模糊控制程序设计报告

PLC，即可编程序控制器，可编程逻辑控制器实质是一种专用于工业控制的计算机，可编程逻辑控制器其硬件结构基本上与微型计算机相同。其结构包括：电源,中央处理单元（CPU） ，存储器 ,输入输出接口电路,功能模块，通信模块。最早出现于上世纪60年代,是一种专门为在工业环境下应用而设计的数字运作的电子装置［2］。它采用可以编制程序的存储器，用来在其内部存储执行逻辑、顺序运算，计时、计数和算术运算等操作指令，并能通过数字式或模拟式输入输出，控制各种类型的机械或生产过程。
4.数据处理
现代PLC具有数学运算（含矩阵运算、函数运算、逻辑运算）、数据传送、数据转换、排序、查表、位操作等功能，可以完成数据的采集、分析及处理。这些数据可以与存储在存储器中的参考值比较，完成一定的控制操作，也可以利用通信功能传送到别的智能装置，或将它们打印制表。数据处理一般用于大型控制系统，如无人控制的柔性制造系统；也可用于过程控制系统,如造纸、冶金、食品工业中的一些大型控制系统。
（2）PLC在闭环过程中应用日益广泛.
（3）不断加强通讯功能。
（4)新器件和模块不断推出。高档的PLC除了主要采用CPU以提高处理速度外，还带有处理器的EPROM或RAM的智能I/O模块、高速计数模块、远程I/O模块等专用化模块。
（5）编程工具丰富多样，功能不断提高，编程语言趋向标准化。有各种简单或复杂的编程器及编程软件，采用梯形图、功能图、语句表等编程语言,亦有高档的PLC指令系统。
（三）系统的设计、建造工作量小，维护方便，易于改造.
PLC用存储逻辑代替接线逻辑，大大减少了控制设别外部恩德接线，是控制系统设计及建造的周期大为缩短，同时维护也变得更为容易。更重要的是使用同一设备经过改变程序改变生产过程成为可能。这很适合多品种、小批量生产。

模糊PID控制温控系统设计C语言程序代码介绍本文介绍了使用模糊PID控制方法来设计温控系统的C语言程序代码。

本温控系统使用传感器读取室内温度，然后根据读取的数值对应调整冷风机的风速和加热器的加热时间，从而控制室内温度达到一个设定值。

系统设计本温控系统采用模糊PID控制方法，具体实现流程如下：1.根据设定温度和当前室内温度计算出误差值2.使用模糊控制方法将误差值转化为温度调节量3.根据模糊控制输出的温度调节量计算出PID控制器的输出4.根据PID控制器的输出调节冷风机的风速和加热器的加热时间系统设计中需要使用的传感器，冷风机和加热器的具体型号及参数需要根据实际情况进行选择。

此处不做详细说明。

程序代码实现以下代码实现了上述系统设计，包括模糊控制和PID控制。

// 温控系统C语言程序代码#include<stdio.h>#include<stdlib.h>// 模糊控制double GetTemperatureByFuzzy(double error){double delta = 0.5; // 设定的温度调节步长double result = 0;if (error <= -5){result = 1;}else if (error > -5 && error < 0){result = (error + 5) / 5.0;}else if (error >= 0 && error < 5){result = (5 - error) / 5.0;}else{result = 0;}return result * delta;}// PID控制double GetTemperatureByPID(double error, double lastError, double integ ral){double Kp = 0.5; // 比例系数double Ki = 0.01; // 积分系数double Kd = 0.1; // 微分系数double deltaT = 0.1; // 采样时间double derivate = (error - lastError) / deltaT;double result = Kp * error + Ki * integral + Kd * derivate;return result;}// 主函数int main(){double setTemp = 25; // 设定温度double curTemp = 24; // 当前温度，需要从传感器读取double lastError = 0; // 上一次的误差值double integral = 0; // 积分项while (1){double error = setTemp - curTemp; // 计算当前误差值double fuzzyTemp = GetTemperatureByFuzzy(error); // 模糊控制integral += error; // 更新积分项double pidTemp = GetTemperatureByPID(error, lastError, integra l); // PID控制lastError = error; // 更新上一次误差值// 根据pidTemp和fuzzyTemp调节冷风机的风速和加热器的加热时间，省略// 读取传感器更新当前温度，省略// curTemp = GetCurTemp();// 采样时间，省略// sleep(1);}}本文介绍了使用模糊PID控制方法来设计温控系统的C语言程序代码。

基于单片机的水温恒温模糊控制系统设计水温恒温在很多工业领域中都是非常重要的，比如在制造过程中需要严格控制水温以确保产品质量，或者在实验室中需要保持水温恒定以保证实验结果的准确性。

为了实现水温恒温，可以采用单片机控制系统进行模糊控制，以更好地调节水温并确保其恒定性。

一、系统设计1.系统组成该水温恒温模糊控制系统包括以下几个部分：1)传感器：用于实时监测水温，通常采用温度传感器来获取水温数据。

2)单片机：作为系统的核心控制部分，负责根据传感器采集的水温数据进行控制算法处理，并输出控制信号给执行器。

3)执行器：负责控制水温调节设备，比如加热器或制冷器，以使水温保持在设定的恒温值附近。

4)人机界面：用于设定水温的目标值、显示当前水温以及系统的工作状态等信息，通常采用液晶显示屏或LED灯来实现。

2.系统工作原理系统工作流程如下：1)单片机通过传感器获取实时水温数据，并与设定的恒温值进行比较。

2)根据实时水温和设定值之间的差异，单片机通过模糊控制算法计算出调节水温的控制信号。

3)控制信号送往执行器，执行器根据信号控制加热器或制冷器对水温进行调节。

4)单片机不断循环执行上述步骤，使水温保持在设定的恒温值附近。

二、模糊控制算法设计模糊控制算法是一种基于模糊逻辑进行推理和决策的控制方法，适用于非线性、不确定性系统的控制。

在水温恒温控制系统中，可以设计如下的模糊控制算法：1.模糊化：将实时水温和设定水温映射到模糊集合，通常包括“冷”、“适中”和“热”等。

2.模糊规则库：根据实际情况，设定一系列的模糊规则，描述实时水温和设定水温之间的关系。

3.模糊推理：通过模糊规则库，进行模糊推理，得到相应的控制信号。

4.解模糊化：将模糊推理的结果映射到实际的控制信号范围内，作为执行器的输入。

通过模糊控制算法设计，可以更加灵活地调节水温，适应各种复杂环境下的恒温控制需求。

三、系统实现在实际系统的实现中，首先需要选择合适的传感器，并设计好传感器的接口电路来获取水温数据。

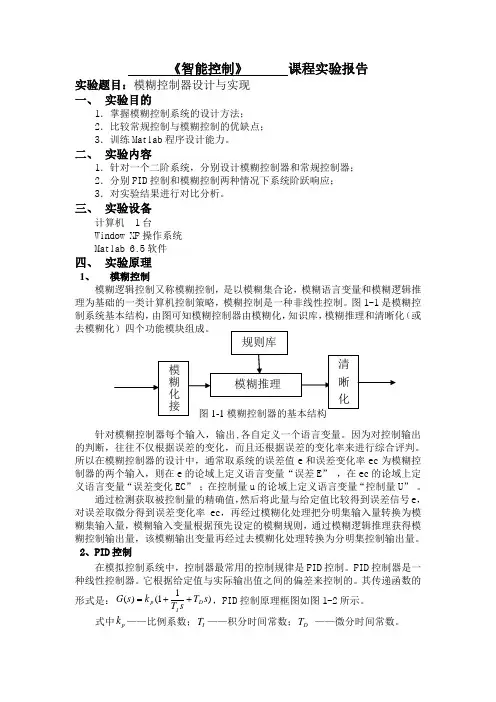
《智能控制》 课程实验报告实验题目：模糊控制器设计与实现 一、 实验目的1．掌握模糊控制系统的设计方法；2．比较常规控制与模糊控制的优缺点； 3．训练Matlab 程序设计能力。

二、 实验内容1．针对一个二阶系统，分别设计模糊控制器和常规控制器； 2．分别PID 控制和模糊控制两种情况下系统阶跃响应； 3．对实验结果进行对比分析。

三、 实验设备计算机 1台Window XP 操作系统 Matlab 6.5软件四、 实验原理1、 模糊控制模糊逻辑控制又称模糊控制，是以模糊集合论，模糊语言变量和模糊逻辑推理为基础的一类计算机控制策略，模糊控制是一种非线性控制。

图1-1是模糊控制系统基本结构，由图可知模糊控制器由模糊化，知识库，模糊推理和清晰化（或针对模糊控制器每个输入，输出,各自定义一个语言变量。

因为对控制输出的判断，往往不仅根据误差的变化，而且还根据误差的变化率来进行综合评判。

所以在模糊控制器的设计中，通常取系统的误差值e 和误差变化率ec 为模糊控制器的两个输入，则在e 的论域上定义语言变量“误差E ” ，在ec 的论域上定义语言变量“误差变化EC ” ；在控制量u 的论域上定义语言变量“控制量U ” 。

通过检测获取被控制量的精确值，然后将此量与给定值比较得到误差信号e ，对误差取微分得到误差变化率ec ，再经过模糊化处理把分明集输入量转换为模糊集输入量，模糊输入变量根据预先设定的模糊规则，通过模糊逻辑推理获得模糊控制输出量，该模糊输出变量再经过去模糊化处理转换为分明集控制输出量。

2、PID 控制在模拟控制系统中，控制器最常用的控制规律是PID 控制。

PID 控制器是一种线性控制器。

它根据给定值与实际输出值之间的偏差来控制的。

其传递函数的形式是：)11()(s T sT k s G D I p ++=，PID 控制原理框图如图1-2所示。

式中p k ——比例系数；I T ——积分时间常数；D T ——微分时间常数。

基于单片机模糊PID控制算法实验设计基于单片机的模糊PID控制算法是一种将模糊逻辑和PID控制相结合的控制方法。

模糊PID控制算法在许多工程和科学领域中具有广泛的应用，用于控制各种物理系统，例如机械系统、电子系统和化学系统等。

本文将介绍基于单片机的模糊PID控制算法的实验设计。

一、实验目的本实验旨在通过使用单片机实现模糊PID控制算法，控制一个虚拟物理系统的运动。

通过这个实验，我们可以了解模糊PID控制算法的原理和实现过程，并通过实验结果对其性能进行评估。

二、实验原理模糊PID控制算法是将模糊逻辑和传统的PID控制算法相结合而得到的一种控制方法。

PID控制算法是一种反馈控制方法，它通过测量和计算系统的误差，调整输出控制量，使得系统的运行状态能够接近期望状态。

模糊PID控制算法的原理是，在PID控制算法的基础上，使用模糊逻辑来处理模糊因素，使得控制系统能够对模糊因素有更好的适应性和鲁棒性。

模糊逻辑是对不确定性和模糊性进行建模和处理的一种方法，它能够通过模糊集合和模糊规则来描述和处理模糊因素。

在模糊PID控制算法中，首先使用一组模糊集合来表示误差和变化率的程度，然后建立一组模糊规则，通过模糊推理得到模糊控制量，最后将模糊控制量经过模糊解模糊化得到实际控制量。

这样，通过模糊逻辑的处理，能够使得控制系统对于模糊因素有更好的适应性和鲁棒性。

三、实验步骤1.设计一个虚拟物理系统，可以使用一个电机控制器和一个电机模拟器来模拟物理系统的运动。

2.根据虚拟物理系统的特性，确定控制系统的输入和输出变量，例如位置和速度。

3.设计一组模糊集合来表示位置和速度的程度，例如“远”、“近”、“大”、“小”等。

4.建立一组模糊规则，通过模糊推理得到模糊控制量。

5.设计一个PID控制算法，用于计算系统的误差和调整输出控制量。

6.将模糊控制量和PID控制量相结合，得到最终的实际控制量。

7.使用单片机编程语言，例如C语言，实现上述的模糊PID控制算法。

AGV小车的导引方式有多种，如激光导引、磁条导引、惯性 导引等，其中激光导引具有精度高、对环境要求低等优点， 是当前主流的导引方式。
倒车入库控制的重要性
倒车入库是AGV小车在仓库、车间等有限空间内进行作业 的重要环节。由于空间有限，障碍物多，倒车入库的控制 难度较大，需要精确控制小车的速度和方向，确保安全、 准确地完成入库操作。
模糊控制的基本原理
通过引入模糊集合和模糊逻辑，模糊控制能够处理不确定性和非线性问题，从而实现对复杂系统的有 效控制。
模糊控制的基本原理包括模糊化、模糊推理和去模糊化三个主要步骤，通过合理设计每个步骤的方法 和参数，实现对系统的精确控制。
04 模糊控制算法在AGV小车 倒车入库中的应用
模糊控制器设计
模糊控制在AGV小车倒车入库中的优势与局限性
优势
模糊控制具有较强的鲁棒性和适应性， 能够处理不确定性和非线性问题，适用 于各种复杂的控制场景。在AGV小车倒 车入库控制中，模糊控制器能够根据实 际情况进行自适应调整，提高控制的准 确性和稳定性。
VS
局限性
模糊控制器的设计过程较为复杂，需要经 验丰富的专业人员进行设计和调整。此外 ，模糊控制器在处理精确度要求较高的控 制任务时可能会存在一定的误差和波动。
导航系统通常采用磁轨导航或激光雷 达导航技术，通过感应器或传感器获 取环境信息，并由控制系统进行解析 和处理，实现小车的精确导航。
AGV小车的运动控制系统
AGV小车的运动控制系统负责控制小 车的运动，包括速度、方向和位置等。
运动控制系统基于模糊控制算法，通 过模糊逻辑控制器对小车的运动状态 进行实时监测和调整，确保小车能够 稳定、准确地完成搬运任务。
模糊控制算法的实现
编程语言选择

//隶属于 Kp 的隶属程度
int code KpRule[7][7]=
//Kp 的模糊控制表
{
3,3,3,3,3,3,3,
2,2,2,2,1,2,2,
1,1,1,1,1,1,1,
1,1,0,1,0,1,1,
0,0,1,0,0,1,0,
0,1,0,1,0,0,2,
3,3,3,3,3,3,3
};
/***** 误差 E 隶属函数描述 *****/
if(KEY1==0) {
delay_ms(1); if(KEY1==0) {
S_temp=S_temp+1; if(S_temp>=200)
S_temp=200; while(!KEY1); } } if(KEY2==0) { delay_ms(1); if(KEY2==0) { if(S_temp>0)
delay_us(10); Show_char(1,1,'T'); delay_us(10); Show_char(2,1,':'); delay_us(10); Show_Num(3,1,3,P_temp); delay_us(10); Show_char(10,1,'S'); delay_us(10); Show_char(11,1,'T'); delay_us(10); Show_char(12,1,':'); delay_us(10); Show_Num(13,1,3,S_temp); delay_us(10); Show_char(0,2,'P'); delay_us(10); Show_char(1,2,':'); delay_us(10); Show_Num(2,2,2,Kp); delay_us(10); Show_char(5,2,'I'); delay_us(10); Show_char(6,2,':'); delay_us(10); Show_char(8,2,'.'); delay_us(10); Show_Ki(Ki); delay_us(10); Show_char(12,2,'D'); delay_us(10); Show_char(13,2,':'); delay_us(10); Show_Num(14,2,2,Kd); delay_us(10); }

洗衣机的模糊控制器设计1 洗衣机的模糊控制传统的洗衣机都是人们用肉眼观看后，根据人的经验来调整洗衣时间和用水量，而模糊控制就是以人对被控对象的控制经验为依据而设计的控制器，这样就能实现控制器模拟人的思维方式来控制洗衣机。

以模糊洗衣机的设计为例其控制是一个开环的决策过程，模糊控制按以下步骤进行。

[4]1.1 洗衣机的时间控制1.1.1 确定模糊控制器的结构选用单变量二维模糊控制器。

控制器的输入为衣物的污泥和油脂，输出为洗涤时间。

1.1.2 定义输入、输出模糊集将污泥分为3个模糊集：SD(污泥少)，MD （污泥中），LD （污泥多）；取值范围为[0,100]。

将油脂分为3个模糊集：NG （油脂少），MG （油脂中），LG （油脂多）； 将洗涤时间分为5个模糊集：VS （很短），S（短），M （中等），L（长），VL （很长）。

1.1.3 定义隶属函数选用如下隶属函数：50/5050/10050/50/50x x x x x x x μLDMD SD污泥1005010050500500 x x x x 采用三角形隶属函数可实现污泥的模糊化。

采用Matlab进行仿真，污泥隶属函数设计仿真程序如下： Close all ； N=2； x=0:0.1:100; for i=1:N+1 f(i)=100/N*(i-1); endu=trimf(x,[f(1),f(1),f(2)]); figure(1)； plot(x,u); for j=2:Nu=trimf(x,[f(j-1),f(j),f(j+1)]); hold on; plot(x,u); endu=trimf(x,[f(N),f(N+1),f(N+1)]); hold on; plot(x,u); xlabel(‘x’);ylabel(‘Degree of membership ’); 污泥程序仿真结果如图1所示：01020304050607080901000.10.20.30.40.50.60.70.80.91xDe g r e e of m e m b e r s h i p图1 污泥隶属函数将油脂分为三个模糊集:NG （无油脂）MG （油脂中）LG(油脂多)，取值范围为[0，100]选用如下隶属函数：50/5050/10050/50/50y y y y y y y LGMG NG油脂1005010050500500 y y y y 采用三角形隶属函数实现油脂的模糊化，仿真程序如下： Clear all; N=2; x=0:0.1:100; for i=1:N+1 f(i)=100/N*(i-1); endu=trimf(y,[f(1),f(1),f(2)]); figure （1）； plot(y,u); for j=2:Nu=trimf(y,[f(j-1),f(j),f(j+1)]); hold on; plot(y,u); endu=trimf(y,[f(N),f(N+1),f(N+1)]); hold on; plot(y,u); xlabel(‘y’);ylabel(‘Degree of membership ’); 油脂程序仿真结果如图2所示：01020304050607080901000.10.20.30.40.50.60.70.80.91yDe g r e e of m e mb e r s h i p图2 油脂隶属函数将洗涤时间分为五个模糊集：VS(很短)S （短）M （中等）L(很长)取值范围为[0,60] 选用如下隶属函数：20/4020/6015/2515/4015/1015/2510/10/10z z z z z z z z z z z z z VLL M S VS洗涤时间604060404025402525102510100100 z z z z z z z z 采用三角形隶属函数实现洗涤时间的模糊化,其Matlab仿真程序如下： Close all; Z=0:0.1:60;U=trimf(z,[0,0,10]); Figure(1); Plot(z,u);U=trimf(z,[0, 10,25]); hold on; plot(z,u);U=trimf(z,[ 10,25,40]); hold on; plot(z,u);U=trimf(z,[ 25,40,60]); hold on; plot(z,u);U=trimf(z,[ 40,60,60]); hold on; plot(z,u); xlabel(‘z’)ylabel(“Degree of membership ”); 洗涤时间仿真程序结果如图3所示：01020304050600.10.20.30.40.50.60.70.80.91zDe g r e e of m e m b e r s h i p图3 洗涤时间隶属函数1.1.4 建立模糊控制规则根据人的操作经验设计模糊规则，模糊规则设计的标准为：“污泥越多，油脂越多，洗涤时间越长”；“污泥适中，油脂适中，洗涤时间适中”；“污泥越少，油脂越少，洗涤时将越短”。

用 PLC 实现模糊控制的程序设计方法摘要：采用 PLC 进行模糊控制操作的程序设计的方法，是我们在应用 PLC 实现一些复杂控制系统时发现的，以前我们经常使用的小型 PLC 由于其不具备现代控制算法植入功能而逐渐被淘汰，文中所述程序设计方法通过实际项目的检验发现可以有效地对系统进行控制，有效缩短控制系统开发周期，其优越性能正在逐步强大起来。

关键词：PLC；模糊控制PLC 即可编程控制器，是为了进行相关数据的计算而发明的一种适用于规模化工业生产条件下使用的设备，通过一定的程序和要求，进行数据的输入和结果的输出，以此来控制工业生产过程。

模糊控制就是将其建立在人类思考问题的方式上形成的一种控制方法，它反映着人类的思维在处理事情上展现出来的一种模糊化的思考，比如对于复杂看似难以解决的问题，人们往往会根据自己的经验对事物进行思考，当我们对被控系统在一定程度上有所认识的前提下，并为解决它需要实现的控制功能而进行适当的思考，这时我们便将其称之为思维的模糊性。

模糊控制就是模仿的人类面对这种状况下的思维，我们只需给予它一定的模糊的指令程序，让其对整个的控制过程进行计算运行，这种看似简单的指令却需要有专业的人士发出以便得到相对更准确的结果。

这种对于控制的模糊性和我们以往进行的自动化的控制有着完全不同的本质，而这种模仿人类思维的控制恰恰体现了它智能化的一面，更适合当今生产对于控制的要求。

一、控制算法面对现今工业生产的复杂性，简单的线性数学模型已经不能满足生产的要求，取而代之的是要建立一个可适应不停变化的、非简单性的控制系统，而这种模型的建立纯在较大的难度。

在过去生产简单产品，不需要过多操作流程的条件下，简单传统的控制就可以实现生产的要求，现在只有找到一种先进的控制模式才能让复杂的生产流程顺利进行，用 PLC 进行模糊控制便是解决这一问题的有效办法。

传统的控制需要基于一定的模型才能准确运行，而模糊控制则完全不需要，正是这一点才让它适应于复杂的条件。

实验二一、实验目的1．通过实验熟悉并掌握GUI(Graph User Interface)的工具箱函数的使用方法2．通过实验熟悉并掌握模糊控制器的设计方法与步骤3．通过实验熟悉并掌握利用GUI建立FIS的方法与步骤2．通过实验进一步熟悉并掌握Matlab软件的使用方法二、实验内容1．根据给定要求，设计炉温控制系统的模糊控制器2．编制炉温模糊控制系统的Matlab仿真程序3．利用GUI建立FIS三、实验步骤1．设计炉温控制系统的模糊控制器①确定模糊控制器的结构②定义输入、输出模糊集③定义输入输出隶属函数④建立模糊控制规则⑤建立模糊控制表⑥进行模糊推理，求出模糊关系作出模糊决策⑦对控制量进行反模糊化2．按上述步骤,设计炉温模糊控制系统的Matlab仿真程序3．针对本例，进一步利用GUI建立FIS①进入FIS编辑器②建立初步的模糊推理系统③建立各变量的隶属函数④设置当前变量的变化范围和其在隶属函数上的显示范围⑤打开模糊规则编辑器加入模糊控制规则⑥打开模糊规则观察器,观察模糊规则⑦打开输出曲面观察器,观察模糊推理系统的输出曲面⑧分析实验结果，完成实验报告。

四、实验要求对于所设计的炉温控制系统，要求温度保持在600°C恒定,针对该控制系统有以下控制经验：1。

若炉温低于600°C,则升压;低得越多升压越高.2.若炉温高于600°C,则降压;高得越多降压越低.3.若炉温等于600°C,则保持电压不变。

(1）设模糊控制器为一维控制器,输入输出变量的量化等级为7级，取5个模糊集。

(2)设模糊控制器为一维控制器，输入输出变量的量化等级为7级,取7个模糊集。

五、实验内容六、实验程序%Fuzzy Control for temperatureclear all;close all；a=newfis（‘fuzzy temperature’）；a=addvar(a,'input’，'e’,［—3 3］);a=addmf（a，’input’，’1’，’NB','zmf'，[-3 -1]);a=addmf（a,’input’，’1’，’NM’，’trimf’，［-3 —1 1］)；a=addmf（a，’input'，’1'，’NS’，’trimf’，［—2 0 2］）;a=addmf（a，’input’,’1’,’Z,'trimf’，［—2 1 1 ]);a=addmf（a，’input',’1’，’PS，’trimf’，[-1 2 1］）;a=addmf(a，’input'，’1’,'PM'trimf',[1 2 3 ]）;a=addmf（a，’input’,'1’，'PM'smf'，［1 3 ］)；a=addvar（a,’output’,’u’,[-3 3])；a=addmf（a，’output’，‘1’，’NB'，’zmf’，［—3 —1］); a=addmf(a，'output’，‘1'，’NS’，'trimf’，［—3 1 1］)；a=addmf(a,’output’, ‘1’,’Z’，'trimf'，[-2 0 2］）；a=addmf(a，'output’，‘1’，'PS’,’trimf’，［-1 1 2］）;a=addmf（a，’output’，‘1’，'PB’，’smf’,[1 3] ）；rulelist=[1 1 1 12 2 1 13 2 1 14 3 1 15 5 1 16 5 1 17 5 1 1］;a=addrule（a,rulelist）;a1=setfis（a,’DeduzzMothod’，’mom’）；writefis（a1，’temperature’）；a2=readfis(’temperature’)；figure（1）；plotfis(a2）；figure(2);plotmf（a，’input’，1）；figure（3）；plotmf(a,’output'，1）;flag=0showrule（a);ruleview(‘temperature’)；enddisp（‘—----—---———------——--—-—-——--—-—----—--—-————-——--——————--‘）;disp(‘fuzzy controller table:e=［-3,3]，u=［-3，3] '）;disp（‘—--—-—-—-——-—--——-———-———----——--——--------——--—--—---———-—-‘)；for i=1:1:7e（i）=i—4;Ulist(i）=evafis（[e(i）],a2）;endUlist=round（Ulist）;e=-3;u=eavlfis（［e］，a2)。

西安交通大学实验报告第1页（共13页）课程：智能控制实验日期：年月日专业班号：自动化交报告日期：年月日姓名：学号：报告退发：（订正、重做）同组者：教师审批签字：实验一模糊控制仿真系统设计实验目的：理解和掌握模糊控制系统的构成和设计方法，为实际工程应用打下基础。

基本要求：掌握以误差及其变化率为输入的典型模糊控制器的设计方法，了解影响模糊控制器性能的关键参数及调节方法。

针对被控对象，构建合适的模糊控制器，搭建模糊控制系统。

实验内容提要：针对典型的二阶以上被控对象，设计模糊控制器。

包括控制器输入输出量的选择，输入输出论域的模糊划分，模糊规则库的建立等。

利用设计完成的模糊控制在Simulink中搭建模糊控制系统，要求该系统稳定且具有良好的动态及稳态特性。

实验工作概述：主要针对倒立摆进行了建模与模糊控制仿真，其中实验1-1是仅针对角度的模糊PID控制，实验1-2是针对位置与角度的分段模糊控制。

后面也尝试进行了二级倒立摆的模糊控制设计，但由于知识水平不够没能完全实现，仅实现了第一级的直立控制。

实验1-1 单级倒立摆的PID模糊控制一、被动对象数学描述与特性分析关于倒立摆的相关背景：倒立摆，Inverted Pendulum ，是典型的多变量、高阶次、非线性、强耦合、自然不稳定系统。

倒立摆系统的稳定控制是控制理论中的典型问题，在倒立摆的控制过程中能有效反映控制理论中的许多关键问题 ，如非线性问题、鲁棒性问题、随动问题、镇定、跟踪问题等。

因此倒立摆系统作为控制理论教学与科研中典型的物理模型 ，常被用来检验新的控制理论和算法的正确性及其在实际应用中的有效性。

所以我此次实验采用一阶倒立摆来验证。

当摆杆夹角很小时，近似线性化处理：(I +ml 2)θ+mglθ=mlẍ (M +m )ẍ+bẋ−mlθ=u根据微分方程组做拉普拉斯变换联立求得外力针对角度的传递函数：Φ(s)U(s)=ml 2qs 2s 4+b(I +ml 2)q s 3−(M +m )mgl q s2−bmql q s将各种参数输入matlab ，编辑一个函数脚本GetPendulum 来求传递函数的系数：当M=2，m=0.8，l=0.25时，求得：这是一个典型的二阶系统二、模糊控制器的设计步骤与具体参数选择模糊集合设计：总共有两个输入三个输出，输入角度和角度微分的模糊集合划分都相同，论域为[-5,5]，模糊集合为3个，分别命名为：[N Z P]，输出P I D三个参数的范围分别为[110，120]，[115，125]，[80，90]，模糊集合为3个命名为：[S M B]它们的分布如上图所示。

编号：实验一普通PI控制方法的设计与实现一、实验目的1. 掌握数字PI及其算法的实现2. 熟悉在在keil环境下进行单片机程序的设计3. 熟悉仿真软件protues的使用二、实验设备及条件1. 计算机系统2. 编程软件keil4和仿真软件protues7.8三、实验原理及其实验步骤(1) PID算法的数字化实现在模拟系统中，PID算法的表达式为u(t)=K P[e(t)+1T I∫e(t)dt+T Dde(t)dt]式中u(t)：调节器的输出信号；e(t)：调节器的偏差信号，它等于测量值与给定值之差；Kp：调节器的比例系数；T I：调节器的积分时间；TD：调节器的微分时间；离散化的PID为：u(k)=K P[e(k)+TT I∑e(j)kj=0+T DT(e(k)−e(k−1))]Δt=T：采样周期，必须使T足够少，才能保证系统有一定的精度；E(k)：第K次采样时的偏差值；E(k-1) ：第K-1次采样时的偏差值；K：采样序号，K=0，1，2……；P(k-1)：第K次采样时调节器的输出；上式计算复杂，经过化简为：u(k)=u(k−1)+K P[e(k)−e(k−1)]+K I e(k)+K D[e(k)−2e(k−1)+e(k −2)]式中：K I=K P TT I为积分系数K D=K P T DT为微分系数要计算第K次输出值u(k)，只需要知道u(k-1)，e(k)，E(k-1)，e(k-2)即可。

上式也称为位置型PID的位置控制算法。

在很多控制系统中，由于执行机构是采用布进电机进行控制，所以只要给一个增量信号即可。

因此得到增量型PID的位置控制算法。

∆u=K P[e(k)−e(k−1)]+K I e(k)+K D[e(k)−2e(k−1)+e(k−2)] (2) 控制系统的结构框图整个系统的控制框图如下所示：图1 PID控制系统结构框图在本次设计中，经过计算，被控对象的传递函数是：G(s)=1 (SCR)2+3SCR+1其中：C=10uf，R=20K；带入上式后可得：G(s)=10.04S2+0.6S+1显然是一个二阶系统。

模糊控制实验报告1.引言随着科技的不断发展，模糊控制理论在控制系统中的应用越来越广泛。

模糊控制通过将精确的数学模型转化为模糊的规则，可以更好地适应复杂、非线性的控制系统。

本实验旨在通过设计一个模糊控制系统来实现对一个简单的水温控制过程的控制，以验证模糊控制在实际系统中的有效性。

2.实验原理本实验将一个简化的水温控制过程作为被控对象，控制目标是使得水温保持在一个设定的温度范围内。

水温的变化是由水流量和加热功率两个因素决定的。

因此，控制系统的输入变量为水流量、加热功率，输出变量为水温。

通过模糊控制器根据当前的水温及其变化率来调节水流量和加热功率，从而实现对水温的控制。

模糊控制器的输入变量为当前的水温和水温变化率，输出变量为水流量和加热功率的控制信号。

通过设定一系列模糊规则，模糊控制器可以根据当前的输入变量来决定输出变量的值，并调整其大小以实现对水温的精确控制。

3.实验步骤1)设定水温的设定值及其变化率，作为模糊控制器的输入变量。

2)使用模糊推理方法，通过设定一系列模糊规则，将输入变量映射到输出变量。

3)根据输出变量的值，调节水流量和加热功率的控制信号。

4)监测水温的变化，根据测量结果对模糊控制器进行调整，以提高控制的精度。

5)重复步骤3和4，直到水温稳定在设定的范围内。

4.实验结果经过多次实验，我们成功地设计出了一个能够稳定控制水温的模糊控制系统。

在不同的设定值和变化率下，模糊控制器都能够根据当前的输入变量来自适应地调节输出变量的值，使水温保持在设定的范围内。

通过对实验数据的分析，我们发现模糊控制系统具有较好的动态性能和鲁棒性。

在水温变化较快的情况下，模糊控制器能够及时地调整输出变量的值，使水温能够迅速回到设定的范围内。

而在水温变化较慢的情况下，模糊控制器能够稳定地控制输出变量的值，使水温能够保持在设定的范围内。

对比传统的PID控制器，我们发现模糊控制系统在对非线性系统和难以建模的系统进行控制方面具有明显的优势。

控制系统中模糊控制器的设计与实现控制系统中采用的控制器可以分为许多种类，其中一种常用的控制器是模糊控制器。

模糊控制器是一种基于模糊逻辑理论的控制器，它可以处理模糊的输入和输出，适用于非线性和复杂的控制系统。

本文将介绍模糊控制器的设计和实现步骤。

一. 模糊控制器的基本原理模糊控制器的基本原理是模糊逻辑理论，它采用了一种模糊的方式来处理不确定性和模糊性的问题。

其基本思想是将系统输入或输出的模糊化，使输入和输出变成了隶属于某种模糊集合之内的量，并根据一定的模糊规则，将输入转化为输出。

模糊控制器的工作流程如下：首先将输入信号进行模糊化，将其转化为一组隶属度值。

然后根据预设的模糊规则，将输入转化为输出信号。

最后将输出信号进行去模糊化，得到具体的控制量，然后输出给被控对象。

二. 模糊控制器的设计步骤模糊控制器的设计步骤主要包括以下几个方面：1. 确定系统的模糊输入和输出模糊控制器的输入和输出通常表示为模糊变量，其基本形式是一个三元组(Name, Universe of discourse, Membership function)。

其中Name表示模糊变量的名称，Universe of discourse表示变量所描述的宇域，Membership function是变量的隶属度函数。

2. 确定模糊控制器的规则库模糊控制器的输入和输出之间建立的模糊规则来自于专家知识和经验。

将这些知识和经验编码成规则库，每个规则的形式为：“If X1 is A1 and X2 is A2 and…Xnis An, Then Y is B”。

其中X1，X2 …Xn 是输入模糊变量，A1，A2…An是它们的隶属程度，Y是输出模糊变量，B是它的隶属程度。

3. 确定模糊控制器的推理机制模糊控制器的推理机制是指如何从规则库中推导出具体的输出。

常用的推理机制有最小最大合成、中心平均合成等。

4. 确定模糊控制器的去模糊化方法模糊控制器的输出是一组隶属度值，需要将其转化为具体的控制量。

实验一熟悉模糊工具箱一、目的和要求1.目的(1)通过本次实验，进一步了解模糊控制的基本原理、模糊模型的建立和模糊控制器的设计过程。

(2)掌握MATLAB模糊逻辑工具箱的图形用户界面设计模糊控制器的过程。

2.要求（1）充分理解实验内容，并独立完成实验报告。

（2）实验报告要求：实验题目、实验具体内容、结果分析、收获或不足。

二、实验内容1、利用matlab中的模糊逻辑工具箱提供的图形用户界面（GUI）工具设计一个两输入、一输出的模糊控制器，控制器的要求如下：（1）设模糊控制器的输入变量为：误差E和误差变化EC，输出量为U。

（2）隶属度函数：◆隶属度函数均为三角函数◆E、EC和U的模糊语言变量集均为{NB,NM,NS,ZO,PS,PM,PB}◆E和EC论域为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}◆U的论域为{-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7}（3）控制规则表如下：表1 模糊控制表三．实验步骤模糊逻辑工具箱提供的图形用户界面（GUI）工具有五个：模糊推理系统（FIS）编辑器；隶属函数编辑器；模糊规则编辑器；模糊规则观察器；输出曲面观察器。

1.模糊控制器结构设计FIS处理系统有多少个输入变量，输出变量，名称是什么，模糊算子“与”(min，prod乘积，custom自定义)，“或”(max大，probor 概率统计方法，custom)，推理方法（min，prod，custom），聚类方法（max，probor，sum，custom），解模糊的方法（centroid 质心法，bisector中位线法，middle of maximum，largest of maximum，smallest of maximum）。

Matlab的FIS界面如图3所示。

图3 模糊推理系统（FIS）界面2.隶属函数编辑器：确定各个变量的论域和显示范围（左下角编辑区内），如图4所示。

《智能控制》课程设计报告专业：自动化班级：学号：学生：时间：13年12月30日～13年1月3日―――――――以下指导教师填写―――――分项成绩：出勤设计报告总成绩：指导教师：设计报告要求和成绩评定1 报告容设计任务书（设计计划），正文，参考资料。

设计任务书（设计计划）由学生所在系安排指导教师编写，容包括设计地点、时间、安排和设计容和要求等。

正文容一般包括：（1）设计简述（设计时间、设计地点，设计方式等）；（2）设计容叙述；（3）设计成品(图纸、表格或计算结果等)；（4）设计小结和建议。

参考资料包括参考书和现场技术资料等。

2 书写用纸A4复印纸；封面、设计任务书要求双面打印。

3 书写要求正文容手工双面或单面书写，字迹清楚，每页20行左右，每行30字左右，排列整齐；页码居中写在页面下方；纸面上下左右4侧边距均为2厘米。

公式单占一行居中书写；插图要有图号和图题，图号和图题书写在插图下方；表格要有表号和表题，表号和表题在表格上方书写；物理量单位和符号、参考文献引用和书写以及图纸绘制要符合有关标准规定；有关细节可参考我院《毕业设计成品规》。

4 装订装订顺序：封面，设计任务书，正文及参考资料，封底；左边为装订边，三钉装订，中间钉反向装订。

5 成绩评定设计成绩一般由出勤（10分）、报告书写规性及成品质量（50分）、考核（40分）三部分成绩合成后折合为优秀（90－100分）、良好（80－89分）、中（70－79分）、及格（60－69分）或不及格（60分以下）。

设计考核可采取笔试、机试或其它合适的方式；不参加考核或不交报告者成绩为零分。

模糊控制算法研究一、课程设计的目的：1. 通过本次课程设计，进一步了解模糊控制的基本原理、模糊模型的建立和模糊控制器的设计过程。

2. 提高学生有关控制系统的程序设计能力；3. 熟悉Matlab语言以及在智能控制设计中的应用。

二、课程设计的基本容：假设系统的模型可以用二阶加纯滞后表示，即传递函数为12()(1)(1)d sf f Ke G s T s T s τ-=++。

522019 年 第 3 期户程序来实现其控制功能，它采用循环扫模糊控制系统与传统的控制系统主要PLC作为工业控制器已广泛应用于描方式，一个扫描周期主要包括输入采不同在于控制器采用了模糊控制器，模糊工业生产的各个领域。

模糊控制系统是样、程序执行、输出刷新等个过程。

控制器应该具备以下功能：①实现系统偏一种典型的智能控制系统，它比传统逻PLC扫描过程如图1所示。

差的数模转换；②由给定的规则对模糊量辑更接近人类的思维和语言。

本文将进行模糊推理；③把推理结果转化为系统PLC控制器与模糊控制相结合，提出了能够接受的数字量或模拟量。

所以，模糊基于PLC控制器实现水温模糊控制系统控制器的设计可以分为模糊化过程、知识的设计方法。

[3]库、推理决策和精确化计算四个过程。

2 水温控制系统模糊化算法实现随着科学技术的发展，控制系统和过 2.1 模糊化过程程日趋复杂，已经很难用传统的数学语言对实际工程设计数学模型和控制程序。

只能由有经验的操作者以模糊方式手动控制。

模糊控制施一种智能控制，它主要是模仿人的经验实现某些控制要求。

PLC模糊控制是利用模糊集合理论，把人的自然语言转化为相应的知识库及PLC程序，从而对一些无法构造精确数学模型的控制对象进行有效控制。

1.2 模糊控制系统目前PLC专用的模糊控制单元还不图3 输入温度隶属度模糊控制系统是一种以模糊数学、模多，本文将PLC与模糊控制相结合，将模糊语言形式的知识表示，以模糊逻辑推理糊控制运用于工程实际，研究以模糊控制为基础，采用计算机控制技术构成的一种的算法去设计PLC的控制程序，使模糊控具有闭环结构的数字控制系统，其组成核制在工业控制中发挥更大的作用。

[2]心是具有智能性的模糊控制，它模拟人1 PLC原理和模糊控制器概述的思维控制复杂过程。

其基本结构如图1.1 PLC的组成和工作原理2所示。

PLC硬件组成包括中央处理器，存储器，输入、输出接口，电源，扩展接口，通信接口，编程工具，智能I/O接口，智图4 阀门开度隶属度函数能单元等。