Simulink中连续与离散模型的区别(DOC)

Simulink中连续与离散模型的区别matlab/simulink/simpowersystem中连续vs离散!本文中的一些具体数学推导见下面链接：计算机仿真技术1.连续系统vs离散系统连续系统是指系统状态的改变在时间上是连续的，从数学建模的角度来看，可以分为连续时间模型、离散时间模型、混合时间模型。

其实在simpowersystem的库中基本所有模型都属于连续系统，因为其对应的物理世界一般是电机、电源、电力电子器件等等。

离散系统是指系统状态的改变只发生在某些时间点上，而且往往是随机的，比如说某一路口一天的人流量，对离散模型的计算机仿真没有实际意义，只有统计学上的意义，所以在simpowersystem中是没有模型属于离散系统的。

但是在选取模型，以及仿真算法的选择时，常常提到的discrete model、discrete solver、discrete simulate type等等中的离散到底是指什么呢？其实它是指时间上的离散，也就是指离散时间模型。

下文中提到的连续就是指时间上的连续，连续模型就是指连续时间模型。

离散就是指时间上的离散，离散模型就是指离散时间模型，而在物理世界中他们都同属于连续系统。

为什么要将一个连续模型离散化呢？主要是是从系统的数学模型来考虑的，前者是用微分方程来建模的，而后者是用差分方程来建模的，并且差分方程更适合计算机计算，并且前者的仿真算法（simulationsolver）用的是数值积分的方法，而后者则是采用差分方程的状态更新离散算法。

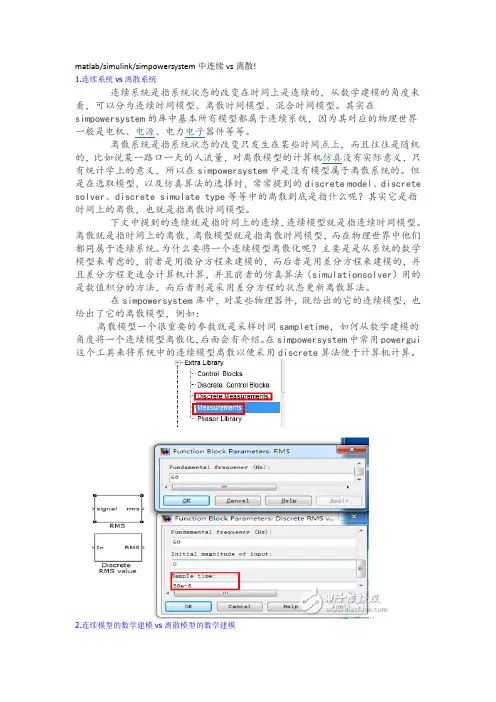
在simpowersystem库中，对某些物理器件，既给出的它的连续模型，也给出了它的离散模型，例如：离散模型一个很重要的参数就是采样时间sampletime，如何从数学建模的角度将一个连续模型离散化，后面会有介绍。

在simpowersystem中常用powergui这个工具来将系统中的连续模型离散以便采用discrete算法便于计算机计算。

Simulink中连续与离散模型的区别matlab/simulink/simpowersystem中连续vs离散!本文中的一些具体数学推导见下面：计算机仿真技术1.连续系统vs离散系统连续系统是指系统状态的改变在时间上是连续的，从数学建模的角度来看，可以分为连续时间模型、离散时间模型、混合时间模型。

其实在simpowersystem的库中基本所有模型都属于连续系统，因为其对应的物理世界一般是电机、电源、电力电子器件等等。

离散系统是指系统状态的改变只发生在某些时间点上，而且往往是随机的，比如说某一路口一天的人流量，对离散模型的计算机仿真没有实际意义，只有统计学上的意义，所以在simpowersystem中是没有模型属于离散系统的。

但是在选取模型，以及仿真算法的选择时，常常提到的discrete model、discrete solver、discrete simulate type等等中的离散到底是指什么呢？其实它是指时间上的离散，也就是指离散时间模型。

下文中提到的连续就是指时间上的连续，连续模型就是指连续时间模型。

离散就是指时间上的离散，离散模型就是指离散时间模型，而在物理世界中他们都同属于连续系统。

为什么要将一个连续模型离散化呢？主要是是从系统的数学模型来考虑的，前者是用微分方程来建模的，而后者是用差分方程来建模的，并且差分方程更适合计算机计算，并且前者的仿真算法（simulationsolver）用的是数值积分的方法，而后者则是采用差分方程的状态更新离散算法。

在simpowersystem库中，对某些物理器件，既给出的它的连续模型，也给出了它的离散模型，例如：离散模型一个很重要的参数就是采样时间sampletime，如何从数学建模的角度将一个连续模型离散化，后面会有介绍。

在simpowersystem中常用powergui这个工具来将系统中的连续模型离散以便采用discrete算法便于计算机计算。

Simulink中连续与离散模型的区别matlab/simulink/simpowersystem中连续vs离散!本文中的一些具体数学推导见下面链接：计算机仿真技术1.连续系统vs离散系统连续系统是指系统状态的改变在时间上是连续的，从数学建模的角度来看，可以分为连续时间模型、离散时间模型、混合时间模型。

其实在simpowersystem的库中基本所有模型都属于连续系统，因为其对应的物理世界一般是电机、电源、电力电子器件等等。

离散系统是指系统状态的改变只发生在某些时间点上，而且往往是随机的，比如说某一路口一天的人流量，对离散模型的计算机仿真没有实际意义，只有统计学上的意义，所以在simpowersystem中是没有模型属于离散系统的。

但是在选取模型，以及仿真算法的选择时，常常提到的discrete model、discrete solver、discrete simulate type等等中的离散到底是指什么呢？其实它是指时间上的离散，也就是指离散时间模型。

下文中提到的连续就是指时间上的连续，连续模型就是指连续时间模型。

离散就是指时间上的离散，离散模型就是指离散时间模型，而在物理世界中他们都同属于连续系统。

为什么要将一个连续模型离散化呢？主要是是从系统的数学模型来考虑的，前者是用微分方程来建模的，而后者是用差分方程来建模的，并且差分方程更适合计算机计算，并且前者的仿真算法（simulationsolver）用的是数值积分的方法，而后者则是采用差分方程的状态更新离散算法。

在simpowersystem库中，对某些物理器件，既给出的它的连续模型，也给出了它的离散模型，例如：离散模型一个很重要的参数就是采样时间sampletime，如何从数学建模的角度将一个连续模型离散化，后面会有介绍。

在simpowersystem中常用powergui这个工具来将系统中的连续模型离散以便采用discrete算法便于计算机计算。

simulink中的欧拉离散化欧拉离散化是数值计算中的一种方法，常用于对连续系统进行离散化处理。

在Simulink中，欧拉离散化是一种常见的模拟仿真方法，可以将连续时间模型转换为离散时间模型，用于系统的数值计算和仿真。

欧拉离散化的基本原理是将连续时间系统的微分方程通过差分逼近的方法离散化，将连续时间的状态和输入变量转换为离散时间的状态和输入信号。

在Simulink中，可以通过选择欧拉离散化方法来对连续时间模型进行离散化处理。

在Simulink中使用欧拉离散化方法，需要注意以下几点。

首先，需要确保所使用的模型是连续时间模型，在模型参数中设置模拟步长，通常选择一个适当的步长值，以保证模拟效果和计算速度的平衡。

接下来，在仿真设置中选择欧拉离散化方法，可以是前向欧拉或后向欧拉方法。

前向欧拉方法是通过使用当前系统状态和输入变量进行差分逼近，计算下一个离散时间步长的状态值；而后向欧拉方法是通过使用下一个离散时间步长的状态值和当前输入变量进行差分逼近，计算当前离散时间步长的状态值。

根据具体系统的特点选择合适的欧拉离散化方法。

在Simulink中使用欧拉离散化方法进行仿真时，还需要关注模型的初值设定和仿真终止条件。

确保模型具有合适的初值设定，以保证仿真的准确性和可靠性。

同时，根据实际需求设置仿真终止条件，例如仿真的时间长度、达到一定精度或满足某些约束条件。

利用Simulink中的欧拉离散化方法，可以方便地对连续时间系统进行仿真和数值计算。

通过选择合适的离散化方法和参数设置，可以得到精确、准确的仿真结果。

同时，结合Simulink中丰富的工具和功能，可以进一步分析和优化系统的性能，提高系统的稳定性和可靠性。

总结来说，Simulink中的欧拉离散化方法是一种常用的连续系统离散化处理方法，通过选择合适的仿真设置和参数配置，可以得到准确、可靠的仿真结果。

在实际应用中，需要根据具体系统的特点和需求，选择合适的离散化方法和参数设置，以确保仿真结果的准确性和可靠性。

simulink中连续与离散的设置在Simulink中，我们可以使用连续与离散的设置来进行系统建模与仿真。

连续与离散是两种不同的系统模型，每种模型都有其适用的场景和特点。

本文将介绍Simulink中如何进行连续与离散的设置，以及它们的应用和区别。

首先，我们来讨论连续系统的建模与仿真。

在连续系统中，信号是连续的，并且在每个时间点都有定义。

对于连续系统的建模，我们可以使用连续的数学方程描述系统的动态行为，例如微分方程。

在Simulink中，我们可以通过添加连续系统的输入和输出信号来建立连续系统的模型。

同时，我们需要选择适当的求解器来求解连续系统的微分方程并进行仿真。

Simulink提供了多种求解器选项，可以根据系统的特点选择合适的求解器。

接下来，我们来讨论离散系统的建模与仿真。

在离散系统中，信号是在离散时间点上采样得到的。

对于离散系统的建模，我们可以使用差分方程来描述系统的动态行为。

在Simulink中，我们可以使用离散的采样和保持模块来建立离散系统的模型。

在进行仿真时，Simulink会根据系统的差分方程进行离散化处理，并使用适当的离散求解器进行仿真。

与连续系统不同，离散系统的仿真是在每个离散时间点上进行的。

在Simulink中，我们可以将连续与离散系统进行组合，建立连续与离散混合系统的模型。

这种混合系统常见于控制系统中，例如连续控制器与离散执行器的组合。

在Simulink中，我们可以使用连续与离散的模块将连续部分和离散部分进行连接，并通过设置适当的采样时间来进行仿真。

同时，我们还可以通过设置不同的触发条件来控制离散模块的执行时机，以满足系统设计的需求。

综上所述，Simulink中提供了丰富的工具和功能来设置连续与离散系统，以及连续与离散混合系统的建模与仿真。

通过合理选择求解器、采样时间和触发条件，我们可以准确地模拟和分析各种系统的动态行为。

无论是连续模型、离散模型还是混合模型，Simulink都能提供强大的支持和灵活性。

matlab/simulink/simpowersystem中连续vs离散!1.连续系统vs离散系统连续系统是指系统状态的改变在时间上是连续的，从数学建模的角度来看，可以分为连续时间模型、离散时间模型、混合时间模型。

其实在simpowersystem 的库中基本所有模型都属于连续系统，因为其对应的物理世界一般是电机、电源、电力电子器件等等。

离散系统是指系统状态的改变只发生在某些时间点上，而且往往是随机的，比如说某一路口一天的人流量，对离散模型的计算机仿真没有实际意义，只有统计学上的意义，所以在simpowersystem中是没有模型属于离散系统的。

但是在选取模型，以及仿真算法的选择时，常常提到的discrete model、discrete solver、discrete simulate type等等中的离散到底是指什么呢？其实它是指时间上的离散，也就是指离散时间模型。

下文中提到的连续就是指时间上的连续，连续模型就是指连续时间模型。

离散就是指时间上的离散，离散模型就是指离散时间模型，而在物理世界中他们都同属于连续系统。

为什么要将一个连续模型离散化呢？主要是是从系统的数学模型来考虑的，前者是用微分方程来建模的，而后者是用差分方程来建模的，并且差分方程更适合计算机计算，并且前者的仿真算法（simulationsolver）用的是数值积分的方法，而后者则是采用差分方程的状态更新离散算法。

在simpowersystem库中，对某些物理器件，既给出的它的连续模型，也给出了它的离散模型，例如：离散模型一个很重要的参数就是采样时间sampletime，如何从数学建模的角度将一个连续模型离散化，后面会有介绍。

在simpowersystem中常用powergui这个工具来将系统中的连续模型离散以便采用discrete算法便于计算机计算。

2.连续模型的数学建模vs离散模型的数学建模Note：这里的连续和离散都是指时间上的连续和离散，无关乎现实世界的连续系统和离散系统。

Simulink模块库简介在进行系统动态仿真之前，应绘制仿真系统框图，并确定仿真所需要的参数。

Simulink 模块库包含有大部分常用的建立系统框图的模块，下面简要介绍常用模块。

1、连续模块（continuous） (1)2、非连续模块（Discontinuous） (2)3、离散模块（Discrete） (3)4、逻辑和位操作模块（Logic and Bit Operation） (4)5、查找表模块（Lookup Table） (5)6．数学模块（Math Operations） (6)7、模型检测模块（Model Verification） (7)8、模型扩充模块（Model-Wide Utilities） (8)9、端口和子系统模块（Prot & Subsystems） (9)10、信号属性模块（Signal Attributes） (10)11、信号路线模块（Signal Routing） (11)12、接收器模块（Sinks） (12)13、输入源模块（Sources） (13)14、用户自定义函数模块（User-Defined Functions） (14)15、Additional Math & Discrete (14)综合 (15)1、连续模块（continuous）（1） Derivative 输入信号微分；（2） Integrator输入信号积分；（3） State-Space状态空间系统模型（4） Transfer-Fcn传递函数模型（5） Transport Delay输入信号延时一个固定时间再输出（6） Variable Transport Delay输入信号延时一个可变时间再输出（7） Zero-Ploe零极点模型2、非连续模块（Discontinuous）（1） Backlash间隙非线性（2） Coulomb&Viscous Friction库仑和粘度摩擦非线性（3） Dead Zone死区非线性（4）Dead Zone Dynamic动态死区非线性（5） Hit Crossing冲击非线性（6） Quantizer量化非线性（7） Rate Limiter静态限制信号的变化速率（8） Rate Limiter Dynamic动态限制信号的变化速率（9） Relay滞环比较器，限制输出值在某一范围内变化（10） Saturation饱和输出，让输出超过某一值是能够饱和（11） Saturation Dynamic动态饱和输出（12） Wrap To Zero3、离散模块（Discrete）（1） Difference差分环节（2） Discrete Derivative 离散微分环节（3） Discrete Filter 离散滤波器（4） Discrete State-Space 离散状态空间系统模型（5） Discrete Transfer Fcn 离散传递函数模型（6） Discrete Zero-Pole 以零极点表示的离散传递函数模型（7） Discrete-Time Integrator 离散时间积分器（8） First-Order Hold 一阶保持器（9） Integer Delay 整数被延迟（10） Memory 输出本模块上一步的输入值（11） Tapped Delay 延迟（12） Transfer Fcn First Order 离散一阶传递函数（13） Transfer Fcn Lead or Lag 传递函数（14） Transfer Fcn Real Zero 离散零点传递函数（15） Unit Delay 一个采样周期的延时（16） Weighted Moving Average 权值移动平均模型（17） Zero-Order Hold 零阶保持器4、逻辑和位操作模块（Logic and Bit Operation）（1） Bit Clear 位清零（2） Bit Set 位置位（3） Bitwise Operator 逐位操作（4） Combinatorial Logic 组合逻辑（5） Compare To Constant 和常量比较（6） Compare To Zero 和零比较（7） Detect Change 检测跳变（8） Detect Decrease 检测递减（9） Detect Fall Negative 检测负上升沿（10） Detect Fall Nonpositive 检测非负下降沿（11） Detect Increase 检测递增（12） Detect Rise Nonnegative 检测非负上升沿（13） Detect Rise Positive 检测正上升沿（14） Extract Bits 提取位（15） Interval Test 检测开区间（16） Interval Test Dynamic 动态检测开区间（17） Logical Operator 逻辑操作符（18） Relational Operator 关系操作符（19） Shift Arithmetic 移位运算5、查找表模块（Lookup Table）（1） Cosine 余弦函数查询表（2） Direct Lookup Table (n-D) n个输入信号的查询表（直接匹配）（3） Interpolation (n-D) using PreLookup n个输入信号的预插值（4） Lookup Table 输入信号的查询表（线性峰值匹配）（5） Lookup Table (2-D) 两维输入信号的查询表（线性峰值匹配）（6） Lookup Table (n-D) n维输入信号的查询表（线性峰值匹配）（7） Lookup Table Dynamic 动态查询表（8） PreLookup Index Search 预查询索引搜索（9） Sine 正弦函数查询表6．数学模块（Math Operations）（1） Abs 取绝对值（2） Add 加法（3） Algebraic Constraint 代数约束（4） Assignment 赋值（5） Bias 偏移（6） Complex to Magnitude-Angle 由复数输入转为幅值和相角输出（7） Complex to Real-Imag 由复数输入转为实部和虚部输出（8） Divide 除法（9） Dot Product 点乘运算（10） Gain 比例运算（11） Magnitude-Angle to Complex 由幅值和相角输入合成复数输出（12） Math Function 包括指数函数、对数函数、求平方、开根号等常用数学函数（13） Matrix Concatenation 矩阵级联（14） MinMax 最值运算（15） MinMax Running Resettable 最大最小值运算（16） Polynomial 多项式（17） Product 乘运算（18） Product of Elements 元素乘运算（19） Real-Imag to Complex 由实部和虚部输入合成复数输出（20） Reshape 取整（21） Rounding Function 舍入函数（22） Sign 符号函数（23） Sine Wave Function 正弦波函数（24） Slider Gain 滑动增益（25） Subtract 减法（26） Sum 求和运算（27） Sum of Elements 元素和运算（28） Trigonometric Function 三角函数，包括正弦、余弦、正切等（29） Unary Minus 一元减法（30） Weighted Sample Time Math 权值采样时间运算7、模型检测模块（Model Verification）（1） Assertion 确定操作（2） Check Discrete Gradient 检查离散梯度（3） Check Dynamic Gap 检查动态偏差（4） Check Dynamic Lower Bound 检查动态下限（5） Check Dynamic Range 检查动态范围（6） Check Dynamic Upper Bound 检查动态上限（7） Check Input Resolution 检查输入精度（8） Check Static Gap 检查静态偏差（9） Check Static Lower Bound 检查静态下限（10） Check Static Range 检查静态范围（11） Check Static Upper Bound 检查静态上限8、模型扩充模块（Model-Wide Utilities）（1） Block Support Table 功能快支持的表（2） DocBlock 文档模块（3） Model Info 模型信息（4） Timed-Based Linearization 时间线性分析（5） Trigger-Based Linearization 触发线性分析9、端口和子系统模块（Prot & Subsystems）（1） Configurable Subsystem 结构子系统（2） Atomic Subsystem 单元子系统（3） CodeReuseSubsystem 代码重用子系统（4） Enable 使能（5） Enabled and Triggered Subsystem 使能和触发子系统（6） Enabled Subsystem 使能子系统（7） For Iterator Subsystem 重复操作子系统（8） Function-Call Generator 函数响应生成器（9） Function-Call Subsystem 函数响应子系统（10） If 假设操作（11） If Action Subsystem 假设动作子系统（12） In1 输入端口（13） Model 模型（14） Out1 输出端口（15） Subsystem 子系统（16） Subsystem Examples 子系统例子（17） Switch Case 转换事件（18） Switch Case Action Subsystem 转换事件子系统（19） Trigger 触发操作（20） Triggered Subsystem 触发子系统（21） While Iterator Subsystem 重复子系统10、信号属性模块（Signal Attributes）（1） Data Type Conversion 数据类型转换（2） Data Type Conversion Inherited 继承的数据类型转换（3） Data Type Duplicate 数据类型复制（4） Data Type Propagation 数据类型继承（5） Data Type Propagation Examples 数据类型继承例子（6） Data Type Scaling Strip 数据类型缩放（7） IC 信号输入属性（8） Probe 探针点（9） Rate Transition 比率变换（10） Signal Conversion 信号转换（11） Signal Specification 信号特征说明（12） Weighted Sample Time 权值采样时间（13） Width 信号带宽11、信号路线模块（Signal Routing）（1） Bus Assignment 总线分配（2） Bus Creator 总线生成（3） Bus Selector 总线选择（4） Data Store Memory 数据存储（5） Data Store Read 数据存储读取（6） Data Store Write 数据存储写入（7） Demux 将一个复合输入转化位多个单一输出（8） Environment Controller 环境控制器（9） From 信号来源（10） Goto 信号去向（11） Goto Tag Visibility 标签可视化（12） Index Vector 索引向量（13） Manual Switch 手动选择开关（14） Merge 信号合并（15） Multiport Switch 多端口开关（16） Mux 将多个单一输入转化为一个复合输出（17） Selector 信号选择器（18） Switch 开关选择，当第二输入端大于临界值时，输出由第一个输入端而来，否则输出由第三输入端而来（1） Display 数字显示器（2） Floating Scope 浮动观察器（3） Out1 输出端口（4） Scope 示波器（5） Stop Simulation 仿真停止（6） Terminator 连接到没有连接到的输出端（7） To File 将输出数据写入数据文件保存（8） To Workspace 将输出数据写入Matlab的工作空间（9） XY Graph 显示二维图形（1） Band-Limited White Noise 带限白噪声（2） Chirp Signal 产生一个频率不断增大的正弦波（3） Clock 显示和提供仿真时间（4） Constant 常数信号（5） Counter Free-Running 无限计数器（6） Counter Limited 有限计数器（7） Digital Clock 在规定的采样间隔产生仿真时间按（8） From File 来自数据文件（9） From Workspace 来自Matlab的工作空间（10） Ground 连接到没有连接到的输入端（11） In1 输入信号（12） Pulse Generator 脉冲发生器（13） Ramp 斜坡信号输入（14） Random Number 产生正态分布的随机数（15） Repeating Sequence 产生规律重复的任意信号（16） Repeating Sequence Interpolated 重复序列内插值（17） Repeating Sequence Stair 重复阶梯序列（18） Signal Builder 信号创建器（19） Signal Generator 信号发生器，可以产生正弦波、方波、锯齿波及任意波形（20） Sine Wave 正弦波信号（21） Step 阶跃信号（22） Uniform Random Number 一致随机数14、用户自定义函数模块（User-Defined Functions）（1） Embedded MATLAB Function 嵌入的Matlab函数（2） Fcn 用自定义的函数（表达式）进行运算（3） Level-2 M-file S-Function M文件编写的S函数（4） MATLAB Fcn 利用Matlab的现有函数进行运算（5） S-Function 调用自编的S函数程序进行运算（6） S-Function Builder S函数建立器（7） S-Function Examples S函数例子15、Additional Math & Discrete（1） Additional Discrete（2） Additional Math: Increment – Decrement综合。

数学模型和模拟中的连续模型与离散模型数学模型和计算机模拟已经成为了许多领域的重要研究手段。

然而，在进行模型建立和模拟过程中，要根据具体问题的特点选择合适的模型类型。

在数学模型和模拟中，常见的模型类型有连续模型和离散模型两种。

连续模型是指一个作用在连续空间上的模型。

例如，微积分中的连续函数模型就是一个常用的连续模型。

这种模型常常用来描述实际问题中的连续过程，如流体力学、热力学等领域。

在连续模型中，物理量在不同时间和空间位置上都可以取到连续的值，因此它通常需要使用微积分的方法来求解。

同时，连续模型可以使用经典的物理方程来描述，如牛顿运动方程和麦克斯韦方程等。

离散模型是指一个作用在离散空间上的模型。

例如，数学中的离散数学模型就是一个常用的离散模型。

这种模型常常用来描述实际问题中的离散现象，如计算机科学、网络科学等领域。

在离散模型中，物理量在不同时间和空间位置上的取值是离散的，因此通常使用离散的数学工具来求解。

同时，离散模型的建立通常需要使用离散数学的方法，如排列组合、图论等。

对于一些实际问题，可以采用混合模型来描述。

例如，植物的生长状态是一个连续过程，可以使用连续模型来描述，但是植物的个体生长是一个离散过程，需要使用离散模型来描述。

因此，可以利用混合模型来描述植物的生长问题。

在建立模型时，需要深入了解问题的特点和要求，选择合适的模型类型进行建模。

同时，需要灵活应用不同模型之间的转化关系，充分利用模型的优势，提高模型的解决问题的能力。

总之，数学模型和模拟在科学研究和工程应用中起着重要的作用，并且连续模型和离散模型都有其独特的适用范围。

因此，我们需要充分了解不同类型的模型特点和应用情况，遵循科学的方法建立模型，提高模型的准确性和实用性。