§7.3 离散时间系统的数学模型
- 格式:ppt
- 大小:468.50 KB
- 文档页数:30


2326.4 离散系统的数学模型为研究离散系统的性能,需要建立离散系统的数学模型。
线性离散系统的数学模型有差分方程、脉冲传递函数和离散状态空间表达式三种。
本节主要介绍差分方程及其解法,脉冲传递函数的定义,以及求开环脉冲传递函数和闭环脉冲传递函数的方法。
有关离散状态空表达式及其求解,将在第8章介绍。
6.4.1 线性常系数差分方程及其解法对于线性定常离散系统,k 时刻的输出)(k c ,不但与k 时刻的输入)(k r 有关,而且与k 时刻以前的输入 ),2(),1(--k r k r 有关,同时还与k 时刻以前的输出 ),2(),1(--k c k c 有关。
这种关系一般可以用n 阶后向差分方程来描述,即∑∑==-+--=mj jni i j k r bi k c a k c 01)()()( (6-34)式中,i a ,i =1,2,…,n 和j b ,j =0,1,…,m 为常系数,n m ≤。
式(6-34)称为n 阶线性常系数差分方程。
线性定常离散系统也可以用n 阶前向差分方程来描述,即∑∑==-++-+-=+mj jni i j m k r bi n k c a n k c 01)()()( (6-35)工程上求解常系数差分方程通常采用迭代法和z 变换法。
1. 迭代法若已知差分方程式(6-34)或式(6-35),并且给定输出序列的初值,则可以利用递推关系,在计算机上通过迭代一步一步地算出输出序列。
例6-10 已知二阶差分方程)2(6)1(5)()(---+=k c k c k r k c输入序列1)(=k r ,初始条件为1)1(,0)0(==c c ,试用迭代法求输出序列)(k c , ,5,4,3,2,1,0=k 。
解 根据初始条件及递推关系,得0)0(=c 1)1(=c6)0(6)1(5)2()2(=-+=c c r c 25)1(6)2(5)3()3(=-+=c c r c 90)2(6)3(5)4()4(=-+=c c r c301)3(6)4(5)5()5(=-+=c c r c2. z 变换法233设差分方程如式(6-34)所示,对差分方程两端取z 变换,并利用z 变换的实数位移定理,得到以z 为变量的代数方程,然后对代数方程的解)(z C 取z 反变换,可求得输出序列)(k c 。

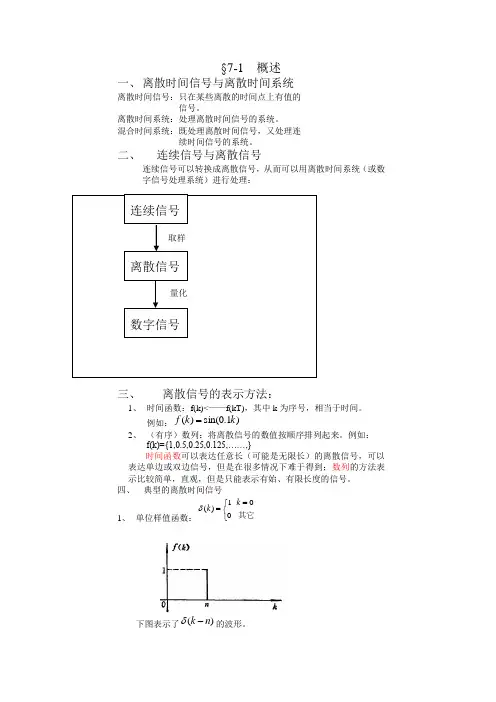
§7-1 概述一、 离散时间信号与离散时间系统离散时间信号:只在某些离散的时间点上有值的信号。
离散时间系统:处理离散时间信号的系统。
混合时间系统:既处理离散时间信号,又处理连续时间信号的系统。
二、 连续信号与离散信号连续信号可以转换成离散信号,从而可以用离散时间系统(或数字信号处理系统)进行处理:三、 离散信号的表示方法:1、 时间函数:f(k)<——f(kT),其中k 为序号,相当于时间。
例如:)1.0sin()(k k f =2、 (有序)数列:将离散信号的数值按顺序排列起来。
例如:f(k)={1,0.5,0.25,0.125,……,}时间函数可以表达任意长(可能是无限长)的离散信号,可以表达单边或双边信号,但是在很多情况下难于得到;数列的方法表示比较简单,直观,但是只能表示有始、有限长度的信号。
四、 典型的离散时间信号1、 单位样值函数:⎩⎨⎧==其它001)(k k δ下图表示了)(n k -δ的波形。
连续信号离散信号 数字信号 取样量化这个函数与连续时间信号中的冲激函数)(t δ相似,也有着与其相似的性质。
例如:)()0()()(k f k k f δδ=, )()()()(000k k k f k k k f -=-δδ。
2、 单位阶跃函数:⎩⎨⎧≥=其它001)(k k ε这个函数与连续时间信号中的阶跃函数)(t ε相似。
用它可以产生(或表示)单边信号(这里称为单边序列)。
3、 单边指数序列:)(k a k ε比较:单边连续指数信号:)()()(t e t e t a at εε=,其底一定大于零,不会出现负数。
4、 单边正弦序列:)()cos(0k k A εφω+(a) 0.9a = (d) 0.9a =-(b) 1a = (e) 1a =-(c) 1.1a = (f) 1.1a =-双边正弦序列:)cos(0φω+k A五、 离散信号的运算1、 加法:)()()(21k f k f k f +=<—相同的k 对应的数相加。






离散时间状态空间模型模型预测控制摘要:1.离散时间状态空间模型的基本概念2.模型预测控制的原理和方法3.离散时间状态空间模型在实际应用中的优势和局限性4.模型预测控制在我国的研究与应用现状5.未来发展趋势和展望正文:一、离散时间状态空间模型的基本概念离散时间状态空间模型(Discrete-Time State Space Model)是一种用于描述离散时间系统中状态随时间变化的数学模型。
它由离散时间、离散状态和系统动态方程三部分组成。
离散时间表示系统状态更新的时刻;离散状态描述了系统在各个离散时刻的状态变量;系统动态方程则描述了状态变量在相邻离散时刻之间的变化规律。
二、模型预测控制的原理和方法模型预测控制(Model Predictive Control,MPC)是一种基于数学模型的控制策略。
其主要思想是在预测未来系统状态的基础上,优化控制输入,使得系统输出尽可能接近期望值。
模型预测控制的实质是在离散时间状态空间模型基础上,通过求解最优控制问题来实现对系统的控制。
三、离散时间状态空间模型在实际应用中的优势和局限性离散时间状态空间模型在许多实际应用领域具有广泛的应用价值,例如工业过程控制、机器人控制、交通运输系统控制等。
其主要优势在于能够有效地描述系统的动态特性,同时具有一定的计算效率。
然而,离散时间状态空间模型也存在一定的局限性,例如对系统噪声的抑制能力较弱,以及对系统不确定性描述的不够准确等。
四、模型预测控制在我国的研究与应用现状近年来,我国在模型预测控制领域的研究取得了显著成果。
不仅在理论研究方面不断深入,而且在实际应用中也取得了良好的效果。
目前,模型预测控制已成功应用于电力系统、化学过程、机械系统等多个领域。
五、未来发展趋势和展望随着科技的不断发展,离散时间状态空间模型和模型预测控制在未来的研究和发展中将具有以下趋势:1.深入研究系统不确定性处理方法,提高模型预测控制的鲁棒性;2.发展多变量、多目标优化算法,提高控制性能;3.结合其他先进控制策略,如自适应控制、优化算法等,实现更高效、更可靠的控制;4.在更多实际应用领域推广和应用模型预测控制技术,为我国的工业发展和科技创新贡献力量。
