极限与配合§1-1 习题

极限配合与技术测量基础（少学时）（第二版）习题册答案绪论一、填空题1.能用来代替同样要求2.产品设计零件加工产品装配使用和维修3.尺寸误差几何误差表面微观形状误差4.允许变动量尺寸公差几何公差二、判断题1.√2.×三、选择题1.C2.A3.A4.B5.B四、简答题1.答：互换性原则广泛用于机械制造中的产品设计、零件加工、产品装配、机器的使用和维修等各个方面。

在设计方面，采用具有互换性的标准件和通用件，可以使设计工作简化，缩短设计周期，并便于应用计算机辅助设计。

在加工和装配方面，当零件具有互换性时，可以分散加工、集中装配。

这样有利于组织跨地域的专业化厂际协作生产；有利于使用现代化的工艺装备，并可提高设备的利用率；有利于采用自动线等先进的生产方式；还可减轻劳动强度，缩短装配周期。

在使用和维修方面，互换性有其不可取代的优势。

当机器的零（部）件突然损坏时，可迅速用相同规格的零（部）件更换，既缩短了维修时间，又能保证维修质量，从而提高机器的利用率和延长机器的使用寿命。

2.答：没有必要。

由于几何量误差的存在，零件几何参数不可能加工得完全一样。

实践证明，虽然零件几何量误差可能影响到零件的使用性能，但只要将这些误差控制在一定的范围内，仍能满足使用功能要求，也就是说，仍可以保证零件互换性要求。

因此，没有必要也不可能将零件几何参数加工得完全一样。

第1章极限与配合基础§1-1 基本术语及其定义一、填空题1.数值特定单位2.测量3.上极限尺寸下极限尺寸公称尺寸4.上极限尺寸下极限尺寸5.上极限实际6.实际尺寸上极限偏差下极限偏差7.零线正偏差负偏差8.公差带大小公差带位置9.公称尺寸公差带10.正负11.间隙配合过渡配合过盈配合12.极限界限值松紧13.极限界限值紧松14.最大间隙最小过盈15.间隙过盈16.过盈过渡间隙过渡17.松紧差别低二、判断题1.×2.√3.×4.×5.√6.×7.×8.×9.√10.×11.√ 12.√ 13.√三、选择题1.B2.D3.A4.B5.C6.C7.C8.B9.D 10.A 11.C12.A 13.D 14.D 15.D四、名词解释1.通过测量获得的尺寸称为实际尺寸。

极限与配合试题及答案注：根据您的要求，我将按照试题和答案的形式为您提供文章内容，请注意仔细阅读。

试题一：极限计算题1. 计算极限：$\lim\limits_{x \to 2} \frac{x^2 - 4}{x - 2} = ?$解答：为了计算该极限，我们可以将分子因式分解：$x^2 - 4 = (x - 2)(x + 2)$。

然后，我们可以简化表达式：$\frac{x^2 - 4}{x - 2} =\frac{(x - 2)(x + 2)}{x - 2} = x + 2$。

因此，当$x$趋近于2时，该极限的值为4。

2. 计算极限：$\lim\limits_{x \to 0} \frac{\sin 3x}{x} = ?$解答：利用泰勒展开公式，我们可以将$\sin 3x$展开为$3x -\frac{(3x)^3}{3!}+\frac{(3x)^5}{5!} - \dots$。

因此，$\lim\limits_{x \to 0} \frac{\sin 3x}{x} = \lim\limits_{x \to 0} \frac{3x -\frac{(3x)^3}{3!}+\frac{(3x)^5}{5!} - \dots}{x} = \lim\limits_{x \to 0} (3 - \frac{(3x)^2}{3!}+\frac{(3x)^4}{5!} - \dots) = 3$。

试题二：配合题1. 将下列函数的图像平移至右方3个单位，并将图像进行上下翻转，得到新的函数。

解答：设原函数为$f(x)$，平移后的函数为$g(x)$，根据平移变换的特性，我们有$g(x) = f(x - 3)$。

而上下翻转则相当于对函数进行纵向伸缩，即$g(x) = -f(x - 3)$。

因此，新的函数可以表示为$g(x) = -f(x - 3)$。

2. 求下列方程组的解：$\begin{cases} x + y = 5 \\ 2x - 3y = 1\end{cases}$解答：我们可以使用消元法来求解这个方程组。

第一章极限与配合练习题一．选择题1.关于孔和轴的概念，下列说法中错误的是（）A、圆柱形的内表面为孔，外表面为轴B、由截面呈矩形的四个内表面或外表面形成一个孔或一个轴C、从装配关系看，包容面为孔，被包容面为轴D、从加工过程看，切削过程中尺寸由小变大的为孔，由大变小的为轴答案：B2.公称尺寸是（）A.测量时得到的B.加工时得到的C.装配后得到的D.设计时给定的答案：D3. 实际偏差是（）。

A、设计时给定的；B、直接测量得到的；C、通过测量，计算得到的；D、最大极限尺寸与最小极限尺寸之代数差。

答案：C4. 关于偏差与公差之间的关系，下列说法正确的是（）。

A、实际偏差愈大，公差愈大；B、上偏差愈大，公差愈大；C、下偏差愈大，公差愈大；D、上下偏差之差的绝对值愈大，公差愈大。

答案：D5.下极限尺寸减其公称尺寸所得的代数差为（）A.上极限偏差B.下极限偏差C. 基本偏差D. 实际偏差答案：B6. 尺寸公差带图的零线表示（）。

A、最大极限尺寸；B、最小极限尺寸；C、公称尺寸；D、实际尺寸答案：C7. 基本偏差确定公差带的位置，一般情况下，基本偏差是（）。

A、上偏差；B、下偏差、C、实际偏差；D、上偏差或下偏差靠近零下的那个。

答案：D8.当孔的下极限尺寸与轴的上极限尺寸之差为正值时，此代数差称为（）A.最大间隙B. 最小间隙C.最大过盈D.最小过盈答案：B9.当孔的下极限尺寸与轴的上极限尺寸之差为负值时，此代数差称为（）A.最大间隙B. 最小间隙C.最大过盈D.最小过盈答案：C10.当孔的上极限偏差大于相配合的轴的下极限偏差时，此配合的性质是（）A. 间隙配合B.过度配合C. 过盈配合D.无法确定答案： D11.确定不在同一尺寸段的两尺寸的精确程度，是根据（）A.两个尺寸的公差数值的大小B. 两个尺寸的基本偏差C. 两个尺寸的公差等级D. 两个尺寸的实际偏差答案： C12.当孔的基本偏差为上极限偏差时，计算下极限偏差数值的计算公式为（）=EI+IT =ES-IT C. EI=ES+IT =es-IT答案：B13.公差带大小是由（）决定的。

第一章 极限与配合 练习题一. 选择题1. 关于孔和轴的概念，下列说法中错误的是（）A 、 圆柱形的内表面为孔，外表面为轴B 、 由截面呈矩形的四个内表面或外表面形成一个孔或一个轴C 、 从装配关系看，包容面为孔，被包容面为轴D 、 从加工过程看，切削过程中尺寸由小变大的为孔，由大变小的为轴 答案：B 2. 公称尺寸是（ A. 测量时得到的 答案：D 3.实际偏差是（ ）。

A 、设计时给定的； C 、通过测量，计算得到的; 答案：C 4.关于偏差与公差之间的关系，下列说法正确的是（）。

A 、实际偏差愈大，公差愈大；B 、上偏差愈大，公差愈大；C 、下偏差愈大，公差愈大；D 、上下偏差之差的绝对值愈大，公差愈大答案：D 5. 下极限尺寸减其公称尺寸所得的代数差为（）A.上极限偏差B.下极限偏差C.基本偏差D.实际偏差 答案：B6. 尺寸公差带图的零线表示（ ）。

A 、最大极限尺寸；B 、最小极限尺寸；C 、公称尺寸；D 、实际尺寸答案：C7. 基本偏差确定公差带的位置，一般情况下，基本偏差是（）。

A 、上偏差；B 、下偏差、C 、实际偏差；D 、上偏差或下偏差靠近零下的那个。

答案：D8•当孔的下极限尺寸与轴的上极限尺寸之差为正值时，此代数差称为（ ）A.最大间隙B.最小间隙C.最大过盈D.最小过盈答案：B9•当孔的下极限尺寸与轴的上极限尺寸之差为负值时，此代数差称为（ ）A.最大间隙B.最小间隙C.最大过盈D.最小过盈 答案：C10. 当孔的上极限偏差大于相配合的轴的下极限偏差时，此配合的性质是（ ） A.间隙配合 B.过度配合 C.过盈配合 D.无法确定答案：DB.加工时得到的C.装配后得到的D.设计时给定的B 、直接测量得到的；D 、最大极限尺寸与最小极限尺寸之代数差11. 确定不在同一尺寸段的两尺寸的精确程度，是根据（）A.两个尺寸的公差数值的大小B.两个尺寸的基本偏差12. 当孔的基本偏差为上极限偏差时，计算下极限偏差数值的计算公式为（ A.ES=EI+IT B.EI=ES-IT C. EI=ES+IT D.ei=es-IT 答案：B 13.公差带大小是由（ ）决定的。

极限与配合练习题极限是微积分中重要的概念之一，它描述了函数在某一点处的趋近行为。

在实际应用中，极限的概念经常需要与其他数学概念配合使用，以求解各种数学问题。

本文将介绍一些与极限配合的练习题，帮助读者加深对极限概念的理解。

练习1：计算极限求解极限是经常出现在数学分析和微积分课程中的问题。

下面我们通过一个具体的练习题来加深对极限概念的理解。

已知函数f(x) = (x^2 - 1) / (x - 1)，计算lim(x->1)f(x)的值。

解析：要计算极限lim(x->1)f(x)，我们可以直接代入x=1得到f(1)=0，但这并不是一个标准的求解极限的方法。

为了使用极限的定义来求解，我们可以对函数进行化简。

将分子的(x-1)因式分解，得到f(x) = [(x-1)(x+1)] / (x-1) = x+1。

此时我们可以发现，在x趋近于1的过程中，f(x)趋近于2。

因此，lim(x->1)f(x) = 2。

练习2：利用极限计算函数的导数极限的概念在微积分中还经常被用于计算函数的导数。

下面我们通过一个练习题来探讨这个应用。

已知函数f(x) = e^x，计算f'(x)。

解析：要计算函数f(x) = e^x的导数，我们可以直接应用指数函数的求导规则得到f'(x) = e^x。

然而，我们也可以利用极限的概念来求解。

令h趋近于0，计算lim(h->0)[f(x+h) - f(x)] / h。

将f(x+h)代入并化简，得到lim(h->0)(e^(x+h) - e^x) / h。

根据指数函数的性质，我们知道e^(x+h) / e^x = e^h。

因此，lim(h->0)e^(x+h) / e^x = e^0 = 1。

所以，将1代入极限式，得到lim(h->0)(e^(x+h) - e^x) / h = lim(h->0)(1 - e^x) / h。

进一步化简可得lim(h->0)(1 - e^x) / h = -e^x。

极限与配合习题及答案极限是高等数学中的一个重要概念，它描述了函数在某一点附近的行为。

极限的理解和应用是解决许多数学问题的基础。

配合极限的概念，我们可以通过极限来研究函数的连续性、导数、积分等。

以下是一些极限与配合的习题及答案。

习题 1：求极限\[ \lim_{x \to 0} \frac{\sin x}{x} \]答案 1：根据极限的定义，我们知道当\( x \)趋近于0时，\( \sin x \)趋近于\( x \)。

因此，这个极限的值为1。

习题 2：求函数的连续性判断函数\( f(x) = x^2 \)在\( x = 1 \)处是否连续。

答案 2：函数\( f(x) = x^2 \)是一个二次函数，它在定义域内处处连续。

因此，\( f(x) \)在\( x = 1 \)处是连续的。

习题 3：求函数的导数求函数\( f(x) = x^3 - 2x + 1 \)的导数。

答案 3：根据导数的定义，我们可以应用幂函数的导数规则，得到：\[ f'(x) = 3x^2 - 2 \]习题 4：求无穷小量的阶确定\( x \)趋近于0时，\( \sin x \)与\( x \)的无穷小量的阶。

答案 4：由于\( \lim_{x \to 0} \frac{\sin x}{x} = 1 \)，我们可以得出\( \sin x \)与\( x \)是同阶无穷小量。

习题 5：求函数的积分求函数\( f(x) = 2x + 3 \)在区间[1, 4]上的定积分。

答案 5：根据积分的基本公式，我们可以得到：\[ \int_{1}^{4} (2x + 3) \, dx = \left[ x^2 + 3x\right]_{1}^{4} = (16 + 12) - (1 + 3) = 28 \]习题 6：求函数的极限求极限\( \lim_{x \to \infty} \frac{2x^2 + 3x}{x^2 - 1} \)。

极限与配合试题及答案一、选择题1.已知函数$f(x)=\frac{3x^2-9x+2}{(x-2)(x+1)}$，则$f(x)$的极限为（）。

A. $x=2$时极限不存在B. $x=-1$时极限为2C. $x=2$时极限为3D. $x=-1$时极限不存在2.若$f(x)=\begin{cases}x^2-4x+3, & x<1\\ ax+b, & x\geq1\end{cases}$在$x=1$处连续，则$a$和$b$的值分别为（）。

A. $a=2, b=-3$B. $a=1, b=-2$C. $a=3, b=0$D. $a=-1, b=3$3.已知函数$f(x)=\frac{\sin^2 x}{x}, g(x)=\frac{1-\cos x}{x}$，则$\lim\limits_{x\to0}\frac{f(x)}{g(x)}=$（）。

A. 0B. 1C. -1D. 不存在4.设函数$f(x)=\begin{cases}x, & x\leq0\\ ax^2+bx+c, & x>0\end{cases}$连续，则$a+b+c$的值为（）。

A. 1B. 2C. 3D. 4二、填空题1.设函数$f(x)=\begin{cases}\sin x+1, & x<0\\ k, & x=0\\ e^{x-1}, & x>0 \end{cases}$，要使$f(x)$在$x=0$处连续，则$k=$\blank.2.已知$f(x)=\frac{e^x-1}{x}$，则$\lim\limits_{x\to0}f(x)=$\blank.3.若$\lim\limits_{x\to0}\frac{f(2x)}{x}=3$，则$\lim\limits_{x\to0}\frac{f(x)}{x}=$\blank.4.设$f(x)=a-bx^2$，若$\lim\limits_{x\to0}\frac{f(x)-f(2x)}{x}=7$，则$a+b=$\blank.三、解答题1.求函数$f(x)=\frac{x^2-3x+2}{x+1}$的极限。

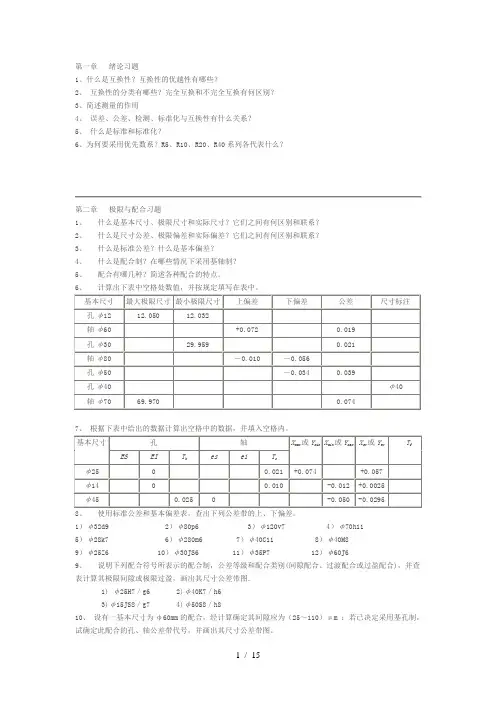
第一章绪论习题1、什么是互换性？互换性的优越性有哪些？2、互换性的分类有哪些？完全互换和不完全互换有何区别？3、简述测量的作用4、误差、公差、检测、标准化与互换性有什么关系？5、什么是标准和标准化？6、为何要采用优先数系？R5、R10、R20、R40系列各代表什么？第二章极限与配合习题1、什么是基本尺寸、极限尺寸和实际尺寸？它们之间有何区别和联系？2、什么是尺寸公差、极限偏差和实际偏差？它们之间有何区别和联系？3、什么是标准公差？什么是基本偏差？4、什么是配合制？在哪些情况下采用基轴制？5、配合有哪几种？简述各种配合的特点。

6、计算出下表中空格处数值，并按规定填写在表中。

7、根据下表中给出的数据计算出空格中的数据，并填入空格内。

8、使用标准公差和基本偏差表，查出下列公差带的上、下偏差。

1）φ32d9 2）φ80p6 3）φ120v7 4）φ70h115）φ28k7 6）φ280m6 7）φ40C11 8）φ40M89）φ25Z6 10）φ30JS6 11）φ35P7 12）φ60J69、说明下列配合符号所表示的配合制，公差等级和配合类别(间隙配合、过渡配合或过盈配合)，并查表计算其极限间隙或极限过盈，画出其尺寸公差带图．1) φ25H7／g6 2)φ40K7／h63)φ15JS8／g7 4)φ50S8／h810、设有一基本尺寸为φ60mm的配合，经计算确定其间隙应为（25～110）μm ；若已决定采用基孔制，试确定此配合的孔、轴公差带代号，并画出其尺寸公差带图。

11、设有一基本尺寸为φ110mm的配合，经计算确定，为保证连接可靠，其过盈不得小于55μm；为保证装配后不发生塑性变形，其过盈不得大于112μm。

若已决定采用基轴制，试确定此配合的孔、轴公差带代号，并画出其尺寸公差带图。

12、被检验工件为φ80h9（）E，试确定验收极限，并选择适当的计量器具。

一、判断题〔正确的打√，错误的打X〕1．公差可以说是允许零件尺寸的最大偏差。

第一章极限与配合§1－1 互换性概念一、填空题1. 对互换性的要求为：2.3.二、判断题（X）1.具有互换性的零件，应该是形状和尺寸完全相同的零件。

（√）2.要使零件具有互换性，只需使零件的加工误差保持在一定的范围内。

（√）3.零件在加工过程中的误差是不可避免的。

三、选择题1. 关于零件的互换性，下列说法中错误的是（A）。

A.凡是合格的零件一定具有互换性。

B.凡是具有互换性的零件必为合格品。

C.为使零件具有互换性，必须把零件的加工误差控制在给定的公差范围内。

2. 实现互换性的基本条件是(B)。

A.对不同规格的零、部件规定统一的技术标准。

B.对同一规格的零、部件规定统一的技术标准。

C.对同一规格的零、部件规定不同的技标准。

3. 不完全互换性与完全互换性的主要区别在于（A）。

A.在装配前允许有附加的选择。

B.在装配时不允许有附加的调整。

C.在装配时允许有适当的修配。

D.装配精度比完全互换性低。

4. 某种零件在装配时需要进行修配，则此种零件（C）。

A.具有完全互换性。

B.具有不完全互换性。

C.不具有互换性。

D.无法确定是否具有互换性。

四、简答题1. 什么是互换性？互换性原则对机械制造有什么意义？答：在机械工业中，互换性是指同一规格的零、部件，任选其一，不需经任何挑选、调整和修配，就能装配到机器上，并完全达到规定的技术性能要求。

互换性具有广泛的技术经济意义，它是现代工业中重要的指导性原则与有效的技术措施。

（1）在设计方面，可以使产品标准化、系列化，从而简化零、部件的设计计算过程，缩短设计周期，并方便应用计算机辅助设计。

（2）在生产制造方面，能组织自动化和专业化的高效生产，应用现代化的技术设备，有利于提高产品质量、降低成本和减轻劳动强度。

（3）在使用维修方面，可以缩短机器维修的时间、减少费用和提高机器的使用率。

2. 具有互换性的零件的几何参数是否必须加工得完全一样？为什么？答：具有互换性的零件的几何参数不要求加工得完全一样。

第一章习题1-1 完全互换和不完全互换有什么区别？各应用于什么场合？零件在装配或更换时，不需选择、调整或辅助加工(修配)的互换性为完今互换性。

当装配精度要求较高时，采用完全互换性将使零件制造公差很小，加工困难，成本很高，甚至无法加工。

这时，将零件的制造公差适当放大，使之便于加工，而在零件完工后再用测量器具将零件按实际尺寸的大小分为若干组，使每组零件间实际尺寸的差别减小，装配时按相应组进行(例如，大孔组零件与大轴组零件装配，小孔组零件与小轴组零件装配)。

这样，既可保证装配精度和使用要求，又能解决加工困难，降低成本。

此种仅组内零件可以互换，组与组之间不能互换的特性，称之为不完全互换性。

1-2 什么是标准、标准化？按标准颁发的级别分，我国有哪几种？标准(Standard):是对重复性事物和概念所做的统一规定。

标准化(Standardization)是指在经济、技术、科学及管理等社会实践中，对重复性事物和概念，通过制订、发布和实施标准达到统一，以获得最佳秩序和社会效益的有组织的活动过程。

按标准颁发的级别分，我国的技术标准有四个层次：国家标准、行业标准、地方标准和企业标准。

1-3 公差、检测、标准化与互换性有什么关系？公差(Tolerance)：允许零件几何参数的变动范围。

检测(Inspection and Measurement)：即检验和测量，是将被测几何参数与单位量值进行比较或判断的过程，由此确定被测几何参数是否在给定的极限范围之内。

标准化(Standardization)是指在经济、技术、科学及管理等社会实践中，对重复性事物和概念，通过制订、发布和实施标准达到统一，以获得最佳秩序和社会效益的有组织的活动过程。

互换性定义（Interchangeability）:指按同一规格标准制成的合格零部件在尺寸上和功能上具有相互替代的性能。

公差、检测、标准化与互换性的关系：A 零件的尺寸大小一定时，给定的公差值越小，精度就越高；但随之而来的是加工困难。

《极限配合与技术测量》第一章极限与配合试卷一、单项选择题1.下列各关系式中,能确定孔与轴的配合一定不是过渡配合的是( )。

(2 分)A.EI=esB.ES≥esC.EI>eiD.ei<ES<es2.对标准公差的论述,下列说法中错误的是( )。

(2 分)A.标准公差的大小与基本尺寸和公差等级有关,与该尺寸是表示孔还是轴无关B.在任何情况下,基本尺寸愈大,标准公差必定愈大C.基本尺寸相同,公差等级愈低,标准公差愈大D.某一基本尺寸段为>50~80mm,则基本尺寸为60mm和75mm的同等级的标准公差数值相同。

3.尺寸公差带图的零线表示( )。

(2 分)A.最大极限尺寸B.最小极限尺寸C.基本尺寸D.实际尺寸。

4.当孔的下偏差大于相配合的轴的上偏差时,此配合性质是( )。

(2 分)A.间隙配合B.过渡配合C.过盈配合D.无法确定5.确定不在同一尺寸段的两尺寸的精确程度,是根据( )。

(2 分)A.两个尺寸的公差数值的大小B.两个尺寸的基本偏差C.两个尺寸的公差等级D.两尺寸的实际偏差6.基本尺寸是( )。

(2 分)A.测量时得到的B.加工时得到的C.装配后得到的D.设计时给定的7.对于孔公差带ZA8,下列说法错误的是( )。

(2 分)A.其标准公差等级为IT8B.其基本偏差是下偏差C.其另一偏差由标准公差确定D.其公差带在零线以下8.下列各关系式中,能确定孔与轴的配合为过盈配合的是( )。

(2 分)A.EI<esB.ES=eiC.ES>esD.EI<ei9.关于实际尺寸,下列说法中正确的是( )。

(2 分)A.零件的实际尺寸就是零件的真实尺寸B.当零件的实际尺寸正好等于其基本尺寸时,该尺寸必然合格C.实际尺寸是零件加工后通过测量获得的D.孔、轴的实际尺寸分别用符号d a、D a表示10.关于偏差与公差之间的关系,下列说法中正确的是( )。

(2 分)A.上偏差越大,公差越大B.实际偏差越大,公差越大C.下偏差越大,公差越大D.上、下偏差之差的绝对值越大,公差越大二、判断题11.( )基轴制的常用配合是由基准轴和孔的常用公差带形成的,孔的常用公差带有44种,因而基轴制的常用配合就有44种。

极限与配合试题及答案一、选择题1. 极限配合的基本概念是什么？A. 零件的制造精度B. 零件的互换性C. 零件的尺寸极限D. 零件的配合性质答案：C2. 基本偏差和标准偏差的区别是什么？A. 基本偏差是设计时确定的，标准偏差是制造时确定的B. 基本偏差是制造时确定的，标准偏差是设计时确定的C. 两者都是设计时确定的D. 两者都是制造时确定的答案：A二、填空题1. 根据配合的松紧程度，配合可以分为______、______和______。

答案：间隙配合；过渡配合；过盈配合2. 当基本偏差为零时，配合的类型是______。

答案：过渡配合三、简答题1. 简述公差与配合的关系。

答案：公差是指在制造过程中允许的尺寸变化范围，而配合是指两个零件之间的相对位置关系。

公差的大小直接影响配合的精度和性质，合理的公差设计可以确保零件的互换性和装配性。

2. 什么是最大实体条件和最小实体条件？答案：最大实体条件是指在给定的尺寸公差范围内，零件的最大可能尺寸；最小实体条件是指在给定的尺寸公差范围内，零件的最小可能尺寸。

这两种条件用于确定零件在装配时的极限尺寸状态。

四、计算题1. 已知一个轴的直径尺寸为50mm，公差为±0.1mm。

请计算其最大极限尺寸和最小极限尺寸。

答案：最大极限尺寸 = 50mm + 0.1mm = 50.1mm最小极限尺寸 = 50mm - 0.1mm = 49.9mm2. 假设一个孔的直径尺寸为40mm，基本偏差为-0.05mm，公差等级为IT7。

根据GB/T 1801-2000标准，计算其标准公差。

答案：根据GB/T 1801-2000标准，IT7公差等级的标准公差为0.04mm。

因此，孔的标准公差为0.04mm。

五、论述题1. 论述在机械设计中，如何合理选择配合类型以满足不同的功能需求。

答案：在机械设计中，合理选择配合类型对于确保机械产品的性能和可靠性至关重要。

间隙配合适用于需要相对运动的场合，如滑动轴承；过渡配合适用于一般定位，要求不高的场合；过盈配合适用于需要传递扭矩或承受较大载荷的场合，如齿轮与轴的连接。

<极限配合与技术测量>习题答案第一章概述1-1 "极限配合与技术测量"是中等职业学校机械加工专业的主干课程,是技术性和实践性都比拟强的一门技术根底课。

主要容包括：极限与配合、形和位公差、外表粗糙度技术测量。

1-2 所谓互换性是指在制成同一规格的零件中，不需要任何挑选或附加加工就可以直接使用，组装成部件或整机，并能到达设计要求。

遵循互换性原那么，不仅能提高生产率，而且能有效地保证产品质量，降低生产本钱，所以互换性是机器和仪表制造中重要的生产原那么。

1-3 互换性可分为完全互换和不完全互换两种。

完全互换是指零、部件在装配时，不需要任何选择或附加加工。

其通用性强，装配方便，可减少修理时间，利于专门化生产，在制造业中被广泛采用。

如螺栓、圆柱销等标准件的装配大都属于此类情况；而不完全互换是指零部件在装配时允许进展附加加工、选择和调整，以提高装配的精度和解决加工的困难。

如精度要求较高的滚动轴承，常采用不完全互换法。

1-4 装配时通常按零件的实际尺寸大小分成假设干组，使同组零件的相配尺寸相差值很小，再与对应组零件进展装配，这种方法称为分组装配法。

该方法既能保证装配精度与使用要求，又降低了本钱。

此时，仅是组零件可以互换，组与组之间不可互换，因此属不完全互换。

如精度要求较高的滚动轴承，常采用分组装配法。

1-5 由于加工中各种因素的影响，不可能把零件加工成理论上准确的尺寸，总会有误差存在，加工误差可分为以下几类：〔1〕尺寸误差：指加工后零件某处的实际尺寸对理想尺寸之差的偏差值。

如图纸上标注的尺寸为30mm，加工后的尺寸为29.98mm，那么尺寸误差为0.02mm。

〔2〕形状误差：指加工后零件上实际的线或面对理想形状的偏差值。

如轴的横截面为圆形，加工后实际形状为椭圆形，这就是形状误差。

〔3〕位置误差：指实际零件形体上的点、线、面对各自要求的理想方向和理想位置的偏差量。

理想方向和理想位置指几何意义上的绝对平行、垂直、同轴及绝对准确的角度和位置关系。

第一章习题1-1．判断下列说法是否正确1）一般来说，零件的实际尺寸愈接近基本尺寸愈好。

( )2）公差通常为正，在个别情况下也可能为负或零。

( )3）过渡配合的孔、轴配合，由于有些可能得到过盈，因此过渡配合可能是间隙配合，也可能是过盈配合。

( )4）公差是零件尺寸允许的最大偏差。

（）5）公差通常为正，在个别情况下也可以为负或零。

（）6）孔和轴的加工精度越高，则其配合精度也越高。

（）7）配合公差总是大于孔或轴的尺寸公差。

（）8）过渡配合可能有间隙，也可能有过盈。

因此，过渡配合可以是间隙配合，也可以是过盈配合。

（）9）零件的实际尺寸就是零件的真实尺寸。

（）10）某一零件的实际尺寸正好等于其基本尺寸，则这尺寸必适合格。

（）11）间隙配合中，孔的公差带一定在零线以上，轴的公差带一定在零线以下。

（）12）零件的最大实体尺寸一定大于其最小实体尺寸。

（）13）公称尺寸一定时，公差值愈大，公差等级愈高。

（）14）不论公差值是否相等，只要公差等级相同，尺寸的精确程度就相同。

（）15）ø75±0.060mm的基本偏差是+0.060mm尺寸公差为0.06mm ( )16）因Js为完全对称偏差，故其上、下偏差相等。

( )17）基准孔的上偏差大于零,基准轴的下偏差的绝对值等于其尺寸公差。

（）18) 因配合的孔和轴基本尺寸相等，故其实际尺寸也相等。

（）19）由于零件的最大极限尺寸大于最小极限尺寸，所以上偏差绝对值大于下偏差绝对值。

（）20）尺寸偏差可以正值，负值或零。

（）21）尺寸误差是指一批零件上某尺寸的实际变动量。

（）22）选择公差等级的原则是，在满足使用要求的前提下，尽可能选择较小的公差等级。

（）1-2．填空1. 国标规定的基本偏差孔、轴各有个，其中H为的基本偏差代号，其基本偏差为，且偏差值为；h为的基本偏差代号，其基本偏差为，且偏差值为。

2. 国标规定有和两种配合制度，一般应优先选用，以减少降低生产成本。