下载文档原格式
2010年江苏省高考预测卷物 理 试 题本试卷共15小题，满分120分。
考试用时100分钟。
注意事项：1．答题前，考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、座位号填写在答题卡上。
用2B 铅笔将试卷类型（A ）填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。
3．非选择题必须用黑色字这的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液；不按以上要求作答的答案无效。
4．作答选做题时，请先用2B 铅笔填涂选做题的题组号对应的信息点，再作答。
漏涂、错涂、多涂的，答案无效。
5．考生必须保持答题卡的整洁。
考试结束后，将试卷和答题卡一并交回。
第I 卷（选择题共31分）一、单项选择题(本题共5小题，每小题3分，共15分．每小题只有一个选项符合题意)． 1．2009年12月19日下午，联合国气候变化大会达成《哥本哈根协议》，为减少二氧化碳 排放，我国城市公交推出新型节能环保电动车，在检测某款电动车性能的实验中，质量 为8×102kg 的电动车由静止开始沿平直公路行驶，达到的最大速度为15m/s ，利用传感 器测得此过程中不同时刻电动车的牵引力F 与对应的速度ν，并描绘出F -1v图象（图中AB 、BO 均为直线），假设电动车行驶中所受的阻力恒定，则根据图象不可确定的是A ．电动车运动过程中所受的阻力B ．电动车的额定功率C ．电动车维持匀加速运动的时间D ．BC 过程电动车运动的时间2．a b 、是某电场线上的两点，如图甲所示。
一带负电的质点只受电场力的作用，沿电场 线从a 点运动到b 点。
在这个过程中，此质点的速度一时间图象图如乙所示，比较a b 、 两点电势a b ϕϕ和，的高低以及场强a E 和b E 的大小，正确的是 A ．,a b a b E E ϕϕ><B ．,a b a b E E ϕϕ>=C ．,a b a b E E ϕϕ>>D ．,a b a bE E ϕϕ<=3．如图所示，质量分别为m 1和m 2的两物块放在水平地面上，与水平地面间的动摩擦因数都是μ(μ≠O)，用轻弹簧将两物块连接在一起．当用水平力F 作用在m 1上时，两物块均以加速度a 做匀加速运动，此时，弹簧伸长量为x 。
2010年普通高等学校招生全国统一考试（江苏卷）数学试题分析2010年6月8日一、2010年江苏高考数学考卷解读2010年高考已经落下帷幕，本次数学试题突出数学学科特点，考查基础与考查能力并重，有创新题、题目梯度明显，区分度较高。
考生的评价集中为一个字“难”，许多题目看似简单，但要真正解决得分却很难。
运算量很大，甚至部分同学的最后两题都没来得及看。
接下来我们来具体分析试题。
1、基础题试题第1题、第2题、第3题、第4题、第5题、第6题、第7题分别考查考纲中的集合的性质与集合的运算、复数的运算、古典概型、频率直方图的运用、函数的奇偶性、双曲线的标准方程与集合性质、算法流程图，基本集中在对A、B级要求的考查。
难度与计算量均不大。
大多数考生都应该能顺利解决。
第9题主要考查直线与圆的位置关系以及点到直线的距离的计算，只要判断准确接下来的计算也不成问题。
第11题主要考查分段函数、函数的单调性以及不等式，难度虽不大，但分情况讨论对于部分函数基础较薄弱的考生稍有难度。
第15题主要考查向量，并与平时常用的解析法结合，在处理过程中需要稍加小心，容易出现计算上的失误。
第16题以四棱锥为模型，主要考查立体几何中线线、线面垂直以及多面体的体积，需要证明过程完整、理由充分，有部分考生虽然会做，但论证过程写的不够完善而导致失分。
总体看以上列举的考题考查的考点明确，难度与平时练习相当，考生的失分会较少。
2、中档题第8题、第10题、第12题主要考查导数的集合意义、数列的概念、三角函数的图像、不等式的解法与不等式的性质中比较容易的考点，只要平时的基本功扎实，解决这几个问题应该不难。
重点在与考题与平时练习题的联系。
第17题测量电视塔的高度，本题的原型在苏教版数学必修5第11页第3题，它进行了改编，并添加了初中的相似三角形、解直角三角形这些知识的运用，在此基础上，考查了解斜三角形、基本不等式的运用。
题目本身难度不大，但在这些知识点的融合中，有部分考生往往会失去方向，似乎有很多途径来解决问题，但要找到一个真正适合的方法不容易。
2010年普通高等学校招生全国统一考试江苏卷数学全解全析数学Ⅰ试题参考公式：锥体的体积公式: V 锥体=13Sh ，其中S 是锥体的底面积，h 是高。
一、填空题：本大题共14小题，每小题5分，共70分。
请把答案填写在答题卡相应的位．．．．．．．置上．．.1、设集合A={-1,1,3}，B={a+2,a 2+4},A ∩B={3}，则实数a =______▲_____.[解析] 考查集合的运算推理。
3∈B, a+2=3, a=1.2、设复数z 满足z(2-3i)=6+4i （其中i 为虚数单位），则z 的模为______▲_____.[解析] 考查复数运算、模的性质。
z(2-3i)=2(3+2 i), 2-3i 与3+2 i 的模相等，z 的模为2。
3、盒子中有大小相同的3只白球，1只黑球，若从中随机地摸出两只球，两只球颜色不同的概率是_ ▲__.[解析]考查古典概型知识。
3162p == 4、某棉纺厂为了了解一批棉花的质量，从中随机抽取了100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间[5,40]中，其频率分布直方图如图所示，则其抽样的100根中，有_▲___根在棉花纤维的长度小于20mm 。
[解析]考查频率分布直方图的知识。
100×（0.001+0.001+0.004）×5=305、设函数f(x)=x(e x +ae -x )(x ∈R)是偶函数，则实数a =_______▲_________[解析]考查函数的奇偶性的知识。
g(x)=e x +ae -x 为奇函数，由g(0)=0，得a =－1。
6、在平面直角坐标系xOy 中，双曲线112422=-y x 上一点M ，点M 的横坐标是3，则M 到双曲线右焦点的距离是___▲_______[解析]考查双曲线的定义。
422MF e d ===，d 为点M 到右准线1x =的距离，d =2，MF=4。
左晓明老师分析的话说今年的江苏省数学卷的关注度那是非同一般地高，难度也不是一般地难，以至于网络上出现了一个新的词汇“数学哥”，诸如“数学哥秒杀了江苏52万考生”“众优生走出考场痛哭流涕”之类的报道一时喧嚣尘上。
笔者也在第一时间完成了江苏高考卷，现在将自己的一点感想写出，以期抛砖引玉。
数学哥是谁？此人乃中国数学界大名鼎鼎的数学教育与奥数培训专家，南京师大的葛军副教授。
在新世纪的最初几年，我曾经在每一期的《数学通讯》的问题征解栏目上面看到他的名字，他是此栏目的主持人。
后来主持人换成了熊斌、冯志刚、田延彦等人，也都是国内数学教育界的一时翘楚。
南京师大数学系的老师们长期关注数学普及工作，从单墫、纪春岗至葛军以降，在国内初等数学教育界享有盛名。
葛军，现任江苏数学普委会主任。
这是一个很重要的职位，承担一个省的数学竞赛的组织与命题工作，一般由各省市竞赛界最德高望重的前辈担任，例如湖北就是由曾任国家队副领队的陈传理教授担任。
那么，由葛军担任命题组组长的2010年江苏数学高考卷，其中必然渗透不少新的理念，包括一些竞赛的思想。
首先来看看江苏数学卷的整体特点。
江苏卷是个很特别的试卷，其特别之处首先在于与其它省市都不一样的，它没有选择题！全卷由14道填空题、6道大题组成试题的主体部分，时长两个小时，总分160分；然后是半个小时的附加题部分，总分40分，其中包括21：选做题，给出四道，分别是几何证明、矩阵变换、坐标系与参数方程、不等式四大选修模块，任选其中两道即可；22题：概率统计问题；23题：竞赛题。
全卷总分200分。
数学考试中只出现填空题和大题的命题风格这两年逐渐开始流传开来。
从去年开始全国高中数学联赛卷就取消了选择题。
江苏卷从去年开始也没有选择题。
应该说，就数学题目的特点来说，取消选择题有助于更真实地了解学生实际水平，杜绝蒙的可能性，唯一的弊端就是稍微增加了阅卷工作量，不过这个弊端显然不值一提。
所以未来的几年可能会有越来越多的省份取消选择题。
2010年普通高等学校招生全国统一考试江苏卷数学全解全析数学Ⅰ试题参考公式：锥体的体积公式: V 锥体=13Sh ，其中S 是锥体的底面积，h 是高。
一、填空题：本大题共14小题，每小题5分，共70分。
请把答案填写在答题卡相应的位．．．．．．．置上．．.1、设集合A={-1,1,3}，B={a+2,a 2+4},A ∩B={3}，则实数a =______▲_____. [解析] 考查集合的运算推理。
3∈B, a+2=3, a=1.2、设复数z 满足z(2-3i)=6+4i （其中i 为虚数单位），则z 的模为______▲_____. [解析] 考查复数运算、模的性质。
z(2-3i)=2(3+2 i), 2-3i 与3+2 i 的模相等，z 的模为2。
3、盒子中有大小相同的3只白球，1只黑球，若从中随机地摸出两只球，两只球颜色不同的概率是_ ▲__.[解析]考查古典概型知识。
3162p ==4、某棉纺厂为了了解一批棉花的质量，从中随机抽取了100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间[5,40]中，其频率分布直方图如图所示，则其抽样的100根中，有_▲___根在棉花纤维的长度小于20mm 。
[解析]考查频率分布直方图的知识。
注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求 1.本试卷共4页，包含填空题（第1题——第14题）、解答题（第15题——第20题）。
本卷满分160分，考试时间为120分钟。
考试结束后，请将本卷和答题卡一并交回。
2.答题前，请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。
4.请在答题卡上按照晤顺序在对应的答题区域内作答，在其他位置作答一律无效。
作答必须用0.5毫米黑色墨水的签字笔。
请注意字体工整，笔迹清楚。
5.如需作图，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗。
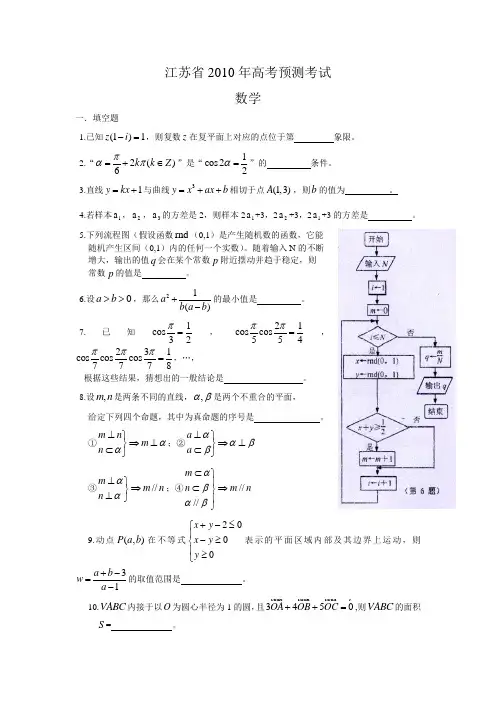
江苏省2010年高考预测考试数学一．填空题1.已知(1)1z i -=，则复数z 在复平面上对应的点位于第 象限。
2.“2()6k k Z παπ=+∈”是“1cos 22α=”的 条件。
3.直线1y kx =+与曲线3y x ax b =++相切于点(1,3)A ，则b 的值为 。
4.若样本1a ，2a ，3a 的方差是2，则样本21a +3，22a +3，21a +3的方差是 。
5.下列流程图（假设函数rnd （0,1）是产生随机数的函数，它能随机产生区间（0,1）内的任何一个实数）。
随着输入N 的不断增大，输出的值q 会在某个常数p 附近摆动并趋于稳定，则常数p 的值是 。
6.设0a b >>，那么21()a b a b +-的最小值是 。
7.已知1c o s 32π=，21cos cos 554ππ=，231cos cos cos 7778πππ=，…， 根据这些结果，猜想出的一般结论是 。
8.设,m n 是两条不同的直线，,αβ是两个不重合的平面，给定下列四个命题，其中为真命题的序号是 。
①m n m n αα⊥⎫⇒⊥⎬⊂⎭；②a a ααββ⊥⎫⇒⊥⎬⊂⎭③//m m n n αα⊥⎫⇒⎬⊥⎭；④////m n m n αβαβ⊂⎫⎪⊂⇒⎬⎪⎭9.动点(,)P a b 在不等式2000x y x y y +-≤⎧⎪-≥⎨⎪≥⎩表示的平面区域内部及其边界上运动，则31a b w a +-=-的取值范围是 。
10.ABC 内接于以O 为圆心半径为1的圆，且3450OA OB OC ++=,则ABC 的面积 S = 。
11.过双曲线22221(0,0)x y a b a b+=>>的右顶点A 作斜率-1的直线，该直线与双曲线的两条渐近线的交点分别为,B C .若12AB BC =,则双曲线的离心率是 。
12.当θ取遍所有值时，直线cos sin )4x y πθθθ⋅+⋅=+所围成的图形面积为。
2010 年普通高等学校招生全国统一考试江苏卷数学全解全析数学Ⅰ试题注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共 4 页，包含填空题（第 1 题——第14 题）、解答题（第15 题——第20 题）。
本卷满分160 分，考试时间为120 分钟。
考试结束后，请将本卷和答题卡一并交回。
2.答题前，请您务必将自己的姓名、准考证号用0.5 毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。
4.请在答题卡上按照晤顺序在对应的答题区域内作答，在其他位置作答一律无效。
作答必须用0.5毫米黑色墨水的签字笔。
请注意字体工整，笔迹清楚。
5.如需作图，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗。
6.请保持答题卡卡面清洁，不要折叠、破损。
参考公式：锥体的体积公式 : V1h 是高。
锥体= Sh，其中 S 是锥体的底面积，3一、填空题：本大题共14 小题，每小题 5 分，共 70分。
请把答案填写在答题卡相应的位．．．．．．．置上 .．．1、设集合 A={-1,1,3}，B={a+2,a 2+4},A ∩ B={3} ，则实数 a=______▲ _____.[ 解析 ] 考查集合的运算推理。
3B, a+2=3, a=1.2、设复数 z 满足 z(2-3i)=6+4i （其中 i 为虚数单位），则 z 的模为 ______ ▲_____.[ 解析 ] 考查复数运算、模的性质。
z(2-3i)=2(3+2 i), 2-3i与 3+2 i 的模相等， z 的模为 2。
3、盒子中有大小相同的 3 只白球， 1 只黑球，若从中随机地摸出两只球，两只球颜色不同的概率是 _ ▲ __.[ 解析 ] 考查古典概型知识。
p316 24、某棉纺厂为了了解一批棉花的质量，从中随机抽取了 100 根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间[5,40] 中，其频率分布直方图如图所示，则其抽样的100 根中，有 _▲ ___根在棉花纤维的长度小于20mm。
2010年普通高等学校招生全国统一考试（江苏卷）数学Ⅰ试题参考公式：锥体的体积公式：13V Sh 锥体，其中S 是锥体的底面面积，h 是高.一、填空题：本大题共14小题，每小题5分，共计70分.请把答案填写在答题卡相应位置上．．．．．．．．.1.设集合{1,1,3}A，4,22aa B ，3BA ，则实数a 的值为____▲____.1.【答案】1.【命题意图】本题考查交集的定义，对求得的集合中的元素要进行检验.【解析】由题意得1,32a a .又由342a不符合题意.经检验得1a.2.设复数z 满足(23)64z i i （i 为虚数单位），则z 的模为____▲____.2.【答案】2.【命题意图】本题考查复数有关运算及复数模的计算.【解析】由i i z 46)32(得,2)32)(32()32)(46(3246i i i i i ii z即2,2z i z.3.盒子里共有大小相同的3只白球，1只黑球.若从中随机摸出两只球，则它们颜色不同的概率是_ ▲__.3.【答案】21.【命题意图】本题考查古典概型知识.【解析】31.62p4.某棉纺厂为了解一批棉花的质量，从中随机抽测了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中，其频率分布直方图如图所示，则在抽测的100根中，有_ ▲__ 根棉花纤维的长度小于20mm.4.【答案】30.【命题意图】本题考查概率统计中频率分布直方图的有关运用,注意纵坐标是频率/组距.【解析】由频率分布直方图得棉花纤维长度小于mm 20的根数为(0.01+0.01+0.04)301005.5.设函数()()xxf x x eae (x R )是偶函数，则实数a 的值为____▲____.5.【答案】1.【命题意图】本题考查函数的奇偶性.【解析】设R xae e x g x x ,)(,由题意分析)(x g 应为奇函数(奇函数奇函数=偶函数),又R x ，0)0(g ，则,01a 所以1a .6.在平面直角坐标系xOy 中，已知双曲线221412xy上一点M 的横坐标为3，则点M 到此双曲线的右焦点的距离为____▲____. 6.【答案】4.【命题意图】本题考查求曲线上点的坐标、双曲线的焦点坐标、两点间距离公式的运用.【解析】由题意得点15,3(M ),双曲线的右焦点的坐标为(4,0)，2MF 22)015()43(=4.或用第二定义：2MF ed，2d，4MF .7.右图是一个算法流程图，则输出的S 的值是____▲____.7.【答案】63.【命题意图】本题考查算法流程图,由流程图得出S 的关系式,比较得出S 的值.【解析】由流程图得12345122222S =1+2+48+16+32=6333,即.63S 8.函数2(0)y x x的图象在点2(,)k ka a 处的切线与x 轴的交点的横坐标为1k a ，其中kN *.若116a ，则123a a a 的值是____▲____.8.【答案】21.【命题意图】考查函数的切线方程、数列的通项.【解析】在点2(,)k k a a 处的切线方程为22(),k k k y a a xa 当0y时，解得2k a x，所以1135,1641212kka a a a a .9.在平面直角坐标系xOy 中，已知圆224x y上有且只有四个点到直线1250x y c 的距离为1，则实数c 的取值范围是____▲____. 9.【答案】(13,13).【命题意图】本题考查直线与圆的位置关系.【解析】如图,圆422yx的半径为2,圆上有且仅有四个点到直线的距离为1,问题转化为原点(0,0)到直线0512cyx 的距离小于1,即1313,13,151222c c c .10.设定义在区间(0,)2上的函数y=6cosx 的图象与y=5tanx 的图象交于点P ，过点P 作x 轴的垂线，垂足为P 1，直线PP 1与函数y=sinx 的图像交于点P 2，则线段P 1P 2的长为____▲____.10.【答案】.32【命题意图】本题考查三角函数问题,由图象相交,即三角函数值相等,建立关系式,求出,32sin x结合图象,数形结合分析P 1P 2的值.xyO 0512cyx1 11【解析】由题意得x x tan 5cos 6，即x x xx xsin 5cos 6,cos sin 5cos 62，226(1sin )5sin ,6sin 5sin 60x x x x 得,32sin x结合图象分析得32sin 21P P x.11.已知函数21,0,()1,0,xx f x x则满足不等式2(1)(2)f x f x 的x 的取值范围是____▲____.11.【答案】).12,1(【命题意图】本题考查分段函数的单调性.【解析】2212,10,x x x解得121x ，所以x 的取值范围是).12,1(12.设x,y 为实数，满足3≤2xy ≤8，4≤2xy≤9，则34xy 的最大值是____▲____. 12.【答案】27.【命题意图】考查不等式的基本性质，等价转化思想.【解析】22()[16,81]xy，2111[,]83xy，322421()[2,27]xxyyxy，43yx 的最大值是27.13.在锐角△ABC 中,角A 、B 、C 的对边分别为a 、b 、c.若6cos b a C ab,则tan tan tan tan C C AB的值是▲.【答案】4.【解析】考查三角函数知识，三角形中的正、余弦定理的应用，等价转化思想.（方法一）考虑已知条件和所求结论对于角A 、B 和边a 、b 具有轮换性.当A=B 或a=b 时满足题意，此时有1cos 3C，21cos 1tan21cos 2C C C ，2tan22C .等腰三角形中，1tan tan 2tan2A BC ，tan tan tan tan C C AB=4.（方法二）226cos 6cos b a C ab Cab ab，2222222236,22a bccabab abab.2tan tan sin cos sin sin cos sin sin()1sin tan tan cos sin sin cos sin sin cos sin sin C C C B A B A C A B CABCA B C A B C A B,由正弦定理，得上式22222214113cos ()662cc cc C abab .14.将边长为1m 的正三角形薄铁皮沿一条平行于某边的直线剪成两块，其中一块是梯形，记2(s梯形的周长）梯形的面积,则s 的最小值是____▲____.【答案】3233.【解析】考查函数中的建模应用，等价转化思想.设剪成的小正三角形的边长为x ，则222(3)4(3)(01)1133(1)(1)22x x sx xx x .（方法一）利用导数求函数最小值.224(3)()13x S x x，22224(26)(1)(3)(2)()(1)3x x x x S x x 2242(31)(3)(1)3x x x 1()0,01,3S x xx.当1(0,]3x时，()0,S x 递减；当1[,1)3x 时，()0,S x 递增.故当13x时，S 取最小值3233.（方法二）利用函数的方法求最小值.令1113,(2,3),(,)32x t t t ，则2224418668331tS tttt .故当131,83xt时，S 取最小值3233.二、解答题：本大题共6小题，共计90分.请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤.15.（本小题满分14分）在平面直角坐标系xOy 中，已知点(1,2)A ，(2,3)B ，(2,1).C (1)求以线段AB 、AC 为邻边的平行四边形的两条对角线的长；(2)设实数t 满足(OC t AB)·OC =0，求t 的值.【解析】本小题主要考查平面向量的几何意义、线性运算、数量积，考查运算求解能力.满分14分.解：（1）由题设知(3,5)AB，(1,1)AC，则(2,6)A B A C ，(4,4).AB AC所以||210AB AC ，||4 2.ABAC 故所求的两条对角线长分别为42，210.（2）由题设知(2,1)OC，(32,5).ABtOCt t由()0AB tOC OC ，得(32,5)(2,1)0t t ，从而511t ，所以11.5t16.（本小题满分14分）如图，在四棱锥P-ABCD 中，PD ⊥平面ABCD ，PD=DC=BC=1，AB=2，AB ∥DC ，∠BCD=900.(1)求证：PC ⊥BC ；(2)求点A 到平面PBC 的距离.【解析】本小题主要考查直线与平面、平面与平面的位置关系，考查几何体的体积，考查空间想象能力、推理论证能力和运算能力.满分14分. 解：（1）因为PD ⊥平面ABCD ，BC 平面ABCD ，所以PD ⊥BC. 由∠BCD=900，得BC ⊥DC. 又PD DC D ，PD平面PCD ，DC平面PCD ，所以BC ⊥平面PCD.因为PC平面PCD ，所以PC ⊥BC.（2）（方法一）分别取AB 、PC 的中点E 、F ，连DE 、DF.则易证DE ∥CB ，DE ∥平面PBC ，点D 、E 到平面PBC 的距离相等. 由（1）知BC ⊥平面PCD ，所以平面PBC ⊥平面PCD.因为PD=DC ，PF=FC ，所以DF ⊥PC ，所以DF ⊥平面PBC 于F. 易知DF=22.又点A 到平面PBC 的距离等于E 到平面PBC 的距离的2倍，故点A 到平面PBC 的距离等于2.（方法二）连结AC.设点A 到平面PBC 的距离h.因为AB ∥DC ，∠BCD=900，所以∠ABC=900. 从而由AB=2，BC=1，得ABC 的面积1ABCS.由PD ⊥平面ABCD 及PD=1，得三棱锥PABC 的体积11.33ABCVSPD因为PD ⊥平面ABCD ，DC 平面ABCD ，所以PD ⊥DC.又PD=DC=1，所以222.PC PDDC由PC ⊥BC ，BC=1，得PBC 的面积2.2PBCS 由11213323PBCVShh ，得2h .因此，点A 到平面PBC 的距离为2.17.（本小题满分14分）某兴趣小组要测量电视塔AE 的高度H(单位：m).如示意图，垂直放置的标杆BC 高度h=4m ，仰角∠ABE=，∠ADE=.（1）该小组已测得一组，的值，算出了tan =1.24，tan =1.20，请据此算出H 的值；。
2010年江苏省高考数学试题预测最后一讲D234数的有界性及其辅助角公式（注意定义域，结合图像解决）；不等式一、恒成立问题――分离参数转化为最值问题。
要能识别并处理两次恒成立问题。
处理方法：（1）分离变量，然后一边构造函数求函数的值域或最值；（2）作差构造函数利用实根分布（作差后构造一个函数若是二次函数可利用实根分布，若不是可以利用求函数的最值或极值与单调性解决。
（3）变更主元（给出谁的范围就以谁作为主元）。
若不等式()A x f >在区间D 上恒成立,则等价于在区间D 上()min f x A >若不等式()B x f <在区间D 上恒成立,则等价于在区间D 上()max f x B <二．能成立问题即不等式有解问题，可以利用其命题的否定将其划归为恒成立问题即将存在性问题转化为全称性问题。
若在区间D 上存在实数x 使不等式()A x f >成立,则等价于在区间D 上()max f x A >；若在区间D 上存在实数x 使不等式()B x f <成立,则等价于在区间D 上的()min f x B <.如：若存在[1,3]a ∈，使得不等式2(2)20ax a x +-->成立，则实数x 的取值范围是 ；四、均值不等式：对于函数 ()k xf x x =+，当0k >符合对勾函数形式，但要注意“一正、二定、三相等”，特别是定义域，有时在定义域内只能是单调的；当0k <时，函数是单调的，注意常见的形式2()(,,,,)ax bx cmx n f x a b c m n +++=为常数，注意换元法的使用。
五、线性规划：注意等号（边界线的虚实），注意目标函数的最优解与x 轴或y 轴上的截距的关系，注意整数解与无穷解的问题。
第一部分 填空题5思想方法填空题解题的基本原则是“小题不能大做”。
解题的基本策略是：巧做。
解题的基本方法一般有：直接求解法，图像法和特殊化法（特殊值法，特殊函数法，特殊角法，特殊数列法，图形特殊位置法，特殊点法，特殊方程法，特殊模型法）等。
2010年江苏省高考数学试题预测最后一讲22010年江苏省高考数学试题预测集合、函数1.充要条件关键是分清条件和结论，注意从集合角度解释，若B A ⊆，则A 是B 的充分条件；若B A ⊆，则A 是B 的必要条件；若A=B ，则A 是B 的充要条件。
注意利用逆否命题的等价性判断。
2．单调性、奇偶性的定义都可以理解为恒成立问题。
注意单调区间不连续，不能写成在并集上单调。
已知函数23()log log 3f x a x b x =-+，若)20101(f ，则)2010(f 的值为 ．3、倒到序相加法在函数中的运用： 已知122()x f x +=则)2010()2009()2008()2007()2008()2009(f f f f f f +++-+-+-＝4．幂函数()f x x α=图象规律：①化为根式求定义域②第一象限五种情况③通过奇偶性作其他象限图象。
注意零指数幂的底数范围与对称性，()0f x x αα=>，抛物线型，1α>开口向上，01α<<开口向右，0α<双曲线型。
已知幂函数223()m m y x m Z --=∈的图像与x 轴、y 轴都无公共点，且关于y 轴对称，则m =5、利用导数研究函数的最值（极值、值域）、单调性；利用导数处理不等式恒成立问题（利用单调性、极值、最值求参数取值范围）；利用导数证明不等式；利用导数研究方程的根的个数（要判断极值点与x 轴的位置关系以及单调性）；因此要特别注意导数与不等式很成立问题、不等式有解问题、根的分布问题结合，经常要构造函数研究其单调性，注意定义域。
★注意熟练掌握指数函数、对数函数、分式函数、三角函数、复合函数的导数6、求函数的值域的方法：二次函数型常用配方法（注意讨论开口方向、对称轴是否属于定义域）； 一次分式型：分离系数法（然后再函数的单调性法及不等式的性质） 、数形结合（转化为动点与定点连线的斜率去解决）； 二次分式型：分离系数法（注意换元法）（再用函数的单调性如)0(＞k x y xk -=及不等式的性质，特别注意是否适合对勾函数)0(＞k x y xk +=）；无理式型常用代数换元 、三角换元法（注意新元的范围的确定）；三角函3数的有界性及其辅助角公式（注意定义域，结合图像解决）；不等式一、恒成立问题――分离参数转化为最值问题。
要能识别并处理两次恒成立问题。
处理方法：（1）分离变量，然后一边构造函数求函数的值域或最值；（2）作差构造函数利用实根分布（作差后构造一个函数若是二次函数可利用实根分布，若不是可以利用求函数的最值或极值与单调性解决。
（3）变更主元（给出谁的范围就以谁作为主元）。
若不等式()A x f >在区间D 上恒成立,则等价于在区间D 上()min f x A >若不等式()B x f <在区间D 上恒成立,则等价于在区间D 上()max f x B <二．能成立问题即不等式有解问题，可以利用其命题的否定将其划归为恒成立问题即将存在性问题转化为全称性问题。
若在区间D 上存在实数x 使不等式()A x f >成立,则等价于在区间D 上()max f x A >；若在区间D 上存在实数x 使不等式()B x f <成立,则等价于在区间D 上的()min f x B <.如：若存在[1,3]a ∈，使得不等式2(2)20ax a x +-->成立，则实数x 的取值范围是 ；四、均值不等式：对于函数 ()k xf x x =+，当0k >符合对勾函数形式，但要注意“一正、二定、三相等”，特别是定义域，有时在定义域内只能是单调的；当0k <时，函数是单调的，注意常见的形式2()(,,,,)ax bx cmx n f x a b c m n +++=为常数，注意换元法的使用。
五、线性规划：注意等号（边界线的虚实），注意目标函数的最优解与x 轴或y 轴上的截距的关系，注意整数解与无穷解的问题。
第一部分 填空题4思想方法填空题解题的基本原则是“小题不能大做”。
解题的基本策略是：巧做。
解题的基本方法一般有：直接求解法，图像法和特殊化法（特殊值法，特殊函数法，特殊角法，特殊数列法，图形特殊位置法，特殊点法，特殊方程法，特殊模型法）等。
1－8题，容易题；9－12题，中等题，13－14难题，估计难度介于08与09之间． 一、填空题：1、将圆()3122=++y x 绕直线01=--y kx 旋转一周，所得几何体的体积为 ．2、抛掷一颗骰子的点数为a ，得到函数π()sin()3a f x x =，则“)(x f y =在[0，4]上至少有5个零点”的概率是 ．3、在平面直角坐标系中，不等式组0,0,,x y x y x a +⎧⎪-⎨⎪⎩≥≥≤（a 为常数）表示的平面区域的面积是4，则y x +2的最小值为 ． 例题解析一、直接求解法——直接从题设条件出发，利用定义、性质、定理、公式等，经过变形、推理、计算、判断得到结论的，称之为直接求解法。
它是解填空题的常用的基本方法。
使用直接法解填空题，要善于透过现象抓本质，自觉地、有意识地采取灵活、简捷的解法。
【例1】已知数列{a n }、{b n }都是等差数列，a 1=0、b 1= -4，用S k 、k S '分别表示数列{a n }、{b n }的前k 项和（k 是正整数），若S k +k S '=0，则a k +b k 的值为 ；4【例2】 若θcos 1－θsin 1=1，则sin2θ的值等于 。
【解】由θcos 1-θsin 1=1得sinθ-cosθ=sinθcosθ ①令sin2θ=t ，则①式两边平方整理得t 2+4t-4=0，解之得t=22-2。
三角函数的有界性5二、图像法——借助图形的直观形，通过数形结合的方法，迅速作出判断的方法称为图像法。
文氏图、三角函数线、函数的图像及方程的曲线等，都是常用的图形。
【例3】 若关于x 的方程21x -=k(x-2)有两个不等实根，则实数k 的取值范围是【解】令y 1=21x -,y 2=k(x-2),由图可知 k AB <k≤0，其中AB 为半圆的切线，计算 k AB = -33,∴-33<k≤0。
1．函数f （x ）＝|x 2－a | 在区间［－1，1］上的最大值M （a ）的最小值是【解析】f （x ）是偶函数，所以M （a ）是在［0，1］内的最大值，当a ≤0时，f （x ）＝x 2－a ，则M （a ）＝1－a ；当a >0时，由图像可知，若12≥a ，则M （a ）＝a ，若12<a ，则M （a ）＝f（1）＝1－a ，从而M （a ）＝ 11212a a a a ⎧-⎪⎪⎨⎪>⎪⎩，≤，，M （a ）min ＝12．3．已知函数4()12f x x =-+的定义域是[],(,)a b a b Z ∈，值域是[]0,1，则满足条件的整数对(,)a b 共有_________________个【解析】()f x 在R 上是偶函数，故()f x 的图象关于y 轴对称，作出()f x 的图象，截取值域是[]0,1的一段，发现a ，b 的取值只可能在－2，－1，0，1，2中取得，但必须取0，－2﹑2必须至少取一个，故有5个．610．若关于x 的方程x ax x =-23有不同的四解，则a 的取值范围为 ．【解析】x ＝0是方程的一个根，其余根即方程12=-ax x （x ＞0）的根．由f （x ）＝ax x -2（x ＞0）与y ＝1的交点个数，可知a ＞0．且f （2a ）＞1，得a ＞2． 1．若1||x a x-+≥12对一切x ＞0恒成立，则a 的取值范围是 ．三、特殊化法——当结论唯一或其值为定值时，我们只须把题中的参变量用特殊值（或特殊函数、特殊角、特殊数列、图形特殊位置、特殊点、特殊方程、特殊模型等）代替之，即可得到结论。
1.特殊值法【例4】设a >b >1，则log a b ,log b a ,log ab b 的大小关系是 。
【解】考虑到三个数的大小关系是确定的，不妨令a=4,b=2，则log a b=21,log b a=2,log ab b=31,∴log ab b<log a b<log b a2．特殊函数法【例5】如果函数f (x )=x 2+bx +c 对任意实数t 都有f (2+t )=f (2-t )，那么f (1)，f (2)，f (4)的大小关系是 。
【解】由于f(2+t)=f(2-t)，故知f(x)的对称轴是x=2。
可取特殊函数f(x)=(x-2)2,即可求得f(1)=1,f(2)=0,f(4)=4。
∴f(2)<f(1)<f(4)。
3．特殊角法【例6】 cos 2α+cos 2(α+120°)+cos 2(α+240°)的值为 。
【解】隐含条件是式子的值为定值，即与α无关，故可令α=0°，计算得上式值为23。
4．特殊数列法【例7】已知等差数列{a n }的公差d≠0，且a 1,a 3,a 9成等比数列，则1042931a a a a a a ++++的值是7y AOxB C 【解】考虑到a 1,a 3,a 9的下标成等比数列，故可令a n =n 满足题设条件，于是1042931a a a a a a ++++=1613。
5．特殊点法【例8】椭圆92x +42y =1的焦点为F 1、F 2，点P 为其上的动点，当∠F 1PF 2为钝角时，点P 横坐标的取值范围是 。
【解】设P(x,y)，则当∠F 1PF 2=90°时，点P 的轨迹方程为x 2+y 2=5，由此可得点P 的横坐标x=±53，又当点P 在x 轴上时，∠F 1PF 2=0；点P 在y 轴上时，∠F 1PF 2为钝角，由此可得点P 横坐标的取值范围是-53<x<53。
7．特殊模型法【例9】 已知m,n 是直线，α、β、γ是平面，给出下列是命题： ①若α⊥γ，β⊥γ，则α∥β；②若n ⊥α，n ⊥β，则α∥β； ③若α内不共线的三点到β的距离都相等，则α∥β； ④若n α，m α且n ∥β,m ∥β，则α∥β；⑤若m,n 为异面直线，n ∈α，n ∥β，m ∈β,m ∥α, 则α∥β；则其中正确的命题是 。
（把你认为正确的命题序号都填上）。
【解】依题意可构造正方体AC 1，在正方体中逐一判断各命题易得正确命题的是②⑤。
8、特殊位置或坐标法2．如图，非零向量,OA OB u u u r u u u r与x 轴正半轴的夹角分别为6π和23π，且0OA OB OC ++=u u u r u u u r u u u r r ，则OC u u u r 与x 轴正半轴 的夹角的取值范围是【解析】OC u u u r 与x 轴正半轴的夹角的取值范围应在向量,OA OB--u u u r u u u r与x 轴正半轴的夹角之间，故OC u u u r与x 轴正半轴的夹角的取值范围8PC AB QP MNCABQ是5(,)36ππ．9．△ABC 内接于以O 为圆心的圆，且3450OA OB OC +-=u u u r u u u r u u u r r．则C ∠ ＝ ．【解析】通过画图，可求AOB ∠，即OA u u u r 与OB u u u r的夹角，再通过圆心角与圆周角的关系，求得135C ∠=o．4．三角形ABC 中AP 为BC 边上的中线，3=AB ，2-=⋅，AC＝【解析】22PCBP=，即22)()(AC PA AP BA =+，5222=⋅+=，=AC 5．12．如图，在ΔABC 中，|AB|=3，|AC|=1，l 为BC 的垂直平分线，E 为l 上异于D 的一点，则⋅AE (AB-AC )u u r u u r u u r等于____．【解析】⊥∴⋅DE BC BC DE =0u u r u u r Q ，又AE =AD+DE u u r u u u r u u r，∴⋅⋅⋅AE(AB-AC )=(AD+DE )CB =AD CBu u u r u u r u u r u u u r u u r u u u r u u u r u u r ⋅22111=(AB+AC )(AB-AC )=(AB -AC )=(9-1)=4222u u r u u r u u r u u r u u r u u r ． 5．如图1，设P 、Q 为△ABC 内的两点，且2155AP AB AC =+u u u r u u u r u u u r ，AQ uuu r ＝23AB u u u r ＋14AC u u ur ，则△ABP 的面积与△ABQ 的面积之比为DABCE9【解析】如图2，设25AM AB =u u u u r u u u r ，15AN AC =u u u r u u u r，则AP AM AN =+u u u r u u u u r u u u r ．由平行四边形法则，知NP ∥AB ，所以ABP AN ABC AC ∆=∆u u u ru u ur ＝15，同理可得14ABQ ABC ∆=∆．故45ABP ABQ ∆=∆， 四、构造法——在解题时有时需要根据题目的具体情况，通过对对与结论的分析，构造适当的辅助量来转换命题，设计新的模式解题，或直接构造结论所述的数学对象，从而使问题得到解决。
