奥数知识点图形计数

四年级奥数第⼆讲图形的计数问题含答案第⼆讲图形的计数问题⼀、知识点：⼏何图形计数问题往往没有显⽽易见的顺序，⽽且要数的对象通常是重叠交错的，要准确计数就需要⼀些智慧了．实际上，图形计数问题，通常采⽤⼀种简单原始的计数⽅法－⼀枚举法．具体⽽⾔，它是指把所要计数的对象⼀⼀列举出来，以保证枚举时⽆⼀重复、．⽆⼀遗漏，然后计算其总和．正确地解答较复杂的图形个数问题，有助于培养同学们思维的有序性和良好的学习习惯．⼆、典例剖析：例（1）数出右图中总共有多少个⾓分析：在∠AOB内有三条⾓分线OC1、OC2、OC3，∠AOB被这三条⾓分线分成4个基本⾓，那么∠AOB内总共有多少个⾓呢？⾸先有这4个基本⾓，其次是包含有2个基本⾓组成的⾓有3个（即∠AOC2、∠C1OC3、∠C2OB），然后是包含有3个基本⾓组成的⾓有2个（即∠AOC3、∠C1OB），最后是包含有4个基本⾓组成的⾓有1个（即∠AOB），所以∠AOB内总共有⾓：4＋3＋2＋1＝10（个）解：4＋3＋2＋1＝10（个）答：图中总共有10个⾓。

练⼀练：数⼀数右图中总共有多少个⾓？答案: 总共有⾓：10+9+8+…+4+3+2+1=55（个）例（2 ）数⼀数共有多少条线段？共有多少个三⾓形？分析：①要数多少条线段：先看线段AB、AD、AE、AF、AC、上各有2个分点，各分成3条基本线段，再看BC、MN、GH这3条线段上各有3个分点，各分成4条基本线段.所以图中总共有线段是：（3+2+1）×5+（4+3+2+1）×3=30+30=60（条）.②要数有多少个三⾓形，先看在△AGH中，在GH上有3个分点，分成基本⼩三⾓形有4个.所以在△AGH中共有三⾓形4+3+2+1=10（个）.在△AMN与△ABC中，三⾓形有同样的个数，所以在△ABC中三⾓形个数总共：（4+3+2+1）×3=10×3=30（个）解：：①在△ABC中共有线段是：（3+2+1）×5+（4+3+2+1）×3=30+30=60（条）②在△ABC中共有三⾓形是：（4+3+2+1）×3=10×3=30（个）答：在△ABC中共有线段60条，共有三⾓形30个。

千里之行，始于足下。

图形的计数【奥数拓展】
【例1】
下面的图形有多少个？你会数吗？
【例2】
你能按照这个侧面图算算砌好这面墙一共需要多少块砖吗？
【例3】
数一数，下面的方块各有多少？
如图所示为一堆转，中央最高一摞是10块，它的左右两边各是9块，再往两边是8块、7块、6块、5块、4块、3块、2块、1块。

问：这堆砖共有多少块？
第 1 页/共 3 页
朽木易折，金石可镂。

【例4】
下面这堆木方块共有多少块？(中间画阴影的部分从上到下是空心)
这堆木方块共有多少块？(中间画阴影的部分从上到下是空心)
【例5】
用10个小正方体摆成一个“工”字形(如下图)，然后又将表面涂成粉色(下面也被涂色)，最后又把小正方体分开，数一数；
⑴3面涂成粉色的小正方体有( )个。

⑵4面涂成粉色的小正方体有( )个。

⑶5面涂成粉色的小正方体有( )个。

千里之行，始于足下。

将8个小立方块组成“丁”字型，再将表面都涂成粉色，然后再把小立方块分开。

⑴3面被涂成粉色的小立方块有( )个。

⑵4面被涂成粉色的小立方块有( )个。

⑶5面被涂成粉色的小立方块有( )个。

第 3 页/共 3 页。

巧数图形例1、数出下图中共有多少条线段。

分析与解：对于基础图形，用最小线段为单位，按序递增。

单拼： 3（段），双拼： 2（段），三拼： 1（段）通过以上的计数方法可以发现：开小火车的方式解决。

最小线段（基础线段）的数量为火车头火车头为基础线段数 3 段： 3+2+1=6（段）或者，线段个数 =基础线段数×端点÷ 2（高阶）基础线段要求：手拉手，肩并肩对于相交的线段，分别计算各个方向，然后加总例2、数出下页左上图中锐角的个数。

分析与解：对于基础图形，可以使用开小火车的方式解决。

最小线段的数量为火车头。

或者，角的个数 =最小角个数×（最小角个数 +1）÷ 2又，角的个数 =射线的个数×（射线个数 -1 ）÷ 2例3、下列各图形中，三角形的个数各是多少？分析与解：对于基础图形，可以使用开小火车的方式解决，最小线段的数量为火车头。

所以，三角形个数 =底边线段个数 ( 每个底边基础线段构成一个基础三角形 )或者，三角形的个数 =最小三角形个数×（最小三角形个数 +1）÷ 2（高阶）以上的内容基本是单层规整图形：数线段（数角，数三角形），解决方法：开小火车！对于多层规整的图形，应该以单层规整图形为基础，运用技术，算出多层规整图形的数量。

例 4、下列图形中各有多少个三角形？分析与解：方法（ 1）使用分层计数法：图（ 1）图（ 2）上层：4+3+2+1=10（个）上层：4+3+2+1=10（个）下层：0（个）中层：0（个）上下层： 4+3+2+1=10（个）下层：0（个）上中层：4+3+2+1=10（个）中下层：0（个）上中下层：4+3+2+1=10总数： 10+0+10=20（个）总数：10+10+10=30（个）方法（ 2）公式法：第一层三角形的总数×层数公式法：第一层三角形的总数×层数图（ 1）图（ 2）第一层：4+3+2+1=10（个）第一层：4+3+2+1=10（个）层数：2（层）层数：3（层）总数：10× 2=20（个）总数：10×3=30（个）例 5、下列图形中各有多少个三角形？分层法：上层： 4+3+2+1=10（个）下层：4（个）（吹泡泡法）上下层：4+3+2+1=10（个）总数： 10+4+10=24（个）小 TIPS：吹泡泡法例 6、右图中有多少个三角形？例7、右图中有多少个三角形？分析与解：对于不规则的图形，数之前，先将每个图形编号，编好后，先数单拼三角形 1、4、3 号，共 3 个。

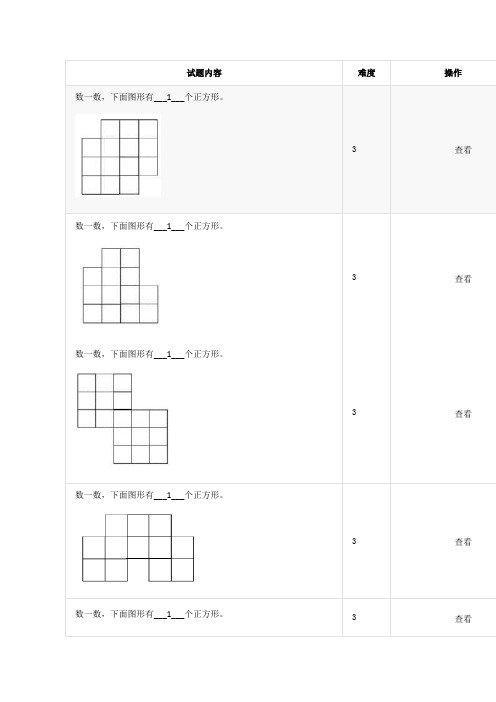
数一数，下面图形有___1___个正方形。

查看数一数，下面图形有___1___个正方形。

查看数一数，下面图形有___1___个正方形。

查看数一数，下面图形有___1___个正方形。

查看
查看
数一数，下面图形有___1___个正方形。

查看数一数，下面图形有___1___个正方形。

查看
查看
数一数，下面图形有___1___个正方形。

查看
数一数，下面图形有___1___个正方形。

查看
查看
数一数，下面图形有___1___个正方形。

查看数一数，下面图形有___1___个正方形。

查看数一数，下面图形有___1___个正方形。

查看
查看
数一数，下面图形有___1___个正方形。

数一数，下面图形有___1___个正方形。

数一数，下面图形有___1___个正方形。

数一数，下面图形有___1___个正方形。

数一数，下面图形有___1___个正方形。

数一数，下面图形有___1___个正方形。

数一数，下面图形有___1___个正方形。

数一数，下面图形有___1___个正方形。

数一数，下面图形有___1___个正方形。

数一数，下面图形有___1___个正方形。

数一数，下面图形有___1___个正方形。

第1步数一数，下面图形有___1___个三角形。

一个三角形：4个二个三角形组合：2个三个三角形组合：2个4+2+2=8（个）故答案为：8第1步数一数，下面图形有___1___个三角形。

一个三角形：4个二个三角形组合：4个4+4=8（个）故答案为：8第1步数一数，下面图形有___1___个三角形。

一个三角形：5个二个组合三角形：6个三个组合三角形：2个四个组合三角形：1个5+6+2+1=14（个）故答案为：14数一数，下面图形有___1___个三角形。

一个三角形：12个二个三角形组合：2个三个三角形组合：2个四个三角形组合：2个五个三角形组合：2个六个三角形组合：2个十二个三角形组合：1个12+2×5+1=23（个）故答案为：23第1步数一数，下面图形有___1___个三角形。

红线上方的有10个添加红线下方的三角形增加了5个三角形共10+5=15（个）故答案为：15数一数，下面图形有___1___个三角形。

第1步一个三角形：8个二个三角形组合：4个四个三角形组合：4个8+4+4=16（个）故答案为：16一个三角形：4个二个三角形组合：6个三个三角形组合：3个四个三角形组合：3个所有三角形组合：1个4+6+3+3+1=17（个）故答案为：17数一数，下面图形有___1___个三角形。

第1步一个三角形：8个二个三角形组合：8个四个三角形组合：2个8+8+2=18（个）故答案为：18数一数，下面图形有___1___个三角形。

第1步1、大三角：4个2、三角形与直线形成的三角形：5个3、大三角型之间形成的三角形：3个4+5+3=12（个）故答案为：12数一数，下面图形有___1___个三角形。

第1步三角形分别有：①、②、④、⑤、①+③+④、②+③+⑤、③+④+⑤共7个故答案为：7第1步一个三角形：9个二个三角形组合：6个三个三角形组合：4个六个三角形组合：2个共9+6+4+2=21（个）故答案为：21第1步数一数，下面图形有___1___个三角形。

一、图形计数
要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数，从中发现规律，以便得到正确的结果。

要正确数出图形的个数，关键是要从基本图形入手。

首先要弄清图形中包含的基本图形是什么，有多少个，然后再数出由基本图形组成的新的图形，并求出它们的和。

例1、数出下图中有多少条线段？
巩固、数出下图中有几个长方形？
例2、数出图中有几个角？
D A B
C O
D C
B
A
巩固、数出图中有几个角？
例3、数出下图中共有多少个三角形？
巩固、数出图中共有多少个三角形？
例4、数出下图中有多少个长方形？
O C B A
P
C B A K G I H G F E A
D C B A
巩固、数出下图中有多少个正方形？
课后练习：
1、数出下图中有多少条线段？
2、数出图中有几个角？
E
A B C D E D
O
C B A
3、数出图中共有多少个三角形？
4、数出下图中有多少个长方形？
A
B A D
C B A。

下图中共有___1___个长方形.第1步中有长方形(4+3+2+1)×(3+2+1)=60(个)，中有长方形(2+1)×(5+4+3+2+1)=45(个)，重叠部分中有长方形(2+1)×(3+2+1)=18(个).所以共有长方形60+45-18=87(个).下图中共有___1___个长方形.中有长方形(3+2+1)×(4+3+2+1)=60(个)，中有长方形(6+5+4+3+2+1)×(2+1)=6 3(个)，重叠部分中有长方形(3+2+1)×(2+1)=18(个).所以共有长方形60+63-18=105(个).数一数，下面图形有___1___个长方形。

1、此长方形含有：6个长方形2、此长方形含有：3个长方形3、组合后增加：2个长方形长方形：6+3+2=11(个)故答案为：111、此长方形含有：10个长方2、此长方形含有：1个长方形3、组合后增加：1个长方形长方形：10+1+1=12(个)故答案为：12数一数，下面图形有___1___个长方形。

1、此长方形含有：10个长方形2、此长方形含有：1个长方形3、组合后增加：1个长方形长方形：10+1+1=12(个)故答案为：12数一数，下面图形有___1___个长方形。

1、中间长方形含有：9个长方形2、上下两个长方形含有：2个长方3、组合后没有增加长方形长方形：9+2=11(个)故答案为：11数一数，下面图形有___1___个长方形。

1、此长方形含有：15个长方形2、此长方形含有：6个长方形3、组合后增加：3个长方形长方形：15+6+3=24(个)故答案为：24数一数，下面图形有___1___个长方形。

1、此长方形含有：15个长方形2、此长方形含有：6个长方形3、组合后增加：6个长方形长方形：15+6+6=27(个)故答案为：27数一数，下面图形有___1___个长方形。

1、此长方形含有：6个长方形2、此长方形含有：1个长方形3、增加这条线：2个4、将小长方形加上去增加：2个6+1+2+2=11(个)故答案为：111、此长方形含有：9个长方形2、此长方形含有：1个长方形增加这个长方形：3个4、将小长方形加上去增加：2个9+1+3+2=15(个)故答案为：15数一数，下面图形有___1___个长方形。

下图是由小正方形组成的大长方形，下图中共有___1___个正方形.这是一个6×3的大长方形，所以正方形有6×3+5×2+4×1=32(个).下图是由小正方形组成的大长方形，下图中共有___1___个正方形.这是一个5×4的大长方形，所以正方形有5×4+4×3+3×2+2×1=40(个).数一数，下面图形有___1___个正方形。

题中3×3的正方形，正方形共有3×3+2×2+1×1=14个题中还有右上角的小正方形，共有14+1=15个正方形故答案为：15数一数，下面图形有___1___个正方形。

题中图分成4×4的正方形加1个小正方形在4×4正方形中，1×1的正方形有4×4=16个，2×2的正方形有3×3=9个，3×3的正方形有2×2=4个，4×4的正方形有1个，总共有（16+9+4+1）+1=31个故答案为：31数一数，下面图形有___1___个正方形。

题中图拆为3×3的正方形加2个小正方形，3×3的正方形中有3×3+2×2+1×1=14个正方形，总共有14+2=16个正方形故答案为：16数一数，下面图形有___1___个正方形。

数一数，下面图形有___1___个正方形。

题中图拆为4×4的正方形和左右2个小正方形，4×4的正方形有4×4+3×3+2×2+1×1=30个，总共有30+2=32个正方形故答案为：32数一数，下面图形有___1___个正方形。

题中图拆为5×5的正方形和1个小正方形，5×5的正方形共有5×5+4×4+3×3+2×2+1×1=55个，总共有55+1=56个正方形故答案为：56数一数，下面图形有___1___个正方形。

第八讲三角形、平行四边形和梯形(图形计数)[知识概述]几何图形计数问题往往没有显而易见的顺序，而且要数的对象通常是重叠交错的,因而，要准确计数就需要些智慧了。

实际上，图形计数问题，通常采用一种简单原始的计数方法一枚举法。

具体而言，它是指把所有要计数的对象一一列举出来，以保证列举时不重复、无遗漏，然后计算其总和,正确地解答较复杂的图形个数问题，有助于培养思维的有序性和良好的学习习惯。

例题精学例1A数一数，下图中有多少条线段?[思路分析]同学们可能会凭直觉脱口而出认为图上有4条线段，分别是AB,BC,CD和DE，其实不然，这4条我们称之为最基本的线段，每几条相邻的基本线段还可以组成新的线段，如AB,BC可以组成线段AC,要想得到正确的结果,必须有次序，有条理地数。

方法一:以线段左端点为起点，分类数的方法。

以A点为左端点的线段有:AB,AC,AD,AE,4条;以B点为左端点的线段有:BC,BD,BE,3条;以C点为左端点的线段有:CD,CE,2条;以D点为左端点的线段有:DE,1条。

所以图中共有线段:4+3+2+1=10(条)。

方法二:把图中线段AB,BC,CD,DE看成基本线段。

由一条基本线段组成的线段有:AB,BC,CD,DE,4条;由两条基本线段组成的线段有:AC,BD,CE,3条;由三条基本线段组成的线段有:AD,BE,2条;由四条基本线段组成的线段有:AE,1条。

图中一共有10条线段:4+3+2+1=10(条)。

同步精练数一数，图中各有几条线段。

一共有()条线段。

一共有()条线段。

一共有()条线段。

例2、数一数.图中有多少个角?[思路分析] 我们可以用数线段的方法类推出数角的方法。

以OA为一边的角有:∠AOB,∠BOC,∠COD和∠DOE,把它们看作基本角:由一个基本角组成的角有:∠AOB, ∠BOC,∠COD和∠DOE4个;由二个基本角组成的角有:∠AOC,∠BOD和∠COE,3个;由三个基本角组成的角有:∠AOD,∠BOE,2个;由四个基本角组成的角有:∠AOE,1个。

小学奥林匹克数学第一集：第五讲：图形的计数一、数一数小朋友，你知道中有多少个三角形吗？我们可以这样想，图中的小三角形一共有4个，大三角形有1个，所以一共有5个三角形。

在数数时，要做到有次序，有条理，不遗漏也不重复，这样才能正确地数数。

例1：数一数下图各有几条线段？分析：我们可以照下面的方法数：解：共有线段4+3+2+1=10（条）例2：图中有多少个小正方体？分析：这个图形是由小正方体组成的。

可以采用数数的方法，按顺序数。

也可以根据图形的组成规律进行计算，如果每2个一摞，一共有4摞。

解：方法一：一个一个地数出8个正方体。

方法二：2×4=8（个）答：共有8个小正方体。

例3：将9个小正方体组成如图所示的“十”字形，再将表面涂成红色，然后将小正方体分开。

问（1）2面涂成红色的有几个？（2）4面涂成红色的有几个？（3）5面涂成红色的有几个？分析：整个图形表面涂成红色。

只有“粘在一起的”面没有涂色。

中间的一个小正方体2面涂色，四端的4个小正方体都是5面涂色，剩下的四个小正方体都是4面涂色。

解：（1）2面涂成红色的小正方体只有1个。

（2）4面涂成红色的小正方体有4个。

（3）5面涂成红色的小正方体有4个。

例4：亮亮从1写到100，他一共写了多少数字“1”？分析：在1到100这100个数中，“1”可能出现在个位、十位或百位上。

应分三种情况计数：“1”在个位上的数有：1、11、21、31、41、51、61、71、81、91共10个；“1”在十位上的数有：10、11、12、13、14、15、16、17、18、19共10个；“1”在百位上的数有：100 只有1个。

解：10+10+1=21（个）答：共写21个。

例5：27个小方块堆成一个正方体。

如果将表面涂成黄色，求：（1）3面涂成黄色的小方块有几块？（2）1面涂成黄色的小方块有几块？（3）2面涂成黄色的小方块有几块？分析：涂色的有26个小方块。

3面涂色的只有顶点上的8个小方块；1面涂色的只有六个面上中间的小方块；其余的必然是2面涂色的小方块。

下图中共有___1___个长方形.长方向线段数有4+3+2+1=10(条)，宽方向线段数有3+2+1=6(条)，所以长方形有10×6=60(个).下图中共有___1___个长方形.长方向线段数有5+4+3+2+1=15(条)，宽方向线段数有4+3+2+1=10(条)，所以长方形有15×10=150(个).数一数，下面图形有___1___个长方形。

横轴上：1+2+3=6条线段纵轴上：1+2=3条线段长方形有：6×3=18（个）故答案为：18数一数，下面图形有___1___个长方形。

横轴上：1+2+3=6条线段纵轴上：1+2+3=6条线段长方形有：6×6=36（个）故答案为：36横轴上：1+2+3+4=10条线段纵轴上：1+2=3条线段长方形有：10×3=30（个）故答案为：30数一数，下面图形有___1___个长方形。

横轴上：1+2+3+4+5=15条线段纵轴上：1+2=3条线段长方形有：15×3=45（个）故答案为：45数一数，下面图形有___1___个长方形。

横轴上：1+2+3+4+5=15条线段纵轴上：1+2=3条线段长方形有：15×3=45（个）故答案为：45数一数，下面图形有___1___个长方形。

横轴上：1+2+3=6条线段纵轴上：1+2+3+4+5=15条线段长方形有：6×15=90（个）故答案为：90横轴上：1+2+3+4=10条线段纵轴上：1+2+3+4+5=15条线段长方形有：10×15=150（个）故答案为：150数一数，下面图形有___1___个长方形。

横轴上：1+2+3+4+5=15条线段纵轴上：1+2+3+4+5=15条线段长方形有：15×15=225（个）故答案为：225数一数，下面图形有___1___个长方形。

横轴上：1+2+3+4+5+6=21条线段纵轴上：1+2+3+4=10条线段长方形有：21×10=210（个）故答案为：210数一数，下面图形有___1___个长方形。

小学四年级数学奥数第17讲数数图形一、知识要点我们已经认识了线段、角、三角形、长方形等基本图形，当这些图形重重叠叠地交错在一起时就构成了复杂的几何图形。

要想准确地计数这类图形中所包含的某一种基本图形的个数，就需要仔细地观察，灵活地运用有关的知识和思考方法，掌握数图形的规律，才能获得正确的结果。

要准确、迅速地计数图形必须注意以下几点：1.线段上有n个端点，那么线段的条数为n+(n-1)+(n-2)+…+3+2+12.从一个顶点引n条射线，那么锐角的个数为n+(n-1)+(n-2)+…+3+2+13. 由相同的n×n个小方格组成的几行几列的正方形其中所含的正方形总数为：1×1＋2×2＋…＋n×n。

4. 如果一个长方形的长被分成m等份，宽被分成n等份（长和宽的每一份都是相等的）那么正方形的总数为：mn+(m－1)(n－1)＋(m－2)(n－2)＋…＋(m－n＋1)n.二、精讲精练【例题1】数出下面图中有多少条线段。

练习1：数出下列图中有多少条线段。

（2）【例题2】数一数下图中有多少个锐角。

练习2：：下列各图中各有多少个锐角？【例题3】数一数下图中共有多少个三角形。

练习3：：数一数下面图中各有多少个三角形。

【例题4】数一数下图中共有多少个三角形。

练习4：：数一数下面各图中各有多少个三角形。

【例题5】数一数下图中有多少个长方形。

练习5：：数一数下面各图中分别有多少个长方形。

【例题6】数一数下图中有多少个长方形？练习6：数一数，下面各图中分别有几个长方形？【例题7】数一数，下图中有多少个正方形？（每个小方格是边长为1的正方形）练习7：：数一数下列各图中分别有多少个正方形？（每个小方格为边长是1的小正方形）【例题8】数一数下图中有多少个正方形？（其中每个小方格都是边长为1个长度单位的正方形）练习8：数一数下列各图中分别有多少个正方形。

【例题9】从广州到北京的某次快车中途要停靠8个大站，铁路局要为这次快车准备多少种不同车的车票？这些车票中有多少种不同的票价？练习9：1.从上海到武汉的航运线上，有9个停靠码头，航运公司要为这段航运线准备多少种不同的船票？2.从上海至青岛的某次直快列车，中途要停靠6个大站，这次列车有几种不同票价？3.从成都到南京的快车，中途要停靠9个站，有几种不同的票价？【例题10】求下列图中线段长度的总和。

图形的计数课kè前qián 活huó动dòng虎hǔ大dà王wáng 捉zhuō鼠shǔ大dà森sēn 林lín 里lǐ的de 老lǎo 鼠shǔ们men 正zhèng 在zài 搬bān 家jiā呢ne ！不bú幸xìng 的de 是shì被bèi 森sēn 林lín 里lǐ的de 老虎lǎohǔ撞见zhuàngjiàn 了le ，老虎lǎohǔ这zhè回huí是shì大展dàzhǎn 拳脚quánjiǎo 呀ya ！一会yīhuì就jiù抓zhuā了le 好hǎo 多duō只zhī老lǎo 鼠shǔ，高gāo 高gāo 兴xìng 兴xìng 的de 回huí到dào 了le 虎hǔ穴xué里lǐ，可kě是shì抓zhuā的de 老lǎo 鼠shǔ太tài 多duō了le ，虎hǔ大dà王wáng 数shù不bù清qīng 楚chǔ到dào 底dǐ有yǒu 几jǐ只zhī？就jiù找zhǎo 来lái 聪cōng 明míng 伶líng 俐lì的de 小xiǎo 青qīng 蛇shé给gěi 它tā数shù数shù，他tā则zé舒shū舒shū服fú服fú地dì躺tǎng 在zài 床chuáng 上shàng 吃chī方fāng 糕gāo 。

小xiǎo 青qīng 蛇shé认rèn 认rèn 真zhēn 真zhēn 地dì数shù了le 半bàn 天tiān ，然rán 后hòu 恭gōng 恭gōng 敬jìng 敬jìng 地dì说shuō：“尊zūn 敬jìng 的de 大dà王wáng ，您nín 只zhǐ需xū数shù一yí下xià你nǐ眼yǎn 前qián 的de 方fāng 糕gāo 就jiù知zhī道dào 您nín 一yí共gòng 抓zhuā了le 多duō少shǎo 只zhī老lǎo 鼠shǔ了le ！”虎hǔ大dà王wáng 忙máng 说shuō：“这zhè些xiē方fāng 糕gāo 有yǒu 多duō少shǎo 块kuài ？我wǒ懒lǎn 得de 数shù了le 。

航创四年级竞赛班图形计数专题一、知识点：几何图形计数问题往往没有显而易见的顺序，而且要数的对象通常是重叠交错的，要准确计数就需要一些智慧了．实际上，图形计数问题，通常采用一种简单原始的计数方法－一枚举法．具体而言，它是指把所要计数的对象一一列举出来，以保证枚举时无一重复、．无一遗漏，然后计算其总和．正确地解答较复杂的图形个数问题，有助于培养同学们思维的有序性和良好的学习习惯．二、典例剖析：例（1）数出右图中总共有多少个角练一练：数一数右图中总共有多少个角？例（2 ）数一数共有多少条线段？共有多少个三角形？练一练：共有多少个三角形？例（3）数一数图中长方形的个数练一练： 数一数图中长方形的个数例（4）数一数图中有多少个正方形（其中每个小方格都是边长为1个长度单位的正方形）.练一练：下图共有几个正方形?例（5）数一数图中三角形的个数练一练：数一数图中三角形的个数例（6）数一数图中一共有多少个三角形？练一练：数一数图中一共有多模拟测试（ 2 ）一、填空题（每小题5分）1、.下列图形各有几条线段( )条 ( )条 ( )条2、一条直线上共有50个点,可以数出( )条线段.3、数一数下图共有( )条线段.( )条. ( )条.4、下图中各有（ ）个三角形.5、数一数下图有（ ）个长方形.6、右图一共有( )个长方形?7、右图一共有( )个正方形？8、下图共有( )个平行四边形.9、一共有( )个梯形.10、下图共有( )个三角形.二、简答题(每小题10分)1、右图的图形中一共有多少个三角形?2、下图共有几个正方形?3、下图共有多少个长方形?4、下图中一共有多少个三角形?5、下图共有几个三角形?.6. 下图中有几个长方形？7.下图中有几个含星号的三角形或者长方形？模拟测试（ 2 ）解答一、填空题1、a有10条, b有15条, c有21条.2、50⨯49÷2=1225(条).3、36; 27.4. 33;5、30个.图中AB边上共有线段4+3+2+1=10条.BC边上共有线段: 2+1=3(条),把AB 上的每一条线段作为长, BC边上每一条线段作为宽,每一个长配一个宽,就组成一个长方形,所以图中共有长方形为:(4+3+2+1)⨯(2+1)=10⨯3=30(个).6、一共有64个.7、一共有18个.解:分三类计算,边长是1的正方形有2+4=13(个),边长为2的正方形有4(个),边长为3 的正方形有1个.因此,图中共有正方形13+4+1=18(个).8、315个=7(=÷⨯÷⨯(个)⨯⨯)215315621)26(59、45个最好的办法是先数出长方形和梯形的总数,再减去长方形的个数.长方形和梯形的总数为:(1+2+3+4+5+6)×(1+2)=63(个)长方形的个数为:(1+2+3)×(1+2)=18(个)梯形的总数为:63-18=45(个)10、 126个Ⅰ.尖朝上的三角形有五种:=8+7+6+5+4=30(1)W①上=7+6+5+4=22(2)W②上(3)W=6+5+4=15③上(4)W=5+4=9④上(5)W=4⑤上∴尖朝上的三角形共有:30+22+15+9+4=80(个)Ⅱ.尖朝下的三角形有四种:(1) W=3+4+5+6+7=25①下=2+3+4+5=14(2)W②下=1+2+3=6(3)W③下=1(4)W④下尖朝下的三角形共有25+14+6+1=46(个)∴80+46=126个.二、简答题1、解：①单个三角形有6个.②两个图形组成的有4个.③三个图形组成的有1个.④四个图形组成的有2个.⑤八个图形组成的有1个.答：一共有: 6+4+1+2+1=14个.2、解：一共有正方形52+42+32+22+12=25+16+9+4+1=55(个).答：一共有正方形55个。