根据二维图画三维图的方法及思路

计算机应用专业《三维图象处理》课程标准一、前言(一)课程定位本课程是全国中等职业学校计算机专业的专业基础课。

本课程的任务是使学生通过本课程的学习使学生掌握使用 3ds max 三维制作软件，实现三维模型与场景制作，毕业后可从事三维产品设计与制作、影视后期三维制作、城市规划、房地产公司、企事业单位的设计部门从事三维建模师、灯光渲染师、设计师等多个工作岗位。

(二)设计思路本课程的设计思路是结合理论与实践、兼顾技术与艺术，培养学生实际操作能力，使学生加深理解，使学生了解与掌握 3ds Max 理论知识；掌握三维模型、场景制作的技术技能；艺术原则与实际操作的方法与技巧，目标在于培养学生从事专业三维项目的模型制作、场景制作、影视后期等方面工作的基本职业能力。

本课程是一门以实际操作为主的课程，在教学过程中注重学生实际操作技能的培养，采用课题教学设计不同的活动，以理论知识与实际操作相结合的结构来展示教学内容。

每一个任务的学习都以任务为载体，以任务为中心整合所需相关知识，实现学中做，做中学的理实一体的教学，给学生提供更多的动手机会，提高基本技能。

本课程总学时为 102 课时。

学时分配方案建议见课程内容和要求表。

二、课程教学目标(一) 知识教学目标1．了解 3ds max 的操作页面。

2．掌握各种绘图工具与操作命令。

3．掌握创建二维图形的操作方法。

4．掌握三维图形的制作方法。

5．掌握三维动画的制作方法。

(二) 技能/能力培养目标1.熟练 3ds max 软件基础操作技能。

2.熟练操作 3ds max 制作三维模型与场景。

3.熟练操作 3ds max 制作模型材质、贴图。

4.熟练操作 3ds max 制作场景光影效果。

5.熟练使用 3ds max 渲染模型和场景效果图。

6.能够根据要求制作出用户满意的各类模型作品。

(三)情感态度培养目标1.热爱三维设计制作，对待工作精益求精，具有吃苦耐劳的精神。

2.具有较好的团队合作精神，严于律已，宽以待人，善于交流沟通。

2011年04月科教纵横浅谈平面设计中二维图形的三维效果文/陈辉摘 要：平面设计中对二维图形的审视不仅仅满足于纯平面的欣赏，更要追寻视觉上三维效果的视觉表现形式。

二维图形三维效果的介入使这种探寻成为可能，它为平面设计带来了新的思路与活力。

关键词：平面设计；图形；二维；三维中图分类号：TB47 文献标识码：A 文章编号：1006-4117（2011）04-0187-01一、二维与三维1、二维的定义在一个平面上的内容就是二维。

二维即左右、上下两个方向，不存在前后。

在一张纸上的内容就可以看做成是二维。

即只有面积，没有立体。

2、三维的定义三维是由二维组成的，二维即只存在两个方向的交错，将一个二维和一个一维叠合在一起就得到了三维。

三维具有立体性，但我们俗语常说的前后，左右，上下都只是相对于观察的视点来说。

没有绝对的前后，左右，上下。

二、平面设计中二维图形——点线面在平面设计中二维图形有着各种各样的元素，但所有的元素概括起来不外乎点线面三种，三种元素的相互结合与相互转换之间就构成了世界上最好的设计。

而点、线、面的关系是什么呢。

那便是：点连续延伸的轨迹成为线，密集成片而成为面。

由于疏密变化而转化为明暗色调；线即可以作为物象的边缘，又可独立的表达一定的形象。

例如线的直与曲，长与短；面在立体艺术中指的是形体，在平面艺术中指两度空间的占有。

在平面设计中，同样一个点，由于大小、形态、位置的不同，所产生的视觉效果和心理作用也不同。

点的缩小起着强调和引起注意的作用，而点的放大有面之感。

它们注重形象的强调和表现给人情感上和心理上的量感。

当点居于几何中心时，上下左右空间对称视觉张力均等。

当居于视觉中心时，有视觉心理的平衡与舒适感。

当点偏左或偏右，产生向心移动趋势，但过于边置也产生离心之动感。

对线的理解，也不仅仅是平面上的一根直线而已，线是空间分割的重要元素，同时在造型中的地位也非常重要。

因为面的形是由线来界定的，也就是形的轮廓线。

从“二维空间”到“三维空间”高考试题的创新性变化,对一线教学具有鲜明的指导意义。

一般而言,高考试题的问题情境都是在“二维空间”内展开,即便是“三维空间”情境,其设问也仅需通过画出侧视图,然后在一个二维空间内就可以解决。

然而2022年高考试题却有了显著变化,试题所呈现的是三维空间情境,需要在三维空间内进行分析和推理才可以解决。

例如2022年高考山东卷第11题、广东卷第10题、河北卷第6题和第7题、全国乙卷第5题等。

本文将依据高考真题,例谈其创新性变化和趋势,并通过变式加以分析和探讨。

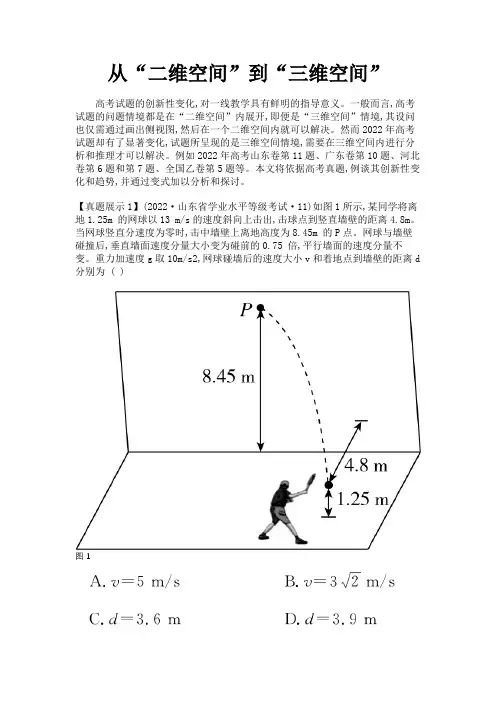
【真题展示1】(2022·山东省学业水平等级考试·11)如图1所示,某同学将离地1.25m 的网球以13 m/s的速度斜向上击出,击球点到竖直墙壁的距离4.8m。

当网球竖直分速度为零时,击中墙壁上离地高度为8.45m 的P点。

网球与墙壁碰撞后,垂直墙面速度分量大小变为碰前的0.75 倍,平行墙面的速度分量不变。

重力加速度g取10m/s2,网球碰墙后的速度大小v和着地点到墙壁的距离d 分别为 ( )图1【解题思路】由于碰墙前后网球的运动轨迹不在同一“二维空间”内,而在三维立体空间内,故该题采用的解题思路是分别对网球在碰墙前和碰墙后运动进行分解与合成。

设网球飞出时的初速度为v0,在竖直方向上代入数据得则在水平方向上网球从抛出点到P点的水平距离画出网球在碰墙前后速度关系的俯视图,如图2所示。

图2根据图2中的几何关系可得,网球打在墙面上时垂直墙面的速度分量故网球着地点到墙壁的距离d＝＝3.9m故BD 正确,AC错误。

【答案】BD【创新点说明】抛体运动是高考常考的重要知识点之一,但常见考查抛体运动试题的情境设置及设问方式与本题有很大差别。

本题的创新点有两个,一是网球虽做斜上抛运动,但因在达到竖直墙壁的最高点P时,竖直分速度为零,只剩下水平分速度,其逆过程即是平抛,因此仍可转换为平抛运动来处理;二是本题创造性地设置研究物体在立体空间,即“三维空间”内的运动,这也是本题最重要的创新点。

《从二维到三维》教学设计方案（第一课时）一、教学目标1. 知识与技能：学生能理解二维图形与三维物体之间的关系，了解从平面图形到立体形态的转换过程。

2. 过程与方法：通过观察、分析和实践，掌握将二维图形转化为三维物体的基本方法。

3. 情感态度价值观：培养学生对美术的兴趣，增强空间感知能力，体验创作的乐趣。

二、教学重难点1. 教学重点：引导学生观察、分析和实践，掌握将二维图形转化为三维物体的基本方法。

2. 教学难点：培养学生的空间想象力，完成从二维到三维的转换，创作出有创意的三维作品。

三、教学准备1. 准备教学用图片、模型和纸艺材料。

2. 安排合适的教室或工作坊，确保光线充足、环境舒适。

3. 确保网络通畅，以便随时查找教学相关资源。

4. 提醒学生携带绘画纸、画笔等美术用具。

四、教学过程：1. 导入环节：老师可以通过展示一些简单的二维图片，引导学生思考如何将这些图片转化为三维立体作品，从而自然过渡到课题。

2. 讲解环节：老师要详细讲解制作三维立体画和三维雕塑的基本步骤和方法，包括构图、着色、塑形、打磨等细节。

同时，老师还要引导学生思考如何将不同的材料、不同的技法运用到三维艺术创作中。

3. 实践环节：学生动手实践，根据老师讲解的方法制作三维立体画或三维雕塑。

老师要巡回指导，解答学生的疑问，并给予必要的帮助和支持。

同时，老师还要鼓励学生发挥自己的想象力和创造力，尝试不同的表现形式和技法。

4. 分享环节：每组选派一名代表展示他们的作品，并分享制作过程中的体会和感受。

同时，老师还可以组织学生互相评价和讨论，交流彼此的创意和心得体会。

5. 拓展环节：引导学生思考如何将三维立体画和三维雕塑的制作方法应用到其他领域，如家居设计、建筑装饰等。

同时，老师还可以组织学生参加一些相关的比赛或展览活动，为学生提供展示自己的机会和平台。

在课程结束后，老师可以鼓励学生将自己的作品整理好，留作纪念。

同时，老师还可以根据学生的兴趣和特长，推荐一些相关的书籍、网站和课程资源，帮助学生进一步拓展自己的艺术视野和学习更多的艺术技能。

Origin二维做图进阶与简单三维做图上次说了Origin的基础与简单二维做图，作为完整的一部份，讲述一下Origin二维做图进阶与简单三维做图，感觉Origin的数据处置不如matlab的好用，而且作为一种工具性的软件，我感觉明白怎么用就能够够了，不需要画太多的东西在这种软件如何利用的问题上。

关于Origin二维图像进阶，要紧有如下几个方面：多层图形的绘制、图层的治理、图形工具的利用。

1、好了，第一，讲一下多层图形的绘制。

咱们能够用到的典型的多层图像有两个，一个是双Y轴图像，若是两个Y轴数据，X轴区间相近，可是Y轴数据相差专门大，就能够够利用双Y轴图像，不然Y数值较小的那个会被紧缩的看不出曲线的转变；另外一个是局部放大图，便于咱们观看所需要的局部区域的曲线转变情形。

菜单栏Plot->Multi-Curve->Double Y，蹦出如图1所示的界面，第一选择做图类型，然后选择X和两个Y，点击OK即可，做出的双Y轴图像如图2所示，能够看出左上角有1、2的注释，别离对应图层1和2（注意：那个地址我为了便于观看，利用的是截屏过来的图像，若是Export Page是没有那个注释的），做出图像后可依照参考[1]进行相应的调整。

图1 双Y轴做图选择界面图2 双Y轴图像那么局部放大图怎么做呢？先选中两列别离做为X和Y轴，菜单栏Plot->Specialized->Zoom，即显现如图3所示的局部放大图形。

上图是完整的图形，基层是局部的放大，用鼠标点击上图中的绿色区域，下面放大部份会随之转变。

图3 局部放大图形2、第二，讲一以下图层的治理。

如何添加图层呢，点击图层空白处，Layer Management，显现如图4所示的操纵界面，点击Add即可添加。

固然了也能够通过菜单栏Graph->New Layer（Axes）或工具栏进行添加。

随之问题来了，如何给图层添加数据或曲线呢？点击图2或图3左上角的图层记号1或2或更多的n，显现如图5所示的操纵界面。

如何快速、准确把CAD二维图转化为PORE三维图
在结构设计、产品设计过程中，经常会遇到需要根据CAD二维图纸转化PROE三维图，以便于零件放于3D设计进行组合、参照。

下面介绍一种方法，可以快速、准确地把CAD二维图转化成为PROE三维图。

步骤1:审核CAD图纸，确保图纸与实物缩放比例为1：1，以保证后继步骤画出图纸的正确性与唯一性。

如下面的一份图纸
步骤2：把后继画图设计不需要用到的东西进行删除、整理，保持图面的整洁性，如下图
步骤3：在轴测图中，利用三维旋转对各图进行投影关系的旋转，方便和保证在PROE中进行绘画拉伸尺寸关系。

同时，把不同视图放于不同的层上并加以颜色，以示区别，方便在后继PROE绘图中辨认不同的线条尺寸。

最后，在图面上确定后继PROE的绘图中心，并加上坐标原点。

如下图
步骤4：把整理、旋转好的CAD图导入PROE中，并插入绘图平面，为下一步的绘图做好准备，如下图
步骤5:根据准备好的二维图，对不同视图面的线条进行3D设计，尺寸关系可以根据不同视图直接拉伸到选定的参照。

最终就可以绘制出完整的3D图，如下图
存图层状态，一个完整的3D零件结构就完成了，如下图。

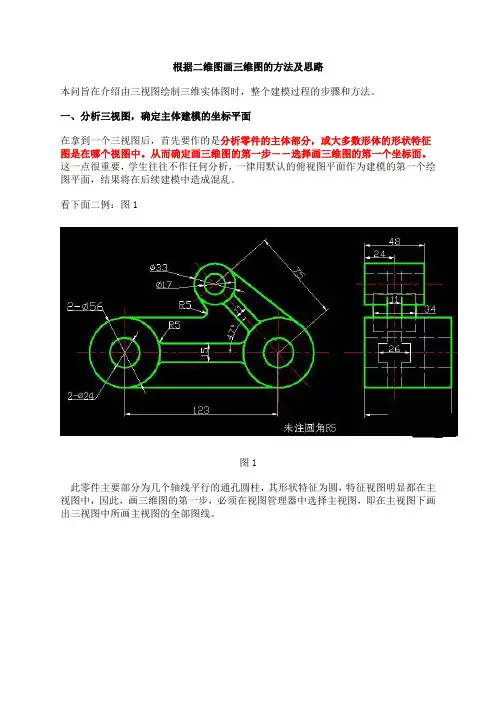
根据二维图画三维图的方法及思路本问旨在介绍由三视图绘制三维实体图时，整个建模过程的步骤和方法。

一、分析三视图，确定主体建模的坐标平面在拿到一个三视图后，首先要作的是分析零件的主体部分，或大多数形体的形状特征图是在哪个视图中。

从而确定画三维图的第一步――选择画三维图的第一个坐标面。

这一点很重要，学生往往不作任何分析，一律用默认的俯视图平面作为建模的第一个绘图平面，结果将在后续建模中造成混乱。

看下面二例：图1图1此零件主要部分为几个轴线平行的通孔圆柱，其形状特征为圆，特征视图明显都在主视图中，因此，画三维图的第一步，必须在视图管理器中选择主视图，即在主视图下画出三视图中所画主视图的全部图线。

图2是用三维图模画三维图，很明显，其主要结构的形状特征――圆是在俯视方向，故应首先在俯视图下作图。

图2二、构型处理，尽量在一个方向完成基本建模操作确定了绘图的坐标平面后，接下来就是在此平面上绘制建模的基础图形了。

必须指出，建模的基础图形并不是完全照抄三视图的图形，必须作构型处理。

所谓构型，就是画出各形体在该坐标平面上能反映其实际形状，可供拉伸或放样、扫掠的实形图。

如图1所示零件，三个圆柱筒，按尺寸要求画出图4中所示6个绿色圆。

与三个圆筒相切支撑的肋板，则用多段线画出图4中的红色图形。

其它两块肋板，用多段线画出图中的两个黄色矩形。

图4：图3这样处理后，该零件的建模操作可在一个方向上完成。

不要担心红色肋板穿过了两圆筒的孔，这可以在对圆筒差集后得到圆满处理。

要注意的是必须先并后差。

这是后话。

再如图2所示零件，左侧半圆筒，用多段线画出图4中所示绿色图形；右侧的内孔及键槽也须用多段线画出；中间的水平肋板，则用多段线画出如图中的红色图形。

该零件中垂直方向的梯形肋板，由于在俯视图中不反映实形，故不能在此构型，需另行处理。

图4三、确定零件上各形体的建模位置画出了各形体的实形图后，即可转到西南等轴测图下，进行拉伸、放样等建模操作。

2d到3d转换转换原理
2D到3D转换是指将二维图像或平面几何对象转换为三维模型或场景的过程。

这种转换可以通过多种方法实现，其中一些常见的原理包括：
1. 视差原理，视差是指当我们从不同位置观察同一个物体时，物体在我们的视野中的位置发生变化。

通过分析图像中物体的视差信息，可以推断出物体的深度信息，从而实现2D到3D的转换。

2. 立体视觉原理，立体视觉是指我们通过两只眼睛同时观察物体时产生的立体感。

通过将两个视角的图像进行比较和匹配，可以计算出物体的深度信息，进而实现2D到3D的转换。

3. 结构光原理，结构光是一种通过投射特定的光纹或模式到物体上，并通过相机捕捉物体表面的形变来计算物体的深度信息的方法。

通过分析光纹的形变，可以实现从2D图像到3D模型的转换。

4. 激光扫描原理，激光扫描是一种通过激光器发射激光束，并通过接收器接收反射回来的激光束来获取物体表面的点云数据的方法。

通过获取物体表面的点云数据，可以重建出物体的三维模型。

5. 纹理映射原理，纹理映射是一种将二维图像或纹理映射到三维物体表面的方法。

通过将2D图像与3D模型进行对应，可以实现从2D到3D的转换。

这些原理可以独立或结合使用，具体的转换方法取决于应用场景和需求。

需要注意的是，2D到3D转换是一个复杂的过程，涉及到计算机视觉、图像处理、几何学等多个领域的知识和技术。

cad2021怎么画三维图形篇一：CAD三维图简单的绘制方法CAD三维图纯粹的绘制方法CAD绘制三维图只需要按下面几步骤操作就行了，下面以绘制长方体为例。

1. 先绘制一个二维长方体，设置好长宽；2. 在工具栏选择“绘图”→“建模”→“拉伸”→设置高度→按enter键→cad自动将矩形拉伸成长方体。

3. 选择“视图”→“三维视图”→“东南等轴测” →得到如下图形；4. 如果在矩形上面想再画个圆柱，则先点击“视图”→ “俯视图”→再用绘图工具绘制一个矩形；5. 在工具栏选择“绘图”→“建模”→“拉伸”→设置高度→按enter键→cad自动将矩形拉伸成八边形。

6. 选择“视图”→“三维视图”→“东南等轴测” →得到如下图形；7. 绘制好图后，选择“视图”→“动态观察”→“受约束的动态观察” →移动得到想要的侧视效果，保存，再打开图时则是下图效果。

如下图所示；篇二：CAD 三维图的绘制教程实例一、工字型的绘制步骤一：设置好绘图单位、绘图范围、线型、图层、颜色，打开捕捉功能。

从下拉菜单View→Display→UCSIcon→On关闭坐标显示。

步骤二：根据图1所示尺寸绘制贴图，得到如图1－1所示封闭图形。

步骤三：创建面域。

在命令栏Command：输入Region，用送走框选方式全部选中该图形，回车。

出现提示：1 loop extracted，1 Region created，表示形成了一个施划图形，创建了一图1－2 三维效果图图1－1 平面图个面域。

步骤四：对该面域进行拉伸操作。

Draw→Solids→Extrude，选中该面域的边框，回车。

在命令栏提示：Specify height of extrusion or [Path]：30，回车，再回车。

三维工字形实体就聚合了。

步骤五：观察三维实体。

View→3D Views→SW Isometric，再从View→Hide进行消除隐藏线处理，观察，最后进行着色渲染，View→Shade→Gouraud Shaded，如图1－2所示。

Python绘图之⼆维图与三维图详解各位⼯程师累了吗? 推荐⼀篇可以让你技术能⼒达到出神⼊化的⽹站"持久男"1.⼆维绘图a. ⼀维数据集⽤ Numpy ndarray 作为数据传⼊ ply1.import numpy as npimport matplotlib as mplimport matplotlib.pyplot as pltnp.random.seed(1000)y = np.random.standard_normal(10)print "y = %s"% yx = range(len(y))print "x=%s"% xplt.plot(y)plt.show()2.操纵坐标轴和增加⽹格及标签的函数import numpy as npimport matplotlib as mplimport matplotlib.pyplot as pltnp.random.seed(1000)y = np.random.standard_normal(10)plt.plot(y.cumsum())plt.grid(True) ##增加格点plt.axis('tight') # 坐标轴适应数据量 axis 设置坐标轴plt.show()3.plt.xlim 和 plt.ylim 设置每个坐标轴的最⼩值和最⼤值#!/etc/bin/python#coding=utf-8import numpy as npimport matplotlib as mplimport matplotlib.pyplot as pltnp.random.seed(1000)y = np.random.standard_normal(20)plt.plot(y.cumsum())plt.grid(True) ##增加格点plt.xlim(-1,20)plt.ylim(np.min(y.cumsum())- 1, np.max(y.cumsum()) + 1)plt.show()4. 添加标题和标签 plt.title, plt.xlabe, plt.ylabel 离散点, 线#!/etc/bin/python#coding=utf-8import numpy as npimport matplotlib as mplimport matplotlib.pyplot as pltnp.random.seed(1000)y = np.random.standard_normal(20)plt.figure(figsize=(7,4)) #画布⼤⼩plt.plot(y.cumsum(),'b',lw = 1.5) # 蓝⾊的线plt.plot(y.cumsum(),'ro') #离散的点plt.grid(True)plt.axis('tight')plt.xlabel('index')plt.ylabel('value')plt.title('A simple Plot')plt.show()b. ⼆维数据集np.random.seed(2000)y = np.random.standard_normal((10, 2)).cumsum(axis=0) #10⾏2列在这个数组上调⽤cumsum 计算赝本数据在0轴(即第⼀维)上的总和print y1.两个数据集绘图#!/etc/bin/python#coding=utf-8import numpy as npimport matplotlib as mplimport matplotlib.pyplot as pltnp.random.seed(2000)y = np.random.standard_normal((10, 2))plt.figure(figsize=(7,5))plt.plot(y, lw = 1.5)plt.plot(y, 'ro')plt.grid(True)plt.axis('tight')plt.xlabel('index')plt.ylabel('value')plt.title('A simple plot')plt.show()2.添加图例 plt.legend(loc = 0)#!/etc/bin/python#coding=utf-8import numpy as npimport matplotlib as mplimport matplotlib.pyplot as pltnp.random.seed(2000)y = np.random.standard_normal((10, 2))plt.figure(figsize=(7,5))plt.plot(y[:,0], lw = 1.5,label = '1st')plt.plot(y[:,1], lw = 1.5, label = '2st')plt.plot(y, 'ro')plt.grid(True)plt.legend(loc = 0) #图例位置⾃动plt.axis('tight')plt.xlabel('index')plt.ylabel('value')plt.title('A simple plot')plt.show()3.使⽤2个 Y轴(左右)fig, ax1 = plt.subplots() ax2 = ax1.twinx() #!/etc/bin/python#coding=utf-8import numpy as npimport matplotlib as mplimport matplotlib.pyplot as pltnp.random.seed(2000)y = np.random.standard_normal((10, 2))fig, ax1 = plt.subplots() # 关键代码1 plt first data set using first (left) axisplt.plot(y[:,0], lw = 1.5,label = '1st')plt.plot(y[:,0], 'ro')plt.grid(True)plt.legend(loc = 0) #图例位置⾃动plt.axis('tight')plt.xlabel('index')plt.ylabel('value')plt.title('A simple plot')ax2 = ax1.twinx() #关键代码2 plt second data set using second(right) axisplt.plot(y[:,1],'g', lw = 1.5, label = '2nd')plt.plot(y[:,1], 'ro')plt.legend(loc = 0)plt.ylabel('value 2nd')plt.show()4.使⽤两个⼦图(上下,左右)plt.subplot(211)通过使⽤ plt.subplots 函数,可以直接访问底层绘图对象,例如可以⽤它⽣成和第⼀个⼦图共享 x 轴的第⼆个⼦图. #!/etc/bin/python#coding=utf-8import numpy as npimport matplotlib as mplimport matplotlib.pyplot as pltnp.random.seed(2000)y = np.random.standard_normal((10, 2))plt.figure(figsize=(7,5))plt.subplot(211) #两⾏⼀列,第⼀个图plt.plot(y[:,0], lw = 1.5,label = '1st')plt.plot(y[:,0], 'ro')plt.grid(True)plt.legend(loc = 0) #图例位置⾃动plt.axis('tight')plt.ylabel('value')plt.title('A simple plot')plt.subplot(212) #两⾏⼀列.第⼆个图plt.plot(y[:,1],'g', lw = 1.5, label = '2nd')plt.plot(y[:,1], 'ro')plt.grid(True)plt.legend(loc = 0)plt.xlabel('index')plt.ylabel('value 2nd')plt.axis('tight')plt.show()5.左右⼦图有时候,选择两个不同的图标类型来可视化数据可能是必要的或者是理想的.利⽤⼦图⽅法: #!/etc/bin/python#coding=utf-8import numpy as npimport matplotlib as mplimport matplotlib.pyplot as pltnp.random.seed(2000)y = np.random.standard_normal((10, 2))plt.figure(figsize=(10,5))plt.subplot(121) #两⾏⼀列,第⼀个图plt.plot(y[:,0], lw = 1.5,label = '1st')plt.plot(y[:,0], 'ro')plt.grid(True)plt.legend(loc = 0) #图例位置⾃动plt.axis('tight')plt.xlabel('index')plt.ylabel('value')plt.title('1st Data Set')plt.subplot(122)plt.bar(np.arange(len(y)), y[:,1],width=0.5, color='g',label = '2nc')plt.grid(True)plt.legend(loc=0)plt.axis('tight')plt.xlabel('index')plt.title('2nd Data Set')plt.show()c.其他绘图样式,散点图,直⽅图等1.散点图#!/etc/bin/python#coding=utf-8import numpy as npimport matplotlib as mplimport matplotlib.pyplot as pltnp.random.seed(2000)y = np.random.standard_normal((1000, 2)) plt.figure(figsize=(7,5))plt.scatter(y[:,0],y[:,1],marker='o')plt.grid(True)plt.xlabel('1st')plt.ylabel('2nd')plt.title('Scatter Plot')plt.show()2.直⽅图 plt.hist#!/etc/bin/python#coding=utf-8import numpy as npimport matplotlib as mplimport matplotlib.pyplot as pltnp.random.seed(2000)y = np.random.standard_normal((1000, 2))plt.figure(figsize=(7,5))plt.hist(y,label=['1st','2nd'],bins=25)plt.grid(True)plt.xlabel('value')plt.ylabel('frequency')plt.title('Histogram')plt.show()3.直⽅图同⼀个图中堆叠#!/etc/bin/python#coding=utf-8import numpy as npimport matplotlib as mplimport matplotlib.pyplot as pltnp.random.seed(2000)y = np.random.standard_normal((1000, 2))plt.figure(figsize=(7,5))plt.hist(y,label=['1st','2nd'],color=['b','g'],stacked=True,bins=20) plt.grid(True)plt.xlabel('value')plt.ylabel('frequency')plt.title('Histogram')plt.show()4.箱型图 boxplot#!/etc/bin/python#coding=utf-8import numpy as npimport matplotlib as mplimport matplotlib.pyplot as pltnp.random.seed(2000)y = np.random.standard_normal((1000, 2))fig, ax = plt.subplots(figsize=(7,4))plt.boxplot(y)plt.grid(True)plt.setp(ax,xticklabels=['1st' , '2nd'])plt.xlabel('value')plt.ylabel('frequency')plt.title('Histogram')plt.show()5.绘制函数from matplotlib.patches import Polygonimport numpy as npimport matplotlib.pyplot as plt#1. 定义积分函数def func(x):return 0.5 * np.exp(x)+1#2.定义积分区间a,b = 0.5, 1.5x = np.linspace(0, 2 )y = func(x)#3.绘制函数图形fig, ax = plt.subplots(figsize=(7,5))plt.plot(x,y, 'b',linewidth=2)plt.ylim(ymin=0)#4.核⼼，我们使⽤Polygon函数⽣成阴影部分，表⽰积分⾯积：Ix = np.linspace(a,b)Iy = func(Ix)verts = [(a,0)] + list(zip(Ix, Iy))+[(b,0)]poly = Polygon(verts,facecolor='0.7',edgecolor = '0.5')ax.add_patch(poly)#5.⽤plt.text和plt.figtext在图表上添加数学公式和⼀些坐标轴标签。