汽车单自由度振动系统强迫振动放大因子分析.
- 格式:doc
- 大小:445.82 KB
- 文档页数:14

汽车产品振动振动的定义和分类振动是指物体在空间中往复运动的一种现象。
对于汽车产品来说,振动是指由于发动机、悬挂系统、轮胎等各种原因引起的汽车整车或车内部件的振动。
振动可以分为三种类型:自由振动、强迫振动和自激振动。
自由振动是指物体自身的固有频率和自身的特性造成的振动。
强迫振动是外界施加在物体上的振动力所引起的振动。
自激振动是指物体内部的非线性元件在发生滞后现象时引起的自激振荡。
汽车产品振动的原因和影响汽车产品振动的原因主要有以下几个方面:1.发动机振动:发动机在运转过程中会产生振动力,特别是在低转速和高转速时振动力更大。
这些振动力会传递到整个车身和底盘系统,引起汽车的振动。
2.悬挂系统振动:悬挂系统是汽车的重要部件之一,它能够缓冲路面的不平,保证驾驶舒适性。
但悬挂系统自身也会发生振动,特别是当经过凸起和凹陷路面时,悬挂系统会受到外力的作用而产生振荡。
3.轮胎振动:轮胎与地面之间的摩擦力会引起轮胎的振动,尤其是在高速行驶时,轮胎的振动会较为明显。
4.车辆失衡:车辆在制造过程中可能会存在零部件制造不精确、安装不准确等问题,这些问题都会导致车辆在行驶过程中出现振动。
汽车产品振动给驾驶者和乘客带来一系列的影响,包括:1.驾驶舒适性下降:汽车振动会导致驾驶者的手臂、脚底、座椅等部位感受到明显的震动,从而降低了驾驶的舒适性。
2.乘坐舒适性下降:汽车振动会使乘客在座椅上感受到明显的震动,影响乘坐舒适性和旅途的愉悦感。
3.安全性降低:汽车振动会影响到车辆的稳定性和操控性能,增加了驾驶的难度,提高了事故的风险。
汽车产品振动的解决方法为了解决汽车产品振动带来的问题,汽车制造商采取了以下一些方法:1.发动机平衡:制造商通过调整发动机的结构和采用平衡装置来减少发动机振动。
这包括使用配重轮、减振器等技术。
2.悬挂系统改进:制造商会通过改进悬挂系统的结构和材料,提高悬挂系统的缓冲效果,减少路面不平带来的振动。
3.轮胎优化:制造商会优化轮胎的结构和材料,改善轮胎的减震性能,减少轮胎振动和噪音。







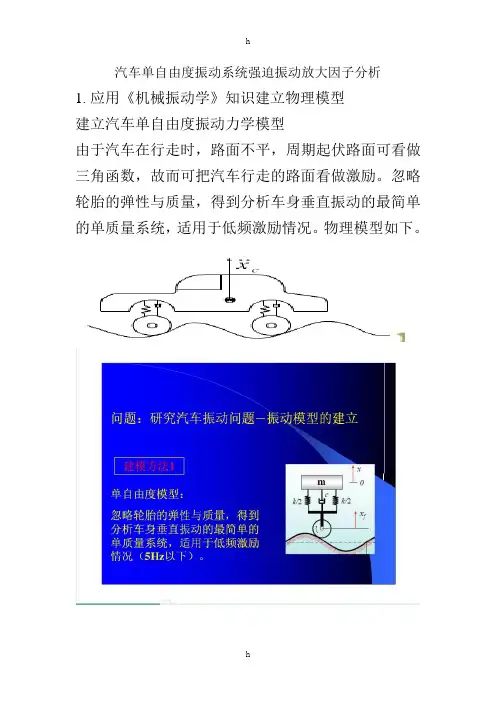
汽车单自由度振动系统强迫振动放大因子分析1.应用《机械振动学》知识建立物理模型建立汽车单自由度振动力学模型由于汽车在行走时,路面不平,周期起伏路面可看做三角函数,故而可把汽车行走的路面看做激励。
忽略轮胎的弹性与质量,得到分析车身垂直振动的最简单的单质量系统,适用于低频激励情况。
物理模型如下。
其中x f =y=Y sin(wt)其中k 为弹性系数,c 为阻尼系数。
2. 根据所建立的力学模型列出微分方程 根据牛顿定律,写出数学方程。
()()"''mx k x y c x y =----"''mx cx kx cy ky ++=+ ⑴由此可见。
基础运动使系统受两个作用力,一个是与y(t)同相位,经弹簧传给质m 的力ky ;一个是与速度y ’同相位,经阻尼器传给质量m 的力cy ’。
利用复指数法求解,用()sin jwtYe Y wt =,并假定方程的解为()jwtx t xe =,代入方程(1)得()()()22221212r X r r ξξ+=-+可表示为()()()22221212r X Yr r ξξ+=-+阻尼比0c c ξ==c 为阻尼系数,0c 为临界阻尼系数 频率比nw r w =,w 为激励频率,nw 为系统固有频率。
3利用MATALB 编程y1=sqrt((1+(2*0.1*x).^2)/((1-x.^2).^2+(2*0.1*x).^2)); y2=sqrt((1+(2*0.15*x).^2)/((1-x.^2).^2+(2*0.15*x).^2)); y3=sqrt((1+(2*0.25*x).^2)/((1-x.^2).^2+(2*0.25*x).^2)); y4=sqrt((1+(2*0.5*x).^2)/((1-x.^2).^2+(2*0.5*x).^2));ezplot('y1=sqrt((1+(2*0.1*x).^2)/((1-x.^2).^2+(2*0.1*x).^2))',[0,6]); hold on;ezplot('y2=sqrt((1+(2*0.15*x).^2)/((1-x.^2).^2+(2*0.15*x).^2))',[0,6])ezplot('y3=sqrt((1+(2*0.25*x).^2)/((1-x.^2).^2+(2*0.25*x).^2))',[0,6])ezplot('y4=sqrt((1+(2*0.5*x).^2)/((1-x.^2).^2+(2*0.5*x).^2))',[0,6]);title('放大因子X/Y 与频率比r 的曲线') xlabel('频率比')ylabel('放大因子X/Y')text(x(20),5,'阻尼比0.1')text(x(20),3,'阻尼比0.15')text(x(20),2,'阻尼比0.25')text(x(20),1,'阻尼比0.5')把程序写入MATALB,用软件开始编程运行程序得如下结果再把该图形做完整X以 为参数,随r变化的曲线表示如下图。
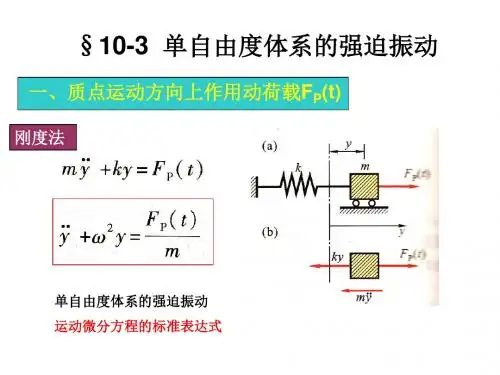
1.2单自由度系统强迫振动一、实验目的1. 理解与掌握单自由度系统强迫振动的基本知识2. 测定带有集中荷重的悬臂梁系统,在自由端部位移激励下引起的强迫振动的振幅频率特性曲线;借助幅频特性曲线,求出系统的固有频率n ω及阻尼常数ζ 3. 初步了解振动测试的仪器设备和工程实验建模方法二、实验内容1. 调节信号源和功率放大器,使系统产生共振 2. 测量系统对应的频率和振幅3. 绘制幅频曲线,得出系统的频率、阻尼等参数三、实验装置和设备单层框架系统实验装置(可视为悬臂梁),如图1所示。
扫频信号源(含功率放大器)DH-1301,激振器JZQ-2 力传感器F.Sen ,加速度传感器A.Sen ,电荷放大器DLF-3 数字式示波器TDS-210图1TDS-210DH-1301DLF-3JZQ-2F.SenA.Sen四、实验原理 1.理论知识单自由度系统在有持续激励时的振动,这类振动称为强迫振动,强迫振动是工程中常见的现象。
激励的来源可分为两类,一类是力激励,它可以是直接作用于机械运动部件上的惯性力,也可以是旋转机械或往复运动机械中不平衡量引起的惯性力,另一类是由于支撑运动而导致的位移激励/速度激励以及加速度激励。
如图2所示的弹簧质量系统为对象,以静平衡位置为坐标原点,根据力系平衡原理,建立动力学方程如下:t F kx x c xm ωsin 0+−−=&&& (2.1) t F kx x c xm ωsin 0=++&&& (2.2) t F x m k x m cxωsin 0=++&&& (2.3)令m k n =2ω,mcn =2 (2.4) nnωζ=(2.5)得到t mF x x n xn ωωsin 202=++&&& (2.6)式(2.6)的稳定解为)sin(φω−=t B x(2.7)将式(2.7)带入式(2.6),求出待定系数B ,得到2222204)(ωδωω+−=n m F B (2.8) 利用共振法得到系统的固有频率n ωn m f f B →→max(2.9) n n f πω2=(2.10)通过幅频特性曲线,如图3所示,利用半功率带宽原理得到系统的阻尼系数ζ 半功率带宽:12f f f −=Δ(2.12)阻尼比ζ:nn f ff f f 2212Δ=−=ζ (2.13)10 36B /B mf (Hz) 10.707n f 1f 2f图32. 实验方法一个单层框架结构组成的悬臂梁系统,固定端固定在底板上,自由端与激振器连接,测试系统,如图3所示,扫频信号发生器(含功率放大器)可调节激振器的激振力的频率和幅值,激振频率由扫频信号发生器直接读得,悬臂梁端部的振幅利用压电加速度传感器(压电加速度传感器是利用振动对压电晶体产生压电效应来测量振动的),经电荷放大器转化并放大,由数字式示波器读得。
单自由度系统强迫振动实验一、实验目的1、 了解学习振动系统和测振系统的组成及原理,掌握测振的一般方法。
2、 观察简支梁振动系统在共振前、共振时、共振后以及快速通过共振区的振幅变化情况。
3、 观察简支梁振动系统在共振前、共振时、共振后干扰力与系统位移的相位关系。
4、 测定简支梁振动系统的固有频率及幅频特性曲线。
二、实验装置 1、 实验装置简图测振仪(11)示波器(12)闪光测速仪(9)闪光灯(8)电动机(3)变压器(2)传感器(10)简支梁(1)偏心轮(4)振标(7)标记线(5)图一2、实验装置上各附件的作用 (1) 简支梁简支梁是由一块截面为矩形的弹性钢板通过轴承支撑在两个刚性很强的固定支架上,它在系统中主要起弹簧作用。
(2) 固定架固定架是用来固定偏心轮、标记盘等部件的,其质量同简支梁质量的一半组成系统的质量(根据能量原理而得)。
故此系统可简化为(图二)所示的弹簧质量系统。
图二图中:M ------系统的质量 m -------偏心质量 0F -------离心惯性力k --------简支梁的弹簧刚度 r --------阻尼系数 (3) 自耦变压器自耦变压器用来启动电机和调节电机转速的设备。
当通过变压器手轮改变变压器输出电压时,即可改变电机的转速,借以达到调速之目的。
(4) 电动机电动机是用来驱动偏心轮旋转的动力源。
在本实验中借助改变电机的转速来实现干扰力频率的变化。
(5) 偏心轮偏心轮在系统中是产生干扰力的元件。
当转轴带动偏心轮以转速N 旋转时,偏心质量m 就以2(1/)60Ns πω=作等速圆周运动,同时产生了一个离心惯性力20F me ω=。
该力通过轴和轴承座传给梁。
这个旋转的离心惯性力在铅直方向的分量就构成了对梁沿铅直方向的简谐干扰力,即20sin sin F F t me t ωωω==。
此干扰力使系统产生强迫振动。
以坐标x 表示偏心轮轴心离开静平衡位置的铅垂位移,如图二,则系统振动的微分方程为:2sin Mx rx kx me t ωω++= (1)设 2r n M = , 2k p M =,2me q Mω=上式可以写成22sin xnx p x q t ω++= (2) 这个微分方程的全解为12()()()x t x t x t =+其中 221()sin()nt x t Ae p n t ϕ-=-+是个衰减振动,在振动开始的一定时间后就完全消失了。
关于单自由度系统的强迫振动分析罗海东【摘要】由单自由度系统中支承的运动规律及达朗伯原理得到运动微分方程,再利用线性系统的叠加原理分析系统中被支承质量的振幅及支承振幅、频率比和阻尼比间的关系,并通过图形对隔振方法进行了分析.%By means of superposition prin ciple of linear system and movement differential equation that is formulated according to d'alembert's principle and law of support motion in a linear system,this paper analyses the relation between the supported amplitude and the support amplitude as well as the relation between frequency ratio and damping ratio. Moreover,it explores the methods to isolate vibration through specific analysis on drawing line.【期刊名称】《南通纺织职业技术学院学报》【年(卷),期】2012(012)004【总页数】2页(P18-19)【关键词】叠加原理;单自由度;振幅;频率比;隔振;阻尼比【作者】罗海东【作者单位】江阴职业技术学院,江阴214433【正文语种】中文【中图分类】O321自然界普遍存在着振动现象.振动的一个重要方面是系统对外部激励的响应,激励的来源可分两类:一类是力激励,可以是直接作用于机械运动部件上的力,也可以是往复运动机械中不平衡量引起的惯性力;另一类是支承运动导致的位移激励、速度激励以及加速度激励.本文讨论的是单自由度系统的强迫振动.单自由度系统在有持续激励时的振动,称之为强迫振动.在科学技术领域以及日常生活里,都会遇到各种不同程度的振动过程,振动过程广泛出现在各生产领域中,有许多的振动问题需我们要去处理.例如,车辆在波形路面上行驶时的振动及固定在机器上的仪表的振动等等,都是支承运动引起的强迫振动.质量块固连的指针与仪表外壳之间的振动是相对运动,车辆及质量块的振动是绝对运动(例举中只讨论车辆及质量块系统的绝对运动).如图1所示,是一单自由度系统的简图,设x(t)及xs(t)分别是质量块及支承的位移,支承的运动规律[1]是:由于支承的运动,质量块受到的弹性恢复力为k(x-xs),阻尼力为c(x′-xs′),根据达朗伯原理可得如下的运动微分方程[2]:为了分析方便,记β为振幅放大因子,在这里把它定义为:β=B/a=,以ξ为参数,画出的幅频响应曲线及相频响应曲线如图2、3所示.由图2、3可见,当频率比时,无论阻尼比ξ为多少,振幅B恒等于支承运动振幅a;振幅B小于a,增加阻尼反而使振幅B增大.在工程机械中超过允许范围的振动影响着本身的正常运行及寿命,还造成环境污染,故有效地隔离振动是相当重要的问题.一类是用隔振器将振动着的机械与地基隔离开,称为积极隔振;另一类是将需要保护的设备用隔振器与振动着的地基隔开,称为消极隔振.两种方法的原理是类似的,隔振效果可以用传递率TR度量,将图2的幅频响应曲线的纵坐标β改为TR,则得到TR随频率比λ的变化规律的特性曲线.从曲线中看到,只有当时,才有隔振效果;当λ>5以后,曲线下降得都慢,通常将λ选在2.5~5的范围内.另外,在λ>以后,增加阻尼反而使隔振效果变坏.因此,为了取得较好的隔振效果,系统应当具有较低的固有频率和较小的阻尼.阻尼也不能太小,否则在经过共振区时会产生较大的振动.利用弹性支撑可使一系统降低对外加激励响应的能力,而将振动源与设备的刚性连接改为弹性连接,能隔绝或减弱振动能量的传递,从而减振降噪.【相关文献】[1] 杨桂通.弹性力学[M].北京:高等教育出版社,1998:163.[2] 钟万勰.弹性力学求解新体系[M].大连:大连理工大学出版社,1995:204.[3] 刘延柱,陈文良,陈立群.振动力学[M].北京:高等教育出版社,1998.。
中北大学
课程设计说明书
学生姓名:学号:********XX
学院:机械工程与自动化学院
专业:机械电子工程
题目:汽车单自由度振动系统强迫振动放大因子分析指导教师:职称:
2013年 1月 7日
课程设计任务书
12/13 学年第一学期
学院:机械工程与自动化学院
专业:机械电子工程
学生姓名:学号:
课程设计题目:汽车单自由度振动系统强迫振动放大
因子分析
起迄日期:2013年1月7日~2013年1月18日课程设计地点:机械自动化系
指导教师:
系主任:
下达任务书日期: 2013年 1月 7日
汽车单自由度振动系统强迫振动放大因子分析
1.应用《机械振动学》知识建立物理模型
建立汽车单自由度振动力学模型
由于汽车在行走时,路面不平,周期起伏路面可看做三角函数,故而可把汽车行走的路面看做激励。
忽略轮胎的弹性与质量,得到分析车身垂直振动的最简单的单质量系统,适用于低频激励情况。
物理模型如下。
其中x f =y=Y sin(wt)
其中k 为弹性系数,c 为阻尼系数。
2. 根据所建立的力学模型列出微分方程 根据牛顿定律,写出数学方程。
()()
"''mx k x y c x y =----
"''mx cx kx cy ky ++=+ ⑴
由此可见。
基础运动使系统受两个作用力,一个是与y(t)同相位,经弹簧传给质m 的力ky ;一个是与速度y ’同相位,经阻尼器传给质量m 的力cy ’。
利用复指数法求解,用()sin jwt
Ye Y wt =,并假定方程的解
为()jwt
x t xe =,
代入方程(1)得
()
()()
2
2
2
21212r X r r ξξ+=-+
可表示为
()
()()
2
2
2
21212r X Y
r r ξξ+=-+
阻尼比0c c ξ=
=
c 为阻尼系数,0
c 为临界阻尼系数 频率比n
w r w =
,
w 为激励频率,n
w 为系统固有频率。
3利用MATALB 编程
y1=sqrt((1+(2*0.1*x).^2)/((1-x.^2).^2+(2*0.1*x).^2)); y2=sqrt((1+(2*0.15*x).^2)/((1-x.^2).^2+(2*0.15*x).^2)); y3=sqrt((1+(2*0.25*x).^2)/((1-x.^2).^2+(2*0.25*x).^2)); y4=sqrt((1+(2*0.5*x).^2)/((1-x.^2).^2+(2*0.5*x).^2));
ezplot('y1=sqrt((1+(2*0.1*x).^2)/((1-x.^2).^2+(2*0.1*x).^2))',[0,6]); hold on;
ezplot('y2=sqrt((1+(2*0.15*x).^2)/((1-x.^2).^2+(2*0.15*x).^2))',[0,6])
ezplot('y3=sqrt((1+(2*0.25*x).^2)/((1-x.^2).^2+(2*0.25*x).^2))',[0,6])
ezplot('y4=sqrt((1+(2*0.5*x).^2)/((1-x.^2).^2+(2*0.5*x).^2))',[0,6]);
title('放大因子X/Y 与频率比r 的曲线') xlabel('频率比')
ylabel('放大因子X/Y')
text(x(20),5,'阻尼比0.1')
text(x(20),3,'阻尼比0.15')
text(x(20),2,'阻尼比0.25')
text(x(20),1,'阻尼比0.5')
把程序写入MATALB,用软件开始编程运行程序得如下结果
再把该图形做完整
X
以ξ为参数,随r变化的曲线表示如下图。
Y
现在经过建立物理模型,构建数学模型,再利用MATALB仿真,最终得出了汽车振动系统强迫振动下的频率放大因子图形。
分析:
当0
M→,而与阻尼无关。
这意味着,当激励r→时,1
频率接近于零时,振幅与静位移相近。
当r→∞时,0
M→。
也与阻尼大小无关。
在激励频率很高时,振幅趋于零。
这意味着,质量不能跟上力的变
化,将停留在平衡位置不动。
当r=1时,若0ξ=,在理论上M →∞,这意味着,当系统中不存在阻尼时,激励频率和系统的固有频率一致,振幅将趋于无限大,这种现象叫做共振。
通常我们称r=1,即w=n
w 时的频率为共振频率。
实际
上,当系统中存在阻尼时,振幅是有限的,其最大值并不在w=n
w 处,
由
0dM
dr
=可得 振幅最大时的频率比
max r =而振幅的最大值为
max M =
只有无阻尼时,共振频率是n
w 。
有阻尼时,最大振幅
n 比n w 小。
当阻尼较小时,可近似的看
做n
w 。
当0ξ≥,即使只有恨微小的阻尼,也使最大振幅限制在有限的范围内。
由式可见,若
ξ=
,则max 0r =。
即振幅的最大值发生在W=0处。
也就是静止时,位移最大,由此可得结论:
① 当2
ξ≥
时,不论r 为何值,1M ≤;
② 当2ξ≤时,对于很小或者很大的r 值,阻尼对响应
的影响可略去。
对远离共振频率的区域,阻尼对减小振幅的作用不大。
只有在共振频率及其近旁,阻尼对减小振幅有明显作用,增加阻尼可使振幅显著的下降。
由r=1, 12M ξ=,,共振时的振幅由阻尼决定。
由图可见,
当r=0和
r =X Y =1,与ξ无关。
当
r ≥
X Y ≤,且阻尼小的X Y 比值要比阻尼大的时候
小。
4. 分析当激振函数)50sin(0
t F F =时,该系统的隔振性能,并作出评价
如图力学模型如上所示。
经隔振装置传递到地基的力有两部分:经弹簧传给地基的力
()sin X F kx kX wt ϕ==-
经阻尼传给地基的力
()'cos d F cx cwX wt ψ==-
Fx 和Fd 是相同频率的,相位差2
π的简协作用力。
因此,传给地基的力的最大值或者振幅T
F 为
T F ==由于在Fsin(wt)作用下,系统稳态响应的振幅为
X =
则
T F =评价积极隔振效果的指标是力传递系数
T F F T F == 合理设计的隔振装置应该选择适当的弹簧常数k 和阻尼系数c,使力传递系数F
T 达到要求的指标,为此,需要讨论F
T 和ξ和r 的关系。
编写程序,用MATALB 编程
x=0:pi/1000:6;
ezplot('y1=sqrt((1+(2*0.1*x).^2)/((1-x.^2).^2+(2*0.1*x).^2))',[0,6]);
hold on;
ezplot('y2=sqrt((1+(2*0.15*x).^2)/((1-x.^2).^2+(2*0.15*x).^2))',[0,6])
ezplot('y3=sqrt((1+(2*0.25*x).^2)/((1-x.^2).^2+(2*0.25*
x).^2))',[0,6])
ezplot('y4=sqrt((1+(2*0.5*x).^2)/((1-x.^2).^2+(2*0.5*x). ^2))',[0,6]);
把所编程序植入MATALB软件,运行,得出模拟图形
横坐标为频率比r,纵坐标为力传递系数
T
F
由图可见,在r=0和2时,
T=1
R
与阻尼无关,即传递的力或位移与施加给系统的力或位移相等。
在02
≤≤的频段内,传递的力或位移都比施加的力或r
位移大。
而当2
r≥
频率的增大而减小,因此可以得到两点结论:
⑴不论阻尼比为多少,只有在2
r≥
⑵对于某个给定的r ≥数也减小。
现在激励频率为w=50HZ, 由n
w
r w =得,
n w
w ≥
,n w ≤==35.7HZ 结论:当系统的初始频率n w 小于等于35.7HZ 时,系统具有明显的隔振性能。