量纲分析基础
- 格式:ppt
- 大小:209.50 KB
- 文档页数:13

量纲分析方法的基本原理是Π定理。
设所选取的单位制中基本量的数目为m,它们是,物理量Q的量纲式为(1)对上式取对数,则有(2)若是m维空间的“正交基矢”,则就是“矢量”ln[Q]在基矢量上的投影,或者说是它的“分量”。
于是,量纲式可以简写为。
所谓几个物理量的量纲独立,是指无法用它们幂次的乘积组成无量纲量。
用矢量语言表达,就是代表它们量纲的“矢量”线性无关。
在m维的空间内最多有m个彼此线性无关的矢量。
m个矢量(i =1,2, …,m)线性无关的条件是它们组成的行列式不等于0:(3)P定理表述为设某物理问题内涉及n个物理量(包括物理常量,而我们所选取的单位制中有m个基本量(n>m),则由此可组成(n-m )个无量纲的量,在物理量之间存在的函数关系式(4)可表示成相应的无量纲形式(5)或者把解出来:(6)n=m的情况下,有两种可能:若的量纲彼此独立,则不能由它们组成无量纲的量;若不独硫还可能组成无量纲的量。
运用P定理作量纲分析示范如下:在力学问题中,选取质量(M)、长度(L)、和时间(T)作为基本物理量,故m=3。
例1:设一均匀细棒,长度为l,质量为m。
求绕过中点O的转轴的转动惯量 J(如右图)。
解:转动惯量的量纲式为,任意形状的转动惯量可写为, 代表一组能确定其几何形状的无量纲参量,如长方形的两边长之比;三角形的底与高之比,对于几何形状相似的物体,函数是等同的,对于那些只用一个特征长度即可完全确定的几何形体,如正方体,长方体,立方体,圆,球……等,退化为一个未知常数,用k表示。
所以,对细棒,转动惯量J可以写成(7)已知平行轴定理(8)(这里是物体对通过其质心的某个特定轴的转动惯量,d是将此转轴平行移动距离。
)设式(7)中的J代表细棒的,即过质心o并垂直于棒的转轴的转动惯量。
将转轴移至端点,则, 按(8)式(9)设想棒平均分成两段,每段质量为,长度为 ,按(9)式, 两段绕同一转轴的转动惯量之和应等于总转动惯量,即: ,∴∴ 由(7)式得, 由(9)式得例2.; 由开普勒第三定律推论万有引力的性质。



2020年注册土木工程师(水利水电工程)《专业基础考试》真题及详解单项选择题(每题2分。
每题的备选项中只有一个最符合题意。
)1.下列哪项是量纲分析的基本原理?()A.动力相似原理B.量纲相似原理C.量纲统一原理D.量纲和谐原理【答案】D【解析】量纲是基本物理量的度量单位,即物理量的属性(类别)。
在每一具体的液体流动中,与之相联系的各物理量之间存在着一定的关系且可用物理方程式表示。
利用量纲和谐原理就可以分析液流物理量之间的关系并在一定程度上导得描述水流运动的物理方程式,这种方法称为量纲分析法。
它是解决水力学问题的有效途径之一。
量纲分析方法的理论基础就是量纲和谐原理,即凡是正确反映客观规律的物理方程式,其各项的量纲都必须是相同的或是一致的,只有方程式两边的量纲相同,方程式才成立。
2.有一河道泄流时,流量Q=120m3/s,过水断面为矩形断面,其宽度b=60m,流速v=5m/s,河道水流的流动类型为()。
A.急流B.缓流C.临界流D.不能确定【答案】A【解析】解法一:比较河流水深(h)与临界水深(h c)的关系,0.742mch===h=Q/(vb)=120/(5×60)=0.4m;由于h c>h,因此判断河道的流动类型为急流。
解法二:计算弗劳德数,2.531Fr===>因此判断河道的流动类型为急流。
3.水力最佳断面是指()。
A.面积一定,湿周最小的断面B.湿周一定,面积最小的断面C.最小糙率的断面D.最低造价的断面【答案】A【解析】明渠均匀流基本公式为:12523122/31i AQ A R in nχ===式中,i为底坡;n为粗糙系数;A为断面面积;R为水利半径;χ为湿周。
当i、n和A一定时,把使流量Q最大的断面形状,或者使水力半径R最大,即湿周最小的断面形状,定义为水力最佳断面。
4.渗流运动在计算总水头时,不需要考虑下列哪项?()A.测压管水头B.流速水头C.压强水头D.位置水头【答案】B【解析】渗流是指流体在孔隙介质中的流动。

《化⼯原理》课程中的量纲分析法教育教学论坛EDUCATION TEACHING FORUM 2019年1⽉第2期Jan.2019NO.2表1基本量、基本量纲及其SI 单位和名称《化⼯原理》课程中的量纲分析法收稿⽇期:2018-04-20作者简介:潘鹤林(1965-),男(汉族),江苏扬州⼈,硕⼠,副教授,主要从事化⼯过程开发和化⼯原理课程教学。
《化⼯原理》课程是化⼯类专业重要的专业基础核⼼课程之⼀,在如数学、⼤学物理和物理化学等学科的基础上,以化⼯过程中的单元操作为对象,研究和解决化⼯过程中的⼯程问题。
化⼯⽣产过程中涉及的物料种类各异,单元操作的类型也较多,过程涉及的设备结构和⼏何形状各不相同,操作条件迥异。
⾯对这些复杂⽽真实的⼯业实际过程,难以采⽤统⼀的研究⽅法处理单元操作问题。
要解决复杂⼯程问题就要求技术⼈员掌握化学⼯程学科的研究⽅法,简便有效地处理实际⼯程问题。
《化⼯原理》课程的学科基础地位由此可见⼀斑。
量纲分析法是⼀种⼯程实验研究⽅法,在《化⼯原理》课程中是有⼴泛应⽤的重要知识点之⼀,正确⽽熟练掌握该⽅法对学⽣解决化⼯上的实际⼯程问题具有重要的指导作⽤。
20世纪初提出的量纲分析法是在经验和实验理论的基础上,根据物理定律量纲齐次性的原则,确定⽣产过程特定现象包含的各物理量之间的关系。
经量纲分析,可以正确地分析各变量之间的关系,从⽽简化实验。
《化⼯原理》课程多次出现复杂问题,如直管湍流摩擦阻⼒损失计算、传热的对流给热系数计算、传质过程中传质系数的计算等均应⽤量纲分析法后得以圆满解决,可见这⼀⽅法能够使复杂问题的处理变得简化、可⾏。
利⽤量纲分析法可将诸多实验因素组合为⽆量纲数群或准数,准数的数⽬⽐实验因素的数⽬少,这样就可以减少实验的次数,并能得到简明的数学关联式,实验数据的整理⼯作得到实质性简化。
⼯程技术上的经验关联式通常是⽐较复杂的,采⽤单因素法进⾏实验时,每次只改变⼀个变量,固定其他变量,在⼯程实验中难以实现。

第七章相似原理与量纲分析第一节相似的概念在几何学的学习中,人们已建立起几何图形的相似概念。
工程中很多物理现象也有相似的特点。
人们把可用同样形式数学式表达的物理现象群称为同类现象。
但属于同类现象的不同物理现象不一定都相似,只有当同类不同物理现象中,它们的各自空间中相对应的各点上的表征现象特性的同类物理量的比例,在时间上相对应的瞬间为常数时,两个同类的不同物理现象才相似。
由于物理现象都是在一定的空间中进行的,相似的物理现象应在相似的空间中进行。
所以完整的物理现象相似应包含两个相似概念,即几何相似和物理现象本身的相似,其中包括初始条件和边界条件的相似。
后者习惯被称为物理现象相似。
一、几何相似几何相似即几何图形相似,如两个相似三角形的对应边长成比例,其比例常数可称为相似常数。
如教材85页图7-1所示。
其中的C l称为相似常数,由于相似常数是同类量之比值,因此相似常数无量纲。
二、物理现象相似如教材86页图7-2所示为物理现象相似。
质点A、B沿几何相似的路径作相似运动。
针对物理现象相似,有如下推论:(1)如果物理现象相似,则在相应的时刻,它们空间任意相应点上的任意同名物理量应该成比例关系;(2)如果物理现象相似,在选取相似的物理量作为量度单位后,将描述物理现象的数学方程式转换成的无量纲方程式应该一样。
需要注意的是,在几何相似时,相似常数只有一个,而物理相似时,由于方程式中的物理量有很多种,不同名的物理量都有各自的相似常数,如空间相似常数C l=l/l’,时间相似常数Ct=t/t’,速度相似常数Cv=v/v’等。
各相似常数又有一定的约束关系,如对两相似质点A和B运动的物理现象,v=l/t和v’=l’/t’,则即或这就是相似物理现象中相似常数关系的附加条件,C称为相似指示数或相似指标,用它来控制相似常数的关系。
如果两现象相似,则其相似指标等于1。
由教材86页图7-2所示物理现象:此式等号左右由物理参数组成的项为无量纲的不变量,或称定数,可取定数的统一符号表示,即此式说明,像质点运动那样的物理现象相似时,则对应点上由各相关参数组成的无量纲数在对应的时间上具有相同的数值,如Ho。

第一讲 1关于量纲分析法量纲分析法是一种解决物理、化学和工程问题的方法,它可以通过分析问题中的物理量的量纲关系,将问题简化,较为准确地估算出某些物理量的数量关系。
量纲是描述物理量的属性的量,它体现在物理量的单位上。
例如,长度的单位是米,质量的单位是千克,时间的单位是秒等等。
在物理、化学和工程问题中,一个物理量的单位需要严格保持一致,因为这个单位可以影响到任何计算结果的准确性。
量纲分析方法可以帮助工程师和科学家在一些情况下,快速地估算某些物理量的数量关系,而不必依靠实验数据或进行复杂的计算。
使用该方法需要首先确定问题中哪些物理量是重要的,然后将它们表示成独立的基本物理量的乘积形式,例如,长度、质量和时间。
接下来,将这些物理量进行量纲分析,确定它们之间的关系,得到以基本物理量的某些函数表示的量纲方程。
该方程描述了物理量之间的数量关系,并且可以用来估算未知的物理量。
例如,当需要知道管道中水流速度的数量关系时,可以使用量纲分析方法来估算它的大小,而不必测量或计算它。
量纲分析法的一个重要应用是在建立数学模型时的物理量选择和相似性问题。
例如,当设计一个飞机模型时,需要考虑到飞机原型中的物理量之间的相似性关系,这可以通过使用量纲分析方法来实现。
该方法还可以帮助工程师和科学家预先估算某些物理量的变化范围,这对于解决实际问题非常有用。
总之,量纲分析法是工程和科学领域中重要的方法之一,它可以帮助工程师和科学家更快速地解决问题。
它的应用范围非常广泛,包括飞机设计、渗透透过、化学反应等等。
然而,该方法仅仅是一个审慎预估的工具,它必须与实验和计算相结合,以确定物理量之间的真实关系。
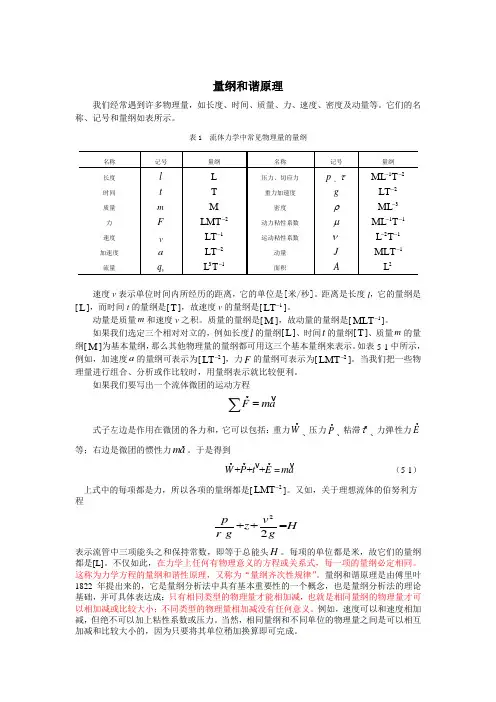
量纲和谐原理我们经常遇到许多物理量,如长度、时间、质量、力、速度、密度及动量等。
它们的名称、记号和量纲如表所示。
表1 流体力学中常见物理量的量纲速度v 表示单位时间内所经历的距离,它的单位是[米/秒]。
距离是长度l ,它的量纲是[L ],而时间t 的量纲是[T ],故速度v 的量纲是[1LT -]。
动量是质量m 和速度v 之积。
质量的量纲是[M ],故动量的量纲是[1MLT -]。
如果我们选定三个相对对立的,例如长度l 的量纲[L ]、时间t 的量纲[T ]、质量m 的量纲[M ]为基本量纲,那么其他物理量的量纲都可用这三个基本量纲来表示。
如表5-1中所示,例如,加速度a 的量纲可表示为[2LT -],力F 的量纲可表示为[2LMT -]。
当我们把一些物理量进行组合、分析或作比较时,用量纲表示就比较便利。
如果我们要写出一个流体微团的运动方程F ma =∑式子左边是作用在微团的各力和,它可以包括:重力W 、压力P 、粘滞τ、力弹性力E等;右边是微团的惯性力ma。
于是得到+++W P E ma t =(5-1)上式中的每项都是力,所以各项的量纲都是[2LMT -]。
又如,关于理想流体的伯努利方程2++=2v p z H g gr 表示流管中三项能头之和保持常数,即等于总能头H 。
每项的单位都是米,故它们的量纲都是[L]。
不仅如此,在力学上任何有物理意义的方程或关系式,每一项的量纲必定相同。
这称为力学方程的量纲和谐性原理,又称为“量纲齐次性规律”。
量纲和谐原理是由傅里叶1822年提出来的,它是量纲分析法中具有基本重要性的一个概念,也是量纲分析法的理论基础,并可具体表达成:只有相同类型的物理量才能相加减,也就是相同量纲的物理量才可以相加减或比较大小;不同类型的物理量相加减没有任何意义。
例如,速度可以和速度相加减,但绝不可以加上粘性系数或压力。
当然,相同量纲和不同单位的物理量之间是可以相互加减和比较大小的,因为只要将其单位稍加换算即可完成。

量纲分析与无量纲化量纲分析是物理学中的一种重要方法,用来研究物质世界中物理量之间的依存关系。
它的基本思想是,将物理量表示成无量纲形式,通过对无量纲式进行分析,可以得到物理量之间的关系,进而推导出各种物理规律和方程。
量纲分析的基本步骤是:选择若干个具有重要意义的物理量作为基本量,通过观察实验结果、提取经验关系或者运用理论推导等方法,找出它们之间的依存关系,建立起无量纲关系式。
然后在物理量之间建立起类似的关系,通过对齐每一项的量纲,可以求得未知物理量的量纲和关键系数。
在量纲分析中,无量纲化是一个非常重要的步骤。
无量纲化的目的是消除物理量的量纲影响,使得物理规律和方程能够更加简洁地表达。
常见的无量纲化方法有:1.选取合适的基本量纲:通常选择与问题相关的几个基本量纲,例如长度(L)、质量(M)和时间(T)。
根据具体问题的特点,还可以引入其他基本量纲,例如温度(Θ)和电流(I)等。
2.选择特征量:根据问题的特点,选择合适的特征量,例如流速、频率或能量等。
特征量可以帮助确定无量纲化中的关键变量。
3.建立无量纲关系:根据选取的基本量纲和特征量,建立起无量纲关系式。
在建立关系式时,需要将问题中的各个物理量分别表示成有关基本量纲和特征量的函数。
4.对无量纲式进行分析:通过对无量纲式进行分析,可以得到物理量之间的关系。
例如,通过无量纲化的关系式可以得到流体力学中的雷诺数和流固耦合问题中的康普顿数等。
量纲分析和无量纲化在科学研究和工程实践中具有广泛的应用。
它能够帮助研究人员理解物理问题的本质,简化问题的描述和计算,加快问题的求解速度,并提高问题的求解精度。
在各个领域中,如物理学、化学、工程、生物学等,都广泛使用了量纲分析和无量纲化方法。
总之,量纲分析和无量纲化是一种有效的工具,它能够帮助解决复杂的物理问题,揭示出物理现象背后的规律与关系。
无量纲化可以让我们更加清晰地认识物理世界的本质,简化问题的描述和计算,加速问题的求解过程,并提高问题的求解精度。


计算实验技术量纲分析指导计算实验技术在各种科学研究中起着重要的作用。
量纲分析是一种常用的方法,用于理解和描述物理系统之中的各个物理量之间的关系。
本文将介绍量纲分析的基本原理,并讨论如何将量纲分析应用于计算实验技术中。
量纲分析是一种将物理量表示为基本量的幂次乘积的方法。
在物理学中,基本量包括长度、质量和时间。
因此,任何物理量都可以由这些基本量表示。
例如,速度可以表示为长度的一次幂、时间的负一次幂的乘积。
在量纲分析中,我们通常使用带有方括号的符号来表示量纲。
例如,[L]代表长度的量纲,[T]代表时间的量纲,[M]代表质量的量纲。
在计算实验技术中,量纲分析可以用于判断模型的有效性和分析模型的特性。
通过将物理系统中的各个变量表示为基本量的幂次乘积,我们可以比较各个物理量之间的量级。
如果两个物理量具有相同的量级,那么它们之间可能存在某种关系,可以通过数学模型来描述。
例如,在流体力学研究中,通过将力、速度、密度和长度表示的量纲进行比较,我们可以得到雷诺数,用于描述流体在不同速度下的行为。
量纲分析也可以用于设计实验和数据处理。
在进行实验研究时,我们可能要调整实验条件,例如改变速度、大小或密度等。
通过量纲分析,我们可以判断哪些因素对实验结果具有重要影响。
如果物理量的量纲相差很大,那么它们可能对实验结果的影响较小。
相反,如果物理量的量纲相差很小,那么它们可能对实验结果的影响较大。
因此,根据量纲分析的结果,我们可以选择适当的实验条件,以提高实验结果的准确性和可靠性。
量纲分析在数据处理中也起着重要的作用。
在分析实验数据时,我们通常会得到一组带有误差的数据。
通过量纲分析,我们可以判断和验证不同物理量之间的关系,并确定合适的数据处理方法。
例如,在传热实验中,我们可以通过量纲分析来确定温度场、传热系数和热流量之间的关系,并根据实验数据进行验证和调整。
除了上述应用,量纲分析还可以用于理解和预测物理系统中的各种现象。
通过对物理量的量纲进行比较,我们可以推导出物理量之间的关系。
物理学中的量纲分析原理物理学在物质世界中发挥着不可替代的作用。
因为物理学是研究物质及其运动规律的学科,所以,衡量器械的量纲便成了物理学的重要方向之一。
量纲分析原理是其中一大重要工具,通过对物理量的分类和内在联系的分析,帮助研究者解决少数特殊情况下的实验与计算问题,它在理论计算方面的应用尤其普遍。
量纲及量纲变量的定义量纲是一个独立的物理量,可更好地描述物理量在物理学理论和应用中的性质和关系。
物理量的范畴包括力、功、势能、速度、加速度、测量、时间等等,它们通过不同的单位来描述规模。
这些单位经常以国际单位制的方式表示。
其中最常见的量纲是质量、长度、时间、温度和电流。
量纲分析原理的基本思路是将物理量分为基本量和衍生量。
基本量,即质量、长度、时间、温度和电流,是建立系统国际单位制的基础,也称作基本量纲。
而衍生量是由基本量纲组成的复杂物理量,尤其重要的是它是无量的。
例如,亮度是一种衍生量纲。
如果某量需要几个量纲乘幂的乘积来表示,它便是衍生量纲。
对应到物理学计算中,如果某个物理量由若干个物理量乘积组成,则称这个物理量具有若干个基本量纲。
对于基本量纲,只有一个单位。
而由多个基本量纲组成的量纲,需要明确选定一个量纲,比如力的量纲可以用牛顿,也可以用磅。
量纲分析原理的实例运用在物理学中,往往需要确定一个物理量的具体数值。
例如,想要用弹簧任务对重物的质量进行测量,并且得到的弹簧的伸长长度是1.2毫米,那么就需要量纲分析来得到相应的公式。
首先,需要将弹簧的伸长长度作为衍生量纲,而重物的质量作为基本量纲。
这样,在衍生量和基本量纲之间就有了一个长度作为衍生数量。
然后,就需要根据这个关系将弹簧的单位长度改变成质量单位。
具体流程可以描述为:量纲分析原理的另一个应用是在研究中解决少数特殊情况下的实验与计算问题。
例如,在气体动力学实验中,如果物理量的变化过快导致实验结果的精度严重受到影响,那么就可以通过将变化过程的变化率用同样的量纲修改得到相对稳定的变化率来解决。
基础课量纲分析法教学举例(下)
第二步,学生进行练。
学生在第一步中研究到的基础知识,在这一步中将掌握并运用到实际情况中去。
比如,学生可以用基础课量纲分析法分析一篇文章,分析出文章的主题、结构、文体等。
例如,学生可以分析一篇关于儿童发展的文章,分析出文章的主题,以及文章中用到的结构和文体。
第三步,学生进行反思。
在这一步,学生可以思考自己在分析文章时遇到的困难,以及自己的分析是否准确、可行。
学生可以思考,自己是否可以从更多的角度准确地分析文章,以及通过什么方式更好地分析文章。
第四步,学生进行检验。
在这一步,学生可以检验自己的分析是否准确,检验自己的理解是否正确。
比如,学生可以找出几篇文章,用刚研究的基础课量纲分析法分析这几篇文章,进行检验。
第五步,让学生进行总结。
在这一步,学生可以总结自己在分析文章时遇到的问题,以及分析文章的技巧。
学生可以总结,基础课量纲分析法能够帮助他们更准确、更有效地把握文章的结构、文体等。
总之,通过基础课量纲分析法教学可以帮助学生更好地分析文章,提高学生的文章分析能力。
在教学过程中,老师可以把学生分成小组,让学生之间进行讨论,激发学生的研究兴趣,
让学生在交流中充分发挥自己的潜力。
同时,老师也可以定期给学生提出分析文章的练,让学生熟练掌握基础课量纲分析法。