统计学原理计算题复习(六种题型重点)

资料内容仅供您学习参考，如有不当或者侵权，请联系改正或者删除。

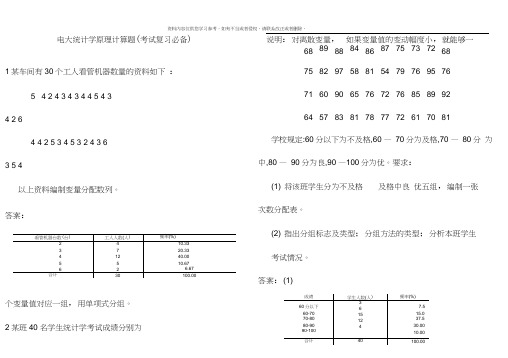
电大统计学原理计算题(考试复习必备) 1某车间有30个工人看管机器数量的资料如下：5 4 2 4 3 4 3 4 4 5 4 34 2 64 4 25 3 4 5 3 2 4 3 63 5 4以上资料编制变量分配数列。

答案：说明：对离散变量，如果变量值的变动幅度小，就能够一68898884868775737268758297588154797695767160906576727685899264578381787772617081学校规定:60分以下为不及格,60 —70分为及格,70 —80分为中,80 —90分为良,90 —100分为优。

要求：(1) 将该班学生分为不及格及格中良优五组，编制一张次数分配表。

(2) 指出分组标志及类型；分组方法的类型；分析本班学生考试情况。

答案：(1)个变量值对应一组，用单项式分组。

2某班40名学生统计学考试成绩分别为（2）分组标志为”成绩”，其类型为”数量标志”； 分组方法为：变量分组中的组距式分组，而且是开口式分 组；本班学生的考试成绩的分布呈两头小 ，中间大的”正态分布”的形态。

3某企业10月份生产情况（单位：台）:计算该企业各车间和全厂产量计划完成 ％。

计算产量计划完成情况全厂产量计划完成96.8%,尚差3.2% 4某工业集团公司工人工资情况按月工资（元）分组 企业个数 各组工人所占比重（％）计算该集团工人的平均工资。

计算表如下月工资组中值X各组工人比重 f（ %）fX?丄f450 20 90.0 550 25 137.5 650 30 195.0 750 15 112.5 850 10 5.0 合计100620.0xx ?f 620元f该工业集团公司工人平均工资 620元。

某厂三个车间一季度生产情况如下 ：第一车间头际产量为 190件，完成计划 95%;第二车间实际产量250件，完成计划100%；第三车间实际产量 609件，完成 计划105%,三个车间产品产量的平均计划完成程度为：95%100% 105% 100%3另外，一车间产品单位成本为18元/件，二车间产品单位成本12元/件，三车间产品单位成本15元/件，则三个车间平均单位成本为：18 12 1515元/件3以上平均指标的计算是否正确？如不正确请说明理由并改正。

统计学原理考试题一、选择题。

1. 下列哪个不是统计学的基本概念？A. 总体。

B. 样本。

C. 参数。

D. 统计量。

2. 在统计学中，描述总体特征的数字指标称为什么？A. 参数。

B. 样本。

C. 统计量。

D. 方差。

3. 下列哪个不是描述数据集中心位置的统计量？A. 均值。

B. 中位数。

C. 众数。

D. 标准差。

4. 如果一个数据集的标准差很大，表示什么？A. 数据集的离散程度大。

B. 数据集的离散程度小。

C. 数据集的中心位置偏移。

D. 数据集的分布形状不规则。

5. 在统计学中，概率分布的形状是由哪个参数控制的？A. 均值。

B. 标准差。

C. 方差。

D. 自由度。

二、填空题。

1. 样本容量为100，样本均值为30，总体标准差为5，样本标准误差为？答，0.5。

2. 一组数据的中位数为35，下四分位数为30，上四分位数为40，该组数据的四分位差为？答，10。

3. 某随机变量X的期望为20，方差为16，标准差为？答，4。

4. 在正态分布曲线上，距离均值两个标准差之外的数据占比约为？答，95.44%。

5. 在t分布中，自由度为10时，t分布的峰度为？答，3。

三、简答题。

1. 请解释参数和统计量的区别。

答，参数是用来描述总体特征的数字指标，如总体均值、总体标准差等；统计量是用来描述样本特征的数字指标，如样本均值、样本标准差等。

参数是对总体进行推断的依据，而统计量是对样本进行推断的依据。

2. 请解释正态分布曲线的特点。

答，正态分布曲线是一个钟形曲线，以均值为中心对称，曲线两侧尾部逐渐下降。

正态分布曲线的均值、中位数、众数重合，曲线的标准差决定了曲线的宽窄。

在正态分布曲线上，距离均值一个标准差之外的数据占比约为68%，距离均值两个标准差之外的数据占比约为95.44%，距离均值三个标准差之外的数据占比约为99.73%。

3. 请解释t分布与正态分布的区别。

答，t分布与正态分布的区别在于t分布是以样本容量为自由度的分布，而正态分布是以总体为基础的分布。

《统计学原理》练习册习题复习重点及参考答案一、填空题（10×1＝10分）第一章：总论1.统计科学3.集合（或整体）4.总体单位6.总体单位名称8.总体单位总体12.品质数量14.定类尺度、定序尺度、定距尺度、定比尺度第二章：统计资料的搜集与整理1. 全面调查非全面调查2. 一次性调查经常性调查 4. 选择分组标志 6. 专门组织一次性全面10.现象一定标志11.分组名称次数15. 普查22. 品质标志数量标志23.各组界限最小最大26.重叠间断27 U型J型第三章：统计数据的描述与显示1.总量指标2.时期指标时点指标6．结构相对数9．变量值次数14分散集中17综合性18集中趋势22零28全距标准差离散系数30. 95％21.8％31最小第四章：抽样调查2正比反比4无偏性一致性有效性9重置抽样不重置抽样10随机原则总体数量特征11样本21抽样极限误差22抽样平均误差第五章：相关分析与回归分析1相关关系3单相关9回归系数11函数r＝114相关16确定的随机的20正相关负相关第六章：时间数列6环比定基定基环比8时间9总规模或总水平16 定基发展速度17环比发展速度第七章：统计指数法3综合指数平均指数12加权算术平均指数加权调和平均指数21基期质量指标报告期数量指标27 0.6％二、单项选择题（15×1＝15分）第一章：总论1④3③4④5.④6.②7②8.②9.①11.③13④17②18①20②22①24①第二章：统计资料的搜集与整理1①5③7③11②13③17④20①21②23②24④27②31②32③36②第三章：统计数据的描述与显示1③2①3④5③7②8②10④18③24①25①31②34①35②38②41②45③48①52③54①67③76④第四章：抽样调查2④4②7①12③15①17①20①21③27②28④34③35④36②37①43②51④53②第五章：相关分析与回归分析2②3②5①6②8①14①16③18①21③29①30①第六章：时间数列2④3③4①6③7②15③19④26②30③第七章：统计指数法2②5②9③13③15③16①17③36②40①44①50②三、多项选择题（5×2＝10分）第一章：总论1①③④2①③⑤3①②⑤5③④7②③④⑤8③⑤10①②③11①④13③⑤18①②③⑤19①③④20②③⑤22①③④⑤第二章：统计资料的搜集与整理2②⑤4①④⑤5①③12④⑤16①④⑤23①②③27①②③④⑤29②④⑤33②③④⑤36①③38②③第三章：统计数据的描述与显示2③④⑤3①③④⑤5②④6①③7①②③④⑤12①③④⑤13①②③⑤15①③20②④⑤24②④32.①④⑤34③⑤36①②④40②④⑤ 47③④50①③第四章：抽样调查1①②⑤2①②③④5①⑤7①②③④8①③④⑤11②③22②③④26①②③⑤31①②第五章：相关分析与回归分析2②③④7①④11①④⑤17①③19①②⑤24②③④⑤27②⑤第六章：时间数列2②④3①②③⑤4①②④⑤8②⑤12①②④⑤18③⑤第七章：统计指数法2②③4②③④11③④24①②③29②⑤四、判断改错题（5×2＝10分）第一章：总论3.错，改正：“不考虑”改“考虑”5.错，改正：“整数和小数”改“整数”6.错，改正：“年龄、性别、民族等”删除7 .错，改正：“离散”改“连续”，“计数”改“测量或计算”第二章：统计资料的搜集与整理1.错，“表现形式”改为“总体数量状况”，4对，6对，10对，11错，“组距和组数”改为“确定分组标志和各组界限”，16错，“定性”改为“定性或定量”，19错，“一部分样本”改为“重点”，“全面调查”改为“非全面调查”第三章：统计数据的描述与显示1错，“平均 ”改“相对”，2错，“时点间隔成正比”改“时点间隔无关”，6对，8对，10对，14错，“简单式”改“加权式”，“加权式”改“简单式”，15对，18错，“平均数”改“相对数”，22错，“越好”改“越差”，27对，32错，“离差”改“离差绝对值”，33对第四章：抽样调查3对，7对，8错，n σ改为nσ，9错，“样本”改“总体”，11对14对16对21对25对 第五章：相关分析与回归分析2对，4对，5错，“数量变动关系”改“相关程度和相关方向”，7错，“可以相同也可以不相同”改“只能相同”，12错，“都是上升的”改“相同方向”，15错，改为“回归分析两个变量，自变量是确定变量，因变量是随机变量；而相关分析两个变量都是随机变量”，17错，“回归系数”改“相关系数”，18对，19对第六章：时间数列1错，“变量”改“时间”，2对，13错，“增长”改“发展”，14对，20对21错，“增长”改“发展”、“增长”改“发展”第七章：统计指数法1错，“数量”改“质量”，2对，11对，15错，“综合”改“总量”五、简答题（4×5＝20分）第一章：总论“统计”一词的涵义及其之间的关系统计信息的主要特征什么是统计学？其研究对象第二章：统计资料的搜集与整理统计调查误差的种类及其产生原因统计分组的类型及其主要内容统计分组中，分组变量的类型有几种，其组限是如何确定的？第三章：统计数据的描述与显示时期指标和时点指标有何不同？权数及其作用第四章：抽样调查什么是抽样调查？它具有哪些提点？抽样误差的影响因素有哪些？第五章：相关分析与回归分析相关关系的种类是如何划分的？第六章：时间数列什么是时间数列？其作用是什么？编制时间数列的原则第七章：统计指数法什么是同度量因素？在综合指数的编制中，同度量因素确定的一般原则指数的分类有哪些？六、计算题（35分）第三章：统计数据的描述与显示P35：16．%95.14,8.188,126311====x v x σσσ%6.16,212,12752222====x v x σσσ 说明：因为甲企业的离散系数小，所以，甲企业的平均工资更具有代表性。

统计学原理题库知识点1、问答题定距尺度与定比尺度有何区别？正确答案：定距尺度也称间隔尺度，是对事物类别或次序之间间距的计量，它通常使用自然或度量衡单位作为计量尺度。

定比尺度是在定距尺度的基础上，确（江南博哥）定可以作为比较的基数，将两种相关的数加以对比，而形成新的相对数，用以反映现象的构成、比重、速度、密度等数量关系。

2、名词解释统计活动正确答案：是在一定的理论指导下，采用适宜的科学方法搜集、处理统计资料的一系列调查研究过程。

3、问答题影响必要样本容量的因素有哪些？正确答案：①总体标志变动度；②抽样极限误差；③概率保证程度；④抽样方式和方法4、单选下列不属于划分控制单元的标准的是()。

A.实际销售额B.现有客户数C.潜在客户数D.地理面积正确答案：A5、名词解释直接观察法正确答案：又称直接观察法，是由调查人员到现场亲自对调查对象进行观察、计量、登记，以取得第一手资料的方法。

6、填空题统计总体具有四个基本特征，即数量性、总体性、变异性和（）正确答案：具体性7、判断题只有在组距中值两侧呈对称分布，才能使用组中值作为该组数据的代表值正确答案：错8、名词解释统计图正确答案：利用统计资料绘制成的几何图形或具体形象9、问答题统计相对数的种类？正确答案：（1）计划完成相对数。

是实际完成数与计划数的比值。

（2）结构相对数。

是总体各组成部分数值与总体总数值的比值。

（3）比例相对数。

总体中某一组的指标数值与总体中另一组的指标数值的比值。

（4）动态相对数。

某现象报告期数值与同一现象基期数值的比值。

（5）比较相对数。

某类现象的数值与不同空间同类现象的数值的比值。

（6）强度相对数。

某一现象数值与另一有联系但性质不同的现象数值的比值。

10、问答题解释拉氏指数和帕氏指数。

正确答案：（1）同度量因素固定在报告期所计算的综合指数成为帕氏指数（2）同度量因素固定在基期水平上所编制的综合指数都统称为拉氏指数。

11、问答题统计调查方案的设计包括哪几部分？正确答案：⑴确定调查目的；⑵确定调查对象和调查单位；⑶确定调查项目和拟定调查表；⑷确定调查时间和调查期限；12、单选当边际产量大于平均产量时，平均产量（）A.递减B.不变C.递增D.先增后减正确答案：C13、单选某机床厂要统计该企业的自动机床的产量和产值，上述两个变量是（）。

第三章：编制次数分配数列1．根据所给资料分组并计算出各组的频数和频率，编制次数分布表；根据整理表计算算术平均数。

例题：某单位40名职工业务考核成绩分别为: 68 89 88 84 86 87 75 73 72 68 75 82 97 58 81 54 79 76 95 76 71 60 90 65 76 72 76 85 89 92 64 57 83 81 78 77 72 61 70 81单位规定：60分以下为不及格，60─70分为及格,70─80分为中，80─90分为良，90─100分为优。

要求：（1）将参加考试的职工按考核成绩分为不及格、及格、中、良、优五组并编制一张考核成绩次数分配表；（2）指出分组标志及类型及采用的分组方法；（3）根据考核成绩次数分配表计算本单位职工业务考核平均成绩； （4）分析本单位职工业务考核情况。

解答：（１）该企业职工考核成绩次数分配表：成 绩(分) 职工人数（人） 频率（％）不及格（60以下） 3 7.5 及格 （60－70） 6 15 中 （70－80） 15 37.5 良 （80－90） 12 30 优 （90－100） 4 10 合 计 40100（2）此题分组标志是按“成绩”分组，其标志类型是“数量标志”； 分组方法是“变量分组中的组距式分组的等距分组，而且是开口式分组”；（3）根据考核成绩次数分配表计算本单位职工业务考核平均成绩。

（4）分析本单位职工考核情况。

本单位的考核成绩的分布呈两头小，中间大的“钟形分布”（即正态分布），不及格和优秀的职工人数较少，分别占总数的7.5%和10%，本单位大部分职工的考核成绩集中在70-90分之间，占了本单位的为67.5%，说明该单位的考核成绩总体良好。

)(774095485127515656553分=⨯+⨯+⨯+⨯+⨯==∑∑f xf x第四章：计算加权算术平均数、加权调和平均数（已知某年某月甲、乙两农贸市场A 、B 、C 三种农产品价格和成交量、成交额资料，试比较哪一个市场农产品的平均价格 较高？并说明原因。

统计学原理题库及真题及答案统计学原理题库1、计算均值与极差：（1）若一组数据来自正态分布，且X的均值为20，极差为2，则X的标准差是多少？答案：标准差为1。

（2）若得到一组数据X=(1,2,3,4,5),求其中的均值和极差？答案：均值为3，极差为4.2、计算样本方差及样本标准差（1）若某一组数据来自正态分布，均值为20，标准差为2，那么它的方差式多少？答案：方差为4。

（2）若得到一组数据X=(1,2,3,4,5),求此时的样本方差和样本标准差？答案：样本方差为2，样本标准差为1.41。

3、计算置信区间（1）若抽样样本的样本均值为21，方差为6，考虑95%置信水平，求此时样本均值的置信区间？答案：置信区间为（19.73，22.27）（2）若样本的样本均值为20，方差为25，考虑99%置信水平，求此时样本均值的置信区间？答案：置信区间为（17.4，22.6）4、计算卡方检验（1）若抽取样本数为1000，平均值为20，标准差为2，求其中的卡方检验值？答案：卡方检验值为0.2。

（2）若抽取样本数为1000，平均值为21，标准差为3，求其中的卡方检验值？答案：卡方检验值为2.4。

5、计算假设检验（1）若某一组数据来自正态分布，且假设检验值为3，假设显著水平为5%，求这次假设检验的结果？答案：假设检验拒绝零假设，支持备择假设。

（2）若某一组数据来自正态分布，且假设检验值为1.5，假设显著水平为5%，求这次假设检验的结果？答案：假设检验不拒绝零假设，也不备择假设。

统计学原理真题及答案：1、某样本抽样后的数据的均值为30，样本方差为25，求这组数据的极值？答案：极差为50。

2、某样本抽取后，总体均值为20，总体标准差为3，全样本大小为100，求95%置信区间？答案：（18.87，21.13）3、某样本抽取后，总体均值为21，方差为25，样本大小为250，求99%置信度时的样本均值置信区间？答案：（20.2，21.8）4、某样本抽样后，样本总体均值为18，样本方差为36，抽取的样本数量为400，求卡方检验的检验结果？答案：拒绝零假设，支持备择假设。

统计学期末（单选、10个填空、5个判断、三个计算、一道论述）第一章导论1、统计学是收集、处理、分析、解释数据并从数据中得出结论的科学。

分析数据：分为描述统计方法和推断统计方法两种方法。

描述统计：研究的是数据收集、处理、汇总、图表描述、概括与分析等统计方法。

推断统计：是研究如何利用样本数据来推断总体特征的统计方法。

推断统计内容包含参数估计和假设检验2、统计数据的类型：（1）按照采用的计量尺度不同，可以将统计数据分为分类数据、顺序数据与数值型数据。

注意：分类数据和顺序数据都是表现事物的品质特征，通常是用文字来表述的，其结果均表现为类别，因此可以通称为定性数据或品质数据(qualitative data)。

数值型数据说明的是现象的数量特征，通常用数值来表现，因此可以统称为定量数据或数量数据(quantitative data)。

(2)按照统计数据的收集方法，可以将统计数据分为观测数据和实验数据。

(3)按照被描述的现象与时间的关系，可以将统计数据分为截面数据、时间序列数据（和面板数据 panal data）。

3、抽样独立性问题：总体区分为有限总体和无限总体，目的是为了判别在抽样中每次抽取是否独立（类似抽小球是否放回的问题）。

在统计推断中，通常是针对无限总体的，因而通常把总体看做随机变量（random variable）。

统计上的总体通常是一组观测数据，而不是一群人或者一些物品的简单集合。

4、统计指标按其所反映的数量特点和作用不同，分为数量指标、质量指标。

样本（sample）是从总体中抽取的一部分元素的集合，构成样本的元素的数目称为样本量（sample size）。

抽样的目的是根据样本提供的信息推断总体的特征。

5、总体参数（parameter）是用来描述总体特征的概括性数字度量，是研究者想要了解的某种特征值。

样本统计量（statistic）是用来描述样本特征的概括性数字度量，是根据样本数量计算出来的一个量。

统计学考试题型及知识点复习在学习统计学的过程中，了解考试题型以及对相关知识点进行系统复习是取得好成绩的关键。

下面我们将详细探讨统计学常见的考试题型，并对重要知识点进行梳理。

一、统计学考试题型1、选择题选择题通常是对基本概念、定义、公式和原理的考查。

题目会给出几个选项，要求考生从中选择正确的答案。

例如：“以下哪个是描述数据集中趋势的指标？（）A 方差 B 标准差 C 均值 D 极差”。

做选择题时，需要对知识点有清晰的理解，能够准确判断每个选项的对错。

2、填空题填空题主要考查对具体数值、公式中的参数或者关键概念的准确记忆。

比如：“样本方差的计算公式为_____。

”这就要求我们对公式和重要概念的细节有扎实的掌握。

3、简答题简答题往往要求考生对某个统计学概念、原理或方法进行简要的阐述。

例如：“请简述假设检验的基本步骤。

”回答此类问题，要条理清晰，语言简洁，突出重点。

4、计算题计算题是统计学考试中的重要部分，通常涉及数据的处理、统计量的计算以及统计方法的应用。

比如：“给定一组数据：12，15，18，20，22，计算其均值和标准差。

”在做计算题时，一定要注意计算的准确性，并且按照规定的步骤进行解答。

5、案例分析题案例分析题通常会给出一个实际的问题情境，要求考生运用所学的统计学知识进行分析和解决。

这需要我们能够将理论知识与实际应用相结合，提出合理的解决方案。

比如：“某工厂生产了一批零件，随机抽取 100 个进行检测，发现其中有 5 个不合格。

请根据此数据估计该批零件的不合格率，并给出置信区间。

”二、知识点复习1、数据的收集与整理（1）数据的来源：包括普查、抽样调查等，要了解它们的特点和适用场景。

（2）数据的整理：包括分组、制表、绘图等，能够根据数据的特点选择合适的整理方法。

2、数据的描述性统计（1）集中趋势的度量：均值、中位数、众数，要掌握它们的计算方法和特点，以及在不同数据分布情况下的适用性。

（2）离散程度的度量：方差、标准差、极差、四分位差，明白如何计算以及它们所反映的数据特征。

00974统计学原理章节基础知识第一章：总论1、统计的三基本方法:大量观察法，综合分析法，归纳推断法（（可扩展未简答）2、凯特乐将统计学的三个主要源泉：英国的政治学派，德国的国势学，法国的概率统计3、“统计”一词的含义：统计包括三个含义：统计工作、统计资料和统计科学。

统计工作、统计资料、统计科学三者之间的关系是：统计工作的成果是统计资料，统计资料和统计科学的基础是统计工作，统计科学既是统计工作经验的理论概括，又是指导统计工作的原理、原则和方法。

（简答）4、统计信息的两大特征：数量性和总体性（多选、简答）5、统计的三大职能：信息，咨询，监督(多选)6、四大计量尺度：定类尺度，定序尺度，定距尺度，定比尺度（重点前两个）7、按度量层次低到高：定类尺度>定序尺度>定距尺度>定比尺度8、区别总体和总体单位（选择，判断）9、统计指标的的三大特性：总体性，数量性，综合性（多选）10、区分变异和变量，变量又可以分为：连续变量和离散变量（多选）第二章：统计资料的收集和整理1.统计资料的三大特性：数量性，总体性，客观性（选择，填空）2.总体性的定义是指统计是从整体上反映和分析事物数量特征，而不是着眼于个别事物，因为事物的本质和发展规律只有从整体上观察，才能作出正确的判断。

(判断)3.原始资料的搜集方法访问方法观察方法实验方法（多选）4.统计调查的方式：1）普查：专门组织进行一次性的全面调查（填空、多选）2）抽样调查：最常用的方法3）统计报表4）重点调查：了解定义（选择）（多年都有考到）5）典型调查6.结论：统计方式是以普查为基础，抽样调查为主体（选择、判断）7.统计调查方案的内容：(1) 调查目的：调查目的要符合客观实际，是任何一套方案首先要明确的问题，是行动的指南。

(2) 调查对象和调查单位：调查对象即总体，调查单位即总体中的个体。

(3) 调查项目：即指对调查单位所要登记的内容。

(4) 调查表：就是将调查项目按一定的顺序所排列的一种表格形式。

统计学原理计算题复习六种题型重点HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第三章：编制次数分配数列1．根据所给资料分组并计算出各组的频数和频率，编制次数分布表；根据整理表计算算术平均数。

例题：某单位40名职工业务考核成绩分别为:68 89 88 84 86 87 75 73 72 6875 82 97 58 81 54 79 76 95 7671 60 90 65 76 72 76 85 89 9264 57 83 81 78 77 72 61 70 81单位规定：60分以下为不及格，60─70分为及格,70─80分为中，80─90分为良，90─100分为优。

要求：（1）将参加考试的职工按考核成绩分为不及格、及格、中、良、优五组并编制一张考核成绩次数分配表；（2）指出分组标志及类型及采用的分组方法；（3）根据考核成绩次数分配表计算本单位职工业务考核平均成绩；（4）分析本单位职工业务考核情况。

解答：（１）（2）分组方法是“变量分组中的组距式分组的等距分组，而且是开口式分组”；（3）根据考核成绩次数分配表计算本单位职工业务考核平均成绩。

（4）分析本单位职工考核情况。

本单位的考核成绩的分布呈两头小，中间大的“钟形分布”（即正态分布），不及格和优秀的职工人数较少，分别占总数的%和10%，本单位大部分职工的考核成绩集中在70-90分之间，占了本单位的为%，说明该单位的考核成绩总体良好。

第四章：计算加权算术平均数、加权调和平均数（已知某年某月甲、乙两农贸市场A、B、C三种农产品价格和成交量、成交额资料，试比较哪一个市场农产品的平均价格较高？并说明原因。

）、标准差、变异系数2．根据资料计算算术平均数指标；计算变异指标；比较平均指标的代表性。

例题：某车间有甲、乙两个生产组，甲组平均每个工人的日产量为36件，标准差为件；乙组工人日产量资料如下：要求：⑴计算乙组平均每个工人的日产量和标准差；⑵比较甲、乙两生产小组哪个组的日产量更有代表性？标准差的计算参考教材P102页.解:类似例题讲解：甲、乙两个生产小组，甲组平均每个工人的日产量为36件，标准差为件；乙组工人日产量资料如下：计算乙组平均每个工人的日产量，并比较甲、乙两生产小组哪个组的日产量更有代表性？解答：第五章：计算抽样平均误差、简单随机抽样条件下估计总体平均数和总体成数的区间范围和总量指标的区间范围。

统计学原理计算题
1. 样本均值的计算
假设有一组数据：7, 8, 9, 10, 11
要计算这组数据的样本均值，首先将数据相加，得到总和：7
+ 8 + 9 + 10 + 11 = 45
然后，将总和除以数据个数得到样本均值：45 / 5 = 9
所以，这组数据的样本均值为9。

2. 方差的计算
假设有一组数据：12, 14, 16, 18, 20
要计算这组数据的方差，首先计算每个数据与样本均值的差值。

样本均值为(12 + 14 + 16 + 18 + 20) / 5 = 16
差值为：12-16 = -4, 14-16 = -2, 16-16 = 0, 18-16 = 2, 20-16 = 4
然后，将差值平方得到如下结果：(-4)^2 = 16, (-2)^2 = 4, 0^2 = 0, 2^2 = 4, 4^2 = 16
计算这些平方结果的和：16 + 4 + 0 + 4 + 16 = 40
最后，将和除以数据个数得到方差：40 / 5 = 8
所以，这组数据的方差为8。

3. 标准差的计算
标准差是方差的平方根。

前面的例子中，方差为8，所以标准差为√8 ≈ 2.828。

因此，这组数据的标准差为约2.828。

《统计学原理》考试计算题类型分析一、 综合指标综合指标计算题主要是平均指标的计算。

计算平均数最基本的公式是简单算术平均数公式，其他公式（加权算术平均数、简单调和平均数及加权调和平均数）都是简单算术平均数公式的变形形式。

例１、某生产车间40名工人日加工零件数（件）如下：30 26 42 41 36 44 40 37 43 35 37 25 45 29 43 31 36 49 34 47 3343 38 42 32 25 30 46 29 3438 46 43 39 35 40 48 33 27 28要求：（1）根据以上资料分成如下几组：25—30，30—35，35—40，40—45，45—50，计算出各组的频数和频率，编制次数分配表。

（2）计算工人的平均日产零件数。

解：（1）所求次数分配表如下：按日加工零件数（件）所分的组各组人数（频数）频率（%）25—30 7 17.5 30—35 8 20 35—40 9 22.5 40—45 10 25 45—50 6 15.0 合计40100.0（2）【分析】平均日产零件数等于日产总件数（标志总量）与总人数（单位总量）之比，由资料可直接求得总件数与总人数，可用加权算术平均数公式。

所求平均日产零件数（件）为：75.3761197765.47115.4295.3775.3275.27=++++⨯+⨯+⨯+⨯+⨯==∑∑fxf x或：75.37%155.425.275.37%5.225.32%5.175.27=⨯+⨯+⨯+⨯==∑∑ffxx例2、已知某局20个企业的有关统计资料如下：按计划完成百分比分组（%）企业数（个）实际产值（万元）90以下 4 68 90—100 5 57 100—110 4 126 110以上 7 184 合计20435试计算产值的平均计划完成程度。

【分析】产值的平均计划完成程度等于实际完成数与计划数之比，资料给出了实际完成数，各组计划数并未直接给出，但各组计划数等于各组实际数与各组计划完成百分比之比求得，故可用加权调和平均数公式计算。

统计学原理学习辅导（一）第一章总论一、社会经济统计的研究对象1、统计的涵义统计一词在不同的场合可以有不同的涵义。

统计有时指统计工作，即统计实践活动，是对社会经济现象的数量方面进行搜集、整理和分析的全过程；统计有时指统计资料，即通过统计工作过程所取得各项数据资料和与之相关的其他实际资料；统计有时指统计科学，即关于认识客观现象数量特征和数量关系的原理原则和方式方法的科学。

统计的三种涵义是密切联系的。

统计工作和统计资料是统计活动和统计成果的关系，统计学和统计工作是理论和实践的关系。

2、社会经济统计学的研究对象社会经济统计学的研究对象是社会经济现象总体的数量特征和数量关系，通过这些数量方面的研究反映社会经济现象发展变化的规律性。

统计学和统计工作是理论和实践的关系，它们所要认识的研究对象是一致的。

3.社会经济统计学研究对象的特点可概括为：数量性；具体性；总体性；社会性；。

二、统计工作过程及统计研究方法1、统计工作过程统计工作过程所包括的环节有统计设计、统计调查、统计整理、统计分析、统计资料的提供与开发。

2、统计研究方法统计研究方法有大量观察法、统计分组法、综合指标法、统计模型法、归纳推断法。

三、国家统计的职能国家统计兼有信息职能、咨询职能、监督职能等三种职能。

四、统计学的几个基本概念及相互关系1、统计总体与总体单位统计总体是根据统计研究的任务目的所确定的研究事物的全体，是客观存在的具有共同性质的个体所构成的整体。

构成统计总体的个体单位称总体单位。

在一次特定范围、目的的统计研究中，统计总体与总体单位是不容混淆的，二者的含义是确切的，是包含与被包含的关系。

但是随着统计研究任务、目的及范围的变化，统计总体和总体单位可以相互转化。

统计总体同时具有大量性、同质性、变异性等特点。

大量性是指构成总体的总体单位数要足够的多，总体应由大量的总体单位所构成，大量性是对统计总体的基本要求；同质性是指总体中各单位至少有一个或一个以上不变标志，即至少有一个具有某一共同标志表现的标志，使它们可以结合起来构成总体，同质性是构成统计总体的前提条件；变异性就是指总体中各单位至少有一个或一个以上变异标志，即至少有一个不同标志表现的标志，作为所要研究问题的对象。

统计学原理计算题练习第 1 页 共 6 页统计学原理计算题练习1．某生产车间30名工人日加工零件数（件）如下：（学习指导P300—1，下同）30 26 42 41 36 44 40 37 37 25 45 29 43 31 36 36 49 34 47 33 43 38 42 32 34 38 46 43 39 35要求：（1）根据以上资料分成如下向组：25—30，30—35，35—40，40—45，45—50，计算出各组频数和频率，编制次数分布表。

（2）根据整理表计算工人平均日产零件数。

2．某公司下属50个企业，生产同种产品，某月对产品质量进行调查，得资料;要求计算该产品的平均合格率。

（P279—1345. 1990试问哪一个市场农产品的平均价格较高?并说明原因。

6.7（P168—21（P166—18（P165—13（P164—10）8．某企业甲、乙两个车间，甲车间平均每个工人日加工零件数65件，标准差11件；乙车间工人日加工零件数资料：计算乙车间工人加工零件的平均数和标准差，并比较甲、乙两车间哪个车间的平均日加工零9．某工厂有2000个工人，用简单随机不重复方法抽出100个工人作为样本，计算出平均工资560元，标准差32.45元。

要求：(1)计算抽样平均误差； (2)以95.45％(t＝2)的可靠性估计该厂工人的月平均工资区间。

（P295—5）10．某乡有5000农户，按随机原则重复抽取100户调查，得平均每户年纯收入12000元，标准差2000元。

要求：（1）以95%的概率（t=1.96）估计全乡平均每户年纯收入的区间。

（2）以同样概率估计全乡农户所纯收入总额的区间范围（P179—14）11．为了解某城市分体式空调的零售价格，随机抽取若干个商场中的40台空调，平均价格为3800元，样本标准差400元。

要求：（1）计算抽样平均误差；（2）以99.73%（t=3）的可靠性估计该城市分体式空调的价格区间。

统计学复习要点第一篇：统计学复习要点第1章统计和统计数据数据类别；总体、样本；几种概率抽样（简单随机抽样，分层抽样，系统抽样，整群抽样）第2章用图表展示数据定性数据表：频数分布表，列联表图：条形图（复式），帕累托图，饼图，环形图定量数据表：频数分布表（分组）图：直方图、茎叶图、箱线图；垂线图、误差图；散点图；雷达图，轮廓图第3章用统计量描述数据水平：均值，中位数，分位数，众数（选择原则）差异：极差，四分位差；方差，标准差，标准分数（经验法则）；离散系数分布：偏态，峰态（解读）第4章概率分布重要分布：二项分布，泊松分布，超几何分布，正态分布（判断）；t分布，卡方分布，F分布统计量分布：参数，统计量，抽样分布，中心极限定理，标准误第5章参数估计点估计：原理，缺陷区间估计：置信区间，置信度评价标准：无偏，有效，一致性单个总体参数估计待估参数均值比例方差大样本小样本大样本χ2分布σ2已知σ2已知Z分布Z分布Z分布σ2未知σ2未知Z分布t分布两个总体参数估计待估参数均值差独立大样本σ12、σ22已Z分布独立小样本正态总体σ12、σ22已知Z分布σ12=σ22t分布比例差独立大样本Z分布方差比匹配样本F分布t分布σ12、σ22未知σ12、σ22未Z分布σ12≠σ22t分布第6章假设检验原假设，备择假设；如何提假设显著性水平，P值，第一、二类错误结果表述（拒绝，不拒绝）参数检验（对照参数估计）第7章分类变量的推断卡方拟合优度检验，卡方独立性检验，相关性度量（3种系数）第8章方差分析与实验设计方差分析研究的问题，基本原理，基本假设方差分析表，参数估计表实验设计3种设计以及与方差分析的对应第9、10章回归分析回归的基本流程：判断有无关系、建模、检验、预测模型好坏的评判标准：判定系数，估计标准误差多元回归特有问题：调整判定系数，多重共线性（产生的问题，识别，处理），哑变量回归（系数解读）第11章时间序列时间序列的几种成分不同类型时间序列对应的预测方法：基本原理第二篇：应用统计学复习要点(09)应用统计学期末复习要点第一章绪论1、知道统计的三种含义及关系（P1）2、知道统计总体与总体单位的概念与特征（P5）3、知道标志与指标的含义与分类(P6)第二章统计数据的搜集1、知道统计调查的方式分类（P15）2、知道统计调查的方法分类(P17)3、知道调查方案的主要内容(P18)第三章统计数据的整理与显示1、知道统计分组的原则与分组整理的步骤（P31）2、知道统计表的构成及设计原则（P38）3、会编制频数分布表（例3.2、计算题1和2）第四章数据分布特征的统计测度1、知道集中趋势的含义及常用测度指标(P63)2、知道离散程度的含义及常用测度指标(P64)3、知道偏度系数和峰度系数与数据分布特征的关系(P70、P72)4、会计算平均数和离散系数（计算题1、2和4）第八章相关与回归分析1、知道相关关系的含义及分类(P130)2、知道相关系数的含义、性质与相关程度的划分(P135)3、知道相关分析和回归分析的含义（P131）4、知道回归参数的经济意义（P138）5、能完成方差分析表并由回归分析表回答相关问题(计算题3)第九章时间序列分析1、知道时间序列的概念、分类及编制原则(P156、P157)2、知道长期趋势、季节变动、循环变动及不规则变动的含义（P169）3、会计算水平分析指标和速度分析指标(计算题1和4。

《统计学原理》复习资料(计算部分）一、 算术平均数和调和平均数的计算 加权算术平均数公式 xfx f=∑∑(常用) fx x f=⋅∑∑(x 代表各组标志值,f 代表各组单位数,ff∑代表各组的比重）加权调和平均数公式 m x m x=∑∑ （x 代表各组标志值,m 代表各组标志总量)分析： m x mx=总产量工人平均劳动生产率（结合题目）总工人人数从公式可以看出，“生产班组"这列资料不参与计算，是多余条件,将其删去.其余两列资料,根据问题“求平均××"可知“劳动生产率”为标志值x ，而剩余一列资料“实际产量”在公式中做分子，因此用调和平均数公式计算,并将该资料记作m .=÷每一组工人数每一组实际产量劳动生产率，即mx。

同上例，资料是组距式分组，应以各组的组中值来代替各组的标志值.解:825065005250255047502730068.25825065005250255047504005565758595m x m x ++++====++++∑∑（件/人)2． 若把上题改成：(作业11P 3）计算该企业的工人平均劳动生产率。

分析： xfx f=总产量工人平均劳动生产率（结合题目）总工人人数从公式可以看出，“生产班组"这列资料不参与计算，是多余条件,将其删去.其余两列资料，根据问题“求平均××”可知“劳动生产率”为标志值x ,而剩余一列资料“生产工人数”在公式中做分母，因此用算术平均数公式计算，并将该资料记作f 。

=⨯每一组实际产量劳动生产率组工人数,即xf 。

同上例，资料是组距式分组,应以各组的组中值来代替各组的标志值.解:5515065100757085309550400xfx f⨯+⨯+⨯+⨯+⨯==∑∑=68.25(件/人）试计算该企业98年、99年的平均单位成本。

分析：mx f=总成本平均单位成本总产量计算98年平均单位成本,“单位成本"这列资料为标志值x ，剩余一列资料“98年产量"在实际公式中做分母,因此用算术平均数公式计算，并将该资料记作f ；计算99年平均单位成本，“单位成本”依然为标志值x ，剩余一列资料“99年成本总额”在实际公式中做分子,因此用调和平均数公式,并将该资料记作m 。

《统计学原理》期末复习指导六、计算题1．某班40名学生统计学考试成绩分别为：57 89 49 84 86 87 75 73 72 68 75 82 97 81 67 81 54 79 87 9576 71 60 90 65 76 72 70 86 85 89 89 64 57 83 81 78 87 72 61学校规定：60分发下为不及格，60－70分为及格，70－80分为中，80－90分为良，90－100分为优。

要求：（1）将该班学生分为不及格、及格、中、良、优五组，编制一张次数分配表。

（2）指出分组标志及类型；方法的类型；分析本班学生考试情况。

（2）分组标志为“成绩”，其类型为“品质标志”。

（3）分组方法为：按品质标志分组（4）本班学生的考试成绩的分布呈两头小，中间大的“正态分布”的形态2、某工业集团公司工人工资情况计算该集团工人的平均工资。

元620=∑∙∑=ff x x该工业集团公司工人平均工资620元。

3．某地区商业局下属20个零售商店，某月按零售计划完成百分比资料分组如下：试计算该局零售计划的平均计划完成百分比。

平均计划完成程度：%6.1034200435015.1160005.1120095.060085.080016001200600800==++++++==∑∑xm m x4、2010年某月份甲、乙两农贸市场某农产品价格和成交量、成交额资料如下：试问哪一个市场农产品的平均价格较高？并说明原因。

成交额单位：万元，成交量单位：万斤。

甲、乙两农贸市场某农产品价格和成交量、成交额统计甲市场平均价格()375.145.5/==∑∑=x m m X （元/斤）乙市场平均价格 325.143.5==∑∑=fxf X （元/斤）说明：两个市场销售单价是相同的，销售总量也是相同的，但甲市场平均收购价高于乙市场，是因为甲市场低价格收购量所占比重（25%）小于乙市场（50%）5、某厂甲、乙两个工人班组，每班组有8名工人，每个班组每个工人的月生产量记录如下：甲班组：20、40、60、70、80、100、120、70 乙班组：67、68、69、70、71、72、73、70 （1）计算甲、乙两组工人平均每人产量；（2）计算全距、标准差、标准差系数；比较甲、乙两组的平均每人产量的代表性。