静止无功补偿器的智能自适应PID控制器设计
- 格式:pdf
- 大小:200.61 KB
- 文档页数:6

基于模糊-PI控制的静止无功补偿器设计的开题报告一、研究背景随着电力系统的不断发展和电器设备的普及,越来越多的非线性负载进入电力系统,导致系统中存在着越来越多的无功损耗和电压波动问题。
因此,为了保证电力系统的稳定运行,需要引入静止无功补偿器,它能够通过补偿无功功率和稳定电压来提高电力系统的可靠性和效率。
目前,静止无功补偿器的控制方式通常是采用PI控制器,但是传统的PI控制器存在着参数不准确、系统性能不稳定等问题。
为此,应用模糊控制理论来设计无功补偿器的控制器,可以得到更加优化的控制效果,提高系统稳定性和响应速度。
二、研究内容本文的研究内容是基于模糊-PI控制的静止无功补偿器的设计。
具体研究内容包括:1.建立无功补偿器的数学模型。
通过分析电力系统的特性和无功补偿器的结构,建立起无功补偿器的数学模型,为后续的控制器设计提供基础。
2.设计模糊-PI控制器。
采用模糊控制理论结合PI控制器设计无功补偿器的控制器,通过模糊化输入变量和输出变量,使得控制器具有智能化的特性,能够更好地适应电力系统的变化。
3.仿真分析控制器的性能。
采用Matlab/Simulink软件对设计的模糊-PI控制器进行仿真分析,探究控制器在不同工况下的性能表现,包括无功功率补偿效果、电压稳定性和控制器的响应速度等方面。
三、研究意义本文的研究意义主要有以下几点:1.优化无功补偿器的控制器设计,提高系统的稳定性和性能。
2.验证模糊-PI控制器在静止无功补偿器控制中的适用性和优越性。
3.为电力系统中无功补偿器的应用提供理论和实践指导,促进电力系统的可靠性和效率的提高。
四、研究方法本文的研究方法包括文献调研法、理论建模法、软件仿真分析法等。
通过查阅相关文献、建立电力系统和无功补偿器的数学模型,采用模糊控制理论结合PI控制器设计无功补偿器的控制器,利用Matlab/Simulink 软件进行仿真分析,探究控制器在不同工况下的性能表现。
最终总结和归纳研究结果,提出进一步的改进和优化措施。
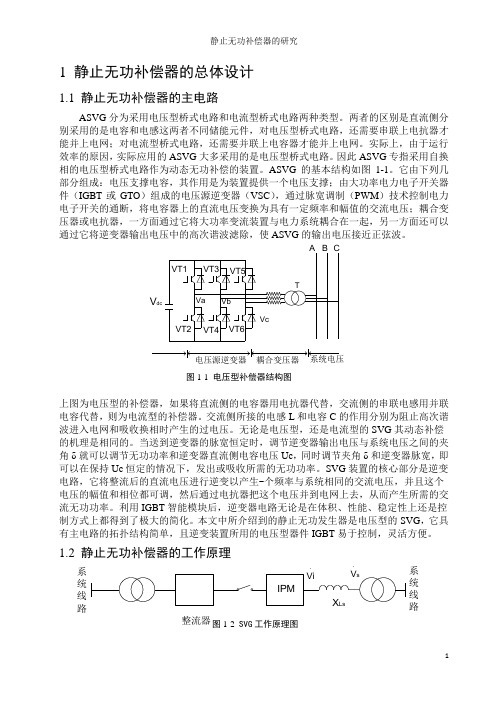
1 静止无功补偿器的总体设计1.1 静止无功补偿器的主电路ASVG 分为采用电压型桥式电路和电流型桥式电路两种类型。
两者的区别是直流侧分别采用的是电容和电感这两者不同储能元件,对电压型桥式电路,还需要串联上电抗器才能并上电网;对电流型桥式电路,还需要并联上电容器才能并上电网。
实际上,由于运行效率的原因,实际应用的ASVG 大多采用的是电压型桥式电路。
因此ASVG 专指采用自换相的电压型桥式电路作为动态无功补偿的装置。
ASVG 的基本结构如图1-1。
它由下列几部分组成:电压支撑电容,其作用是为装置提供一个电压支撑;由大功率电力电子开关器件(IGBT 或GTO )组成的电压源逆变器(VSC ),通过脉宽调制(PWM )技术控制电力电子开关的通断,将电容器上的直流电压变换为具有一定频率和幅值的交流电压;耦合变压器或电抗器,一方面通过它将大功率变流装置与电力系统耦合在一起,另一方面还可以通过它将逆变器输出电压中的高次谐波滤除,使ASVG 的输出电压接近正弦波。
图1-1 电压型补偿器结构图上图为电压型的补偿器,如果将直流侧的电容器用电抗器代替,交流侧的串联电感用并联电容代替,则为电流型的补偿器。
交流侧所接的电感L 和电容C 的作用分别为阻止高次谐波进入电网和吸收换相时产生的过电压。
无论是电压型,还是电流型的SVG 其动态补偿的机理是相同的。
当送到逆变器的脉宽恒定时,调节逆变器输出电压与系统电压之间的夹角δ就可以调节无功功率和逆变器直流侧电容电压Uc ,同时调节夹角δ和逆变器脉宽,即可以在保持Uc 恒定的情况下,发出或吸收所需的无功功率。
SVG 装置的核心部分是逆变电路,它将整流后的直流电压进行逆变以产生-个频率与系统相同的交流电压,并且这个电压的幅值和相位都可调,然后通过电抗器把这个电压并到电网上去,从而产生所需的交流无功功率。
利用IGBT 智能模块后,逆变器电路无论是在体积、性能、稳定性上还是控制方式上都得到了极大的简化。


静止无功发生器控制策略研究随着电力系统的发展,无功发生器的应用越来越广泛,而静止无功发生器(SVC)作为一种重要的无功补偿设备,在电力系统稳定控制中具有重要的作用。
如何控制SVC,让其更加有效地进行无功补偿,成为了研究的重点。
本文将介绍静止无功发生器控制策略的研究进展。
一、静止无功发生器静止无功发生器是一种基于电容、电感、限流电抗、动态电阻等器件,通过控制这些器件的传导和断开,来实现修正三相电压、提高电力系统静态稳定性的无功补偿设备。
二、静止无功发生器控制策略研究历程1.传统的PI控制策略传统的PI控制策略是一种广泛应用的静止无功发生器控制方法,该控制器通过对电路参数进行调整,使SVC输出的无功电流与系统所需的无功电流相一致,从而维持系统电压稳定。
但是,传统的PI控制策略难以应对大范围电压变化和有功负荷扰动导致的无功需求变化,而且一旦系统发生电网故障,传统的PI控制策略很难保证控制的有效性,因此,需要一种更加精密的控制算法。
2.自适应控制策略自适应控制策略是一种能够根据电力系统的实时状态变化自动调整静止无功发生器控制策略的算法。
自适应控制策略可以实现对系统电压、有功负荷变化的自适应响应,从而达到更加精准的无功补偿效果。
目前,基于模糊控制、神经网络、遗传算法等智能算法的自适应控制策略广泛应用于静止无功发生器控制领域,可以提高控制的精度和鲁棒性,提高了系统稳定性和可靠性。
3.多变量控制策略传统的静止无功发生器控制策略只考虑了有功负荷对系统电压的影响,然而在实际电力系统中,无功负荷和电路参数的变化同样会对系统电压产生影响。
因此,多变量控制策略旨在通过同时控制系统的多个因素,提高无功补偿效果和电力系统的稳定性。
该策略需要对系统的多个变量进行实时监测和控制,从而能够更好地适应不同的电力系统需求,提高了系统的可靠性和稳定性。
三、结论与展望静止无功发生器作为一种重要的电力系统无功补偿设备,其控制策略的研究虽取得了一定进展,但仍需要不断地进行探究和改进。

静止无功补偿器的控制方式SVC 输出容量控制主要有电压控制和恒导纳控制两种方式,可以在运行人员的指令下互相切换。
3.1.1电压控制模式这种控制模式下控制系统将测量所得到的母线电压Vmeas与一个设定的参考电压Vref 进行比较,然后将差值进行计算, 得到一个标么值电纳信号Bref ,该电纳值除以单组机械可投切电容(电抗) 器的电纳值可以确定需要的电容(电抗)器数目,而差值由TCR来补充。
随后将该标么值电纳送往脉冲触发发生电路,控制TCR 的触发角。
SVC稳态特性曲线的斜率采用电流反馈来实现,这种方法能够保证在SVC 控制范围内使端电压和端电流之间保持线性关系。
实测的SVC电流ISVC与代表调差率的系数KSL相乘,构成信号VSL再输入到加法节点。
当ISVC为感性时, VSL取正;当ISVC为容性时,VSL取负。
其传递函数为:G( s) =K1(1+s T Q)/s(1+s Tp),其中T Q=Tp+Kp/K1由于Tp通常设为零,因而控制器转化为简单的比例积分器,比例系数Kp 反映响应速度。
电压调节器输出的电纳参考信号被送到触发计算单元,该单元计算出6 组触发角,送至脉冲发生电路,从而在SVC 母线上得到期望的电纳值,达到设定的控制目标。
3.1.2恒导纳控制模式在该模式下,SVC 的等效导纳Bord 由运行人员设定,且该导纳可以在规定范围内连续可调。
Bref来自电压调节器的输出,在恒导纳模式下被偏置。
首先根据监控单元提供的开入量需要确定已投运的电容(电抗) 器组的等效电纳,然后经过电纳计算,得出仍需投切的电容(电抗) 器组以及需要的TCR 触发角连续调节的等效感性电纳。
最后换算成触发角发送到触发脉冲发生电路。
3.1.3 PWM电流控制对PWM电路的电流控制可分为间接电流控制和直接电流控制。
前者通过控制整流器产生的交流电压基波分量的相位和幅值来实现PWM 交流侧的电流控制;后者采用跟踪型PWM控制技术对交流侧的电流进行直接控制。

一、毕业设计(论文)的内容目前,随着电力电子技术的迅速发展,工厂大量使用大功率开关器件组成的设备对大型,冲击型负载供电,这使电能质量问题日益严重。
如果不进行无功补偿,在正常运行时,会反复地使负载的无功功率在很大范围内波动,这不仅使电气设备得不到充分利用,网络传输能力下降,损耗增加,甚至还会导致设备损坏,系统瘫痪,因此,装设无功补偿装置是十分必要的。
目前的主要无功补偿装置主要有静止无功补偿器(SVC)和静止无功发生器(SVG),静止无功补偿器(SVC)又可分为饱和电抗器型无功补偿装置(SR)、晶闸管控制电抗器(TCR)和晶闸管投切电容器(TSC)。
相比较,尽管SVG在理论上拥有无法比拟的优势,能达到快速、安全的补偿效果。
但由于控制元件价格昂贵且控制系统较复杂,使得这种系统的可靠性差,容量产生误动作。
根据我国目前的发展状况煤矿、农村等35KV变电站安装的大多数还是分组投切无功补偿装置,因此采用分组投切无功补偿仍然具有广阔的发展前景。
论文的主要内容:1、熟悉静止无功补偿装置TSC在无功补偿中的相关知识。
2、熟悉静止无功补偿装置TSC控制方式相关内容。
3、设计控制器。
4、制作基本的硬件、编写软件并调试。
5、编写相关软件程序。
二、毕业设计(论文)的要求与数据1、能够根据投切方法实现对TSC的投切控制。
2、能够对系统故障进行相应的保护和警告。
3、能够显示各组TSC的投切状态。
4、具有和电脑进行通信的功能。
5、画出PCB制作电路板,能够用三相标准电源对各部分功能进行验证。
6、附录包含有程序清单,原理图和PCB图。
三、毕业设计(论文)应完成的工作1、完成二万字左右的毕业设计说明书(论文);在毕业设计说明书(论文)中必须包括300-500个单词的英文摘要;附15篇以上参考文献,其中英文文献不少于2篇。
2、独立完成与课题相关,不少于四万字符的指定英文资料翻译(附英文原文)。
3、电气设计图纸两张(A3)。
4、毕业设计的工作量要满足16周的工作量要求。
无功补偿装置的智能控制与自适应优化技术无功补偿装置是电力系统中的重要设备,用于调节系统中的无功功率,提高系统的功率因数,稳定电压,改善电力质量。
随着电力系统的发展和智能化技术的提升,无功补偿装置的控制方式也在不断深化和创新。
本文将介绍智能控制与自适应优化技术在无功补偿装置中的应用。
一、智能控制技术1. 控制策略智能控制技术在无功补偿装置中的应用主要体现在控制策略的优化上。
现代无功补偿装置采用模糊控制、神经网络控制、遗传算法等人工智能方法,通过对系统运行状态的监测与判断,实现对无功补偿装置的智能控制。
例如,采用模糊控制可以根据系统的负载变化情况自动调节无功补偿装置的容量以提高无功功率的补偿效果。
2. 数据采集与处理智能控制技术还要求对系统运行数据进行实时采集和处理。
无功补偿装置通过传感器获取电网的电压、电流等参数,并将这些数据传输给智能控制系统。
智能控制系统通过对数据的分析和处理,实现对无功补偿装置的精确控制。
数据采集与处理的准确性和实时性对于智能控制的有效实施至关重要。
二、自适应优化技术1. 参数自适应无功补偿装置的最优补偿效果需要根据电网的实际运行状态来确定。
自适应优化技术通过对电网参数进行实时监测和分析,根据电网的实时需求自动调整补偿装置的参数,以实现最佳的无功补偿效果。
例如,如果电网的功率因数较低,自适应优化技术可以调整无功补偿装置的容量和补偿角度,使功率因数得到改善。
2. 优化算法自适应优化技术还包括用于无功补偿装置优化的算法。
常见的优化算法包括遗传算法、蚁群算法、粒子群算法等。
这些算法根据无功补偿装置的目标函数和约束条件,通过迭代计算和优化搜索,得到最优的补偿参数。
自适应优化技术的引入可以极大地提高无功补偿装置的效率和准确性。
综上所述,智能控制与自适应优化技术在无功补偿装置中发挥着重要作用。
通过采用智能控制技术,可以实现对无功补偿装置的智能化控制和操作,提高系统的无功功率补偿效果。
同时,自适应优化技术的应用可以根据电网实际需求,自动调整无功补偿装置的参数,使其达到最佳状态。
第26卷 第5期湖 南 大 学 学 报 (自然科学版)Vo1.26,No.5 1999年10月Jour nal o f Hunan U niv ersit y(N at ur al Sciences Editio n)Oct.1999文章编号:1000-2472(1999)05-0050-06静止无功补偿器的智能自适应PID控制器设计a彭建春,黄 纯,王耀南(湖南大学电气与信息工程学院,湖南长沙 410082) 摘 要:将神经网络和模糊控制与有着广泛应用的PID控制相结合,设计了一种静止无功补偿器(SVC)的智能自适应PID控制器.利用神经网络实现系统模型辨识,采用模糊逻辑和神经网络相结合对PID控制器参数动态寻优.使SVC的控制既具有模糊控制的简单、有效的非线性控制作用,又具有神经网络的自学习、自适应能力.关键词:静止无功补偿器;神经网络;模糊控制;自适应PID控制中图分类号:T M761 文献标识码: AIntellig ent A daptive PID Controller Design forStatic Var CompensatorPENG Jian-chun,HUA NG Chun,WANG Yao-nan (Colleg e o f Electr ical&Infor mation Eng ineer ing,Hunan U niv,Changsha 410082,China) Abstract:The neural netw o rk and fuzzy control theories are fused into PID co ntroller.An intellig ent adaptive PID controller for static var compensator(SVC)is desig ned.Neural-netw ork is used to identify dynamically the plant m odel.Fuzzy log ic and neur al-netw ork are fused to determ ine the o ptimal PID controller param eters by dy nam ic o ptimization.The SVC contr oller is adaptiv e and nonlinear in contr ol actio n.Key words:static var compensato r;neur al-netwo rk;fuzzy contro l;adaptive PID co ntrol在电力系统控制的发展过程中,比例、微分和积分控制(PID控制)是历史最悠久、生命力最强的控制方式.即使是在美、日等发达国家,目前将高新控制技术应用于电力系统的情况也只占很小的比例,绝大部分的控制回路基本上还是采用比例、微分和积分控制. PID控制在电力系统控制中占据非常重要的地位,因此,研究电力系统中PID控制的智能化方法具有重大的理论意义和广阔的应用前景.a基金项目:国家863计划资助项目(863-511-9485-002)收稿日期:1998-11-25.作者简介:彭建春(1964-),男,湖南常德人,湖南大学副教授,博士1 SVC 智能自适应PID 控制器设计对连续PID 控制,有如下的控制算式 u (t )=K P [e (t )+1/T I ∫t0e (t )d t +T D d e (t )/d t ],相应的增量式数值PID 控制算式为 u (k )=u (k -1)+K P [e (k )-e (k -1)]+K I e (k )+ K D [e (k )-2e (k -1)+e (k -2)],(1)式中K P ,K I 和K D 分别为比例、积分和微分系数,K I =K P T /T I ,K D =K P T D /T ,T 为采样周期.比例、积分和微分三种控制作用对获得良好的控制效果来说都是必要的,但这并不是图1 SV C 智能自适应PI D 控制系统充分条件.如果让控制算式跳出上述P,I,D 线性组合的结构,就有可能找到某种非线性组合的最佳控制规律.对此,在本文中,将模糊逻辑与神经网络引入SVC 的控制系统,构造了如图1所示的智能自适应PID 控制器,利用模糊逻辑简单和有效的非线性控制作用以及神经网络的自学习、自适应能力,动态地求解某一最优控制律下的P ,I ,D 参数.从图中可见,这种智能自适应PID 控制系统的结构由以下4个部分组成.1)传统的PID 控制器,直接对SVC 构成闭环控制.2)模糊量化模块,对补偿点母线电压偏差量$V 做归一化和模糊量化.NN2的输入被模糊量化的目的在于:¹利用模糊逻辑控制的鲁棒性和非线性控制作用;º相当于对神经网络NN2的输入进行了预处理,当神经网络的激活函数采用Sigmo id 函数或双曲正切函数时,避免了由于输入过大而使输出趋于饱和、导出输出对输入不敏感的现象.3)神经网络NN1,用于建立电力系统及其装置的动态模型,并为神经网络NN2的学习训练提供所需梯度信息5V /5A .4)神经网络N N 2,根据系统的状态调节PID 控制器的参数,以达到选定的某一性能指标最优的目的.具体实现时,使NN2的三个输出对应PID 控制器的被调参数K P ,K I 和K D ,通过神经网络自身权系数的调整,使得NN 2在稳定状态时,输出某种最优控制律下的PID 控制器参数.2 控制器的算法实现2.1 电压偏差的模糊量化对$V (k )=V r (k )-V (k )按下面的方法进行模糊量化处理,令51 第5期 彭建春等:静止无功补偿器的智能自适应P ID 控制器设计 $V ′(k )=100$V (k )/V e ,其中V e 为补偿点母线电压的额定值. E =5sgn($V ′(k )) $V ′(k )≥104sgn($V ′(k )) $V ′(k )≥83sgn($V ′(k )) $V ′(k )≥62sgn($V ′(k )) $V ′(k )≥41sgn($V ′(k )) $V ′(k )≥20 $V ′(k )<2,E 为补偿点母线电压偏差的模糊论域.将上述论域作为横坐标并向正方向平移5个单位,再乘以缩减系数0.1,则电压偏差的模糊值被调整到0~1数量级,补偿点母线电压偏差就被转换成适合于作神经网络输入量的“概念”值,送给优化神经网络NN2.2.2 辨识网络NN1输电网中用作电压控制的SVC 可以看成是一个单输入-单输出的非线性系统,其离散时间模型可以描述为 V m (k )=y [V (k -1),…,V (k -n ),A (k -1),…,A (k -m )],其中V (k )和A (k )为系统的输出(补偿点母线电压)和控制量(可控硅触发角)[1,2],它们被用作辨识网络的输入,V m (k )为辨识网络的输出.n 和m 分别为V (k )和A (k )的阶次,y [・]是非线性函数.采用3层串并联动态BP 神经网络[3]作为辨识网络,这种网络的反馈信号取自被控对象的实际输出,从而保证了输出误差趋于零,与其它相似的神经网络相比,这种神经网络更适合实际应用.定义辨识网络的性能指标J 1为 J 1=[V (k )-V m (k )]2/2,最小化性能指标可得相应的权系数与阈值的修正公式[4].2.3 自适应神经网络NN 2由式(1),对SVC 控制问题可以用一个函数h [・]来描述增量式数值PID 控制算式 A (k )=h [A (k -1),K P ,K I ,K D ,$V (k ),$V (k -1),$V (k -2)],h [・]是与K P ,K I ,K D ,$V (k ),A(k -1)和V (k )等有关的非线性函数.此外,通过自适应神经网络NN2的学习训练来寻找这样的一个控制规律.选取NN2为一个3层BP 神经网络,它有n 1个输入节点(n 1的大小取决于被控系统的复杂程度,此处取n 1=4),n 2个隐含层节点和n 3=3个输出节点.NN 2的输入层对应n 1个电压偏差的模糊量化值序列,3个输出节点分别对应PID 控制器的3个参数K P ,K I 和K D ,显然,它们不能为负值,神经元活化函数取Sigm oid 函数就能保证它们的非负性.对神经网络NN2的输入层有 O (1)j (k )=E (k -j ) j =0,1,…,n 1-1,(2)网络隐含层节点的输入和输出为 net (2)l (k )=∑n 1-1j =0W (2)lj (k )O (1)j (k ) l =0,1,…,n 2-1;(3) O (2)l (k )=g l [net (2)l (k )] l =0,1,…,n 2-1.(4)对应网络的输出层有52 湖南大学学报(自然科学版) 1999年 net (3)i (k )=∑n 2-1l =0W (3)il (k )O (2)l (k ) i =0,1,2;(5) O (3)i (k )=g i [net (3)i (k )] i =0,1,2.(6)即K P =O (3)0(k ),K I =O (3)1(k ),K D =O (3)2(k ).取性能指标为J 2=[V r (k +1)-V (k +1)]2/2,用最速下降法,并考虑搜索方向的惯性,对输出层神经元的权系数和阈值(H (3)i =W (3)in 2)有如下的修正公式 $W (3)il (k )=-G ・5J 2/5W (3)il (k )+B$W (3)il (k -1) (i =0,1,2;l =0,1,n 2-1),而 5J 25W (3)il (k )=5J 25V (k +1)・5V (k +1)5A (k )・5A (k )5O (3)i (k )・5O (3)i (k )5net (3)i (k )・5net (3)i (k )5W (3)il (k ), i =0,1,2;l =0,1,…,n 2-1,电力系统是复杂的非线性系统,梯度信息5V (k +1)/5A (k )难于求取,因此用辨识网络NN 1的输出V m (k +1)近似代替V (k +1),即用5V m (k +1)/5A (k )来近似5V (k +1)/5A(k ).而由辨识网络NN 1可以推得 5V m (k +1)5A (k )=5V m (k +1)5net (3)0(k )∑l 5net (3)0(k )5O (2)l (k )・5O (2)l (k )5net (2)l (k )・5net (2)l (k )5A (k )= g ′0[net (3)0(k )]∑l [W (3)0l (k )・g ′l [net (2)l (k )]・W (2)l ,n (k )].(7)对NN 2输出层的第i 个神经元,由式(1)并考虑用A 和$V 代替u 和e ,则有当i =0时,对应输出为K P ,5A (k )/5O (3)0(k )=$V (k )-$V (k -1);当i =1时,对应输出为K I ,5A (k )/5O (3)1(k )=$V (k );当i =2时,对应输出为K D ,5A (k )/5O (3)2(k )=$V (k )-2$V (k -1)+$V (k -2).则得N N2网络输出层权系数的修正量为 $W (3)il (k )=G D (3)i (k )O (2)l (k )+B$W (3)il (k -1);(8) D (3)i (k )=$V (k +1)・5V m (k +1)/5A (k )・5A (k )/5O (3)i (k )・g ′i [net (3)i (k )], i =0,1,2;l =0,1,…,n 2-1.(9)隐含层权系数的修正量为 $W (2)lj (k )=G D (2)l (k )O (1)j (k )+B$W (2)lj (k -1), l =0,1,…,n 2-1;j =0,1,…,n 1-1.(10) D (2)l (k )=g ′l [net (2)l (k )]∑2i =0D (3)i (k )W (3)il (k ) l =0,1,…,n 2-1.(11)2.4 控制算法综上所述,SVC 智能自适应PID 控制算法可归纳如下1)通过采样得到V (k ),V r (k ),然后计算$V (k );2)对$V (k )进行模糊量化处理;3)按式(2)~(6)计算NN2各层神经元的输入和输出,其输出对应PID 控制器的3个参数;4)PID 控制器的输出A (k )同时送被控对象和NN 1,产生下一步实际输出和辨识输出;5)采用有监督的广义D 学习规则对神经网络NN1进行训练.NN1网络的输出为V m (k +1),目标值为补偿点母线的实际电压V (k +1);53 第5期 彭建春等:静止无功补偿器的智能自适应P ID 控制器设计 6)将补偿母线期望电压V r (k +1)与实际电压V (k +1)的偏差,逐层反向传播修正网络NN 2的权系数及阈值,修正的具体步骤为:¹由式(7)计算5V m (k +1)/5A(k );º按式(9)计算输出层等效误差D (3)i (k );»根据式(8)修正NN 2输出层的权系数;¼由式(11)计算隐含层等效误差D (2)l (k );½按式(10)修正NN 2中隐含层的权系数;7)令k =k +1,将{V (k )},{A (k )}和{$V (k )}移位处理后返回1).3 仿真算例图2为一单机无穷大系统,SVC 接在线路的中间(线路电抗为2X L ),发电机及网络参数见表1.设零秒时d 点三相短路,0.08秒故障清除.取计算步长为0.02秒,对系统的动态过程进行仿真.图2 仿真系统图表1 仿真系统参数X ′dX d X q D 0.0340.1700.16510X L X T T J T C0.0160.01063.500.10 和本文控制器作对比的是常规PID (电压型)控制器,此处称之为传统控制器,其模型取自文献[5]中图4的连续控制模型,其控制器增益按Ziegler -Nicho ls 经验公式整定[6].考虑到可控硅本身动作的快速性,忽略了上述原始模型中对应可控硅单元的延时环节,发电机采用暂态电抗后电势恒定的经典模型,且不计原动机调速器的影响.神经网络中隐层神经元的个数取输入层节点的个数,学习率取0.9,冲量因子取0.7,系统的收敛误差取0.001.针对SVC 采用传统控制器和本文设计的控制器两种情况进行了仿真.图3给出了本文控制器作用下补偿点母线电压的变化情况.SVC 在智能自适应PID 控制器作用下,补偿点母线电压经过衰减振荡过渡到稳态电压,使系统得以继续稳定运行.而在传统控制器的作用下,补偿点母线电压呈增幅振荡(见图4),最后导至系统解列,失去稳定.本文设图3 智能PID 控制 图4 常规P ID 控制计的SVC 智能自适应PID 控制器改善了系统的稳定性,比常规PID 控制方式具有更好54 湖南大学学报(自然科学版) 1999年的动态性能.4 结 论本文作者设计的SVC 智能自适应PID 控制器,将模糊逻辑、神经网络和常规PID 控制有机地结合起来,既发挥了智能控制的优势,又迎合了PID 控制的广泛适应性;这种控制器不需要电力系统及其设备的数学模型,而且对电网结构和系统工作点的变化具有良好的自适应性和鲁棒性,有助于进一步改善补偿点母线电压的动态特性.本文的研究对实际静止无功补偿器之智能控制器的开发具有指导意义.参考文献:[1] 刘 取,马维新.静止补偿器用于电力系统无功控制[M ].北京:水利电力出版社,1989.[2] 卢 强,孙元章.电力系统非线性控制[M ].北京:科学出版社,1993.[3] 舒迪前.预测控制系统及其应用[M ].北京:机械工业出版社,1996.[4] 王耀南.智能控制系统[M ].长沙:湖南大学出版社,1996.[5] K oessler R J.Dy nam ic simulation of static v ar co mpensato rs in distr ibut ion systems [J].IEEET rans PS ,1992,7(3):1285~1291.[6] 薛定宇.控制系统计算机辅助设计[M ].北京:清华大学出版社,1996.(上接第33页)10mL 硝酸和2.0mLH 2SO 4在电炉上消化2h 、直到冒白烟,冷却后用稀碱溶液调节酸度近中性,用水定容于25mL 容量瓶中,摇匀.分取适量男女青年发样于25m L 比色管中,按绘制工作曲线方法进行,分析结果列于表4.表4 人发中痕量锰的分析结果及其回收率发样名称单次测定值/(L g ・g -1)123平均值/(L g ・g -1)相对标准偏差/%加入锰量/L g 测得锰量/(L g ・g -1)回收率/%青年男发0.2290.2250.2240.2160.2200.2210.223 2.00.50.71098.20.1 3.2099.1青年女发0.1820.1900.1840.1830.1870.1880.186 1.70.50.711103.60.1 2.8097.9参考文献:[1] Ishii H ,K oh H ,Satoh K .Spectr o phot ometr ic deter minatio n of ma ng anese ut ilizing met al ionsudstit ut ion in t he cadmium -A ,B ,C ,D -T etr akis (4-Carbo xy phchyl )P or phine Complex [J ].A na l Chim A cta ,1982(136):347.[2] 汤福隆,王莉红,陈秀华,江明泽.5,10,15,20-四(3-溴-4-磺酸苯基)卟啉的合成及其光度法测定痕量锰的研究[J ].化学试剂,1993,15(4):199.[3] 霍广进,贾静娴.m eso -四(4-甲氧基苯基)卟啉与锰显色反应的研究[J].理化检验(化学分册),1993,29(6):334.[4] 林瑞英.卟啉胶束增敏导数分光光度法测定微量锰[J].分析化学,1987,15(4):318.[5] L ong G L ,Winefo rdner J D .L imit o f detectio n a closer loo k at the T U P AC definitio n [J ].A na l Chem,1983,55(7):712A.55 第5期 彭建春等:静止无功补偿器的智能自适应P ID 控制器设计 。