chap 9 概率论与数理统计问题的求解

概率论及数理统计习题解答（第2章）.doc习题⼆（A ）三、解答题1．⼀颗骰⼦抛两次，以X 表⽰两次中所得的最⼩点数 (1) 试求X 的分布律； (2) 写出X 的分布函数．解: (1)分析：这⾥的概率均为古典概型下的概率，所有可能性结果共36种，如果X=1，则表明两次中⾄少有⼀点数为1，其余⼀个1⾄6点均可，共有1-612?C （这⾥12C 指任选某次点数为1，6为另⼀次有6种结果均可取，减1即减去两次均为1的情形，因为612?C 多算了⼀次）或1512+?C 种，故{}36113615361-611212=+?=?==C C X P ,其他结果类似可得.(2)≥<≤=+=+=+=+=<≤=+=+=+=<≤=+=+=<≤=+=<≤=<=6165}5{}4{}3{}2{}1{54 }4{}3{}2{}1{43 }3{}2{}1{32}2{}1{21}1{1 0 )(x x X P X P X P X P X P x X P X P X P X P x X P X P X P x X P X P x X P x x F ，，，，，，，≥<≤<≤<≤<≤<≤<=6 165363554 363243 36273236202136111 0 x x x x x x x ，，，，，，，2．某种抽奖活动规则是这样的：袋中放红⾊球及⽩⾊球各5只，抽奖者交纳⼀元钱后得到⼀次抽奖的机会，然后从袋中⼀次取出5只球，若5只球同⾊，则获奖100元，否则⽆奖，以X 表⽰某抽奖者在⼀次抽取中净赢钱数，求X 的分布律．解：注意，这⾥X 指的是赢钱数，X 取0-1或100-1，显然{}1261299510===C X P . 3．设随机变量X 的分布律为0;,2,1,0,! }{>===λλΛk k ak X P k为常数，试求常数a ．解：因为1!==-∞=∑λλae k ak k，所以λ-=e a .4．设随机变量X 的分布律为(1) 求X 的分布函数；(2) 求}21{≤X P ，}2523{≤解：(1)≥<≤<≤-<=??≥<≤=+-=<≤--=<=3x 13 2432141-1x 03x 132}2{}1{21}1{-1x 0)(，，，，，，，，x x x X P X P x X P x f ，(2) {}41121=-==≤X p X P 、 {}2122523===≤<x p="" x="" ,="" {}{}{}{}{}{}4<="" bdsfid="126">。

概率论与数理统计常见问题解答1.概率论研究的对象是什么？现实生活中有两类现象。

必然现象：一定条件下，结果是肯定的。

如：一定大气压下，水加温到100℃：沸腾随机现象：一定条件下，结果不肯定的。

如：实弹射击，打一发子弹：可能中或不中概率论是研究随机现象规律性的一门学科。

2.随机现象有规律性吗？有。

例如：两人打枪。

甲是神枪手，乙是普通射手。

如果打一发子弹，甲可能打中也可能打不中，乙也可能打中也可能打不中，看不出什么规律。

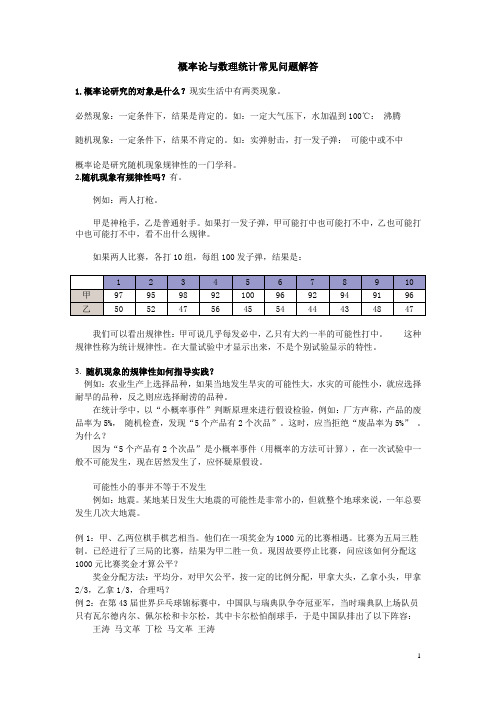
如果两人比赛，各打10组，每组100发子弹，结果是：我们可以看出规律性：甲可说几乎每发必中，乙只有大约一半的可能性打中。

这种规律性称为统计规律性。

在大量试验中才显示出来，不是个别试验显示的特性。

3.随机现象的规律性如何指导实践？例如：农业生产上选择品种，如果当地发生旱灾的可能性大，水灾的可能性小，就应选择耐旱的品种，反之则应选择耐涝的品种。

在统计学中，以“小概率事件”判断原理来进行假设检验，例如：厂方声称，产品的废品率为5%，随机检查，发现“5个产品有2个次品”。

这时，应当拒绝“废品率为5%” 。

为什么？因为“5个产品有2个次品”是小概率事件（用概率的方法可计算），在一次试验中一般不可能发生，现在居然发生了，应怀疑原假设。

可能性小的事并不等于不发生例如：地震。

某地某日发生大地震的可能性是非常小的，但就整个地球来说，一年总要发生几次大地震。

例1：甲、乙两位棋手棋艺相当。

他们在一项奖金为1000元的比赛相遇。

比赛为五局三胜制。

已经进行了三局的比赛，结果为甲二胜一负。

现因故要停止比赛，问应该如何分配这1000元比赛奖金才算公平？奖金分配方法：平均分，对甲欠公平，按一定的比例分配，甲拿大头，乙拿小头，甲拿2/3，乙拿1/3，合理吗？例2：在第43届世界乒乓球锦标赛中，中国队与瑞典队争夺冠亚军，当时瑞典队上场队员只有瓦尔德内尔、佩尔松和卡尔松，其中卡尔松怕削球手，于是中国队排出了以下阵容：王涛马文革丁松马文革王涛决策时已经估计到瑞典队有两种可能的选择：或以卡尔松打第三单打去碰削球手丁松或以佩尔森打第三单打，以便卡尔松避开丁松最后，中国队战胜瑞典队（3：2），夺回了阔别六年之久的斯韦思林杯。

概率论与数理统计答案
1. 概率论中，事件的概率是什么？
事件的概率是指该事件发生的可能性大小。

通常用0到1之间的数值表示，0表示不可能发生，1表示一定会发生。

2. 如何计算联合概率和条件概率？
联合概率指两个事件同时发生的概率，可以用乘法原理计算。

条件概率是指已知一个事件发生的前提下，另一个事件发生的概率，可以用条件概率公式P(A|B) = P(A∩B) / P(B)来计算。

3. 如何计算期望和方差？
期望是指随机变量取值的平均值，可以用加权平均数来计算。

方差是指随机变量的取值与其期望之差的平方的平均数，可以用期望和平方的期望之差来计算。

4. 什么是正态分布？
正态分布是一种常见的连续概率分布，也称为高斯分布。

其具有对称、单峰、钟形曲线的特点，通过平均数和标准差来描述。

5. 如何进行假设检验？
假设检验是一种基于样本数据推断总体参数的方法。

通常先提出一个假设（原假设或备择假设），根据样本数据计算出一个统计量，然后根据这个统计量的概率分布来判断原假设是否成立。

1、排列组合：)1)...(1()(!1)...1()1)...(1(m!m n m n +--=-=⨯-+--==m n n n m n n A m m m n n n A C m n 性质!10n A C C C C n n m n n m n n n n ====-2、事件运算律：①AB=BA ②A ∪B=B ∪A③ABC=A(BC)④A ∪B ∪C=A ∪(B ∪C)④A(B ∪C)=(A ∪B)(B ∪C)=(BC)∪A ⑤德摩根率：____________A ∪B =__A ∩__B ____AB=__A ∪__B⑥加法公式：P(A ∪B)=P(A)+P(B)-P(AB)P(A ∪B ∪C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC)⑦减法公式：P(A-B)=P(A ___B)=P(A)-P(BA)⑧独立事件：P(AB)=P(A)*P(B)P(AB)=P(B)*P(AlB)=P(A)P(B)☆P(AlB)=P(A)↔A,B 独立⑨三个事件两两独立：P(AB)=P(A)P(B)P(AC)=P(A)P(C)P(BC)=P(B)P(C)P(ABC)=P(A)P(B)P(C)四个条件缺一不可，少了第四个就只有两两互相独立了3、条件概率：)()()(A P AB P A B P =乘法公式：)()()()()(B A P B P A B P A P AB P ==,P(A)>0)()()()(AB C P A B P A P ABC P =4、全概率公式：∑==ni Bi A P Bi P A P 1)()()((B1,B2,......Bn ，是完备事件组)5、贝叶斯公式：)()()()i ()()i ()i (1A P ABi P Bi A P B P Bi A P B P A B P n i ==∑-6、切比雪夫不等式：[][][]εεεεε≥--=<->≤≥-)(1)()0()()(2X E X P X E X P X D X E X P 7、多项独立同分布，求总和怎样的概率。

数据统计与概率问题的解题技巧在数学学科中，数据统计与概率问题是一个重要的部分，它涉及到统计学和概率论的知识与应用。

正确解答这类问题需要掌握一些解题技巧和方法。

本文将介绍一些在数据统计与概率问题中常用的解题技巧，帮助读者更好地解决相关问题。

一、数据统计问题的解题技巧1. 了解不同统计指标的含义与应用：在数据统计问题中，常常会涉及到不同的统计指标，例如平均值、中位数、众数等。

在解题过程中，应该明确每个指标的定义和应用场景，以便正确使用。

2. 注意样本容量和总体容量的关系：在进行数据统计时，我们通常只能获得样本数据，而无法得知整个总体的情况。

因此，需要根据样本特征推断总体特征时，应该注意样本容量与总体容量的关系，以避免推理错误。

3. 熟练掌握频数表和频率表的制作和应用：频数表和频率表是解决数据统计问题时常用的工具。

通过制作频数表和频率表，可以清晰地了解数据的分布情况，从而更好地进行分析和推理。

4. 注意异常值对统计结果的影响：在进行数据统计时，有时会遇到一些异常值，例如极大值或极小值。

这些异常值可能会对统计结果产生影响，因此在解题过程中要注意排除这些异常值，以减少误差。

二、概率问题的解题技巧1. 熟悉概率基本概念：解决概率问题的第一步是熟悉概率的基本概念，例如随机事件、样本空间、事件概率等。

只有清楚了解这些基本概念，才能更好地解答概率问题。

2. 灵活运用概率公式：在解决概率问题时，利用概率公式是一个常见的方法。

例如，计算事件的概率可以使用频率公式，计算相互独立事件的联合概率可以使用乘法公式等。

熟练掌握这些公式的使用，有助于解答复杂的概率问题。

3. 注意条件概率与独立性的关系：在解决概率问题中，常常会涉及到条件概率和事件的独立性。

要正确应用条件概率公式，需要先判断事件之间是否相互独立，如果相互独立，则条件概率可以简化为事件概率。

4. 利用概率模型进行建模：对于一些复杂的概率问题，可以利用概率模型进行建模，以便更好地分析和解答问题。

概率统计的解题技巧即可查看其他科目资源《概率论与数理统计》期末考试试题概率统计的解题技巧一、重点解析1．了解随机事件的发生存在着规律性和随机事件概率的意义．2．了解等可能性事件的概率的意义，会用排列组合的基本公式计算一些等可能性事件的概率.3．了解互斥事件、相互独立事件的意义，会用互斥事件的概率加法公式与相互独立事件的概率乘法公式计算一些事件的概率．4．会计算事件在 n 次独立重复试验中恰好发生 k 次的概率．5．掌握离散型随机变量的分布列.6．掌握离散型随机变量的期望与方差.7．掌握抽样方法与总体分布的估计.8．掌握正态分布与线性回归.二、例题解析考点 1. 求等可能性事件、互斥事件和相互独立事件的概率解此类题目常应用以下知识:考点 4 抽样方法与总体分布的估计抽样方法1．简单随机抽样：设一个总体的个数为N，如果通过逐个抽取的方法从中抽取一个样本，且每次抽取时各个个体被抽到的概率相等，就称这样的抽样为简单随机抽样. 常用抽签法和随机数表法.2．系统抽样：当总体中的个数较多时，可将总体分成均衡的几个部分，然后按照预先定出的规则，从每一部分抽取 1 个个体，得到所需要的样本，这种抽样叫做系统抽样（也称为机械抽样） .3．分层抽样：当已知总体由差异明显的几部分组成时，常将总体分成几部分，然后按照各部分所占的比进行抽样，这种抽样叫做分层抽样.总体分布的估计由于总体分布通常不易知道，我们往往用样本的频率分布去估计总体的分布，一般地，样本容量越大，这种估计就越精确.总体分布：总体取值的概率分布规律通常称为总体分布.当总体中的个体取不同数值很少时，其频率分布表由所取样本的不同数值及相应的频率表示，几何表示就是相应的条形图.当总体中的个体取值在某个区间上时用频率分布直方图来表示相应样本的频率分布.总体密度曲线：当样本容量无限增大，分组的组距无限缩小，那么频率分布直方图就会无限接近于一条光滑曲线，即总体密度曲线.后面会附有答案解析答案。

初中数学解题技巧掌握解决概率与统计题目的窍门初中数学是中学阶段的必修课程之一，其中概率与统计是数学中的一个重要内容。

解决概率与统计题目需要掌握一些解题技巧和窍门。

本文将介绍一些初中数学解题技巧，帮助学生们更好地解决概率与统计题目。

一、概率题目的解题技巧概率是数学中的一个重要概念，也是我们生活中经常会遇到的概念。

解决概率题目需要掌握以下几个技巧：1. 确定样本空间：样本空间是指一个随机试验可能结果的集合，确定样本空间有助于我们对概率问题的整体了解。

2. 列举事件：根据题目要求，列举可能发生的事件，并计算事件出现的次数。

3. 计算概率：根据事件发生的次数和样本空间来计算概率，概率的计算公式是：事件发生的次数/样本空间中可能结果的总数。

4. 判断独立事件：如果两个事件发生与否互相不会影响，我们可以将其看作是独立事件，此时可以通过将事件的概率相乘来计算同时发生的概率。

二、统计题目的解题技巧统计是数学中与概率相关的内容，解决统计题目需要掌握以下几个技巧：1. 理解统计图表：在解决统计问题时，学生要能够理解并分析给定的统计图表，如条形图、折线图、饼图等，从图表中获取相关信息。

2. 确定数据类型：在解决统计问题时，要根据题目给出的问题确定所需的数据类型，如平均数、中位数、众数等。

3. 进行数据分析：根据题目要求进行数据分析，计算相关统计量，并进行适当的比较和推理。

4. 注意问题中的陷阱：有时统计题目中会设置一些陷阱，会有一些与问题无关的数据和信息，学生需要有辨别能力，避免被这些干扰信息所迷惑。

三、解决概率与统计题目的窍门除了上述的解题技巧外，还有一些解决概率与统计题目的窍门可以帮助学生们更快更准确地解题。

1. 多做练习：解决概率与统计题目需要不断的练习，熟能生巧。

学生们可以多做相关习题或者模拟试题，加深对解题方法和技巧的理解。

2. 理清思路：在解题过程中，学生们应该先理清思路，明确问题的要求，然后再根据题目给出的条件和已有的知识来解决问题。

概率与统计常见问题的解题技巧一、引言概率与统计是数学中重要的分支，它们在实际生活和科学研究中都有广泛的应用。

在解题过程中，我们常常会遇到一些常见的问题和难题。

本文将介绍一些解题技巧，帮助读者更好地解决概率与统计领域的常见问题。

二、概率问题的解题技巧概率问题涉及到随机事件的发生概率。

以下是其中一些常见问题的解题技巧：1. 互斥事件的概率计算当两个事件是互斥事件（即两个事件不可能同时发生）时，可以通过计算两个事件的概率之和来得到它们的并集概率。

2. 独立事件的概率计算当两个事件是独立事件（即一个事件的发生不影响另一个事件发生的概率）时，可以通过计算两个事件的概率之积来得到它们的交集概率。

3. 条件概率的计算当两个事件的发生概率有关联时，需要利用条件概率的概念来计算它们的概率。

条件概率可以通过给定条件下的概率计算得出。

4. 贝叶斯定理的应用贝叶斯定理可以用于计算反向条件概率，即已知结果的情况下，计算其引起的原因的概率。

它在概率问题中有重要的应用价值。

三、统计问题的解题技巧统计问题涉及到数据的收集、整理和分析。

以下是其中一些常见问题的解题技巧：1. 数据统计的基本概念在进行统计分析时，需要了解一些基本概念，如均值、中位数、标准差等，这些概念能够帮助我们更好地理解数据的分布情况。

2. 数据收集和整理在进行统计分析之前，需要进行数据收集和整理。

这包括选择合适的样本，设计问卷调查或实验，并对数据进行清洗和归纳整理。

3. 统计推断统计推断是根据样本数据对总体进行推断。

通过样本平均值和样本标准差等统计量，可以对总体平均值和总体标准差进行估计。

4. 假设检验假设检验是用来检验研究者对总体参数的假设是否成立。

它可以帮助我们判断某个因素对样本数据是否有显著影响。

四、总结概率与统计是数学中重要的分支，解决概率与统计问题需要一定的技巧和方法。

本文简要介绍了概率问题和统计问题的一些常见解题技巧，希望能对读者在解决概率与统计问题时提供一些帮助。

概率论数理统计答案概率论、数理统计是我们生活中不可避免地遇到的问题。

这些问题的解决离不开概率论和数理统计的知识。

然而，这两门学科并不是一见倾心，即使学了也未必能轻松掌握，尤其是对于初学者来说。

下面，我将通过几个问题的答案，来阐述概率论和数理统计的相关知识。

问题1：某科目的考试成绩满分为100分，进行了300人的考试，平均分为70分，标准差为15分，问该科成绩在80分以上的学生占总人数的比例是多少？答：根据正态分布理论，假设该科目的成绩服从正态分布，可以通过标准正态分布表确定得分区间的分位点。

首先，计算该科考试的标准化分数：z = (80-70)/15 = 0.67，然后查表可知，该分数区间的累积概率为0.2514。

也就是说，80分以上的学生人数占总人数的比例为25.14%。

问题2：某家超市进货的鸡蛋尺寸有偏差，但保证平均每箱鸡蛋数量为24个。

现在有一个顾客随机挑选一箱鸡蛋，请问该顾客选择到数量小于20个的概率是多少？答：假设每箱鸡蛋的数量服从正态分布，那么该超市的进货量应该符合中心极限定理。

设每个鸡蛋的数量的均值为μ，标准差为σ，则该超市进货24个鸡蛋的标准化分数为z = (20-24μ)/σ。

根据正态分布的特性，计算可得符合条件的概率为P(Z<z)，Z为标准正态分布，z的值可以从标准正态分布表中查找得知。

如此算下来，该顾客选择到数量小于20个的概率为0.0003。

问题3：某手机厂商有两种机型，分别为A、B型。

现在调查了10000名用户，发现喜欢A型机的用户有4000人，喜欢B型机的用户有6000人，而两种机型都喜欢的用户有2000人。

那么，随机选择一个用户，问TA喜欢B型机的概率是多少？答：根据全概率公式，随机选择一个用户个体喜欢B型机的概率为P(B) = P(B|A)P(A) + P(B|A')P(A')，其中，P(B|A)表示个体喜欢A型机的条件下喜欢B型机的概率，P(A)表示个体喜欢A型机的概率，P(B|A')表示个体不喜欢A型机的条件下喜欢B型机的概率，P(A')表示个体不喜欢A型机的概率。

概率论与数理统计例题和知识点总结概率论与数理统计是一门研究随机现象统计规律的学科，它在自然科学、工程技术、经济管理、社会科学等众多领域都有着广泛的应用。

下面将通过一些例题来帮助大家理解和掌握这门学科的重要知识点。

一、随机事件与概率随机事件是指在一定条件下，可能出现也可能不出现的事件。

概率则是衡量随机事件发生可能性大小的数值。

例 1：抛掷一枚均匀的硬币，求正面朝上的概率。

解：因为硬币只有正反两面，且质地均匀，所以正面朝上的概率为1/2。

知识点：古典概型中，事件 A 的概率 P(A) ＝ A 包含的基本事件数／基本事件总数。

例 2：一个袋子里有 5 个红球和 3 个白球，从中随机取出一个球，求取出红球的概率。

解：袋子里一共有 8 个球，其中 5 个是红球，所以取出红球的概率为 5/8。

知识点：概率的性质：0 ≤ P(A) ≤ 1；P(Ω) ＝ 1，P(∅）＝ 0。

二、条件概率与乘法公式条件概率是指在已知某一事件发生的条件下，另一事件发生的概率。

例 3：已知在某疾病的检测中，阳性结果中真正患病的概率为 09，而总体人群中患病的概率为 001。

如果一个人的检测结果为阳性，求他真正患病的概率。

解：设 A 表示患病，B 表示检测结果为阳性。

则 P(A) ＝ 001，P(B|A) ＝ 09，P(B|A'）＝ 1 P(B|A) ＝ 01。

根据全概率公式：P(B) ＝P(A)×P(B|A) ＋ P(A'）×P(B|A'）＝ 001×09 ＋099×01 ≈ 0108。

再根据贝叶斯公式：P(A|B) ＝ P(A)×P(B|A) ／ P(B) ＝ 001×09 ／0108 ≈ 0083。

知识点：条件概率公式：P(B|A) ＝ P(AB) ／ P(A)；乘法公式：P(AB) ＝ P(A)×P(B|A)。

三、独立性如果两个事件的发生与否互不影响，那么称它们是相互独立的事件。