精编2018高考数学(理科)习题第四章三角函数422和答案

2018年高考数学分类汇编之三角函数和解三角形、选择题B • 305)的图象向右平移10个单位长度，所得图象对应的函数3 5A 在区间［-，—］上单调递增4 4 3B 在区间［―,］上单调递减45 3C 在区间［予‘专］上单调递增3D 在区间［厅,2 ］上单调递减7.【2018浙江卷5］函数y= 2|x|sin2x 的图象可能是1.【2018全国二卷 6】在厶ABC 中,C cos— 2，BC 1，AC 5，则 AB52.【2018全国二卷 10]若 f(x) cosxsinx 在［a, a ］是减函数，贝U a 的最大值是3.【2018全国三卷 4] 若sin1 … 3，则cos24. 5. 0, C . 【2018全国三卷9］ △ ABC 的内角 A, B, C 的对边分别为 2 2 2a ，b ，c ,若△ ABC 的面积为-— -，4【2018北京卷7］在平面直角坐标系中，记m 变化时，d 的最大值为d 为点P A. 1(COS 0 sin 0到直线x my 2 0的距离，当B. 2C. 3D.4C . . 296.【2018天津卷6］将函数y sin(2x1. 【2018全国一卷16】已知函数f x 2sinx sin2x ，则f x 的最小值是 _______________ .2.【2018 全国二卷 15】已知 sin a cos 3 1 , cos a sin 3 0，则 sin( a ® __________________ .3. 【2018全国三卷15】函数f x cos 3x n在0, n 的零点个数为6 ---------------------------------------------------4. 【2018北京卷11】设函数f (x ) =cos( x n ( 0),若f(x) f (n)对任意的实数x 都成立，则co的最小值为 _________ . 5.【2018江苏卷7】已知函数y sin(2x _______________________ )(--)的图象关于直线x -对称，则 的值是 ____________________ .2236. 【2018江苏卷13】在厶ABC 中，角A, B,C 所对的边分别为a,b,c , ABC 120 , ABC 的平分线 交AC 于点D ，且BD 1，则4a c 的最小值为 _________ .7. 【2018浙江卷13】在厶ABC 中，角A ，B ，C 所对的边分别为a ，b ，c •若a= 7，b=2, A=60°，贝U sin B= _________ , c= _________.、填空题B .三.解答题1. [2018 全国一卷17】在平面四边形ABCD 中，ADC 90°, A 45°, AB 2 , BD 5.12. 【2018 北京卷15】在厶ABC 中，a=7, b=8, cosB=—.(△)求/ A ；(△)求AC边上的高.3. 【2018天津卷15】在厶ABC中，内角A,B,C所对的边分别为a,b,c.已知bsinAacos(B ). 6(I)求角B的大小；(II)设a=2, c=3,求b和sin(2A B)的值.4. 【2018江苏卷16】已知，为锐角‘tan 3 ,迹()舟.(1)求cos2的值；(2)求tan( )的值.5. 【2018江苏卷17】某农场有一块农田，如图所示，它的边界由圆O的一段圆弧MPN (P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米，点P到MN的距离为50米.现规划在此农田上修建两个温室大棚，大棚I内的地块形状为矩形ABCD，大棚U内的地块形状为△ CDP，要求A,B均在线段MN上，C,D均在圆弧上.设OC与MN所成的角为.(1)用分别表示矩形ABCD和厶CDP的面积，并确定sin的取值范围；(2)若大棚I内种植甲种蔬菜，大棚U内种植乙种蔬菜，且甲、乙两种蔬菜的单位面积年产值之比为4 ：3 .求当为何值时，能使甲、乙两种蔬菜的年总产值最大.6. 【2018浙江卷18】已知角a的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边过点P345'(I)求sin (a + n 的值; (U)若角B满足sin (a+B=13，求cos B的值・7.【2018上海卷18】设常数a R，函数f(x) a sin 2x c 22cos x(1)若f(x)为偶函数，求a的值; (2) 若〔匸〕1，求方程f(x) 1 .2在区间［，的解.参考答案、选择题 1.A 2.A 3.B 4.C 5.C 6.A 7.D、填空题 1. 3.3223. 34.235. 7.3 ；37三•解答题 1.解: (1)在厶ABD中，由正弦定理得一BLsin AABsin ADB由题设知,5sin 452 sinADB，所以sin ADB -5由题设知, ADB 90，所以cos ADB 1225 5(2)由题设及(1) 知, cos BDC sin ADB 辽在△ BCD 中,5 由余弦定理得2 2 2BC BD DC 2 BD DC cos BDC 25 8 25. 所以BC 5.32.解：(1)在厶ABC 中,1 n _________________________________ 2—T cosB= —7 ,二 B €( — , n ，二 sinB= 1 cos B<3 7由正弦定理得—sin A bsin B8 -二=<3，二 sinA= £ . T B €( f ,sin A227•- A €( 0,亍)，(n )在厶ABC 中,■/ sinC=sin (A+B ) =sinAcosB+sinBcosA=—3 21 (-)71 4.3_ 3.3 2714女口图所示，在△ ABC 中sinC=g ,二 h=BC sinC = 7 3 弓BC14••• AC 边上的高为子.3.解：在厶ABC 中，由正弦定理— sin A—，可得 bsinA asinB sin B又由 bsinA acos(B n ),6得 as in B acos(B n ),6即sinB cos(B ，可得tanB 3 .又因为 B (0 ,可得(n)解：在△ ABC 中,由余弦定理及a =2, c=3, B =^,有 b 2 a 2 c 2 2accosB 7，故 b= J7 .由 bsin A acos(B —), 6可得sin A因为 a<c , 故cosA因此 sin 2 A 2sin AcosA2,cos2 A 2cos A所以，si n(2A B)sin 2Acos Bcos2 A sinB ^^3 73 3 3 2144.解：(1)因为tan4, tan 3汇，所以sin4c o s cos因为sin 22cos1，所以 2cos25，因此,cos222cos7 25(2)因为，为锐角，所以(0, n .又因为cos()寻，所以sin()厂曲( )害，因此tan( ) 2.因为tan -，所以tan232ta n 242 , 1 tan 7因此，tan( ) tan[2 ( )]；+；爲；：；(—5 2115•解：(1)连结PO并延长交MN于H,贝U PH丄MN , 所以OH=10.过O作OE丄BC于E,贝U OE// MN，所以/ COE书故OE=4Ocos0, EC=40sin B,则矩形ABCD 的面积为2X40cos((40sin 0 +10=800(4sin 0 cos 0 +cOs B △ CDP的面积为 1 x 2X 40co(40 - 40sin) 0=1600 (cos 0 - sin 0)cos 0过N作GN丄MN，分别交圆弧和OE的延长线于G和K，则GK=KN=10 .令/GOK=0,则sin0=4 2(0, n)・当濮[0, n)时，才能作出满足条件的矩形所以sin(的取值范围是[〔，1).4答：矩形ABCD的面积为800 (4sin 0 cos 0 +cQs平方米，△ CDP的面积为1600 (cos 0 - sin 0)cos0n 的取值范围是[1 , 1).4(2)因为甲、乙两种蔬菜的单位面积年产值之比为 4 : 3,设甲的单位面积的年产值为4k，乙的单位面积的年产值为3k (k>0).则年总产值为4k X 800(4sin 0 cos 0 +cbs+Bk x 1600( cos 0 - sin 0 cos 0=8000k (sin 0 cos 0 +)s [ 0, n)2设 f ( 0) =sin 0 cos 0 +cos 0€ [ 0, n),2则f'( ) cos2sin2 sin (2sin2 sin 1) (2sin 1)(sin 1).令 f'( )=0，得 B =,6当9€( (0, n 时，f '( )>0，所以f (0)为增函数;6当0€(J ,匸)时，f '( )<0 ,所以f (0)为减函数,6 2因此，当0=时，f ((取到最大值.6答：当吧时，能使甲、乙两种蔬菜的年总产值最大•［来源:学§科§网］,］时，即2x(U)由角的终边过点 P( 3,得cos35 55由 sin() —得 cos( )121313由( )得coscos()cossin( )s in,5616所以cos或cos6565 .解：(1) f(x ； )asin 2x2 cos 2 x 1 1 =asi n2x cos2x 1 ,6. ( I)由角的终边过点P(4)得 sin 5所以sin( 冗)sin -5f ( x) a sin(当f (x)为偶函数时：f (x)f( x)，则 a a，解得a 0 o2(2) f ( ) a sin 2 cos —,424由题意f (一)a 13 1 ,4、.3sin 2x 2cos 2 xa .3 , f (x) 3sin2x cos2x1 2sin(2x6)1,令 f (x) 1血，则2sin 2x1151319解得：x ,2424，24或x248. 解: (1) f(x)asin 2x c 22cos x 1 1 = asin2x cos2x 1 , f( x) a sin( 2x)cos(2x)1asin2x cos2x 1当f(x)为偶函数时:f(x)f( x)，则a a，解得a 0。

1．y＝A sin(ωx＋φ）的有关概念y＝A sin(ωx ＋φ）(A〉0，ω〉0），x∈R 振幅周期频率相位初相A T＝错误!f＝错误!＝错误!ωx＋φφ2.用五点法画y＝A sin（ωx＋φ）一个周期内的简图时，要找五个特征点如下表所示：x错误!错误!错误!错误!错误!ωx＋φ0π2π错误!2πy＝A sin（ωx＋φ）0A0－A03.函数y＝sin x的图象经变换得到y＝A sin(ωx＋φ) （A>0，ω>0）的图象的步骤如下：【知识拓展】1．由y＝sin ωx到y＝sin（ωx＋φ)(ω>0，φ〉0）的变换：向左平移φω个单位长度而非φ个单位长度．2．函数y＝A sin（ωx＋φ）的对称轴由ωx＋φ＝kπ＋错误!,k∈Z确定;对称中心由ωx＋φ＝kπ，k∈Z确定其横坐标．【思考辨析】判断下列结论是否正确(请在括号中打“√”或“×")(1)y＝sin错误!的图象是由y＝sin错误!的图象向右平移错误!个单位得到的．( √）（2）将函数y＝sin ωx的图象向右平移φ（φ>0)个单位长度，得到函数y＝sin（ωx－φ）的图象．（×)（3）利用图象变换作图时“先平移，后伸缩"与“先伸缩,后平移”中平移的长度一致．( ×)（4)函数y＝A sin（ωx＋φ）的最小正周期为T＝错误!。

( ×) (5）把y＝sin x的图象上各点纵坐标不变，横坐标缩短为原来的错误!,所得图象对应的函数解析式为y＝sin 12x。

（×)(6)若函数y＝A cos（ωx＋φ）的最小正周期为T，则函数图象的两个相邻对称中心之间的距离为错误!.（√）1．(教材改编）y＝2sin(错误!x－错误!）的振幅，频率和初相分别为( ）A．2，4π，错误!B．2，错误!，错误!C．2，错误!，－错误!D．2，4π,－错误!答案C解析由题意知A＝2，f＝错误!＝错误!＝错误!，初相为－错误!. 2．（2015·山东）要得到函数y＝sin错误!的图象，只需将函数y＝sin 4x 的图象( )A．向左平移π12个单位B．向右平移错误!个单位C．向左平移错误!个单位D．向右平移错误!个单位答案B解析∵y＝sin错误!＝sin错误!，∴要得到y＝sin错误!的图象,只需将函数y＝sin 4x的图象向右平移错误!个单位．3．（2016·青岛模拟）将函数y＝sin x的图象上所有的点向右平行移动错误!个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变），所得图象的函数解析式是( ）A．y＝sin（2x－错误!）B．y＝sin（2x－错误!）C．y＝sin（错误!x－错误!）D．y＝sin（错误!x－错误!）答案C解析y＝sin xπ10右移个单位−−−−−→y＝sin（x－错误!)错误!y＝sin(错误!x－错误!）．4．(2016·临沂模拟）已知函数f(x)＝A cos(ωx＋θ）的图象如图所示,f(错误!)＝－错误!,则f(－错误!）＝________。

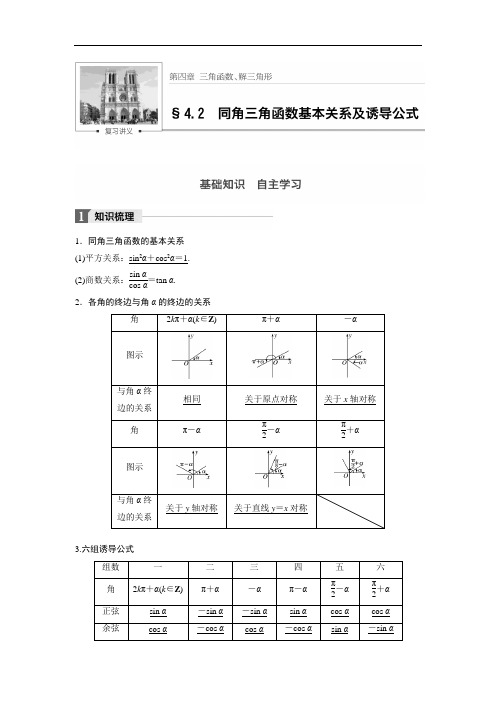
1．同角三角函数的基本关系(1)平方关系：sin2α＋cos2α＝1.(2)商数关系：sin αcos α＝tan α.2．各角的终边与角α的终边的关系3.六组诱导公式【知识拓展】1．诱导公式的记忆口诀：奇变偶不变，符号看象限． 2．同角三角函数基本关系式的常用变形： (sin α±cos α)2＝1±2sin αcos α； (sin α＋cos α)2＋(sin α－cos α)2＝2； (sin α＋cos α)2－(sin α－cos α)2＝4sin αcos α.【思考辨析】判断下列结论是否正确(请在括号中打“√”或“×”) (1)若α，β为锐角，则sin 2α＋cos 2β＝1.( × ) (2)若α∈R ，则tan α＝sin αcos α恒成立．( × )(3)sin(π＋α)＝－sin α成立的条件是α为锐角．( × )(4)诱导公式的记忆口诀中“奇变偶不变，符号看象限”，其中的奇、偶是指π2的奇数倍和偶数倍，变与不变指函数名称的变化．( √ )1．(2015·福建)若sin α＝－513，且α为第四象限角，则tan α的值等于( )A.125 B ．－125 C.512 D ．－512 答案 D解析 ∵sin α＝－513，且α为第四象限角，∴cos α＝1213，∴tan α＝sin αcos α＝－512，故选D.2．(教材改编)已知sin(π＋α)＝12，则cos α的值为( )A ．±12B.12C.32D ．±32答案 D解析 ∵sin(π＋α)＝－sin α＝12.∴sin α＝－12，cos α＝±1－sin 2α＝±32.3．(2016·东营模拟)计算：sin 116π＋cos 103π等于( ) A ．－1 B ．1 C ．0 D.12－32答案 A 解析 ∵sin 116π＝sin(π＋56π)＝－sin 5π6＝－12， cos103π＝cos(2π＋4π3)＝cos 4π3＝－12， ∴sin116π＋cos 103π＝－1. 4．(教材改编)若tan α＝2，则sin α＋4cos α5sin α－2cos α＝ .答案 34解析sin α＋4cos α5sin α－2cos α＝tan α＋45tan α－2＝2＋45×2－2＝34. 5．已知函数f (x )＝⎩⎪⎨⎪⎧2cos π3x ，x ≤2 000，x －18，x >2 000，则f (f (2 018))＝ .答案 －1解析 ∵f (f (2 018))＝f (2 018－18)＝f (2 000)， ∴f (2 000)＝2cos 2 000π3＝2cos 23π＝－1.题型一 同角三角函数关系式的应用例1 (1)已知sin αcos α＝18，且5π4<α<3π2，则cos α－sin α的值为( )A ．－32B.32C ．－34D.34(2)化简：(1＋tan 2α)(1－sin 2α)＝ . 答案 (1)B (2)1 解析 (1)∵5π4＜α＜3π2，∴cos α＜0，sin α＜0且cos α>sin α， ∴cos α－sin α＞0.又(cos α－sin α)2＝1－2sin αcos α＝1－2×18＝34，∴cos α－sin α＝32. (2)(1＋tan 2α)(1－sin 2α)＝(1＋sin 2αcos 2α)·cos 2α＝cos 2α＋sin 2αcos 2α·cos 2α＝1. 思维升华 (1)利用sin 2α＋cos 2α＝1可以实现角α的正弦、余弦的互化，利用sin αcos α＝tan α可以实现角α的弦切互化．(2)应用公式时注意方程思想的应用：对于sin α＋cos α，sin αcos α，sin α－cos α这三个式子，利用(sin α±cos α)2＝1±2sin αcos α，可以知一求二．(3)注意公式逆用及变形应用：1＝sin 2α＋cos 2α，sin 2α＝1－cos 2α，cos 2α＝1－sin 2α.已知sin α－cos α＝2，α∈(0，π)，则tan α等于( )A ．－1B ．－22C.22D ．1答案 A解析 由⎩⎨⎧sin α－cos α＝2，sin 2α＋cos 2α＝1，消去sin α得2cos 2α＋22cos α＋1＝0， 即(2cos α＋1)2＝0， ∴cos α＝－22. 又α∈(0，π)， ∴α＝3π4，∴tan α＝tan 3π4＝－1.题型二 诱导公式的应用例2 (1)(2016·长春模拟)已知f (x )＝sin (2π－x )·cos (32π＋x )cos (3π－x )·sin (112π－x )，则f (－21π4)＝ .(2)已知A ＝sin (k π＋α)sin α＋cos (k π＋α)cos α(k ∈Z )，则A 的值构成的集合是( )A ．{1，－1,2，－2}B ．{－1,1}C ．{2，－2}D ．{1，－1,0,2，－2}答案 (1)－1 (2)C解析 (1)f (x )＝－sin x ·sin x－cos x ·(－cos x )＝－tan 2x ，f (－21π4)＝－tan 2(－21π4)＝－tan 234π＝－1.(2)当k 为偶数时，A ＝sin αsin α＋cos αcos α＝2；当k 为奇数时，A ＝－sin αsin α－cos αcos α＝－2.∴A 的值构成的集合是{2，－2}． 思维升华 (1)诱导公式的两个应用①求值：负化正，大化小，化到锐角为终了． ②化简：统一角，统一名，同角名少为终了． (2)含2π整数倍的诱导公式的应用由终边相同的角的关系可知，在计算含有2π的整数倍的三角函数式中可直接将2π的整数倍去掉后再进行运算，如cos(5π－α)＝cos(π－α)＝－cos α.(1)化简：tan (π＋α)cos (2π＋α)sin (α－3π2)cos (－α－3π)sin (－3π－α)＝ .(2)已知角α终边上一点P (－4,3)，则cos (π2＋α)·sin (－π－α)cos (11π2－α)·sin (9π2＋α)的值为 ．答案 (1)－1 (2)－34解析 (1)原式＝tan αcos αsin[－2π＋(α＋π2)]cos (3π＋α)[－sin (3π＋α)]＝tan αcos αsin (π2＋α)(－cos α)sin α＝tan αcos αcos α(－cos α)sin α＝－tan αcos αsin α＝－sin αcos α·cos αsin α＝－1.(2)原式＝(－sin α)sin α(－sin α)cos α＝tan α，根据三角函数的定义得tan α＝－34.题型三 同角三角函数关系式、诱导公式的综合应用例3 (1)已知α为锐角，且有2tan(π－α)－3cos(π2＋β)＋5＝0，tan(π＋α)＋6sin(π＋β)－1＝0，则sin α的值是( ) A.355B.377C.31010D.13答案 C解析 2tan(π－α)－3cos(π2＋β)＋5＝0化简为－2tan α＋3sin β＋5＝0，① tan(π＋α)＋6sin(π＋β)－1＝0化简为 tan α－6sin β－1＝0.②由①②消去sin β，解得tan α＝3. 又α为锐角，根据sin 2α＋cos 2α＝1， 解得sin α＝31010.(2)已知－π<x <0，sin(π＋x )－cos x ＝－15.①求sin x －cos x 的值； ②求sin 2x ＋2sin 2x 1－tan x的值．解 ①由已知，得sin x ＋cos x ＝15，sin 2x ＋2sin x cos x ＋cos 2x ＝125，整理得2sin x cos x ＝－2425.∵(sin x －cos x )2＝1－2sin x cos x ＝4925.由－π<x <0，知sin x <0， 又sin x ＋cos x >0， ∴cos x >0，sin x －cos x <0， 故sin x －cos x ＝－75.②sin 2x ＋2sin 2x 1－tan x＝2sin x (cos x ＋sin x )1－sin x cos x＝2sin x cos x (cos x ＋sin x )cos x －sin x＝－2425×1575＝－24175.引申探究本例(2)中若将条件“－π<x <0”改为“0<x <π”，求sin x －cos x 的值． 解 若0<x <π，又2sin x cos x ＝－2425，∴sin x >0，cos x <0，∴sin x －cos x >0，故sin x －cos x ＝75.思维升华 (1)利用同角三角函数关系式和诱导公式求值或化简时，关键是寻求条件、结论间的联系，灵活使用公式进行变形． (2)注意角的范围对三角函数符号的影响．已知sin ⎝⎛⎭⎫π2＋α＝35，α∈⎝⎛⎭⎫0，π2，则sin(π＋α)等于( ) A.35 B ．－35C.45 D ．－45答案 D解析 由已知sin ⎝⎛⎭⎫π2＋α＝35， 得cos α＝35，∵α∈⎝⎛⎭⎫0，π2， ∴sin α＝45，∴sin(π＋α)＝－sin α＝－45.7．分类讨论思想在三角函数中的应用典例 (1)已知sin α＝255，则tan(α＋π)＋sin ⎝⎛⎭⎫5π2＋αcos ⎝⎛⎭⎫5π2－α＝ .(2)(2016·湛江模拟)已知k ∈Z ，化简：sin (k π－α)cos[(k －1)π－α]sin[(k ＋1)π＋α]cos (k π＋α)＝ .思想方法指导 (1)在利用同角三角函数基本关系式中的平方关系时，要根据角的范围对开方结果进行讨论．(2)利用诱导公式化简时要对题中整数k 是奇数或偶数进行讨论． 解析 (1)∵sin α＝255＞0，∴α为第一或第二象限角． tan(α＋π)＋sin ⎝⎛⎭⎫5π2＋αcos ⎝⎛⎭⎫5π2－α＝tan α＋cos αsin α＝sin αcos α＋cos αsin α＝1sin αcos α. ①当α是第一象限角时，cos α＝1－sin 2 α＝55， 原式＝1sin αcos α＝52.②当α是第二象限角时，cos α＝－1－sin 2α＝－55， 原式＝1sin αcos α＝－52.综上①②知，原式＝52或－52.(2)当k ＝2n (n ∈Z )时，原式＝sin (2n π－α)cos[(2n －1)π－α]sin[(2n ＋1)π＋α]cos (2n π＋α)＝sin (－α)·cos (－π－α)sin (π＋α)·cos α＝－sin α(－cos α)－sin α·cos α＝－1；当k ＝2n ＋1(n ∈Z )时，原式＝sin[(2n ＋1)π－α]·cos[(2n ＋1－1)π－α]sin[(2n ＋1＋1)π＋α]·cos[(2n ＋1)π＋α]＝sin (π－α)·cos αsin α·cos (π＋α) ＝sin α·cos αsin α(－cos α)＝－1. 综上，原式＝－1. 答案 (1)52或－52(2)－11．(2016·西安模拟)已知cos α＝45，α∈(0，π)，则tan α的值等于( )A.43B.34 C ．－43D ．－34答案 B解析 ∵α∈(0，π)， ∴sin α＝1－cos 2α＝1－(45)2＝35，由tan α＝sin αcos α，得tan α＝34. 2．已知tan(α－π)＝34，且α∈(π2，3π2)，则sin(α＋π2)等于( )A.45 B ．－45C.35 D ．－35答案 B解析 由tan(α－π)＝34，得tan α＝34，∴α∈(π，3π2)，由⎩⎪⎨⎪⎧tan α＝34，sin 2α＋cos 2α＝1及α∈(π，3π2)，得cos α＝－45，而sin(α＋π2)＝cos α＝－45.3．若角α的终边落在第三象限，则cos α1－sin 2 α＋2sin α1－cos 2 α的值为( )A ．3B ．－3C ．1D ．－1答案 B解析 由角α的终边落在第三象限， 得sin α＜0，cos α＜0，故原式＝cos α|cos α|＋2sin α|sin α|＝cos α－cos α＋2sin α－sin α＝－1－2＝－3.4．若sin(π－α)＝－2sin(π2＋α)，则sin α·cos α的值等于( )A ．－25B ．－15C.25或－25D.25答案 A解析 由sin(π－α)＝－2sin(π2＋α)，可得sin α＝－2cos α，则tan α＝－2，sin α·cos α＝sin α·cos αsin 2α＋cos 2α＝tan α1＋tan 2α＝－25. 5．已知函数f (x )＝a sin(πx ＋α)＋b cos(πx ＋β)，且f (4)＝3，则f (2 017)的值为( ) A ．－1 B ．1 C ．3 D ．－3答案 D解析 ∵f (4)＝a sin(4π＋α)＋b cos(4π＋β) ＝a sin α＋b cos β＝3，∴f (2 017)＝a sin(2 017π＋α)＋b cos(2 017π＋β) ＝a sin(π＋α)＋b cos(π＋β) ＝－a sin α－b cos β ＝－3.*6.(2016·揭阳模拟)若sin θ，cos θ是方程4x 2＋2mx ＋m ＝0的两根，则m 的值为( ) A ．1＋ 5 B ．1－ 5 C ．1±5 D ．－1－ 5答案 B解析 由题意知sin θ＋cos θ＝－m 2，sin θcos θ＝m 4，又(sin θ＋cos θ)2＝1＋2sin θcos θ，∴m 24＝1＋m 2， 解得m ＝1±5，又Δ＝4m 2－16m ≥0，∴m ≤0或m ≥4，∴m ＝1－ 5.7．已知α为钝角，sin(π4＋α)＝34，则sin(π4－α)＝ . 答案 －74解析 因为α为钝角，所以cos(π4＋α)＝－74， 所以sin(π4－α)＝cos[π2－(π4－α)]＝cos(π4＋α)＝－74. 8．若f (cos x )＝cos 2x ，则f (sin 15°)＝ .答案 －32解析 f (sin 15°)＝f (cos 75°)＝cos 150°＝cos(180°－30°)＝－cos 30°＝－32. 9．已知角θ的顶点在坐标原点，始边与x 轴正半轴重合，终边在直线2x －y ＝0上，则sin (3π2＋θ)＋cos (π－θ)sin (π2－θ)－sin (π－θ)＝ . 答案 2解析 由题意可得tan θ＝2，原式＝－cos θ－cos θcos θ－sin θ＝－21－tan θ＝2. 10．(2016·长春模拟)已知α为第二象限角，则cos α1＋tan 2α＋sin α1＋1tan 2α＝ . 答案 0解析 原式＝cos α sin 2α＋cos 2αcos 2α＋sin α sin 2α＋cos 2αsin 2α＝cos α1|cos α|＋sin α1|sin α|， 因为α是第二象限角，所以sin α>0，cos α<0，所以cos α1|cos α|＋sin α1|sin α|＝－1＋1＝0，即原式等于0. 11．已知sin(3π＋α)＝2sin ⎝⎛⎭⎫3π2＋α，求下列各式的值：(1)sin α－4cos α5sin α＋2cos α； (2)sin 2α＋sin 2α.解 由已知得sin α＝2cos α.(1)原式＝2cos α－4cos α5×2cos α＋2cos α＝－16. (2)原式＝sin 2α＋2sin αcos αsin 2α＋cos 2α＝sin 2α＋sin 2αsin 2α＋14sin 2α＝85. 12．已知在△ABC 中，sin A ＋cos A ＝15. (1)求sin A cos A 的值；(2)判断△ABC 是锐角三角形还是钝角三角形；(3)求tan A 的值．解 (1)∵(sin A ＋cos A )2＝125， ∴1＋2sin A cos A ＝125， ∴sin A cos A ＝－1225. (2)∵sin A cos A <0，又0<A <π，∴cos A <0，∴A 为钝角，∴△ABC 为钝角三角形．(3)(sin A －cos A )2＝1－2sin A cos A ＝4925. 又sin A －cos A >0，∴sin A －cos A ＝75， ∴sin A ＝45，cos A ＝－35， 故tan A ＝－43. *13.已知关于x 的方程2x 2－(3＋1)x ＋m ＝0的两根为sin θ和cos θ，θ∈(0,2π)．求：(1)sin 2θsin θ－cos θ＋cos θ1－tan θ的值； (2)m 的值；(3)方程的两根及此时θ的值．解 (1)原式＝sin 2θsin θ－cos θ＋cos θ1－sin θcos θ＝sin 2θsin θ－cos θ＋cos 2θcos θ－sin θ＝sin 2θ－cos 2θsin θ－cos θ＝sin θ＋cos θ. 由条件知sin θ＋cos θ＝3＋12， 故sin 2θsin θ－cos θ＋cos θ1－tan θ＝3＋12. (2)由sin 2θ＋2sin θcos θ＋cos 2θ＝1＋2sin θcos θ＝(sin θ＋cos θ)2， 得m ＝32. (3)由⎩⎪⎨⎪⎧sin θ＋cos θ＝3＋12，sin θ·cos θ＝34， 知⎩⎨⎧ sin θ＝32，cos θ＝12或⎩⎨⎧ sin θ＝12，cos θ＝32. 又θ∈(0,2π)，故θ＝π3或θ＝π6.。

2018三角函数专题（理）1.已知集合22{(,)|3,,}A x y x y x y =+∈∈Z Z ≤，则A 中元素的个数为( ) A ．9 B ．8 C ．5 D ．42.已知向量a ，b 满足||1=a ，1⋅=-a b ，则(2)⋅-=a a b ( ) A ．4B ．3C ．2D ．03.在ABC △中，cos 2C =1BC =，5AC =，则AB =( ) A．BCD．4.若()cos sin f x x x =-在[,]a a -是减函数，则a 的最大值是( ) A ．π4B ．π2C ．3π4D ．π5.若，则( ) A ．B ．C ．D ． 6.的内角的对边分别为，，，若的面积为，则( ) A ．B ．C ．D ．7.在ABC △中，AD 为BC 边上的中线，E 为AD 的中点，则EB =（ ） A ．3144AB AC - B ．1344AB AC - C ．3144AB AC +D ．1344AB AC +8.设R x ∈，则“11||22x -<”是“31x <”的 （ ） A. 充分而不必要条件 B. 必要而不重复条件 C.充要条件 D. 既不充分也不必要条件 9.已知a ∈R ，则“1a >”是“11a<”的（ ） A. 充分非必要条件 B.必要非充分条件 C. 充要条件 D. 既非充分又非必要条件1sin 3α=cos 2α=897979-89-ABC △A B C ，，a b c ABC △2224a b c +-C =π2π3π4π610．已知2log e =a ，ln 2b =，121log 3c =，则a ，b ，c 的大小关系为 （ ） A. a b c >> B. b a c >> C. c b a >> D. c a b >> 11．将函数sin(2)5y x π=+的图象向右平移10π个单位长度，所得图象对应的函数（ ） A. 在区间35[,]44ππ上单调递增 B. 在区间3[,]4ππ上单调递减 C. 在区间53[,]42ππ上单调递增 D. 在区间3[,2]2ππ上单调递减 12．如图，在平面四边形ABCD 中，AB BC ⊥，AD CD ⊥，120BAD ∠=︒，1AB AD ==. 若点E 为边CD 上的动点，则 的最小值为（ ） A.2116 B. 32 C. 2516D. 313.设a ，b 均为单位向量，则“33-=+a b a b ”是“a ⊥b ”的（ ） A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件D. 既不充分也不必要条件14．在平面直角坐标系中，记d 为点P （cos θ，sin θ）到直线20x my --=的距离，当θ，m 变化时，d 的最大值为（ ） A. 1B. 2C. 3D. 415．设集合{(,)|1,4,2},A x y x y ax y x ay =-≥+>-≤则（ ） A. 对任意实数a ，(2,1)A ∈B. 对任意实数a ，（2，1）A ∉C. 当且仅当a <0时，（2，1）A ∉D. 当且仅当32a ≤时，（2，1）A ∉ 16．已知a ，b ，e 是平面向量，e 是单位向量．若非零向量a 与e 的夹角为，向量b 满足b 2−4e ·b +3=0，则|a −b |的最小值是()π3A−1B+1C．2D．217.在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ．若a ，b =2，A =60°，则sin B =___________，c =___________．18.已知向量，，．若，则________．19.在平面直角坐标系中，已知点(1,0)A -，(2,0)B ，E 、F 是y 轴上的两个动点，且2EF =，则AE BF ∙的最小值为_________.20.设函数f （x ）=πcos()(0)6x ωω->，若π()()4f x f ≤对任意的实数x 都成立，则ω的最小值为__________．21.若x ，y 满足x +1≤y ≤2x ，则2y –x 的最小值是__________． 22.已知函数)22)(2sin(πϕπϕ<<-+=x y 的图象关于直线3π=x 对称，则ϕ的值是______23.在平面直角坐标系xOy 中，A 为直线l ：x y 2=上在第一象限内的点，B (5，0)，以AB 为直径的圆C 与l 交于另一点D ，若0=⋅，则点A 的横坐标为_______24.在ABC ∆中角A ，B ，C 所对的边分别为a ，b ，c ，︒=∠120ABC ，ABC ∠的平分线交AC 与点D ，且BD ＝1，则4a ＋c 的最小值为_______25.已知函数()2sin sin 2f x x x =+，则()f x 的最小值是________．26.已知sin cos 1αβ+=，cos sin 0αβ+=，则sin()αβ+=__________．27．已知圆2220x y x +-=的圆心为C ，直线1,23⎧=-+⎪⎪⎨⎪=⎪⎩x y (t 为参数)与该圆相交于A ，B 两点，则ABC ∆的面积为 . 28.已知,R a b ∈，且360a b -+=，则128ab+的最小值为 . ()=1,2a ()=2,2-b ()=1,λc ()2∥c a +b λ=29.在平面四边形ABCD 中，90ADC =︒∠，45A =︒∠，2AB =，5BD =． ⑴求cos ADB ∠；⑵若DC =，求BC ．30.在△ABC 中，a =7，b =8，cos B =–17． （Ⅰ）求∠A ； （Ⅱ）求AC 边上的高．31.在ABC ∆中，内角A ，B ，C 所对的边分别为a ，b ，c.已知sin cos()6b A a B π=-.（I ）求角B 的大小；（II ）设a =2，c =3，求b 和sin(2)A B -的值.32.已知βα,为锐角，34tan =α，55)cos(-=+βα， (1)求α2cos 的值； (2)求)tan(βα-的值．33.已知角α的顶点与原点O 重合，始边与x 轴的非负半轴重合，它的终边过点P （）．（Ⅰ）求sin （α+π）的值； （Ⅱ）若角β满足sin （α+β）=，求cos β的值．34.设常数a ∈R ，函数2()sin 22cos f x a x x =+。

1．用五点法作正弦函数和余弦函数的简图正弦函数y＝sin x,x∈[0，2π]的图象中,五个关键点是：（0，0），(错误!,1),（π，0),(错误!，－1)，（2π,0)．余弦函数y＝cos x，x∈［0，2π］的图象中，五个关键点是：(0，1)，（错误!，0)，(π，－1),(错误!，0)，(2π，1)．2．正弦函数、余弦函数、正切函数的图象与性质函数y＝sin x y＝cos x y＝tan x图象定义域R R ｛x｜x∈R 且x≠错误!＋kπ，k∈Z}值域[－1,1］[－1,1]R【知识拓展】1．对称与周期(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个周期，相邻的对称中心与对称轴之间的距离是错误!个周期．（2)正切曲线相邻两对称中心之间的距离是半个周期．2．奇偶性若f(x)＝A sin（ωx＋φ）(A，ω≠0），则(1)f（x)为偶函数的充要条件是φ＝错误!＋kπ(k∈Z）；（2）f(x)为奇函数的充要条件是φ＝kπ(k∈Z)．【思考辨析】判断下列结论是否正确(请在括号中打“√”或“×”)（1)y＝sin x在第一、第四象限是增函数．（×)(2)常数函数f(x)＝a是周期函数,它没有最小正周期．（√）(3）正切函数y＝tan x在定义域内是增函数．（×）（4)已知y＝k sin x＋1，x∈R,则y的最大值为k＋1.（×)（5)y＝sin ｜x|是偶函数．( √)(6)若sin x>错误!，则x>错误!.（×)1．函数f（x）＝cos（2x－错误!)的最小正周期是( ）A.错误!B．πC．2π D．4π答案B解析最小正周期为T＝错误!＝错误!＝π.故选B.2．（教材改编）函数f(x）＝3sin(2x－错误!)在区间［0，错误!］上的值域为( ）A．［－错误!，错误!] B．[－错误!，3]C．［－错误!，错误!］D．[－错误!，3]答案B解析当x∈［0，错误!］时,2x－错误!∈［－错误!，错误!]，sin（2x－错误!）∈［－错误!，1],故3sin(2x－错误!）∈[－错误!，3]，即f（x)的值域为［－32，3]．3．函数y＝tan 2x的定义域是（) A。

2018年高考数学——三角函数解答1.(18北京理（15）（本小题13分）)在△ABC 中，a =7，b =8，cos B =–17． （Ⅰ）求∠A ；（Ⅱ）求AC 边上的高．2.（18江苏16．（本小题满分14分））已知,αβ为锐角，4tan 3α=，cos()αβ+=． （1）求cos2α的值；（2）求tan()αβ-的值．3.（18全国一理17．（12分））在平面四边形ABCD 中，90ADC ∠=o ，45A ∠=o ，2AB =，5BD =.（1）求cos ADB ∠；（2）若DC =，求BC .4.（18天津理（15）（本小题满分13分））在ABC △中，内角A ，B ，C 所对的边分别为a ，b ，c.已知sin cos()6b A a B π=-. （I ）求角B 的大小；学科*网（II ）设a =2，c =3，求b 和sin(2)A B -的值.5.（18浙江18．（本题满分14分））已知角α的顶点与原点O 重合，始边与x 轴的非负半轴重合，它的终边过点P （3455-，-）． （Ⅰ）求sin （α+π）的值；（Ⅱ）若角β满足sin （α+β）=513，求cos β的值．6.（18北京文（16）（本小题13分））已知函数2()sin cos f x x x x =+.（Ⅰ）求()f x 的最小正周期；（Ⅱ）若()f x 在区间[,]3m π-上的最大值为32，求m 的最小值.参考答案：1.解：（Ⅰ）在△ABC 中，∵cos B =–17，∴B ∈（π2，π），∴sin B =2431cos B -=． 由正弦定理得sin sin a b A B =⇒7sin A =43，∴sin A =3． ∵B ∈（π2，π），∴A ∈（0，π2），∴∠A =π3． （Ⅱ）在△ABC 中，∵sin C =sin （A +B ）=sin A cos B +sin B cos A =31143()72⨯-+⨯=33． 如图所示，在△ABC 中，∵sin C =h BC ，∴h =sin BC C ⋅=33337⨯=， ∴AC 边上的高为33．2.解：（1）因为4tan 3α=，sin tan cos ααα=，所以4sin cos 3αα=． 因为22sin cos 1αα+=，所以29cos 25α=， 因此，27cos22cos 125αα=-=-． （2）因为,αβ为锐角，所以(0,π)αβ+∈．又因为5cos()αβ+=，所以225sin()1cos ()αβαβ+=-+=， 因此tan()2αβ+=-．因为4tan 3α=，所以22tan 24tan 21tan 7ααα==--， 因此，tan 2tan()2tan()tan[2()]1+tan 2tan()11ααβαβααβααβ-+-=-+==-+．3.解：（1）在ABD △中，由正弦定理得sin sin BD AB A ADB=∠∠. 由题设知，52sin 45sin ADB=︒∠，所以2sin ADB ∠=. 由题设知，90ADB ∠<︒，所以223cos 1255ADB ∠=-=.（2）由题设及（1）知，cos sin BDC ADB ∠=∠=在BCD △中，由余弦定理得 2222cos BC BD DC BD DC BDC =+-⋅⋅⋅∠258255=+-⨯⨯ 25=.所以5BC =.4.（Ⅰ）解：在△ABC 中，由正弦定理sin sin a b A B=，可得sin sin b A a B =，又由πsin cos()6b A a B =-，得πsin cos()6a B a B =-，即πsin cos()6B B =-，可得tan B =．又因为(0π)B ∈，，可得B =π3． （Ⅱ）解：在△ABC 中，由余弦定理及a =2，c =3，B =π3，有2222cos 7b a c ac B =+-=，故b由πsin cos()6b A a B =-，可得sin A =．因为a <c ，故cos A ．因此sin 22sin cos A A A =21cos22cos 17A A =-=．所以，sin(2)sin 2cos cos2sin A B A B A B -=-=1127-=5.（Ⅰ）由角α的终边过点34(,)55P --得4sin 5α=-， 所以4sin(π)sin 5αα+=-=. （Ⅱ）由角α的终边过点34(,)55P --得3cos 5α=-， 由5sin()13αβ+=得12cos()13αβ+=±. 由()βαβα=+-得cos cos()cos sin()sin βαβααβα=+++， 所以56cos 65β=-或16cos 65β=-.6.【解析】（Ⅰ）1cos 211π1()22cos 2sin(2)22262x f x x x x x -=+=-+=-+， 所以()f x 的最小正周期为2ππ2T ==. （Ⅱ）由（Ⅰ）知π1()sin(2)62f x x =-+. 因为π[,]3x m ∈-，所以π5ππ2[,2]666x m -∈--. 要使得()f x 在π[,]3m -上的最大值为32，即πsin(2)6x -在π[,]3m -上的最大值为1. 所以ππ262m -≥，即π3m ≥. 所以m 的最小值为π3.。

真题演练集训1．若cos ⎝ ⎛⎭⎪⎫π4－α＝35，则sin 2α＝( ) A.725 B.15C ．－15D ．－725 答案：D解析：因为cos ⎝ ⎛⎭⎪⎫π4－α＝cos π4cos α＋sin π4·sin α＝22(sin α＋cos α)＝35，所以sin α＋cos α＝325，所以1＋sin 2α＝1825，所以sin 2α＝－725，故选D. 2．设α∈⎝ ⎛⎭⎪⎫0，π2，β∈⎝⎛⎭⎪⎫0，π2，且tan α＝1＋sin βcos β，则( ) A ．3α－β＝π2B ．2α－β＝π2C ．3α＋β＝π2D ．2α＋β＝π2答案：B解析：解法一：由tan α＝1＋sin βcos β，得 sin αcos α＝1＋sin βcos β， 即sin αcos β＝cos α＋cos αsin β， ∴sin(α－β)＝cos α＝sin ⎝ ⎛⎭⎪⎫π2－α. ∵α∈⎝ ⎛⎭⎪⎫0，π2，β∈⎝⎛⎭⎪⎫0，π2， ∴α－β∈⎝ ⎛⎭⎪⎫－π2，π2，π2－α∈⎝⎛⎭⎪⎫0，π2， ∴由sin(α－β)＝sin ⎝ ⎛⎭⎪⎫π2－α，得 α－β＝π2－α，∴2α－β＝π2. 解法二：tan α＝1＋sin βcos β＝1＋cos ⎝ ⎛⎭⎪⎫π2－βsin ⎝ ⎛⎭⎪⎫π2－β＝2cos 2⎝ ⎛⎭⎪⎫π4－β22sin ⎝ ⎛⎭⎪⎫π4－β2cos ⎝ ⎛⎭⎪⎫π4－β2＝cot ⎝ ⎛⎭⎪⎫π4－β2 ＝tan ⎣⎢⎡⎦⎥⎤π2－⎝ ⎛⎭⎪⎫π4－β2tan ⎝ ⎛⎭⎪⎫π4＋β2， ∴α＝k π＋⎝ ⎛⎭⎪⎫π4＋β2，k ∈Z ∴2α－β＝2k π＋π2，k ∈Z . 当k ＝0时，满足2α－β＝π2，故选B. 3．已知2cos 2x ＋sin 2x ＝A sin(ωx ＋φ)＋b (A >0)，则A ＝________，b ＝________. 答案： 2 1解析：由于2cos 2x ＋sin 2x ＝1＋cos 2x ＋sin 2x ＝2sin ⎝⎛⎭⎪⎫2x ＋π4＋1，所以A ＝2，b ＝1.4．已知函数f (x )＝3sin(ωx ＋φ)⎝⎛⎭⎪⎫ω＞0，－π2≤φ＜π2的图象关于直线x ＝π3对称，且图象上相邻两个最高点的距离为π.(1)求ω和φ的值；(2)若f ⎝ ⎛⎭⎪⎫α2＝34⎝ ⎛⎭⎪⎫π6＜α＜2π3，求cos ⎝⎛⎭⎪⎫α＋3π2的值． 解：(1)因为f (x )的图象上相邻两个最高点的距离为π，所以f (x )的最小正周期T ＝π，从而ω＝2πT＝2. 又因为f (x )的图象关于直线x ＝π3对称， 所以2×π3＋φ＝k π＋π2，k ＝0，±1，±2，…. 因为－π2≤φ＜π2得k ＝0， 所以φ＝π2－2π3＝－π6. (2)由(1)得f ⎝ ⎛⎭⎪⎫α2＝3sin ⎝⎛⎭⎪⎫2·α2－π6＝34， 所以sin ⎝⎛⎭⎪⎫α－π6＝14.由π6＜α＜2π3得0＜α－π6＜π2， 所以cos ⎝⎛⎭⎪⎫α－π6＝1－sin 2⎝ ⎛⎭⎪⎫α－π6 ＝1－⎝ ⎛⎭⎪⎫142＝154. 因此cos ⎝ ⎛⎭⎪⎫α＋3π2＝sin α＝sin ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α－π6＋π6 ＝sin ⎝ ⎛⎭⎪⎫α－π6cos π6＋cos ⎝⎛⎭⎪⎫α－π6sin π6 ＝14×32＋154×12＝3＋158. 课外拓展阅读给值求角忽视角的范围致误已知α，β为三角形的两个内角，cos α＝17，sin(α＋β)＝5314，则β＝________. ∵0<α<π，cos α＝17， ∴sin α＝1－⎝ ⎛⎭⎪⎫172＝437. 又∵sin(α＋β)＝5314， ∴cos(α＋β)＝－1－⎝ ⎛⎭⎪⎫53142＝－1114. ∴sin β＝sin ＝sin(α＋β)cos α－cos(α＋β)sin α＝32. 又∵0<β<π，∴β＝π3或2π3. (1)不能根据题设条件缩小α，β及α＋β的取值范围，在由同角基本关系式求sin(α＋β)时不能正确判断符号，产生两角解．(2)结论处应由cos β的值确定β的取值，由sin β确定结论时易出现两解而造成失误．因为0<α<π，cos α＝17，所以sin α＝1－cos 2α＝437，故π3<α<π2.又因为0<α＋β<π，sin(α＋β)＝5314<32，所以0<α＋β<π3或2π3<α＋β<π. 由π3<α<π2，知2π3<α＋β<π， 所以cos(α＋β)＝－1－sin2α＋β＝－1114， 所以cos β＝cos ＝cos(α＋β)cos α＋sin(α＋β)sin α＝12， 又0<β<π，所以β＝π3. π3答题启示利用三角函数值求角时，要充分结合条件，确定角的取值范围，再选取合适的三角函数进行求值，最后确定角的具体取值．。

2018年高考真题解答题专项训练：三角函数（理科）教师版1．已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边过点P（，）．（Ⅰ）求sin（α+π）的值；（Ⅱ）若角β满足sin（α+β）=，求cosβ的值．【来源】2018年全国普通高等学校招生统一考试数学（浙江卷）详解：（Ⅰ）由角的终边过点得，所以.（Ⅱ）由角的终边过点得，由得.由得，所以或.2．在中，内角A，B，C所对的边分别为a，b，c.已知.（1）求角B的大小；（2）设a=2，c=3，求b和的值.【来源】2018年全国普通高等学校招生统一考试理科数学（天津卷）详解：（Ⅰ）在△ABC中，由正弦定理，可得，又由，得，即，可得．又因为，，可得B=．（Ⅱ）在△ABC中，由余弦定理及a=2，c=3，B=，有，故b=．由，可得．因为a<c，故因此，．所以，．3．在ABC中，a=7，b=8，cos B= –．（Ⅰ）求∠A；（Ⅱ）求AC边上的高．【来源】2018年全国普通高等学校招生统一考试理科数学（北京卷）详解：解：（1）在△ABC中，∵cos B=–，∴B∈（，π），∴sin B=．由正弦定理得=，∴sin A=．∵B∈（，π），∴A∈（0，），∴∠A=．（2）在ABC中，∵sin C=sin（A+B）=sin A cos B+sin B cos A==．如图所示，在△ABC中，∵sin C=，∴h==，∴AC边上的高为．4．已知为锐角，，．（1）求的值；（2）求的值．【来源】2018年全国普通高等学校招生统一考试数学（江苏卷）详解：解：（1）因为，，所以．因为，所以，因此，．（2）因为为锐角，所以．又因为，所以，因此．因为，所以，因此，．5．在平面四边形中，，，，.（1）求；（2）若，求.【来源】2018年全国普通高等学校招生统一考试理科数学（新课标I卷）详解：（1）在中，由正弦定理得.由题设知，，所以.由题设知，，所以.（2）由题设及（1）知，.在中，由余弦定理得.所以.。

第四章 三角函数第2节 三角函数的图像与性质题型51 已知解析式确定函数性质1.（2013浙江文6）函数()sin cos f x x x x =⋅+的最小正周期和振幅分别是 A.π1， B.π2， C. 2π1， D. 2π2，1.分析 把函数的解析式化简为只含一个三角函数名的三角函数式，再求周期和振幅.解析 ()1sin 22sin 223f x x x x π⎛⎫==+ ⎪⎝⎭，所以最小正周期为22T π==π，振幅1A =.故选A.2.（2013江苏1）函数π3sin 24y x ⎛⎫=+⎪⎝⎭的最小正周期为 . 2.分析 利用函数()sin y A x ωϕ=+的周期公式求解. 解析 函数3sin 24y x π⎛⎫=+⎪⎝⎭的最小正周期T 2π==π2. 3.（2014陕西文2）函数()πcos 2+4f x x ⎛⎫= ⎪⎝⎭的最小正周期是（ ）.A.π2B.πC.2πD.4π 4.（2014新课标Ⅰ文7）在函数①cos 2y x =，②cos y x =，③cos 26y x π⎛⎫=+⎪⎝⎭， ④tan 24y x π⎛⎫=- ⎪⎝⎭中，最小正周期为π的所有函数为（ ）A.①②③B. ①③④C. ②④D. ①③5.（2014天津文8）已知函数()()cos 0,.f x x x x ωωω=+>∈R 在曲线()y f x =与直线1y =的交点中，若相邻交点距离的最小值为π3，则()f x 的最小正周期为（ ）.A.π2 B.2π3C.πD.2π 6. （2014山东文12）函数22cos y x x =+的最小正周期为 . 7.（2014福建文18）（本小题满分12分） 已知函数()2cos (sin cos )f x x x x =+.（1）求5()4f π的值； （2）求函数()f x 的最小正周期及单调递增区间.8.（2015四川文5）下列函数中，最小正周期为π的奇函数是（ ）. A.πsin 22y x ⎛⎫=+⎪⎝⎭ B. πcos 22y x ⎛⎫=+ ⎪⎝⎭C.sin 2cos 2y x x =+D. sin cos y x x =+ 8.解析 由2πT ω=，可知选项A ，B ，C 的周期都是π，选项D 的周期为2π.通过化简可得，选项A ：cos 2y x =，为偶函数； 选项B 为：sin 2y x =-，为奇函数； 选项C为：π24y x ⎛⎫=+ ⎪⎝⎭，为非奇非偶函数.故选B.9.（2015全国1文8）函数则()cos()f x x ωϕ=+的部分图像如图所示，()f x 的单调递减区间为（ ）.A. ()13π,π44k k k ⎛⎫-+∈ ⎪⎝⎭ZB. ()132π,2π44k k k ⎛⎫-+∈ ⎪⎝⎭Z C. ()13,44k k k ⎛⎫-+∈ ⎪⎝⎭Z D. ()132,244k k k ⎛⎫-+∈ ⎪⎝⎭Z 9.解析 由图可知511244T =-=，得2T =，2ππTω==. 画出图中的一条对称轴0x x =，如图所示. 由图可知034x =，则3πcos 14ϕ⎛⎫+=- ⎪⎝⎭， 可得3π2ππ4k ϕ+=+， 则()π2π4k k ϕ=+∈Z ，得()πcos π4f x x ⎛⎫=+ ⎪⎝⎭.由π2ππ2ππ4k x k ++， 得132244k xk -+.故选D. 4.（2015湖南文）已知0ω>，在函数的交点2sin y xω=与2cos y x ω=的图像中，距离最短的两个交点的距离为则ω= .4.解析 令2sin 2cos x x ωω=，解得2ππ4k x ωω=+和2π5π4k x ωω=+，k ∈Z . 2ππ2sin 4k ωωω⎛⎫+= ⎪⎝⎭2π5π2sin 4k ωωω⎛⎫+=⎪⎝⎭所以交点的坐标为2ππ4k ωω⎛+⎝，2π5π,4k ωω⎛+ ⎝.k ∈Z .距离最短的两个交点一定在同一个周期内，所以((2222π5π2ππ44k k ωωωω⎡⎤⎛⎫⎛⎫+-++= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，解得π2ω=. 5.（2015浙江文）函数()2sin sin cos 1f x x x x =++的最小正周期是 ，最小值是 ．5.解析 ()1cos 21π3sin 21sin 222242x f x x x -⎛⎫=++=-+ ⎪⎝⎭，所以2ππ2T ==，()min 32f x =. 6.（2015天津文）已知函数()()sin cos 0,,f x x x x ωωω=+>∈R 若函数()f x 在区间(),ωω-内单调递增，且函数()f x 的图像关于直线x ω=对称，则ω的值为 ．6.解析 由()f x 在区间(),ωω-内单调递增，且()f x 的图像关于直线x ω=对称，可得π2ωω，即2π2ω，且()222πsin cos sin 14f ωωωω⎛⎫=+=+= ⎪⎝⎭，所以2ππ422ωω+=⇒= 7.（2015安徽文）已知函数2()(sin cos )cos 2f x x x x =++（1）求()f x 的最小正周期；（2）求()f x 在区间π0,2⎡⎤⎢⎥⎣⎦上的最大值和最小值.7.解析 （1）因为()()2sin cos cos21sin 2cos2f x x x x x x =++=++=π214x ⎛⎫++ ⎪⎝⎭，所以()f x 的最小正周期2π2ππ2T ω===.（2）因为π0,2x ⎡⎤∈⎢⎥⎣⎦，所以ππ5π2,444x ⎡⎤+∈⎢⎥⎣⎦，则πsin 242x ⎡⎤⎛⎫+∈-⎢⎥ ⎪⎝⎭⎣⎦，所以()max 1f x =()min 0f x =.8.（2015北京文）已知函数()2sin 2xf x x =- （1）求()f x 的最小正周期；（2）求()f x 在区间2π0,3⎡⎤⎢⎥⎣⎦上的最小值. 8. 解析 （1）()21cos sin sin 22x xf x x x -=-=-=πsin 2sin 3x x x ⎛⎫+=+ ⎪⎝⎭，函数()f x 的最小正周期2πT =.（2）当（1）知()π2sin 3f x x ⎛⎫=+⎪⎝⎭，当2π03x，πππ33x +，π0sin 13x ⎛⎫+ ⎪⎝⎭，()323f x --，函数()f x 在区间2π0,3⎡⎤⎢⎥⎣⎦上的最小值为. 9.（2016浙江文3）函数2sin y x =的图像是（ ）.A. B. C. D.9. D 解析 易知2sin y x =为偶函数，所以它的图像关于y 轴对称，排除A ，C 选项；当2π2x =，即x =max 1y =，排除B 选项.故选D.10.（2016上海文8）方程3sin 1cos2x x =+在[]0,2π区间上的解为 . 10.π6，5π6解析 23sin 22sin x x =-，即22sin 3sin 20x x +-=， 所以()()2sin 1sin 20x x -+=，故1sin 2x =.由于[]0,2πx ∈，故π6x =，5π6. 11.（2016江苏9）定义在区间[]0,3π上的函数sin 2y x =的图像与cos y x =的图像的交点个数是 .11.7解析 解法一（图像法）：画出函数图像草图，如图所示.共7个交点.解法二（解方程）：即解方程sin2cos x x =，即2sin cos cos x x x =. 所以cos 0x =或1sin 2x =，由[]0,3πx ∈. 当cos 0x =时，,,222x π3π5π=；当1sin 2x =时，,,,6666x π5π13π17π=. 共7个根，即共7个交点.12.（2016山东文17）设2()π)sin (sin cos )f x x x x x =---.（1）求()f x 的单调递增区间；（2）把()y f x =的图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），再把得到的图像向左平移π3个单位，得到函数()y g x =的图像，求π6g ⎛⎫⎪⎝⎭的值. 12.解析 （1）由()()()2πsin sin cos f x x x x x =---=()212sin cos x x x --)1cos 2sin 21x x =-+-=sin 221x xπ2sin 213x ⎛⎫=- ⎪⎝⎭，由()πππ2π22π232k x k k --+∈Z ，得()π5πππ1212k x k k -+∈Z ， 所以()f x 的单调递增区间是()π5ππ,π1212k k k ⎡⎤-+∈⎢⎥⎣⎦Z ，（或写为()π5ππ,π1212k k k ⎛⎫-+∈ ⎪⎝⎭Z ）.（2）由（1）知()f x π2sin 213x ⎛⎫=-⎪⎝⎭， 把()y f x =的图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），得到y =π2sin 13x ⎛⎫=-⎪⎝⎭的图像，再把得到的图像向左平移π3个单位，得到y 2sin 1x =+的图像，即()2sin 1.g x x =所以ππ2sin 166g ⎛⎫=+=⎪⎝⎭13.（2017全国2文3）函数()sin 23f x x π⎛⎫=+ ⎪⎝⎭的最小正周期为（ ）.A.4πB.2πC. πD. π213.解析 由题意，22T π==π.故选C.14.（2017山东文7）函数2cos 2y x x =+的最小正周期为（ ）.A.π2 B.2π3C.πD. 2π 14.解析 由题意，得2sin 26y x π⎛⎫=+⎪⎝⎭，其最小正周期22T π==π.故选C.15.（2017浙江18）已知函数()()22sin cos cos f x x x x x x =--∈R . （1）求23f π⎛⎫⎪⎝⎭的值； （2）求()f x 的最小正周期及单调递增区间.15.解析 （1）由2sin 3π=21cos 32π=-，得222112322f π⎛⎫⎛⎫⎛⎫=----= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. （2）由22cos2cos sin x x x =-，sin22sin cos x x x =，得()cos 222sin 26f x x x x π⎛⎫=--=-+ ⎪⎝⎭，所以()f x 的最小正周期是2π2T ==π.由正弦函数的性质得3222,262k x k k πππ+π++π∈Z ，解得2,63k x k k ππ+π+π∈Z . 所以()f x 的单调递增区间是2,63k k k ππ⎡⎤+π+π∈⎢⎥⎣⎦Z ，.题型52 函数的值域(最值)1. (2013天津文6）函数π()sin 24f x x ⎛⎫=-⎪⎝⎭在区间π0,2⎡⎤⎢⎥⎣⎦上的最小值是( ). A. 1-B.C.D. 01.分析：确定出π24x -的范围，根据正弦函数的单调性求出最小值. 解析 因为π0,,2x ⎡⎤∈⎢⎥⎣⎦所以ππ3π2,444x --≤≤所以当ππ244x -=-时，()πsin 24f x x ⎛⎫=- ⎪⎝⎭有最小值2-故选B. 2.（2013江西文13）设sin 3cos3f x x x =+（），若对任意实数x 都有||f x a （），则实数a的取值范围是 .2.解析 由于()π3cos32sin 36f x x x x ⎛⎫=+=+ ⎪⎝⎭，则()π2sin 326f x x ⎛⎫=+ ⎪⎝⎭≤，要使()f x a ≤恒成立，则2a ≥.答案[)2,+∞.3. (2013陕西文14）在如图所示的锐角三角形空地中，欲建一个面积最大的内接矩形花园（阴影部分），则其边长x 为 m . 3.解析 设矩形花园的宽为y m ，则404040x y-=，即40y x =-,矩形花园的面积()()22404020400S x x x x x =-=-+=--+，当20x =m 时，面积最大．4. （2013江苏18）如图，游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C ，另一种是先从A 沿索道乘缆车到B ，然后从B 沿直线步行到C .现有甲.乙两位游客从A 处下山，甲沿AC 匀速步行，速度为50m /min .在甲出发min 2后，乙从A 乘缆车到B ，在B 处停留min 1后，再从匀速步行到C .假设缆车匀速直线运动的速度40m为130m /min ，山路AC 长为1260m ，经测量，1312cos =A ，53cos =C . （1）求索道AB 的长；（2）问乙出发多少分钟后，乙在缆车上与甲的距离最短？ （3）为使两位游客在C 处互相等待的时间不超过3分钟，乙步行的速度应控制在什么范围内？4.分析 （1）由cos A ，cos C 的值可求得sin B 的值，然后在ABC △中利用正弦定理可得AB 的长度；（2）利用余弦定理将乙与甲之间的距离表示为出发时间的函数，然后求得函数的最小值，即得最短距离.（3）利用正弦定理求出BC 的长，再根据题 意列不等式求解.解析 （1）在ABC △中，因为12cos 13A =，3cos 5C =，所以54sin ,sin 135A C ==.从而()()sin sin sinB AC A C =π-+=+⎡⎤⎣⎦sin cos cos sin A C A C=+531246313513565=⨯+⨯=. 由正弦定理sin sin AB ACC B=，得()12604sin 1040m 63sin 565AC AB C B =⋅=⨯=. 所以索道AB 的长为1040m .（2）假设乙出发min t 后，甲、乙两游客距离为d ，此时，甲行走了()10050m t +，乙距离A 处130m t ，所以由余弦定理得()()22210050130d t t =++()213010050t t -⨯⨯+⨯()212200377050.13t t =-+ 由于10400130t ≤≤，即08t ≤≤，故当()35min 37t =时，甲、乙两游客距离最短.（3）由正弦定理sin sin BC ACA B=，得()12605sin 500m 63sin 1365AC BC A B =⋅=⨯=. 乙从B 出发时，甲已走了()()50281550m ⨯++=，还需走710m 才能到达C .CBA设乙步行的速度为m/min v ，由题意得5007103350v --≤≤，解得1250625434v ≤≤， 所以为使两游客在C 处互相等待的时间不超过3min ，乙步行的速度应控制在()1250625,m /min 4314⎡⎤⎢⎥⎣⎦单位：范围内.5.（2013山东文18）设函数2()sin cos (0)f x x x x ωωωω=->，且y =()f x图象的一个对称中心到最近的对称轴的距离为π4．（1） 求ω的值；（2）求()f x 在区间3ππ,2⎡⎤⎢⎥⎣⎦上的最大值和最小值． 5.分析 （1）先利用倍角公式，两角和、差的三角公式把函数()f x 的解析式进行化简整理， 再利用对称中心到最近的对称轴的距离为4π求出ω；（2）先根据x 的取值范围求出23x π-的取值范围，然后利用三角函数的图象，并结合其单调性求出()f x 的最值.解析 （1）()2sin cos f x x x x ωωω=--1cos 21sin 222x x ωω-=-12sin 22x x ωω=-sin 23x ωπ⎛⎫=-- ⎪⎝⎭. 因为图象的一个对称中心到最近的对称轴的距离为4π，又0ω，所以24ωππ=⨯24.因此1ω=.（2）由（1）知()sin 2f x x π⎛⎫=-- ⎪3⎝⎭. 当x 3ππ2≤≤时，2x 5ππ8π-332≤≤.所以sin 2x π⎛⎫-1 ⎪3⎝⎭≤.因此()f x -1≤.故()f x 在区间3,2π⎡⎤π⎢⎥⎣⎦，1-.6. (2013安徽文16）设函数()sin sin 3f x x x π⎛⎫=++⎪⎝⎭. （1）求()f x 的最小值，并求使()f x 取得最小值x 的集合；（2）不画图，说明函数()y f x =的图象可由sin y x =的图象经过怎样变化得到.6. 分析 （1）先逆用两角和正弦公式把()f x 化成关于一个角的三角函数，再利用正弦函 数性质计算；（2）利用三角函数图象的变换规律求解.解析 （1）因为()1sin sin cos 22f x x x x =++3sin cos 226x x x π⎛⎫=+=+ ⎪⎝⎭.所以当()26x k k ππ+=π-∈2Z ，即()223x k k π=π-∈Z 时，()f x 取得最小值. 此时x 的取值集合为22,3x x k k ⎧π⎫=π-∈⎨⎬⎩⎭Z .（2）先将sin y x =y x =的图象；再将y x =的图象上所有的点向左平移π6个单位，得()y f x =的图象.7. (2013陕西文16）已知向量)1cos cos22x x x x ⎛⎫=-=∈ ⎪⎝⎭R ，，，，a b ，设函数()f x =⋅a b .（1）求()f x 的最小正周期；（2）求()f x 在π02⎡⎤⎢⎥⎣⎦，上的最大值和最小值.7.分析 利用向量数量积运算及辅助角公式将()f x 化为一个角的一种三角函数，利用公式 确定周期；利用正弦函数的性质确定最值．解析 ())1cos ,,cos 22f x x x x ⎛⎫=-⋅ ⎪⎝⎭11sin cos 22cos 222x x x x x =-=-πππcos sin 2πsin cos 2πsin 2666x ⎛⎫=-=- ⎪⎝⎭.（1）()f x 的最小正周期为2π2ππ2T ω===，即函数()f x 的最小正周期为π.（2）因为π02x ≤≤，所以ππ5π2666x --≤≤.由正弦函数的性质，得当ππ262x -=，即π3x =时，()f x 取得最大值1；当ππ266x -=-，即0x =时，()102f =-；当π52π66x -=，即π2x =时，π122f ⎛⎫= ⎪⎝⎭，所以()f x 的最小值为12-. 因此，()f x 在π0,2⎡⎤⎢⎥⎣⎦上的最大值是1，最小值是12-．8. (2013重庆文18）在ABC △中，内角A B C ，，的对边分别是a b c ，，，且222a b c =++.（1）求A ；（2）设a S =为ABC △的面积，求3cos cos S B C +的最大值，并指出此时B 的值.8.分析 利用正、余弦定理及差角三角函数直接运算解答.解析 （1）由余弦定理得222cos 2b c a A bc +-===.又因为0πA <<，所以5π6A =.（2）由（1）得1sin 2A =.又由正弦定理及a = 11sin sin sin 3sin sin 22sin a B S ab C a C B C A==⋅⋅=，因此，3cos cos S B C +()3sin sin cos cos B C B C =+()3cos B C =-. 所以，当B C =，即ππ212A B -==时，2cos cos S B C +取最大值3.9.（2013辽宁文17） 设向量)()πsin cos sin 02a x x b x x x ⎡⎤==∈⎢⎥⎣⎦，，，，，.（1）若a b =，求x 的值；（2）设函数()f x a b =⋅，求()f x 的最大值.9.分析 分别表示两向量的模，利用相等求解x 的值；利用数量积运算及辅助角公式化为一 个角的一种函数求解.解析 （1）由)2222sin 4sin xx x =+=a ，222cos sin 1x x =+=b ，及=a b ，得24sin 1x =.又π0,2x ⎡⎤∈⎢⎥⎣⎦，从而1sin 2x =，所以π6x =.（2）()2cos sin f x x x x =⋅=⋅+a b 112cos 222x x =-+1sin 262x π⎛⎫=-+ ⎪⎝⎭， 当ππ0,32x ⎡⎤=∈⎢⎥⎣⎦时，πsin 26x ⎛⎫- ⎪⎝⎭取最大值1． 所以()f x 的最大值为32． 10.（2014新课标Ⅱ文14）函数()sin()2sin cos f x x x ϕϕ=+-的最大值为 .11.（2014江苏14）若ABC △的内角满足sin 2sin A B C +=，则cos C 的最小值是 ．12.（2014北京文16）（本小题满分13分）函数()π3sin 26f x x ⎛⎫=+ ⎪⎝⎭的部分图像如图所示.（1）写出()f x 的最小正周期及图中0x ，0y 的值； （2）求()f x 在区间ππ,212⎡⎤--⎢⎥⎣⎦上的最大值和最小值.12. 解析 （I ）()f x 的最小正周期为π.007π36x y =⋅=. （II ）因为ππ,212x ⎡⎤∈--⎢⎥⎣⎦，所以π5π2,066x ⎡⎤+∈-⎢⎥⎣⎦.于是，当π206x +=，即π12x =-时，()f x 取得最大值0；当ππ262x +=-，即π3x =-时，()f x 取得最小值3-. 评注 本题主要考查函数()sin y A x ωϕ=+的图像和性质，熟练掌握三角函数的图像是解题的关键，属基础题.13．（2014湖北文18）（本小题满分12分） 某实验室一天的温度（单位：C ）随时间t （单位：h ）的变化近似满足函数关系：()ππ10sin 1212f t t t =-，[)024t ∈，. （Ⅰ）求实验室这一天上午8时的温度； （Ⅱ）求实验室这一天的最大温差.14.（2016全国甲文11）函数()πcos26cos 2f x x x ⎛⎫=+-⎪⎝⎭的最大值为（ ）. A.4 B.5 C.6 D.714. B 解析 ()()cos 26sin f x x x =+22sin 6sin 1x x =-++23112sin 22x ⎛⎫=--+ ⎪⎝⎭，所以当sin 1x =时，()f x 取得最大值2615-++=.故选B.15.（2016江苏14）在锐角三角形ABC 中，若sin 2sin sin A B C =，则tan tan tan A B C 的最小值是 .15.8分析 求解多元最值问题，首要的关键是考虑如何消参.解析 解法一：由()sin sin A B C =+sin cos cos sin 2sin sin B C B C B C =+= （*） 由三角形ABC 为锐角三角形，则cos 0,cos 0B C >>， 同时除以cos cos B C 得tan tan 2tan tan B C B C +=. 又()tan tan tan tan 01tan tan B CA B C B C+=-+=->-，所以tan tan 1B C >.故tan tan tan A B C tan tan 2tan tan 1tan tan B C B C B C +⎛⎫=-⎪-⎝⎭，不妨设tan tan t B C =()1t >，故2222tan tan tan 111t A B C t t t==--+， 所以当112t =，即2t =时，()min tan tan tan 8A B C =. 此时tan tan 4B C +=，tan tan 2B C =，解得tan 2tan 2tan 4B C A ==+=（或tan ,tan B C 互换）， 此时,,A B C 均为锐角，满足条件.解法二：由解法一部分可知tan tan 2tan tan B C B C +=， 在锐角三角形中，tan ,tan ,tan 0A B C >， 而()tan tan tan tan 1tan tan B CA B C B C+=-+=--，即()tan 1tan tan tan tan A B C B C -+=+，从而tan tan tan tan tan tan A B C A B C =++（这个公式课本中作为例题出现要求证明）. 故tan tan tan tan 2tan tan A B C A B C=+22tan tan tan A B C整理得tan tan tan 8A B C ，当且仅当tan tan 4B C +=，tan 2tan tan 4A B C==，解得tan 2tan 2tan 4B C A ==+=（或tan ,tan B C 互换）， 此时,,A B C 均为锐角，满足条件.评注 从表面此题看似,B C 等价，但构造等腰三角形求解出的最值却不正确，因此等价的思想也需慎用.如果注意到此题的结构，我们优先考虑切化弦，且优先考虑sin sin B C 搭配， 则有：解法三：sin sin sin tan tan tan =cos cos cos A B C A B C A B C =()22sin sin 1sin sin cos cos cos cos B C B C B C B C⨯-()222sin sin 8sin sin 2B C B C =⎛⎫⎪⎝⎭（因为22a b ab +⎛⎫⎪⎝⎭）.最后检验一下是否存在即可. 16.（2017全国2文13）函数()cos sin =2+f x x x 的最大值为.16.解析 因为()())tan 2f x x ϕϕ=+=，所以()max f x 17.（2017全国3文6）函数()1ππsin cos 536f x x x ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭的最大值为（ ）. A ．65B ．1C ．35D ．1517.解析 11()sin sin sin sin 5362533f x x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫=++-+=+++= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 6sin 53x π⎛⎫+ ⎪⎝⎭.故选A. 评注 本题属于中档题，基础差一点的学生在解题思路方面可能会存在一定问题，三角恒等变换中公式的选择对于学生来说是一个难点，对于老师教学来说是一个重点，选择合适的公式能起到事半功倍的效果！18.（2017江苏16）已知向量()cos ,sin x x =a ，(3,=b ，[]0,πx ∈． （1）若∥a b ，求x 的值；（2）记()f x =⋅a b ，求()f x 的最大值和最小值以及对应的x 的值．18.解析 （1）因为()cos ,sin x x =a ，(3,=b ，∥a b ，所以3sin x x =， 若cos 0x =，则sin 0x =，与22sin cos 1x x +=矛盾，因此cos 0x ≠．所以tan x =，由[]0,πx ∈，所以56x =π． （2）()()(cos ,sin 3,x x f x =⋅=⋅ab 3cos 6x x x ⎛⎫=-=+⎝π⎪⎭． 因为[]0,πx ∈，所以,666x ππ7⎡⎤+∈⎢⎥⎣⎦π，所以31cos 62x ⎛⎫-+ ⎪⎝⎭π． 所以当66x +ππ=，即0x =时，()f x 的最大值为3； 当6x +π=π，即6x 5π=时，()f x 的最小值为-题型53 根据条件确定解析式1. （2013四川文6）函数()()ππ2sin >0<<22f x x ωϕωϕ⎛⎫=+- ⎪⎝⎭，的部分图象如图所示，则ωϕ，的值分别是（ ）.A. π23-，B. π26-，C. π46-，D. π43， 1.分析 借助三角函数的图象和性质求解.解析 因为115,21212T =π-π所以T =π. 又()20T ωωπ=>，所以2ωπ=π，所以2ω=.由五点作图法可知当512x =π时，x ωϕπ+=2，即52122ϕπ⨯π+=，所以3ϕπ=-. 故选A.2.（2014江苏5）已知函数cos y x =与()sin 2y x ϕ=+()0ϕ<π≤，它们的图像有一个横坐标为3π的交点，则ϕ的值是 ． 3.（2014大纲文16）直线1l 和2l 是圆222x y +=的两条切线，若1l 与2l 的交点为（1，3），则1l 与2l 的夹角的正切值等于.4.（2016全国甲文3）函数的部分图像如图所示，则（ ）. A.π2sin 26y x ⎛⎫=-⎪⎝⎭B.π2sin 23y x ⎛⎫=-⎪⎝⎭C.π2sin 6y x ⎛⎫=+ ⎪⎝⎭D.π2sin 3y x ⎛⎫=+ ⎪⎝⎭4.A 解析 解法一：当0x =时，0y <，排除C ，D.当3x π=时，2y =，代入A 满足.故选A.5.（2016上海文17）设a ∈R ，[]0,2πb ∈.若对任意实数x 都有πsin 33x ⎛⎫-= ⎪⎝⎭()sin ax b +，则满足条件的有序实数对(),a b 的对数为（ ）.A.1B.2C.3D.4 5.解析 ①当3a =时，则3b 5π=；②当3a =-时，则4π3b =.共2组.故选B. 评注 事实上a 确定了，则b 能唯一确定，因此共2组. 6.（2016天津文8）已知函数)0(21sin 212sin )(2>-+=ωωωx xx f ，x ∈R .若)(x f 在区间(π,2π)内没有零点，则ω的取值范围是（ ）. A.10,8⎛⎤ ⎥⎝⎦ B.150,,148⎛⎤⎡⎫ ⎪⎥⎢⎝⎦⎣⎭ C.50,8⎛⎤ ⎥⎝⎦ D.1150,,848⎛⎤⎡⎤⎥⎢⎥⎝⎦⎣⎦6. D 解析 由题意()f x =1cos 2x ω-+sin 122x ω-=πsin 24x ω⎛⎫- ⎪⎝⎭. 由()0f x =，即πsin 04x ω⎛⎫-= ⎪⎝⎭，得()ππ+4k x k ω=∈Z .又()()ππ+4π,2πk x k ω=∉∈Z ，因此115599,,,848484ω⎛⎫⎛⎫⎛⎫∉⋅⋅⋅= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭115,,848⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭，所以1150,,848ω⎛⎤⎡⎤∈ ⎥⎢⎥⎝⎦⎣⎦.故选D. 7.（2016全国乙文12）若函数1()sin 2sin 3f x x x a x =-+在(),-∞+∞上单调递增，则a 的取值范围是（ ）.A.[]1,1-B.11,3⎡⎤-⎢⎥⎣⎦ C.11,33⎡⎤-⎢⎥⎣⎦ D.11,3⎡⎤--⎢⎥⎣⎦7. C 解析 问题转化为()21cos2cos 03f x x a x '=-+对x ∈R 恒成立， 故()2212cos 1cos 03x a x --+，即245cos cos 033a x x -+恒成立. 令cos x t =，得245033t at -++对[]1,1t ∈-恒成立. 解法一：构造()24533g t t at =-++，开口向下的二次函数()g t 的最小值的可能值为端点值，故只需保证()()11031103g a g a ⎧-=-⎪⎪⎨⎪=+⎪⎩，解得1133a -.故选C.解法二：①当0t =时，不等式恒成立； ②当01t <时，1543at t ⎛⎫- ⎪⎝⎭恒成立，由y =1543t t ⎛⎫- ⎪⎝⎭在01t <上单调递增， 所以()1511445333t t ⎛⎫--=- ⎪⎝⎭，故13a -； ③当10t -<时，1543at t ⎛⎫- ⎪⎝⎭恒成立.由y =1543t t ⎛⎫- ⎪⎝⎭在10t -<上单调递增， ()1511445333t t ⎛⎫--+= ⎪⎝⎭，所以13a . 综上可得，1133a -.故选C. 评注 曾经谈到必要条件的问题，如取cos 1x =，则转化为13a-，因此直接选择C 选项.这缘于运气好，若不然取cos 0x =，则式子恒成立；取cos 1x =-，则13a ，此时只能排除A 选项.此外，可在未解题之前取1a =-，此时()1sin 2sin 3f x x x x =--，则()21cos2cos 3f x x x '=--，但此时()22011033f '=--=-<，不具备在(),-∞+∞上单调递增，直接排除A ，B ，D.故选C.8. （2016浙江文11）已知22cos sin 2sin()(0)x x A x b A ωϕ+=++>，则A =________，b =________.8.；1 解析 2π2cos sin 2214x x x ⎛⎫+=++ ⎪⎝⎭，所以A =1b =.9.（2016上海文5）若函数()4sin cos f x x a x =+的最大值为5，则常数a = .9.3±解析 由辅助角公式可知函数()f x 5=，故3a =±.10.（2016北京文16）已知函数()()2sin cos cos20f x x x x ωωωω=+>的最小正周期为π.（1）求ω的值；（2）求()f x 的单调递增区间. 10.解析 （1）因为()2sin cos cos2sin2cos2f x x x x x x ωωωωω=+=+=π24x ω⎛⎫+ ⎪⎝⎭，所以()f x 的最小正周期2ππ2T ωω==.依题意ππω=，解得1ω=.（2）由（1）知，()π24f x x ⎛⎫=+ ⎪⎝⎭.函数sin y x =的单调递增区间为()ππ2π,2π22k k k ⎡⎤-+∈⎢⎥⎣⎦Z . 由πππ2π22π242k x k -++，得3ππππ88k xk -+.所以()f x 的单调递增区间为()3πππ,π88k k k ⎡⎤-+∈⎢⎥⎣⎦Z .11.（2017天津文7）设函数()2sin(),f x x x ωϕ=+∈R ，其中0,||πωϕ><.若5π28f ⎛⎫= ⎪⎝⎭，11π08f ⎛⎫= ⎪⎝⎭，且()f x 的最小正周期大于2π，则（ ）. A.2π,312ωϕ== B.211π,312ωϕ==- C.111π,324ωϕ==- D.17π,324ωϕ== 11.解析 解法一：由题意，得125π282118k k ωϕωϕπ⎧+=π+⎪⎪⎨π⎪+=π⎪⎩，其中12,k k ∈Z ，所以()2142233k k ω=--.又22T ωπ=>π，所以01ω<<，所以23ω=，11212k ϕ=π+π，由ϕ<π，得π12ϕ=.故选A ．解法二：由5π28f ⎛⎫=⎪⎝⎭，11π08f ⎛⎫= ⎪⎝⎭，知()11π5π3π214884T k +=-=，所以3π21T k =+.又()f x 的最小正周期2πT >，故0k =，3πT =，2π23T ω==，所以将5π8x =代入()2sin()f x x ωϕ=+，得125ππ2π382k ϕ⨯+=+，1k ∈N ，||πϕ<，解得π12ϕ=.题型54 三角函数图像变换1. （2013湖北文6）将函数sin ()y x x x =+∈R 的图象向左平移(0)m m >个单位长度后，所得到的图象关于y 轴对称，则m 的最小值是（ ）. A ．π12B ．π6C ．π3D ．5π61.分析 先将函数解析式化简，再写出平移后的解析式，然后根据函数为偶函数求得m 的值.解析由于πsin 2cos 6y x x x ⎛⎫=+=- ⎪⎝⎭，向左平移()0m m >个单位长度后得到函数π2cos 6y x m ⎛⎫=+- ⎪⎝⎭的图象，由于该图象关于y 轴对称，所以()ππ6m k k -=∈Z ，于是()ππ6m k k =+∈Z ，又0m >，故当0k =时，m 取最小值π6.故选B.2．(2013福建文9）将函数()()ππsin 222f x x θθ⎛⎫=+-<< ⎪⎝⎭的图像向右平移()1ϕϕ>个单位长度后得到函数()g x 的图像，若()(),f x g x 的图像都经过点02P ⎛⎝⎭，，则ϕ的值可以是（ ）.A ．5π3 B ．5π6 C ．π2 D ．π62.分析 先求出解析式中的字母的聚取值，再利用代入法确定答案.解析 因为P ⎛ ⎝⎭在()f x 的图象上，所以()0sin f θ==因为ππ22θ⎛⎫∈- ⎪⎝⎭，，所以π=3θ，所以()πsin 23f x x ⎛⎫=+ ⎪⎝⎭，所以()()πsin 23g x x ϕ⎡⎤=-+⎢⎥⎣⎦.因为()02g =，所以sin 232ϕπ⎛⎫-= ⎪⎝⎭.验证，5π6ϕ=时，ππ54sin 2sin πsin π33332ϕ⎛⎫⎛⎫⎛⎫-=-=-=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭成立.故选B. 3.（2014四川文3）为了得到函数()sin 1y x =+的图像，只需把函数sin y x =的图像上所有的点（ ）.A.向左平行移动1个单位长度B.向右平行移动1个单位长度C.向左平行移动π个单位长度D.向右平行移动π个单位长度 4.（2014福建文7）将函数sin y x =的图像向左平移2π个单位，得到函数()y f x =的图像，则下列说法正确的是（ ）. A.()y f x =是奇函数 B. ()y f x =的周期是πC. ()y f x =的图像关于直线2x π=对称 D. ()y f x =的图像关于点02π⎛⎫- ⎪⎝⎭，对称 5. （2014安徽文7）若将函数()sin2cos2f x x x =+的图像向右平移ϕ个单位，所得图像关于y 轴对称，则ϕ的最小正值是（ ） A.8π B.4π C.83π D.43π5. 解析 由()πsin 2cos 224f x x x x ⎛⎫=+=+ ⎪⎝⎭知()f x 图像的对称轴方程为()ππ28k x k =+∈Z ，因此在y 轴左侧且离y 轴最近的对称轴方程为3π8x =-.依题意结合图像知，ϕ的最小正值为3π8，故选C.评注 本题考查三角函数的图像和性质.6. （2014辽宁文11）将函数3sin 23y x π⎛⎫=+ ⎪⎝⎭的图像向右平移2π个单位长度，所得图像对应的函数（ ）. A ．在区间7,1212ππ⎡⎤⎢⎥⎣⎦上单调递减 B ．在区间7,1212ππ⎡⎤⎢⎥⎣⎦上单调递增 C ．在区间,63ππ⎡⎤-⎢⎥⎣⎦上单调递减 D ．在区间,63ππ⎡⎤-⎢⎥⎣⎦上单调递增 7.（2014浙江文4）为了得到函数x x y 3cos 3sin +=的图像，可以将函数y x =的图像（ ）.A ．向右平移π12个单位 B ．向右平移π4个单位 C ．向左平移π12个单位 D ．向左平移π4个单位8.（2014重庆文13）将函数()()sin 022f x x ωφωφππ⎛⎫=+>-< ⎪⎝⎭，≤图像上每一点的横坐标缩短为原来的一半，纵坐标不变，再向右平移6π个单位长度得到x y sin =的图像，则6f π⎛⎫= ⎪⎝⎭______. 9.（2015山东文）要得到函数sin 43y x π⎛⎫=- ⎪⎝⎭的图像，只需将函数sin 4y x =的图像（ ）. A. 向左平移12π个单位 B. 向右平移12π个单位 C. 向左平移3π个单位D. 向右平移3π个单位 9.解析 因为ππsin 4sin 4312y x x ⎡⎤⎛⎫⎛⎫=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，所以要得到πsin 43y x ⎛⎫=- ⎪⎝⎭的图像， 只需要将函数sin 4y x =的图像向右平移π12个单位.故选B. 10.（2015陕西文）如图，某港口一天6时到18时的水深变化曲线近似满足函数π3sin()6y x k ϕ=++，据此函数可知，这段时间水深（单位：m ）的最大值为（ ）．A ．5B ．6C ．8D ．1010.解析 由图像得，当πsin 16x ϕ⎛⎫+=-⎪⎝⎭时min 2y =，即π3sin 6y k ϕ⎛⎫=++ ⎪⎝⎭的最小值 为2，求得5k =，所以π3sin 56y ϕ⎛⎫=++⎪⎝⎭，max 358y =+=. 11.（2015重庆文）已知函数()21sin22f x x x =-. （1）求()f x 的最小周期和最小值；到原来（2）将函数()f x 的图像上每一点的横坐标伸长的两倍，纵坐标不变，得到函数()g x 的图像.当时间/hπ,π2x ⎡⎤∈⎢⎥⎣⎦时，求()g x 的值域.11.解析 （1）())211sin 2sin 21cos 2222f x x x x x ==-+=1sin 2cos 2sin 222232x x x π⎛⎫--=--⎪⎝⎭．因此()f x 的最小正周期为π，最小值为．（2）由条件可知：()sin 23x g x f x π⎛⎫⎛⎫==-⎪ ⎪⎝⎭⎝⎭当,2x π⎡⎤∈π⎢⎥⎣⎦时有，2,363x πππ⎡⎤-∈⎢⎥⎣⎦，从而sin 3x π⎛⎫- ⎪⎝⎭的值域为1,12⎡⎤⎢⎥⎣⎦，那么sin 32x π⎛⎫-- ⎪⎝⎭的值域为1222⎡⎢⎣⎦，故()g x 在区间,2π⎡⎤π⎢⎥⎣⎦上的值域是⎣⎦.12.（2015福建文）已知函数()2cos 10cos 222x x xf x =+. （1）求函数()f x 的最小正周期； （2）将函数()f x 的图像向右平移π6个单位长度，再向下平移a （0a >）个单位长度后得到函数()g x 的图像，且函数()g x 的最大值为2． （ⅰ）求函数()g x 的解析式；（ⅱ）求证：存在无穷多个互不相同的正整数0x ，使得()00g x >．12.分析 （1）先利用二倍角公式和余弦降幂公式将()f x 化为()π10sin 56f x x ⎛⎫=++ ⎪⎝⎭，然后利用2πT ω=求最小正周期；（2由函数()f x 的解析式中给x 减π6，再将所得解析式整体减去a 得()g x 的解析式为()10sin 5g x x a =+-，当sin x 取1时，()g x 取得最大值105a +-，列方程求得13a =，从而()g x 的解析式可求；欲证明存在无穷多个互不相同的正整数0x ，使得()00g x >，可解不等式()00g x >，只需解集的长度大于1，此时解集中一定含有整数，由周期性可得，必存在无穷多个互不相同的正整数0x ． 解析 （1因为()2103sincos 10cos 222x x x f x =+=π535cos 510sin 56x x x ⎛⎫++=++ ⎪⎝⎭.所以函数()f x 的最小正周期2πT =． （2（i ）将()f x 的图像向右平移π6个单位长度后得到10sin 5y x =+的图像，再向下平移()0a a >个单位长度后得到()10sin 5g x x a =+-的图像．又函数()g x 的最大值为2，所以1052a +-=，解得13a =． 所以()10sin 8g x x =-．（ii ）要证明存在无穷多个互不相同的正整数0x ，使得()00g x >，就是要证明存在无穷多个互不相同的正整数0x ，使得010sin 80x ->，即04sin 5x >． 由435<知，存在0π03α<<，使得04sin 5α=． 由正弦函数的性质可知，当()00,πx αα∈-时，均有4sin 5x >． 因为sin y x =的周期为2π，所以当()()002π,2π+πx k k k αα∈+-∈Z 时，均有4sin 5x >． 因为对任意的整数k ，()()000π2π+π2ππ213k k ααα--+=->>，所以对任意的正整数k ，都存在正整数()()002π,2ππk x k k k αα∈++-∈Z ，使得4sin 5k x >．即存在无穷多个互不相同的正整数0x ，使得()00g x >． 13.（2015湖北文）某同学将“五点法”画函数()()πsin 02f x A x ωϕωϕ，⎛⎫=+>< ⎪⎝⎭在某一个时期内的图像时，列表并填入部分数据，如表所示：（1）请将上述数据补充完整，填写在答题卡上相应位置，并直接写出函数()f x 的解析式；（2）将(y f x =()y g x =图像，求()y g x =的图像离原点O 最近的对称中心.13.解析 (1)根据表中已知数据，解得π5,2,6A ωϕ===. 数据补全如表所示：且函数表达式为()π5sin 26f x x ⎛⎫=- ⎪⎝⎭.(2由(1)知π()5sin(2)6f x x =-，因此 πππ()5sin 25sin 2666g x x x ⎡⎤⎛⎫⎛⎫=+-=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.因为sin y x =的对称中心为()π0k ，，k ∈Z . 令π2π6x k +=，解得ππ212k x =-，k ∈Z ，即()y g x =图像的对称中心为ππ0212k ⎛⎫- ⎪⎝⎭，，k ∈Z ， 其中离原点O 最近的对称中心为π012⎛⎫- ⎪⎝⎭，.14.（2016四川文4） 为了得到函数πsin 3y x ⎛⎫=+ ⎪⎝⎭的图像，只需把函数sin y x =的图像上所有的点（ ）.A. 向左平行移动π3个单位长度 B. 向右平行移动π3个单位长度 C. 向上平行移动π3个单位长度 D. 向下平行移动π3个单位长度14.A 解析 由题意，为得到函数πsin 3y x ⎛⎫=+ ⎪⎝⎭，只需把函数sin y x =的图像上所有的点向左移π3个单位.故选A. 15.（2016全国乙文6）若将函数π2sin 26y x ⎛⎫=+ ⎪⎝⎭的图像向右平移14个周期后，所得图像对应的函数为（ ）. A.π2sin 24y x ⎛⎫=+⎪⎝⎭ B.π2sin 23y x ⎛⎫=+ ⎪⎝⎭C.π2sin 24y x ⎛⎫=-⎪⎝⎭ D.π2sin 23y x ⎛⎫=- ⎪⎝⎭15. D 解析 将函数π2sin 26y x ⎛⎫=+⎪⎝⎭的图像向右平移14个周期，即向右平移π4个单位， 故所得图像对应的函数为ππ2sin 246y x ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦π2sin 23x ⎛⎫=- ⎪⎝⎭.故选D.16.（2014全国丙文14）函数sin y x x =图像可由函数2sin y x =的图像至少向右平移______个单位长度得到.16.π3解析 由sin y x x =，得π2sin 3y x ⎛⎫=- ⎪⎝⎭，所以可由函数2sin y x =至少向右平移π3才能得到.感谢您的下载!快乐分享，知识无限！由Ruize收集整理！。

2018年全国各地高考数学分类汇编4-三角函数一、选择题（共13小题；共65分）1. 若sinα=13，则cos2α= A. 89B. 79C. −79D. −892. 在△ABC中，cos C2=55，BC=1，AC=5，则AB= A. 4B. 30C. 29D. 23. △ABC的内角A，B，C的对边分别为a，b，c，若△ABC的面积为a2+b2−c24，则C= A. π2B. π3C. π4D. π64. 在平面直角坐标系中，AB，CD，EF，GH是圆x2+y2=1上的四段弧（如图），点P在其中一段上，角α以Ox为始边，OP为终边．若tanα<cosα<sinα，则P所在的圆弧是 A. ABB. CDC. EFD. GH5. 将函数y=sin2x+π5的图象向右平移π10个单位长度，所得图象对应的函数 A. 在区间 −π4,π4上单调递增 B. 在区间π4,0上单调递减C. 在区间π4,π2上单调递增 D. 在区间π2,π 上单调递减6. 将函数y=sin2x+π5的图象向右平移π10个单位长度，所得图象对应的函数 A. 在区间3π4,5π4上单调递增 B. 在区间3π4,π 上单调递减C. 在区间5π4,3π2上单调递增 D. 在区间3π2,2π 上单调递减7. 若f x=cos x−sin x在0,a是减函数，则a的最大值是 A. π4B. π2C. 3π4D. π8. 函数f x=tan x1+tan x的最小正周期为 A. π4B. π2C. πD. 2π9. 已知角α的顶点为坐标原点，始边与x轴的非负半轴重合，终边上有两点A1,a，B2,b，且cos2α=23，则 a−b = A. 15B. 55C. 255D. 110. 已知函数f x=2cos2x−sin2x+2，则 A. f x的最小正周期为π，最大值为3B. f x的最小正周期为π，最大值为4C. f x的最小正周期为2π，最大值为3D. f x的最小正周期为2π，最大值为411. 函数y=2 x sin2x的图象可能是 A. B.C. D.12. 设F1，F2是双曲线C：x2a2−y2b2=1a>0,b>0的左、右焦点，O是坐标原点．过F2作C的一条渐近线的垂线，垂足为P．若PF1=6 OP ，则C的离心率为 A. 5B. 2C. 3D. 213. 已知F1，F2是椭圆C:x2a +y2b=1a>b>0的左，右焦点，A是C的左顶点，点P在过A且斜率为36的直线上，△PF1F2为等腰三角形，∠F1F2P=120∘，则C的离心率为 A. 23B. 12C. 13D. 14二、填空题（共11小题；共55分）14. 函数f x=cos3x+π6在0,π的零点个数为．15. 能说明“若f x>f0对任意的x∈0,2都成立，则f x在0,2上是增函数”为假命题的一个函数是．16. 在△ABC中，角A，B，C所对的边分别为a，b，c．若a=7，b=2，A=60∘，则sin B=，c=．17. △ABC的内角A，B，C的对边分别为a，b，c，已知b sin C+c sin B=4a sin B sin C，b2+c2−a2=8，则△ABC的面积为．18. 若△ABC的面积为34a2+c2−b2，且∠C为钝角，则∠B=；ca的取值范围是．19. 已知sinα+cosβ=1，cosα+sinβ=0，则sinα+β=．20. 已知tan α−5π4=15，则tanα=．21. 已知函数y=sin2x+φ −π2<φ<π2的图象关于直线x=π3对称，则φ的值为．22. 设函数f x=cos ωx−π6ω>0．若f x≤fπ4对任意的实数x都成立，则ω的最小值为．23. 在△ABC中，角A，B，C所对的边分别为a，b，c，∠ABC=120∘，∠ABC的平分线交AC于点D，且BD=1，则4a+c的最小值为．24. 函数f x满足f x+4=f x x∈R，且在区间−2,2上，f x=cosπx2,0<x≤2x+12,−2<x≤0，则f f15的值为．三、解答题（共7小题；共91分）25. 设常数a∈R，函数f x=a sin2x+2cos2x．（1）若f x为偶函数，求a的值；（2）若fπ4=3+1，求方程f x=1−2在区间−π,π上的解．26. 在△ABC中，a=7，b=8，cos B=−17．（1）求∠A；（2）求AC边上的高．27. 在平面四边形ABCD中，∠ADC=90∘，∠A=45∘，AB=2，BD=5．（1）求cos∠ADB；（2）若DC=22，求BC．28. 在△ABC中，内角A，B，C所对的边分别为a，b，c．已知b sin A=a cos B−π6．（1）求角B的大小；（2）设a=2，c=3，求b和sin2A−B的值．29. 已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边过点P −35,−45．（1）求sinα+π的值；（2）若角β满足sinα+β=513，求cosβ的值．30. 已知α，β为锐角，tanα=43，cosα+β=−55．（1）求cos2α的值；（2）求tanα−β的值．31. 已知函数f x=sin2x+3sin x cos x．（1）求f x的最小正周期；（2）若f x在区间 −π3,m 上的最大值为32，求m的最小值．答案第一部分1. B2. A3. C4. C5. A6. A7. C8. C9. B10. B11. D12. C13. D第二部分14. 315. f x=sin x（答案不唯一）16. 217，317. 23318. π3，2,+∞19. −1220. 3221. −π622. 2323. 924. 22第三部分25. （1）由f x是偶函数，所以f−x=f x，即a sin2−x+2cos2−x=a sin2x+2cos2x，即−a sin2x=a sin2x，即a=0．（2）由fπ4=a sinπ2+2cos2π4=3+1，即a=3，所以f x=3sin2x+2cos2x，解方程3sin2x+2cos2x=1−2，即sin2x+π6=−22，所以2x+π6=2kπ−π4或2kπ−34πk∈Z，即x=kπ−524π或kπ−1124πk∈Z，因为x∈−π,π，所以x=−1124π或−524π或1324π或1924π，所以f x=1−在−π,π上的解为 −1124π,−524π,1324π,1924π ．26. （1）在△ABC中，因为cos B=−17，所以B为钝角，所以sin B=1−cos2B=437．根据正弦定理asin A =bsin B，即7sin A=437，得到sin A=32，所以A=π3．（2）过B作BD⊥AC于D．在△ABC中，sin C=sin A+B=sin A cos B+cos A sin B=32× −17+12×437=33 14,所以BD=a⋅sin C=7×3314=332，所以AC边上的高为332．27. （1）在△ABD中，由正弦定理得BDsin∠A =ABsin∠ADB．由题设知，5sin45=2sin∠ADB，所以sin∠ADB=25．由题设知，∠ADB<90∘，所以cos∠ADB=1−225=235．（2）由题设及（1）知，cos∠BDC=sin∠ADB=25．在△BCD中，由余弦定理得BC2=BD2+DC2−2⋅BD⋅DC⋅cos∠BDC=25+8−2×5×22×2 5=25.所以BC=5．28. （1）在△ABC中，由正弦定理asin A =bsin B，可得b sin A=a sin B，又由b sin A=a cos B−π6，得a sin B=a cos B−π6，即sin B=cos B−π6，可得tan B=3．又因为B∈0,π，可得B=π3．（2）在△ABC中，由余弦定理及a=2，c=3，B=π3，有b2=a2+c2−2ac cos B=7，故b=7．由b sin A=a cos B−π6，可得sin A=37．因为a<c，故cos A=7．因此sin2A=2sin A cos A=437，cos2A=2cos2A−1=17．所以，sin2A−B=sin2A cos B−cos2A sin B=437×12−17×32=3314．29. （1）由角α的终边过点P −35,−45得sinα=−45，所以sinα+π=−sinα=45．（2）由角α的终边过点P −35,−45得cosα=−35，由sinα+β=513得cosα+β=±1213．由β=α+β−α得cosβ=cosα+βcosα+sinα+βsinα，所以cosβ=−5665或cosβ=−1665．30. （1）因为tanα=43，tanα=sinαcosα，所以sinα=43cosα．因为sin2α+cos2α=1，所以cos2α=925，因此，cos2α=2cos2α−1=−725．（2）因为α，β为锐角，所以α+β∈0,π．又因为cosα+β=−55，所以sinα+β=1−cos2α+β=255，因此tanα+β=−2．因为tanα=43，所以tan2α=2tanα1−tan2α=−247，因此，tanα−β=tan2α−α+β=tan2α−tanα+β1+tan2αtanα+β=−211．31. （1）f x=sin2x+3sin x cos x=1−cos2x2+32sin2x=12+sin2x−π6.所以f x的最小正周期为T=2π2=π．（2）f x在区间 −π3,m 上最大值为32，故sin2x−π6在 −π3,m 上最大值为1，x∈ −π3,m 时，2x−π6∈ −56π,2m−π6，令t=2x−π6，所以sin t在t∈ −56π,2m−π6上最大值为1，所以2m−π6≥π2，m≥π3，所以m的最小值为π3．。