圆的面积二

《圆的面积（二）》教学简案
【教学内容】
北师大版六年级上册第一单元第9课时
【教学目标】
1能正确运用圆的面积公式计算圆的面积，并能解决一些简单的实际问题。

2在多个探究圆面积公式的活动中、体会圆的半径、周长、面积之间的关系。

3结合剪杯垫的活动，进一步丰富学生探索圆面积公式的方法，并体会“等积变形”的数学思想。

【教学重、难点】
教学重点：圆面积公式的应用。

教学难点：圆周长与面积的综合应用。

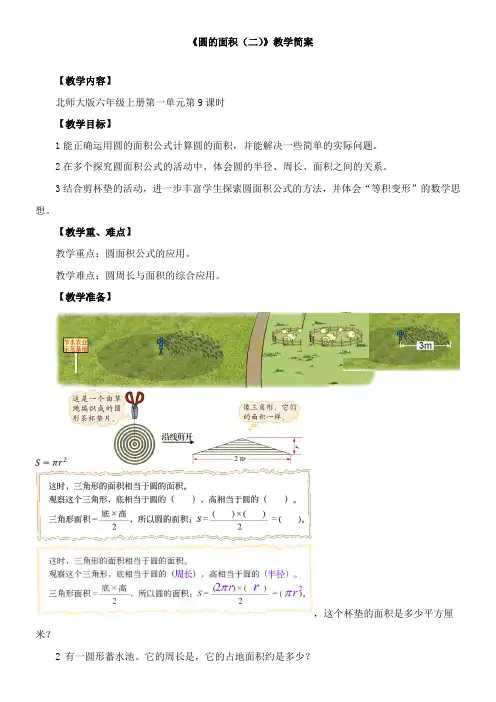
【教学准备】
，这个杯垫的面积是多少平方厘米？
2有一圆形蓄水池。

它的周长是，它的占地面积约是多少？
3一个运动场跑道的形状与大小如图。

两边是半圆形，中间是长方形，
这个运动场的占地面积是多少？
4拓展练习。

（1）如上图，这个运动场的周长是多少？（2）同一个运动场，在计算它的面积和周长时有什么不同？
四、全课回顾，总结收获
回顾本课重点研究的三个问题，进一步梳理和总结本课学习的收获。

第06讲 圆的面积（二）【知识梳理】1、圆的面积计算公式的应用已知半径求面积，直接用公式S=πr 2计算；已知周长求面积，用公式S=π（）2计算。

2、圆的面积计算公式的有趣推导由三角形的面积公式推导圆的面积公式的方法：圆的面积=三角形的面积=2高底⨯=2r r 2⨯π=πr 2【典型例题】例1 大圆的周长是小圆周长的2倍，如果小圆的面积是26.28dm ，那么大圆的面积是（ ）。

A ．212.56dmB ．218.84dmC ．225.12dmD ．237.68dm【分析】圆的周长＝π×2×半径，大圆的周长是小圆的2倍，即大圆半径是小圆半径的2倍，由此可知，大圆的面积是小圆面积的4倍，由此求出大圆的面积。

【详解】6.28×4＝25.12（dm 2）故答案为：C【点睛】本题主要考查圆的周长公式、面积公式的灵活运用，关键熟记公式。

例2把半径1分米的圆沿半径平均分成32份，然后拼成一个近似的长方形，这个长方形的长是( )分米，面积是( )分米2。

π2C【分析】这个长方形的长相当于圆周长的一半，长方形的宽就是圆的半径，长方形的面积等于长×宽，据此解答。

【详解】3.14×（1×2）÷2＝3.14×2÷2＝3.14（分米）3.14×1＝3.14（分米2）【点睛】考查了圆的面积的公式的推导，学生应理解掌握。

例3某学校有一个周长为24m的正方形花园，在它的中央有一个直径为4m的圆形花圃，园艺工王师傅想。

在花圃周围修建一个尽可能宽的环形走道，剩下的四个角再种上各种各样的花。

（1）请在图中画出环形走道。

（2）如果环形走道每平方米的造价是250元，那么修建这个环形走道一共要花费多少元？【分析】（1）根据题意，在正方形中画出最大的圆即是尽可能宽的环形走道。

测量出图上正方形的边长，以圆形花圃的圆心为圆心，以正方形边长的一半为半径画圆即可。

1.6《圆的面积（二）》（教案）六年级上册数学北师大版一、教学内容1. 复习圆的面积公式和基本概念。

2. 探讨圆的面积与半径的关系。

3. 学习圆的面积在实际问题中的应用。

二、教学目标1. 熟练掌握圆的面积公式，并能够灵活运用。

2. 理解圆的面积与半径的关系，并能解释实际问题中的现象。

3. 培养同学们的观察能力、思考能力和解决问题的能力。

三、教学难点与重点本节课的重点是圆的面积公式的运用和理解，以及圆的面积与半径的关系。

难点在于如何将实际问题与圆的面积公式相结合，灵活运用所学知识解决问题。

四、教具与学具准备为了更好地进行课堂教学，我准备了一些教具和学具，包括黑板、粉笔、圆规、直尺、练习本等。

五、教学过程1. 实践情景引入：我拿出一个圆形桌面，让同学们观察并思考，如果我们知道这个圆的半径，我们能否计算出它的面积呢？2. 复习圆的面积公式：3. 探讨圆的面积与半径的关系：4. 例题讲解：我给出一个例题：一个圆的半径是5厘米，求这个圆的面积。

我带领同学们一起运用圆的面积公式进行计算，得到答案是78.5平方厘米。

5. 随堂练习：我给同学们发放一些练习题，让同学们独立完成。

这些题目包括计算给定半径的圆的面积，以及解决一些实际问题。

6. 作业布置：我布置了一个作业：请同学们回家后，用圆的面积公式计算一下家里的圆桌的面积，并写下计算过程和答案。

六、板书设计圆的面积公式：S = πr²圆的面积与半径的关系：面积随半径的增加而增加。

七、作业设计作业题目：计算家里的圆桌的面积，并写下计算过程和答案。

答案：待同学们完成作业后，我会在课堂上进行讲解和批改。

八、课后反思及拓展延伸通过本节课的学习，我发现同学们对圆的面积公式掌握得比较好，但在解决实际问题时，有些同学可能会忽略圆的半径单位的重要性。

在课后，我需要加强对这部分同学的辅导，帮助他们更好地理解和运用圆的面积公式。

拓展延伸：同学们可以进一步学习圆的周长和直径的概念，探讨它们与圆的面积的关系。

第7课时圆的面积（二）教学内容：教材第16~17页的内容。

教学目标：1进一步掌握圆面积的计算公式，并能正确地计算圆面积。

2能计算简单的有关圆的组合图形的面积。

3进一步认识数学与人类生活的密切联系，体验数学活动充满探索和创造的乐趣。

教学重点：进一步掌握圆的面积的计算公式，能够正确地计算不同条件下圆的面积。

教学难点：正确地进行简单的有关圆的组合图形的面积的计算。

教学准备：教学课件。

（2）学生观看圆的转变过程，展开的图形像什么？并说说它们的面积的关系。

生：像三角形，它们的面积一样。

（3）让学生观察这个三角形和圆，在小组内说说圆的周长和半径在三角形中去哪儿了？（4）根据交流引导学生填空并推导出圆的面积公式。

三角形的底相当于圆的（周长），高相当于圆的（半径）。

三角形的面积=底×高÷2，所以圆的面积=（周长）×（半径）÷2=（）=（πr 2）。

四、巩固练习1完成教材第17页“练一练”第3题。

（1）学生观察圆形茶杯垫片和平行四边形的面积关系。

（相等） （2）引导学生观察并讨论平行四边形底、高分别来自于圆的哪部分。

（3）学生独立在书上填空，推导出来圆的面积公式。

然后全班订正。

2完成教材第17页“练一练”第4题。

学生说一说解题思路：由直径先求半径，再利用公式分别求圆面积和周长。

3完成教材第17页“练一练”第5题。

让学生观察图形看看运动场的面积是由哪几个图形的面积组成的，每个图形的面积如何求。

五、拓展提升1一个圆的半径由6 cm 增加到8 cm ，增加的面积是多少？ ×（82-62）=（cm 2）2求右图中阴影部分的面积。

（×22÷4-2×2÷2×2=dm 2六、课堂总结学生谈学习收获。

师生共同对重点内容进行归纳整理。

七、作业布置教材第17页“练一练”第1、2、6题。

板书设计教学反思。

北师大版数学六年级上册《圆的面积（二）》教学设计3一. 教材分析北师大版数学六年级上册《圆的面积（二）》这一节课，是在学生已经掌握了圆的面积公式的基础上进行教学的。

本节课的主要内容是让学生进一步理解圆的面积公式的推导过程，提高学生解决实际问题的能力。

教材通过例题和练习题的形式，帮助学生巩固圆的面积公式的应用，并引导学生将所学知识运用到生活实际中。

二. 学情分析六年级的学生已经具备了一定的逻辑思维能力和解决问题的能力。

他们对于圆的面积公式已经有了一定的了解，但可能对于公式的推导过程并不是很清楚。

因此，在教学过程中，教师需要引导学生通过观察、操作、思考、讨论等方式，深入理解圆的面积公式的推导过程，提高他们解决问题的能力。

三. 教学目标1.知识与技能：进一步理解圆的面积公式的推导过程，掌握圆的面积公式的应用。

2.过程与方法：通过观察、操作、思考、讨论等方式，提高学生解决问题的能力。

3.情感态度与价值观：培养学生对数学的兴趣，培养学生合作、交流、探究的学习态度。

四. 教学重难点1.重点：圆的面积公式的推导过程，圆的面积公式的应用。

2.难点：圆的面积公式的推导过程，以及如何将所学知识运用到实际问题中。

五. 教学方法1.情境教学法：通过创设情境，激发学生的学习兴趣，引导学生主动参与学习。

2.探究教学法：引导学生通过观察、操作、思考、讨论等方式，自主探究圆的面积公式的推导过程。

3.案例教学法：通过分析实际问题，引导学生运用圆的面积公式解决问题。

六. 教学准备1.教具：圆的面积公式课件，实物模型，练习题。

2.学具：学生用书，练习本，铅笔，橡皮。

七. 教学过程1.导入（5分钟）教师通过创设情境，引出本节课的主题——圆的面积（二）。

例如，可以给学生展示一个圆形场地，让学生计算这个场地的面积。

2.呈现（10分钟）教师通过课件或者实物模型，呈现圆的面积公式的推导过程。

引导学生观察、思考，并解释圆的面积公式的推导过程。

3.操练（10分钟）教师出示一些练习题，让学生运用圆的面积公式进行计算。

圆的面积2教学设计圆的面积（二）教学目标：1. 知识目标：了解圆的面积公式，并能够应用公式计算圆的面积。

2. 能力目标：培养学生分析和解决问题的能力，以及运用数学知识进行推理和论证的能力。

教学重点和难点：1. 重点：掌握圆的面积公式。

2. 难点：能够应用圆的面积公式解决实际问题。

教学准备：1. 教师准备：教学课件、教学板书、白板、计算器。

2. 学生准备：直尺、圆周率的近似值（如3.14）。

教学过程：Step 1：导入新知识1. 教师出示一张圆形物体的图片，引导学生观察，并提问：这个物体有哪些特点？与之前学过的图形有什么相同和不同之处？2. 引导学生回忆椭圆的面积公式，并提问：椭圆的面积公式是怎样的？是否可以应用到圆上？3. 引导学生思考，提出圆的面积公式：S = πr²，其中S表示圆的面积，r表示圆的半径。

Step 2：圆的面积公式的推导1. 教师引导学生思考圆的面积公式的推导过程。

可以通过剖析圆，将圆分成无数个与直径垂直的扇形，然后将这些扇形排列起来，形成一个近似于二维的曲线，即圆的面积，最终推导出圆的面积公式S = πr²。

2. 教师进行示范计算一个具体大小的圆的面积，并解释计算过程。

Step 3：运用圆的面积公式解决问题1. 教师出示一些实际问题，引导学生运用圆的面积公式解决。

2. 学生针对问题进行小组讨论，然后展示自己的解答并解释解题过程。

3. 教师进行点评和总结，让学生对圆的面积公式有更深入的理解。

Step 4：练习和巩固1. 学生进行课堂练习，运用圆的面积公式计算不同大小圆的面积。

2. 学生进行课后作业，进一步巩固和加深对圆的面积公式的理解和应用。

Step 5：归纳和总结1. 通过课堂练习和作业的讲解，学生对圆的面积公式应用有了更深入的理解。

2. 教师进行总结，强调圆的面积公式的重要性和应用价值。

Step 6：课堂小结教师对本节课的内容进行小结，并给予学生一定的学习反馈。