立体及其表面交线
- 格式:ppt
- 大小:4.91 MB
- 文档页数:99

第三章立体及立体表面交线目的要求:1)掌握平面立体和回转体的投影特性,以及表面取点线的方法2)熟悉立体表面上常见交线的画法(截交线、相贯线)重点难点:1)掌握和熟练运用各种立体的投影特性求解表面取点线的方法2)熟练求解立体表面上截交线和相贯线授课学时:8学时主要作图练习:1)完成平面立体、回转体的三面投影,平面立体、回转体表面找点、找线。
2)单个截平面截棱柱、棱锥后的三面投影。
3)多个截平面(切口)截棱柱、棱锥的三面投影,尤其是长方体截切后的三面投影。
4)单个和多个截平面截切圆柱、圆锥、圆球后的三面投影,尤以带槽的圆柱和圆球为主。
5)圆柱与圆柱相贯、同轴回转体相贯的各种情况作图、综合作图。
6)授课内容:机件形状是多种多样的,经过分析,都是由一些基本几何体所组成。
而几何体又是由一些表面所围成,根据这些表面的性质,几何体可分为两类:平面立体——由若干个平面所围成的几何体,如棱柱、棱锥等。
曲面立体——由曲面或曲面与平面所围成的几何体,最常见的是回转体,如圆柱、圆锥、圆球、圆环等。
用投影图表示一个立体,就是把围成立体的这些平面和曲面表达出来,然后根据可见性判别哪些线是可见的,哪些线是不可见的,把其投影分别画成粗实线和虚线,即可得立体的投影图。
§3-1 平面立体的投影平面立体各表面都是平面图形,各平面图形均由棱线围成,棱线又由其端点确定。
因此,平面立体的投影是由围成它的各平面图形的投影表示的,其实质是作各棱线与端点的投影。
一、棱柱以正六棱柱为例,其顶面、底面均为水平面,它们的水平投影反映实形,正面及侧面投影积聚为一直线。
棱柱有六个侧棱面,前后棱面为正平面,它们的正面投影反映实形,水平投影及侧面投影积聚为一直线。
棱柱的其它四个侧棱面均为铅垂面,水平投影积聚为直线,正面投影和侧面投影为类似形。
图3-1 正六棱柱的投影二、棱锥以四棱锥为例,其底面为一长方形,呈水平位置,水平投影反映底面的实形。
左右两个棱面是正垂面,其正面投影积聚为直线,水平和侧面投影均为类似三角形,前后两个棱面为侧垂面,其侧面投影积聚为直线,水平和正面投影同样为类似的三角形。



立体几何表面交线问题
解决立体几何表面交线问题,可以采用以下方法:
1. 确定交线的位置:首先需要确定立体几何的表面交线的位置,可以通过观察立体几何的形状和相对位置来确定。
2. 建立坐标系:为了方便计算和分析,需要建立一个适当的坐标系。
可以选择一个适当的点作为原点,并确定x、y、z轴的方向。
3. 计算交线的方程:根据立体几何的表面方程和相对位置,可以计算出交线的方程。
一般情况下,可以使用线性方程或者二次方程来表示交线的方程。
4. 分析交线的性质:通过分析交线的方程,可以确定交线的形状、长度、方向等性质。
5. 求解交点:如果需要求出立体几何表面交线的交点,可以将交线的方程代入各个表面的方程中进行求解。
6. 应用定理或公式:在某些情况下,可以利用定理或公式来简化计算或推导出更一般的结论。
例如,对于圆锥和圆柱相交的情况,可以利用相关线的性质求解。
两个回转体表面相交时,在两个立体外表面所产生的交线就是相关线,也是两个回转体的公有线。
此外,对于平面与平面的交线问题,可以根据基本事实3(如
果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线)进行求解。
以上是解决立体几何表面交线问题的一般方法,具体应用时需要根据具体情况进行分析和计算。




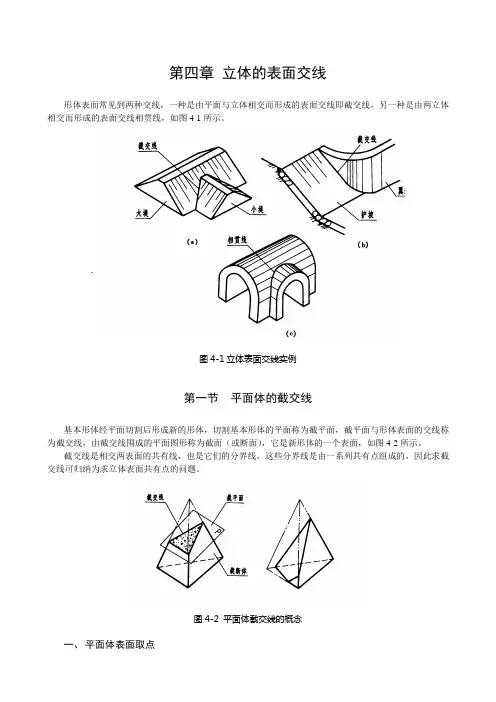
第四章立体的表面交线形体表面常见到两种交线,一种是由平面与立体相交而形成的表面交线即截交线,另一种是由两立体相交而形成的表面交线相贯线,如图4-1所示。
图4-1立体表面交线实例第一节平面体的截交线基本形体经平面切割后形成新的形体,切割基本形体的平面称为截平面,截平面与形体表面的交线称为截交线,由截交线围成的平面图形称为截面(或断面),它是新形体的一个表面,如图4-2所示。
截交线是相交两表面的共有线,也是它们的分界线,这些分界线是由一系列共有点组成的,因此求截交线可归纳为求立体表面共有点的问题。
图4-2 平面体截交线的概念一、平面体表面取点平面体表面取点就是根据平面体表面上的一个投影,求作该点其余的投影,并判别其可见性。
在特殊位置平面上的点可利用该平面的积聚性投影作图求得;在一般位置平面上的点,则要利用“找点先找线”的方法求得,即过已知点作一辅助直线,求出辅助直线的投影,再求辅助直线上已知点的投影。
其次要注意判别点的可见性,即点的投影的可见性与它所在立体表面的可见性一致。
【例4-1】如图4-3所示,已知三棱柱的表面上点A和点B的正面投影(a’)和b’,求出它们的水平投影和侧面投影。
图4-3 三棱柱表面取点分析:由图4-3(a)可以看出,点A的正面投影不可见,可判断A在三棱柱的后棱面上;点B正面投影可见,又位于右侧,可判断B在三棱柱的右侧棱面上,由于三棱柱棱面的水平投影及后棱面的侧面投影均有积聚性,因此可利用积聚性直接作图。
作图:①根据“长对正”的投影规律,如图4-3(b)所示,由点a´和b’向下引一条铅垂线与正三棱柱后棱面及右侧棱面的水平投影(斜直线)相交,交点即为A点、B点的水平投影a和b。
②根据“高平齐,宽相等”的投影规律,由a'、b'和a、b求得a"、b"。
③判别可见性,点A所在的平面,其水平投影和侧面投影均具有积聚性,所以无需判别它的可见性。
点B所在的右侧棱面其侧面投影不可见,故b" 不可见,标记为(b")。
第二章立体及其表面交线平面立体2.1.1 棱柱1. 棱柱的投影如下图的正六棱柱,其顶面、底面均为水平面,它们的水平投影反映实形,正面和侧面投影积聚为一直线。
棱柱有六个侧面,前后为正平面,其正面投影反映实形,水平投影及侧面投影积聚为一直线。
棱柱的其他四个侧面均为铅垂面,水平投影积聚为直线,正面投影和侧面投影为类似形。
直棱柱的投影特点:一个投影为多边形,反映棱柱的形状特点,另外两个投影是由矩形(实线和虚线)组成的矩形线框。
作图时,先画反映棱柱形状特点的投影——多边形,再依照棱柱的高作出其他两个投影。
2. 棱柱表面上的点在平面立体表面上的点,实质上确实是平面上的点。
正六棱柱的各个表面都处于特殊位置,因此在表面上的点可利用平面投影的积聚性来作图。
如已知棱柱表面上M点的正面投影m′,求水平、侧面投影m、m″。
由于正面投影m′是可见的,因此M点必然在棱柱的前半部平面ABCD上,而平面ABCD为铅垂面,水平投影abcd具有积聚性,因此m必在abcd上。
依照m′和m,由点的投影规律可求出m″。
2.1.2 棱锥1. 棱锥的投影如下图的正三棱锥,锥顶为S,其底面△ABC为水平面,水平投影△abc反映实形。
棱面△SAB、△SBC是一样位置平面,它们的各个投影均为类似形,棱面△SAC 为侧垂面,其侧面投影s″a″(c″)积聚为一直线。
棱锥的投影特点:一个投影为由三角形组成的多边形线框,外形轮廓反映底面实形,另外两个投影为由三角形(实线和虚线)组成的三角形线框。
作图时,先画出棱锥底面的各个投影,再作出锥顶的各个投影,然后连接各棱线,并判别可见性。
2. 棱锥表面上的点若是点在棱线上,那么可利用点在直线上,其投影必然在该直线的同面投影上求得。
若是点所在的平面具有积聚性,那么可利用积聚性直接求得。
若是点所在的平面为一样位置平面,可通过在该平面上作辅助线的方式求得。
例如,已知棱锥表面上M点的正面投影m′,求水平、侧面投影m、m″。