立体及立体表面交线
- 格式:doc
- 大小:7.99 MB
- 文档页数:13

第三章立体及立体表面交线目的要求:1)掌握平面立体和回转体的投影特性,以及表面取点线的方法2)熟悉立体表面上常见交线的画法(截交线、相贯线)重点难点:1)掌握和熟练运用各种立体的投影特性求解表面取点线的方法2)熟练求解立体表面上截交线和相贯线授课学时:8学时主要作图练习:1)完成平面立体、回转体的三面投影,平面立体、回转体表面找点、找线。
2)单个截平面截棱柱、棱锥后的三面投影。
3)多个截平面(切口)截棱柱、棱锥的三面投影,尤其是长方体截切后的三面投影。
4)单个和多个截平面截切圆柱、圆锥、圆球后的三面投影,尤以带槽的圆柱和圆球为主。
5)圆柱与圆柱相贯、同轴回转体相贯的各种情况作图、综合作图。
6)授课内容:机件形状是多种多样的,经过分析,都是由一些基本几何体所组成。
而几何体又是由一些表面所围成,根据这些表面的性质,几何体可分为两类:平面立体——由若干个平面所围成的几何体,如棱柱、棱锥等。
曲面立体——由曲面或曲面与平面所围成的几何体,最常见的是回转体,如圆柱、圆锥、圆球、圆环等。
用投影图表示一个立体,就是把围成立体的这些平面和曲面表达出来,然后根据可见性判别哪些线是可见的,哪些线是不可见的,把其投影分别画成粗实线和虚线,即可得立体的投影图。
§3-1 平面立体的投影平面立体各表面都是平面图形,各平面图形均由棱线围成,棱线又由其端点确定。
因此,平面立体的投影是由围成它的各平面图形的投影表示的,其实质是作各棱线与端点的投影。
一、棱柱以正六棱柱为例,其顶面、底面均为水平面,它们的水平投影反映实形,正面及侧面投影积聚为一直线。
棱柱有六个侧棱面,前后棱面为正平面,它们的正面投影反映实形,水平投影及侧面投影积聚为一直线。
棱柱的其它四个侧棱面均为铅垂面,水平投影积聚为直线,正面投影和侧面投影为类似形。
图3-1 正六棱柱的投影二、棱锥以四棱锥为例,其底面为一长方形,呈水平位置,水平投影反映底面的实形。
左右两个棱面是正垂面,其正面投影积聚为直线,水平和侧面投影均为类似三角形,前后两个棱面为侧垂面,其侧面投影积聚为直线,水平和正面投影同样为类似的三角形。






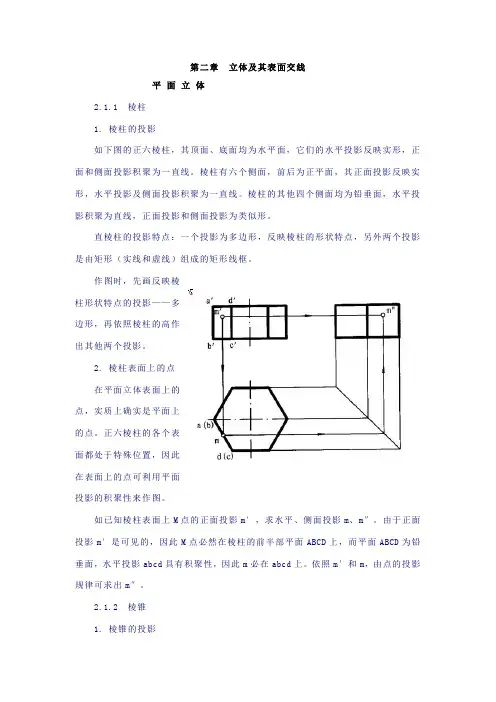
第二章立体及其表面交线平面立体2.1.1 棱柱1. 棱柱的投影如下图的正六棱柱,其顶面、底面均为水平面,它们的水平投影反映实形,正面和侧面投影积聚为一直线。
棱柱有六个侧面,前后为正平面,其正面投影反映实形,水平投影及侧面投影积聚为一直线。
棱柱的其他四个侧面均为铅垂面,水平投影积聚为直线,正面投影和侧面投影为类似形。
直棱柱的投影特点:一个投影为多边形,反映棱柱的形状特点,另外两个投影是由矩形(实线和虚线)组成的矩形线框。
作图时,先画反映棱柱形状特点的投影——多边形,再依照棱柱的高作出其他两个投影。
2. 棱柱表面上的点在平面立体表面上的点,实质上确实是平面上的点。
正六棱柱的各个表面都处于特殊位置,因此在表面上的点可利用平面投影的积聚性来作图。
如已知棱柱表面上M点的正面投影m′,求水平、侧面投影m、m″。
由于正面投影m′是可见的,因此M点必然在棱柱的前半部平面ABCD上,而平面ABCD为铅垂面,水平投影abcd具有积聚性,因此m必在abcd上。
依照m′和m,由点的投影规律可求出m″。
2.1.2 棱锥1. 棱锥的投影如下图的正三棱锥,锥顶为S,其底面△ABC为水平面,水平投影△abc反映实形。
棱面△SAB、△SBC是一样位置平面,它们的各个投影均为类似形,棱面△SAC 为侧垂面,其侧面投影s″a″(c″)积聚为一直线。
棱锥的投影特点:一个投影为由三角形组成的多边形线框,外形轮廓反映底面实形,另外两个投影为由三角形(实线和虚线)组成的三角形线框。
作图时,先画出棱锥底面的各个投影,再作出锥顶的各个投影,然后连接各棱线,并判别可见性。
2. 棱锥表面上的点若是点在棱线上,那么可利用点在直线上,其投影必然在该直线的同面投影上求得。
若是点所在的平面具有积聚性,那么可利用积聚性直接求得。
若是点所在的平面为一样位置平面,可通过在该平面上作辅助线的方式求得。
例如,已知棱锥表面上M点的正面投影m′,求水平、侧面投影m、m″。


第三章立体及立体表面交线目的要求:1)掌握平面立体和回转体的投影特性,以及表面取点线的方法2)熟悉立体表面上常见交线的画法(截交线、相贯线)重点难点:1)掌握和熟练运用各种立体的投影特性求解表面取点线的方法2)熟练求解立体表面上截交线和相贯线授课学时:8学时主要作图练习:1)完成平面立体、回转体的三面投影,平面立体、回转体表面找点、找线。
2)单个截平面截棱柱、棱锥后的三面投影。
3)多个截平面(切口)截棱柱、棱锥的三面投影,尤其是长方体截切后的三面投影。
4)单个和多个截平面截切圆柱、圆锥、圆球后的三面投影,尤以带槽的圆柱和圆球为主。
5)圆柱与圆柱相贯、同轴回转体相贯的各种情况作图、综合作图。
6)授课内容:机件形状是多种多样的,经过分析,都是由一些基本几何体所组成。
而几何体又是由一些表面所围成,根据这些表面的性质,几何体可分为两类:平面立体——由若干个平面所围成的几何体,如棱柱、棱锥等。
曲面立体——由曲面或曲面与平面所围成的几何体,最常见的是回转体,如圆柱、圆锥、圆球、圆环等。
用投影图表示一个立体,就是把围成立体的这些平面和曲面表达出来,然后根据可见性判别哪些线是可见的,哪些线是不可见的,把其投影分别画成粗实线和虚线,即可得立体的投影图。
§3-1 平面立体的投影平面立体各表面都是平面图形,各平面图形均由棱线围成,棱线又由其端点确定。
因此,平面立体的投影是由围成它的各平面图形的投影表示的,其实质是作各棱线与端点的投影。
一、棱柱以正六棱柱为例,其顶面、底面均为水平面,它们的水平投影反映实形,正面及侧面投影积聚为一直线。
棱柱有六个侧棱面,前后棱面为正平面,它们的正面投影反映实形,水平投影及侧面投影积聚为一直线。
棱柱的其它四个侧棱面均为铅垂面,水平投影积聚为直线,正面投影和侧面投影为类似形。
图3-1 正六棱柱的投影二、棱锥以四棱锥为例,其底面为一长方形,呈水平位置,水平投影反映底面的实形。
左右两个棱面是正垂面,其正面投影积聚为直线,水平和侧面投影均为类似三角形,前后两个棱面为侧垂面,其侧面投影积聚为直线,水平和正面投影同样为类似的三角形。
底边中两条为正垂线,两条为侧垂线。
可对照立体图及投影图分析其每一条棱线的投影。
图3-2 正四棱锥的投影§3-2 平面与平面立体相交在机件上常有平面与立体相交(平面截割立体)而形成的交线,平面与立体表面相交ZVXHO W YA BCD E a'b'd'c'e'a (b)(d)c ea''b''d''(e'')c''a (b)(d)c ea'b'd'c'e'a''d''(e'')b''c''ZXY HY WZVXHWYyy截断面截断体截交线图3-3 截交线的概念的交线,称为截交线。
这个平面称为截平面,形体上截交线所围成的平面图形称为截断面。
被截切后的形体称为截断体,如图3-3所示。
从图中可以看出,截交线既在截平面上,又在形体表面上,它具有如下性质:(1)截交线上的每一点既是截平面上的点又是形体表面的点,是截平面与立体表面共有点的集合。
(2)因截交线是属于截平面上的线,所以截交线一般是封闭的平面图形。
平面立体被截切后所得到的截交线,是由直线段组成的平面多边形。
此多边形的各边是立体表面与截平面的交线,而多边形的各顶点是立体各棱线与截平面的交点。
截交线既在立体表面上,又在截平面上,所以它是立体表面和截平面的共有线,截交线上的各顶点都是截平面与立体各棱线的共有点。
因此,求截交线实际上是求截平面与立体各棱线的交点,或求截平面与平面立体各表面的交线。
以平面截切六棱柱为例:图3-4 平面截切六棱柱作图步骤:①先画出完整六棱柱的侧面投影图;②因截平面为正垂面,六棱柱的六条棱线与截平面的交点的正面投影1′、2′、3′、4′、5′、6′可直接求出;③六棱柱的水平投影有积聚性,各棱线与截平面的交点的水平投影1、2、3、4、5、6可直接求出;④根据直线上点的投影性质,在六棱柱的侧面投影上,求出相应点的侧面投影1″、2″、3″、4″、5″、6″;⑤将各点的侧面投影依次连接起来,即得到截交线的侧面投影,并判断其可见性;⑥在图上将被截平面切去的顶面及各条棱线的相应部分去掉,并注意可能存在的虚线。
图3-5 切口三棱锥的投影三棱锥所形成的缺口是由一个水平面和一个正垂面切割三棱锥而形成的,由于水平面和正垂面的正面投影有积聚性,故截交线的正面投影已知。
因为水平截面平行于底面,所以它与前棱面的交线DE必平行于底边AB,与后棱面的交线DF必平行于底边AC。
正垂面分别与前、后棱面相交于直线GE、GF。
由于两个截平面都垂直于正面,所以它们的交线EF一定是正垂线。
画出这些交线的投影,也就画出了这个缺口的投影作图步骤:①因为两截平面都垂直于正面,所以d′e′、d′f′和g′e′、g′f′都分别重合在它们的有积聚性的正面投影上,e′f′则位于它们的有积聚性的正面投影的交点处;②根据点在直线上的投影特性,由d′在sa 上作出d。
由d作de∥ab、df∥ac,再分别由e′、f′在de、df上作出e、f。
由d′e′、de和d′f′、df作出d″e″、d″f″,都重合在水平截面的积聚成直线的侧面投影上;③由g′分别在sa、s″a″上作出g、g″,并分别与e、f和e″、f″连成ge、gf和g″e″、g″f″;④连接e、f,由于ef被三个棱面SAB、SBC、SCA的水平投影所遮而不可见,画成虚线;e″f″则重合在水平截面的积聚成直线的侧面投影上;⑤加粗实际存在的左棱线的SG、DA段的水平和侧面投影。
§3-3 曲面立体的投影曲面立体是由曲面或曲面与平面所围成。
曲面可分为规则曲面和不规则曲面两种。
规则曲面可看作由一条线按一定的规律运动所形成,运动的线称为母线,而曲面上任一位置的母线称为素线。
母线绕轴线旋转则形成回转面。
回转面的形状取决于母线的形状及母线与轴线的相对位置。
母线任一点绕轴线回转一周所形成的轨迹称为纬圆。
纬圆的半径是该点到轴线的距离,纬圆所在的平面垂直于轴线。
本节仅讨论由回转面组成的立体——回转体。
作回转体的投影主要是画出回转面投影的转向轮廓线。
转向轮廓线是切于曲面的投影线与投影面的交点的集合,也就是曲面的最外围轮廓线,在投影图中,也常常是曲面的可见投影与不可见投影的分界线。
需注意,回转面在正面投影、水平投影、侧面投影中的转向轮廓线,是曲面上不同位置的曲线或直线的投影。
一、圆柱体1、圆柱体的投影圆柱体是由圆柱面和顶面、底面组成。
圆柱面是由一条直母线,绕与它平行的轴线旋转而形成,圆柱面上的素线都是平行于轴线的直线。
圆柱的顶面、底面是水平面,所以水平投影反映圆的实形,即投影为圆。
其正面投影和侧面投影积聚为直线,直线的长度就等于圆的直径。
由于圆柱的轴线垂直于水平面,圆柱面的所有素线都垂直于水平面,故其水平投影积聚为圆,与上下底面的圆的投影重合。
在圆柱的正面投影中,前、后两半圆柱面的投影重合为一矩形,矩形的两条竖线分别是圆柱最左、最右素线的投影,也就是圆柱前后分界的转向轮廓线的投影。
在圆柱的侧面投影中,左右两半圆柱面重合为一矩形,矩形的两条竖线分别是最前、最后素线的投影,也就是圆柱左右分界的转向轮廓线的投影。
转向轮廓线对于回转体而言是一个十分有用的概念,要认真体会,分清其在三个投影面中的投影。
图3-6 园柱的投影2、圆柱表面找点圆柱表面找点,若点在转向轮廓线上,可直接根据线上取点的方法直接找出点的投影,注意可见性,应熟悉各转向轮廓线在三投影面上的投影。
若点不在转向轮廓线上,可根据圆柱面的积聚性,先找出点的积聚性投影,然后再根据点的投影规律找点的其余投影。
二、圆锥体1、圆锥体的投影圆锥体由圆锥面和底面组成。
(见图3-7)圆锥面是由一条直母线,绕与它相交的轴线旋转而形成。
在圆锥面上任意位置的素线,均交于锥顶。
圆锥面上的纬圆从锥顶到底面直径是越来越大的,底面可看作为圆锥面上直径最大的纬圆。
以直立圆锥为例,它的正面和侧面投影为同样大小的等腰三角形。
正面投影的等腰三角形的两腰是圆锥的最左和最右转向轮廓线的投影,其侧面投影与轴线重合,它们将圆锥面分为前、后两半;侧面投影的等腰三角形的两腰是圆锥面对侧面转向轮廓线,亦即圆锥面上最前和最后素线的投影,其正面投影与轴线重合,它们将圆锥面分为左、右两半。
圆锥面的水平投影为圆,因为圆锥面的素线相对于底面的位置均是倾斜的,故圆周只是底面圆的投影,而非圆锥面的投影。
最左和最右转向轮廓线为正平线,其水平投影与圆的水平对称线重合;最前和最后转向轮廓线为侧平线,其水平投影与圆的垂直对称线重合。
图3-7 圆锥的投影2、圆锥表面找点(见图3-8)在转向轮廓线上找点同圆柱。
在圆锥面上取点,因为圆锥面没有积聚性,所以只能应用作辅助线的方法,在圆锥面上的辅助线有纬圆和素线两种图3-8 圆锥表面上取点素线法,即过点A与锥顶S作锥面上的素线SB,即先过a′作s′b′,由b′求出b、b″,连接sb和s″b″,它们是辅助线SB的水平投影及侧面投影。
而点A的水平投影及侧面投影必在SB的同面投影上,从而求出a和a″。
纬圆法,即过点A在锥面上作一水平辅助纬圆,纬圆与圆锥的轴线垂直。
该纬圆在正面及侧面投影中积聚为直线,直线长度即为纬圆直径,水平投影反映纬圆的实形。
点A的投影必在纬圆的同面投影上。
先过a′作垂直于轴线的直线,得到纬圆的直径;画出纬圆的水平投影,由a′找出a,注意A点的正面投影可见,所以其应在圆锥的前半部分,即a为a′a连线与纬圆水平投影两交点中前面的一个;再由a′、a求出a″,因点A在圆锥面的左半部,所以a″为可见。
三、圆球体1、圆球体的投影圆球体由圆球面围成。
圆球面是一圆母线绕其直径旋转一周形成的。
如图3-9所示,圆球的三个投影是圆球上平行相应投影面的三个不同位置的转向轮廓圆。
正面投影的轮廓圆是前、后两半球面的可见与不可见的分界线。
水平投影的轮廓圆是上、下两半球面的可见与不可见的分界线。
侧面投影的轮廓圆是左、右两半球面的可见与不可见的分界线。
图3-9 圆球的投影2、圆球表面找点若所找点在转向轮廓线上,同样可根据线上找点的方法来求,但应注意圆球的转向轮廓线为圆。
若点在一般位置,则应作辅助线,在球面上只能以辅助纬圆作辅助线。
如图3-10所示,若已知圆球面上的点A、B、C的正面投影a′、b′、c′,要求各点的其它投影。
A、B两点均为处于转向轮廓线上的特殊位置点,可直接作图求出其另外两投影。
因a′可见,且在正面的转向轮廓圆上,故其水平投影a在水平对称线上,侧面投影a″在竖直对称线上;b′为不可见,且在水平对称线上,故点B在水平面的转向轮廓圆的后半部,可由b′先求出b,最后求出b″;由于点B在侧面转向轮廓园的右半部,故b″不可见。