二维随机变量的函数
- 格式:ppt
- 大小:1007.50 KB
- 文档页数:42

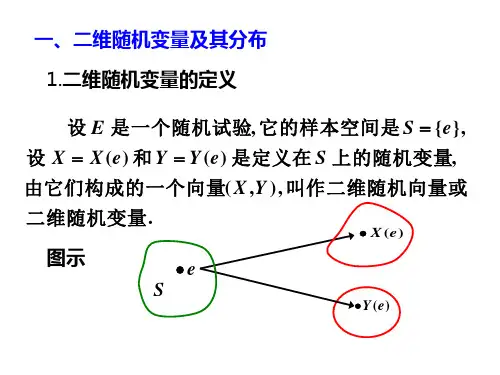
定义3-1 n个随机变量X1,X2,…,X n构成的整体X=(X1,X2,…,X n)称为一个n维随机变量或n维随机向量,X i称为X的第i(i=1,2,…,n)个分量.
定义3-2 设(x,Y)为一个二维随机变量,记
F(x,y)=P{X≤x,Y≤y},-∞<z<+∞,-∞<y<+∞,< p="" style="padding: 0px; list-style: none;">
称二元函数F(x,y)为X与y的联合分布函数或称为(X,Y)的分布函数.
(X,Y)的两个分量X与y各自的分布函数分别称为二维随机变量(X,Y)关于X与关于y的边缘分布函数,记为F X(x)与F Y(y).
边缘分布函数可由联合分布函数来确定,事实上,一元函数
几何上,若把(X,Y)看成平面上随机点的坐标,则分布函数F(x,y)在(x,y)处的函数值就是随机点(X,Y)落在以(x,y)为顶点、位于该点左下方的无穷矩形D内的概率.
分布函数F(x,y)具有下列性质:
(1)F(x,y)是变量x(或y)的不减函数.
(2)0≤F(x,y)≤l,
对任意固定的y,F(-∞,y)=0
对任意固定的x,F(x,-∞)=0;
F(-∞, -∞)=0,F(+∞,+∞)=1. (3)F(x,y)关于x和关于y均右连续,即F(x,y)=F(x+0,y);F(x,y)=F(x,y+0). (4)对任意固定的x1<x2,y1<y2
F(x2 ,y2)-F(x2,yl)-F(xl,y1)+F(x1+yl)≥0.。


第五章 二维随机变量第一节 二维随机变量及其分布一、二维随机变量1、定义:设),,(P S F 为一概率空间,X 、Y 均为S 上的一维随机变量,称二维向量X ),(Y X =为S 上的二维随机变量.2、X 的分布:}{B P ∈X , 2B ∈B . 其中可证:=∈}{B X F ∈∈∈},))(),((|{S e B e Y e X e .若取},|),{(2121y y y x x x y x B ≤<≤<=,那么},{}{2121y Y y x X x P B P ≤<≤<=∈X},{22y Y x X P ≤≤=},{21y Y x X P ≤≤- },{},{1112y Y x X P y Y x X P ≤≤+≤≤-.3、分布函数(1)定义:设),,(P S F 为一概率空间,),(Y X 为S 上的二维随机变量,R ∈∀y x ,,规定:},{),(y Y x X P y x F ≤≤=. 称),(y x F 为),(Y X 的分布函数.显然: },{2121y Y y x X x P ≤<≤<),(),(),(),(11122122y x F y x F y x F y x F +--=.(2)性质① R ∈∀y x ,,1),(0≤≤y x F .② ),(y x F 关于y x ,均为单调不减函数.③ 0),(=-∞y F ,0),(=-∞x F ,0),(=-∞-∞F ,1),(=+∞+∞F . ④ ),(y x F 关于y x ,均为为右连续函数.⑤ R ∈<<∀2121,y y x x ,0),(),(),(),(11122122≥+--y x F y x F y x F y x F .注:①~⑤为分布函数的特征性质.反之亦然.例1掷硬币三次,X 表示出现正面的次数,|)3(|X X Y --=,求),(Y X 的分布函数),(y x F .解:(1) X 的所有可能取值为3,2,1,0,依次记为4321,,,x x x x ,Y 的所有可能取值为3,1,依次记为21,y y .列表如下X样 本 点Y0 (反反反)3 1 (正反反) (反正反) (反反正) 1 2(正正反) (正反正) (反正正)13 (正正正)3(2) 概率情况列表 81},{21===y Y x X P ,83},{12===y Y x X P , 83},{13===y Y x X P ,81},{24===y Y x X P ,其他0},{===j i y Y x X P .(3)求分布. 记}2,1 ,3,2,1|),{(===j i y x A j i ,YX1 3 0 0 8/1 1 8/3 02 8/3 0 38/1A B BA B +=, 显然φ=∈}),{(A B Y X ,那么}),{(}),{(}),{(A B Y X P BA Y X P B Y X P ∈+∈=∈∑∈===∈=By x j i j i y Y x XP BA Y X P )(,},{}),{((4)求分布函数. ∑≤≤===≤≤=yy x x j i j i y Y x XP y Y x X P y x F ,},{},{),(.⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥≥≥<≤<≤≥≥<≤<≤<≤≥<≤<<<<=.3 ,3 1, ,3 ,32 ,8/7 ;31 ,3 ,8/6 ;3 ,21 ,8/4 ;31 ,21 ,8/3 ;3 ,10 ,8/1;3 ,1 1 0 0,),(y x y x y x y x y x y x y x y x y x F 或或二、边缘分布1、),(Y X 关于X 的边缘分布: ),(lim }{)(y x F x X P x F y X +∞→=≤=.证明:取}{},{},{x X Y x X n Y x X A n ≤=+∞<≤→≤≤=不减,由①②知),(lim y x F y +∞→存在,故)(}{)lim ()(lim ),(lim ),(lim x F x X P A P A P n x F y x F X n n n n n y =≤====∞→∞→∞→+∞→.2、),(Y X 关于Y 的边缘分布: ),(lim }{)(y x F y Y P y F x Y +∞→=≤=. (略)三、随机变量相互独立、定义:设),(y x F 为),(Y X 的分布函数,X 、Y 的分布函数分别为 )(x F X 、)(y F Y ,若R ∈∀y x ,,恒有=),(y x F )(x F X )(y F Y , 则称X 与Y 相互独立.2、X 与Y 相互独立⇔R ∈<<∀2121,y y x x ,恒有}{}{},{21212121y Y y P x X x P y Y y x X x P ≤<≤<=≤<≤<.证明:“⇐” R ∈∀y x ,,由于},{},{y Y x X y Y n x X n ≤≤→≤<-≤<-, }{}{x X x X n ≤→≤<-, }{}{y Y y Y n ≤→≤<-均不减,则},{),(y Y x X P y x F ≤≤=},{lim y Y n x X n P n ≤<-≤<-=∞→}]{}{[lim y Y n P x X n P n ≤<-≤<-=∞→}]{lim }{lim y Y n P x X n P n n ≤<-≤<-=∞→∞→)()(}{}{y F x F y Y P x X P Y X =≤≤=.“⇒”R ∈<<∀2121,y y x x ,有 },{2121y y x x P ≤<≤<ηξ ),(),(),(),(11122122y x F y x F y x F y x F +--=)()()()()()()()(11122122y F x F y F x F y F x F y F x F Y X Y X Y X Y X +--= )]()()][()([1212y F y F x F x F Y Y X X --= }{}{2121y y P x x P ≤<≤<=ξξ.3、X 与Y 相互独立⇔R ⊂∀21,B B ,恒有}{}{},{2121B Y P B X P B Y B X P ∈∈=∈∈.第二节 二维离散型随机变量一、二维离散型随机变量 1、定义:设),,(P S F 为一概率空间,),(Y X 为S 上的二维随机变量,若),(Y X 的取值为有限个或可数个(至多可数),称),(Y X 为S 上的二维离散型随机变量. 显然:),(Y X 为S 上的二维离散型随机变量⇔X 与Y 均为S 上的一维离散型随机变量.2、概率分布:设),(Y X 所有可能取的值为),(j i y x ,令 },{j i ij y Y x X P p ===,称其为二维随机变量),(Y X 的概率分布(分布率)。







二维随机变量及其概率分布复习资料内容摘要一、二维随机变量设随机试验的样本空间为Ω,X 和Y 是定义在Ω上的两个随机变量(X ,Y )为二维随机变量或二维随机向量。
1. 联合分布函数设(X ,Y )是二维随机变量,y x ,是任意实数,函数F (x ,y )=P{X ≤x ,Y ≤y}称为(X ,Y )的分布函数,或称随机变量X 与Y 的联合分布函数. 2. 联合分布函数的性质(1) 0≤F (x ,y )≤1;(2) F(x ,- ∞)= F(-∞,y)= F(-∞,- ∞)=0F(+∞,+ ∞)=1;(3) F(x ,y)对x 和y 分别是不减的.即对于固定的y ,若x 1<x 2,则F (x 1,y )(),y x F 2≤;对于固定的x ,若y 1<y 2,则F(x ,y 1)≤F(x ,y 2);(4) F (x ,y )关于x 右连续,关于y 右连续,即 F (x +0,y )=F (x ,y ),F (x ,y+0)=F (x ,y )。
(5) 对于任意的点(x 1,y 1),(x 2,y 2),x 1<x 2,y 1<y 2,有 F(x 2,y 2)-F(x 2,y 1)-F(x 1,y 2)+F(x 1,y 1)≥0. 3.二维离散型随机变量如果二维随机变量(X ,Y)所有可能取的数对为有限个或可数个,则称(X ,Y )为二维离散型随机变量.并且称P{X=i , Y=y j }=ij p ,i ,j=1,2…为(X,Y)的分布律,或称做X与Y的联合分布律. 分布律也可用表格列出:分布律满足下列3条性质:4.二维连续型随机变量设(X,Y)的分布函数为F(x,y),如果存在非负函数f(x,y),使得对任意实数x,y都有则称(X,Y)为二维连续型随机变量,函数f(x,y)称做(X,Y)的概率密度,或X,Y的联合概率密度.f(x,y)具有下列性质:(1)f(x,y)≥0,(2)⎰+∞∞-⎰+∞∞- f(x,y)d x dy=1(3)若f(x,y)在点(x,y)连续,则有(4)设D为x Oy平面上的区域,则f(x,y)d x dyP{(x,y)∈D}=⎰⎰D二、边缘分布1.边缘分布函数设F(X,Y)是X与Y的联合分布函数,则FX(x)=P{X≤x,Y<+∞}=F(x,+∞)F Y(y)=P{ X<+∞,Y≤y } =F(+∞)分别称为(X,Y)关于X与Y的边缘分布律。