第7章现代控制理论简介

现代控制理论
目录
• 引言 • 线性系统理论 • 非线性系统理论 • 最优控制理论 • 自适应控制理论 • 鲁棒控制理论
01
引言
什么是现代控制理论
现代控制理论是一门研究动态系统控制的学科，它利用数学模型和优化方法来分析 和设计控制系统的性能。
它涵盖了线性系统、非线性系统、多变量系统、分布参数系统等多种复杂系统的控 制问题。
20世纪60年代
线性系统理论和最优控制理论得到发展，为现代控制理论的建立奠定 了基础。
20世纪70年代
非线性系统理论和自适应控制理论逐渐发展起来，进一步丰富了现代 控制理论的应用范围。
20世纪80年代至今
现代控制理论在智能控制、鲁棒控制、预测控制等领域取得了重要进 展，为解决复杂系统的控制问题提供了更有效的工具。
01
利用深度学习算法对系统进行建模和学习，实现更高
效和智能的自适应控制。
多变量自适应控制
02 研究多变量系统的自适应控制方法，以提高系统的全
局性能。
非线性自适应控制
03
发展非线性系统的自适应控制方法，以处理更复杂的
控制系统。
06
鲁棒控制理论
鲁棒控制的基本概念
鲁棒控制是一种设计方法，旨在 提高系统的稳定性和性能，使其 在存在不确定性和扰动的情况下
自适应逆控制
一种基于系统逆动态特性的自适应控制方法，通过对系统 逆动态特性的学习和控制，实现系统的自适应控制。
自适应控制系统设计
系统建模
建立被控对象的数学模型，包括线性系统和非线性系统。
控制器设计
根据系统模型和性能指标，设计自适应控制器，包括线性自适应控制器和 非线性自适应控制器。
参数调整
根据系统运行状态和环境变化，调整控制器参数，以实现最优的控制效果 。

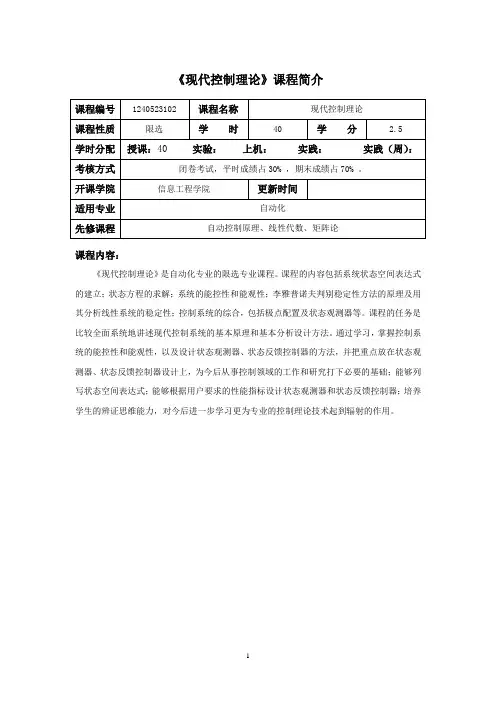
《现代控制理论》课程简介课程内容：《现代控制理论》是自动化专业的限选专业课程。

课程的内容包括系统状态空间表达式的建立；状态方程的求解；系统的能控性和能观性；李雅普诺夫判别稳定性方法的原理及用其分析线性系统的稳定性；控制系统的综合，包括极点配置及状态观测器等。

课程的任务是比较全面系统地讲述现代控制系统的基本原理和基本分析设计方法。

通过学习，掌握控制系统的能控性和能观性，以及设计状态观测器、状态反馈控制器的方法，并把重点放在状态观测器、状态反馈控制器设计上，为今后从事控制领域的工作和研究打下必要的基础；能够列写状态空间表达式；能够根据用户要求的性能指标设计状态观测器和状态反馈控制器；培养学生的辨证思维能力，对今后进一步学习更为专业的控制理论技术起到辐射的作用。

Brief IntroductionCourse Description:This course is the limited subject course for the college students.The contents of this course include: system state space expressions, state equation, controllability and observability, Lyapunov stability method, the pole placement , observer and controller.The mission of this course is:1st, to introduce the basic principle and basic method of modern control system ，through the study, master control system controllability and observability;2nd, to design state observer, state feedback controller, state space expression;3rd, to design state observer and state feedback controller according to the user request performance index .《现代控制理论》课程教学大纲一、教学内容第一章控制系统的状态空间表达式1.1 状态变量及状态空间表达式1.2 状态空间表达式的模拟结构图1.3 由微分方程列写状态空间表达式1.4 由传递函数列写状态空间表达式1.5 状态向量的线性变换1.6 传递函数矩阵教学难点：传递函数矩阵。

最优估计理论的内容
参数估计法；（最小方差、最小二乘法） 状态估计法（卡尔曼滤波）
§ 1.3 现代控制理论与经典控制理论的差异
庞特里亚金 L.S.Pontryagin
4. 罗森布洛克（H.H.Rosenbrock）、欧文斯（D.H.Owens） 和麦克法仑（G.J.MacFarlane）研究了用于计算机辅助设计的 现代频域法理论，将经典控制理论传递函数的概念推广到多变 量系统，并探讨了传递函数矩阵与状态方程之间的等价转换关 系，为进一步建立统一的线性系统理论奠定了基础。
赫尔维茨（Hurwitz）
3.由于两次世界大战中军事 工业需要控制系统具有准确 跟踪与补偿能力，1932年奈 奎斯特（H.Nyquist）提出 了复数域内研究系统的频率 响应法，为具有高质量动态 品质和静态准确度的军用控 制系统提供了急需的分析工 具。
奈奎斯特
4.1948年伊文思（W.R.Ewans）提出了用图解方式研 究系统的根轨迹法。
1.五十年代后期，贝尔曼（Bellman）等人提出了状态空间法； 在1957年提出了基于动态规划的最优控制理论。
2.1959年匈牙利数学家卡尔曼（Kalman） 和布西创建了卡尔曼滤波理论；1960年 在控制系统的研究中成功地应用了状态 空间法，并提出了可控性和可观测性的 新概念。
卡尔曼
3. 1961年庞特里亚金（俄国人）提出 了极小（大）值原理。
现代控制理论基础
Modern Control Theory
绪论
§ 1.1 现代控制理论的产生与发展 § 1.2 现代控制理论的内容 § 1.3 现代控制理论与经典控制理论的差异 § 1.4 现代控制理论的应用
§ 1.1 现代控制理论的产生与发展
同学们，我们都知道：控制理论作为一门科 学技术，已经广泛地运用于我们社会生活的方 方面面。

第六次课小结一、 Lyapunov 意义下的稳定性问题基本概念● 平衡状态的概念● Lyapunov 意义下的稳定性定义（稳定，一致稳定，渐进稳定，一致渐进稳定，大范围渐进稳定等）● 纯量函数的正定性，负定性，正半定性，负半定性，不定性 ● 二次型，复二次型（Hermite 型）二、 Lyapunov 稳定性理论● 第一方法 ● 第二方法三、 线性定常系统的Lyapunov 稳定性分析● 应用Lyapunov 方程Q PA P AH-=+来进行判别稳定性四、 线性定常系统的稳定自由运动的衰减率性能估计● 衰减系数，一旦定出min η，则可定出)(x V 随时间t 衰减上界。

● 计算min η的关系式五、 离散时间系统的状态运动稳定性及其判据● 离散系统的大范围淅近稳定判据，Lyapunov 稳定判据在离散系统中的应用六、 线性多变量系统的综合与设计的基本问题●问题的提法●性能指标的类型●研究的主要内容七、极点配置问题●问题的提出●可配置条件●极点配置算法5.2.5 爱克曼公式(Ackermann ’s Formula) 考虑由式（5.1）给出的系统，重写为Bu Ax x +=假设该被控系统是状态完全能控的，又设期望闭环极点为n s s s μμμ===,,,21 。

利用线性状态反馈控制律Kx u -=将系统状态方程改写为x BK A x )(-=(5.14)定义BK A A -=~则所期望的特征方程为)())((~11121=++++=---=-=+-**--*n n n nn a s a sa s s s s A sI BK A sI μμμ由于凯莱-哈密尔顿定理指出A ~应满足其自身的特征方程，所以0~~~)~(**11*1*=++++=--I a A a A a A A n n n n φ (5.15)我们用式（5.15）来推导爱克曼公式。

为简化推导，考虑n = 3的情况。

需要指出的是，对任意正整数，下面的推导可方便地加以推广。

现代控制理论⾮线性动态系统的稳定性和鲁棒控制理论研究上世纪50年代，Kallman成功的将状态空间法引⼊到系统控制理论中，从⽽标志着现代控制理论研究的开始。

现代控制理论的研究对象是系统的数学模型，它根据⼈们对系统的性能要求，通过对被控对象进⾏模型分析来设计系统的控制律，从⽽保证闭环系统具有期望的性能。

其中，线性系统理论已经形成⼀套完整的理论体系。

过去⼈们常⽤线性系统理论来处理很多⼯程问题，并在⼀定范围内取得了⽐较满意的效果。

然⽽，这种处理⽅法是以忽略系统中的动态⾮线性因素为代价的。

实际中很多物理系统都具有固有的动态⾮线性特性，如库仑摩擦、饱和、死区、滞环等，这些⾮线性动态⾮线性特性的存在常常使系统的控制性能下降，甚⾄变得不稳定。

这就使得利⽤线性系统理论处理⾮线性动态系统⾯临巨⼤的困难。

此外，在控制系统运⾏过程中，环境的变化或者元件的⽼化，以及外界⼲扰等不确定因素也会造成系统实际参数和标称值之间出现较⼤差别。

因此，基于标称数学模型所设计的控制律⼀般很难达到期望的性能指标，甚⾄会使系统不稳定。

综上所述，研究不确定条件下⾮线性动态系统的鲁棒稳定性及鲁棒控制间题具有重要的理论意义和迫切的实际需要。

⾮线性动态系统是指按确定性规律随时间演化的系统，⼜称动⼒学系统，其理论来源于经典⼒学，⼀般由微分⽅程来描述。

美国数学家Birkhoff[1]发展了法国数学家Poincare在天体⼒学和微分⽅程定性理论⽅⾯的研究，奠定了动态系统理论的基础。

在实际动态系统中，对象往往受到各种各样的不确定的影响，所以其数学模型⼀般不可能精确得到。

因此，我们只能⽤近似的标称数学模型来描述被控对象，并据此来设计控制系统,动态系统鲁棒控制由此产⽣。

所谓鲁棒性就是指系统预期⾮线性动态系统的稳定性和鲁棒控制理论研究的设计品质不因不确定性的存在⽽遭到破坏的特性，鲁棒控制是⾮线性动态系统控制理论研究的⼀个⾮常重要的分⽀。

现代控制理论的发展促进了对动态系统的研究，使它的应⽤从经典⼒学扩⼤到⼀般意义下的系统。

现代控制理论及应用李嗣福教授、博士生导师中国科学技术大学自动化系一、现代控制理论及应用发展简介1. 控制理论及应用发展概况2. 自动控制系统和自动控制理论以单容水槽水位控制和电加热器温度控制为例说明什么是自动控制、控制律（或控制策略）、自动控制系统以及自动控制系统组成结构和自动控制理论所研究的内容。

2.1自动控制：利用自动化仪表实现人的预期控制目标。

2.2自动控制系统及其组成结构自动控制系统：指为实现自动控制目标由自动化仪表与被控对象所联接成闭环系统。

自动控制系统组成结构：是由被控对象、测量代表、控制器或调节器和执行器构成反馈闭环结构，其形式有单回路形式和串级双回路形式。

控制系统性能指标：定性的有稳（定性）、准（确性）、快（速性）。

控制律（或控制策略、控制算法）：控制系统中控制器或调节器所采用的控制策略，即用系统偏差量如何确定控制量的数学表示式。

2.3自动控制系统类型主要有：按系统参数输入信号形式分：定值控制系统或调节系统和随动系统。

按系统结构形式分：前馈控制系统（即开环系统）和反馈控制系统以及复合控制系统；按系统中被控对象的控制输入量数目和被控输出量数目分：单变量控制系统和多变量控制系统；按被控对象特性分：线性控制系统和非线性控制系统；按系统中的信号形式分：模拟（或时间连续）控制系统、数字（或时间离散）控制系统以及混合控制系统。

2.4自动控制理论：研究自动控制系统分析与综合设计的理论和方法。

3. 古典（传统）控制理论：采用数学变换方法（即拉普拉斯变换和富里叶变换）按照系统输出量与输入量之间的数学关系（即系统外部特性）研究控制系统分析和综合设计问题。

具体方法有：根轨迹法；频率响应法。

主要特点：理论方法的物理概念清晰，易于理解；设计出控制律一般较简单，易于仪表实现主要缺点：① 设计需要凭经验试凑，设计结果与设计经验关系很大； ② 系统分析和设计只着眼于系统外部特性；③一般只能处理单变量系统分析和设计问题，而不能处理复杂的多变量系统分析和设计。

(3)控制规律：
u* kx(t)
P由黎卡提微分k 方Q2程1BT得P 到 边界条件：P(tf)=Q0

PA AT P PBQ21BT P Q1 P(t)
例：求解使：J最小的u*(t)
0 1 0 x 0 0x 1u,
பைடு நூலகம்
J
第二节 状态调节器
在不消耗过多控制能量的前提下，使系统各状态在受 到外界干扰作用下，维持平衡状态。
一.无限长时间状态调节器
1.原系统：可控系统

2.性能指标： 说明：(1) J

x Ax Bu, y Cx
12表0 (示xTQ1系x u统TQ2要u)d求t 状态变量偏离平衡点的累积
u* kx(t)
3.控制规律
k Q21BT P
正定实对称P由黎卡提代数方程得到：
PA AT P PBQ21BT P Q1 0
例：求使J最小的u*(t)。 0 1 0
解：
x 0 0x 1u,
J

1

(xT
x uTu)dt
误差最小，这xTQ意1x 味着因某种原因系统状态偏离平衡点，控制
作用应使它很快回复到平衡点，调节器的名称由此而来
(2) 表示在控制过程中，消耗的能量最小
J中(3的u)TQ权Q2u1重半正定，Q2正定，用来确定状态变量与控制能量在
即寻求控制规律，使系统的状态变量x(t)按性能指标J的要 求，在无限长的时间内达到平衡点
1.原系统：可控、可观系统
x Ax Bu, y Cx

2.性能指标：J

1 2

[(y
0

统安全监测等方面。
THANKS FOR WATCHING和优化控制，注重系统的全局性、 最优性和鲁棒性。
现代控制理论的重要性
工业自动化
现代控制理论为工业自动化提供了理论基础和技 术支持，提高了生产效率和产品质量。
航天与航空
在航天和航空领域，现代控制理论的应用对于飞 行器的稳定性和安全性至关重要。
能源与环境
在能源和环境领域，现代控制理论有助于实现能 源的高效利用和环境的可持续发展。
VS
详细描述
线性二次型最优控制基于最优控制理论， 通过最小化系统状态和控制输入的二次型 代价函数来寻找最优的控制策略。这种方 法能够有效地优化系统的性能，提高系统 的稳定性和动态响应能力。
预测控制
总结词
预测控制是一种基于模型预测和滚动优化的 控制方法。
详细描述
预测控制通过建立系统的预测模型，对未来 的系统行为进行预测，并滚动优化控制策略 以减小预测误差。这种方法具有较好的鲁棒 性和适应性，广泛应用于工业过程控制和智 能控制等领域。
现代控制理论的历史与发展
历史
现代控制理论起源于20世纪50年代，随着计算机技术和数学理论的不断发展而 逐步完善。
发展
现代控制理论的发展涉及多个学科领域，如线性系统理论、最优控制、鲁棒控 制、自适应控制等，为复杂系统的控制提供了更广泛和深入的理论基础。
02 现代控制理论的基本概念
系统建模
总结词
系统建模是现代控制理论的基础，它通过数学模型描述系统的动态行为。
详细描述
性能指标是用来评估控制系统性能的关键因素，包括稳定性、准确性、快速性和鲁棒性 等。稳定性表示系统在受到扰动后恢复平衡的能力；准确性表示系统输出与理想输出之 间的误差大小；快速性表示系统达到稳定状态所需的时间；鲁棒性表示系统在存在不确

现代控制理论简介下列几方面为现代控制理论发展的促进因素:1.处理更多的现实模型系统的必要性2.强调向最佳的控制和最佳的系统设计的升级3.数字化计算机技术的持续发展.4.当前技术的不成熟.众所周知的方法在其它知识领域的适用性得到承认.从容易解决的简单近似的模型到更多的现实模型的转变产生了两种效果：首先，模型必须包括很多的变量。

其次，一个十分逼真的模型是尽可能的包括非线性和随时间变化的参数。

早先的忽略了系统的一些方面，例如很有可能的一方面就是在环境中有着反馈的交互作用。

在现代科技高度发达的社会，存在一种非常雄心的目标的趋势，这也意味着要处理有着很多相互关联成分的复杂系统，高精确度与高效率的需要改变了控制系统的执行重点。

在超频百分比，时间设置，频宽等等方面的经典规范，在很多情况下解决了优化标准如最小能量，最小花费，最小时间控制，优化这些标准时很难避免和不开心的非线性打交道。

即使基础系统是线性的和不随时间变化的，优化控制理论显示非线性时间变化控制也被应用到了。

不停发展的计算机技术在控制领域创造了三条最重要的影响。

其中一项是有关数字化的超级计算机，较之这本书首印时期，现在能模拟，分析，控制的问题的大小和种类都要大得惊人。

计算机技术的第二个问题就是必须处理微型计算机在家庭和工作地的扩散与广泛的可靠性。

古典的控制理论是以图画似的方法为主导的. 因为在时间那是唯一的解决确定的问题的途径。

为了系统分析和设计,现在每一个控制设计者很容易有机会接近强大的计算机内部。

老的图画似的方法不但没有消失, 并且还使其自动化了.它们之所以能生存是因为提供了洞察力与直觉，许多不同的技术经常能更适合于计算机。

虽然计算机能被用于执行经典的改变-到转的改变方法，但它通常更多的有效用于直接整合微分方程。

计算机的第三个，也是最重要的方面，就是它们现在已经如此普遍地应用于控制系统，俨然其中的一员。

其价格，型号和稳定性使得能够在许多系统中常规的使用。

数字仿真实验结果分析 阐述如何对数字仿真实验结果进 行分析，包括性能指标的计算和 评估，以及对实验结果进行解释 和讨论。
数字仿真软件 介绍常用的数字仿真软件，如 MATLAB/Simulink等，并解释其 基本原理和使用方法。
数字仿真实验设计 详细说明数字仿真实验的设计方 法，包括如何建立系统模型、如 何设计控制器、如何设置仿真参 数等。
该方法能够全面地反映系统的性能，具有较强的适用性和实用 性。同时，该方法可通过实验手段进行验证，可靠性高。
设计过程相对较为复杂，需要一定的专业知识和经验。
适用于高阶系统和多变量系统的控制器设计，广泛应用于工程 实践中。
最优控制设计法
定义
最优控制设计法是一种基于最优化理论进行控制器设计的 方法。
缺点
现代控制理论阶段
自20世纪60年代开始，状态空间 法成为主导，适用于多输入多输 出、非线性、时变系统的分析与 设计。
现代控制理论的特点
状态空间描述
现代控制理论基于状态空间描述 ，通过状态变量全面反映系统内 部状态，提供更深入的系统分析
。
时域分析法
相比古典控制理论的频域分析法， 现代控制理论采用时域分析法，能 够直接反映系统的时间响应特性。
05
现代控制理论进阶知 识
系统的数学模型 ，包括微分方程、差分方程和状态方程等
。
A 非线性现象
介绍系统中的非线性现象，如死区 、饱和、滞后等，并分析其对系统
性能的影响。
B
C
D
非线性系统设计
探讨非线性控制系统的设计方法，如反馈 线性化、滑模变结构控制、反步法等。
稳定性分析
利用状态空间方程的特征值分析系统的稳定性，通过判断 特征值的分布来确定系统的稳定性。

现代控制理论HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】1、什么是对偶系统，从传递函数矩阵，特征多项式和能控、能观性说明互为对偶的两个系统之间的关系。

答：定义：如果两个系统满足A2=A1T，B2=C1T,C2=B1T，则称这两个系统互为对偶函数。

互为对偶系统传递函数矩阵互为转置特征多项式相同，一个函数的能控性等价于另一个函数的能观性。

2、什么是状态观测器？简述构造状态观测器的原则。

答：系统的状态不易检测，以原系统的输入和输出为输入量构造，一动态系统，使其输出渐近于原系统状态，此动态系统为原系统的状态观测器。

原则：（1）观测器应以原系统的输入和输出为输入量；（2）原系统完全能观或不能观于系统是渐近稳定的；（3）观测器的输出状态应以足够快速度超近于原系统状态；（4）有尽可能低的维数，以便于物理实现。

3、说明应用李氏第二法判断非线性系统稳定性基本思想和方法步骤和局限性。

答：基本思想：从能量观点分析平衡状态的稳定性。

（1）如果系统受扰后，其运动总是伴随能量的减少，当达到平衡状态时，能量达到最小值，则此平衡状态渐近稳定：（2）如果系统不断从外界吸收能量，储能越来越大，那么这个平衡状态就是不稳定的：（3）如果系统的储能既不增加也不消耗，那么这个平衡状态时李亚普诺夫意义下的稳定。

方法步骤：定义一个正定的标量函数V（x）作为虚构的广义能量函数，然后根据V（x）=dV（x）/dt的符号特征来判别系统的稳定性。

局限性：李雅普诺夫函数V(x)的选取需要一定的经验和技巧。

4、举例说明系统状态稳定和输出稳定的关系。

答：关系：（1）状态稳定一定输出稳定，但输出稳定不一定状态稳定；（2）系统状态完全能观且能控=状态稳定与输出稳定等价。

举例：A的特征值 =-1 =1 所以状态不是渐进稳点的，W(s)的极点S=-1，所以输出稳点。

5、什么是实现问题什么是最小实现说明实现存在的条件。

现代控制理论摘要最优控制，又称无穷维最优化或动态最优化，是现代控制理论的最基本，最核心的部分。

它所研究的中心问题是：如何根据受控系统的动态特性，去选择控制规律，才能使得系统按照一定的技术要求进行运转，并使得描述系统性能或品质的某个“指标”在一定的意义下达到最优值。

最优控制问题有四个关键点：受控对象为动态系统；初始与终端条件（时间和状态）；性能指标以及容许控制。

一个典型的最优控制问题描述如下：被控系统的状态方程和初始条件给定，同时给定目标函数。

然后寻找一个可行的控制方法使系统从输出状态过渡到目标状态，并达到最优的性能指标。

系统最优性能指标和品质在特定条件下的最优值是以泛函极值的形式来表示。

因此求解最优控制问题归结为求具有约束条件的泛函极值问题，属于变分学范畴。

变分法、最大值原理（最小值原理）和动态规划是最优控制理论的基本内容和常用方法。

庞特里亚金极大值原理、贝尔曼动态规划以及卡尔曼线性二次型最优控制是在约束条件下获得最优解的三个强有力的工具，应用于大部分最优控制问题。

尤其是线性二次型最优控制，因为其在数学上和工程上实现简单，故其有很大的工程实用价值。

关键词：最优控制；控制规律；最优性能指标；线性二次型一绪论1.1背景和意义要求将最优控制问题典型解决方法变分法、极值原理和动态规划及其在时间最短控制问题的应用和线性二次型最优控制问题（包括线性二次型实验及仿真结果）作为主要内容。

其中有关线性二次型的实验要利用MATLAB软件建立数学模型及仿真并作对结果一定的分析。

通过理论与实践操作加深对最优控制这门课程的理解，使之能应用于以后的学习和工作。

1.2主要内容现代控制理论是在经典控制理论基础上逐步发展起来的。

其基本内容包括：线性系统的状态空间理论，最优估计与最优滤波、最优控制理论，系统辨识理论、鲁棒控制、自适应控制。

它以状态空间法为基础，研究多输入多输出、变参数、非线性、高精度、高效能等控制系统的分析与设计问题。

迹(root locus)等
●现代控制理论 (modern control
theory)
采用方法：是以时域中（状态变量）描述 系统内部特征的状态空间方法为基础的内 部描述方法 。the concept of state and of
state variable state-space form 主要研究：多输入——多输出系统
现代控制理论基础
授课教师：刘洪锦 天津理工大学自动化系 •E-mail ：liu200718@
现代控制理论是在50年代末，60年代初 形成的。称其为现代控制理论是与经典控 制理论比较而言的。
无论在分析方法还是在使用工具上与经典 理论比较，均有许多本质的不同。
●经典控制理论(classical
目前发展的方向：大系统理论、复杂系
统、人工智能、模糊控制等分支。
对现代控制理论做出杰出贡献的有：
贝尔曼Bellman——动态规划法 庞特里亚金Ponteryagin——极值原理（苏） 卡尔曼Kalman——能控性、能观测性、
Kalman滤波（美）
本课介绍：现代控制理论基础
主要内容：多变量系统的分析方法与 设计（线性系统理论） 具体内容： 1、状态空间的表达式 2、能控性、能观测性 3、李亚谱诺夫稳定性方法 4、线性系统的综合（状态反馈、观 测器）
(multiple inputs and multiple outputs MIMO system)的分析与设计问题。 复杂
系统（complex system） 采用工具：更多地采用计算机软硬件。目 前世界上流行的MATLAB软件就是对系统
进行计算机辅助设计的有力工具。
现代控制理论主要内容：
1、多变量系统的分析与设计 2、最优控制 3、估计理论 4、自适应理论 5、系统辨识

奈奎斯特
四 标志阶段
1.1947年控制论的奠基人美国 数学家韦纳（N.Weiner）把控制 论引起的自动化同第二次产业革 命联系起来，并与1948年出版了 《控制论—关于在动物和机器中 控制与通讯的科学》，书中论述 了控制理论的一般方法，推广了 反馈的概念，为控制理论这门学 科奠定了基础。
控制论之父——韦纳
自适应控制：也是现代控制理论中近十几年 来发展比较快的一个活跃的分支。对于控 制对象的结构或参数会随环境条件的变化 而有大的变化的情况，为了保证控制系统 在整个控制过程中都满足某一最优准则， 那么最优控制器的参数就需要随时加以调 节变化才行。换句话说，控制器的参数要 适应环境条件的变化而自动地调整其参数， 使得整个系统仍然满足最优准则。因此， 这类控制系统称为自适应控制系统。
马克斯韦尔
2. 1895年劳斯（Routh）与赫
尔维茨（Hurwitz）把马克 斯韦尔的思想扩展到高阶微 分方程描述的更复杂的系 统中,各自提出了两个著名
的稳定性判据—劳斯判据
和赫尔维茨判据。基本上 满足了二十世纪初期控制
工程师的需要。
赫尔维茨（Hurwitz）
3.由于第二次世界大战需要 控制系统具有准确跟踪与补 偿能力，1932年奈奎斯特 （H.Nyquist）提出了频域 内研究系统的频率响应法， 为具有高质量的动态品质和 静态 准确度的军用控制系 统提供了所需的分析工具。

这类控制问题十分复杂，采用经典控制 理论难以解决。1958年，苏联科学家Л.С. 庞特里亚金提出了名为极大值原理的综 合控制系统的新方法。在这之前,美国学 者R.贝尔曼于1954年创立了动态规划,并 在1956年应用于控制过程。他们的研究 成果解决了空间技术中出现的复杂控制 问题，并开拓了控制理论中最优控制理 论这一新的领域。

• •
根据控制变量的取值范围有无限制，可将最优控制问题分为无约束最优控制 无约束最优控制和 根据控制变量的取值范围有无限制，可将最优控制问题分为无约束最优控制和有约 束最优控制。 束最优控制。 本章主要介绍求解无约束最优控制问题的变分法和有约束最优控制问题的最小值原 求解最优控制问题等内容。 理、动态规划、线性二次型最优控制和应用MATLAB求解最优控制问题等内容。 动态规划、线性二次型最优控制和应用 求解最优控制问题等内容
2012年3月9日 年 月 日 章第7页 第7章第 页 章第
（4）容许控制的集合 。每一个实际的控制问题， 控制向量 ） 容许控制的集合。每一个实际的控制问题，控制向量u(t)都有 都有 一个规定的取值范围，这个取值范围对应于m维控制空间 维控制空间R 一个规定的取值范围，这个取值范围对应于 维控制空间 m中的一 个集合Ω， 的每一个取值对应于集合Ω中的一个元素 个集合 ，而u(t)的每一个取值对应于集合 中的一个元素。凡属于 的每一个取值对应于集合 中的一个元素。 集合Ω的控制称为容许控制。如果容许控制受到限制， 集合 的控制称为容许控制。如果容许控制受到限制，如 u(t ) ≤ U m则 的控制称为容许控制 ， 称容许控制属于某一闭集；如果容许控制向量u(t)的取值不受限制， 的取值不受限制， 称容许控制属于某一闭集；如果容许控制向量 的取值不受限制 则容许控制属于某一开集。容许控制属于闭集和开集的两类问题， 则容许控制属于某一开集。 容许控制属于闭集和开集的两类问题 ， 在处理方法上有较大差别。 在处理方法上有较大差别。
从上述实例可以看出， 从上述实例可以看出，最优控制理论通常是将控制问题严格地 抽象为数学模型后再求解的。 抽象为数学模型后再求解的。 最优化问题的数学描述，应包括以下四个方面的内容： 最优化问题的数学描述，应包括以下四个方面的内容： 数学模型， （ 1） 受控动态系统的 数学模型 ， 即受控系统动力学特性的系统状 ） 受控动态系统的数学模型 态方程，它反映了动态系统在运动过程中所应遵循的客观规律， 态方程，它反映了动态系统在运动过程中所应遵循的客观规律，是 描述被控系统各状态变量之间关系的一组等式。 描述被控系统各状态变量之间关系的一组等式。 （ 2）动态系统的初态和终态 （ 末态 ） 即 状态方程的边界条件 。 一 ） 动态系统的初态和终态（末态） 状态方程的边界条件。 个动态过程，归根到底是状态空间从一个状态转移到另一个状态。 个动态过程，归根到底是状态空间从一个状态转移到另一个状态。 （3）目标函数（又称性能指标或性能泛函或目标泛函等）。目标 ）目标函数（又称性能指标或性能泛函或目标泛函等） 函数是一个衡量“ 控制作用” 效果的性能指标。 函数是一个衡量 “ 控制作用 ” 效果的性能指标 。 为了实现动态过 程中状态从初态转移到终态， 可以通过不同的控制来完成， 程中状态从初态转移到终态 ， 可以通过不同的控制来完成 ， 而各 种控制效果的好坏， 可通过能否达到所规定的目标函数来判别。 种控制效果的好坏 ， 可通过能否达到所规定的目标函数来判别 。 对于最优化问题的目标函数， 对于最优化问题的目标函数 ， 其内容与形式主要取决于具体最优 化问题所要解决的主要矛盾。 化问题所要解决的主要矛盾。

2
现代控制理论与经典控制理论的差异
经典控制理论 研究对象 研究方法 研究工具 分析方法 设计方法 其他 单输入单输出系统（SISO） 高阶微分方程 传递函数法（外部描述） 拉普拉斯变换 复域，频率响应和根轨迹法 PID控制和校正网络 现代控制理论 多输入多输出系统（MIMO） 一阶微分方程组 状态空间法（内部描述） 线性代数矩阵 复域、实域，能控和能观测 状态反馈和输出反馈
参数设置
• 假定倒立摆系统的参数如下。 • 摆杆的质量：m=0.1g • 摆杆的长度：2l=1m • 小车的质量：M=1kg • 重力加速度：g=10/s2 • 摆杆惯量：I=0.003kgm2 • 摆杆的质量在摆杆的中心。
SIMULINK仿真设计
倒立摆控制系统结构框图
MATLAB演示
整理后得到系统状态空间方程：
0 x 0 x 0 0
1 ( I m l2 )b I ( M m) Mm l2 0 m lb I ( M m) Mm l2
0 m gl 2 I ( M m) Mm l2 0 m gl( M m) I ( M m) Mm l2
自适应控制：通过控制器与具有随机动态特性的被控 过程相匹配来克服、解决被控对象不确定给控制系统带 来的影响。如何利用各种间接或直接辨识系统动态特性 的方法随时调整控制规律达到最优控制。
非线性系统理论：主要研究非线性系统状态的运动规 律和改变这些规律的可能性和实施方法，建立和揭示系 统结构、参数、行为和性能之间的关系。其主要包括能 控性、能观性、稳定性、线性化、解耦以及反馈控制、 状态估计等理论。 随着现代控制理论的不断发展，还出现了大系统理论、智 能控制理论、鲁棒控制理论以及离散事件系统理论等。

建立方程：
L
di(t dt
)
Ri(t
)
uC
(t
)
u(t
)
i C duC (t) dt
初始条件：
i(t) t t0
i(t0 )
uC (t) tt0 uC (t0 )
i(t) 和 uC (t) 可以表征该电路系统的行为，就是该系统的一组状态
变量
9
1.1.2 状态空间表达式
前面电路的微分方程组可以改写如下，并且写成矩阵形式：
本章内容为：
1、状态空间表达式 2、由微分方程求出系统状态空间表达式 3、传递函数矩阵 4、离散系统的数学模型 5、线性变换 6、组合系统的数学描述 7、利用MATLAB进行模型之间的变换
7
1.1 状态空间表达式
1.1.1 状态、状态变量和状态空间 状态——动态系统的状态是一个可以确定该系统行为的信息集合。 这些信息对于确定系统未来的行为是充分且必要的。
（一）待定系数法 首先考察三阶系统，其微分方程为
y a2 y a1 y a0 y b3u b2u b1u b0u
选择状态变量： x1 y 0u x2 y 0u 1u x1 1u x3 y 0u 1u 2u x2 2u
其中，待定系数为： 0 b3 1 b2 a20 2 b1 a10 a21 2 b0 a00 a11 a22
) 2
( sin
)
线性化：当 和 较小时 ，有 sin cos 1 2 0
化简后，得
(M m)y ml u
my ml mg
求解得： y mg 1 u MM
(M m)g 1 u
Ml
Ml
21
选择状态变量 x1 y ，x2 x1 y ，x3 ，x4 x3