第七讲练习答案

第7讲一般应用题（一）一、知识要点一般复合应用题往往是有两组或两组以上的数量关系交织在一起，有的已知条件是间接的，数量关系比较复杂，叙述的方式和顺序也比较多样。

因此，一般应用题没有明显的结构特征和解题规律可循。

解答一般应用题时，可以借助线段图、示意图、直观演示手段帮助分析。

在分析应用题的数量关系时，我们可以从条件出发，逐步推出所求问题（综合法）；也可以从问题出发，找出必须的两个条件（分析法）。

在实际解时，可以根据题中的已知条件，灵活运用这两种方法。

二、精讲精练【例题1】五年级有六个班，每班人数相等。

从每班选16人参加少先队活动，剩下的同学相当于原来4个班的人数。

原来每班多少人？练习1：1.五个同学有同样多的存款，若每人拿出16元捐给“希望工程”后，五位同学剩下的钱正好等于原来3人的存款数。

原来每人存款多少？2.把一堆货物平均分给6个小组运，当每个小组都运了68箱时，正好运走了这堆货物的一半。

这堆货物一共有多少箱？3.老师把一批树苗平均分给四个小队栽，当每队栽了6棵时，发现剩下的树苗正好是原来每队分得的棵数。

这批树苗一共有多少棵？【例题2】某车间按计划每天应加工50个零件，实际每天加工56个零件。

这样，不仅提前3天完成原计划加工零件的任务，而且还多加工了120个零件。

这个车间实际加工了多少个零件？练习2：1.汽车从甲地开往乙地，原计划每小时行40千米，实际每小时多行了10千米，这样比原计划提前2小时到达了乙地。

甲、乙两地相距多少千米？2.小明骑车上学，原计划每分钟行200米，正好准时到达学校，有一天因下雨，他每分钟只能行120米，结果迟到了5分钟。

他家离学校有多远？3.加工一批零件，原计划每天加工80个，正好按期完成任务。

由于改进了生产技术，实际每天加工100个，这样，不仅提前4天完成加工任务，而且还多加工了100个。

他们实际加工零件多少个？【例题3】甲、乙二人加工零件。

甲比乙每天多加工6个零件，乙中途停了15天没有加工。

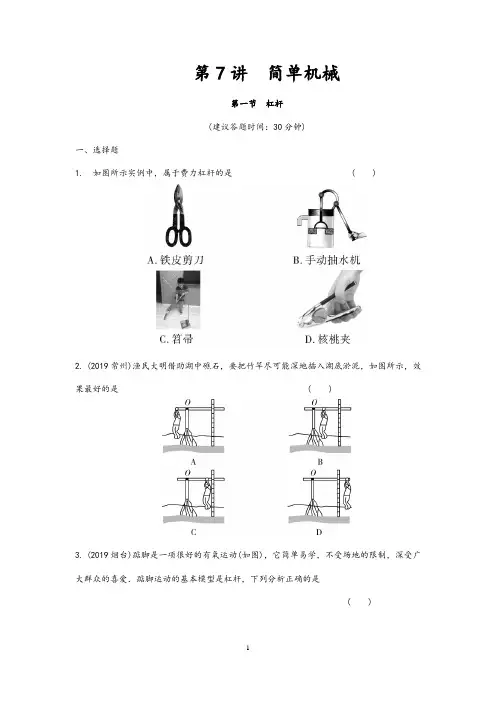
第7讲简单机械第一节杠杆(建议答题时间：30分钟)一、选择题1. 如图所示实例中，属于费力杠杆的是 ( )2. (2019常州)渔民大明借助湖中礁石，要把竹竿尽可能深地插入湖底淤泥，如图所示，效果最好的是 ( )3. (2019烟台)踮脚是一项很好的有氧运动(如图)，它简单易学，不受场地的限制，深受广大群众的喜爱．踮脚运动的基本模型是杠杆，下列分析正确的是( )第3题图A. 脚后跟是支点，是省力杠杆B. 脚后跟是支点，是费力杠杆C. 脚掌与地面接触的地方是支点，是省力杠杆D. 脚掌与地面接触的地方是支点，是费力杠杆4. (2019雅安)如图所示，在轻质杠杆上吊一重物G，在一端施加一个始终与杠杆垂直的动力F，使杠杆缓慢地从OA转到OB，则在转动过程中 ( )第4题图A. F不变，杠杆是省力杠杆B. F变大，杠杆是省力杠杆C. F不变，杠杆是费力杠杆D. F变大，杠杆是费力杠杆5. (2019永川区指标到校)如图所示，将杠杆在水平位置调节至平衡后，两侧分别挂上相同规格的钩码，杠杆处于平衡状态．如果两侧各增加一个钩码，则会( )第5题图A. 仍然平衡B. 左端下降C. 右端下降D. 无法判断6. (2019聊城)如图所示，在“探究杠杆的平衡条件”实验中，已知杠杆上每个小格长度为2 cm ，当弹簧测力计在A 点斜向上拉(与水平方向成30°角)杠杆，使杠杆在水平位置平衡时，下列说法正确的是 ( )第6题图A. 动力臂为0.08 mB. 此时为省力杠杆C. 弹簧测力计的示数为4 ND. 钩码总重为2 N7. (2019南岸区二诊)如图所示是抽水马桶水箱进水自动控制的结构原理图，AOB 为一可绕固定点O 转动的轻质杠杆，已知OA ∶OB ＝1∶2，A 端所挂空心合金球质量为0.3 kg(ρ合金＝3.0×103 kg/m 3)，圆柱形容器底面积为100 cm 2.当合金球体积的13浸在水中，在B 端施加1 N 的竖直向下的拉力F 时，杠杆恰好在水平位置平衡．下列结果正确的是( )第7题图A. 该合金球的体积为1×10－4 m 3B. 该合金球空心部分的体积为1×10－4 m 3C. 该合金球浸入水中后，容器底部所受压强增加100 PaD. 该合金球排开水的重力为2 N二、填空作图题8. (2019贺州)如图所示是赛艇比赛，赛艇的桨是________杠杆，杠杆的平衡条件是________．第8题图9. (2019哈尔滨)如图所示，杠杆水平放置且自重忽略不计，O 是支点，左侧挂一重物，动力F 1大小为 3 N ，整个装置处于静止状态，则物体的重力为________N ，此时杠杆属于________杠杆(选填“省力”或“费力”)．第9题图10. (2019安徽)如图所示，将一把薄木尺的13长度用多层报纸紧密地覆盖在水平桌面上．已知报纸的上表面积为0.25 m 2，则大气对报纸上表面的压力为________N ；在木尺右端快速施加竖直向下的力F，要将报纸掀开，则力F至少为________N(假设报纸对木尺的压力全部作用在木尺的最左端，大气压取1.0×105 Pa，报纸和薄木尺的重力忽略不计)．第10题图11. (2019南岸区指标到校)如图所示是人们利用杠杆拉起吊桥的情景，其中O为支点，请在图中画出动力F的动力臂(用l表示)．第11题图12. (2019河池)如图是使用手机和自拍杆进行自拍时的示意图，将自拍杆看作一个杠杆，O 为支点，请在图中画出手机受到重力的示意图和F1的力臂l1.第12题图13. (2019铜仁)如图所示的杠杆中，O为支点，在一个最小的拉力F1的作用下，在图示位置保持静止，请在图中画出最小拉力F1的示意图和力F2的力臂L2.第13题图三、实验探究题14. 小明在探究杠杆的平衡条件的实验中，以杠杆中点为支点．第14题图(1)在调节杠杆平衡时，小明发现杠杆右端低左端高，此时应将杠杆右端的平衡螺母向________(选填“左”或“右”)调节，使它在________位置平衡．(2)如图甲所示，杠杆在水平位置平衡，记录数据．根据这一次实验数据，小明立即分析得出杠杆的平衡条件，小明这种做法的不足之处是：__________________________________________．(3)如图乙所示，小明设计了两种实验方案：第一种弹簧测力计沿竖直方向拉，其读数为F1；第二种弹簧测力计倾斜拉，其读数为F2.第______(选填“一”或“二”)种实验方案更为方便，理由是：___________．四、论述计算题15. (2019重庆一中一模)小渝同学体重为600 N，正方体M的边长为0.2 m，重为150 N.(1)当他站在水平地面上时，对地面的压强为1.5×104 Pa，求小渝双脚的面积是多少？(2)小渝同学用如图所示杠杆AB提升物体M，当物体M对地面的压强为0时，物体M没有离开地面，且杠杆保持水平位置平衡，已知OB＝3OA.求此时人对绳子的拉力？第15题图答案2. D 【解析】要把竹竿尽可能深地插入湖底淤泥，在其他条件相同的情况下，应使动力臂最大(渔民离支点的距离)，由图可知，D中动力臂最大，效果最好．故选D.3.C 【解析】踮脚运动的基本模型是杠杆，脚掌与地面接触的地方是支点，阻力即人的重力，作用点在脚掌中心，而动力在脚踝附近，动力臂大于阻力臂，是省力杠杆．故选C.4. B 【解析】杠杆缓慢由A到B的过程中，动力臂OA的长度没有变化，阻力G的大小没有变化，而阻力臂L却逐渐增大；由杠杆的平衡条件知：F·OA＝G·L，当OA、G不变时，L 越大，那么F越大，因此拉力F在这个过程中逐渐变大．并且动力臂始终大于阻力臂，这一过程中杠杆始终是省力杠杆．故选B.5.C 【解析】设一个钩码的重为G，一个小格的长度为L，则原来杠杆：3G×2L＝2G×3L，处于平衡状态，现在在两侧各增加一个钩码后，左边＝4G ×2L ，右边＝3G ×3L ，右边的力和力臂的乘积大，杠杆不再平衡，并且右端下降．故选C.6. D 【解析】OA ＝2 cm×4＝8 cm ＝0.08 m ，由于30°所对的直角边等于斜边的一半，所以动力臂l 1＝12OA ＝12×0.08 m ＝0.04 m ，A 错误；阻力臂l 2＝2 cm×3＝6 cm ＝0.06 m ＞l 1，所以为费力杠杆，B 错误；从图中可直接读出弹簧测力计的示数为3 N ，C 错误；由杠杆平衡条件得，钩码的总重G ＝F 2＝F 1l 1l 2＝3 N ×0.04 m 0.06 m＝2 N, D 正确．故选D. 7. C 【解析】根据杠杆平衡条件得F A ×OA ＝F B ×OB ，由F B ＝1 N ，OA ∶OB ＝1∶2，即：F A ×1＝1 N×2，解得：F A ＝2 N ；此时合金球受到竖直向上的拉力、竖直向上的浮力和竖直向下的重力，则合金所受的浮力F 浮＝G －F A ＝mg －F A ＝0.3 kg×10 N/kg－2 N ＝1 N ，此时合金球排开液体的体积V 排＝F 浮ρ水g ＝ 1 N 1×103 kg/m 3×10 N/kg＝1×10－4 m 3，故该合金球的体积V 球＝3×1×10－4 m 3＝3×10－4 m 3，故A 错误；合金球实心部分的体积V 实＝m 球ρ合金＝0.3 kg 3×103 kg/m 3＝1×10－4 m 3，故该合金球空心部分的体积V 空＝V 球－V 实＝3×10－4 m 3－1×10－4 m 3＝2×10－4 m 3，故B 错误；该合金球浸入水中，容器中液面升高的高度为Δh ＝V 排S 容＝1×10－4 m 3100×10－4 m 2＝1×10－2m ，则容器底部增加的压强Δp ＝ρ水g Δh ＝1×103 kg/m 3×10 N/kg ×1×10－2 m ＝100 Pa ，故C 正确；由阿基米德原理可知：该合金球排开水的重力G 排＝F 浮＝1 N ，故D 错误．故选C.8. 费力 F 1L 1＝F 2L 2 【解析】运动员在使用赛艇桨的过程中，动力臂小于阻力臂，属于费力杠杆；杠杆的平衡条件是：F 1L 1＝F 2L 2.9. 6 省力 【解析】由图可知动力臂是阻力臂的2倍，根据杠杆平衡条件F 1L 1＝F 2L 2，知动力是阻力的12，即阻力是动力的二倍，为 6 N ，而阻力的大小等于物体的重力，所以物体的重力为6 N ；动力臂大于阻力臂，所以此杠杆是省力杠杆．10. 2.5×104 1.25×104 【解析】大气对报纸上表面的压力为F上压＝pS ＝1.0×105 Pa ×0.25 m 2＝2.5×104 N ；要将报纸掀开，则薄木尺对报纸向上的力的大小就等于大气对报纸上表面向下的压力；设杠杆的总长度为L ，O 为支点，则根据杠杆平衡条件得：F ×23L ＝F 上压×1 3L，代入数值得F×23L＝2.5×104 N×13L，解得F＝1.25×104 N.11.如答图所示第11题答图12.如答图所示第12题答图13.如答图所示第13题答图14. (1)左水平(2)没有进行多次实验，结论不具有普遍性 (3)一便于测量力臂【解析】(1)在调节杠杆平衡时，若杠杆右端低左端高，要使杠杆在水平位置平衡，应将杠杆右端的平衡螺母向左调节；(2)根据仅有的一次实验数据总结实验结论是不合理的，因为一次实验具有偶然性，要多进行几次实验，使结论具有普遍性；(3)力臂等于支点到力的作用线的距离；当杠杆在水平位置平衡时，力的方向与杠杆垂直，力臂可以从杠杆标尺刻度上直接读出来；若弹簧测力计倾斜拉，力的方向与杠杆不垂直，力臂不能从杠杆标尺刻度上直接读出来；因此第一种实验方案更方便.15. 解：(1)S ＝F p ＝G p ＝600 N 1.5×104 Pa＝4×10－2 m 2 (2)M 对地面的压力为0时，杠杆B 点所受的拉力F 2＝G M ＝150 N ，根据杠杆平衡条件可知：F 1×OA ＝F 2×OB ，又由于OB ＝3OA ，所以F 1＝3F 2＝3×150 N＝450 N。

待定系数法求二次函数的解析式—知识讲解（基础）【学习目标】1. 能用待定系数法列方程组求二次函数的解析式；2. 经历探索由已知条件特点，灵活选择二次函数三种形式的过程，正确求出二次函数的解析式，二次函数三种形式是可以互相转化的．【要点梳理】要点一、用待定系数法求二次函数解析式 1.二次函数解析式常见有以下几种形式 ：(1)一般式：2y ax bx c =++(a ，b ，c 为常数，a ≠0)； (2)顶点式：2()y a x h k =-+(a ，h ，k 为常数，a ≠0)；(3)交点式：12()()y a x x x x =--(1x ，2x 为抛物线与x 轴交点的横坐标，a ≠0)． 2.确定二次函数解析式常用待定系数法，用待定系数法求二次函数解析式的步骤如下第一步，设：先设出二次函数的解析式，如2y ax bx c =++或2()y a x h k =-+，或12()()y a x x x x =--，其中a ≠0；第二步，代：根据题中所给条件，代入二次函数的解析式中，得到关于解析式中待定系数的方程(组)； 第三步，解：解此方程或方程组，求待定系数； 第四步，还原：将求出的待定系数还原到解析式中． 要点诠释：在设函数的解析式时，一定要根据题中所给条件选择合适的形式：①当已知抛物线上的三点坐标时，可设函数的解析式为2y ax bx c =++；②当已知抛物线的顶点坐标或对称轴或最大值、最小值时．可设函数的解析式为2()y a x h k =-+；③当已知抛物线与x 轴的两个交点(x 1，0)，(x 2，0)时，可设函数的解析式为12()()y a x x x x =--．【典型例题】类型一、用待定系数法求二次函数解析式1．已知二次函数的图象过（－1，－9）、（1，－3）和（3，－5）三点，求此二次函数的解析式. 【答案与解析】本题已知三点求解析式，可用一般式.设此二次函数的解析式为y=ax 2+bx+c(a ≠0)，由题意得：⎪⎩⎪⎨⎧-=++-=++-=+-53939c b a c b a c b a 解得⎪⎩⎪⎨⎧-==-=531c b a∴所求的二次函数的解析式为y=-x 2+3x-5.【总结升华】若给出抛物线上任意三点，通常可设一般式：y=ax 2+bx+c (a ≠0). 举一反三：【变式】（秋•岳池县期末）已知二次函数图象过点O （0，0）、A （1，3）、B （﹣2，6），求函数的解析式和对称轴．【答案与解析】解：设二次函数的解析式为y=ax 2+bx+c ，把O （0，0）、A （1，3）、B （﹣2，6）各点代入上式得解得，∴抛物线解析式为y=2x 2+x ； ∴抛物线的对称轴x=﹣=﹣=﹣．2．（•巴中模拟）已知抛物线的顶点坐标为M （1，﹣2），且经过点N （2，3），求此二次函数的解析式．【答案与解析】解：已知抛物线的顶点坐标为M （1，﹣2）， 设此二次函数的解析式为y=a （x ﹣1）2﹣2， 把点（2，3）代入解析式，得： a ﹣2=3，即a=5，∴此函数的解析式为y=5（x ﹣1）2﹣2． 【总结升华】本题已知顶点，可设顶点式. 举一反三：【变式】在直角坐标平面内，二次函数图象的顶点为(14)A -，，且过点(30)B ，.（1）求该二次函数的解析式；（2）将该二次函数图象向右平移几个单位，可使平移后所得图象经过坐标原点？并直接写出平移后所得图象与x 轴的另一个交点的坐标.【答案】（1）223y x x =--．（2）令0y =，得2230x x --=，解方程，得13x =，21x =-．∴二次函数图象与x 轴的两个交点坐标分别为(30)，和(10)-，． ∴二次函数图象向右平移1个单位后经过坐标原点．平移后所得图象与x 轴的另一个交点坐标为(40)，. 3．（•丹阳市校级模拟）抛物线的图象如图，则它的函数表达式是 ．当x时，y ＞0．【思路点拨】观察可知抛物线的图象经过（1，0），（3，0），（0，3），可设交点式用待定系数法得到二次函数的解析式．y ＞0时，求x 的取值范围，即求抛物线落在x 轴上方时所对应的x 的值． 【答案】y=x 2﹣4x +3．x ＜1，或x ＞3 【解析】解：观察可知抛物线的图象经过（1，0），（3，0），（0，3）， 由“交点式”，得抛物线解析式为y=a （x ﹣1）（x ﹣3）， 将（0，3）代入， 3=a （0﹣1）（0﹣3）， 解得a=1．故函数表达式为y=x 2﹣4x +3．由图可知当x ＜1，或x ＞3时，y ＞0．【总结升华】在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x 轴有两个交点时，可选择设其解析式为交点式来求解．类型二、用待定系数法解题4．已知抛物线经过(3，5)，A(4，0)，B(-2，0)，且与y 轴交于点C ．(1)求二次函数解析式； (2)求△ABC 的面积． 【答案与解析】(1)设抛物线解析式为(2)(4)y a x x =+-(a ≠0)，将(3，5)代入得5(32)(34)a =+-，∴ 1a =-．∴ (2)(4)y x x =-+-． 即228y x x =-++．(2)由(1)知C(0，8)， ∴ 1(42)8242ABC S =+⨯=△． 【总结升华】此题容易误将(3，5)当成抛物线顶点．将抛物线解析式设成顶点式．待定系数法求二次函数的解析式—巩固练习（基础）【巩固练习】一、选择题1. （•厦门校级模拟）已知一条抛物线经过E （0，10），F （2，2），G （4，2），H （3，1）四点，选择其中两点用待定系数法能求出抛物线解析式的为（ ） A ．E ，F B ．E ，G C ．E ，H D ．F ，G 2．二次函数225y x x =+-有( )A ．最小值-5B ．最大值-5C ．最小值-6D ．最大值-63．把抛物线y=3x 2先向上平移2个单位再向右平移3个单位，所得的抛物线是（ ）A . y=3(x －3)2+2B .y=3(x+3)2+2C .y=3(x －3)2－2D . y=3(x+3)2－24．如图所示，已知抛物线y ＝2x bx c ++的对称轴为x ＝2，点A ，B 均在抛物线上，且AB 与x 轴平行，其中点A 的坐标为(0，3)，则点B 的坐标为 ( )A.(2，3)B.(3，2)C.(3，3)D.(4，3)5．将函数2y x x =+的图象向右平移a(a ＞0)个单位，得到函数232y x x =-+的图象，则a 的值为( )A ．1B ．2C ．3D ．46．若二次函数2y ax bx c =++的x 与y 的部分对应值如下表：x -7 -6 -5 -4 -3 -2 Y-27-13-3353则当x ＝1时，y 的值为 ( )A ．5B ．-3C ．-13D ．-27二、填空题7．抛物线2y x bx c =-++的图象如图所示，则此抛物线的解析式为____ ____．第7题 第10题8．（•河南）已知A （0，3），B （2，3）是抛物线y=﹣x 2+bx +c 上两点，该抛物线的顶点坐标是 ．9．已知抛物线222y x x =-++．该抛物线的对称轴是________，顶点坐标________；10．如图所示已知二次函数2y x bx c =++的图象经过点（-1，0），（1，-2），当y 随x 的增大而增大时，x 的取值范围是____ ____．11．已知二次函数2y ax bx c =++ (a ≠0)中自变量x 和函数值y 的部分对应值如下表：x (3)2- -1 12- 0 12 1 32 … y…54- -294- -254- 074…则该二次函数的解析式为_____ ___．12．已知抛物线2y ax bx c =++的顶点坐标为(3，-2)，且与x 轴两交点间的距离为4，则抛物线的解析式为___ _____．三、解答题13．根据下列条件，分别求出对应的二次函数解析式． (1)已知抛物线的顶点是(1，2)，且过点(2，3)；(2)已知二次函数的图象经过(1，-1)，(0，1)，(-1，13)三点； (3)已知抛物线与x 轴交于点(1，0)，(3，0)，且图象过点(0，-3)．14．如图，已知直线y ＝-2x+2分别与x 轴、y 轴交于点A ，B ，以线段AB 为直角边在第一象限内作等腰直角三角形ABC ，∠BAC ＝90°，求过A 、B 、C 三点的抛物线的解析式．15．（•齐齐哈尔）如图，在平面直角坐标系中，正方形OABC 的边长为4，顶点A 、C 分别在x 轴、y 轴的正半轴，抛物线y=﹣x 2+bx+c 经过B 、C 两点，点D 为抛物线的顶点，连接AC 、BD 、CD ． （1）求此抛物线的解析式．（2）求此抛物线顶点D 的坐标和四边形ABCD 的面积．【答案与解析】 一、选择题 1.【答案】C ．【解析】∵F （2，2），G （4，2）， ∴F 和G 点为抛物线上的对称点， ∴抛物线的对称轴为直线x=3， ∴H （3，1）点为抛物线的顶点，设抛物线的解析式为y=a （x ﹣3）2+1， 把E （0，10）代入得9a +1=10，解得a=1， ∴抛物线的解析式为y=（x ﹣3）2+1．2.【答案】C ；【解析】首先将一般式通过配方化成顶点式，即2225216y x x x x =+-=++-2(1)6x =+-，∵ a ＝1＞0，∴ x ＝-1时，6y =-最小． 3.【答案】A ； 4.【答案】D ；【解析】∵ 点A ，B 均在抛物线上，且AB 与x 轴平行， ∴ 点A 与点B 关于对称轴x ＝2对称， 又∵ A(0，3)，∴ AB ＝4，y B ＝y A ＝3， ∴ 点B 的坐标为(4，3)． 5.【答案】B ；【解析】抛物线的平移可看成顶点坐标的平移，2y x x =+的顶点坐标是11,24⎛⎫-- ⎪⎝⎭，232y x x =-+的顶点坐标是31,24⎛⎫-⎪⎝⎭，∴ 移动的距离31222a ⎛⎫=--= ⎪⎝⎭．6.【答案】D ；【解析】此题如果先用待定系数法求出二次函数解析式，再将x ＝1代入求函数值，显然太繁，而由二次函数的对称性可迅速地解决此问题．观察表格中的函数值，可发现，当x ＝-4和x ＝-2时，函数值均为3，由此可知对称轴为x ＝-3，再由对称性可知x ＝1的函数值必和x ＝-7的函数值相等，而x ＝-7时y ＝-27．∴ x ＝1时，y ＝-27． 二、填空题7．【答案】223y x x =-++；【解析】由图象知抛物线与x 轴两交点为(3，0)，(-1，0)，则(1)(3)y x x =-+-． 8.【答案】（1，4）． 【解析】∵A （0，3），B （2，3）是抛物线y=﹣x 2+bx +c 上两点，∴代入得：，解得：b=2，c=3， ∴y=﹣x 2+2x +3 =﹣（x ﹣1）2+4， 顶点坐标为（1，4）， 故答案为：（1，4）． 9．【答案】(1)x ＝1；(1，3)；【解析】代入对称轴公式2b x a =-和顶点公式24,24b ac b aa ⎛⎫-- ⎪⎝⎭即可.10．【答案】12x ≥； 【解析】将(-1，0)，(1，-2)代入2y x bx c =++中得b ＝-1， ∴ 对称轴为12x =，在对称轴的右侧，即12x ≥时，y 随x 的增大而增大. 11．【答案】22y x x =+-；【解析】此题以表格的形式给出x 、y 的一些对应值．要认真分析表格中的每一对x 、y 值，从中选出较简单的三对x 、y 的值即为(-1，-2)，(0，-2)，(1，0)，再设一般式2y ax bx c =++， 用待定系数法求解．设二次函数解析式为2y ax bx c =++(a ≠0)，由表知2,2,0.a b c c a b c -+=-⎧⎪=-⎨⎪++=⎩ 解得1,1,2.a b c =⎧⎪=⎨⎪=-⎩∴ 二次函数解析式为22y x x =+-． 12．【答案】21(3)22y x =--； 【解析】由题意知抛物线过点(1，0)和(5，0)． 三、解答题13.【答案与解析】(1)∵ 顶点是(1，2)，∴ 设2(1)2y a x =-+(a ≠0)．又∵ 过点(2，3)，∴ 2(21)23a -+=，∴ a ＝1． ∴ 2(1)2y x =-+，即223y x x =-+． (2)设二次函数解析式为2y ax bx c =++(a ≠0)．由函数图象过三点(1，-1)，(0，1)，(-1，13)得1,1,13,a b c c a b c ++=-⎧⎪=⎨⎪-+=⎩ 解得5,7, 1.a b c =⎧⎪=-⎨⎪=⎩故所求的函数解析式为2571y x x =-+．(3)由抛物线与x 轴交于点(1，0)，(3，0)，∴ 设y ＝a(x-1)(x-3)(a ≠0)，又∵ 过点(0，-3)， ∴ a(0-1)(0-3)＝-3，∴ a ＝-1，∴ y ＝-(x-1)(x-3)，即243y x x =-+-．14.【答案与解析】过C 点作CD ⊥x 轴于D ．在y ＝-2x+2中，分别令y ＝0，x ＝0，得点A 的坐标为(1，0)，点B 的坐标为(0，2)． 由AB ＝AC ，∠BAC ＝90°，得△BAO ≌△ACD ， ∴ AD ＝OB ＝2，CD ＝AO ＝1， ∴ C 点的坐标为(3，1)．设所求抛物线的解析式为2(0)y ax bx c a =++≠，则有0,9312,a b c a b c c ++=⎧⎪++=⎨⎪=⎩，解得5,61762.a b c ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩，∴ 所求抛物线的解析式为2517266y x x =-+．（15.【答案与解析】 解：（1）由已知得：C （0，4），B （4，4），把B 与C 坐标代入y=﹣x 2+bx+c 得：，解得：b=2，c=4，则解析式为y=﹣x 2+2x+4；（2）∵y=﹣x 2+2x+4=﹣（x ﹣2）2+6，∴抛物线顶点坐标为（2，6），则S四边形ABDC=S△ABC+S△BCD=×4×4+×4×2=8+4=12．。

1．学校的占地面积约为3000（）。

A．平方分米B．平方厘米C．平方米2．一块橡皮的面积大约是（）。

A．4厘米B．4平方厘米C．4平方分米3．下面几件事情中，（）与周长有关。

A．给墙刷漆B．给照片加个边框C．给操场铺草坪4．如图所示，三边长度相等的三角形被分成两部分，其中图①和图②相比，表述正确的是（）。

A．图①比图②周长长B．图①比图②周长短C．图①比图②面积小D．图①和图②周长相等5．用两个同样的长方形分别拼成下面的形状，说法正确的是（）。

A．三个图形的周长都不相等，面积都相等B．③的面积最大C．①的周长最小6．图中每个小方格代表1平方厘米，那么阴影部分的面积是（）平方厘米。

A．18B．19C．20D．217．用20个面积为1平方厘米的小正方形拼成一个长方形，这个长方形的面积是（）平方厘米。

A．400B．24C．208．下面每个小方格表示1平方厘米，对下图描述正确的是（）。

A．周长和面积都相等B．周长相等，面积不相等C．周长不相等，面积相等二、填空题9．在（）里填上合适的单位。

一块橡皮擦的面积是4( )；一个篮球场的面积是420( )；一块黑板长4( )。

10．填写适当的单位名称。

餐桌的面积大约是100( )；莉莉的身高123( )；黑板的面积约4( )。

11．图中每个小正方形代表1平方厘米，涂色部分的面积是( )平方厘米，未涂色部分的面积是( )平方厘米。

12．图中每个□代表1平方厘米，写出每个图形的面积各是多少。

( )平方厘米( )平方厘米13．在实际生活中，面积接近1平方厘米的物体有( )（写一个），你正在做的这张试卷的面积大约13( )。

14．下图中每个小方格面积是1cm²，图中阴影部分面积是( )cm²。

三、连线题15．将面积相等的图形连一连。

16．连一连。

四、作图题17．把下面三个图形的面积用铅笔涂出来。

18．下面每个□代表1平方厘米。

在方格纸上，画出三个面积是8平方厘米的形状不同图形。

第七讲生活中的可能性前续知识点：一年级第一讲；XX模块第X讲后续知识点：X年级第X讲；XX模块第X讲阿瓜卡莉娅卡莉娅阿瓜把相应的人物换成红字标明的人物．把熊大玩偶换成一只普通熊玩偶即可．在任何情况下都会发生的事件，是“一定”会发生的事件；在任何情况下都不会发生的事件，是“不可能”发生的事件；在某种情况下会发生，而在其他情况下不会发生的事件，是“可能”发生的事件．【提示】“可能”跟“一定”有什么区别？判断：“一定”的画“√”，“不可能”的画“×”，“可能”的画“○”．世界上每天都有人出生．三天后下雨．太阳从西边升起．我从出生到现在，没吃过一点儿东西．吃饭时，人用左手拿筷子．地球每天都在转动．例题1哪个盒子里一定能摸到红球？哪个盒子里不可能摸到绿球？哪个盒子里可能摸到蓝球？A B C练习1【提示】图形的数量和摸到的可能性有什么关系？按要求涂一涂．例题3 看图回答问题．摸到什么颜色球的可能性最小？ 摸到什么颜色球的可能性最大？可能摸出 ：摸出的不可能是◆：例题2按要求涂一涂．摸出的一定是●：摸出的可能是▲：练习2【提示】球的数量和摸到的可能性有什么关系？ 在下图的扑克牌中摸一张．摸到哪种花色的牌的可能性最大呢？在可能性最大的花色下面的括号中画“√”．【提示】总挑不到他要的水果说明什么？ 小敏准备联欢会的抽奖箱，每张奖券上画着一个符号．有24张画❀的、13张画☆的和1张画☀的．请将相应奖项和奖券连线．一等奖 二等奖 三等奖❀ ☆☀水果篮里面装有多种水果，有雪梨、苹果和香瓜，数量分别是23个、17个和2个．小熊挑水果吃，它多次取出水果又放回，总挑不到它要的水果，你知道小熊要吃哪种水果吗？例题4♠ ♥ ♣ ♦（ ） （ ） （ ） （ ）练习3练习4数量越多，可能性越大；反之，数量越少，可能性越小．如果题目中没有告诉我们具体的数量，我们就要先进行计算，再比较数量多少，从而判断可能性大小．【提示】每种彩票分别剩下多少？例题5彩票站设有5个一等奖，10个二等奖，15个三等奖．丁丁购买时已经出现了2个一等奖，8个二等奖，9个三等奖，如果丁丁能够中奖，那么她中几等奖的可能性最大呢？例题6 从下面6个箱子里，分别摸出一个球，结果是哪个？用线连一连．不可能是绿色的球一定是蓝色的球不可能是蓝色的球蓝色的球可能性很小蓝色的球可能性很大【提示】逐一分析每个箱子，分别做判断即可．一天，阿凡提骑着毛驴，驮着和富人打赌赢来的一袋金币往回走，路上碰见了巴依老爷．巴依老爷听说阿凡提赢了一袋金币，就指挥他的仆人拦住了阿凡提，蛮不讲理地说：“阿凡提，如果你能做到我的一个要求，我就让你把金币带回家去．否则，你别想占便宜，拿了别人的金币就走!”阿凡提看了看巴依老爷，胸有成竹地说：“好吧，把你的要求说出来．”巴依老爷不怀好意地说：“阿凡提，你把袋子里的金币全部抛向空中，落地后金币朝上的要全部都是正面．不然的话，你就别想拿走金币，金币就要全部归我所有!”阿凡提想了想，说道：“好吧．”你知道阿凡提用了什么办法吗？阿凡提抛金币课外阅读作业1. 判断：“一定”的画“√”，“不可能”的画“×”，“可能”的画“○”．（1） 公鸡长期在水中生活．（ ） （2）花是香的．（ ）（3） 月球绕着地球转．（ ） （4） 公鸡下蛋．（ ） （5） 每个星期有7天．（ ）2. 按要求涂一涂．3. 盒子里面放了9只红色袜子，1只蓝色袜子，从中任取一只，摸到什么颜色袜子的可能性大？4. 超市举行幸运大抽奖活动，抽奖转盘如图，转到几等奖的可能性最大？摸出的可能是★：不可能摸出♡：5. 小伟去买彩票，一等奖有2个，二等奖有10个，三等奖有15个．小伟购买时已经出现了1个一等奖，2个二等奖，9个三等奖．小伟中几等奖的可能性最大？第七讲 生活中的可能性1. 例题1答案：B ；B 、C ；A 、C 详解：A 中有红球、蓝球和绿球，所以可能摸到3种颜色的球；B 中只有红球，所以一定摸到红球；C 中有红球、蓝球，没有绿球，所以可能摸到红球、蓝球，不可能摸到绿球． 2. 例题2答案：详解：摸出的可能是▲，则至少有一个▲即可（答案不唯一）；摸出的一定是●，则需要全部是●． 3.例题3答案：蓝；黄详解：第一个图中可以看出有4个红球、3个黄球和1个蓝球，数量越少摸到的可能性就越小，所以摸到蓝球的可能性最小；第二个图中可以看出有4个黄球、2个蓝球和2 个红球，数量越多摸到的可能性就越大，所以摸到黄球的可能性最大． 4.例题4答案：香瓜详解：三种水果中，香瓜的数量最少，被小熊抽到的可能性最小，小熊多次取出又放回，说明它想吃的水果抽到的可能性最小，所以小熊要吃香瓜． 5.例题5答案：三等奖 详解：丁丁购买时还剩下一等奖：523-=（个），二等奖：1082-=（个），三等奖：1596-=（个）．三等奖剩下的最多，所以中三等奖的可能性最大． 6.例题6 答案：7. 练习1答案：简答：根据常识进行判断即可．8. 练习2答案：世界上每天都有人出生． 三天后下雨． 太阳从西边升起． 我从出生到现在，没吃过一点儿东西． 吃饭时，人用左手拿筷子．地球每天都在转动． √ × ○√× ○不可能是绿色的球一定是蓝色的球不可能是蓝色的球蓝色的球可能性很小蓝色的球可能性很大简答：摸出的不可能是◆，则全部是◇即可；可能摸出●，则至少有一个●即可（答案不唯一）．9. 练习3答案：♠简答：♠有3张，♥有0张，♣有1张，♦有2张．所以摸到♠的可能性最大．10. 练习4答案：简答：三种奖券中，画☀的数量最少，则为一等奖，画❀的数量最多，则为三等奖，剩下的为二等奖．11. 作业1答案：（1）×；（2）○；（3）√；（4）×；（5）√简答：根据生活常识判断即可．12. 作业2答案：★ ☆ ☆ ☆ ☆ ☆ ☆ ☆ ☆ ☆♥ ♥ ♥ ♥ ♥ ♥ ♥简答：（1）摸出的可能是★，则只要有★且不全是★即可．（答案不唯一）（2）不可能摸出♡，则全部为♥即可．13. 作业3答案：红色简答：红色袜子有9只，蓝色袜子有1只，摸到红色袜子的可能性大．一等奖二等奖三等奖14.作业4答案：幸运简答：通过观察可以发现抽奖转盘中幸运奖占得地方比较大，所以抽中幸运奖的可能性最大．15.作业5答案：二简答：根据题意，一等奖剩下1个，二等奖剩下8个，三等奖剩下6个，二等奖剩下的最多，所以小伟中二等奖的可能性最大．。

第7讲一年级语文课外阅读专项练习3（含答案）一、阅读理解题1．课内阅读有时候,我觉得自己很大。

我自己穿衣服的时候,我自己系鞋带的时候,我觉得自己很大。

有时候,我觉得自己很小。

我够不到按钮的时候,我听到雷声喊妈妈的时候,我觉得自己很小。

（1）短文中出现了一对反义词是________和________。

（2）照样子填空。

穿衣服系鞋带________水果 ________玻璃（3）我会说________的时候,我觉得自己很大。

________的时候,我觉得自己很小。

【答案】（1）大；小（2）吃；擦（3）我帮妈妈做事；我不会写作业【考点】课文内容理解,大还是小【解析】【分析】本题关键要理解原句中的“很大”和“很小”的意思。

“很大”是指自己懂事时,自己能做事情时；“很小”是指很多事情自己还不能做好时。

2．读一读,做一做。

大萝卜,水盈盈,小白菜,绿盈盈,西红柿像灯笼,黄瓜一咬脆生生,多吃蔬菜身体好,壮壮实实少生病。

（1）儿歌中的整体认读音节有：。

（重复的只写一个）（2）连一连。

（3）请你再写出两种你爱吃的蔬菜。

________、 ________【答案】（1）yíng shì yi chī shí（2）（3）qié zi；qín cà【考点】儿歌【解析】3．读一读,完成练习。

傍晚,我在院里的地上画了一只青蛙,希望它跑到池塘。

早上,我走出屋一看：果然没有了!原来是雨水爷爷把它带走了。

（1）用“△”圈出逗号,用“○”圈出句号。

（2）是谁把青蛙带走了?用横线画出来。

【答案】（1）略（2）雨水爷爷【考点】语段阅读【解析】4．阅读下文,回答问题香蕉树妈妈,个子高又大,生下胖娃娃,长得像月牙,从小手拉手,兄弟不分家。

（1）香蕉树妈妈长什么样？（2）谁长得像月牙,从小手拉手？（3）读儿歌,“我”又认识了新的生字宝宝,“我”用线画出来了。

它的读音是（）A. xiānɡjiāoB. xiānɡjāo（4）这首儿歌写的是________,它的特点是________。

中考数学复习一元一次方程及分式方程【基础演练】1．(2013·滨州)把方程12x＝1变形为x＝2，其依据是() A．等式的性质1B．等式的性质2C．分式的基本性质D．不等式的性质1解析把方程12x＝1变形为x＝2，其依据是等式的性质2.答案B2．(2013·泰安)某电子元件厂准备生产4600个电子元件，甲车间独立生产了一半后，由于要尽快投入市场，乙车间也加入该电子元件的生产，若乙车间每天生产的电子元件是甲车间的1.3倍，结果用33天完成任务，问甲车间每天生产电子元件多少个？在这个问题中设甲车间每天生产电子元件x个，根据题意可得方程为()A.2300x＋23001.3x＝33 B.2300x＋2300x＋1.3x＝33C.2300x＋4600x＋1.3x＝33 D.4600x＋2300x＋1.3x＝33解析设甲车间每天能加工x个，则乙车间每天能加工1.3x个，根据题意可得：2300 x＋2300x＋1.3x＝33.答案B3．(2013·丽水)分式方程1x－2＝0的解是________．解析方程两边同乘以x，得1－2x＝0，解得x＝12.检验：当x＝12时，x＝12≠0，所以，原方程的解为x ＝12.答案x ＝124．(2012·宁波)分式方程x －2x ＋4＝12的解是________．解析方程的两边同乘2(x ＋4)，得2(x －2)＝x ＋4，2x －4＝x ＋4，解得x ＝8.检验：把x ＝8代入x ＋4＝12≠0.故原方程的解为x ＝8.答案x ＝85．(2013·绍兴)分式方程2xx －1＝3的解是________．解析方程两边同乘以x －1，得2x ＝3(x －1)，解得x ＝3.检验：当x ＝3时，x －1＝3－1＝2≠0，所以，原方程的解为x ＝3.答案x ＝36．(2013·滨州)解方程：3x ＋52＝2x －13.解去分母得：3(3x ＋5)＝2(2x －1)，去括号得：9x ＋15＝4x －2，移项合并得：5x ＝－17，解得：x ＝－175.7．(2010·台州)解方程：3x ＝2x －1.解方程两边同乘以x (x －1)，得3(x －1)＝2x ，解得x ＝3.经检验：x ＝3是原方程的解，所以原方程的解是x ＝3.8．(2010·义乌市)解分式方程：2x2＋1x＋2＝2x.解方程的两边同乘x＋2，得2x2＋1＝2x2＋4x，∴4x＝1，∴x＝1 4 .经检验，x＝14是原方程的解．9．(2012·北京)列方程或方程组解应用题：据林业专家分析，树叶在光合作用后产生的分泌物能够吸附空气中的一些悬浮颗粒物，具有滞尘净化空气的作用．已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少4毫克，若一年滞尘1000毫克所需的银杏树叶的片数与一年滞尘550毫克所需的国槐树叶的片数相同，求一片国槐树叶一年的平均滞尘量．解设一片国槐树叶一年的平均滞尘量为x毫克，则一片银杏树叶一年的平均滞尘量为(2x－4)毫克，由题意得：10002x－4＝550x，解得：x＝22.经检验：x＝22是所列方程的解．答：一片国槐树叶一年的平均滞尘量为22毫克．【能力提升】10．(2013·台湾)附表为服饰店贩卖的服饰与原价对照表．某日服饰店举办大拍卖，外套依原价打六折出售，衬衫和裤子依原价打八折出售，服饰共卖出200件，共得24000元．若外套卖出x件，则依题意可列出下列哪一个一元一次方程式？()服饰原价(元)外套250衬衫125裤子125A．0.6×250x＋0.8×125(200＋x)＝24000B．0.6×250x＋0.8×125(200－x)＝24000C．0.8×125x＋0.6×250(200＋x)＝24000D．0.8×125x＋0.6×250(200－x)＝24000解析若外套卖出x 件，则衬衫和裤子卖出(200－x )件，由题意得：0．6×250x ＋0.8×125(200－x )＝24000，答案B11．(2012·山西)图1是边长为30cm 的正方形纸板，裁掉阴影部分后将其折叠成如图2所示的长方体盒子，已知该长方体的宽是高的2倍，则它的体积是________cm 3.解析长方体的高为x cm ，然后表示出其宽为30－4x ，根据题意得：30－4x ＝2x ，解得：x ＝5.故长方体的宽为10cm ，长为20cm 则长方体的体积为5×10×20＝1000cm 3.答案100012．(2012·攀枝花)若分式方程：2＋1－kx x －2＝12－x有增根，则k ＝________.解析∵2＋1－kx x －2＝12－x，去分母得：2(x －2)＋1－kx ＝－1，整理得：(2－k )x ＝2，当2－k ＝0时，此方程无解，不符合题意．∵分式方程2＋1－kx x －2＝12－x 有增根，∴x －2＝0，2－x ＝0，解得：x ＝2，把x ＝2代入(2－k )x ＝2得：k ＝1.答案113．(2010·嘉兴)解方程：x x ＋1＋x ＋1x＝2.解设x x ＋1＝y ，则原方程化为y ＋1y ＝2.整理得，y 2－2y ＋1＝0，解之得，y ＝1.当y ＝1时，xx ＋1＝1，此方程无解．故原方程无解．14．(2010·义乌市)我市举办的“义博会”是国内第三大展会，从1995年以来已成功举办了15届．(1)1995年“义博会”成交金额为1.01亿元，1999年“义博会”成交金额为35.2亿元，求1999年的成交金额比1995年的增加了几倍？(结果精确到整数)(2)2000年“义博会”的成交金额与2009年的成交金额的总和是153.99亿元，且2009年的成交金额是2000年的3倍少0.25亿元，问2009年“义博会”的成交金额是否突破了百亿元大关？解(1)(35.2－1.01)÷1.01≈34.答：1999年的成交金额比1995年约增加了34倍；(2)设2000年成交金额为x 亿元，则2009年成交金额为(3x －0.25)亿元．由题意得x ＋3x －0.25＝153.99，解得x ＝38.56，∴3x －0.25＝115.43＞100，∴2009年“义博会”的成交金额突破了百亿元大关．。

第7讲方阵问题一、【知识要点】1、方阵问题：把若干人或物排列成正方形队列的形式，根据排列规律，引出的计算问题就叫做方阵问题2、方阵问题的特点是：方阵每边的实物数量相等，相邻两边的实物数量相差2，相邻两层的实物数量相差83、方阵问题的解题思路是：（1）实心方阵：每边数×每边数＝总数（每边数－1）×4＝每层数每层数÷4＋1＝每边数（2）空心方阵：大实心方阵－小实心方阵＝总数（每边数－层数）×层数×4＝总数二、【典型题解】例1：四年级同学举行广播操比赛，排成了8行8列。

如果去掉一行一列，要去掉几人？还剩多少人？针对练习11、同学们排队，要排成每行10人，共10行的方阵，共需要多少人？2、同学们排成十行十列的方阵，如果去掉一行一列，要去掉多少人？3、小明用棋子摆了一个实心方阵，后来他又加上15个棋子，使横竖各增加一排，成为一个大的实心方阵，原来的实心方阵每排有几个棋子？例2：菊花展上，园丁李师傅要摆一个正方形空心花坛，已知四边各摆5盆菊花，且四个角上都有一盆，请计算李师傅摆这个花坛共要用多少盆菊花？针对练习21、一个正方形池塘四周栽满了树，已知每边栽了9棵，并且四个角上都有一棵，这个池塘四周一共栽了多少棵树？2、学校的升旗台成正方形，在四周共放了40盆花，每个角放一盆，每边放花多少盆？3、沿一个正方形水池的四周栽树一行，四角都要栽1棵，共载树152棵。

问每边栽多少棵树？例3：某校180名学生，排成一个三层空心方阵，这个方阵外层每边有多少名学生？针对练习31、一个两层空心花盆阵，最外层每边放了10盆，一共用花多少盆？2、由24人组成两层中空方阵，现在外面增加2层，要增加多少人？3、一个三层的中空方阵，最内层共有80人，这个方阵共有多少人？例4：某班抽出一些学生参加节日活动表演，如果排成一个正方形实心方阵多7人，如果每行每列增加1人，就少4人，共抽出学生多少人？三、能力训练题：1、同学们站队，一共站了15行，如果要去掉2行2列，一共要去掉多少人？2、一些战士排成一个方阵，横竖各增加一人，就要增加11人。

第7讲 圆与扇形综合同步练习：1. 如图，已知正方形的面积为8平方厘米，求图中谷子形（阴影部分）的面积.（π取3.14）【答案】4.56【解析】设正方形的边长（或扇形的半径）为a ，则28=a ，再来求谷子形的面积，有多种求法：法1：谷子形的面积等于弓形面积的两倍，即：2211112=22 3.1488 4.564242π⎛⎫⎛⎫=⨯-=⨯⨯⨯-⨯= ⎪ ⎪⎝⎭⎝⎭谷子形弓形S S a a 平方厘米法2：谷子形等于正方形面积减去两个弯角，即：12828 3.148 4.564⎛⎫=-=-⨯-⨯⨯= ⎪⎝⎭谷子形正方形弯角S S S 平方厘米法3：谷子形等于两个直角扇形减去一个正方形，即：122 3.1488 4.564=-=⨯⨯⨯-=谷子形正方形扇形S S S 平方厘米.2. 如图，大正方形的面积是400平方厘米，则圆环的面积是 平方厘米．（π取3.14）【答案】157平方厘米．【解析】将小正方形转45°，如下图，可以看出大正方形的面积是小正方形面积的两倍，所以大圆面积是小圆面积的两倍．因为大正方形面积是400平方厘米，所以大圆面积为314平方厘米，小圆面积为157平方厘米，圆环面积为157平方厘米．3. 如下图所示，半圆1S 的面积是14.13平方厘米.圆2S 的面积是5198平方厘米，求阴影部分的面积.（π取3.14）【答案】5平方厘米【解析】设半圆1S 和圆2S 的半径分别是12,r r ，则22121514.13,1928ππ==r r ，可分别解得13=r 厘米，2 2.5=r 厘米，所以阴影部分长方形的长为225=r 厘米，宽为1222651-=-=r r 厘米，面积为515⨯=平方厘米.4. 如图，正方形的边长为3厘米，求阴影部分的周长.（π取3.14）【答案】9.28【解析】如下图，将各点标上字母，连接AE 、BE ，因为AE 、BE 、AB 都等于正方形的边长，因此△ABE 是正三角形，因此弧BE 、AE 所对的圆心角都是60°，阴影部分的周长等于弧AE 、弧BE 和线段AB 的和，为：122 3.14339.286⨯⨯⨯⨯+=厘米.5. 如图，已知圆环的面积是141.3平方厘米，那么阴影部分的面积是______平方厘米．(π取3.14)【答案】45【解析】设大圆半径为R ，小圆半径为r ，则圆环面积为()22141.3π-=R r 平方厘米，所以阴影部分面积为22141.3 3.1445-=÷=R r （平方厘米）．6. 如图，ABCD 是边长为10厘米的正方形，且AB 是半圆的直径，则阴影部分的面积是 平方厘米.（π取3.14）【答案】17.875．【解析】如图，两个阴影部分的面积相当于正方形面积—三角形DOC 的面积—半圆面积， 所以该面积=()101010104 3.14552217.875⨯-⨯÷-⨯⨯÷÷=（平方厘米）.7. 如图所示，曲线ACDB 和COD 是两个半圆，CD 平行于AB ，大半圆的半径是1米，那么阴影部分的面积是______．A ．12π- B ．3142π- C ．1 D ．2π【答案】A ．【解析】因为大半圆半径为1，所以大半圆的面积为2π， 14=+-阴影小半圆大圆等腰直角三角形S S S S ，即为111+-=4422πππ⨯-．8. 如右图，正方形的边长为5厘米，则图中阴影部分的面积是_____平方厘米，(π取3.14)【答案】7.125【解析】观察可知阴影部分是被以AD 为半径的扇形、以AB 为直径的半圆形和对角线BD 分割出来的，分头求各小块阴影部分面积明显不是很方便，我们发现如果能求出左下边空白部分的面积，就很容易求出阴影部分的面积了，我们再观察可以发现左下边空白部分的面积就等于三角形ABD 的面积减去扇形ADE 的面积，那么我们的思路就很清楚了． 因为45∠=︒ADB ， 所以扇形ADE 的面积为：224545π 3.1459.8125360360⨯⨯=⨯⨯=AD (平方厘米)， 那么左下边空白的面积为：1559.8125 2.68752⨯⨯-=(平方厘米)，又因为半圆面积为：215π9.812522⎛⎫⨯⨯= ⎪⎝⎭(平方厘米)，所以阴影部分面积为：9.8125 2.68757.125-=(平方厘米)．9. 如图，梯形ABCD 中的两个阴影部分的面积相等，DE =1cm ，∠A =∠B =45°，则CD = ______cm ．（其中π取3.14）【答案】0.57．【解析】由于两个阴影部分面积相等，可知扇形面积为梯形面积的一半，又知道扇形面积为221+=84ππ⨯⨯（11），所以梯形面积为2π，设CD 的长为x cm ，那么(11)122π+++⨯÷=x x ， 求得CD 的长为12π-=0.57cm ．C10. 三个半圆、两个圆如图摆放，两个小半圆和两个小圆的半径都是5厘米,大半圆外的阴影面积比大半圆内的阴影面积大______平方厘米.（π取3.14）【答案】78.5【解析】大半圆外的阴影面积和大半圆内的阴影面积都不好直接求，题目只要求计算它们的差，同时加上图中的所有空白部分，它们的差不变.大半圆外的阴影部分加上所有空白以后是两个小圆和两个小半圆，实际等于三个小半圆的面积，为23 3.145235.5⨯⨯=平方厘米；大半圆内的阴影部分加上所有空白以后是一个大半圆的面积，为213.14101572⨯⨯=平方厘米，它们的差为78.5平方厘米. 深化练习11. 如图，已知圆心是O ，半径9=r 厘米，1215∠=∠=︒，那么阴影部分的面积是______平方厘米．（π取3.14）【答案】42.39．【解析】因为圆的半径都相等，于是=OA OB ．在等腰三角形AOB 中两个底角都是15︒．又知道三角形内角之和是180︒，所以，三角形AOB 的顶角180(1515)150∠=︒-︒+︒=︒AOB ．同理150∠=︒AOC ，因此360(150150)60∠=︒-︒+︒=︒BOC ．这就是说，阴影部分扇形的面积是圆面积的16，即2211π 3.14942.3966⨯⨯≈⨯⨯=r （平方厘米）．12. 在下图中，AC 为圆O 的直径，三角形ABC 为等腰直角三角形，其中90∠=︒C ．以B 为圆心，BC 为半径作弧CD 交线段AB 于D 点．若AC =10cm ， 试求下图中阴影部分面积之和．(π取3)【答案】62.5cm 2．【解析】阴影部分面积为圆加扇形减三角形，阴影面积为：222115101062.582ππ⨯+⨯⨯-⨯=（cm 2）．13. 如图，圆中有四条弦，每一条弦都把圆分割成面积比为13∶的两个部分，而这些弦在圆正中正好围出一个正方形．已知这个正方形的面积为2100cm ，请问图中阴影部分的面积为多少2cm ？【答案】25cm 2．【解析】因每一条弦都把圆分割成面积比为13∶的两个部分，其中较小的部分是圆的14，四块加起来应该等于整个圆的面积，因此得知正方形面积为阴影部分面积的4倍，即阴影部分的面积为2100425(cm )÷=．14. 图中3=AB ，阴影部分的面积是______.【答案】4.5．【解析】图中有两种半径的圆弧，其中半径大的所对应的圆的面积是小的2倍，小半圆面积等于大的90°扇形的面积，可以得出下图两块小阴影面积之和等于大阴影的面积，所以原题阴影面积等于中间正方形的面积3×3÷2=4.5．15. 直线上并排放置着两个紧挨着的圆，它们的面积都等于1680平方厘米．阴影部分是夹在两圆及直线之间的部分．如果要在阴影部分内部放入一个尽可能大的圆，则这个圆的面积等于______平方厘米．【答案】105【解析】设小圆半径为r ，大圆半径为R ，则()()222-+=+R r R R r ， 4=R r ，所以大圆面积是小圆的16倍，所以小圆面积为105平方厘米．。

六年级第7讲线索及作用（含答案）x叙事线索“线索”是叙事性文艺作品中贯穿整个情节发展的脉络,它把作品中的各个事件联成一体,其表现形式可以是人物的活动、事件的发展或某一贯穿始终的事物,一部叙事作品通常都有一条或有一条以上的线索,但起主导作用的只有一条。

叙事线索及作用：线索：能把文章中表达的思想内容贯穿起来,组成一个整体,使文章条理清楚,文脉贯通。

题型一、指出文章的线索对策：1、了解叙事线索的几种类型：①人物线索（人物的见闻感受或事迹）②物品线索（某一有特殊意义的物品）③事件线索（中心事件）④时间线索⑤地点线索⑥感情线索（作者或作品中主要人物的思想感情变化）2、寻找线索的几种方法：①文章的标题②各段反复出现的事物③文中议论抒情的语句④作者的思想感情⑤某一人物的见闻感受题型二、说说叙事线索的作用对策：是贯穿全文的脉络,把文中的人物和事件有机的连在一起,使文章条理清楚,层次清晰。

安排线索应注意的问题：1.注意线索必须和所写的内容紧密相关,必须有利于情节的展开,必须有助于表达文章的中心思想。

2.线索一经确定,就要用它组织要表达的内容。

3.线索的安排还要做到首尾呼应,使全文上下一贯,结构严谨。

（一）珍珠项链（1）去鼓浪屿旅游,给母亲挑了一串珍珠项链。

淡粉色的,光泽很柔和,珠子大小也均匀,虽然比不上名贵的珍珠,但已经花去我一个月的工资。

母亲生日那天,很恭敬地送给了她。

（2）母亲很高兴,那天父亲在森林公园附近的一家酒店里订了房间,想让母亲高高兴兴地度过一个休闲周末。

母亲虽然嘴里说太浪费了但还是很高兴。

她戴上了那淡粉色的珍珠项链,穿了一件墨蓝色的领口和袖子上有镂空花纹的长裙。

然后一家人出去拍照,六十岁的母亲那天依然十分美丽。

（3）中午,我们在酒店的餐厅吃饭,母亲说要去一趟洗手间,谁知一去半天都没回来。

我和姐姐纳闷了,赶紧去找。

在洗手间门口,看见母亲在跟一个年轻的女孩说话,很客气的样子。

见我们来了,母亲对那女孩子说：我女儿来了,那么我们再见了！女孩微微地向母亲弯了弯腰,匆匆走了。

人教版数学四年级春季第七讲《小数的意义和性质下》知识点1、小数点的移动复习小绿，小棕，小紫三个小妖怪身高分别是2.35米23.5米和235米，它们三个谁更高?答案：小紫最高2.35米 23.5米 235米思考：这三个数组成数字都相同，但是什么不同?小数点的位置不同。

总结：小数点右移，小数变大；小数点左移，小数变小。

练习小数点的移动对于数的大小改变具体有什么影响呢？1小数点往左移动_1_位，小数变小2 小数点往右移动_1_位，小数变_大_。

3 小数点往左移动_2_位，小数变_小_。

思考：思考价签一般是精确到“分”的，怎么表示呢?10元=10.00元1元=_1.00元1角= 0.10元1分=_0.01元思考：(1)0.01→0.10，小数点右移1位，x10。

(2)0.10→1.00，小数点右移1位，x10。

(3)1.00→10.00，小数点右移1位，x10(4)0.01→1.00，小数点右移2位， x100总结：小数点向右移动一位，小数x10;小数点向右移动两位，小数x100;小数点向右移动三位，小数x1000……思考(1)10.00→1.00，小数点左移1位，÷10.(2)1.00→0.10小数点左移1位，÷10(3)0.10→0.01，小数点左移1位，÷10 .(4)1.00 →0.01，小数点左移2位，÷100总结：小数点向左移动一位，小数÷10小数点向左移动两位，小数÷100;小数点向左移动三位，小数÷1000……思考小高骑车的速度是3分钟骑1000米，那么按照同样的速度，那小高300分钟能骑多少米?小高骑了0.1米需要多少分钟?思考：单位换算。

(1) 1.9米=1900毫米;(2)0.5平方分米=0.005平方米。

分析 (1)1米=1000毫米;1.9米小数点向右移动3位变成1900毫米。

(2)1平方米=100平方分米0.5平方分米小数点向左移动2位变成0.005平方米小练习：小练习：判断对错1、3.76去掉小数点后所得的数是原来的100倍（）2、0.8平方米=80000平方厘米（）3、一个数先缩小到原来的一百分之一，再扩大到所得数的100倍，小数点位置没有变化; （）4 将最大的两位数缩小到它的十分之一是0.99。

第七讲不定方程前我们学习的方程一般都有唯一解，比如方程 3x 4 19只有一个解x 5，方程组x 2y 5只有一组解 2x 3y 8什么样的方程，解不唯一呢？举个简单的例子，二元一次方程唯一，因为每当y 取定一个数值时，x 就会有相应的取值和它对应，使方程成立，这样一来就会有无穷多组解.通常情况下，当未知数的个数大于方程个数时.，这个方程.(或 方程组).就会有无穷多个解.可是方程的解那么多， 究竟哪个才是正确的呢？应该说，如果不加任何额外的限制条件，这 无穷多个解都是正确的. 但在实际情况中，我们通常会限定方程的解必须是自然数， 这样一来，往往就只有少数几个解能符合要求，甚至在某些情况下所有的解都不对.x 2y 5的解就不求下列方程的自然数解:(1) x 2y 5 ;(2) 2x 3y 8 ;(4) 4x 5y20 .対刖•所以这杆的方程才 囚平处方程啊x+y=10陕。

一个右程龙么含右两个木 如数啊”这样的力稈论町好 多桦1方程个数小于未知数个数怖方 程如叫不罡方4T.不定方程，顾名思义就是“不确定”的方程，这里的不确定主要体现在方程的解上.之本讲我们要学习的就是这样的一类方程（或方程组） ：它们所含未知数的个数往往大于方程的个数， 而未知数本身又有一定的取值范围， 这个范围通常都是自然数——这 类方程就是“不定方程” ．形如 ax by c （ a 、b 、c 为正整数）的方程是二元一次不定方程的标准形式．解 这样的方程， 最基本的方法就是枚举． 那怎样才能枚举出方程的全部自然数解呢？我们 下面结合例题来进行讲解．例1．甲级铅笔 7角一支，乙级铅笔 3角一支，张明用 5元钱买这两种铅笔， 钱恰好花完． 请问：张明共买了多少支铅笔？「分析」设张明买了甲级铅笔 x 支，乙级铅笔y 支，可以列出不定方程：7x 3y 50, 其中x 和y 都是自然数.怎么求解呢？x 19 x 22 x 25 、、 y 4 y 2 y 0 的不定方程的自然数解时,我们可以先找出一组解,之后其余的所有解都可由这一组解的次变化 a 得到（注意变化的方向相反, 一个增加, 另一个就得减少, 才能保证 ax by 的 大小不变）练习 1、（1）求3x5y 35的所有自然数解；（2）求11x 12y160 的所有自然数解.般地,如果m是ax nby xmax byc 的一组解,那么yn这naam abbn abam bn c .另外,也是 ax by c 的一组解,理由相同.2x 这条性质有什么用呢？我们以求x 10一组自然数解x 10.应用上面的规律,y 10 然数）,所得结果仍然是x 25都是 2x 3y y0增加 2,所得结果也是 b（当n a 时）也是3y 50的自然数解为例, 2x 3y 50的一组解, 所以y 50的自然数解.另外x 每次减少2x 是2x 3y 50的自然数解.而且这样就已经求出了2x 是： 因 b . , （当 m b 时） a我们容易看出它有13 x 16 x 19 x 228 、 y 、 6 y 、 4 y 2 、 3（只要 x 还是自然数） ,y 每次 x 7x 4x 1、、也都y12 y 14 y16 3y 50的自然数解,所以50 的所有自然数解,它们3y x 每次增加3, y 每次减少2 （只要y 还是自x x 16 y6 ax by c （ a 、b 、c 为正整数） 7 x 10 x 13 、、 12 y 10 y 8x 值每次变化 b , y 值每例2．采购员去超市买鸡蛋．每个大盒里有23 个鸡蛋，每个小盒里有16 个鸡蛋．采购员要恰好买500 个鸡蛋，他一共要买多少盒？「分析」采购员要买多少个大盒，多少个小盒？大盒个数与小盒个数之间有什么联系？练习2、点心店里卖大、小两种蛋糕．一个大蛋糕恰好够7 个人吃，一个小蛋糕恰好够4 个人吃，现在有100 个人要吃蛋糕，应该准备大、小蛋糕各多少个才不浪费？如果每个大蛋糕10 元，每个小蛋糕7 元，那么至少要花多少钱？前面的两道例题只要求方程的解是自然数即可，但有的问题除了要求“解必须是自然数”外，还会有一些其它的约束．下面我们就来看几道这样例题．例3．甲、乙两个小队去植树．甲小队有一人植树12 棵，其余每人植树13 棵；乙小队有一人植树8 棵，其余每人植树10 棵．已知两小队植树棵数相等，且每小队植树的棵数都是四百多棵．问：甲、乙两小队共有多少人？「分析」不妨设甲小队有X人，乙小队有y人•由“两小队植树棵数相等”，你能列出一个关于x与y的不定方程吗？所列出来的不定方程又该如何求解？练习3、天气炎热，高思学校购置了大、小空调若干．每台大空调每天耗电38 度，每台小空调每天耗电13 度．已知所有大空调日耗电量之和恰好比所有小空调日耗电量之和少 1 度．请问：单位里最少购进了多少台空调？例4．将一根长为380厘米的合金铝管截成若干根长为36厘米和24 厘米两种型号的短管，加工损耗忽略不计．问：剩余部分最少是多少厘米？「分析」不妨设已经截出了x根长36厘米的管子和y根长24厘米的管子.合金铝管如果刚好能够被用完，方程应该怎么列？列出来的方程有自然数解吗？练习4、酒店里有500 升女儿红，李一白每次路过这里就打走35 升，杜二甫每次路过这里就打走21 升．那么若干天后，酒店剩余的女儿红最少是多少升？二元一次不定方程只要找到一组自然数解，就能利用方程系数有规律地写出所有自然数解•而含有更多未知数的不定方程又当如何求解呢?例5.我国古代数学家张丘建在《算经》一书中提出了“百鸡问题”：鸡翁一值钱五，鸡母一值钱三，鸡雏三值钱一.百钱买百鸡，问鸡翁、鸡母、鸡雏各几何？这个问题是说：每只公鸡价值5文钱，每只母鸡价值3文钱，每3只小鸡价值1文钱•要想用100文钱恰好买100只鸡，公鸡、母鸡和小鸡应该分别买多少只？「分析」题中有几个未知量？由这些未知量你能列出几个方程？:；《张丘建算经》■- 张丘建，北魏清河（今山东邢台市清河县）人，中国古代数学家，著有《张丘建算.经》.该书的体例为问答式，条理精密、文辞古雅，是中国古代数学史上少有的杰作.；；《张丘建算经》现传本有92问，比较突出的成就有最大公约数与最小公倍数的计算，:各种等差数列问题的解决，某些不定方程问题的求解. 百鸡问题就是其中一个著名的不定方程问题.- 张丘建所处的年代是中国古代的南北朝时期•尽管当时的中国战火连年，朝代更迭::频繁，且一直处于分裂状态，但数学发展的脚步依然没有停下•与《张丘建算经》同时代的算经还有《孙子算经》和《夏侯阳算经》，而与张丘建本人同时代的数学家还有大＞名鼎鼎的祖冲之.例6.卡莉娅到商店买糖，巧克力糖13元一包，奶糖17元一包，水果糖7.8元一包，酥糖10.4元一包，最后她共花了360元，且每种糖都买了•请问：卡莉娅买了多少包奶糖？「分析」题目中出现了四种糖果，我们不妨设巧克力糖、奶糖、水果糖和酥糖分别有x 包、y包、z包和w包，再由已知的单价、总价可以列出方程13x 17y 7.8z 10.4w 360 .这是一个四元一次方程，如果按通常的解法枚举出所有解，势必会有太多可能性需要讨论，过于繁琐•而且题目也没要我们求出所有解，只要我们求出奶糖的数量即可.那有没有办法不求其它糖果，只求奶糖的数量呢？练习6、求22x 26y 33z 65w 194的所有自然数解.气象学家Lorenz 提出一篇论文，名叫“一只蝴蝶拍一下翅膀会不会在德克萨斯州引起 龙卷风？”论述某系统如果初期条件差一点点，结果会很不稳定，他把这种现象戏称做「蝴 蝶效应」•就像我们投掷骰子两次，无论我们如何刻意去投掷，两次的物理现象和投出的点 数也不一定是相同的.Lorenz 为何要写这篇论文呢?这故事发生在1961年的某个冬天，他如往常一般在办公室操作气象电脑.平时，他只 需要将温度、湿度、压力等气象数据输入，电脑就会依据三个内建的微分方程式，计算出下 一刻可能的气象数据，因此模拟出气象变化图.这一天，Lorenz 想更进一步了解某段纪录的后续变化， 他把某时刻的气象数据重新输入电脑，让电脑计算出更多的后续结果•当时，电脑处理数据资料的数度不快，在结果出来之 前，足够他喝杯咖啡并和友人闲聊一阵•在一小时后，结果出来了，不过令他目瞪口呆•结 果和原资讯两相比较，初期数据还差不多，越到后期，数据差异就越大了，就像是不同的两 笔资讯.而问题并不出在电脑，问题是他输入的数据差了0.000127,而这些微的差异却造成天壤之别•所以长期的准确预测天气是不可能的.蝴蝶效应课 内 外堂作业5x 2 y 4z 601. （1）求5x 7y 31的所有自然数解；（2）求5x 2y 4z 60的所有自然数解．x 2 y z 362. 在一次植树节的活动中，参加活动的男生每个人种11 棵树，女生每个人种7棵树，最后所有人一共种了100棵树，那么参加活动的一共有多少人？3. 一张纸上写有25个1.21 和25个1.3．现在要划去其中的一些数，使留下来的数的总和为20.08，那么应划去多少个 1.3？4. 樱木同学特别喜欢吃包子，每天早上都到学一食堂买包子吃．（1）第一天早上，樱木同学花了6元买了一些冬菜包和豆香包，两种包子他都买了．已知冬菜包每个7 角，豆香包每个 5 角，那么樱木同学一共买了多少个包子？（2）第二天早上，樱木同学去学一食堂的路上遇到了晴子．于是樱木邀请晴子一起去吃包子．到学一食堂后，两人除了吃冬菜包和豆香包以外还点了几串羊肉串．已知羊肉串每串1 .2元，最后一共花了18元，所点包子与羊肉串数量总和是25．那么两人最多吃了多少串羊肉串？5. 甲、乙、丙三个班向希望工程捐赠图书．已知甲班有1 人捐6册，有2人各捐7册，其余都各捐11 册；乙班有 1 人捐6册，3人各捐8册，其余各捐 1 0册；丙班有2人各捐4册，6人各捐7册，其余各捐9册．已知甲班捐书总数比乙班多28册，乙班比丙班多101 册，且每个班捐赠的册数都在400与600之间．各班各有多少人？第七讲不定方程例题：例题1. 答案：14 或10详解：由于方程两边除以 3 的余数相同, 7x 3y x mod3 , 50 2 mod3 ,所以x除以3余2 .又因为7x 50，所以x是不超过7的自然数，只能取2或5.当x 2时，y 50 2 7 3 12 , x y 14；当x 5 时, y 50 5 7 3 5 , x y 10．所以张明共买了14支或10支铅笔．例题2. 答案：26详解：设买了大盒鸡蛋x盒，小盒鸡蛋y盒，则23x 16y 500 .考虑方程两边除以16 的余数，得：7x除以16的余数是4.首先要求7x是4的倍数，所以x是4的倍数，验证x 4、8、12、……发现满足7x除以16的余数是4的最小x值是12,相应的y的值是14,即x 12．由于12 16 且14 23,所以方程没有其它自然数解,采购员一共y 14买了12 14 26 盒鸡蛋．例题3. 答案：76详解：设甲、乙两小队分别有x人和y人.则两队植树棵数分别为13x 1棵和10y 2棵.由分析得：10y 13x 1 .将y 0、1、2、……代入方程验证x是否是自然数，可以求出方程的y值最小的一组自然数解y 4，此时每队的植树棵数均为38棵.x3方程的所有其他的自然数解都可以由进行若干次的“y值增加13且同时x值增加10”得到（也就是方程的其他所有自然数解是y 17, y 30, y 43,……），每次“ yx 13 x 23 x 33值增加13且同时x值增加10”意味着每队植树棵数增加130棵，38棵要变为四百多棵，意味着要增加 3 次，符合要求的自然数解是y 43.所以甲队有33 人，乙队有x 3343 人，两队共有33 43 76 人.例题4. 答案：8详解：设已经截出了x根长36厘米的管子和y根长24厘米的管子，那么被截出的管子一共长36x 24y厘米.由36,24 12，得：36x 24y一定是12的倍数.而380不是12 的倍数，所以36x 24y 380是没有自然数解的！管子不可能刚好被用尽，那么最少会剩下多少厘米呢？由于36x 24y —定是12的倍数，小于 380且能被12整除的最大自然数是372，而36x 24y 372的自然数解是存在的，如X 1，也就是截出1根长36厘米的管子和y 1414根长24厘米的管子，能够使得截出的管子总长度达到最大值 372厘米•所以剩余部分最少是380372 8厘米.x y z 100详解：设公鸡、母鸡和小鸡分别买了 x 只、y 只和z 只•依题意，得： 1•要5x 3y - z 100 3求这个方程的自然数解， 我们用“消元”的想法把它转化成二元一次不定方程求自然 数解的问题.我们选择“消去” z :将第二个方程乘以3,然后减去第一个方程， 得:例题6.答案：12详解：不妨设巧克力糖、奶糖、水果糖和酥糖分别有 x 包、y 包、z 包和w 包，则13x 17y 7.8z 10.4w 360 .把系数都化成整数，得：65x 85 y 39z 52w 1800 .由于我们只关心奶糖的数量，我们将未知数y 分为一组，其余未知数分为另一组：65x39z 52w85y1800 .也就是 13 5x 3z 4w 85y1800 .令 u 5x 3z 4w ，则13u 85y 1800 .它的自然数解只有U 60，所以阿奇共买了 12包奶糖.y 12x 0 x 4 x 8 x 12有自然数解是：y 25、 y 18、 y 11和 y 4 .所以我们有四种符合要求的买z 75z 78 z 81z 84x y 4z 值分别为75、78、81、84都是自然数，于是原不定方程的所鸡方案：公鸡 0只，母鸡25只，小鸡75只；公鸡4只，母鸡18只，小鸡78只；公例题5.答案：有四种符合要求的买鸡方案：公鸡 母鸡18只，小鸡78只；公鸡8只，母鸡 小鸡84只0只，母鸡25只，小鸡75只；公鸡4只, 11只，小鸡81只；公鸡12只，母鸡4只，14x 8y 200，即 7x 4y100，它的所有自然数解是x 0 x 4 x 8 、 、y25y 18y1112.它们对应的鸡8只，母鸡 11只，小鸡81只；公鸡12只，母鸡4只，小鸡84只.练习：1. 答案： ( 1 )有三组解： x 0 ； x 5；x 1010；(2)有一组解：x8y 7 y 4y1 y6简答： ( 1)考虑方程两边除以 3 的余数； ( 2) 考虑方程两边除以11 的余数2.答案：有四种购买方案： 1 2个大蛋糕， 4个小蛋糕； 8个大蛋糕， 11 个小蛋糕； 4个大 蛋糕， 18 个小蛋糕； 0 个大蛋糕， 25 个小蛋糕；第一个方案最省钱，只要花12 10 4 7 148 元 简答：求不定方程 7x 4y 100的自然数解即可.3. 答案： 4 台简答： 38x 13y 1 的最小自然数解为x 1， 最少需要大空调 1 台，小空调 3 台y34. 答案：3简答： 注意 35x 21y 是7的倍数.x7 x 6x 55. 答案： ( 1) 有三组解： y 1 、 y3 、 y5； (2) 1； 2； 6z2 x 1x简答： ( 1)消去 x 可解；( 2)求 x yz 9的正整数解即可.16x12y 1 0z 1006 x 015 ； y 140 z 83的余数；(2)消去未知数y ,转化成二元一次不定方程.2. 答案： 12x4x 4，所以参加活动的共有 4 8 12 人. y83. 答案： 17简答：设留下来的数中有 x 个 1.21 和 y 个 1.3，则 1.21x 1.3y 20.08.由于总和的百分作业：x x2 1. 答案：( 1 )x 2；( 2) yy3z 简答：( 1 )考虑方程两边除以简答：由 11x 7y 100 ，得：位是8，说明x 8或18.仅当x 8相应的y 是整数，求得y 8，所以应该划去25 8 17 个 1.3.4. 答案：( 1) 10；(2) 7x5简答：( 1)设买了冬菜包x 个，豆香包y 个.由7x 5y 60，得：x 5，所以樱木同y5x24x17x10学一共买了5 5 10个包子；( 2)由7x 5y 12z 180,得：y0、y5、y10 x y z 25135z z zx3或y 15 ，所以羊肉串最多有7 串. z75. 答案：甲51 ；乙53；丙49 简答：设甲、乙、丙三个班分别有x 人、y人、z 人，则由已知可得：20 11(x 3) 30 10(y 4) 28 11x 31 10y，即，所以可知x 是除以10 余 1 的数，y30 10(y 4) 50 9(z 8) 101 10y 89 9z是除以9余8的数.又因为每班捐书册数在400与600之间，所以x只能取51,此时才同时满足y是除以9余8的数，即为53,则z为49.x 1 x 4 x、、y 16 y 14 y 这就告诉我们,在求形如。

Ⅰ单句语法填空1．(2017·北京卷单项填空)Jane moved aimlessly down the tree-lined street, not knowing ____________she was heading.where解析：句意：Jane漫无目的地沿着绿树成荫的街道往前走，不知道要去哪里。

此处应用where引导宾语从句。

2．(2018·河北保定、唐山联考)I asked him ____________his father had done so that he became such a good person.what解析：句意：我问他他的父亲做了什么，使他成为一个如此好的人。

设空处引导宾语从句，作asked的宾语，从句中缺少had done的宾语，指“什么”，因此用what引导该从句。

3．(2018·福建安溪模拟)Success partially depends on ____________you have the patience to do simple things perfectly.whether解析：句意：成功部分取决于你是否有耐心把简单的事情做得完美。

设空处引导宾语从句，作介词on的宾语，意为“是否”，故填whether。

4．(2018·山东师大附中模拟)My first task was to decide where to go and ____________to get there.how解析：句意：我的第一项任务是决定去哪里及如何到达那里。

根据常识可知设空处表示“如何”，故填how。

5．(2018·山东泰安期中)Students can choose __________they want to do and register online.what/whatever解析：句意：学生们可以选择他们想做的(任何)事情并在网上注册。

第七讲简单机械——机械效率[知识新授]一有用功使用机械做功时，对人们有用的功叫有用功，用W有用表示。

也就是人们不用机械而直接用手时必须做的功，也等于在理想情况下(即不考虑摩擦和机械本身的重力)人们所做的功，或者是机械对物体做的功。

在提升物体时，W有用＝；在水平拉动物体时，W有用＝。

二额外功使用机械时，对人们没有用但又不得不做的功叫额外功，用W额表示。

额外功的来源主要有：①提升物体时，克服机械自重、容器重、绳重等所做的功；②克服机械的摩擦所做的功。

三总功人们在使用机械做功的过程中实际所做的功叫总功，用W总表示。

它等于有用功和额外功的总和，即W总＝W有用＋W额，或人对机械的动力为F，则W总＝Fs。

四机械效率①定义：有用功与总功的比值叫做机械效率。

②公式：η＝由于总是存在额外功，使得W有用＜W总，所以η总是1；影响机械效率的主要因素有摩擦和机械自重等。

五探究定滑轮，动滑轮，滑轮组，斜面，杠杆的机械效率表达式（标注出重要物理量）机械效率分析W有用W额外W总η提升η的方法[经典例题][例1]从井中提水时，常常会发生吊水桶落入井里的事情．用物理知识分析下列说法，其中错误的是（）A．用吊水桶向上提水，人对桶和水做的功都是有用功B．用吊水桶向上提水，人对桶做的功是额外功C．吊水桶掉在井里，打捞水桶时桶里会带些水，这时人对水做的功是额外功D．吊水桶掉在井里，打捞水桶时，人对桶做的功是有用功[例2]利用如图所示的滑轮，在粗糙水平面上匀速拉动物体，下列叙述正确的是（）A．克服物体重力做的功是有用功B．克服物体受地面摩擦力做的功是有用功C．绳子自由端的拉力F做的功是有用功D．克服物体受地面摩擦力做的功是额外功[例3]如图，已知斜面倾角为30°，斜面高2m．小明沿斜面将重为400N的货物由底端匀速拉到顶端，用时10s．已知拉力大小为300N，绳重不计，则下列说法中正确的是（）A．小明对货物做的有用功是1200JB．小明对绳的拉力的功率是80WC．斜面的机械效率是66.7%D．物体受到斜面的摩擦力是90N[例4]如图所示，把一个重400N的物体沿竖直方向上在10s内匀速提升了2m，所用拉力F为140N，不计摩擦和绳重．则下列计算结果错误的是（）A．动滑轮重20NB．拉力F做功840JC．拉力F做功的功率为84WD．此滑轮组机械效率为80%[例5]用如图所示的滑轮组拉动水平地面上重1000N的物体A，使物体A在4s内匀速前进了4m，物体A受到地面的摩擦力f=300N，所用拉力F=120N，忽略绳重、滑轮重及绳与滑轮间的摩擦．下列说法中正确的是（）A．绳子自由端在4s内移动了8mB．物体A重力做功的功率为1000WC．物体A克服摩擦力做的功为480JD ．滑轮组的机械效率约为83.3%[例6]如图所示，小明测量动滑轮的机械效率，他用弹簧测力计拉动绳子的自由端，将质量为500g 的重物从A 位置沿竖直方向匀速提升到A′位置，弹簧测力计的示数如图乙所示，在这个过程中，该动滑轮的额外功和机械效率分别是（ ）A ．0.14J 78%B ．0.5J 78%C ．0.14J 81%D ．0.12J 81%[例7]在“探究影响滑轮组机械效率的因素”实验中，某实验小组用如图所示的同一滑轮组提升不同钩码的方法，分别做了甲、乙、丙3组实验，实验数据记录如下： 次数 钩码重/N动滑轮重/N钩码上升 的距离/cm弹簧测力计 的示数/N弹簧测力计 上升的距离/cm机械效率 1 2 0.8 5 1 15 66.7% 2 4 0.8 5 1.7 15 \ 360.85\1583.3%（1）在实验操作中应该使钩码 （选填“快速”或“缓慢”）上升；（2）进行第2次测量时滑轮组的机械效率约为 （保留三位有效数字）；（3）进行第3次测量时，弹簧测力计示数为 N ，滑轮组做的有用功是 J ；（4）分析实验数据，实验小组得出的实验结论是：滑轮组的机械效率与 有关； （5）分析表中数据可知，F≠3G G +动，可能的原因是： ；（6）某次实验时将绳子自由端匀速拉动时弹簧测力计的读数记为F ，钩码重记为G ，动滑轮重记为G’，绳自由端移动距离记为s ，钩码提升高度记为h ，不计绳子重及摩擦．则下列关于滑轮组机械效率的计算关系中错误的是 ．A ．η=s F h G B ．η=F G C ．η=GG G'+ D ．η=1﹣s F h G [例8]甲乙两位同学合作完成“测滑轮组的机械效率”，装置如图，现已测得所挂物体重为G ，动滑轮重为G 1，于是甲同学认为操作可以结束了，可令重物上升h 米，可以计算出滑轮组的机械效率为η=h G Gh h G 1+×100%=1G G G+×100%．乙同学认为这样不妥，他认为还是要用弹簧测力计匀速竖直地拉动绳子的自由端，并读出弹簧测力计的示数，记为F ，然后根据公式η=s F h G ×100%=F3h h G ×100%=3FG×100%． ①你认为 （选填：甲或乙）操作合理．②操作欠妥的一次，测得机械效率偏 （选填：大或小） ③引起误差的原因 ．[例9]在“测定动滑轮机械效率”的实验中，小明用如图所示的动滑轮提升钩码，改变钩码的数量，正确操作，实验数据如表： 实验序号 钩码重 钩码上升高度h/cm拉力F/N 绳端移动的距离s/cm一 1.0 20.0 0.7 40.0 二2.020.01.240.0三 3.0 20.0 1.7 40.0（1）实验时，用手 拉动弹簧测力计，使持在动滑轮下的钩码缓缓上升． （2）第一次实验时测得动滑轮的机械效率为 ．（百分号前保留一位小数） （3）第三次实验时，钩码上升的速度为0.1m/s ，则拉力的功率为 W ．（4）由表中实验数据分析可知，同一动滑轮，所提升物重增大，机械效率将 （选填“增大”、“减小”或“不变”）．[例10]如图所示，重350N 的物体在100N 的拉力作用下10秒钟上升30cm ，若不计摩擦和绳子重，求：（1）物体上升速度； （2）拉力的功率；（3）若物体再增加100N ，滑轮组的机械效率为多大．[例11]工人用平行于斜面向上的500N的推力将重800N的物体匀速推上高1.5m的车厢，所用的斜面长是3m．求：（1）推力做的功；（2）斜面的机械效率；（3）斜面对物体的摩擦力．[例12]如图所示，某工人用平行于斜面的力F将重为G的木箱匀速拉上斜边长为S、高为h的斜面，斜面的倾角为θ．（1）请推导，若不计摩擦：F=G•sinθ（2）实际的斜面存在摩擦，若木箱质量为100kg，所用拉力为400N，斜面长为5m，高为1.6m，则斜面的机械效率为多少？木箱所受摩擦力的大小为多少？[课后作业]1．一个滑轮组经改装后提高了机械效率，用它把同一物体匀速提升同样的高度，改进后与改进前相比较（）A．总功减少，额外功增多B．机械效率提高，机械做功加快C．功率变大，机械做功更多D．有用功不变，总功减少2．如图所示，用一个重为4N的动滑轮来提升物体，若在实际工作中竖直向上的拉力为5N，则动滑轮的机械效率η（）A．一定小于40%B．一定小于60%C．40%＜η＜60%D．60%＜η＜100%3．用一个定滑轮和一个动滑轮组成的滑轮组把重150N的物体匀速提升1m，不计摩擦和绳重，滑轮组的机械效率为60%．则下列选项中错误的是（）A．有用功一定是150J B．拉力大小一定是125NC．总功一定是250J D．动滑轮重一定是100N4．一个重为G的物体分别沿如图所示的左右两个斜面，被推上同一个平台，如果沿两个斜面推动物体时所受摩擦力一样大，那么两个斜面相比（）A．用左斜面省力少，机械效率比右高B．用右斜面省力多，机械效率比左高C．两个斜面做的有用功一样，效率也一样D．条件不足，无法判断5．如图所示是建筑工地上的塔式起重机，它通过电动机带动滑轮组吊起重物．滑轮组在10s内把6×103N的重物匀速提升10m，绳索自由端的拉力是2.1×103N．不计一切摩擦和绳重，下列说法中错误的是（）A．拉力做的功是6.3×104JB．绳索自由端的速度是3m/sC．该滑轮组的动滑轮重300ND．该滑轮组的机械效率是80%6．如图所示，有一斜面长为L，高为h，现用力F沿斜面把物重为G的物体从底端匀速拉到顶端．已知物体受到斜面的摩擦力为f，则下列关于斜面机械效率η的表达式正确的是（）A ．η=Lf h G hG +×100%B ．η=L f F hG ）（-×100%C ．η=L f F hG ）（+×100%D ．η=Lf hG ×100%7．如图甲是小红“测量滑轮组的机械效率”的实验装置．（1）实验时小红沿竖直方向 拉动弹簧测力计，使钩码上升10cm ，弹簧测力计的示数如图甲所示，其拉力为 N ，若每个钩码重2N ，则滑轮组的机械效率为 ． （2）小红做完实验，通过和其他小组交流，了解到滑轮组的机械效率η与动滑轮重G 动有关系，接在她改变动滑轮重，提升同一物体进行多次实验，获得数据丙绘制出如图乙的图象．由图象可知：被提升物体所受的重力相同时，动滑轮越重，滑轮组的机械效率越 ．8．斜面的机械效率与斜面的哪些因素有关呢？小刚猜想：斜面的机械效率可能跟斜面的粗糙程度、斜面的倾斜程度有关．他将一木板的一端垫高，构成长度一定、高度可调的斜面，用弹簧测力计拉着同一块木块沿不同的斜面匀速向上运动．下表是他们实验记录的有关数据： 次数斜面 倾角 斜面材料物重G/N斜面高度h/m沿斜面拉力F/N斜面长s/m有用功W 有/J总功W 总/J机械效率η1 30° 木板 7 0.5 6.0 12 30° 毛巾 7 0.5 6.5 1 3.5 6.5 53.8% 320°木板70.344.912.384.948.6%（1）请将第1次实验表格的空补充完整．（2）在第2次实验中，木块与斜面的摩擦力为 N ．（3）分析第1、2次实验数据，可以得出：当其他条件一定时， 斜面机械效率越低．（4）分析第1、3次实验数据，可以得出：斜面材料相同时，斜面倾角越大，斜面的机械效率越，斜面在生活中有着广泛的应用，例如．9．工人用图所示的滑轮组运送建材上楼，每次运送量不定，滑轮组的机械效率随建材重量变化的图象如图乙，机械中摩擦力及绳重忽略不计，g=10N/kg．（1）从图乙中看出，建材重400N时，滑轮组的机械效率为50%，则动滑轮重为多少？（2）若工人在1min内将建材匀速竖直向上提升了12m，作用在钢绳上的拉力为300N，求拉力的功率；（3）当滑轮组的机械效率为60%时，运送建材的重力是多大？10．某同学在探究滑轮组的机械效率与被提升物体重力的关系时，采用了如图甲所示的滑轮组，每个滑轮等重．不计绳重和摩擦，物体重G从200N开始逐渐增加，直到绳子被拉断．每次均匀速拉动绳子将物体提升同样的高度．图乙记录了在此过程中滑轮组的机械效率随物体重力的增加而变化的图象．请根据图象回答：（1）每个滑轮重为多少N？（2）当物重多少N时，滑轮组的机械效率可达到75%．11．钱老师在“探究斜面的额外功（W额外）与斜面的水平长度（L）是否有关”的实验中，如图所示，将弹簧测力计将重力G=5.0N的物块从长度S=0.50m的木板搭成一个斜面底端匀速拉至斜面顶端．（1）钱老师在实验中，调整斜面的高度为h=0.20m，将物块从斜面底端匀速拉至顶端的过程中，弹簧测力计的示数F=4.0N，则有用功为J，机械效率为．（2）将物块从斜面底端匀速拉至斜面顶端的过程中，额外功W额外与斜面的水平长度L（木板在水平面上的正投影长度﹣工具所限，测量的为近似值）有如下关系：L（m）0.45 0.40 0.35 0.30W额外（J）0.90 0.80 0.70 0.60通过数据分析，钱老师得出初步结论：．钱老师查阅资料后证实此结论是正确的．根据此结论，当斜面的水平长度L=0.40m时，斜面的机械效率为；（保留一位小数）（3）当木板平放在水平桌面上，水平匀速拉动木板上的物块时，弹簧测力计的示数约为N．在上述实验过程中，A木块除了能长木板搭组成一个斜面之外，它的主要作用是．[参考答案][经典例题]1．A．2．B．3．C．4．D．5．D．6．A．7．（1）缓慢；（2）78.4%；（3）2.4；0.3；（4）被提升物体的重力；（5）拉动过程中需克服滑轮的转轴处的摩擦；（6）BD．8．①乙；②大；③没有考虑绳重和摩擦．9．（1）竖直向上匀速；（2）71.4%；（3）0.34；（4）增大．10．（1）物体上升速度为0.03m/s；（2）拉力的功率为12W；（3）若物体再增加100N，滑轮组的机械效率为90%．11．（1）推力做的功为1500J；（2）斜面的机械效率为80%；（3）斜面对物体的摩擦力为100N．12．（1）若不计摩擦，拉力做的功等于克服物体重力所做的功，即Fs=Gh，则F==G=G•sinθ．（2）斜面的机械效率为80%，木箱所受摩擦力为80N．[课后作业]1．D．2．B．3．B．4．A．5．D6．A．7．（1）匀速；2.4；83.3%；（2）低．8．（1）3.5；6.0；58.3%；（2）3；（3）斜面越粗糙；（4）高；盘山公路．9．（1）动滑轮重为400N；（2）拉力的功率为120W；（3）当滑轮组的机械效率为60%时，运送建材的重力是600N．10．（1）每个滑轮重为100N；（2）当物重为600N时，滑轮组的机械效率可达到75%．11．（1）1；50%；（2）斜面的长不变时，斜面的额外功与斜面的水平长度成正比；65.2%；（3）2；调节斜面的水平长度．6。

第7讲力的概念重力7.1 学习提要7.1.1 力的概念1. 力的定义力是物体对物体的作用。

例如：用手压篮球时，球会凹进去，手对球有力的作用；人推着自行车前进，人对车有力的作用。

2. 力的作用效果（1）力可以使受力的物体发生形变。

如手捏面团，面团变形等。

（2）力可以改变受力物体运动的速度大小或方向。

例如：足球守门员用力将球扑出去时，足球受到守门员力的作用，其运动方向发生了改变。

3. 力的三个属性（1）力的物质性：力是施力物体对受力物体的作用，任何力都不能离开物体而单独存在。

（2）力的相互性：力是两个物体间的相互作用，受力物体在受到施力物体作用的同时，必然会给施力物体一个反作用。

施力物体和受力物体是相对而言的，施力物体同时也是受力物体。

物体间的相互作用力，即作用力与反作用力是一对同时产生、同时消失、大小相等、方向相反的力，且力的性质也相同。

（3）力的方向性：力是有方向的，比较两个力是否相同，不但要比较他们的大小，还需要比较他们的方向是否一致。

4. 力的单位力的符号是F。

在国际单位制（SI）中，力的单位是牛顿，简称牛，用N表示。

5. 力的三要素及图示法力对物体产生的作用效果与力的大小、方向和作用点有关。

因此通常我们把力的大小、方向、作用点就叫做力的三要素。

用一根带箭头的比例线段可以把力的三要素表示出来：箭头的指向表示力的方向，比例线段的长短表示力的大小，线段的起点表示力的作用点。

这就是力的图示法。

例如：用3N 的水平拉力F向右拉A物体，则力F可用图7-1的图示法表示。

此外，还有一种表示力的方法，叫做力的示意图，它只表示出力的方向和作用点，不严格表示力的大小。

6. 力的测量测量力的仪器叫做测力计，常用的测力计是弹簧测力计，如图7-2所示。

该测力计的测量范围是0~5牛，最小分度是0.2牛，使用前要观察指针是否与零刻线对齐，并进行调零，弹簧测力计是利用弹簧的伸长量与弹簧受到的拉力的大小成正比的原理制成的。

使用弹簧测力计测力时，不能超出弹簧测力计的测量范围。

第7讲盈亏问题2有记载《九章算术》于公元前1世纪成书，是中国最重要的数学经典，也是世界古代数学史上一颗璀璨的明珠。

这一讲，我们将讨论复杂一些的盈亏问题。

例1友爱中心小学师生乘车到公园春游，如果每车坐65人，则有15人不能乘上车;如果每车坐70人，恰好可以少用一辆汽车。

问一共有几辆汽车? 有多少人去春游?解(15+70)÷(70-65)=17(辆);70×(17-1)=1120(人)。

答:一共有17辆汽车,有1120人去春游。

【思路点拨】第一种分配方案:“每车坐65人，多15人”，而第二种分配方案只告诉“每车坐70人，恰好少用一辆汽车”，分配的结果究竟是盈数还是亏数呢?可以这样想:每车坐70人，恰好少用一辆汽车，而这辆车还可以坐70人。

这辆车按原定计划开到公园总人数就少70人，也就是可以将这个数看作“亏”。

也就是每辆车坐70人，总人数少70人，把第二种分配方案转化为盈亏问题的一般情形。

例2少先队员去植树，如果每人挖5个树坑还有3个树坑没人挖;如果其中2人各挖4个树坑，其余的人每人各挖6个树坑，就恰好挖完所有树坑。

一共要挖多少个树坑?解 [3+(6-4)x2]÷(6-5)=7(人);5x7+3=38(个)。

答:少先队员一共要挖38个树坑。

【思路点拨】这道题与例1比较相似，关键是要把第二种分配方案转化成盈亏问题的一般情形。

转化第二种分配方案是这道题的关键。

可这样想:第二种方案中挖4个树坑的2人，也各挖6个，这样每人就多挖2个，共多挖4个，结果就会多挖4个树坑。

第二种分配方案就转化为:每人挖6个，总数就少4个树坑。

这样就可以用盈亏问题的方法求出一共挖多少个树坑。

例3一些学生搬一批砖，如果每人搬4块，其中5人要搬两次;如果每人搬5块，就有两人没有砖可搬。

搬砖的学生有多少人?这批砖一共有多少块?解(4x5+5x2)÷(5-4)=30(人);4x30+4x5=140(块)。