周炳琨激光原理答案第七章习题

第七章 激光特性的控制与改善习题1．有一平凹氦氖激光器，腔长0.5m ，凹镜曲率半径为2m ，现欲用小孔光阑选出TEM 00模，试求光阑放于紧靠平面镜和紧靠凹面镜处的两种情况下小孔直径各为多少？(对于氦氖激光器，当小孔光阑的直径约等于基模半径的3.3倍时，可选出基模。

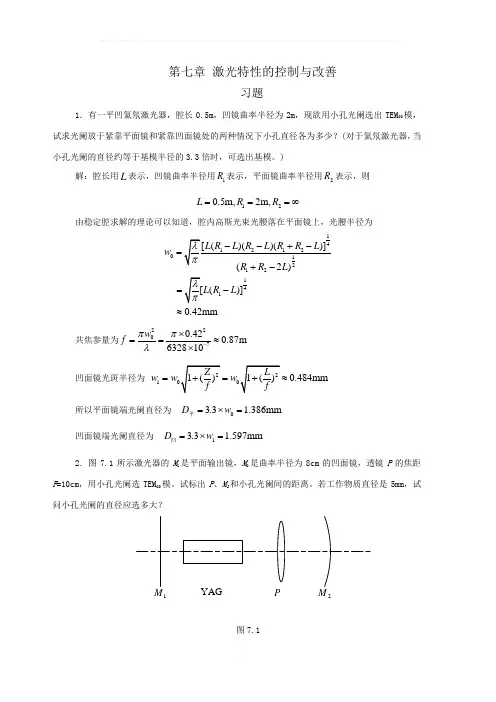
)解：腔长用L 表示，凹镜曲率半径用1R 表示，平面镜曲率半径用2R 表示，则120.5m,2m,L R R ===∞由稳定腔求解的理论可以知道，腔内高斯光束光腰落在平面镜上，光腰半径为012141 ()] 0.42mmw L R L ==-≈共焦参量为22070.420.87m 632810w f ππλ-⨯==≈⨯ 凹面镜光斑半径为10.484mm w w w ==≈ 所以平面镜端光阑直径为 03.3 1.386mm D w =⨯=平 凹面镜端光阑直径为 13.3 1.597mm D w =⨯=凹2．图7.1所示激光器的M 1是平面输出镜，M 2是曲率半径为8cm 的凹面镜，透镜P 的焦距F =10cm ，用小孔光阑选TEM 00模。

试标出P 、M 2和小孔光阑间的距离。

若工作物质直径是5mm ，试问小孔光阑的直径应选多大？图7.112解：如下图所示：12P小孔光阑的直径为：31.061010022mm 0.027mm 2.5f d a λππ-⨯⨯==⨯≈⨯其中的a 为工作物质的半径。

3．激光工作物质是钕玻璃，其荧光线宽F ν∆=24.0nm ，折射率η=1.50，能用短腔选单纵模吗？解：谐振腔纵模间隔222q q c LLνηλλη∆=∆=所以若能用短腔选单纵模，则最大腔长应该为215.6μm 2L ληλ=≈∆所以说，这个时候用短腔选单纵模是不可能的。

6．若调Q 激光器的腔长L 大于工作物质长l ，η及'η分别为工作物质及腔中其余部分的折射率，试求峰值输出功率P m 表示式。

解：列出三能级系统速率方程如下：2121 (1)2 (2)R dN l NcN n dt L d nN n dtστσυ=∆-'∆=-∆式中，()L l L l ηη''=+-，η及'η分别为工作物质及腔中其余部分的折射率，N 为工作物质中的平均光子数密度，/,/R c L c υητδ'==。

激光原理(周炳琨)激光（Light Amplification by Stimulated Emission of Radiation，即激发辐射的光放大）是一种特殊的电磁辐射，它的特点是具有高度的方向性、高度的空间和频率的纯度、高度的能量聚集度以及高度的能量稳定性。

激光是由一个叫做激光源的装置产生的，它是一种特殊的电磁辐射，它的特点是具有高度的方向性、高度的空间和频率的纯度、高度的能量聚集度以及高度的能量稳定性。

激光源的工作原理是通过利用激发辐射的原理来产生激光，它是一种特殊的电磁辐射，它的特点是具有高度的方向性、高度的空间和频率的纯度、高度的能量聚集度以及高度的能量稳定性。

激发辐射的原理是一种物理现象，它指的是一个原子或分子在受到外部光激发作用时，在其能级之间跃迁时发射出跟外部激发光一样频率的光，这种光称为激发辐射。

激发辐射的原理是激光源的基本工作原理，它的特点是具有高度的方向性、高度的空间和频率的纯度、高度的能量聚集度以及高度的能量稳定性。

激光源的结构一般包括激光器件、激光器件驱动电路、激光调谐电路、激光调制电路以及激光输出系统等组成部分。

激光器件是激光源的核心部件，它决定了激光源的性能。

激光器件分为半导体激光器件、离子激光器件、气体激光器件和激光晶体等类型。

激光器件的工作原理是在激光器件内部，电路设计的特殊形式和特殊的结构，使得原子或分子在受到外部光激发作用时，发生激发辐射，从而产生激光。

激光器件驱动电路是激光器件的基本组成部分，它的作用是将外部的电源转换成激光器件所需的电压和电流，从而使激光器件能够正常工作。

激光调谐电路是激光器件驱动电路的基本组成部分，它的作用是通过调节电路中的参数，使激光器件能够输出一定的频率和能量，从而使激光器件能够正常工作。

激光调制电路是激光调谐电路的基本组成部分，它的作用是通过调节电路中的参数，使激光器件能够输出一定的频率和能量，从而使激光器件能够正常工作。

激光输出系统是激光器件的基本组成部分，它的作用是将激光器件输出的激光聚焦到一个特定的位置，从而使激光器件能够正常工作。

激光原理习题答案激光是一种特殊的光源，它具有高度的单色性、相干性、方向性和亮度。

激光的产生基于受激辐射原理，即当原子或分子被激发到高能级状态后，受到外部光子的激发，以相同的频率、相位和方向释放出光子。

以下是一些激光原理习题的答案：1. 激光的产生条件：- 粒子数反转：在激光介质中，高能级上的粒子数必须大于低能级上的粒子数。

- 光学谐振腔：激光器内部需要有一个反射镜和一个半反射镜构成的谐振腔，以形成反馈机制。

2. 激光的分类：- 固体激光器：如红宝石激光器、Nd:YAG激光器等。

- 气体激光器：如氦氖激光器、CO2激光器等。

- 半导体激光器：也称为激光二极管，广泛应用于通信和数据存储。

3. 激光的特性：- 单色性：激光的波长非常窄，颜色非常纯净。

- 相干性：激光的光波具有相同的频率和相位。

- 方向性：激光束具有很好的方向性，发散角很小。

4. 激光的应用：- 医学：用于手术切割、治疗等。

- 工业：用于材料加工，如焊接、切割、打标等。

- 通信：光纤通信中使用激光作为信号载体。

5. 激光的安全问题：- 激光可能对眼睛造成损伤，使用时应采取适当的防护措施。

- 激光器应按照安全等级分类，并遵守相应的操作规程。

6. 激光器的工作原理：- 泵浦源提供能量，将介质中的粒子激发到高能级。

- 高能级粒子在受到外部光子的激发下，通过受激辐射释放出光子。

- 释放的光子在谐振腔中来回反射，不断被放大，最终形成激光束输出。

7. 激光的调制和调Q技术：- 调制：通过改变激光的参数（如频率、强度）来传输信息。

- 调Q：通过改变谐振腔的品质因数，实现激光脉冲的压缩和放大。

8. 激光的光谱特性：- 激光的光谱非常窄，通常用线宽来描述。

- 线宽越窄，激光的单色性越好。

9. 激光的相干长度：- 相干长度是激光在保持相干性的情况下能够传播的最大距离。

10. 激光的发散角：- 发散角是激光束在传播过程中的扩散程度，与激光的模式有关。

以上是一些基本的激光原理习题答案，希望能够帮助理解激光的基本原理和特性。

激光原理(周炳琨)概述激光（Laser）是指由物质在受到外界能量激发时，通过放射出的光束具有高度的单色性、相干性和方向性的一种光源。

激光原理是指实现激光的产生以及激光的特性与作用的基本原理。

激光技术已经广泛应用于科学研究、医疗、通信、材料加工等领域。

激光产生原理1. 激光器的构成激光器通常由激活介质、光腔和泵浦三部分构成。

其中，激活介质是激光的源头，光腔用于放大激光信号，而泵浦则用于向激活介质输送能量。

2. 激活介质激活介质是产生激光所必需的物质，它具有可以被激活、通过受激辐射放出高度单色的光等特性。

常见的激活介质有气体、固体和液体。

2.1 气体激光气体激光器是使用气体作为激活介质的激光器，常见的气体激光器有CO2激光器、氦氖激光器等。

它们的激活介质分别是二氧化碳和氦氖气体，通过电子激活气体分子，使其达到受激辐射的能级，从而产生激射。

2.2 固体激光固体激光器是使用固体晶体作为激活介质的激光器，常见的固体激光器有Nd:YAG激光器、Nd:YVO4激光器等。

它们的激活介质通常是镨钇掺杂的钇铝石榴石晶体，通常使用光泵或电泵的方式来激发晶体。

2.3 液体激光液体激光器是使用液体作为激活介质的激光器，常见的液体激光器有染料激光器、红宝石激光器等。

它们的激活介质通常是含有染料的溶液，通过外界刺激能激活染料分子，产生激射。

3. 光腔光腔是激光器中光信号的放大装置，其作用类似于谐振腔。

光腔有两端透明的镜子，称为半反射镜和全透射镜。

其中，半反射镜只透过一部分光，而全透射镜使光完全透过。

4. 泵浦泵浦是为激活介质提供能量的装置，通过各种能量输入方式将能量输入到激活介质中。

常用的泵浦方式有光泵和电泵两种。

光泵是指通过光能量向激活介质输送能量，而电泵则是指通过电流向激活介质输送能量。

激光特性与应用1. 激光特性激光具有以下几个独特的特性：•高度单色性：激光光束的频率很单一，其波长非常狭窄，通常只有几个纳米的范围。

•相干性：激光具有相位高度一致的性质，可以保持光束的干涉性质，实现干涉光的实验和应用。

《激光原理》习题解答第一章习题解答1 为了使氦氖激光器的相干长度达到1KM ，它的单色性0λ∆应为多少？解答：设相干时间为τ，则相干长度为光速与相干时间的乘积，即c L c ⋅=τ根据相干时间和谱线宽度的关系 cL c ==∆τν1又因为 0γνλλ∆=∆，00λνc=，nm 8.6320=λ由以上各关系及数据可以得到如下形式： 单色性=0ννλλ∆=∆=cL 0λ=101210328.61018.632-⨯=⨯nmnm解答完毕。

2 如果激光器和微波激射器分别在10μｍ、500nm 和Z MH 3000=γ输出1瓦连续功率，问每秒钟从激光上能级向下能级跃迁的粒子数是多少。

解答：功率是单位时间内输出的能量，因此，我们设在dt 时间内输出的能量为dE ，则功率=dE/dt激光或微波激射器输出的能量就是电磁波与普朗克常数的乘积，即d νnh E =，其中n 为dt 时间内输出的光子数目，这些光子数就等于腔内处在高能级的激发粒子在dt 时间辐射跃迁到低能级的数目（能级间的频率为ν）。

由以上分析可以得到如下的形式：ννh dth dE n ⨯==功率 每秒钟发射的光子数目为：N=n/dt,带入上式，得到：()()()13410626.61--⨯⋅⨯====s s J h dt n N s J νν功率每秒钟发射的光子数 根据题中给出的数据可知：z H mms c13618111031010103⨯=⨯⨯==--λν z H mms c1591822105.110500103⨯=⨯⨯==--λνz H 63103000⨯=ν把三个数据带入，得到如下结果：19110031.5⨯=N ，182105.2⨯=N ，23310031.5⨯=N3 设一对激光能级为E1和E2（f1=f2），相应的频率为ν（波长为λ），能级上的粒子数密度分别为n2和n1，求(a)当ν=3000兆赫兹，T=300K 的时候，n2/n1=? (b)当λ=1μm ，T=300K 的时候，n2/n1=? (c)当λ=1μm ，n2/n1=0.1时，温度T=？解答:在热平衡下，能级的粒子数按波尔兹曼统计分布，即： TK E E T k h f f n n b b )(expexp 121212--=-=ν（统计权重21f f =） 其中1231038062.1--⨯=JK k b 为波尔兹曼常数，T 为热力学温度。

《激光原理及应用》习题参考答案思考练习题11•解答：设每秒从上能级跃迁到下能级的粒子数为n 。

单个光子的能量：g = h v = he / Z 连续功率：p 二n ； 则,n = p/ ；a.对发射■ = 0.5000的光:p 1 0.5000 10-6 n — —he 6.63 10 ⑶ 3.0 108-2.514 1018(个)b.对发射、• = 3000 MHz 的光_________ 16.63 10 "4 3000 106= 5.028 1023(个)E 2 a 匹Tn 1hv些=小-1n 1hc 3T6.26 103(K)'■ ln 匹3.解答：(1) 由玻耳兹曼定律可得_E 2 -E 1e '丁 , m/g20且4g 1 =g 2, m • n 2 =10代入上式可得: n 2 :30 (个)(2 )由 (a ), (b ) ,(c)式可得:2.解答:E 2 - E<| = h..(a).(b) (1 )由 ■■■. = c/ ■ .......(a ), (b )式可得:.(c)n 2 /g 2(2) p =108 n 2(E 2 -EJ =5.028 10-(W) 4•解答：(1)由教材(1-43)式可得e kT —1因此：fT ' =2.82kh ，hc同样可求得： 一丄 =4.96九m kT故' m - m = 0.568c8h1 3 A-2000J s/m 3 -3.860 10, J s/m 3 (0.6328 10冷3 5.0 10*8- 6.63 10 ^4= 7.592 10 5•解答：(1)红宝石半径 r = 0.4cm ，长L -8cm ，铬离子浓度匸=2 1018cm‘，发射波长• =0.6943 10 “m ，巨脉冲宽度 -T = 10 ns 则输出最大能量2 ,、he18E - (：r L) 2 1034826.63 1030 108二 0.42 86(J)二 2.304(J)0.6943 10」脉冲的平均功率:P =E /.「23041010"2.304 叫) (2)自发辐射功率 _ hcN 2heP (兀r 2L)Q 自皿z-X663计 3° IO 8 *1。

第二章5）激发态的原子从能级E2跃迁到E1时，释放出m μλ8.0=的光子，试求这两个能级间的能量差。

若能级E1和E2上的原子数分别为N1和N2，试计算室温（T=300K ）时的N2/N1值。

【参考例2-1，例2-2】 解：（1）J hcE E E 206834121098.310510310626.6---⨯=⨯⨯⨯⨯==-=∆λ （2）52320121075.63001038.11098.3exp ---∆-⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯-==T k Eb e N N10）激光在0.2m 长的增益物质中往复运动过程中，其强度增加饿了30%。

试求该物质的小信号增益系数0G .假设激光在往复运动中没有损耗。

104.0*)(0)(0m 656.03.1,3.13.014.02*2.0z 0000---=∴===+=====G e e I I me I I G z G ZzG Z ααα即且解：第三章2．CO 2激光器的腔长L=100cm ，反射镜直径D=1.5cm ，两镜的光强反射系数分别为r 1=0.985，r 2=0.8。

求由衍射损耗及输出损耗分别引起的δ、τc 、Q 、∆νc (设n=1) 解：衍射损耗:1880107501106102262.).(.a L =⨯⨯⨯=λ=δ-- s ..c L c 881075110318801-⨯=⨯⨯=δ=τ输出损耗:1190809850502121.)..ln(.r r ln =⨯⨯-=-=δ s ..c L c 881078210311901-⨯=⨯⨯=δ=τ4.分别按图(a)、(b)中的往返顺序，推导旁轴光线往返一周的光学变换矩阵⎪⎪⎭⎫ ⎝⎛D C B A ，并证明这两种情况下的)(21D A +相等。

（a ）（b ）解： 矩阵乘法的特点：1、只有当乘号左边的矩阵（称为左矩阵）的列数和乘号右边的矩阵（右矩阵）的行数相同时，两个矩阵才能相乘；这条可记为左列=右行才能相乘。

第七章习题 1．有一平凹氦氖激光器，腔长m 5.0，凹镜曲率半径为m 2，现欲用小孔光阑选出00TEM模，试求光阑放于紧靠平面镜和紧靠凹面镜处两种情况下小孔直径各为多少？（对于氦氖激光器，当小孔光阑的直径约等于基模半径的3.3倍时，可选出基横模。

）解：由RL g -=1，可计算出75.01=g ，0.12=g ，满足1021<⋅<g g ，故该腔为一稳定腔。

对He-Ne 激光器的nm 8.632=λ，则m L os 41017.3-⨯==πλω。

由公式（2.8.7）,当光阑放于紧靠凹面镜的情况下，44/121121082.4])1([1-⨯=⋅-=g g g g oss ωω，故小孔直径应为m d s 311059.13.31-⨯=⋅=ω。

当光阑放于紧靠平面镜的情况下，44/121211017.4])1([2-⨯=⋅-=g g g g os s ωω，故小孔直径应为m d s 321038.13.32-⨯=⋅=ω。

2．图7.1所示激光器的1M 是平面输出镜，2M 是曲率半径为cm 8的凹面镜，透镜P 的焦距cm F 10=，用小孔光阑选00TEM模。

试标出P 、2M 和小孔光阑间的距离。

若工作物质直径是mm 5，试问小孔光阑的直径应选多大？解：m f 5.1820==λπωmm F f 0135.0)(120=+='ωω小孔光阑直径为mm 027.020='ω 距透镜P :cm FF F l 10])(1[22022=+-='λπω 距凹面镜2M :cm F l 4222==。

3．激光工作物质是钕玻璃，其荧光线宽nm F 0.24=∆λ，折射率50.1=η，能用短腔选单纵模吗？解：1421014.2)1(-⨯=∆=∆m λλλHz c 12104.6)1(⨯=∆⋅=∆λν由短腔选模条件：ν∆>'L c 2（7.1.3）5103.22-⨯=∆<'νc Lm L μη6.15103.25max ≈⨯=-。