数学人教版初中三年级下册 黄冈中学2017年理科实验班预录考试数学模拟B卷

黄冈中学2017年自主招生(理科实验班)预录考试化学模拟试题(F卷)(分值：50分，时间：45分钟；物理化学合卷，物理80分，总时间：120分钟)(可能用到的相对原子质量: H:1,C:12,O:16, Na:23, Mg:24，Al：27，S:32,Ca:40,Fe:56，)一、选择题(每小题有1个或2个选项符合题意,每小题2分,共24分，答案填写在下列答题卡中)1、网络神曲“化学是你，化学是我”揭示了化学与生活的密切关系。

下列有关说法中正确的是：A．碳酸钠俗名纯碱，也叫苏打，可用于清洗厨房用具的油污B．84消毒液在日常生活中使用广泛，溶液无色、有漂白作用，它的有效成分为Ca(ClO)2 C．青铜是我国使用最早的合金材料，目前世界上使用量最大的合金材料是铝合金D．明矾[KAl(SO4)2·12H2O]溶于水会形成胶体，因此可用于自来水的消毒杀菌2、为检验某化合物是否含碳、氢、氧三种元素，取一定质量该化合物在氧气中充分燃烧，接下来还须进行的实验有：①用带火星的木条检验氧气；②用无水硫酸铜检验是否有水生成；③用澄清石灰水检验是否有二氧化碳生成；④测定生成水和二氧化碳的质量。

A．①②③④B．①②③C．②③④D．②③3、已知所含元素化合价发生变化的反应是氧化还原反应，其中被还原的元素化合价降低，被氧化的元素化合价升高。

海洋中有丰富的资源，如下图所示利用海水可获得许多化工产品。

下列有关说法正确的是：A．第①步中除去粗盐中的SO42－、Ca2＋、Mg2＋等杂质，加入的试剂顺序为：Na2CO3溶液、NaOH溶液、BaCl2溶液，过滤后加盐酸B．第②步中加入的试剂为CaCl2溶液C．第③步中发生分解反应D．在第④步中溴元素被还原4、新型纳米材料MFe2O x （3＜x＜4）中M表示+2价的金属元素，在反应中化合价不发生变化。

常温下，MFe2O x能使工业废气中的SO2转化为S，在反应中M的化合价不发生改变。

黄冈中学2017年自主招生(理科实验班)预录考试化学模拟试题(A卷)(分值：50分，时间：45分钟；物理化学合卷，物理80分，总时间：120分钟)(可能用到的相对原子质量: H:1,C:12,O:16, Na:23,Mg:24,S：32，Cl:35.5,K:39,Cu:64) 一、选择题(每小题有1个或2个选项符合题意,每小题2分,共24分，答案填写在下列答题卡中)1、燃放烟花爆竹是我国春节的一项传统习俗。

烟花点燃后绽放出的鲜艳夺目、五彩缤纷的图案是一些金属离子魅力的展示。

焰火的主要原料是黑火药，还有草酸钠、碳酸铜（发出绿色的光）等发色剂和氯酸钾、金属镁、铝粉末等添加剂。

下列说法正确的是：A．碳酸铜因为受热分解才发出绿色的光B．氯酸钾的主要用途是产生紫色的焰火C．镁、铝在焰火中发出耀眼的白光D．黑火药是我国古代的发明之一2、下列CO2的制备装置中，不能起到“随开随制，随关随停”效果的是：A B C D3、人们可从铁钛矿（主要成分FeTiO3）制取金属钛（Ti），其在一定条件下的主要反应有：①FeTiO3+H2 ==Fe+TiO2+H2O；② TiO2+2C+2Cl2 ==TiCl4+2CO；③ TiCl4+2Mg ==2MgCl2+Ti下列叙述正确的是：A．反应①中的H2被氧化 B．反应②中钛元素的化合价升高C．反应③是复分解反应 D．反应②Cl2中的“Cl”得到电子4、已知复分解反应2 CH3COOH + Na2CO3 == 2 CH3COONa + H2O + CO2↑可进行。

在常温下，的物质。

依照该规律，请你判断下列反应不能．．成立的是：A．CO2 + H2O + 2NaClO == Na2CO3 + 2HClOB．CO2 + H2O + NaClO == NaHCO3 + HClOC．CH3COOH + NaCN == CH3COONa + HCND．NaClO + CH3COOH == HClO + CH3COONa5、实验室需要把烧杯A中的氢氧化钠溶液转移到烧杯B中，将烧杯A内的液体倒入烧杯B 后，烧杯A内会残留1 mL液体，之后用19 mL蒸馏水清洗烧杯A的内壁，这部分液体也倾倒至烧杯B，烧杯A内仍残留1 mL液体……需要几次这样的清洗，才能保证原烧杯中的氢氧化钠溶液99.9%都被转移至新烧杯：A．2次B．3次C．4次D．5次6、在Na2SO4、NaCl、NaNO3的混合溶液中，含有Na+、SO42-、Cl-、NO3-，已知其中Na+、SO42-、NO3-的个数比为8：1：2，则溶液中Na2SO4、NaCl、NaNO3的“分子”个数比为：A．1：1: 1 B．1: 4: 2 C．1: 2 : 4 D．1: 3 : 27、下列从原料及试剂分别制取相应的最终产物的设计中，理论上正确、操作上可行、经济上合理的是：黄冈中学2017年自主招生(理科实验班)预录考试化学模拟试题(A卷)黄冈中学2017年自主招生(理科实验班)预录考试化学模拟试题(A 卷)8、下图是甲、乙两种物质的溶解度曲线。

黄冈中学2017年理科实验班预录模拟试题数学C 卷时间120分钟 满分120分一、 选择题（本大题共6小题，每小题5分，共30分）1、小明设计了一个电子游戏：一电子跳蚤从横坐标为t(t ＞0)的P 1点开始，按点的横坐标依次增加1的规律，在抛物线a ax y (2=＞0)上向右跳动，得到点P 2、P 3，这时△P 1P 2P 3的面积为（ ）A ．2B ．3C ．4D ．1 2、如图，边长为1的正方形ABCD 绕点A 逆时针旋转30︒到正方形AB C D '''，图中阴影部分的面积为（ ）A ．313-B ．33C ．314-D ．123、代数式9)12(422+-++x x 的最小值为（ ）A ．12B ．13C ．14D ．114、设1x 、2x 是方程02=++k x x 的两个实根，若恰有22221212k x x x x =++成立，则k 的值为（ ） A ．1- B ．21或 1- C ．21D ．21-或 1 5、如图，AB 是半圆的直径，点C 是弧AB 的中点，点E 是弧AC 的中点，连结EB 、CA交于点F ，则=（ ） A. B. C. D.6、如图，设AD ，BE ，CF 为三角形ABC 的三条高，若6AB =，5BC =，3EF =，则线段BE 的长为 （ ）A185. B 4. C 215. D 245一、填空题（本大题共6小题，每小题5分，共30分）7、、已知x 、y 均为实数，且满足17=++y x xy ，6622=+xy y x ，则代数式432234y xy y x y x x ++++的值为BFEF1314212-212- ABC DB 'D 'C '(第5题)8、若222a b c bc =+- 则ca b+++b a c 的值是 9、已知ABC ∆的顶点A 、C 在反比例函数3y =（0x >）的图象上，090ACB ∠=,030ABC ∠=,AB x ⊥轴，点B 在点A 的上方，且6,AB =则点C 的坐标为 .10、如图，E ，F 是正方形ABCD 的边AD 上两个动点，满足AE=DF ．连接CF 交BD 于点G ，连接BE 交AG 于点H ．若正方形的边长为2，则线段DH 长度的最小值是 ．11、对于正数x ，规定f （x ）＝ x1x+， 计算f （1001）＋ f （991）＋ f （981）＋ …＋ f （13）＋ f （12）＋ f （1）＋ f （2）＋ f （3）＋ … ＋ f （98）＋ f （99）＋ f （100）＝__________． 12、设直线(1)10kx k y ++-=与坐标轴所构成的直角三角形的面积为k S ，则=+++201721S S S Λ ．二、解答题（本大题共4小题，共60分，解答应写出文字说明、证明、过程或演算步骤） 13、（15分）在直角ABC ∆中，ο90=∠C ，直角边BC 与直角坐标系中的x 轴重合，其内切圆的圆心坐标为)1,0(p ，若抛物线122++=kx kx y 的顶点为A 。

黄冈中学自主招生考试 数学模拟试题（C 卷）（满分：120分 考试时间：120分钟）一、选择题（每小题4分，共8题，在给出的四个选项中，只有一项是符合题目要求的） 1.在直角坐标系xOy 中，点P (4,)y 在第一象限内，且OP 与x 轴正半轴的夹角为60°，则y 的值为（ ）.A.3B.2.将二次函数2y x =的图像向右平移1个单位，再向上平移2个单位后，所得图像的函数表达式是（ ）．A.2(1)2y x =-+ B. 2(1)2y x =++ C. 2(1)2y x =-- D. 2(1)2y x =+- 3．x 、y 都是正数，并且成反比，若x 增加了p ﹪，设y 减少的百分数为q ﹪，则q 的值为（ ）. A.1001%p p + B. 100%p C. 100p p + D. 100100pp+4.在凸多边形中，四边形有两条对角线，五边形有五条对角线.观察探索凸十边形有（ ）条对角线.A.29B. 32C. 35D.385．已知△ABC 的三边长为a 、b 、c ，且满足方程222222()0a x c a b x b ---+=.则方程根的情况是（ ）.A.有两相等实根B. 有两相异实根C. 无实根D.不能判定 6．关于x的方程1x x -=的根的个数为（ ）.A.0B. 1C. 3D.47．如图所示，两个边长都为2的正方形ABCD 和OPQR ，如果O 点正好是正方形ABCD 的中心，而正方形OPQR 可以绕O 点旋转，那么它们重叠部分的面积是（ ）.A.4B. 2C. 1D.128.折叠圆心为O 、半径为10cm 的圆纸片，使圆周上的某一点A 与圆心O 重合.对圆周上的每一点都这样折叠纸片，从而都有一条折痕.那么，所有折痕所在直线第7题上点的全体为（ ）.A.以O 为圆心、半径为10cm 的圆周B. 以O 为圆心、半径为5cm 的圆周C. 以O 为圆心、半径为5cm 的圆内部分D. 以O 为圆心、半径为5cm 的圆周及圆外部分 二、填空题（每小题4分，共8小题）9．如图，⊙C 通过原点，并与坐标轴分别交于A 、D 两点.已知∠OBA=30°，点D 的坐标为（0，2）,则点C 的坐标为 .10.如图，已知3个边长相等的正方形相邻并排.则∠EBF ＋∠EBG= . 11．若函数(0)y kx k =>与函数1y x=的图像相交于A 、C 两点，AB 垂直x 轴于点B ，则△ABC 的面积为 .12．设二次函数222(0)2a y x ax a =++<的图像顶点为A ，与x 轴交点为B 、C.当△ABC 为等边三角形时，a 的值为 .13．甲在汽车上发现乙正往相反的方向走去。

黄冈中学2017年自主招生（理科实验班）预录考试化学模拟试题可能用到的相对原子质量 H=1 O=16 S=32 C=12 Cu=64 Mg=24 Al=27 Ca=40 Ba=137 Fe=56一、选择题。

（每小题只有1个答案，共18分）1. 下列实验操作能达到目的的是 ( )A. 向滴有酚酞的Na2CO3溶液中加入BaCl2溶液，溶液褪色，则证明BaCl2有酸性B. 准确称取2.80gCa(OH)2，加入97.2g水中配制100g 2.8%的Ca(OH)2溶液C. 在实验室，可无需查阅资料用50%的硝酸来配制50g20%的硝酸溶液D. 通过灼热的镁粉除去CO2中的O22. 实验室制备氯气：MnO2+4HCl(浓)MnCl2+ Cl2↑+2 H2O反应会因盐酸浓度下降而停止。

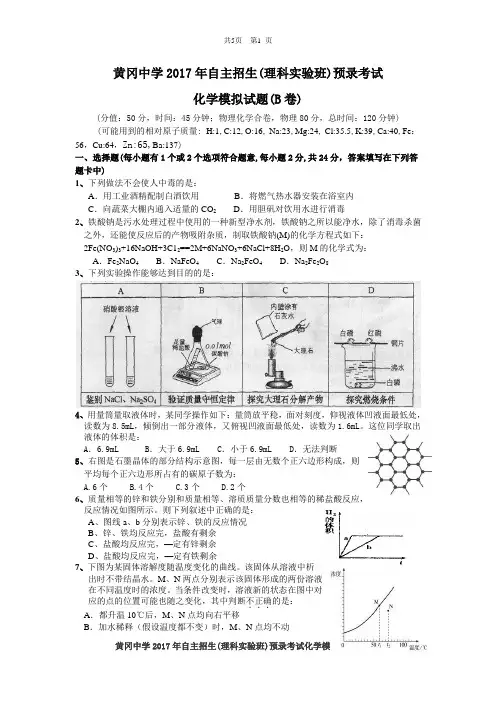
为测定反应残余液中盐酸的浓度，探究小组同学设计了4组实验方案（每次均量取20 g反应残余液进行实验），其中正确的是（）A. 与足量AgNO3溶液反应，过滤、洗涤、干燥，称量生成的沉淀质量为a gB. 稀释10倍后取20 mL用已知浓度的NaOH溶液滴定，消耗NaOH的体积为b gC. 与足量NaHCO3固体反应，逸出气体用足量碱石灰吸收，增重c gD. 加入d1g CaCO3（过量）充分反应后，过滤、洗涤、干燥，称量剩余固体质量为d2 g （已知：相同条件下 MnCO3的溶解度远远小于CaCO3）3. 甲、乙两烧杯内盛有等质量、等质量分数的盐酸．将镁逐渐加入甲烧杯，铁逐渐加入乙烧杯，测量加入的金属质量m和相应的烧杯内物质质量变化量△m，画出△M﹣m曲线oac和obc的示意图，如图所示．根据图中信息，下列说法错误的是（）A. m1：m2=3：7B. m1﹣△M1＜m2﹣△M2C. 曲线oac表示的是甲烧杯中△M与m的变化关系D. 当乙烧杯内加入铁的质量为m1时，溶液中溶质不止一种4. 小明向盛有盐酸和MgCl2溶液的烧杯中加入一定量的NaOH溶液，为判断反应后溶液的成分，他分别取少量反应后的溶液a于试管中，用下表中的试剂进行实验，相应结果错误的是（）A. AB. BC. CD. D5. 列表和作图是常用的数据处理方法．结合所绘图表判断下列说法正确的是（）氢氧化钠、碳酸钠分别在水、酒精中的溶解度学.科.网...学.科.网...学.科.网...学.科.网...A. 图象与表格均能反映温度对固体物质溶解度的影响，其中表格的优点是变化规律更直观B. 由表格数据可知，物质的溶解度只受温度影响C. 40℃时，将50g NaOH分别投入到100g水和酒精中都能得到饱和溶液D. 40℃时，将CO2通入饱和的NaOH酒精溶液中有沉淀生成6. 下列有关实验现象和解释或结论都正确的是（）A. AB. BC. CD. D7. 对下列各组物质的鉴别分析错误的是 ( )A. 黑色粉末：FeO、Fe、CuO、C 只用一种试剂即可鉴别B. 无色溶液：KOH、H2SO4、CuCl2、NaNO3只用一种试剂即可鉴别C. 无色溶液：Na2CO3、AgNO3、BaCl2、HCl 不用其他试剂就可以鉴别D. 无色溶液：Ba(OH)2、Na2CO3、BaCl2、HNO3不用其他试剂就无法鉴别8. 某溶液可能含有盐酸、硫酸、硫酸镁、碳酸钠、硝酸钠、氯化铜中的一种或几种，为了探究其组成，向一定质量的该溶液中逐滴加入氢氧化钡溶液，生成沉淀的质量与所加氢氧化钡溶液的质量之间的关系如图所示。

黄冈中学2017年自主招生(理科实验班)预录考试化学模拟试题(B卷)(分值：50分，时间：45分钟；物理化学合卷，物理80分，总时间：120分钟)(可能用到的相对原子质量: H:1,C:12,O:16, Na:23,Mg:24, Cl:35.5,K:39,Ca:40,Fe：56，Cu:64，Zn:65,Ba:137)一、选择题(每小题有1个或2个选项符合题意,每小题2分,共24分，答案填写在下列答题卡中)1、下列做法不会使人中毒的是：A．用工业酒精配制白酒饮用B．将燃气热水器安装在浴室内C．向蔬菜大棚内通入适量的CO2D．用胆矾对饮用水进行消毒2、铁酸钠是污水处理过程中使用的一种新型净水剂，铁酸钠之所以能净水，除了消毒杀菌之外，还能使反应后的产物吸附杂质，制取铁酸钠(M)的化学方程式如下：2Fe(NO3)3+16NaOH+3C12==2M+6NaNO3+6NaCl+8H2O，则M的化学式为：A．Fe2NaO4B．NaFeO4C．Na2FeO4D．Na2Fe2O83、下列实验操作能够达到目的的是：4、用量筒量取液体时，某同学操作如下：量筒放平稳，面对刻度，仰视液体凹液面最低处，读数为8.5mL，倾倒出一部分液体，又俯视凹液面最低处，读数为1.6mL。

这位同学取出液体的体积是：A．6.9mL B．大于6.9mL C．小于6.9mL D．无法判断5、右图是石墨晶体的部分结构示意图，每一层由无数个正六边形构成，则平均每个正六边形所占有的碳原子数为：A.6个B.4个C.3个D.2个6、质量相等的锌和铁分别和质量相等、溶质质量分数也相等的稀盐酸反应，反应情况如图所示。

则下列叙述中正确的是：A、图线a、b分别表示锌、铁的反应情况B、锌、铁均反应完，盐酸有剩余C、盐酸均反应完，—定有锌剩余D、盐酸均反应完，—定有铁剩余7、下图为某固体溶解度随温度变化的曲线。

该固体从溶液中析出时不带结晶水。

M、N两点分别表示该固体形成的两份溶液在不同温度时的浓度。

理科实验班预录数学模拟试题(B 卷)一、选择题（每小题 5 分，共 30 分） 1．已知a+b=3，a 3+b 3=9，则a 7+b 7=（ ） A ．129 B ．225 C ．125 D ．6752．如图，⊙O 内的点P 在弦AB 上，点C 在⊙O 上，PC ⊥OP ，若BP=2，AB=6，则CP 的长等于（ ） A ．32B ．4C ．22D ．233．已知215-=m ，则1122223+++-+m m m m m =( )A ．253-B ．453-C ．235-D ．435-4．如图，△ABC 中，AB=AC ，∠ABC=40°，BD 是∠ABC 的平分线，延长BD 至E ，使DE=AD ，则∠ECA=（ ） A ．30° B ．35° C ．40° D ．45°5．如图，在平面直角坐标系中，四边形OBCD 是边长为4的正方形，平行于 对角线BD 的直线l 从O 出发，沿x 轴正方向以每秒1个单位长度的速度 运动，运动到直线l 与正方形没有交点为止．设直线l 扫过正方形OBCD 的面积为S ，直线l 运动的时间为t （秒），下列能反映S 与t 之间函数关 A ．B ．C ．D ．6．如图，点O 在△ABC 内，点P 、Q 、R 分别在边AB 、BC 、CA 上，且OP ∥BC ，OQ ∥CA ，OR ∥AB ，OP=OQ=OR=x ，BC=a ，CA=b ，AB=c ，则x =( )A ．cb a 1111++B ．3cb a ++ C ．331222c b a ++D ．331cabc ab ++二、填空题（每小题 5分，共30 分）7．实数a 、b 、x 、y 满足ax+by=3，ax 2+by 2=7，ax 3+by 3=16, ax 4+by 4=42, 那么ax 5+by 5= . 8．如图，在边长为26的正方形ABCD 中，E 是AB 边上一点，G 是 AD 延长线上一点，BE =DG ，连接EG ，CF ⊥EG 交EG 于点H ，交 AD 于点F ，连接CE ，BH ．若BH =8，则FG = ．9．已知函数|x |x y 22--=的图象与x 轴相交于A 、B 两点，另一条抛物线422+-=x ax y 也过A 、B 两点，则a= .10.如图，在梯形ADEB 中，∠D=∠E=90°，△ABC 是等边三角形，且点C 在DE 上，如果AD=7，BE=11，则S △ABC = .11.设f(a)是关于a 的多项式，f(a)除以2(a+1)，余式是3；2f(a)除以3(a -2)，余式 是-4. 那么3f(a)除以4(a 2-a -3)，余式是 .12.如图，已知圆的内接△ABC ，AB=AC ，D 是弦AC 上的一点，连接AD 并延长，与BC 的延长线交于点E ，且AE=5，则AB 2+EB ·EC= . 三、解答题（共60分）13.(10分)解方程：.)x (x 082244=--+14.（12分）如图，已知等边△ABC ，AB =12，以AB 为直径的半圆与BC 边交于点D ，过点D 作DF ⊥AC ，垂足为F ，过点F 作FG ⊥AB ，垂足为G ，连结GD ． （1）求证：DF 是⊙O 的切线； （2）求FG 的长；（3）求tan ∠FGD 的值．15.(12分)经统计分析，某市跨河大桥上的车流速度v （千米／小时）是车流密度x （辆／千米） 的函数，当桥上的车流密度达到220辆／千米时，造成堵塞，此时车流速度为O 千米/小时；当车流密度不超过20辆／千米时，车流速度为80千米／小时．研究表明：当20≤x ≤220时，车流速度v 是车流密度x 的一次函数．(1)求大桥上车流密度为100辆／千米时的车流速度．(2)在交通高峰时段，为使大桥上的车流速度大于40千米／小时且小于60千米／小时时，应控制大桥上的车流密度在什么范围内？(3)车流量（辆／小时）是单位时间内通过桥上某观测点的车辆数，即：车流量=车流速度×车流密度．求大桥上车流量y 的最大值．16.(13分)设).x (x x x x x )x (f 094932424>+--+-=(1)将f(x)化成b)x (g a )x (g +++221(a 、b 是不同的整数)的形式；(2)求f(x)的最大值及相应的x 值.17.(13分)如图，在直角梯形ABCD中，AB∥CD，AD⊥AB，∠B=60°，AB=10，BC=4，点P沿线段AB从点A向点B运动，设AP=x．(1)求AD的长；(2)点P在运动过程中，是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似？若存在，求出x的值；若不存在，请说明理由；(3)设△ADP与△PCB的外接圆的面积分别为S1、S2，若S=S1+S2，求S的最小值．参考答案：1.A 2.A 3.B 4.C 5.D 6.A7.20 8．25 9. -2 10. 33 11.-5a+4 12.2514.（1）证明：连结OD ，如图，∵△ABC 为等边三角形，∴∠C =∠A =∠B =60°， 而OD =OB ，∴△ODB 是等边三角形，∠ODB =60°，∴∠ODB =∠C ，∴OD ∥AC ， ∵DF ⊥AC ，∴OD ⊥DF ，∴DF 是⊙O 的切线；（2）解：∵OD ∥AC ，点O 为AB 的中点，∴OD 为△ABC 的中位线，∴BD =CD =6． 在Rt △CDF 中，∠C =60°，∴∠CDF =30°，∴CF =CD =3，∴AF =AC ﹣CF =12﹣3=9，在Rt △AFG 中，∵∠A =60°，∴FG =AF ×sinA =9×=；（3）解：过D 作DH ⊥AB 于H ．∵FG ⊥AB ，DH ⊥AB ， ∴FG ∥DH ，∴∠FGD =∠GDH ． 在Rt △BDH 中，∠B =60°，∴∠BDH =30°， ∴BH =BD =3，DH =BH =3．在Rt △AFG 中，∵∠AFG =30°，∴AG =AF =，∵GH =AB ﹣AG ﹣BH =12﹣﹣3=，∴tan ∠GDH ===，∴tan ∠FGD =tan ∠GDH =．15.(1)由题意得：当20≤x ≤220时，v 是x 的一次函数，则可设v =kx +b （k ≠O ）， 由题意得：当x =20时，v =80,当x =220时，v =0所以⎩⎨⎧=+=+02208020b k b k 解得：⎪⎩⎪⎨⎧=-=8852b k ,所以当20≤x ≤220时，v =－52x +88 ， 则当x =100时,y =一52×100+88=48.即当大桥上车流密度为100辆／千米时，车流速度为48千米／小时． (2)当20≤v ≤220时，v =一52x +88(0≤v ≤80), 由题意得：⎪⎪⎩⎪⎪⎨⎧+-+-608852408852x x ．解得70＜x ＜120, 所以应控制车流密度的范围是大于70辆／千米且小于120辆／千米. (3)①当0≤x ≤20时，车流量y 1=vx =80x , 因为k =80>0，，所以y 1随x 的增大面增大，故当x =20时，车流量y 1的最大值为1600． ②当20≤x ≤220时，车流量y 2=vx =(一52x +88)x =一(x －110)2+4840, 当x =110时，车流量y 2取得最大值4840，因为4840>1600，所以当车流密度是110辆／千米，车流量y 取得最大值.17.解：（1）过点C 作CE ⊥AB 于E ，在Rt △BCE 中，∵∠B =60°，BC =4，∴CE =BC •sin ∠B =4×=2，∴AD =CE =2．（2）存在．若以A 、P 、D 为顶点的三角形与以P 、C 、B 为顶点的三角形相似， 则△PCB 必有一个角是直角．①当∠PCB=90°时，在Rt△PCB中，BC=4，∠B=60°，PB=8，∴AP=AB﹣PB=2．又由（1）知AD=2，在Rt△ADP中，tan∠DP A===，∴∠DP A=60°，∴∠DP A=∠CPB，∴△ADP∽△CPB，∴存在△ADP与△CPB相似，此时x=2．②∵当∠CPB=90°时，在Rt△PCB中，∠B=60°，BC=4，∴PB=2，PC=2，∴AP=3．则≠且≠，此时△PCB与△ADP不相似．（3）如图，因为Rt△ADP外接圆的直径为斜边PD，则S1=x•（）2=x•，①当2＜x＜10时，作BC的垂直平分线交BC于H，交AB于G；作PB的垂直平分线交PB于N，交GH于M，连结BM．则BM为△PCB外接圆的半径．在Rt△GBH中，BH=BC=2，∠MGB=30°，∴BG=4，∵BN=PB=（10﹣x）=5﹣x，∴GN=BG﹣BN=x﹣1．在Rt△GMN中，∴MN=GN•tan∠MGN=（x﹣1）．在Rt△BMN中，BM2=MN2+BN2=x2﹣x+，∴S1=x•BM2=x（x2﹣x+）．②∵当0＜x≤2时，S2=x（x2﹣x+）也成立，∴S=S1+S2=x•+x（x2﹣x+）=x（x﹣）2+x．∴当x=时，S=S1+S2取得最小值x．。

错B 1 D C B EE A 1 黄冈中学2017年自主招生数学模拟试题A 卷一、选择题：（每个5分，共30分）1.已知错误！未找到引用源。

，则s 的整数部分为（ ）A 163 B.165 C.167 D.1692.甲杯中盛有m 毫升红墨水，乙杯中盛有m 毫升蓝墨水，从甲杯中倒出a 毫升到乙杯里（0＜a ＜m ），搅匀后，又从乙杯倒出a 毫升到甲杯里，则这时（ ）A.甲杯中混入的蓝墨水比乙杯中混入的红墨水少B. 甲杯中混入的蓝墨水比乙杯中混入的红墨水多C. 甲杯中混入的蓝墨水和乙杯中混入的红墨水相同D. 甲杯中混入的蓝墨水与乙杯中混入的红墨水多少关系不定3.如图，△ABC 是顶角为100°的等腰三角形，将它绕C 旋转到△CA 1B 1的位置，D 、E 、F 分别是AB 、BA 1、A 1B 1的中点，则∠DEF 为（ ） A.90º B.100º C.80º D.60º 4. 如图，DC ∥AB ，∠BAE=∠BCD,AE ⊥DE,∠D=130°,则∠B=（ ）A. 30°B. 40°C. 45°D. 50° 5.如果同时满足不等式错误！未找到引用源。

和错误！未找到引用源。

的整数仅为1，2，3，那么整数a, b 有序数对（a, b ）有( )A.17对B.64对C.72对D.81对6.已知一次函数错误！未找到引用源。

的图象经过一、二象限，且与错误！未找到引用源。

轴交于（-2，0），则不等式错误！未找到引用源。

的解集为（ ）A.错误！未找到引用源。

B.错误！未找到引用源。

C.错误！未找到引用源。

D.错误！未找到引用源。

二、填空题：（每个5分，共30分）7.某商铺专营A ，B 两种商品，试销一段时间，总结得到经营利润y 与投入资金错误！未找到引用源。

（万元）的经验公式分别是y A =错误！未找到引用源。

黄冈中学理科实验班预录考试数学模拟试题五（时间：120分钟 满分：120分 命题人：金小雷）一、选择题：（下列各小题都给出了四个选项，其中只有一项是符合题目要求.本大题共8小题，每小题5分，计40分）1．下列说法中，正确的是（ ） A ．如果a b c d b d ++=，那么a cb d= B3 C ．当1x <D ．方程220x x +-=的根是2112x x =-=，2．将函数2y x x =+的图象向右平移a (0)a >个单位，得到函数232y x x =-+的图象，则a 的值为 （ ）A ．1B ．2C ．3D ．43．下列图形中，对称轴有且只有3条的是（ ） A ．菱形 B ．等边三角形 C ．正方形 D ．圆 4、方程1)1(32=-++x x x 的所有整数解的个数是（ ） A.．5个 Ｂ．4个 Ｃ．3个 Ｄ．2个 5．如图，AB 是圆O 的直径，点D 在AB 的延长线上，DC 切圆O 于C ，若25A =∠．则D ∠等于（ ）A ．40︒B ．50︒C ．60︒D ．70︒ 6．已知二次函数的图象如图所示，有以下结论：①；②；③；④；⑤其中所有正确结论的序号是（ ） A ．①② B ．①③④ C ．①②③⑤ D．①②③④⑤ 7. 如图,已知等边ABC ∆外有一点P ，P 落在ABC ∠ 内，设P 到B C 、CA 、AB 的距离分别为123,,h h h ， 满足1236h h h -+=，那么等边ABC ∆的面积为（ ）A ．B ．C ．D ．8. 若1xy ≠，且有272009130x x ++=及213200970y y ++=，则xy的值是 （ ） A ．137 B ．713 C ．20097- D ．200913- 二、填空题：本大题共6个小题，每小题5分，共30分． 9. 104cos30sin60(2)2008)-︒︒+--=_____________ 10. 函数y ____________11．如图，在Rt ABC △中，9042C AC BC ===∠°，，，分别以AC 、BC 为直径画半圆，则图中阴影部分的面积 为 ．（结果保留π）12. 对于每个非零自然数n ，抛物线2211(1)(1)n n n n n y x x +++=-+与x 轴交于A n 、B n 两点，以n nA B 表示这两点间的距离，则112220092009A B A B A B +++的值是____________13、已知a 、b 、c 102b 2－＝，则代数式a ＋c 的值是 14．如果三位数abc (表示百位数字为a,十位数字为b,个位数字为c 的三位数),且满足b ＜a 或b ＜c ，则称这个三位数为“凹数”。