北京理工大学20172018学年工数上期末试题A及答案.docx

华南农业大学期末考试试卷（A 卷）2017~2018学年第2学期 考试科目：高等数学B Ⅱ 考试类型：（闭卷）考试 考试时间： 120 分钟 学号 姓名 年级专业一、填空题（本大题共5小题，每小题3分，共15分） 1．设{3,1,1}=a,{2,0,1}=b ，则23-=a b .2．函数zy u x ⎛⎫= ⎪⎝⎭在点(1,1,2)处的全微分为 ．3．设{(,)1}D x y x y =+≤，则二重积分(||)Dx y dxdy +=⎰⎰ ．4．幂级数21(1)2nn n n x +∞=-∑的收敛区间为 ．5．微分方程2(1)2x y xy '''+=满足初始条件(0)1,(0)3y y '==的特解为 ．二、单项选择题（本大题共5小题，每小题3分，共15分） 1．平面3380x y --=与z 轴的位置关系是（ ）A ．平行于z 轴；B ．垂直于z 轴；C ．斜交于z 轴；D ．包含z 轴．2．函数(3)zxy x y =--的极值点是（）（A ）(0,0)； （B ）(1,1)； （C ）(3,0)； （D ）(0,3) 3．2111(,)xdx f x y dy =⎰⎰ （ ）A ．12112(,)xdy f x y dx ⎰⎰； B ．2111(,)xd y f x y dx ⎰⎰；C ．12112(,)ydy f x y dx ⎰⎰； D ．2211(,)ydy f x y dx ⎰⎰．4．下列级数收敛的是 （ ）A ．11(2)n n n n +∞=++∑； B ．132nn n n +∞=⋅∑； C ．11ln n n n +∞=+∑； D．1n +∞=． 5．差分方程120t ty y +-=的通解为 （ ）A ．2t t y C =；B ．2t t y Ct =⋅；C ．12()2t t y C t C =+⋅；D ．12()2t t y t C t C =+⋅．三、计算题（本大题共6小题，每小题8分，共48分） 1. 求过点(2,0,2)-且与212:123x y z L --==垂直的平面方程．2. 设函数ln()z y xy =，求2z x y ∂∂∂及22zy ∂∂．3. 设2ln z u v =，32,yu x y v x=+=，求dz ．4．试将函数()lg f x x =展开成1x -的幂级数，并求展开式成立的区间．5．计算二重积分sin DyI dxdy y=⎰⎰，其中D 是由直线y x =及2y x =所围成的闭区域．6．设方程组dD Y dt αβ=+；dYY dtγ=，其中，()D D t =表示国民债务，()Y t 表示国民收入， 0,0,0αβγ>>>均为已知常数,若0(0)D D =，0(0)Y Y =，求()D t 和()Y t四、解答题（本大题共3小题，第1题 10分，第2、3题各6分，共 22 分） 1．某工厂生产甲、乙两种产品的日产量分别为x 件和y 件，总成本函数为22(,)1000812C x y x xy y =+-+ (元)。

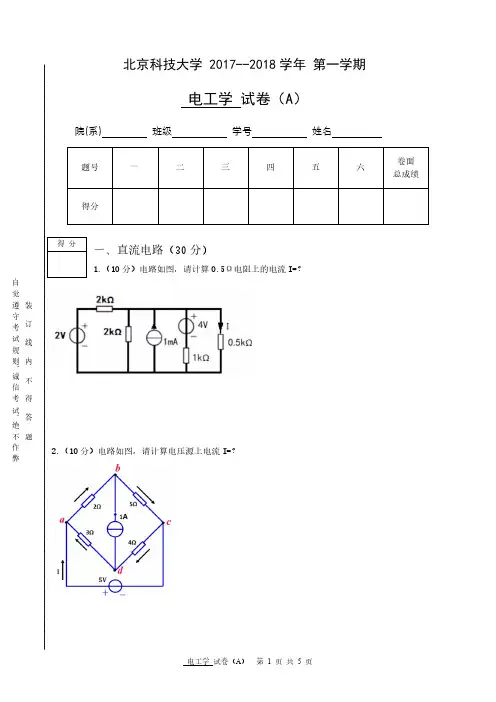
3.（10分）电路如图，开关K 原来在1位置停留较久，现在t=0时刻切换到2位置，请计算图中2k Ω电阻上电流)(t i 的变化情况？
二、交流电路（8分）
4.（8分）如图所示电路，求：（a ）输出与输入之间的关系方程；（b ）当R R R ==21，C C C ==21时，电路什么时候输出幅值最大？最大幅值为多少？
得 分
21分）
(a)静态分析的任务是什么？(b)动态分析请问是什么原因？应如何
，使u o =8u i1 + 6u i2 - 3u i3，并将下列电路图补充完整。

W7805为例），并标出其中的4个主要功能部
四、门电路和组合逻辑电路（18分） 8.（9分）请设计一个逻辑电路，输入有A 、B 、C 三个逻辑变量，要求输出：当C=0时，输
出A ；当C=1时，输出B 。

并要求全部使用与非门来实现你的电路。

9.（9分）如图所示，74LS138为3-8线译码器，输入有A 、B 、C 三个逻辑变量，请写出如图所示输出Z 与输入之间的关系。

（提示：译码器输出可描述为i i m Y =）
五、时序逻辑电路（18分） 10.（9分）如图所示电路，输入A 和CP 的波形如图，请画出输出信号Q 的波形。

CP
A
Q
得 分
得 分
2片74LS290芯片及少量门电路，实现十进制数28进制的计数器。

六、AD/DA 电路（5分） 12.（5分）请用200字左右简述教材上AD 变换电路的主要原理。

1、水平梁由AC、BC二部分组成，A端插入墙内，B端搁在辊轴支座上，Ｃ处用铰连接，受F、M作用。

已知F＝４ｋＮ，M＝６ｋＮ·ｍ，求A、B两处的反力。

2、一外形为半圆弧的凸轮A，半径r=500mm，沿水平方向向右作匀加速运动，
=800mm/s2。

凸轮推动直杆BC沿铅直导槽上下运动。

设在图所示瞬其加速度a
Ａ
=600mm/s，若用点的合成运动的方法求解
时，v
Ａ
（1）选动点、动系、静系
动点
动系
静系
绝对运动
相对运动
牵连运动
（2）求图示瞬时B点相对凸轮的速度
（3）求图示瞬时B点相对凸轮的加速度
3、已知A、B的质量为m1、m2，鼓轮半径为r，绳子过B的质心在
常力偶M 作用下，轮B 拖动A 沿倾角为θ的斜面运动，不计摩擦试求物块沿斜面向上运动S 时，A 的速度、加速度及轮轴O 处的约束
力。

1、外伸梁受力如图，求支座反力
2、刚架受力如图，F=5KN, M=2.5KN.m 求支座处的约束力（长度单位为m ）
B
M
3、曲柄OA 长为r ，以角速度ω转动，圆盘半径为R ，在固定水平面上只滚不滑。

试在图上画出作平面运动的构件的速度瞬心，并求图示
瞬
时
B
点
的
速
度。

4、平面力系如图，已知F1=F2=F,M=Fa
若将力系向O 点简化，试计算该力系主矢和主矩的大小
5、均质杆长为l ，重P ，可绕水平轴O 转动。

在图示瞬时杆的角速度为ω，角加速度为α，试求惯性力系向点O 简化结果，并将结果画在图上
a
a
O。

第一学期高中新课程模块考试试题（卷）高一数学第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知变量a b 、已被赋值，要交换a b 、的值，采用的算法是（ ）A ．a b =，b a =B ．a c =，b a =，c b =C ．a c =，b a = ，c a =D ．c a =，a b =，b c =2.从某年纪1000名学生中抽取125名学生进行体重的统计分析，就这个问题来说，下列说法正确的是（ ）A ．1000名学生是总体B ．每个被抽查的学生是个体C ．抽查的125名学生的体重是一个样本D ．抽取的125名学生的体重是样本容量3.阅读下边的程序框图，运行相应的程序，则输出s 的值为（ ）A ．-1B ．0C ．1D ． 34.一个年级有12个班,每个班有50名同学,随机编号1,2，…，50，为了了解他们在课外的兴趣，要求每班第40号同学留下来进行问卷调查,这里运用的抽样方法是（ ）A.抽签法B.有放回抽样C.随机抽样D.系统抽样5.下列抽样实验中,最适宜用系统抽样的是（ ）A.某市的4个区共有2000名学生,且4个区的学生人数之比为3: 2 :8 :2,从中抽取200人入样B 从某厂生产的2000个电子元件中随机抽取5个入样C.从某厂生产的2000个电子元件中随机抽取200个入样D.从某厂生产的20个电子元件中随机抽取5个入样6.某学院A B C 、、三个专业共有1200名学生,为了调查这些学生勤工俭学的情况，拟采用分层抽样的方祛抽取一个容量为120的样本,已知该学院的A 专业有380名学生,B 专业有420名学生，则在该学院的C 专业应抽取的学生人数为（ ）A ．30B ．40 C. 50 D ．607.当5x =，20y =-时，下边程序运行后输出的结果为（ ）A ．22，-22B ．22,22 C. 12，-12 D ．-12,128.现要完成下列3项抽样调查:①从10盒酸奶中抽取3盒进行食品卫生检查;②科技报告厅有32排，每排有40个座位，有一次报告会恰好坐满了听众，报告会结束后，为了听取意见，需要请32名听众进行座谈;③东方中学共有160名教职工，其中一般教师120名,行政人员16名,后勤人员24名,为了了解教职工对学校在校务公开方面的意见，拟抽取一个容量为20的样本。

2017-2018学年度第二学期期末质量监测七年级数学试卷注意事项：1.本次考试试卷共6页，试卷总分120分，考试时间90分钟。

2.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答题前，务必在答题卡规定的地方填写自己的姓名、准考证号，并认真核对答题卡上所粘贴的条形码中姓名、准考证号和本人姓名、准考证号是否一致。

3.回答第Ⅰ卷时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再涂选其它答案标号。

写在本试卷上无效。

一、精心选一选，慧眼识金（本大题共16个小题：每小题3分，共48分。

在每小题给出的四个选项中，只有一个是符合题目要求的）1.计算23a a ⋅正确的是A.aB.5aC.6aD.9a2.某种细菌直径约为0.00000067mm ，若将0.00000067mm 用科学记数法表示为n 107.6⨯mm （n 为负整数），则n 的值为A.-5B.-6C.-7D.-83.下列三天线段不能构成三角形的三边的是A.3cm ，4cm ，5cmB.5cm ，6cm ，11cmC.5cm ，6cm ，10cmD.2cm ，3cm ，4cm4.如图，直线a ，b 被直线c 所截，若a ∥b ，=∠︒=∠︒=∠3702401，则，A.70°B.100°C.110°D.120°5.当x ＜a ＜0时，2x 与ax 的大小关系是A.2x ＞axB.2x ≥axC.2x ＜axD.2x ≤ax6.不等式组⎩⎨⎧≤+x4-168-x 213x 4＞的最小整数解是A.0B.-1C.1D.27.如图，下列能判定AB ∥EF 的条件有①︒=∠+∠180BFE B ②21∠=∠③43∠=∠ ④5∠=∠BA.1个B.2个C.3个D.4个8.当a ，b 互为相反数时，代数式2a +ab-4的值为A.4B.0C.-3D.-49.下列运算正确的是A.222b a b a +=+）（B.（-2ab 3）622b a 4-= C.3a 632a a 2-= D.a 3-a=a （a+1）（a-1）10.（-8）201320148-）（+能被下列整数除的是 A.3 B.5 C.7 D.911.若不等式组⎩⎨⎧-a x ＜＜x 312的解集是x ＜2，则a 的取值范围是 A.a ＜2 B.a ≤2 C.a ≥2 D.无法确定12.如图，是三个等边三角形（注：等边三角形的三个内角都相等）随意摆放的图形，则321∠+∠+∠等于A.90°B.120°C.150°D.180°13.把三张大小相同的正方形卡片A 、B 、C 叠放在一个底面为正方形的盒底上，底面未被卡片覆盖的部分用阴影表示，若按图1摆放时，阴影部分的面积为S 1；若按图2摆放时，阴影部分的面积为S 2，则S 1和S 2的大小关系是A.S 1＞S 2B.S 1＜S 2C.S 1=S 2D.无法确定14.已知的结果为，则计算：2m -m -m 01-m -m 342+= A.3 B.-3 C.5 D.-515.甲、乙两人从相距24km 的A 、B 两地沿着同一条公路相向而行，如果甲的速度是乙得速度的两倍，要保证在2小时以内相遇，则甲的速度A.小于8km/hB.大于8km/hC.小于4km/hD.大于4km/h16.如图，E 是△ABC 中BC 边上的一点，且BE=31BC ；点D 是AC 上一点，且AD=41AC ，S=-=∆∆∆AD F EF ABC S S ，则24A.1B.2C.3D.4第Ⅱ （非选择题，共72分）二、细心填一填，一锤定音（每小题3分，共12分）17.分解因式：2-x 22= 。

课程编号：100172003 北京理工大学2017-2018学年第二学期2016级概率与数理统计试题（A 卷）座号 班级 学号 姓名附表：φ(2)=0.9772, φ(1.64)=0.95,φ(1.96)=0.975,0.025(15) 2.1314 t ,0.025(16) 2.1199 t ,0.05(15) 1.7531 t ,0.05(16) 1.7459 t ,20.025(4)11.1433 ,20.975(4)0.4844 ,20.025(5)12.8325 , 20.975(5)0.8312 ，20.05(4)9.4877 , 20.95(4)0.7107 ,20.5845(4)=2.8428一、填空题（12分）1．设 A ，B 为两个事件，则事件 A B 表示 （回答该事件表示的含义）. 2. 若P (A )=0.6, ()0.84P A B ，(|)0.4P B A 则P (B )= .3. 设随机变量X 的密度函数为 2,01,0,x x f x其他，用Y 表示对X 的3次独立重复观察中事件1{}2X 出现的次数，则 2P Y .4. 设随机变量X 和Y 相互独立，都服从参数为2的泊松分布，则P {X+Y=0}=________ .5.已知EX = −2, EX 2= 5，则D (1−3X )= .6. 设随机变量X 满足E (X )=μ，D (X )=σ2，则由切比雪夫不等式可得 P (|X-μ|>3σ)≤ .7. 设随机变量序列X 1, X 2,… , X n ,…相互独立, 都服从参数λ=1的泊松分布，则)2(lim 1n n X X P n n= .8. 设随机变量 和 相互独立且)(~),(~22m n ，则 )( E , )( D . 9. 已知一批零件的长度X (单位：cm)服从正态分布N (μ,1), 从中随机的取出16个零件，得到长度的平均值为40cm ，则μ的置信水平为95%的置信区间是___________.10. 设总体X ~N ( , 2)， , 2 均未知，x 1, …, x 5是总体X 的样本值，假设H 0: 2 = 4 , H 1: 2 = 1.在显著性水平 = 0.05下的拒绝域是s 2 0.7107，则该检验犯第一类错误的概率是_________，犯第二类错误的概率是__________.二、（12甲、乙、丙3台机床各自独立的加工同一种零件，已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为14，乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为112，甲、丙两台机床加工的零件都是一等品的概率为320.1. 分别求甲、乙、丙3台机床各自加工的零件是一等品的概率；2. 从甲、乙、丙加工的零件中各自取一个检验，求至少有一个一等品的概率.三、（161.设离散型随机变量X 的分布律为令2X Y .（1）确定常数c 的值；（2）求Y 的分布律；（3）求Y 的分布函数。

《高等数学B(一)》 A 卷 共（6）页，第（1）页河北科技大学2017—2018学年第一学期高等数学考试试卷 (A 卷)一、单项选择题 （每小题3分，共15分）1．当0x →时，与x 等价的无穷小是（）.(A) 1x e - (B) 1cos x - (C) 1cos x + (D) ln(1)x + 2．微分方程650y y y '''-+=的通解为（ ）. (A)512x x y C e C e -=+ (B) 512x x y C e C e =+ (C) 512x x y C e C e -=+ (D) 512x x y C e C e --=+ 3．曲线3y x =在点(1,1)处的切线方程为 ( ) . (A) 320y x +-= (B) 320y x ++= (C) 320y x -+= (D) 320y x --=4．二阶微分方程2x y y y e '''++=的特解形式应设为（ ）. (A)*x y ae = (B) *()x y ax b e =+ (C) *x y axe = (D) *2x y ax e = 5．设()f x 在区间(,)a b 内可导，1x ,2x 是(,)a b 内的任意两点，且12x x <，则至少存在一点ξ，使得下列等式成立的是( ) .(A) ()()()()f b f a f b a ξ'-=-，(,)a b ξ∈学院 考场号 座位号 班级 姓名 学号密 封 线 内 不 要 答 题《高等数学B(一)》 A 卷 共（6）页，第（2）页(B) 11()()()()f b f x f b x ξ'-=-，1(,)x b ξ∈(C) 2121()()()()f x f x f x x ξ'-=-，12(,)x x ξ∈ (D) 22()()()()f x f a f x a ξ'-=-，2(,)a x ξ∈二、填空题 （每小题3分，共15分）1．积分()121sin x x xx -+=⎰d ___________.2．积分211x x +∞=+⎰d ___________. 3．极限011lim sin sin x x x x x →⎛⎫+= ⎪⎝⎭_________.4．已知函数()1(12),0,,0x x x f x a x ⎧⎪+≠=⎨⎪=⎩在0x =处连续，则=a ________.5．若()cos f x x x C =+⎰d ，则()f x '=_____________.三、（6分）验证罗尔定理对函数22()(1)f x x x =-在区间[0,1]上的正确性，并求出相应的点ξ的值.《高等数学B(一)》 A 卷 共（6）页，第（3）页四、计算下列各题 （每小题7分，共28分）1．若函数()y y x =由参数方程00sin ,02(1cos )t tx u u t y u uπ⎧=⎪⎛⎫≤≤⎨ ⎪⎝⎭⎪=-⎩⎰⎰d d 确定， 求(1) ()y x '；(2) 0lim ()x y x →'.2．求积分0x π⎰.学院 考场号 座位号 班级 姓名 学号密 封 线 内 不 要 答 题《高等数学B(一)》 A 卷 共（6）页，第（4）页3．求积分ln x x x ⎰d .4．求函数y =的间断点，并讨论这些间断点是第一类还是第二类间断点？《高等数学B(一)》 A 卷 共（6）页，第（5）页五、解答下列各题 （每小题9分，共36分）1. 求微分方程23yxy x x+=d d 的通解.2. 求函数22,0,()31,0,x e x f x x x ⎧≤⎪=⎨+>⎪⎩求30(1)f x x -⎰d .学院 考场号 座位号 班级 姓名 学号密 封 线 内 不 要 答 题《高等数学B(一)》 A 卷 共（6）页，第（6）页3.设D 是由曲线3y x =，与直线2x =及x 轴所围成的平面图形，求(1) D 的面积S ；(2) 平面图形D 绕y 轴旋转一周所形成的立体的体积V .4.求函数23()3xf x x =-的单调区间与极值.。

2017-2018学年度第二学期高二年级化学期末练习考试时间90分钟Ⅰ卷（共60分）本部分共30道小题，每小题2分，共60分。

请在每小题列出的四个选项中，选出最符合题目要求的一项。

1．下列电池工作时，O2在正极放电的是（）【答案】B2．我国酒文化源远流长。

下列古法酿酒工艺中，以发生化学反应为主的过程是（）【答案】B3．下列化合物中，属于弱电解质的是（）A．NaOH B．CH3COOH C．NH4Cl D．H2SO4【答案】B4．下列与化学反应能量变化相关的叙述正确的是（）A ．同时改变两个变量来研究反映速率的变化，能更快得出有关规律B ．从HF 、HCl 、HBr 、HI 酸性递增的事实，推出F 、Cl 、Br 、I 的非金属递增的规律C ．利用盖斯定律，可计算某些难以直接测量的反应对应的焓变D ．同温同压下，1mol 甲烷完全燃烧生成CO 2气体和水蒸气时放出的热量称之为燃烧热 【答案】C5．下列化学用语表述正确的是（ ） A ．二氧化碳的结构式：O=C=OB ．氯化氢的电子式：H [:Cl :]+-ggggC ．31H 的原子结构示意图：D ．水的电离方程式：H 2O=H ++OH -【答案】A6．下列关于金属腐蚀与防护的说法正确的是（ ） A ．金属腐蚀就是金属失去电子被还原的过程 B ．铝制品的耐腐蚀性强，说明铝的化学性质不活泼C ．将海水中钢铁闸门与电源的负极相连，可防止闸门被腐蚀D ．铁门上的铜铆钉处在潮湿的空气中直接发生反应：Fe-3e -=Fe 3+ 【答案】C7．下列离子方程式书写正确的是（ ） A ．FeCl 3水解：Fe 3++3H 2OFe(OH)3↓+3H +B ．氯化铵溶液呈酸性：4NH ++2H 2OH 3O ++NH 3·H 2O C ．碳酸钠溶液呈碱性：23CO -+2H 2OH 2CO 3+2OH -D ．碳酸氢钠水解：3HCO -+H 2OH 2O+CO 2↑+OH -【答案】B8．下列离子方程式中，不正确．．．的是（）A．用NaOH溶液除去铝箔表面的氧化膜Al2O3+2OH-===2AlO-+H2O2B．向AlCl3溶液中加入过量氨水Al3++3NH3·H2O===Al(OH)3↓+3NH+4 C．用胃舒平（复方氢氧化铝）缓解胃酸（HCl）过多OH-+H+===H2OD．向污水中投放明矾，生成能凝聚悬浮物的胶体Al3++3H 2O Al(OH)3(胶体)+3H+ 【答案】C9．室温下，关于1.0mL0.1mol/L氨水，下列判断正确的是（）A．溶液的pH等于13 B．加入少量NH4Cl固体，c(OH-)不变C．c(OH-)=c(NH+)+c(H+) D．与1.0mL0.1mol/L盐酸混合后，溶4液呈中性【答案】C10．用Cl2生产某些含氯有机物时会生成副产物HCl，利用下列反应可实现氯的循环利用：(g)2Cl2(g)+H2O(g)ΔH=-115.6kJ/mol4HCl(g)+O恒温恒容的密闭容器中，充入一定量的反应物发生上述反应，能充分说明该反应达到化学平衡状态的是（）A．气体的质量不再改变B．氯化氢的转化率不再改变C．断开4molH-Cl键的同时生成4molH-O键D．n(HCl)：n(O2)：n(Cl2)：n(H2O)=4：1：2：2【答案】B(g)+O2(g)2SO3(g)ΔH=akJ·mol-1，反应能量变化如图所示。

北京海淀区2017-2018高二数学上学期期末试题（理科带答案）海淀区高二年级第一学期期末练习数学（理科）2018.1第一部分（选择题共40分）一、选择题共8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）直线在轴上的截距为A.B.C.D.（2）在空间直角坐标系中，已知点，则线段的中点的坐标是A.B.C.D.（3）已知圆经过原点，则实数等于A.B.C.D.（4）鲁班锁是曾广泛流传于民间的智力玩具，它起源于中国古代建筑中首创的榫卯结构，不用钉子和绳子，完全靠自身结构的连接支撑.它看似简单，却凝结着不平凡的智慧.下图为鲁班锁的其中一个零件的三视图，则该零件的体积为A.32B.34C.36D.40（5）已知平面，直线，下列命题中假命题是A.若，，则B.若，，则C.若，，则D.若，，，则（6）椭圆的焦点为，若点在上且满足，则中最大角为A.B.C.D.（7）“”是“方程表示双曲线”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件（8）平面两两互相垂直，在平面内有一个点到平面，平面的距离都等于1.则在平面内与点，平面，平面距离都相等的点的个数为A.1B.2C.3D.4第二部分（非选择题共110分）二、填空题共6小题，每小题4分，共24分。

（9）直线的倾斜角为,经过点且与直线平行的直线方程为. （10）直线被圆所截得的弦长为.（11）请从正方体的8个顶点中，找出4个点构成一个三棱锥，使得这个三棱锥的4个面都是直角三角形，则这4个点可以是.（只需写出一组）（12）在空间直角坐标系中，已知点，若三点共线，则. （13）已知椭圆和双曲线的中心均在原点，且焦点均在轴上，从每条曲线上取两个点，将其坐标记录于下表中，则双曲线的离心率为.04（14）曲线的方程为①请写出曲线的两条对称轴方程；②请写出曲线上的两个点的坐标；③曲线上的点到原点的距离的取值范围是.三、解答题共4小题，共44分。

河南理工大学 2017-2018 学年第 一 学期《高等数学b1》期末试卷（A 卷）本次考试时长110分钟，满分100分。

试卷共3页，第三页是演草纸，请取下使用，不要把试卷当演草纸，本次考试没有答题卡和答题纸，答案务必写在试卷上，考试结束时试卷上交。

请在密封线外填写专业班级、姓名和学号，不填或填错可能会影响成绩。

1．函数()x ee xf xx sin )(-+=在定义域上是 ( )（A ）若函数)(x f 在0x 处可导，则函数)(x f 在0x 处连续； （B ）若函数)(x f 在0x 处不连续，则函数)(x f 在0x 处不可导； （C ）若函数)(x f 在0x 处可导，则函数)(x f 在0x 处可微； （D ）若函数)(x f 在0x 处连续，则函数)(x f 在0x 处可导．2．如果)(lim 0x f x x →存在，)(lim 0x g x x →不存在，则下面一定正确的是（ ）（A ）)]()([lim 0x g x f x x +→不存在；（B ）)]()([lim 0x g x f x x +→存在；（C ）)()(lim 0x g x f x x →不存在；（D ）)()(lim 0x g x f x x →存在．3．当+∞→x 时，关于函数x x sin 的说法正确的是（ ） （A ）是无穷大； （B ）不是无穷大但有界； （C ）不是无穷大但无界； （D ）是无穷大但有界． 4．设函数)(x f y =在0x 处的导数2)(0='x f ，则当0→x ∆时，)(x f 在0x 处的微分y d 是（ ）． （A ）比x ∆高阶的无穷小 （B ）比x ∆低阶的无穷小（C ）与x ∆等价的无穷小（D ）与x ∆同阶的无穷小但不是等价无穷小5．设在]1,0[上0)(>''x f ，则)0()1(),1(),0(f f f f -''的大小关系为（ ）． （A ）)0()1()0()1(f f f f ->'>'； （B ）)0()0()1()1(f f f f '>->'； （C ）)0()1()0()1(f f f f '>'>-； （D ）)1()0()1()0(f f f f '>->' 6．设)(x f 的定义域为]1,1[-，则)(a x f -的定义域是．7．=∞→n nn 23sin2lim ．8．=--+→hh x h x h )ln()ln(lim000．9．设x e y xsin =，则='y． 10．函数xe y =的n 阶麦克劳林公式．11．求)2sin(10)1(lim x x x +→．12．设)(sin 2x f y =，求22d d xy．13．)31ln()1cos(1lim 20x e x x ---→．一、选择填空题（共10题，每题4分，请把正确答案填在括号内或横线上，不写在括号内或横线上不得分.）二、计算题（共6题，每题6分,请写出必要的文字说明和做题过程．）14．求函数2332)(x x x f -=在]4,1[-上最大值和最小值．15．设)(x f y =是由e xy e y =+确定的函数，求)0(y ''．16．指出函数xx y 1+=的凹凸区间．17．当0>x 时，试证221)1ln(x x x ->+．18．设)(x f 在],0[a 上连续，在),0(a 内可导，且0)(=a f ，证明：存在一点)(0,a ∈ξ，使0)()(='+ξξξf f ．19．设,00||sin 24)(21⎪⎪⎩⎪⎪⎨⎧=≠+++=x x x x e e x f xx讨论函数)(x f 的连续性，并指明间断点类型．三、解答题（共3题，每题8分，请写出必要的文字说明和做题过程．）。

2017-2018学年北京市101中学高二（上）期末数学试卷（理科）一、选择题共8小题．在每小题列出的四个选项中，选出符合题目要求的一项．1．（5分）双曲线的两焦点坐标是F1（3，0），F2（﹣3，0），2b=4，则双曲线的标准方程是（）A．﹣=1 B．=1 C．﹣=1 D．﹣=12．（5分）命题“∃x0∈（0，+∞），lnx0=x0﹣1”的否定是（）A．∀x∉（0，+∞），lnx=x﹣1 B．∀x∈（0，+∞），lnx≠x﹣1C．∃x0∈（0，+∞），lnx0≠x0﹣1 D．∃x0∉（0，+∞），lnx0=x0﹣13．（5分）抛物线y=4x2的焦点坐标是（）A．（0，1） B．（0，）C．（1，0） D．（，0）4．（5分）有下列三个命题：①“若x+y=0，则x，y互为相反数”的逆命题；②“若x＞y，则x2＞y2”的逆否命题；③“若x＜﹣3，则x2+x﹣6＞0”的否命题．则真命题的个数是（）A．3 B．2 C．1 D．05．（5分）4名大学生到三家企业应聘，每名大学生至多被一家企业录用，则每家企业至少录用一名大学生的情况有（）A．24种B．36种C．48种D．60种6．（5分）已知圆M：x2+y2﹣2ay=0截直线x+y=0所得的线段长是2，则a的值为（）A．B．2 C．D．±27．（5分）从0、2中选一个数字．从1、3、5中选两个数字，组成无重复数字的三位数．其中奇数的个数为（）A．24 B．18 C．12 D．68．（5分）设双曲线C的中心为点O，若有且只有一对相交于点O，所成的角为60°的直线A1B1和A2B2，使|A1B1|=|A2B2|，其中A1、B1和A2、B2分别是这对直线与双曲线C的交点，则该双曲线的离心率的取值范围是（）A．B．C．D．二、填空题共6小题．9．（5分）双曲线3x2﹣y2=﹣3的渐近线方程为．10．（5分）设常数a∈R，若（x2+）5的二项展开式中x7项的系数为﹣10，则a=．11．（5分）设F1、F2分别是椭圆+=1的左、右焦点．若点P在椭圆上，且•=0，则|+|=．12．（5分）若双曲线=1与直线y=kx﹣l有且仅有一个公共点，则这样的直线有条．13．（5分）已知点P在抛物线y2=4x上，那么当点P到点Q（3，4）的距离与点P到抛物线准线的距离之和取得最小值时，点P的坐标为．14．（5分）下列四个命题中①“k=1”是“函数y=cos2kx﹣sin2kx的最小正周期为π”的充要条件；②“a=3”是“直线ax+2y+3a=0与直线3x+（a﹣1）y=a﹣7相互垂直”的充要条件；③函数的最小值为2其中假命题的为（将你认为是假命题的序号都填上）三、解答题共5小题，每小题10分，共50分．解答应写出文字说明、演算步骤或证明过程．15．（10分）命题p：关于x的不等式x2+2ax+4＞0对一切x∈R恒成立；命题q：函数f（x）=log a x（a＞0且a≠1）在（0，+∞）上单调递增．若p∨q为真，而p∧q为假，求实数a的取值范围．16．（10分）已知P是椭圆上的一点，F1，F2是椭圆上的两个焦点，（1）当时，求△F1PF2的面积（2）当∠F1PF2为钝角时，求点P横坐标的取值范围．17．（10分）如图所示，在Rt△ABC中，已知点A（﹣2，0），直角顶点B（0，﹣2），点C在x轴上．（1）求Rt△ABC外接圆的方程；（2）求过点（﹣4，0）且与Rt△ABC外接圆相切的直线的方程．18．（10分）定长为2的线段AB的两个端点在以点（0，）为焦点的抛物线x2=2py 上移动，记线段AB的中点为M，求点M到x轴的最短距离，并求此时点M的坐标．19．（10分）已知椭圆C的中心在原点，焦点在x轴上，左右焦点分别为F1，F2，且|F1F2|=2，点（1，）在椭圆C上．（Ⅰ）求椭圆C的方程；（Ⅱ）过F1的直线l与椭圆C相交于A，B两点，且△AF2B的面积为，求以F2为圆心且与直线l相切的圆的方程．2017-2018学年北京市101中学高二（上）期末数学试卷（理科）参考答案与试题解析一、选择题共8小题．在每小题列出的四个选项中，选出符合题目要求的一项．1．（5分）双曲线的两焦点坐标是F1（3，0），F2（﹣3，0），2b=4，则双曲线的标准方程是（）A．﹣=1 B．=1 C．﹣=1 D．﹣=1【解答】解：∵双曲线的两焦点坐标是F1（3，0），F2（﹣3，0），2b=4，∴焦点在x轴上，且c=3，b=2，∴a=，∴双曲线的标准方程是﹣=1．故选：A．2．（5分）命题“∃x0∈（0，+∞），lnx0=x0﹣1”的否定是（）A．∀x∉（0，+∞），lnx=x﹣1 B．∀x∈（0，+∞），lnx≠x﹣1C．∃x0∈（0，+∞），lnx0≠x0﹣1 D．∃x0∉（0，+∞），lnx0=x0﹣1【解答】解：命题“∃x0∈（0，+∞），lnx0=x0﹣1”的否定是“∀x∈（0，+∞），lnx ≠x﹣1”故选：B．3．（5分）抛物线y=4x2的焦点坐标是（）A．（0，1） B．（0，）C．（1，0） D．（，0）【解答】解：抛物线y=4x2的标准方程为x2=y，p=，开口向上，焦点在y 轴的正半轴上，故焦点坐标为（0，），故选：B．4．（5分）有下列三个命题：①“若x+y=0，则x，y互为相反数”的逆命题；②“若x＞y，则x2＞y2”的逆否命题；③“若x＜﹣3，则x2+x﹣6＞0”的否命题．则真命题的个数是（）A．3 B．2 C．1 D．0【解答】解：①“若x+y=0，则x，y互为相反数”的逆命题为：“若x，y互为相反数，则x+y=0”正确；②“若x＞y，则x2＞y2”的逆否命题为：“若x2≤y2，则x≤y”，不正确；③“若x＜﹣3，则x2+x﹣6＞0”的否命题为：“若x≥﹣3，则x2+x﹣6≤0”不正确．综上可知：真命题的个数是1个；故选：C．5．（5分）4名大学生到三家企业应聘，每名大学生至多被一家企业录用，则每家企业至少录用一名大学生的情况有（）A．24种B．36种C．48种D．60种【解答】解：分两类，第一类，有3名被录用，有=24种，第二类，4名都被录用，则有一家录用两名，有=36，根据分类计数原理，共有24+36=60（种）故选：D．6．（5分）已知圆M：x2+y2﹣2ay=0截直线x+y=0所得的线段长是2，则a的值为（）A．B．2 C．D．±2【解答】解：化圆M：x2+y2﹣2ay=0为x2+（y﹣a）2=a2．∴圆M的圆心为（0，a），半径r=|a|，∴圆心M到直线x+y=0的距离d=，=|a|2，解得a=±2．故选：D．7．（5分）从0、2中选一个数字．从1、3、5中选两个数字，组成无重复数字的三位数．其中奇数的个数为（）A．24 B．18 C．12 D．6【解答】解：从0、2中选一个数字0，则0只能排在十位，从1、3、5中选两个数字排在个位与百位，共有=6种；从0、2中选一个数字2，则2排在十位，从1、3、5中选两个数字排在个位与百位，共有=6种；2排在百位，从1、3、5中选两个数字排在个位与十位，共有=6种；故共有3=18种故选：B．8．（5分）设双曲线C的中心为点O，若有且只有一对相交于点O，所成的角为60°的直线A1B1和A2B2，使|A1B1|=|A2B2|，其中A1、B1和A2、B2分别是这对直线与双曲线C的交点，则该双曲线的离心率的取值范围是（）A．B．C．D．【解答】解：不妨令双曲线的方程为，由|A1B1|=|A2B2|及双曲线的对称性知A1，A2，B1，B2关于x轴对称，如图，又∵满足条件的直线只有一对，当直线与x轴夹角为30°时，双曲线的渐近线与x轴夹角大于30°，双曲线与直线才能有交点A1，A2，B1，B2，若双曲线的渐近线与x轴夹角等于30°，则无交点，则不可能存在|A1B1|=|A2B2|，当直线与x轴夹角为60°时，双曲线渐近线与x轴夹角大于60°，双曲线与直线有一对交点A1，A2，B1，B2，若双曲线的渐近线与x轴夹角等于60°，也满足题中有一对直线，但是如果大于60°，则有两对直线．不符合题意，∴tan30°，即，∴，∵b2=c2﹣a2，∴，∴，∴，∴双曲线的离心率的范围是．故选：A．二、填空题共6小题．9．（5分）双曲线3x2﹣y2=﹣3的渐近线方程为y=±x．【解答】解：双曲线3x2﹣y2=﹣3的标准形式为，其渐近线方程是，整理得y=±x．故答案为：y=±x．10．（5分）设常数a∈R，若（x2+）5的二项展开式中x7项的系数为﹣10，则a=﹣2．【解答】解：的展开式的通项为T r=C5r x10﹣2r（）r=C5r x10﹣3r a r+1令10﹣3r=7得r=1，∴x7的系数是aC51∵x7的系数是﹣10，∴aC51=﹣10，解得a=﹣2．故答案为：﹣2．11．（5分）设F1、F2分别是椭圆+=1的左、右焦点．若点P在椭圆上，且•=0，则|+|=6．【解答】解：由椭圆+=1，得a=4，c2=a2﹣b2=9，又•=0，∴，即，∴4×16﹣2，即．∴|+|2=2•==4a2﹣2×14=36．∴|+|=6．故答案为：6．12．（5分）若双曲线=1与直线y=kx﹣l有且仅有一个公共点，则这样的直线有4条．【解答】解：把直线y=kx﹣1代入双曲线=1中，消y，得（4﹣9k2）x2+18kx ﹣45=0，当4﹣9k2=0，即k=±时，直线与双曲线相交有一个交点，当4﹣9k2≠0，△=0，即182k2+4（4﹣9k2）×45=0，k=±时，直线与双曲线相切，有一个交点，∴k的值有4个，故答案为：4．13．（5分）已知点P在抛物线y2=4x上，那么当点P到点Q（3，4）的距离与点P到抛物线准线的距离之和取得最小值时，点P的坐标为（，+1）．【解答】解：Q在抛物线的外侧，点P到抛物线焦点距离等于点P到抛物线准线距离，如图PF+PQ=PM+PQ，故最小值在QF的连线上，F（1，0），QF的方程为：2x﹣y﹣2=0，，结合图形，解得P（，+1）．故答案为：（，+1）．14．（5分）下列四个命题中①“k=1”是“函数y=cos2kx﹣sin2kx的最小正周期为π”的充要条件；②“a=3”是“直线ax+2y+3a=0与直线3x+（a﹣1）y=a﹣7相互垂直”的充要条件；③函数的最小值为2其中假命题的为①②③（将你认为是假命题的序号都填上）【解答】解：①y=cos2kx﹣sin2kx=cos2kx，最小正周期为π，则k=±1，即①“k=±1”是“函数y=cos2kx﹣sin2kx的最小正周期为π”的充要条件，①是个假命题；②若直线ax+2y+3a=0与直线3x+（a﹣1）y=a﹣7相互垂直，根据两条线垂直的充要条件，可得3a+2（a﹣1）=0，解可得a=，这是一个假命题；③函数y==，由于≥，则≥＞2，③是假命题，综上可知假命题有①②③，故答案为：①②③．三、解答题共5小题，每小题10分，共50分．解答应写出文字说明、演算步骤或证明过程．15．（10分）命题p：关于x的不等式x2+2ax+4＞0对一切x∈R恒成立；命题q：函数f（x）=log a x（a＞0且a≠1）在（0，+∞）上单调递增．若p∨q为真，而p∧q为假，求实数a的取值范围．【解答】解：若p为真，则△=（2a）2﹣42＜0，即﹣2＜a＜2．若q为真，则a＞1．因为p∨q为真，而p∧q为假，所以p，q一真一假．当p真q假时，，所以0＜a＜1．当p假q真时，，所以a≥2．综上，a的取值范围为（0，1）∪[2，+∞）．16．（10分）已知P是椭圆上的一点，F1，F2是椭圆上的两个焦点，（1）当时，求△F1PF2的面积（2）当∠F1PF2为钝角时，求点P横坐标的取值范围．【解答】解：（1）由椭圆的定义，得|PF 1|+|PF2|=4，且①在△F1PF2中，由余弦定理得，②由①②得，所以（2）设点P（x，y），由已知∠F1PF2为钝角，得即，即：x2+y2﹣3＜0，又，所以，解得，所以点P横坐标的取值范围是：．17．（10分）如图所示，在Rt△ABC中，已知点A（﹣2，0），直角顶点B（0，﹣2），点C在x轴上．（1）求Rt△ABC外接圆的方程；（2）求过点（﹣4，0）且与Rt△ABC外接圆相切的直线的方程．【解答】解：（1）设点C（a，0），由AB⊥BC可得k AB•k BC=﹣1，即，解得a=4．则所求的圆的圆心为AC的中点（1，0），半径为3，∴所求圆的方程为（x﹣1）2+y2=9；（2）由题意知直线的斜率存在，设所求直线的方程为y=k（x+4），即kx﹣y+4k=0．当直线和圆相切时，圆心到直线的距离等于半径，∴，解得k=，∴所求直线的方程为y=（x+4）或y=﹣（x+4），即3x﹣4y+12=0或3x+4y+12=0．18．（10分）定长为2的线段AB的两个端点在以点（0，）为焦点的抛物线x2=2py 上移动，记线段AB的中点为M，求点M到x轴的最短距离，并求此时点M的坐标．【解答】解：依题意点（0，）为焦点的抛物线x2=2py可得抛物线的方程为x2=y．设直线AB的方程为y=kx+b（k∈R），联立方程组得2x2﹣kx﹣b=0．设A（x1，y1），B（x2，y2），则x1+x2=，x1x2=﹣，y1+y2=．因为|AB|=2，所以（1+k2）[（x1+x2）2﹣4x1x2]=4，所以b=，所以y M==+b===．当且仅当k=±时取等号，所以点M到x轴的最短距离为，此时点M的坐标为（，）．19．（10分）已知椭圆C的中心在原点，焦点在x轴上，左右焦点分别为F1，F2，且|F1F2|=2，点（1，）在椭圆C上．（Ⅰ）求椭圆C的方程；（Ⅱ）过F1的直线l与椭圆C相交于A，B两点，且△AF2B的面积为，求以F2为圆心且与直线l相切的圆的方程．【解答】解：（Ⅰ）设椭圆的方程为，由题意可得：椭圆C两焦点坐标分别为F1（﹣1，0），F2（1，0）．∴．∴a=2，又c=1，b2=4﹣1=3，故椭圆的方程为．（Ⅱ）当直线l⊥x轴，计算得到：，，不符合题意．当直线l与x轴不垂直时，设直线l的方程为：y=k（x+1），由，消去y得（3+4k2）x2+8k2x+4k2﹣12=0显然△＞0成立，设A（x1，y1），B（x2，y2），则，又即，又圆F2的半径，所以，化简，得17k4+k2﹣18=0，即（k2﹣1）（17k2+18）=0，解得k=±1所以，，故圆F2的方程为：（x﹣1）2+y2=2．。

2017—2018学年度第二学期期末考试高二数学（理）试题一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 设集合A=｛4，5，7，9｝，B=｛3，4，7，8，9｝，全集U A B =U ，则集合）（B A C U I 中的元素共有（ ） A .3个 B. 4个C.5个D.6个2. 复数3223ii+=-( ) A.1 B.1-C.iD.i -3．已知)1,1(),2,(a n a m -=-=，且n m //，则a=（ ） A ．﹣1B ．2或﹣1C ．2D ．﹣24. 在区间[]1,1-上随机选取一个实数x ，则事件"210"x -< 的概率为（ ）A ．12B ．34C ．23D ．145. 已知tan a =4,cot β=13,则tan(a+β)=（ ）A.711B.711-C. 713D.713-6．在6)2(y x -的展开式中，含24y x 的项的系数是（ ） A ．15 B ．-15C ．60D ． -607.执行如图所示的程序框图，若输入的a 为2，则输出 的a 值是（ ）A. 2B. 1C.21D.1-8. 设非零向量a 、b 、c 满足c b a c b a =+==|,|||||，则>=<b a ,（ ） A.150°B.120°C.60°D.30°9. 甲组有5名男同学、3名女同学；乙组有6名男同学、2名女同学，若从甲、乙两组中各选出2名同学，则选出的4人中恰有1名女同学的不同选法共有（ ） A.150种B.180种C.300种D.345种10．下列四个结论中正确的个数是（1）对于命题,:0R x p ∈∃使得0120≤-x ，则,:R x p ∈∀⌝都有012>-x ； （2）已知),2(~2σN X ，则 (2)0.5P X >=（3）已知回归直线的斜率的估计值是2，样本点的中心为（4,5），则回归直线方程为32ˆ-=x y； （4）“1≥x ”是“21≥+xx ”的充分不必要条件. A ．1B ．2C ．3D ．411.正方体1111ABCD A B C D -中，若1D AC △外接圆半径为26，则该正方体外接球的表面积为( ) A.2πB.8πC.12πD.16π12.已知奇函数()f x 的导函数为()f x '，当0x ≠时，()()0f x f x x'+>，若11(),()a f b ef e e e==--，()1c f =，则,,a b c 的大小关系正确的是（ ） A ．a b c << B ．b c a << C ．c a b << D ．a c b <<二、填空题：本题共4小题，每小题5分，共20分。