稳态温度场求解

二维稳态温度场控制方程二维稳态温度场控制方程是描述二维空间内物体温度分布的方程，它是热传导定律的数学表达形式。

稳态温度场意味着物体内部的温度分布不随时间变化，只与空间位置有关。

此外，控制方程还考虑了边界条件和材料性质。

二维稳态温度场的控制方程可以用偏微分方程形式表示，对于矩形区域内的二维空间来说，控制方程如下：【注】用户在问题陈述中可能会给出具体的条件，如热源和边界条件，因此，参考以下方程时可以结合具体情况适当添加这些条件。

热传导方程：∂²T/∂x² + ∂²T/∂y² = 0热传导方程是一个椭圆型偏微分方程，它描述了温度分布在空间中的流动和变化。

其中T表示温度，x和y分别表示空间坐标。

边界条件：1.第一类边界条件：指定边界上的温度值。

可以是恒定的温度，如T(x,y)=T0，表示边界上的温度值为常量T0。

2.第二类边界条件：指定边界上的温度梯度。

可以是传热率，如q_n = -k * ∂T/∂n，表示边界上的传热速率等于热传导率乘以温度梯度，其中q_n是与边界垂直的热通量；k是材料的热传导率；∂T/∂n是温度沿着边界法向量方向的梯度。

材料性质：材料性质包括热扩散率和热导率。

其中热扩散率表示材料对热的传递速度的能力，热导率表示材料在单位时间内单位面积的热流量，两者通常用D和k表示。

通过数值解法，可以求解出二维稳态温度场控制方程的解析解。

数值解法中常用的方法有有限差分法和有限元法。

有限差分法将偏微分方程离散化为差分方程，通过迭代计算得到数值解。

有限元法将二维空间划分为小的有限元单元，并通过插值计算得到节点上的温度值，然后利用元素之间的关系求解整个二维区域内的温度分布。

在实际应用中，二维稳态温度场控制方程被广泛应用于热传导、传热分析、热工程和工业制造等领域。

例如，它可以用于预测电子设备中的热分布，优化散热系统设计。

也可以用于分析材料加工过程中的温度变化，以便提高生产效率和产品质量。

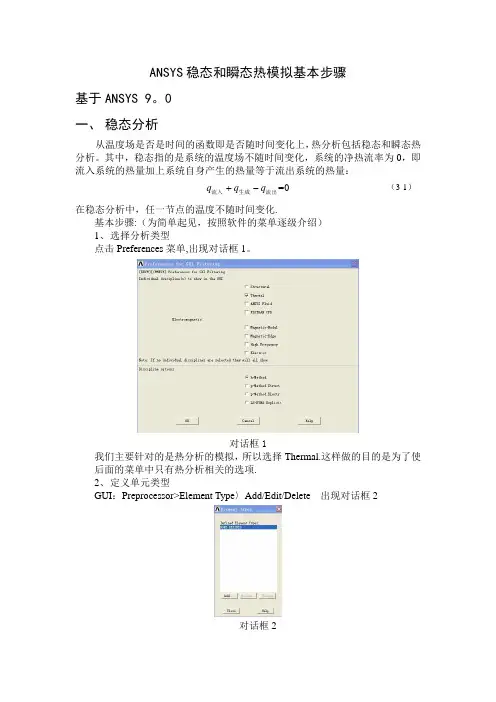
ANSYS稳态和瞬态热模拟基本步骤基于ANSYS 9。

0一、稳态分析从温度场是否是时间的函数即是否随时间变化上，热分析包括稳态和瞬态热分析。

其中，稳态指的是系统的温度场不随时间变化，系统的净热流率为0，即流入系统的热量加上系统自身产生的热量等于流出系统的热量：（3-1）=0+-q q q流入生成流出在稳态分析中，任一节点的温度不随时间变化.基本步骤:（为简单起见，按照软件的菜单逐级介绍）1、选择分析类型点击Preferences菜单,出现对话框1。

对话框1我们主要针对的是热分析的模拟，所以选择Thermal.这样做的目的是为了使后面的菜单中只有热分析相关的选项.2、定义单元类型GUI：Preprocessor>Element Type〉Add/Edit/Delete 出现对话框2对话框2点击Add，出现对话框3对话框3在ANSYS中能够用来热分析的单元大约有40种，根据所建立的模型选择合适的热分析单元。

对于三维模型，多选择SLOID87:六节点四面体单元。

3、选择温度单位默认一般都是国际单位制，温度为开尔文(K）.如要改为℃，如下操作GUI：Preprocessor>Material Props>Temperature Units选择需要的温度单位。

4、定义材料属性对于稳态分析,一般只需要定义导热系数，他可以是恒定的，也可以随温度变化。

GUI: Preprocessor〉Material Props> Material Models 出现对话框4对话框4一般热分析，材料的热导率都是各向同性的，热导率设定如对话框5.对话框5若要设定材料的热导率随温度变化,主要针对半导体材料。

则需要点击对话框5中的Add Temperature选项，设置不同温度点对应的热导率，当然温度点越多，模拟结果越准确.设置完毕后,可以点击Graph按钮,软件会生成热导率随温度变化的曲线。

对话框5中，Material菜单，New Model选项，添加多种材料的热参数。

汽车轮胎二维稳态温度场的数值分析李杰魏建华赵旗(吉林大学汽车动态模拟国家重点实验室)摘要: 通过对滚动轮胎进行合理假设，在MSC.Patran系统中建立了国产9.00-2012PR尼龙斜交轮胎二维稳态温度场有限元分析模型，用MSC.Nastran热分析求解器计算了轮胎的温度场分布，计算结果反映了轮胎的温度分布。

通过拟合得到最高温升与车速的基本线性关系，该公式可以用来简单预测轮胎不同车速稳态的最高稳升，对轮胎结构设计与使用有一定的指导意义。

1 前言对轮胎生热及其温度场的研究有试验法和数值计算法[1-3]。

试验法是通过试验直接测量轮胎温度场的分布，这种方法有一定的局限性。

随着有限元技术和计算机技术的发展，越来越多的研究者采用数值计算法获得轮胎温度场的分布，以便在设计之初就能优化轮胎结构和进行配方设计，提高轮胎的使用寿命。

本文应用MSC.Patran系统对汽车轮胎二维稳态温度场进行数值分析，通过计算得到轮胎达到生热与散热平衡时的温度场，以便为轮胎寿命预测提供依据。

2 汽车轮胎二维稳态温度场的有限元建模2.1 汽车轮胎二维稳态温度场的基本假设汽车轮胎温度场分析是一个非常复杂的课题，为了简化计算，对轮胎温度场模型提出如下假设：（1）轮胎形状是轴对称，不计花纹的影响。

（2）轮胎滚动过程中，其周向方向不存在温度梯度，任一微元体从地面所吸收的功，被均匀分配到整个圆周上，即周向无温度梯度假设。

（3）轮胎在定载和定压状态下工作，由橡胶组成，且材料为各向同性。

（4）轮胎在连续行驶一段时间后，达到热平衡状态，可看作稳态热传导问题。

（5）忽略接触摩擦生热和辐射换热。

根据上述假设，可将汽车轮胎温度场分析问题简化为通过对称轴的一个子午线平面来计算模拟轮胎内部温度分布的二维平面问题。

2.2 MSC.Nastran的热分析功能MSC.Patran系统中链接的求解器MSC.Nastran具有较强的传热分析能力，提供了一维、二维、三维、轴对称等传热分析单元，可求解各种形式的传热问题：传导、对流和辐射，可以进行稳态或瞬态传热分析，线性和非线性传热分析。

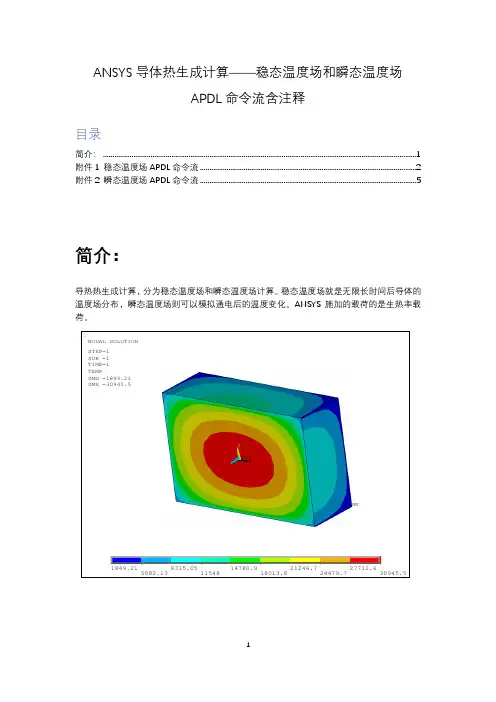
ANSYS 导体热生成计算——稳态温度场和瞬态温度场APDL 命令流含注释目录简介： (1)附件1 稳态温度场APDL 命令流 (2)附件2 瞬态温度场APDL 命令流 (5)简介：导热热生成计算，分为稳态温度场和瞬态温度场计算。

稳态温度场就是无限长时间后导体的温度场分布，瞬态温度场则可以模拟通电后的温度变化。

ANSYS 施加的载荷的是生热率载荷。

MNMX XYZ 5082.138315.0511********.918013.821246.724479.727712.6附件1 稳态温度场APDL命令流!注1：本例温度单位为℃，其余物理量采取国际单位制。

!注2：导热系数、比热等物性参数是假定的，请根据实际情况更改! ***************环境设置************************finish/clear/filn,Heat_generation/title,!基本参数h1=160e-3 !导体块体长，本例为块体X轴方向尺寸h2=100e-3 !导体块体宽，本例为块体Z轴方向尺寸h3=100e-3 !导体块体高，本例为块体Y轴方向尺寸d1=5e-3 !PC壳体厚度temp_1=0 !第一个温度点温度temp_2=50 !第二个温度点温度temp_3=100 !第三个温度点温度kxx_1_1=0.5 !导体块体在第一个温度点的导热系数kxx_1_2=0.6 !导体块体在第二个温度点的导热系数kxx_1_3=0.7 !导体块体在第三个温度点的导热系数kxx_2_1=0.21 !PC壳体在第一个温度点的导热系数kxx_2_2=0.22 !PC壳体在第二个温度点的导热系数kxx_2_3=0.23 !PC壳体在第三个温度点的导热系数C_1_1=4e3 !导体块体在第一个温度点的比热容C_1_2=4e3 !导体块体在第二个温度点的比热容C_1_3=4e3 !导体块体在第三个温度点的比热容C_2_1=1.2e3 !PC壳体在第一个温度点的比热容C_2_2=1.2e3 !PC壳体在第二个温度点的比热容C_2_3=1.2e3 !PC壳体在第三个温度点的比热容U=36 !电压伏R=60e-3 !电阻欧姆e_size=10e-3 !单元边长，此变量可以调整模型规模temp_air=20 !空气温度conv_air=25 !空气自然对流换热系数!导出参数h4=h1+2*d1 !PC壳体外部尺寸,长h5=h2+2*d1 !PC壳体外部尺寸,宽h6=h3+2*d1 !PC壳体外部尺寸,高QR=U**2/R/(h1*h2*h3) !热生成率!****************前处理*************************** /prep7et,1,70 ! 定义1号单元类型tref,20 !基准温度mptemp,1,temp_1,temp_2,temp_3 !一个温度序列mpdata,Kxx,1,1,kxx_1_1,kxx_1_2,kxx_1_3 mpdata,C,1,1,C_1_1,C_1_2,C_1_3mpdata,Kxx,2,1,kxx_2_1,kxx_2_2,kxx_2_3 mpdata,C,2,1,C_2_1,C_2_2,C_2_3!*******************建模************************** block,-h4/2,h4/2,-h6/2,h6/2,0,-h5/2wpoff,,,-h2/2vsbw,allwpcsys,-1,0wprota,,,90wpoff,,,h1/2vsbw,allwpcsys,-1,0wprota,,,90wpoff,,,-h1/2vsbw,allwpcsys,-1,0wprota,,90wpoff,,,h3/2vsbw,allwpcsys,-1,0wprota,,90wpoff,,,-h3/2vsbw,allwpcsys,-1,0nummrg,allnumcmp,all!*******************分网************************** vsel,s,,,18vatt,1allsel,allvsel,u,,,18vatt,2allsel,alllesize,all,e_size !设定单元尺寸vsweep,14vsweep,2vsweep,10vsweep,5vsweep,6vsweep,1vsweep,18vsweep,13vsweep,12vsweep,11vsweep,17vsweep,7vsweep,3vsweep,15vsweep,8vsweep,9vsweep,16vsweep,4!*******************边界条件************************** asel,s,loc,x,-h4/2 !选择PC壳体外壁asel,a,loc,x,h4/2asel,a,loc,y,-h6/2asel,a,loc,y,h6/2asel,a,loc,z,-h5/2sfa,all,,conv,conv_air,temp_airallsel,allvsel,s,mat,,1bfv,all,hgen,QRallsel,all!*******************求解**************************/soluANTYPE,STATIC !稳态热分析solve附件2 瞬态温度场APDL命令流!注1：本例温度单位为℃，其余物理量采取国际单位制。

第一章1. 热传导物体各部分之间不发生相对位移，依靠分子、原子及自由电子等微观粒子的热运动而产生的热能传递。

2. 热流量单位时间内通过某一给定面积的热量。

3. 热对流指由于流体的宏观运动而引起的流体各部分之间发生相对位移，冷、热流体相互掺混所导致的热量传递过程。

4. 导热系数表征材料导热性能优劣的参数，数值上等于在单位温度梯度作用下物体内热流密度矢量的模。

取决于物质的种类和热力状态（温度和压力等）5. 对流换热流体流过固体表面时，对流和导热的联合作用，使流体与固体壁面之间产生热量传递的过程。

6. 辐射物体通过电磁波来传递能量的方式。

7. 热辐射物体因热的原因而发出辐射能的现象。

8. 辐射传热物体不断向空间发出热辐射，又不断吸收其他物体的热辐射，辐射与吸收过程的综合结果就造成了以辐射方式进行的物体间的热量传递。

9. 传热过程热量由壁面一侧的流体通过壁面传到另一侧流体中去的过程。

10. 传热系数表征传热过程强烈尺度的标尺，数值上等于冷热流体间温差1℃、传热面积 1 ㎡时的热流量的值。

11. 传热过程热阻面积热阻（见P14）第二章1. 温度场各个时刻物体中各点温度所组成的集合。

2. 稳态温度场物体中各点温度不随时间变化的温度场。

3. 非稳态温度场物体中各点温度随时间变化的温度场。

4. 均匀温度场物体中各点温度相同的温度场。

5. 一维温度场物体中各点温度只在一个坐标方向变化的温度场。

6. 二维温度场物体中各点温度只在二个坐标方向变化的温度场。

7. 等温面温度场中同一瞬间相同温度各点连成的面。

8. 等温线在任何一个二维截面上等温面表现为等温线。

9. 导热基本定律在导热过程中，单位时间内通过给定截面的导热量，正比于垂直该截面方向上的温度变化率和截面面积，而热量传递的方向则与温度升高的方向相反。

（傅里叶定律）10. 热流线一组与等温线处处垂直的曲线，通过平面上任一点的热流线与该点的热流密度矢量相切。

11. 热流通道相邻两条热流线之间所传递的热流量处处相等，相当于构成一个热流通道。

采空区稳态流场及温度场的数学模型采空区稳态流场及温度场的数学模型是指在采空区内的流场中求解稳态流场和温度场的数学模型。

稳态流场及温度场的模拟是建立矿山安全防护工作的一个重要基础，在这里我们将深入探讨采空区稳态流场及温度场的数学模型。

首先，对采空区稳态流场和温度场的数学模型进行讨论。

采空区稳态流场及温度场的数学模型是由质量守恒方程和能量守恒方程构成的。

稳态流场模型通过考虑涡流阻力、压力阻力、喷流损失、湍流损失等因素，从几何形式上，用解析法或数值法求解流场的流动情况。

另外，稳态温度场模型主要是通过考虑对流换热、辐射换热、潜热换热等方式，从物理形式上，用解析法或数值法求解温度场的温度分布情况。

接着，我们来看看采空区内稳态流场及温度场模型的应用。

采空区稳态流场及温度场模型应用于分析采空区内空气对灰尘的传输，对污染物的传输，维护采空区内空气质量的稳定，预测和模拟火灾的发生及发展，以及其他研究。

此外，采空区内稳态流场及温度场模型也可以应用于节能优化，空调系统的设计，采空区内气象条件的监测等。

最后，我们来看看采空区稳态流场及温度场模型的研究前景。

随着采空区稳态流场及温度场的数学模型在实际应用中的日益深入，为研究工作带来的挑战也在增加。

为了满足采空区安全监督和节能优化的要求，研究者们正不断尝试更丰富的模型，并为模型的参数匹配、计算的性能及实际应用上的适应性等领域提出新的模型。

此外，研究人员还运用采空区稳态流场及温度场模型，在研究过程中将其与新兴技术如无人机、虚拟现实等相结合，探索更深层次的应用场景和可能性。

以上就是关于采空区稳态流场及温度场的数学模型的介绍，希望能够对大家有所帮助。

由于采空区从地质学，物理学，化学，机械，数学等方面都复杂且深刻，所以研究采空区稳态流场及温度场的数学模型要更加深入，以达到更好的研究成果。

在 cfd 计算中，稳态结果的中间过程是指在计算过程中所产生的各种中间变量、中间结果以及对流动和传热特性的影响。

这个主题虽然听起来有些抽象，但是却是cfd 计算中不容忽视的重要部分。

在本文中，我们将深入探讨 cfd 计算中稳态结果的中间过程，从而帮助你更全面地理解这一主题。

1.计算域的离散化在 cfd 计算中，首先需要对计算域进行离散化处理，将其分割成若干个网格单元。

这一过程中，不仅需要考虑网格尺寸的选择，还要进行网格质量的评估，以确保计算结果的准确性和稳定性。

随着计算域的复杂性增加，离散化过程中需要考虑的问题也变得更加繁杂。

2.流场和温度场的解算在 cfd 计算中，对流动和传热问题的求解是其中的核心部分。

通过对navier-stokes 方程和能量方程的离散化处理，可以得到流场和温度场的解算结果。

在这一过程中，需要考虑流动的湍流特性、流场的速度分布、压力分布以及温度场的分布情况，通过对这些中间结果的分析，可以更好地理解流动和传热特性。

3.网格独立性和收敛性分析为了验证 cfd 计算结果的准确性和可靠性，需要进行网格独立性和收敛性分析。

通过对不同网格尺寸下的计算结果进行比较，可以得到计算结果的收敛性情况，从而评估计算结果的稳定性。

这一过程中，需要不断调整网格尺寸，进行多次计算，以确保最终得到的稳态结果具有良好的收敛性。

4.边界条件和物性参数的选择在 cfd 计算中，边界条件和物性参数的选择对计算结果有着重要的影响。

通过对不同边界条件和物性参数的设定，可以得到不同的计算结果，从而进一步分析稳态结果的中间过程。

在这一过程中，需要考虑流场和温度场的边界情况、物性参数的变化对计算结果的影响，以及不同边界条件下的流动和传热特性。

总结回顾在本文中，我们深入探讨了 cfd 计算中稳态结果的中间过程。

通过对计算域的离散化、流场和温度场的解算、网格独立性和收敛性分析、边界条件和物性参数的选择等多个方面进行分析，可以更全面地理解cfd 计算中稳态结果的形成过程。

稳态温度场中,固体的热流密度与温度梯度呈正比,称为热导率,即满足关系1.引言1.1 概述概述热传导是热学中的一项重要研究内容，它描述了固体中热量传输的过程。

在稳态温度场中，固体的热流密度与温度梯度呈正比的关系，这个比例关系称为热导率。

热导率是描述固体导热性能的物理量，对于我们理解和应用热传导过程具有重要意义。

本文将首先介绍稳态温度场中的热流密度的定义以及它所描述的物理原理，然后深入探讨温度梯度与热导率之间的关系。

热导率的定义将会被详细解释，并且我们将看到热导率如何与温度梯度形成正比关系。

通过本文的研究，我们可以更好地理解固体中热传导的机制，并且能够更准确地描述和预测热传导的过程。

这对于工程领域的热设计、材料科学以及能源利用等方面具有重要意义。

本文将按照上述大纲的结构进行展开，接下来将首先详细介绍稳态温度场中的热流密度的定义和物理原理。

然后我们将探讨热导率的定义以及它与温度梯度的正比关系。

最后在结论部分，我们将对本文的内容进行总结，并得出一些结论。

随着社会的不断发展和科学技术的进步，对于热传导过程的研究变得越来越重要。

通过对热导率和温度梯度之间关系的深入研究，我们可以更好地掌握热传导的规律，为解决能源转换和热管等热学问题提供更有效的解决方案。

1.2文章结构文章结构部分的内容可以如下所示：1.2 文章结构本文将分为三个主要部分进行论述和分析。

第一部分是引言部分，主要包括以下内容：- 概述：对稳态温度场中固体的热流密度与温度梯度的关系进行简要介绍，并指出其重要性。

- 文章结构：介绍整篇文章的组织结构和各个部分的内容安排，以帮助读者了解整体框架。

- 目的：明确文章的研究目的和意义，阐述为什么对该热导率与温度梯度的正比关系进行研究和分析很重要。

第二部分是正文部分，将分为两个小节进行讨论和分析。

- 2.1 稳态温度场中的热流密度：首先给出热流密度的定义，然后介绍稳态温度场中固体的热流密度的特点和测量方法，进一步说明其重要性和应用场景。

稳态温度场与热应力分析算例稳态温度场问题与热应力分析2014年3月5日星期三1 前言最近，本人需要做一个涉及热应力、疲劳分析的综合问题。

之前对热应力分析没有接触，看了几天书后，根据前人的经验，动手做了一个简单的稳态温度场问题与热应力分析算例，小试牛刀一把，现拿出来晒晒，请高手过来拍砖指点。

2 问题描述一块等厚的均质矩形薄板，如下图所示，其长20米，宽16米，厚1米。

板顶面温度为22?，底面温度为176.67 ?，左、右面绝热，并且顶面、底面固定约束。

板的材料是结构钢(系统默认)，材料参数取系统默认，不做任何修改。

图1 问题描述问题:2.1 分析薄板内的温度分布;2.2 分析薄板内的应力分布。

3 稳态温度场分布模拟3.1 创建稳态温度场分析系统进入ansys workbench后，在Project Schematic窗口中，单击右键，在弹出的菜单中，选择“New analysis systems->steady-state thermal(ANSYS)”，创建稳态温度场分析系统，见下图。

图2 创建稳态温度场分析系统图3 创建好的稳态温度场分析系统3.2创建薄板模型在创建的稳态温度场分析系统中，材料采用默认的结构钢，材料参数不做任何修改。

单击“Geometry”，进入MD系统，创建一个简单的等厚均质矩形薄板，几何尺寸见2问题描述。

创建好几何模型后，保存后退出。

图4 创建的薄板几何模型3.3 创建稳态温度场模型单击图3所示的系统中的“Model”，进入“Multiple Systems-Mechanical”系统中，单击“Steady-State Thermal”，在此处定义顶面、底面温度，定义左、右面为完全绝热状态。

单击“Solution”，定义求取结果“Temperature”。

单击右键，选择“solve”，进行分析。

温度场分布云图见下图。

图5 温度场分布云图4 热应力分析稳态温度场分析完成后，退出“Multiple systems-Mechanical”系统，在下图中“steady-state thermal”的“solution”上，单击右键，在弹出的菜单中，选择“New analysis systems->staticstructural(ANSYS)”，创建热应力分析系统。