专题三基础计算

专题三-弹簧与受力分析弹簧是一种用于弹性成分的机械构件，它通常由能够弯曲和变形的金属制成。

在物理学中，弹簧是一个非常重要的概念，因为它是弹性力学的基础。

在本篇文章中，我们将学习弹簧的基础知识和受力分析。

弹性力学弹性力学是物理学中研究材料弹性的分支学科。

材料的弹性是指其在受到外力作用后，能够恢复到原来的形态和大小。

弹性力学主要研究材料受力的变形、应力分布、变形量、变形速率、破坏条件等方面，其中弹簧作为弹性体的一种常见构件，也是弹性力学的重要内容之一。

弹簧的基础知识弹簧的定义弹簧是一种弹性成分，通常由金属制成。

它可以被弯曲或压缩，但一旦没有外力作用，它将恢复到原始状态。

弹簧的种类弹簧可以分为两种类型：压缩弹簧和拉伸弹簧。

压缩弹簧是通常被挤压的弹簧，而拉伸弹簧则通常被拉伸。

弹簧的形态弹簧可以有各种形状和大小。

最常见的是圆弧形和线形。

弹簧的系数弹簧的系数是一个重要的参数，它用于描述弹簧的强度和弹性。

弹簧系数越高，弹簧所能承受的重量也就越大。

受力分析受力分析的基本概念受力分析是物理学中的基本概念，它用于描述物体在受到外部力作用时的运动状态。

在物理学中，我们通常使用牛顿第二定律来描述物体的运动状态。

牛顿第二定律的公式如下所示：F=ma其中“F”是物体所受的外力，“m”是物体的质量，“a”是物体的加速度。

受力分析的应用在物理学中，我们可以利用受力分析来计算物体所承受的力的大小和方向。

例如，在弹簧中，我们可以利用受力分析来计算所需弹簧的系数，以便将所需的重量承载在弹簧上。

受力分析还可以用于解决其他许多问题，如力的矢量分解、摩擦力、重力和弹力等等。

弹簧作为物理学中非常重要的概念，是弹性力学的基础。

在物理学的研究中，我们可以利用受力分析来计算弹簧所需系数，并解决其他许多问题。

通过本篇文章对弹簧和受力分析的学习，我们可以更好地理解物理学的相关概念，为我们的学习和生活带来便利。

初中化学总复习专题三初中化学基础知识总结和常用口诀一、物质的俗名、学名、及化学式⑴碳、金刚石、石墨：C ⑵水银、汞：Hg (3)生石灰、氧化钙：CaO(4) 熟石灰、消石灰：Ca(OH)2 （5）干冰（固体二氧化碳）：CO2(6)亚硫酸：H2SO3 (7)盐酸、氢氯酸：HCl (8)氢硫酸：H2S (9) 苛性钠、火碱、烧碱：NaOH (11)纯碱：Na2CO3碳酸钠、纯碱（苏打）(12)碳酸氢钠：NaHCO3 (小苏打） (13)胆矾、蓝矾、硫酸铜晶体：CuSO4·5H2O (14)铜绿、孔雀石：Cu2(OH)2CO3（分解生成三种氧化物的物质）((15)酒精、乙醇：C2H5OH (17)醋酸、乙酸CH3COOH（CH3COO-醋酸根离子）(18)氨气：NH3（碱性气体） (19)氨水、一水合氨：NH3·H2O（为常见的碱是一种不含金属离子的碱） (20)亚硝酸钠：NaNO2（工业用盐、有毒）二、常见物质的颜色的状态1、白色固体：MgO、P2O5、CaO、 NaOH、Ca(OH)2、KClO3、KCl、Na2CO3、NaCl、无水CuSO4；铁、镁为银白色（汞为银白色液态）2、黑色固体：石墨、炭粉、铁粉、CuO、MnO2、Fe3O4 ▲KMnO4为紫黑色3、红色固体：Cu、Fe2O3、HgO、红磷▲硫：淡黄色▲ Cu2(OH)2CO3为绿色4、溶液的颜色：凡含Cu2+的溶液呈蓝色；凡含Fe2+的溶液呈浅绿色；凡含Fe3+的溶液呈棕黄色，其余溶液一般无色。

（高锰酸钾溶液为紫红色）5、沉淀(即不溶于水的盐和碱）：①盐：白色↓：CaCO3、BaCO3（溶于酸） AgCl、BaSO4(也不溶于稀HNO3) 等②碱：Cu(OH) 2：蓝色↓：Fe(OH)3红褐色↓其余碱：白色↓6、气体（1）具有刺激性气体的气体：NH3、SO2、HCl（皆为无色）（2）无色无味的气体：O2、H2、N2、CO2、CH4、CO（剧毒）▲注意：具有刺激性气味的液体（易挥发）：盐酸、硝酸、醋酸。

专题3 实数的运算考点一：实数的大小比较1．（2022·四川成都·中考模拟）在实数 3.14-，－3，3-π-中，最小的数是（ ） A ． 3.14-B ．－3C ．3D ．π-2．（2022·湖南益阳·21，2，13中，比0小的数是（ ）A 2B ．1C ．2D ．133．（2022·吉林长春·中考真题）实数a ，b 在数轴上对应点的位置如图所示，下列结论正确的是（ ） A ．0a > B ．a b <C ．10b -<D ．0ab >4．（2022·广东深圳·中考二模）下列数中，大于－1且小于0的是（ ） A ．3B ．32-C ．23-D ．235．（2022·天津红桥·中考三模）估计17- ）． A ．5-和4-之间 B ．4-和3-之间 C ．3-和2-之间D ．2-和1-之间6．（2022·山东临沂·23“>”或“<”或“＝”）．7．（2022·海南·310___________．考点二：实数的基本运算8．（2022·浙江·杭州中考模拟预测）下列计算结果是正数的是（ ） A ．1﹣2B ．﹣π＋3C ．（﹣3）×（﹣5）2D ．|59．（2022·河北唐山·中考三模）运算后结果正确的是（ ） A ．12332=B 342 C 8220= D 2632=10．（2022·天津·中考模拟预测）计算sin30tan 45︒-︒（ ） A 31- B ．12-C 32D ．3211．（2022·重庆中考二模）计算：1122-⎛⎫-+= ⎪⎝⎭（ ） A ．0 B ．4 C ．-2D ．3212．（2022·广东深圳·01(1+的结果是（ ）A ．1BC ．2D ．113．（2022·山东威海·中考真题）按照如图所示的程序计算，若输出y 的值是2，则输入x 的值是 _____．14．（2022·陕西·中考真题）计算：3=______．15．（2022·四川攀枝花·0(1)=-__________．16．（2022·辽宁阜新·中考真题）计算：22-=______．17．（2022·广东肇庆·______________．18．（2022·湖北黄石·中考真题）计算：20(2)(2022--=____________．考点三：实数的混合运算19．（2022·广东·佛山市中考模拟）计算0312(2017)()2π----+的结果为（ ）A ．3-B ．3C ．6D ．920．（2022·山东威海·302(1)(1)2π-----的结果是（ ）A ．74B ．34C ．14D ．14-21．（2022·江苏南京·中考模拟）计算20212020的结果是（ ）A B ．C ．D 22．（2022·广东·东莞市中考三模）计算：10|2|3sin 302(2022)π--+---︒等于（ ）A ．2-B ．12-C ．2D ．023．（2022·广东惠州·中考二模）101tan60|(3)2π-︒⎛⎫---+-= ⎪⎝⎭__________．24．（2022·山东泰安·中考三模）()022112cos 45π--+-︒=________．25．（2022·重庆长寿·中考模拟）计算：20112160π1tan --+-︒+⋅=-（）__________．26．（2022·内蒙古内蒙古·中考真题）计算：1012cos30(3π)2-︒⎛⎫-++- ⎪⎝⎭27．（2022·湖南·中考真题）计算：0112cos 45( 3.14)1()2π-︒+-+．28．（2022·湖南郴州·中考真题）计算：()12022112cos3013-⎛⎫--︒+ ⎪⎝⎭．29．（2022·广东北江实验学校三模）计算：()20120222sin 6023π-⎛⎫+-+︒ ⎪⎝⎭30．（2022·湖南·(032cos 60π+︒．31．（2022·四川德阳·()()023.143tan 6012π---︒+-．答案与解析考点一：实数的大小比较1．（2022·四川成都·中考模拟）在实数 3.14-，－3，π-中，最小的数是（ ） A． 3.14- B ．－3C ．D ．π-∴33 3.14＜，在实数 3.14-，－3，3-，故选：D ．【点睛】本题主要考查实数的比较大小，关键在于绝对值符号的去掉，根据负数绝对值越大，反而越小．2．（2022·湖南益阳·中考真题）四个实数﹣1，2，13中，比0小的数是（ ）A B ．1 C ．2D ．133．（2022·吉林长春·中考真题）实数a ，b 在数轴上对应点的位置如图所示，下列结论正确的是（ ）A ．0a >B ．a b <C ．10b -<D ．0ab >【答案】B【分析】观察数轴得：2123a b -<<-<<<，再逐项判断即可求解．【详解】解：观察数轴得：2123a b -<<-<<<，故A 错误，不符合题意；B 正确，符合题意； ∴10b ->，故C 错误，不符合题意； ∴0ab <，故D 错误，不符合题意； 故选：B【点睛】本题主要考查了实数与数轴，实数的大小比较，利用数形结合思想解答是解题的关键． 4．（2022·广东深圳·中考二模）下列数中，大于－1且小于0的是（ ）A ．B ．32-C ．23-D ．23【详解】解：13<<，故A 不符合题意；B 不符合题意；，故C 符合题意；5．（2022·天津红桥·中考三模）估计 ）． A ．5-和4-之间 B ．4-和3-之间 C ．3-和2-之间 D ．2-和1-之间【详解】解：1617<5-【点睛】本题考查无理数的估算，是基础考点，掌握相关知识是解题关键．6．（2022·山东临沂·“>”或“<”或“＝”）．【详解】解：22()2=1123>，∴223>故答案为：．【点睛】本题考查了实数的大小比较，解题的关键是灵活变通，比较两者平方后的结果．7．（2022·海南·___________．考点二：实数的基本运算8．（2022·浙江·杭州中考模拟）下列计算结果是正数的是（ ）A ．1﹣2B ．﹣π＋3C ．（﹣3）×（﹣5）2D ．|【点睛】本题考查了实数，有理数的混合运算，熟练掌握运算法则是解本题的关键． 9．（2022·河北唐山·中考三模）运算后结果正确的是（ ）A．12=B 2 C 0= D =10．（2022·天津·中考模拟预测）计算sin30tan 45︒-︒（ ）A 1B ．12-C D ．3211．（2022·重庆中考二模）计算：1122-⎛⎫-+= ⎪⎝⎭（ ）A ．0B ．4C ．-2D ．32故选：B ．【点睛】本题考查了实数的运算，正确理解实数的运算法则是解本题的关键．12．（2022·广东深圳·01(1+的结果是（ ）A．1 B C ．2D ．113．（2022·山东威海·中考真题）按照如图所示的程序计算，若输出y 的值是2，则输入x 的值是 _____．14．（2022·陕西·中考真题）计算：3-=______．15．（2022·四川攀枝花·0-__________．(1)=-【答案】3【分析】根据立方根的定义，零指数次幂的定义以及有理数减法法则，进行计算即可．=--=-．【详解】解：原式213-．故答案为：3【点睛】本题考查了立方根的定义，零指数次幂的定义以及有理数减法法则，正确进行计算是解题的关键．16．（2022·辽宁阜新·中考真题）计算：22-______．17．（2022·广东肇庆·中考二模）计算：=______________．18．（2022·湖北黄石·中考真题）计算：20--=____________．(2)(2022【答案】3【分析】根据有理数的乘法与零次幂进行计算即可求解．-=．【详解】解：原式＝413故答案为：3．【点睛】本题考查了实数的混合运算，掌握零次幂以及有理数的乘方运算是解题的关键．考点三：实数的混合运算19．（2022·广东·佛山市中考模拟）计算0312(2017)()2π----+的结果为（ ） A ．3-B ．3C ．6D ．920．（2022·山东威海·302(1)(1)2π-----的结果是（ ）A ．74B ．34C ．14D ．14-21．（2022·江苏南京·中考模拟）计算20212020的结果是（ ）A B ．C ．D 【答案】A【分析】把较高次幂拆分后逆用积的乘方法则，进行运算即可得解．22．（2022·广东·东莞市中考三模）计算：10|2|3sin 302(2022)π--+---︒等于（ ）A ．2-B ．12-C ．2D ．01123122 312122=+-- =2，23．（2022·广东惠州·中考二模）101tan60|(3)2π-︒⎛⎫---+-= ⎪⎝⎭__________． 【答案】-1【分析】根据负整数指数幂，特殊角三角函数值，绝对值，零指数幂，二次根式的性质化简等计算法则求解即可．24．（2022·山东泰安·中考三模）()022112cos 45π--+-︒=________．25．（2022·重庆长寿·中考模拟）计算：20112160π1tan --+-︒+⋅-（）__________．26．（2022·内蒙古内蒙古·中考真题）计算：1012cos30(3π)2-︒⎛⎫-++- ⎪⎝⎭27．（2022·湖南·中考真题）计算：0112cos 45( 3.14)1()2π-︒+-++．28．（2022·湖南郴州·中考真题）计算：()12022112cos3013-⎛⎫--︒+ ⎪⎝⎭．=3．【点睛】本题考查了特殊角的三角函数值、绝对值的意义和负整数指数幂的运算法则等知识，熟记特殊角的三角函数值是解答本题的关键．29．（2022·广东中考三模）计算：()20120222sin 6023π-⎛⎫+-+︒ ⎪⎝⎭30．（2022·湖南·(032cos 60π+︒．31．（2022·四川德阳·()()023.143tan 6012π---︒++-．。

初一数学专题三多边形、轴对称考点例析华东师大版【本讲教育信息】一. 教学内容：专题三多边形、轴对称考点例析二、知识点分析1.三角形内角和、外角的性质、三角形的三边关系，会根据三边关系判断已知的三条线段能否组成三角形.2.三角形的分类.3.三角形具有稳定性.4.多边形的内角和与多边形的外角和的探索过程.5.理解某些正多边形能够铺满地面的道理，会欣赏丰富多彩的图案.6.了解轴对称的概念，能够判断一个图形是不是轴对称图形，并能找出对称轴.7.会画和一个简单图形关于某条直线成轴对称的图形，会设计简单的轴对称图形. 特别是在坐标系中对一些图形会以坐标轴为对称轴进行轴对称变换.8.认识线段的垂直平分线的性质，并能用来解决相关的简单问题.9.理解等腰三角形的性质与判定，了解等边三角形是特殊的等腰三角形，以及等边三角形的性质与判定，能用来解决相关的简单问题.10.等腰三角形性质表示如果一个三角形是等腰三角形，那么可以得出：两底角相等；而要判定一个三角形是等腰三角形，必须先说明三角形中有两个角相等. 两者是实现“等角”与“等边”相互转化的重要依据，常用来说明两条线段、两个角相等.三、典型例题求正多边形的边数例1．若一个正多边形的内角和是其外角和的3倍，则这个多边形的边数是______．分析:根据由多边形的内外角和公式列出边数的方程解题.解:设多边形的边数为n，则（n-2）×180°＝3×360°，解得n＝8求正多边形的内角例2.如图是一个五角星图案，中间部分的五边形ABCDE是一个正五边形，则图中∠ABC的度数是.分析:根据多边形内角和及正多边每个内角相等.解:正五边形的内角和为：（5－2）×180°＝540°，又因为正五边形内角相等，故∠ABC＝540°÷5＝108°.点评:正多边形既具有一般凸多边形的内角和关系：（n－2）×180°，同时它还具有各角都相等，各边都相等的特性.求多边形的个数例3.若n边形所有的边都相等，所有的内角都相等，则这样的n边形叫做正n边形，如果一个正n边形的每个内角的度数都是整数，那么这样的正n边形共有＿＿＿＿个.分析:因为这个正n边形的每个内角的度数都是整数，所以这个正n边形的每个外角的度数也是整数，所以n应是360的约数．解: 易求得360的大于2的约数共有22个：3，4，5，6，8，9，10，12，15，18，20，24，30，36，40，45，60，72，90，120，180，360，所以这样的正n边形共有22个．求正多边形的对角线条数例4. 如果多边形的每个内角都比它相邻的外角的4倍还多30°，则这个多边形的对角线的总条数为＿＿＿＿．分析: 本题首先根据多边形的内外角的关系求出多边形的边数，再联系对角线的条数计算可求得这个多边形的对角线的总数.解:设外角为x ，则内角为（4x+30°）因为每一个内角与它的外角互为邻补角所以：x+(4x+30°)=180°x=30°.因为多边形的外角和为360°，所以360°÷30°=12这个多边形的内角和为（12-2）×180°=1800°，因为12边形从任意顶点出发均可以画出9条对角线所以对角线的总条数为：21×9×12=54， 这个多边形的对角线的总条数为21×12×（12-3）=54.求不规则的多边形的角度和例5. 如图，∠A+∠B+∠C+∠D+∠E+∠F 的度数为＿＿＿＿＿.分析:我们观察整个图形，里面包含着三角形和四边形，我们可以借助四边形的内角和解决问题.解:四边形ABPO 的内角和为∠A+∠B+∠BPO+∠POA=360°.因为∠BPO 是△PDC 的外角，所以∠BPO=∠C+∠D.因为∠POA 是△OEF 的外角，所以∠POA=∠E+∠F.所以∠A+∠B+∠C+∠D+∠E+∠F=360°.点评:把这些分散的角集中到一起构成多边形，借助多边形内角和求解，体现转化的思想.正多边形的操作例6. 将一正方形纸片按下列顺序折叠，然后将最后折叠的纸片沿虚线剪去上方的小三角形.将纸片展开，得到的图形是（）分析: 把一个正方形按如图所示进行四次折叠，将最后折叠的纸片沿虚线剪去上方的小三角形，展开，得到的图形是C.解:C.点评: 本题无论是内容还是方法都更重视动手实验操作的作用.要改变以往数学学习过分依赖模仿与记忆的学习方式.正多边形的密铺例7. 如图，用灰白两色正方形瓷砖铺设地面。

2025届高三化学一轮专题复习讲义（12）专题三基本理论3-5 化学平衡（二）（1课时，共2课时）【复习目标】1．了解化学平衡常数(K)的含义，能利用化学平衡常数进行相关计算。

2．理解外界条件(浓度、温度、压强、催化剂等)对化学平衡的影响，能用相关理论解释其一般规律。

3．了解化学平衡的调控在生活、生产和科学研究领域中的重要作用【重点突破】1．能运用平衡移动原理，解决生活中的相关问题，讨论化学反应条件的选择和优化。

综合考虑化学反应速率、原料利用率、设备要求、催化剂的活性等，控制合适的反应条件。

2．联想外界条件的改变对化学反应速率和化学平衡的影响规律，根据图像中表现的关系与所学规律相对比，做出符合题目要求的判断。

能充分考查学生读图、提取信息、解决问题的能力。

【真题再现】例1．（2023·江苏卷）二氧化碳加氢制甲烷过程中的主要反应为CO2(g)+4H2(g)===CH4(g)+2H2O(g) △H=-164.7kJ·mol-1CO2(g)+H2(g) ===CO(g)+H2O(g) △H=41.2kJ·mol-l在密闭容器中，1.01×10-5Pa、n起始(CO2)︰n起始(H2)=1︰4时，CO2平衡转化率、在催化剂作用下反应相同时间所测得的CO2实际转化率随温度的变化如题13图所示。

CH4的选择性可表示为n生成(CH4)n反应(CO2)×100%。

下列说法正确的是A．反应2CO(g)+2H2(g)===CO2(g)+CH4(g)的熔变△H=-205.9kJ·mol-1B．CH4的平衡选择性随着温度的升高而增加C．用该催化剂催化二氧化碳反应的最佳温度范围约为480～530℃D．450℃时，提高n起始(H2)n起始(CO2)的值或增大压强，均能使CO2平衡转化率达到X点的值解析：A项，由盖斯定律可知反应2CO(g)+2H2(g)===CO2(g)+CH4(g)的焓变△H=-2×41.2 kJ·mol-1-164.7 kJ·mol-1=-247.1 kJ·mol-1，错误；B项，CO2(g)+4H2(g)===CH4(g)+2H2O(g)为放热反应，升高温度平衡逆向移动，CH4的含量降低，故CH4的平衡选择性随着温度的升高而降低，错误；C项，由图可知，已知条件之下，该催化剂催化二氧化碳反应温度范围约为380℃时二氧化碳转化率最大，此时为最适温度，温度继续增加，催化剂活性下降，错误；D项，450℃时，提高n起始(H2)n起始(CO2)的值可提高二氧化碳的平衡转化率，增大压强反应I平衡正向移动，可提高二氧化碳的平衡转化率，均能使CO2平衡转化率达到X点的值，D正确。

初中数学基础计算专题训练专题一：有理数的计算1. ( 3)2 22. 1 ( 2 ) 4 (1)(1)2 3 5 2 33.1 14. 8(5) 63 ( 1.5) 4 2.75(5)4 25.45( 1 )36. ( 2 )( 5) ( 4.9)0.62 5 67( 10)2 5 ( 2)8. ( 5)3(3)25 59.5(6) (4)2( 8) 10. 21( 6) (1 2)4 7 211.( 16 50 32) ( 2) 12.(6)8 (2)3( 4)2 5513. (1)2 1 ( 2 2 2 ) 14. 11997 (1 0.5) 12 23 3 315. 3 [ 32( 2)2 2] 16. (3)2( 2 1) 02 3 4 317. 14(1 0.5) 1[2 ( 3)2] 18. ( 81) ( 2.25) (4) 163 919. 52[ 4 (1 0.21) ( 2)] 20. ( 5) ( 36) (7)(36) 12 ( 36)5 7 7 721.(5) ( 4)2 0.25 ( 5) ( 4)322. ( 3)2(11 )3 2 6 28 2 9 31、化简（ 40 分）(1) 12( x－ 0.5)（2）3x+ (5y-2x)（3）8y-(-2x+3y) （ 4） -5a+(3a-2)-(3a-7)（5）7-3 x-4x2+ 4x-8x2-15 (6) 2(2a2-9b)-3(－4a2+b)（7）－2（8a+2b）+4(5a＋b)（ 8） 3 （ 5a-3c ）－ 2(a-c) (9)8x 2-[-3x-(2x2-7x-5)+3]+4x（10）(5a-3b) – 3(a 2-2b)+7(3b+2a) 2、先化简，后求值；（ 1） (5x-3y-2xy)-(6x+5y-2xy)，其中x5 ，y1 （ 2） 1 1 3 1 )x 2( x y) ( x3 y ，其中 x1, y 22 3 2（ 3）若a2 b 3 20 ，求3a2b－[2ab2－2（ab－1.5a2b）+ab]+3ab2的值；1、计算：② ( － 8a b c ÷4ab ) ·(3ab )① (6a 5－ 7a 2+36a 3) ÷3a 25 34 5 2③（ 3x － 2）2④（ 2x － 3）（－ 2x － 3）2⑤ 79.8⑥ 2003 1997⑦ （2a ＋1）2－(2a ＋1)(－1＋2a)2005 2004 2 2002 2003 20048. 40.259.( 3 ) × (1.5) ÷(－1)＝ 10. (a 2)4a-(a 3)2a 311. (5a 3b) ·(-4abc) (-5ab)· 2、化简求值 2a 3b 22a 3b 2 a 3b2a 3b 2，a2 , b13(x+3)(x-4)-x(x-2) , 其中 x=112 1a b a ba b ，其中 a ＝3， b ＝－ .3已知 2x － y ＝10，求x 2 y 2x y 22y x y4y 的值.专题四：因式分解1.（1） 3p2﹣ 6pq（2）2x2+8x+83 3 2 2（ 3）x y﹣xy （ 4） 3a ﹣ 6a b+3ab．2 2 2 2 2 2（ 5） a （ x﹣ y） +16（ y﹣x）（ 6）（ x +y ）﹣ 4x y 2.（ 1） 2x2﹣ x（2）16x2﹣1（3）6xy2﹣9x2y﹣y3（ 4）4+12 （ x﹣ y） +9 （x﹣y）2 2 3 2 2（ 5） 2am ﹣8a （6） 4x +4x y+xy（ 7） 3x﹣12x 3 2 2 2﹣4x2 2 2 23 2 2（ 8）（x +y ）y （ 9） x y﹣2xy +y（ 10）（ x+2y ）﹣y（ 11） n2（m﹣ 2）﹣ n（ 2﹣ m）（12）（x﹣1）（x﹣3）+12 2 2 2（ 13）a﹣ 4a+4﹣b（ 14） a ﹣ b ﹣2a+1专题五：二次根式的运算（1）3 25（2）8136（ 3）0.040.25 （4）6 2 3（ 5）0.36 46 （ 6）121(7)2734 （9）38 2 32503 （8）2 1248 （10）(31)2（11）93 712 548（12）805502（ 13） (1)5 15- 4 3 ；（ 14）250325 9（ 15）0.2 900 0.5 121 （16）( 31 )23（ 17）(74 3)(23) 2（ 19）4 3 93 2 8（ 21）( 1) 2006 ( 3 2 ) 0 1 1( ) 2 （ 23）123 ( 2006) 0(1)12217（ 18）3 （20）(15)( 52)（ 22）(3 2) 2002 ( 32)20031（24）3 20455（ 25） 1 11 1 4 32 75 （ ） 12 2 326 32 3（ 27）48412 120.25 1 0.75 （28）(11)2(2)24 25 5 （29）( 3)28122(63)0（ 30）18 1 126 1 4 0.752 2（31）3 40 2 2 1 （32）4( 37)018 (1 2)25 10 224 1 4 1 (1 2) 0.3 8(33)解下列一元一次方程：（ 1） 3（ x-2） =2-5(x-2)(2) 2(x+3)－ 5(1－x)=3(x － 1)(3) 3( x1) 2( x 2) 2x 3(4) 3( x2)1 x (2 x1)2x－1 x+2 1 x 1(5) 3 =2+1 (6) 3 2 1(7) x 8x (8) 3 1.2x 4 x 123 53 1 3x 1 4x 2(9 ) x 0.4 x 0.3 (10)5 14 2 2(11) 3 y 12 2 5 y 7 (12) 5 6 x 7 x 14 3 3 21 m 3 3m(14) y 1 y 2(13) 1 y 22 4 2 5(15) x 1 x x 2 1(16) 3 x x 8 13 6 2 3(17) 1 (x-3)=2- 1 (x-3) (18) x 2x 1 32 2 0.2 0.5(19)x 1 x 3 3 (20) x 2 2 x 3 10.2 0.01 4 6（ 21）x 1x 2 4 x (22) 3 4 x 1 2 2x3 6 2 2 3 3专题七：解二元一次方程组（1）x y 3（）4x 3y 0 （）4x 3y 5 （）4x y 5 x y 1234 12x 3y 84x 6y 143x 2y 1 （5）5x 4y 6（）3x 2y 7 （7） y 2x 3 （）7x 5y 3 2x 3y 163x 2y 18 2x 3y 172x y 4（ 9）x y（）x 5y 6（）3( y 2) x 1（） xy 2 3 10 6y 4 0 111) 5y 8122 33x 2(x 3x 4y 18 3x 4y 184x 15y 170 6x 25y 23 0 x y 13 1 x 2 y 2 1x 2 3y 24 3 2 3 24 3 x y 33y 2 3x 21y 2 413 4 2x 122x 1 3y 2 3x 2y 2x 3y （7）5 4 2 （） 18 6 73x 1 3y 2 3x 2y 2x 3y 5 4 0 6 5 7专题八：分式方程1.3x= 1 。

专题03 有理数的加减法重点突破知识点一 有理数的加法（基础）有理数的加法法则：（先确定符号，再算绝对值） 1. 同号两数相加，取相同的符号，并把绝对值相加；2. 异号两数相加，绝对值不相等时，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值；3. 互为相反数的两个数相加得0；（如果两个数的和为0，那么这两个数互为相反数）4. 一个数同0相加，仍得这个数。

有理数的加法运算律：1. 两个数相加，交换加数的位置，和不变。

即a b b a +=+；2. 三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。

即()()a b c a b c ++=++。

知识点二 有理数的减法（基础） 有理数的减法法则：减去一个数等于加上这个数的相反数。

即()a b a b -=+-。

【注意减法运算2个要素发生变化】：减号变成加号；减数变成它的相反数。

有理数减法步骤： 1.将减号变为加号。

2.将减数变为它的相反数。

3.按照加法法则进行计算。

考查题型考查题型一 有理数加法运算典例1．（2018·广东初一期中）计算－(－1)＋|－1|，其结果为( ) A ．－2 B ．2 C ．0 D ．－1【答案】B 【解析】试题提示：由题可得：原式=1+1=2，故选B．a b的值（）变式1-1．（2019·呼伦贝尔市期末）有理数a、b在数轴上的位置如图所示，则A．大于0B．小于0C．小于a D．大于b【答案】A【提示】先根据数轴的特点判断出a，b的符号，再根据其与原点的距离判断出其绝对值的大小，然后根据有理数的加法法则得出结果．【详解】根据a，b两点在数轴上的位置可知，a＜0，b＞0，且|b|＞|a|，所以a+b＞0．故选A．【名师点拨】此题考查数轴,绝对值,有理数的加法法则．解题关键在于用几何方法借助数轴来求解，非常直观，体现了数形结合的优点．变式1-2．（2019·庆阳市期中）若a＝2，|b|＝5，则a＋b＝( )A．－3 B．7 C．－7 D．－3或7【答案】D【提示】根据|b|=5，求出b=±5，再把a与b的值代入进行计算，即可得出答案．【详解】∵|b|=5，∴b=±5，∴a+b=2+5=7或a+b=2-5=-3；故选D．【名师点拨】此题考查了有理数的加法运算和绝对值的意义，解题的关键是根据绝对值的意义求出b的值．变式1-3．（2019·扬州市期中）若|m|=3，|n|=5，且m-n＞0，则m+n的值是（）A．-2 B．-8或8 C．-8或-2 D．8或-2【答案】C【详解】∵|m|=3，|n|=5，∴m=±3，n=±5，∵m-n＞0，∴m=±3，n=-5，∴m+n=±3-5，∴m+n=-2或m+n=-8．故选C ．变式1-4．（2018·上饶市期末）若m 是有理数，则m m +的值是（ ） A ．正数 B ．负数C ．0或正数D ．0或负数【答案】C【提示】根据：如果m>0,则|m|=m; 如果m<0,则|m|=-m; 如果m=0,则|m|=0.【详解】如果m 是正数，则m m +是正数；如果m 是负数，则m m +是0；如果m 是0，则m m +是0. 故选C【名师点拨】本题考核知识点：有理数的绝对值.解题关键点：理解绝对值的意义. 考查题型二 有理数加法中的符号问题典例2．（2018·重庆市期末）将 6-(+3)+(-2) 改写成省略括号的和的形式是（ ） A ．6-3-2 B ．-6-3-2C ．6-3+2D ．6+3-2【答案】A【提示】先把加减法统一成加法，再省略括号和加号．【详解】将6﹣（+3）+（﹣2）改写成省略括号的和的形式为6﹣3﹣2． 故选A ．【名师点拨】本题考查了有理数的加减混合运算，将算式写成省略括号的形式必须统一成加法后，才能省略括号和加号．变式2-1．（2020·银川市期中）把（+3）﹣（+5）﹣（﹣1）+（﹣7）写成省略括号的和的形式是（ ）． A ．﹣3﹣5+1﹣7 B ．3﹣5﹣1﹣7 C ．3﹣5+1﹣7 D ．3+5+1﹣7 【答案】C【解析】（+3）﹣（+5）﹣（﹣1）+（﹣7）=（+3）+（-5）+（+1）+（﹣7）=3﹣5+1﹣7, 故选：C.变式2-2．（2020·邯郸市期末）若两个非零的有理数a ，b 满足：|a|＝－a ，|b|＝b ，a ＋b ＜0，则在数轴上表示数a ，b 的点正确的是（ ） A ．B ．C ．D ．【答案】D【提示】根据|a|=-a 得出a 是负数，根据|b|=b 得出b 是正数，根据a+b ＜0得出a 的绝对值比b 大，在数轴上表示出来即可．【详解】解：∵a 、b 是两个非零的有理数满足：|a|=-a ，|b|=b ，a+b ＜0， ∴a ＜0，b ＞0， ∵a+b ＜0， ∴|a|＞|b|，∴在数轴上表示为：故选D.【名师点拨】本题考查数轴，绝对值，有理数的加法法则等知识点，解题关键是确定出a ＜0，b ＞0，|a|＞|b|． 变式2-3．（2019·深圳市期中）如果a ＜0，b ＞0，a ＋b ＜0 ，那么下列关系式中正确的是（ ） A ．a b b a ->>-> B ．a a b b >->>- C ．a b b a >>->- D ．b a b a >>->-【答案】A【提示】由于a ＜0，b ＞0，a+b ＜0，则|a|＞b ，于是有-a>b ，-b>a ，易得a ，b ，-a ，-b 的大小关系． 【详解】∵a ＜0，b ＞0，a+b ＜0， ∴|a|＞b ， ∴-a>b ，-b>a ，∴a ，b ，-a ，-b 的大小关系为：-a>b>-b>a ， 故选A ．【名师点拨】本题考查了有理数的加法法则，有理数的大小比较，异号两数的加法法则确定出|a|＞b 是解题的关键. 考查题型三 有理数加法在实际生活中的应用典例3（2018·厦门市期末）下列温度是由－3℃上升5℃的是（ ） A ．2℃ B ．－2℃C ．8℃D ．－8℃【答案】A【提示】物体温度升高时，用初始温度加上上升的温度就是上升之后的温度，即是所求 【详解】（－3℃）+5℃= 2℃ 故本题答案应为：A【名师点拨】此题考查了温度的有关计算，是一道基础题．熟练掌握其基础知识是解题的关键变式3-1．（2019·石家庄市期中）在学习“有理数的加法与减法运算”时，我们做过如下观察：“小亮操控遥控车模沿东西方向做定向行驶练习，规定初始位置为0，向东行驶为正，向西行驶为负．先向西行驶3m ，在向东行驶lm ，这时车模的位置表示什么数？”用算式表示以上过程和结果的是（ ）A．（﹣3）﹣（+1）=﹣4 B．（﹣3）+（+1）=﹣2C．（+3）+（﹣1）=+2 D．（+3）+（+1）=+4【答案】B【详解】由题意可得：（﹣3）+（+1）=﹣2．故选B．变式3-2．（2019·石家庄市期中）一家快餐店一周中每天的盈亏情况如下（盈利为正）：37元，-26元，-15元，27元，-7元，128元，98元，这家快餐店总的盈亏情况是（）A．盈利了290元B．亏损了48元C．盈利了242元D．盈利了-242元【答案】C【提示】利用有理数的加法求出已知各数的和即可求出一周总的盈亏情况．【详解】∵37+(−26)+(−15)+27+(−7)+128+98=242（元），∴一周总的盈亏情况是盈利242元.故选择C.【名师点拨】本题考查正数和负数、有理数的加法，解题的关键是掌握正数和负数、有理数的加法.±kg，现随机选取10袋面粉进行质量变式3-3．（2020·沈阳市期末）面粉厂规定某种面粉每袋的标准质量为500.2检测，结果如下表所示：则不符合要求的有（）A．1袋B．2袋C．3袋D．4袋【答案】A【提示】提示表格数据,找到符合标准的质量区间即可解题.±kg，即质量在49.8kg——50.2kg之间的都符合要求,【详解】解：∵每袋的标准质量为500.2根据统计表可知第5袋49.7kg不符合要求,故选A.【名师点拨】本题考查了有理数的实际应用,属于简单题,熟悉概念是解题关键.考查题型四有理数加法运算律典例4．（2019·忠县期中）计算1﹣3+5﹣7+9=（1+5+9）+（﹣3﹣7）是应用了（）A．加法交换律B．加法结合律C．分配律D．加法交换律与结合律【答案】D【提示】根据加法交换律与结合律即可求解．【详解】计算1-3+5-7+9=（1+5+9）+（-3-7）是应用了加法交换律与结合律．故选：D．【名师点拨】考查了有理数的加减混合运算，方法指引：①在一个式子里，有加法也有减法，根据有理数减法法则，把减法都转化成加法，并写成省略括号的和的形式．②转化成省略括号的代数和的形式，就可以应用加法的运算律，使计算简化．变式4-1．（2018·新蔡县期中）计算()+()+()+()等于（）A．-1 B．1 C．0 D． 4【答案】A【提示】有理数的加减运算，适当运用加法交换律.【详解】解：故选：A.【名师点拨】本题考查有理数的加减运算，熟记有理数的加减运算法则，同时能够题目数字特点进行灵活计算.变式4-2．（2019淮南市期中）－1＋2－3＋4－5＋6＋…－2017＋2018的值为()A．1 B．－1 C．2018 D．1009【答案】D【提示】从左边开始，相邻的两项分成一组，组共分成1009组，每组的和是1，据此即可求解．【详解】原式=(−1+2)+(−3+4)+(−5+6)+…(−2015+2016)+(−2017+2018),=1+1+1+…+1=1×1009,=1009.故选D.【名师点拨】属于规律型：数字的变化类，考查有理数的加减混合运算，掌握运算法则是解题的关键.变式4-3．（2019·南阳市期中）下列交换加数的位置的变形中，正确的是A．1-4+5-4=1-4+4-5B．13111311 34644436 -+--=+--C．1-2+3-4=2-1+4-3D．4.5-1.7-2.5+1.8=4.5-2.5+1.8-1.7 【答案】D【详解】A. 1−4+5−4=1−4−4+5，故错误；B. 13111311=-34644436-+--+--，故错误； C. 1-2+3-4=-2+1-4+3，故错误；D. 4.5−1.7−2.5+1.8=4.5−2.5+1.8−1.7，故正确． 故选D.考查题型五 有理数减法运算典例5．（2020·济南市期末）﹣3﹣（﹣2）的值是（ ） A ．﹣1 B ．1C ．5D ．﹣5【答案】A【提示】利用有理数的减法的运算法则进行计算即可得出答案． 【详解】﹣3﹣（﹣2）=﹣3+2=﹣1，故选A ．【名师点拨】本题主要考查了有理数的减法运算，正确掌握运算法则是解题关键． 变式5-1．（2019·郯城县期末）比﹣1小2的数是（ ） A ．3 B ．1C ．﹣2D ．﹣3【答案】D【提示】根据题意可得算式，再计算即可． 【详解】-1-2=-3， 故选D ．【名师点拨】此题主要考查了有理数的减法，关键是掌握减去一个数，等于加上这个数的相反数． 变式5-2．（2019·重庆市期末）若 |a |= 3， |b | =1 ，且 a > b ，那么 a -b 的值是（ ） A ．4 B ．2C ．-4D ．4或2【答案】D根据绝对值的性质可得a =±3，b =±1，再根据a ＞b ，可得①a =3，b =1②a =3，b =﹣1，然后计算出a －b 即可． 【详解】∵|a |=3，|b |=1，∴a =±3，b =±1． ∵a ＞b ，∴有两种情况： ①a =3，b =1，则：a －b =2； ②a =3，b =﹣1，则a －b =4． 故选D ．【名师点拨】本题考查了绝对值的性质，以及有理数的减法，关键是掌握绝对值的性质，绝对值等于一个正数的数有两个．变式5-3．（2018·自贡市期中）若x ＜0，则()x x --等于（ ）A ．－xB ．0C ．2xD ．－2x【答案】D【提示】根据有理数的加法法则和绝对值的代数意义进行提示解答即可. 【详解】()2x x x x x --=+=， ∵0x <， ∴20x <， ∴原式=22x x =-. 故选D.【名师点拨】“由已知条件0x <得到20x <，进而根据绝对值的代数意义得到：22x x =-”是解答本题的关键. 考查题型六 有理数减法在实际生活中的应用典例6．（2019临河区期末）某市有一天的最高气温为2℃，最低气温为﹣8℃，则这天的最高气温比最低气温高（ ） A ．10℃ B ．6℃ C ．﹣6℃ D ．﹣10℃ 【答案】A【解析】提示：用最高温度减去最低温度，然后根据减去一个数等于加上这个数的相反数进行计算即可得解． 详解：2-（-8） =2+8 =10（℃）． 故选：A ．名师点拨：本题考查了有理数的减法，是基础题，熟记减去一个数等于加上这个数的相反数是解题的关键． 变式6-1．（2019·长兴县月考）某地一周前四天每天的最高气温与最低气温如右表，则这四天中温差最大的是（ ）A ．星期一B ．星期二C ．星期三D ．星期四【答案】C【提示】利用每天的最高温度减去最低温度求得每一天的温差，比较即可解答. 【详解】星期一温差：10﹣3＝7℃； 星期二温差：12﹣0＝12℃； 星期三温差：11﹣（﹣2）＝13℃；星期四温差：9﹣（﹣3）＝12℃； 综上，周三的温差最大. 故选C ．【名师点拨】本题考查了有理数的减法的应用，根据题意正确列出算式，准确计算有理数减法是解题的关键． 变式6-2．（2018·吕梁市期末）我市冬季里某一天的最低气温是-10℃，最高气温是5℃，这一天的温差为 A ．-5℃ B ．5℃C ．10℃D ．15℃【答案】D【详解】解：5−(−10) =5+10=15℃． 故选D.变式6-3．（2020·寿阳县期末）甲、乙、丙三地海拔分别为20m ，15m -，10m -，那么最高的地方比最低的地方高( ) A ．10m B ．25mC ．35mD ．5m【答案】C【提示】根据正数与负数在实际生活中的应用、有理数的减法即可得．【详解】由正数与负数的意义得：最高的地方的海拔为20m ，最低的地方的海拔为15m - 则最高的地方比最低的地方高20(15)201535()m --=+= 故选：C ．【名师点拨】本题考查了正数与负数在实际生活中的应用、有理数的减法，理解负数的意义是解题关键． 考查题型七 有理数加减混合运算典例7（2018·南阳市期中）计算：①﹣13+（﹣20）﹣（﹣33）；②（+12）﹣（﹣13）+（﹣14）﹣（+16） 【答案】①0；②512． 【解析】①﹣13+（﹣20）﹣（﹣33） =﹣33+33 =0；②（+12）﹣（﹣13）+（﹣14）﹣（+16） =12+13﹣14﹣16 =643212121212+-- =512.变式7-1．（2019·河池市期中）计算：（1） 6789-+- （2） 2(5)(8)5---+-- 【答案】（1）-2；（2）-10 【详解】解：（1）6789-+- =189-+- =79-2=-（2）2(5)(8)5---+--2585=-+--385=--55=-- 10=-【名师点拨】此题考查的是有理数的加减法混合运算，掌握有理数的加、减法法则是解决此题的关键． 变式7-2．（2019·枣庄市期中）请根据如图所示的对话解答下列问题．求：(1)a ，b ，c 的值； (2)8－a ＋b －c 的值．【答案】(1)a ＝－3，b ＝±7,c=-1或-15; (2)33或5. 【详解】解：（1）∵a 的相反数是3，b 的绝对值是7， ∴a=-3，b=±7； ∵a=-3，b=±7，c 和b 的和是-8， ∴当b=7时，c= -15， 当b= -7时，c= -1，（2）当a=-3，b=7，c=-15时，8-a+b-c=8-（-3）+7-（-15）=33； 当a=-3，b=-7，c=-1时，8-a+b-c=8-（-3）+（-7）-（-1）=5． 故答案为（1）a=-3，b=±7；c=-1或-15;（2）33或5. 【名师点拨】本题考查有理数的加减混合运算，掌握相反数和绝对值的概念是解题关键.。

专题三三角形模型8 “8字”形模型展现基础模型怎么用?1.找模型两条相交的线段构成含对顶角的两个三角形,简称“有交点，想8字”2.用模型“8字”型的实质是利用三角形内角和定理进行角度转化来解题∠结论分析结论1:∠A+∠B=∠C+∠D证明:AC与BD相交于点0 , 连接AB,CD,在∠ABO中,∠.A+∠B+∠.AOB= 180°在OCD0中，∠C+∠D+∠COD= 180°因为∠AOB=∠COD(对顶角相等),所以∠A+∠B=∠C+∠D.拓展延伸角度和相等,是解决角度转化的重要思想。

“8字”型虽简单,但往往在几何综合题中推导角度时用到.∠模型拓展典例小试例1如图,线段AB , CD,EF两两相交,交点分别为G,H,I,连接AC,BE,DF，则∠A+∠B+∠C+∠D+∠E+∠F的度数是（）出现多个模型,分离模型,逐个计算A.180°B.360°C.540°D.720°考什么?对顶角相等,三角形的内角和例2如图,A,B,C,D,E是同一平面上的点,F是AB上一点,则∠A+∠B+∠C+∠D+∠E+∠DFE的度数是( )试着转化到一个四边形中,利用内角和求解A.180°B.360°C.540°D.720°考什么?对顶角相等,四边形的内角和思路点拨“8字”型能得到角度和的关系,在题目未给出具体角度的情况下,考虑将所求角度和转化到同一个多边形中,再利用多边形内角和求解.实战演练1.如图,AB∠BD,AC∠CD,∠A=30°,则∠.D的度数为____.2.一副三角板如图摆放,其中一块三角板的直角边EF落在另.一块三角板的斜边AC上,边BC与DF交于点0,则∠BOD的度数是____。

模型9 “燕尾”型模型展现基础模型怎么用?1．找模型遇到凹四边形的角度问题，考虑用“燕尾”型基础模型1 2.用模型通过“燕尾”型把“凹”的角转换成三个内角之和结论分析结论1:∠BDC=∠A+∠B+∠C证法1:如解图,延长BD交AC于点E.∠∠BEC是∠ABE的外角∠∠BEC=∠A+∠B又∠∠BDC是∠CDE的外角，∠BDC=∠BEC+∠C=∠A+∠B+∠C证法2:如解图，连接AD并延长，则∠1=∠B+∠3,∠2=∠C+∠4，∠BDC=∠1+∠2=∠B+∠3+∠C+∠4=∠A+∠B+∠C.∠∠BDC=∠A+∠B+∠C.结论2:AB+AC>BD+CD证明:如解图,延长BD交AC于点E，则AB+AE>BD+DE , DE+CE>CD，∠AC=AE+CE，∠AB+AC=AB+AE+CE>BD+DE+CE>BD+CD.巧学巧记简记:“凹角等于凸角之和”.拓展延伸也可以连接BC,使用三角形内角和定理来证明,同学们可以试试哦.:AOBAOCS S BD =:AOB COBS S AE =:BOC AOCSSBF =怎么用? 1．找模型遇到共边的两个三角形的面积相关问题,考虑用“燕尾”型基础模型2 2.用模型通过模型将面积问题转化为边的问题 满分技法燕尾相邻的两个三角形共底不等高,常根据三角形的面积公式“12×底×高”可推导“共底不等高”的三角形的面积比即为应高的比. 结论分析 结论3:∠::;AOBAOCSSBD CD =证明:如解图,分别过点B ,C 作 BH , CG 垂直于AD 交于点H , G ,在∠ABC 中,∠11,,22AOBAOCSAO BH S AO CG ==∠11:::,22AOB AOCSSAO BH AO CG BH CG ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭在∠BHD 和∠CGD 中，∠BHD =∠CGD =90°，∠BDH =∠CDG ， ∠∠BHD ∠∠CGD ，∠BH BDCG CD =， ∠::.AOBAOCSSBD CD =典例小试例1如图，已知点D ,E 分别在∠ABC 的边AB ,AC 上，将∠A 沿DE 折叠 （点拨：折叠产生相等的角）使点A 落在点F 的位置，已知∠A =50°（点拨：∠F =50°），∠1=130°，则∠2的度数为（ ） A .130° B .120° C .150° D .140°考什么?三角形外角的性质,折叠的性质思路点拨 折叠产生三角形全等，即ADE FDE ∆≅∆例2(2021河北)如图是可调躺椅示意图(数据如图),AE 与BD 的交点为C ,且∠A ,∠B ,∠E 保持不变.为了舒适,需调整∠D 的大小（点拨：先分析哪个角的大小随着D 点变化）,使∠EFD =110°，则图中∠D 应(填“增加”或“减少”)____度.考什么?三角形的内角和,对顶角相等实战实演1．将一副直角三角板如图放置,使两直角边重合,则∠1的度数为 （） A .75° B .105° C .135° D .165°2.如图,是一块不规则的纸片,∠ABC =∠DEF = 80°,则∠A +∠C +∠D +∠F 的度数为( )A . 80°B . 160°C .240°D . 360°3.如图,∠A = 45°, ∠BDC = 135°，∠ABE =13∠ABD ，∠ACE =13∠ACD ,则∠BEC 的度数是（ ）A . 30°B .45°C .75°D .90°4．如图,矩形ABCD 中,点E ,F 分别是边AB ,BC 的中点,连接AF ,CE 交于点G ,若矩形ABCD 的面积为3,则四边形AGCD 的面积为________5.如图,在∠ABC 中,点 D ,E 分别在BC ,AC 边上,AD 与BE 交于点F ,若CD =3BD ,EC =4AE ,四边形CDFE 的面积是10,则∠ABC 的面积为________模型10 “风筝”型模型展现基础模型怎么用?1.找模型三角形折叠或者在角内部的角容易产生“风筝”型2.用模型三角形外角性质是解决问题的关键结论分析结论1:∠DBF+∠ECF= ∠A+∠F证明:如解图,连接AF，∠∠DBF是∠ABF的外角，∠∠DBF=∠BAF+∠BF A.∠∠FCE是∠ACF的外角，∠∠FCE=∠CAF+∠CF A，∠∠DBF+∠FCE=∠BAF+∠BF A+∠CAF+∠CF A=∠BAC+∠BFC，即∠DBF+∠ECF= ∠BAC+∠BFC.怎么用?1．找模型遇到与四边形(含对角线)相关的面积问题,考虑用“风筝”型2.用模型共边三角形面积问题可转化为线段问题例1如图,已知点D,E分别在∠ABC的边AB,AC上,将∠A沿DE 折叠(注：折叠性质产生相等的角,且有“风筝”型),使点A落在BC上,对应点为F,已知∠B=50°,∠C=60°,则么∠1+∠2的度数为（）A.100°B. 120°C. 140°D. 135°例2如图,∠ABC中,AB=BC,(等腰三角形)延长AB,AC至点D,E,点F是∠DAE内部一点,连接BF,CF.若∠ABC= 40°，∠F= 50°则∠DBF+∠ECF(寻找与求解有关的角度关系)的度数为（）A. 90°B. 100°C. 110°D. 120°实战实演1.如图,在平行四边形ABCD中,∠B= 50°,点E是BC上一点,将∠ABE沿边AE翻折得到∠AFE,延长BA至点M.若∠FEC=70°,则∠MAF的度数为（）A. 20° B．30° C. 40° D. 50°2.如图,在等边∠ABC中,点D 、E 分别是AB, BC边上一点,把∠BDE沿DE 折叠,使点B落在点B'处, DB', EB'分别交边AC于点F、G ,若∠ADF=70°,则∠AGE的度数为.3.如图,在四边形ABCD中,点E, F分别是AD, BC上的点,将四边形ABCD 沿直线EF折叠,若∠A =130°, ∠B =110°,则∠1+∠2的度数为.4.如图,在四边形ABCD中,对角线AC , BD相交于点E ,∠ADE , ∠ABE ,∠CDE 的面积分别为2,3,4,则∠BCE的面积为, AE : CE的值为.5.如图,平行四边形ABCD 的对角线交于点O,点E , F分别在BC , CD上,连接EF交OC于点G ,连接OE , OF , S∠OEF= S∠ODF =2S∠CEF, S∠BOE =6,则∠OCF的面积为；∠GCE的面为.模型11 角平分线模型模型展现基础模型结论分析结论: P A = PB , OA = OB , ∠APO = ∠BPO 证明:OP 平分∠MON , ∠∠AOP = ∠BOP ,在∠AOP 和∠BOP 中,90AOP BOPOAP OBP OPOP ∠＝∠∠＝∠＝＝∠∠AOP ∠∠BOP ,∠P A = PB , OA = OB , ∠APO = ∠BPO .怎么用? 1.找模型遇到图形中含角平分线,考虑用角平分线模型 2.用模型一般直接用角平分线的性质,或者构造等腰三角形或全等三角形解决线段和角度问题模型拓展满分技法角平分线性质:角平分线上的点到角两边的距离相等.碰到角平分线,常需要截相等线段来构造三角形全等或者作平行线产生等腰三角形来解决问题.例1(2021青海)如图,在四边形ABCD中, ∠A =90°, AD=3,BC=5,对角线BD平分∠ABC（点拨:考虑角平分线的性质）,则∠BCD 的面积为A .8B .7.5 C.15 D .无法确定考什么?角平分线的性质,三角形的面积计算公式思路点拨已知角平分线+边的垂直(直角),考虑作垂直,应用角平分线上的点到角两边的距离相等.例2(2019青岛)如图,BD是∠ ABC的角平分线, AE∠BD（点拨：角平分线的垂线产生全等），垂足为 F .若∠ABC =35°, ∠C =50°,则∠CDE 的度数为A .35°B .40°C .45°D .50°考什么?角平分线的性质,三角形的内角和,全等三角形的判定与性质,三角形的内外角关系,等腰三角形的性质思路点拨已知角平分线+角平分线的垂线,构造出等腰三角形.例3如图,已知∠ABC的平分线交AC于点E ,过点E作DE∠BC（点拨：过角平分线上的点作平行线产生等腰三角形及角相等）,交AB于点D.若∠A =70°, ∠AED =50°, BD =2,则BE长为.考什么?角平分线的性质,平行线的性质,三角形的内角和,等腰三角形的判定与性质,特殊角的三角函数值思路点拨已知角平分线+平行线,构造出等腰三角形.实战演练1.如图,已知三角形ABC 中, ∠ABC =60°, BD 是∠ABC的平分线, CE ∠AB于点E ,交BD于点F,若EF =4,则FC 的长为.2.如图,在∠ABC中, BD平分∠ABC,以点B为圆心,AB长为半径画弧,交BC于点E,连接DE,已知∠A=70° ,则∠CED的度数为______.3.如图,在∠ABC中,D,E分别是AB,AC的中点,CF平分∠ACB，交DE于点F,若AC=10,BC=12,则DF的长为________.4.如图,在矩形ABCD中,点E,F分别是BC,CD上的点,连接EF,AE,AF,若AE,AF恰好平分∠BEF,∠DFE.(1)则∠EAF的度数为__________;(2)求证:四边形ABCD是正方形;(3)若BE=EC=3,则DF的长为________.模型12 双角平分线模型模型展现基础模型111怎么用?1. 找模型三角形中,遇到两角平分线，考虑用双角平分线模型2.用模型通过三角形的内角和,内外角关系及角平分线的性质，建立两角之间的数量关系结论分析结论1:∠D=90°+12∠A证明:∠ BD平分∠ABC,CD平分∠ACB∠∠DBC=12∠ABC,∠DCB=12∠ACB∠∠D= 180°-(∠DBC+∠DCB)= 180°-(12∠ABC+12∠ACB)=180°-12(∠ABC+∠ACB)= 180°-12(180°-∠A)=90°+12∠A拓展延伸结论2的证明同学们可参考结论1和结论3,利用三角形的内外角关系进行证明.结论3：∠D =90°-12∠A证明:∠BD平分∠EBC,CD平分∠FCB，∠∠DBC=12∠EBC,∠DCB=12∠FCB，∠∠D= 180°-(∠DBC+∠DCB)= 180°-(12∠EBC +12∠FCB)= 180°-12(∠ACB+∠A+∠ABC+∠A)= 180°-12( 180°+∠A )= 90°-12∠A.模型拓展333111满分技法若将角平分线改为三等分角线,同样根据三角形的内角和及角度的倍数关系求解.典例小试例1 如图,在∠ABC中,∠ B=40°,CD∠AB于点D,∠BCD和∠BDC的平分线相交于点E（结合图形可知是双内角平分线型），则∠E的度数为（)A.105°B.110°C.140°D.145°考什么?角平分线的性质,三角形的内角和万唯中考几何模型例2如图,在四边形ABCD中，∠DAB的平分线与∠ABC的外角平分线相交于点P，且∠D+∠C=210°,则∠P=（）A. 10°B.15° C．30° D.40°考什么?角平分线的性质,三角形外角的性质,三角形的内角和思路点拨结合图形可知两角平分线分别为内角、外角平分线,根据“一内一外”角平分线结论求解即可.实战实演1.如图,在∠ABC中, ∠C= 110°，AE平分∠DAB,延长EA,交∠ABC的平分线于点F,则∠F= 。

§ 2 三角恒等变换一、复习要点三角函数式的恒等变换是解答三角函数问题的方法基础．所谓三角式的恒等变换，就是运用有关概念和公式把给定的三角式化为另一等价形式．同一式子的不同形状，可以暴露式子的不同整体性质，我们对式子作恒等变换的目的，就是要把我们所需的整体性质显现出来．对式子的一次变形常常不能得到所需形状，须经过数次变形转化，才能达到目的．如何选择变形起步点?如何一步一步把给定式子转化为所需形状?通过对例题及训练题的分析，总结归纳出思维规律来，这是本节复习的重难点；本节复习的另一重点是，如何把一个三角函数问题化归为三角式的恒等变形问题．三角式的化简、求值问题，是训练三角恒等变换的基本题型．求三角函数的最小正周期、求三角函数最值、证明三角恒等式、解证三角方程或三角不等式问题，一般都要借助三角恒等变换而完成．联想三角公式与基本题型，并把二者与方程、不等式观点综合运用，这是运用三角恒等变换解答三角函数问题的思维关键．例1 （1）函数ｙ＝2ｓｉｎｘｃｏｓｘ＋2ｃｏｓ２ｘ的最小正周期是（）；Ａ．（π／2）Ｂ．πＣ．2πＤ．4π（2）函数y=2sinxsin2x的最大值是（）；A．（64／27）B．（8／9）C．2D．（／2）（3）若（1／cosθ）-（1／sinθ）=1，则sin2θ的值等于_________.讲解：（1）本题是判定一个较复杂三角函数的最小正周期问题．联想与此问题有关的基础知识与方法，想起我们会求角为ωｘ＋φ的基本三角函数的最小正周期，自然产生这样一个解题念头：希望运用三角公式和概念把原函数式变形为ｙ＝Ａｓｉｎ（ωｘ＋φ）＋Ｂ（或ｙ＝Ａ²ｃｏｓ（ωｘ＋φ）＋Ｂ）的形式，然后用熟知方法求出最小正周期．在这一思路指导下，着重观察已知三角函数式的结构特点，朝着既定目标方向，发现用倍角公式与和角公式能完成变形工作，得解法如下：ｙ＝2ｓｉｎｘｃｏｓｘ+2ｃｏｓ２ｘ＝ｓｉｎ2ｘ＋ｃｏｓ2ｘ＋1＝2ｓｉｎ（2ｘ＋（π／6））＋1，∴Ｔ＝（2π／2）＝π，故选B．（2）本题是一道无附加条件的最值问题.回忆求三角函数最值的基本模型方法，想到用三角恒等变换向基本模型转化，但转化方向一下看不透，应在变形过程中逐步明朗化．首先想到应用倍角公式，把原式化为y=4sin２xcosx，接着思考第二步变形．想法一：希望把原式化为y=Asin（ωx+φ）＋Ｂ的形式；想法二：希望把原式化为二次函数模型．这两种转化思维均受阻以后，应重新深入分析y=4sin２xcosx的结构特点，从中找出转化的新出路．注意到y的最大值应在cosx＞0时取得，因此：①y=4sin２xcosx可视为正变量的乘积，所以y与y２＝16sin４xcos２x同时取得最大值；②由y２的表达形式与sin２x+cos２x=1，联想到均值不等式，产生出想用均值不等式实施转化的思维方向——设法把式子变形为能用均值不等式求最值的形式．构思后，可得如下解法：当cosx＞0时，当且仅当sin２x=2cos２x，即cos２x=（1／3）时，等号成立．故选B．（3）这是一道填空题.条件为：sinθ与cosθ满足的一个方程式；目标为：求sin2θ的值．由目标首先联想到正弦倍角公式，得sin2θ＝2ｓｉｎθ²cosθ，看到了目标与条件的内在联系，萌发出解题的方程观点，想到由方程组（1／ｃｏｓθ）－（1／ｓｉｎθ）＝1，求出sin2θ.ｓｉｎ２θ＋ｃｏｓ２θ＝1，细思考感觉，先求出sinθ与cosθ的方法比较繁，暂不采取．转而思考：能否对条件中的方程式实施三角恒等变换，产生出关于sin2θ的方程而求得其值．朝着这一既定方向，运用三角恒等变换和解方程的方法，便可获得如下两种解法：解法1 （1／ｃｏｓθ）－（1／ｓｉｎθ）＝1（（1／ｃｏｓθ）－（1／ｓｉｎθ））２＝11／ｃｏｓ２θ）－（2／ｓｉｎθｃｏｓθ）＋（1／ｓｉｎ２θ）＝1（1／ｓｉｎ２θcos２θ）－（2／ｓｉｎθｃｏｓθ）＝1，即（1／ｓｉｎθｃｏｓθ）２－2（1／ｓｉｎθｃｏｓθ）－1＝0．解得（1／ｓｉｎθｃｏｓθ）＝1±．又由|ｓｉｎθｃｏｓθ|≤1｜（1／ｓｉｎθｃｏｓθ）｜≥1，∴（1／ｓｉｎθｃｏｓθ）＝1＋，∴ ｓｉｎθｃｏｓθ＝－1．故ｓｉｎ2θ＝2（－1）．解法2 （1／ｃｏｓθ）－（1／ｓｉｎθ）＝1ｓｉｎθ－ｃｏｓθ＝sinθｃｏｓθ1－2（ ｓｉｎθ－ｃｏｓθ）＝1－2ｓｉｎθｃｏｓθ＝（ｓｉｎθ－ｃｏｓθ）２，即（sinθ－ｃｏｓθ）２＋2（ｓｉｎθ－ｃｏｓθ）－1＝0．解得 sinθ－ｃｏｓθ＝－1±．又因｜ｓｉｎθ－ｃｏｓθ｜＝｜ｓｉｎθｃｏｓθ｜≤1，∴ ｓｉｎθ－ｃｏｓθ＝－1．故ｓｉｎ2θ＝2ｓｉｎθｃｏｓθ＝2（ｓｉｎθ－ｃｏｓθ）＝2（－1）．例2 （1）计算ctg10°－4ｃｏｓ10°的值;（2）化简ｓｉｎ２α＋ｓｉｎ２β＋2ｓｉｎαｓｉｎβ²ｃｏｓ（α＋β）．讲解：（1）本题是具体角的两个基本三角函数求差，形状虽简单，但两项角度均非特殊角，其倍、半角也非特殊角，也不能分拆为含特殊角的和或差，所以既无法分别求得其值，又不能用拆分角的方法，通过展开、抵消、合并得出结果．这种情况下，一个有效的策略思想是，先设法将两项分散的信息聚笼贯通，希望从中能看到“某种整体特殊性”或“内在联系”，在这一思想下，想到从“切化弦”并通分入手，得ｃｔｇ10°－4ｃｏｓ10°＝（ｃｏｓ10°／ｓｉｎ10°）－4ｃｏｓ10° ＝（ｃｏｓ10°－4ｃｏｓ10°ｓｉｎ10°／ｓｉｎ10°）．分子中第二项能用倍角公式将角扩大，出现一新角，得（ｃｏｓ10°－2ｓｉｎ20°／ｓｉｎ10°）．思路1．经观察可见，分子中两项的角度之和恰为特殊角30°，且分母的角度与分子中第一项的角度均为10°，由这种关系想到拆角法：20°＝30°－10°，得（ｃｏｓ10°－2ｓｉｎ（30°－10°）／ｓｉｎ10°）＝（ｃｏｓ10°－2［（1／2）ｃｏｓ10°－（／2）ｓｉｎ10°］／ｓｉｎ10°＝（ｓｉｎ10°）／ｓｉｎ10°．至此求解思路已贯通．整理以上分析，得出解答如下：原式＝（ｃｏｓ10°／ｓｉｎ10°）－4ｃｏｓ10°＝（ｃｏｓ10°－2ｓｉｎ20°）／ｓｉｎ10°＝（ｃｏｓ10°－2ｓｉｎ（30°－10°））／ｓｉｎ10°＝（ｃｏｓ10°－2［（1／2）ｃｏｓ10°－（／2）ｓｉｎ10°］／ｓｉｎ10°）＝．思路2．注意到分式化简的基本思想是对分子、分母因式分解，再行约分，而ｃｏｓ10°与2ｓｉｎ20°的系数不同，不便于化积，加之化为同名（ｓｉｎ80°与ｓｉｎ20°）后两角之差的一半为30°，想到拆项处理：（ｃｏｓ10°－2ｓｉｎ20°）／ｓｉｎ10°＝（ｓｉｎ80°－ｓｉｎ20°－ｓｉｎ20°）／ｓｉｎ10°＝（2ｃｏｓ50°ｓｉｎ30°－ｓｉｎ20°）／ｓｉｎ10°＝（ｃｏｓ50°－ｃｏｓ70°）／ｓｉｎ10°）＝（2ｓｉｎ60°ｓｉｎ10°）／ｓｉｎ10°＝．（2）这是一道二元三角多项式的化简问题．从式子各项中含基本三角函数的名称、幂次、角度及其组合关系看式子的结构特点：第三项比前两项角度复杂，组合关系复杂，而前两项为单角正弦的平方，幂次具有特殊性．由此可以产生出如下三个变形方向：①从分解较复杂的第三项入手，先把和角的三角函数化为单角的三角函数，从角度和幂次方面把第三项向前两项靠拢；②从分解较复杂的第三项入手，先把单角化为和差角，并从角度和幂次方面把第三项向前两项靠拢；③从前两项幂次的特殊性入手，先降幂，再从角度方面向第三项靠拢．若选定第一方向，则先用和角公式展开第三因子，得ｓｉｎ２α＋ｓｉｎ２β＋2ｓｉｎαｓｉｎβ［ｃｏｓαｃｏｓβ－ｓｉｎαｓｉｎβ］＝ｓｉｎ２α＋ｓｉｎ２β＋2ｓｉｎαｓｉｎβｃｏｓαｃｏｓβ－2ｓｉｎ２αｓｉｎ２β．看到第四项与前两项已经相通，拆开第四项与前两项分别合并，得ｓｉｎ２α（1－ｓｉｎ２β）＋ｓｉｎ２β（1－ｓｉｎ２α）＋2ｓｉｎαｓｉｎβｃｏｓαｃｏｓβ＝ｓｉｎ２αｃｏｓ２β＋ｓｉｎ２βｃｏｓ２α＋2ｓｉｎαｓｉｎβｃｏｓαｃｏｓβ．仔细观察发现：式子整体已呈现出两数和的平方展开式的形状，即式子的各部分用两数和的平方公式能贯通为一个整体：（ｓｉｎαｃｏｓβ＋ｃｏｓαｓｉｎβ）２．再用正弦和角公式，立得化简出结果：ｓｉｎ２（α＋β）．整理以上变形过程，得出解法一如下：原式＝ｓｉｎ２α＋ｓｉｎ２β＋2ｓｉｎαｓｉｎβ［ｃｏｓαｃｏｓβ－ｓｉｎαｓｉｎβ］＝ｓｉｎ２α（1－ｓｉｎ２β）＋ｓｉｎ２β（1－ｓｉｎ２α）＋2ｓｉｎαｓｉｎβｃｏｓαｃｏｓβ＝ｓｉｎ2αｃｏｓ2β＋ｃｏｓ2αｓｉｎ2β＋2ｓｉｎαｓｉｎβｃｏｓαｃｏｓβ＝（ｓｉｎαｃｏｓβ＋ｃｏｓαｓｉｎβ）２＝ｓｉｎ２（α＋β）．若选定第二变形方向，并在变形中运用积化和差公式，可得解法二如下：原式＝ｓｉｎ２α＋ｓｉｎ２β＋［ｃｏｓ（α－β）－ｃｏｓ（α＋β）］²ｃｏｓ（α＋β）＝ｓｉｎ２α＋ｓｉｎ２β＋ｃｏｓ（α－β）ｃｏｓ（α＋β）－ｃｏｓ２（α＋β）＝ｓｉｎ２α＋ｓｉｎ２β＋（1／2）（ｃｏｓ2α＋ｃｏｓ2β）－ｃｏｓ２（α＋β）＝ｓｉｎ２α＋ｓｉｎ２β＋（1／2）（1－2ｓｉｎ２α＋1－ｓｉｎ２β）－ｃｏｓ２（α＋β）＝1－ｃｏｓ２（α＋β）＝ｓｉｎ２（α＋β）．若选定第三变形方向，并在变形中运用和差化积公式，可得解法三如下：原式＝1－（1／2）（ｃｏｓ2α＋ｃｏｓ2β）＋2ｓｉｎαｓｉｎβｃｏｓ（α＋β）＝1－ｃｏｓ（α＋β）ｃｏｓ（α－β）＋2ｓｉｎαｓｉｎβｃｏｓ（α＋β）＝1－ｃｏｓ（α＋β）［ｃｏｓ（α－β）－2ｓｉｎαｓｉｎβ］＝1－ｃｏｓ（α＋β）［ｃｏｓαｃｏｓβ－ｓｉｎαｓｉｎβ］＝1－ｃｏｓ２（α＋β）＝ｓｉｎ２（α＋β）．例3 （1）求（1＋ｔｇ7°＋ｔｇ8°－ｔｇ7°ｔｇ8°／1－ｔｇ7°－ｔｇ8°－ｔｇ7°ｔｇ8°）的值；（2）若ｔｇθ、ｃｔｇθ是方程2ｘ２－2ｋｘ＝3－ｋ２的两个实根，且π＜θ＜（5π／4），求ｃｏｓθ－ｓｉｎθ的值．讲解：（1）从表达式中含有ｔｇ7°＋ｔｇ8°和ｔｇ7°ｔｇ8°能想到什么呢?在ｔｇ（7°＋8°）的展式中将会出现这样的式子!于是想到思路：ｔｇ15°＝（ｔｇ7°＋ｔｇ8°）／（1－ｔｇ7°ｔｇ8°）．故原式＝[（1＋ｔｇ15°（1－ｔｇ7°ｔｇ8°）－ｔｇ7°ｔｇ8°]／[[1－ｔｇ15°（1－ｔｇ7°ｔｇ8°）－ｔｇ7°ｔｇ8°）]＝[（1＋ｔｇ15°）（1－ｔｇ7°ｔｇ8°）]／（1－ｔｇ15°）（1－ｔｇ7°ｔｇ8°）） ＝（1＋ｔｇ15°）／（1－ｔｇ15°）＝ｔｇ（45°＋15°）＝．本题中运用的结构联想的思维方法在数学解题中是十分重要的．（2）由这样的条件想到韦达定理是很自然的：ｔｇθ＋ｃｔｇθ＝ｋ，ｔｇθ²ｃｔｇθ＝（1／2）（ｋ２－3）＝1，ｋ２＝5，ｋ＝±．对吗?注意θ的范围！由此应有ｋ＝．由于ｋ的确定，不难求出ｔｇθ＝（－1）／2（也要注意由θ的范围，0＜ｔｇθ＜1），∴（ｃｏｓθ－ｓｉｎθ）２＝1－ｓｉｎ2θ＝1－（2ｔｇθ／1＋ｔｇ２θ）＝（1／5）（5－2）．又∵ｃｏｓθ＜ｓｉｎ θ，∴ ｃｏｓθ－ｓｉｎθ ＝－． （本题也可由ｔｇθ＋ｃｔｇθ＝后直接变形得 ｓｉｎθｃｏｓθ＝（1／）代入上式）例4 设ａｓｉｎｘ＋ｂｃｏｓｘ＝0，Ａｓｉｎ2ｘ＋Ｂｃｏｓ2ｘ＝Ｃ（ａ，ｂ不同时为0）．证明：2Ａａｂ＋（ｂ２－ａ２）Ｂ＋（ａ２＋ｂ２）Ｃ＝0．讲解：本题要证明的是一个条件等式，其条件可看成关于ｘ的两个三角方程组成的方程组．可由前式解出ｘ再代入后式得出求证不等式．但ｘ不是特殊角，这样做计算量大，不可取．若由前式分别求出ｓｉｎｘ和ｃｏｓｘ再代入后式也可以，但求ｓｉｎｘ、ｃｏｓｘ时涉及到符号问题，这样处理也很麻烦．运用思维模块对ａｓｉｎｘ＋ｂｃｏｓｘ进行变形：ａ ｓｉｎｘ＋ｂｃｏｓｘ＝（（ａ／）ｓｉｎｘ＋（ｂ／）ｃｏｓｘ）．令ｓｉｎｙ＝－（ｂ／），ｃｏｓ ｙ＝（ａ／），则ｓｉｎ（ｘ－ｙ）＝0，由此得ｘ＝ｙ＋ｋπ（ｋ∈Ｚ），并求出ｃｏｓ2ｘ和ｓｉｎ2ｘ的值（ｃｏｓ2ｘ＝ｃｏｓ2（ｙ＋ｋπ）＝ｃｏｓ2ｙ＝2ｃｏｓ２ｙ－1＝…）代入后式即可得求证的结论．如果联想到ｓｉｎ2ｘ、ｃｏｓ2ｘ与ｔｇｘ的关系，可由前式求得ｔｇｘ＝（ｂ／ａ）（ａ＝0时另证），用万能公式求得ｓｉｎ2ｘ、ｃｏｓ2ｘ后代入后式也可得证．三、专题训练1．已知ｃｏｓ78°约等于0．20，那么ｓｉｎ66°约等于（）．A．0．92B．0．85C．0．88D．0．952．复数z= ｃｏｓ 2＋i的模为 （）．A．-cos2B．-cos2C．cos2D．cos23．函数ｙ＝｜ｓｉｎｘ｜＋｜ｃｏｓｘ｜的最小正周期是（）．Ａ．（π／4）Ｂ．（π／2）Ｃ．πＤ．2π4．设（1－ｔｇα）／（1＋ｔｇα）＝3－2，则ｓｉｎ2α的值是 （）．Ａ．（／2）Ｂ．（2／3）Ｃ．（3／4）Ｄ．（3／8）5．化简（ｓｉｎ（α／2）＋ｃｏｓ（α＋β／2）ｓｉｎ（β／2）／ｃｏｓ（α／2）－ｓｉｎ（α＋β）／2ｓｉｎ（β／2）），得______________．6．已知α、β为锐角，2ｔｇ（α＋3）ｓｉｎβ＝7，ｔｇα－6ｓｉｎβ＝1，则ｓｉｎα＝________．7．已知ｃｔｇα＝2，ｔｇ（α－β）＝－（2／3），则ｔｇ（β－2α）＝______________． 8．求下列三角式的值：（1）ｓｉｎ80°ｃｔｇ20°（ｔｇ20°－1）；（2）ｓｉｎ（60°－（α／2））ｃｏｓ（30°－（α／2））²（ｓｉｎ（α／2）／ｓｉｎ（3α／2））．9．（1）化简：（1＋ｓｉｎα／ｃｔｇ（α／2）－ｔｇ（α／2）［（3ｃｏｓα／2ｃｏｓ2（（π／4）－（α／2）））－2ｔｇ（（π／4）－（α／2）］；（2）证明：2sin4x+（3／4）sin22x+5cos4x-cos3xcosx=2（1+cos2x）.10．已知α、β、γ为锐角，ｔｇ（α／2）＝ｔｇ3（γ／2），2ｔｇβ＝ｔｇγ，求证：α，β，γ成等差数列．。

专题三：绝对值（基础专题）一．选择题1．若a＝﹣5，|a|＝|b|，则b的值等于（）2．下列判断正确的是（）A．若|a|＝|b|，则a＝b B．若|a|＝|b|，则a＝﹣bC．若a＝b，则|a|＝|b|D．若a＝﹣b，则|a|＝﹣|b|3．有下列结论：①|a|一定是正数；②只有两个数相等时，它们的绝对值才相等；③绝对值最小的数是0；④在数轴上表示﹣a的点一定在原点的左边；⑤有理数分为正有理数和负有理数；其中正确的结论的个数为（）A．1个B．2个C．3个D．4个4．如图，四个有理数在数轴上的对应点分别为点M，P，N，Q，若点P，Q表示的有理数互为相反数，则图中表示绝对值最大的有理数的点是（）A．点M B．点P C．点N D．点Q二．填空题5．若a＞0，b＜0，化简a+3b﹣|a|+|2b|得．6．绝对值不大于3的整数是______________．绝对值小于2015的所有整数之积为_____．7．数轴上到原点的距离小于3的整数的个数为x，不大于3的正整数的个数为y，绝对值等于3的整数的个数为z，则x+y+z＝_____．三．解答题8．已知|x﹣4|+|y+2|＝0，求x与y的值．9．已知|x﹣4|+|5﹣y|＝0，求12（x+y）的值．10．若|a|＝4，|b|＝2，且a，b异号，求a与b的值．11．有理数a，b，c在数轴上的对应点如图所示．（1）在横线上填入“＞”或“＜”：a______0；b______0；c______0；|c|______|a|．（2）试在数轴上找出表示﹣a，﹣b，﹣c的点；（3）试用“＜”将a，﹣a，b，﹣b，c，﹣c，0连接起来．12．已知数a ，b 表示的点在数轴上的位置如图所示．（1）在数轴上表示出a ，b 的相反数的位置，并将这四个数从小到大排列；（2）若数b 与其相反数相距16个单位长度，则b 表示的数是多少？（3）在（2）的条件下，若数a 与数b 的相反数表示的点相距4个单位长度，则a 表示的数是多少？【参考答案】1。

专题三角平分线的性质与判定一、单选题1．如图，在△ABC中，∠C=90°，AD平分∠BAC交BC于点D，若BC=15，且BD:CD=3:2，则点D到AB的距离为（）2345．如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，AB+BC+CA=18，过O作OD⊥BC于点D，且OD=3，则△ABC的面积是．6．如图，AD∥BC，∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P，作PE⊥AB于点E．若PE7得8910．如图，△ABC中，∠ABC，∠ACB的角平分线交于点O，过O点作MN∥BC分别交AB，AC于M，N 两点，AB=6，ΔAMN的周长是15．则AC的长为．三、解答题11．如图1，△ABC的两条外角平分线AO，BO相交于点O，∠ACB=50°．(1)直接写出∠AOB的大小；(2)如图2，连接OC交AB于K．①求∠BCK的大小；②如图3，作AF⊥OC于F，若∠BAC=105°，求证：AB=2CF．12．如图，四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，DF平分∠CDA，若∠ABC=60°，FD=10，求DC的长．13．如图，四边形ABCD中，∠B=90°，AB∥CD，M是BC边上的一点，且AM平分∠BAD,DM平分∠ADC,求证：(1)BM=MC；(2)AM⊥MD．14．定义：如果一个三角形的一个内角等于另一个内角的两倍，则称这样的三角形为“倍角三角形”．(1)如图1，△ABC中，AB=AC,∠A=36°，求证：△ABC是倍角三角形；(2)如图2，△ABC的外角平分线AD与CB的延长线相交于点D，延长CA到点E，使得AE=AB，若AB+AC=BD，请你找出图中的倍角三角形，并进行证明．15．如图，四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，DF平分∠CDA，设∠ABC=α．(1)α=50°时，求∠DFC的度数；(2)证明：BE∥DF．16．在△ABC中，AO、BO分别平分∠BAC、∠ABC．(1)如图1，若∠C=32°，则∠AOB=________；(2)如图2，连结OC，求证：OC平分∠ACB；(3)如图3，若∠ABC=2∠ACB，AB=4，AC=7，求OB的长．17．如图，在△ABC中，D在BC边的延长线上，∠ACD的平分线CE交BA的延长线于点E，已知∠B=30°，∠E=40°，求证：AE=CE．18．如图，在四边形ABCD中，AB∥CD，∠C=90°，点E为BC的中点，DE平分∠CDA.(1)求证：AD=AB+CD；(2)若S△CDE=3，S△ABE=4，则四边形ABCD的面积为______.（直接写出结果）19．如图，在△ABC中，BO平分∠ABC，CO平分∠ACB，MN经过点O与AB，AC分别相交于点M，N，且MN∥BC．(2)已知AB=7，AC=6，求△AMN的周长．参考答案题号12答案B B1．B【分析】本题考查的是角平分线的性质，作DE⊥AB于E，根据角平分线的性质得到CD=DE，根据题意求出CD的长即可．∵∴∵∴2∴3【详解】试题分析：本题需要分两种情况进行讨论：如图1所示：根据∠B=40°，∠C=70°可得：∠BAC=70°，根据高线以及角平分线的性质可得：∠DAC=20°，∠EAC=35°，则∠DAE=35°-20°=15°；如图2所示：根据∠B=40°，∠ACD=70°可得：∠BAC=30°，根据高线以及角平分线的性质可得：∠DAC=20°，∠EAC=15°，则∠DAE=15°+20°=35°.点睛：对于这种在三角形中求角度问题的时候，如果题目中没有给出图形，我们首先一定要根据题意画出图形，然后根据图形求出角的度数.特别要注意分类讨论的思想，在画图时一定要注意锐角三角形和钝角三角形两种情况.在画垂线的时候要注意高线在三角形内部和三角形外部两种情况.4．3：2【分析】过点D作DE⊥AB于点E，由角平分线的性质得到DE=CD，再根据三角形面积公式解答即可．【详解】解：过点D作DE⊥AB于点E，∵AD是Rt△ABC的角平分线，CD⊥AC,DE⊥AB∴DE=CDS△ABD S△ACD =12AB⋅DE12AC⋅CD=ABAC=128=32故答案为：3：2．【点睛】本题考查角平分线的性质、三角形面积公式等知识，是基础考点，掌握相关知识是解题关键．5．27【分析】作OE⊥AB于E,OF⊥AC于F，连接OA，根据角平分线的性质求出OE=OD=3和OF=OD=3，根据三角形面积公式计算即可．【详解】解：作OE⊥AB于E,OF⊥AC于F，连接OA，∵OB是∠ABC的平分线，OD⊥BC,OE⊥AB，∴OE=OD=3，同理OF=OD=3，∵AB+BC+CA=18．∴△ABC的面积=12×AB×3+12×AC×3+12×BC×3=27．故答案为：27．【点睛】本题主要考查角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．6．4【分析】根据角平分线的性质以及平行线的性质即可得出PM =PE =2，PE =PN =2，即可得出答案．【详解】解：过点P 作MN ⊥AD ，∵AD ∥BC ，∠ABC 的角平分线BP 与∠BAD 的角平分线AP 相交于点P ，PE ⊥AB 于点E ，∴AP ⊥BP ，PN ⊥BC ，∴PM =PE =2，PE =PN =2，∴MN =2+2=4．故答案为：4．7．2【分析】连接PC 、PB 、PA ，作PD ⊥AB 于D ，PE ⊥AC 于E ，PF ⊥BC 于F ，根据三角形的面积公式计算即可．【详解】连接PC 、PB 、PA ，作PD ⊥AB 于D ，PE ⊥AC 于E ，PF ⊥BC 于F ，由题意得，PE=PD=PF ， S △APC +S △APB +S △BPC =S △ACB ，∴12AC·PE+12AB·PD+12BC·PF=12AC·BC ，即12×12·PD+12×13•PD+12×5•PD=12×5×12，解得，PD=2，故答案为：2．【点睛】本题考查的是三角形的面积计算，掌握三角形的面积公式是解题的关键．8．60【分析】根据五边形的内角和求出∠BCD和∠CDE的和，再根据角平分线及三角形内角和求出∠CPD．【详解】解：∵五边形的内角和等于540°，∠A+∠B+∠E＝300°，∴∠BCD+∠CDE＝540°﹣300°＝240°，∵∠BCD、∠CDE的平分线在五边形内相交于点O，（∠BCD+∠CDE）＝120°，∴∠PDC+∠PCD＝12∴∠CPD＝180°﹣120°＝60°．故答案是：60．【点睛】本题解题的关键是知道多边形内角和定理以及角平分线的性质．9．5【分析】本题考查角平分线的性质定理，过点P作PE⊥OB，垂足为E，过点P作PF⊥MN，垂足为F，过点P作PG⊥OA，垂足为G，连接OP，利用角平分线的性质可得PF=PG=PE，然后根据三角形的面积求出PF=PE=PG=2，再利用△OMP的面积+△ONP的面积−△PMN的面积=4，进行计算即可解答．根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．【详解】解：过点P作PE⊥OB，垂足为E，过点P作PF⊥MN，垂足为F，过点P作PG⊥OA，垂足为G，连接OP，∵MP平分∠AMN，NP平分∠MNB，∴PF=PG=PE，∵MN=1，△PMN的面积是1，∴ 12MN ⋅PF =1，∴PF =2，∴PG =PE =2，∵△OMN 的面积是4，∴△OMP 的面积+△ONP 的面积−△PMN 的面积=4，∴ 12OM ⋅PG +12ON ⋅PE−1=4，∴OM +ON =5．故答案为：5．10．9【分析】本题考查了等腰三角形的判定与性质，平行线的性质，根据角平分线的定义和平行线的性质可得△MOB 和△NOC 是等腰三角形，从而可得MO =MB ，NO =NC ，然后利用等量代换可得ΔAMN 的周长=AB +AC ，从而进行计算即可解答．【详解】解：∵BO 平分∠ABC ，CO 平分∠ACB ，∴∠ABO =∠OBC ，∠ACO =∠OCB ，∵MN ∥BC ，∴∠MON =∠OBC ，∠NOC =∠OCB ，∴∠ABO =∠MON ，∠ACO =∠NOC ，∴MO =MB ，NO =NC ，∵△AMN 的周长是15，∴AM +MN +AN =15，∴AM +MO +ON +AN =15∴AM +MB +NC +AN =15，∴AB +AC =15，∵AB =6，∴AC =15−6=9，故答案为：9．11．(1)65°；(2)①25°；②证明见解析．【分析】（1）根据三角形内角和定理求得∠CBA +∠CAB =130°，则∠EBA +∠BAD =230°，再由角平分线的定义求出∠OBA +∠OAB =115°，根据四边形内角和求出∠AOB 即可；（2）①过点O作OM⊥AD于点M，ON⊥BE于点N，OP⊥AB于点P，根据角平分线的性质求解即可；②先求出KB=KC，过点A作AH∥BC交CO于点H，再求出KA=KH，则AB=CH，分别求出AH=AC，HF=CF，即可得出结论．【详解】（1）解：∵AO平分∠BAD，∴∠DAO=∠OAB，∵BO平分∠EOA，∴∠EBO=∠OBA，∵∠ACB=50°，∴∠CBA+∠CAB=130°，∴∠EBA+∠BAD=360°−130°=230°，∴∠OBA+∠OAB=115°，∴∠AOB=360°−50°−115°−130°=65°；（2）解：如图2，①过点O作OM⊥AD于点M，ON⊥BE于点N，OP⊥AB于点P，∵AO、BO分别平分∠DAB、∠EBA，∴OM=OP，OP=ON，∴OM=ON，∴CO平分∠ACB，∵∠ACB=50°，∴∠BCK=∠ACK=25°；②证明：∵∠BAC=105°，∠ACB=50°，∴∠ABC=25°，∵∠KCB=25°，∴∠KBC=∠KCE，∴KB=KC，如图3，过点A作AH∥BC交CO于点H，∴∠AHK=∠KCB，∠HAK=∠KBC，∴∠AHK=∠HAK，∴KA=KH，∴AB=CH，∵∠AHK=∠ACH，∴AH=AC，∵AF⊥CO，∴HF=CF，∴CH=2CF，∴AB=CH=2CF．12∴∵∴∴∵∴∴故DC=5．【点睛】此题主要考查了角平分线的定义，四边形内角和定理，含30°角的直角三角形的性质等知识，解题关键是熟练掌握各性质与定理．13．(1)见详解(2)见详解【分析】（1）作NM⊥AD，根据角平分线的性质得到BM=MN,MN=CM，等量代换得到答案．（2）根据平行线的性质得到∠BAD+∠ADC=180°，根据角平分线的定义得到∠MAD+∠ADM=90°，根据垂直的定义得到答案；【详解】（1）作NM⊥AD交AD于N，∵∠B=90°,AB∥CD,∴BM⊥AB,CM⊥CD,∵AM平分∠BAD,DM平分∠ADC,∴BM=MN,MN=CM,∴BM=CM；（2）证明：∵AB∥CD，∴∠BAD+∠ADC=180°,∵AM平分∠BAD,DM平分∠ADC,∴2∠MAD+2∠ADM=180°,∴∠MAD+∠ADM=90°,∴∠AMD=90°,即AM⊥DM；【点睛】本题考查的是角平分线的性质，掌握平行线的性质和角的平分线上的点到角的两边的距离相等是解题的关键．14．(1)见解析(2)△ADC和△ABC是倍角三角形，见解析【分析】（1）利用等边对等角及三角形的内角和求出∠B=∠C=72°，得到2∠A=∠C即可；（2）根据SAS证明△ABD≌△AED，得到∠ADE=∠ADB，BD=DE，证明CE=DE，得出∠C=∠BDE=2∠ADC，可得出∠ABC=2∠C．则结论得证．【详解】（1）证明：∵AB=AC，∴∠B=∠C，∵∠A+∠B+∠C=180°，∠A=36°，∴∠B=∠C=72°，∴2∠A=∠C，即△ABC是倍角三角形；（2）解：△ADC和△ABC是倍角三角形，证明如下：∵AD平分∠BAE，∴∠BAD=∠EAD，∵AB=AE，AD=AD，∴∴又∴∴∴∴∵15(2)∠EBC=∠DFC即可得出结论．【详解】（1）解：在四边形ABCD中，∠A=∠C=90°，∠ABC=α，α=50°，∴∠ADC=360°−∠A−∠C−∠ABC=130°，∵DF平分∠CDA，∠ADC=65°，∴∠FDC=12∴∠DFC =90°−65°=25°；（2）证明：在四边形ABCD 中，∠A =∠C =90°，∠ABC =α，∴∠ADC =360°−∠A−∠C−∠ABC =180°−α，∵DF 平分∠CDA ，∴∠FDC =12∠ADC =12(180°−α)，∴∠DFC =90°−12(180°−α)=12α，∵BE 平分∠ABC ，∴∠EBC =12α，∴∠EBC =∠DFC ，∴BE ∥DF ．16．(1)106°；(2)见解析；(3)3；【分析】（1）本题考查与角平分线有关的三角形内角和关系，根据∠C =32°得到∠CAB +∠CBA ，再结合角平分线求出∠CAO +∠CBO ，即可得到答案；（2）本题考查角平分线判定与性质，过O 作OD ⊥AC ，OE ⊥AB ，OF ⊥BC ，根据角平分线性质得到OD =OF =OE ，结合角平分线的判定即可证明；（3）本题主要考查三角形全等的性质与判定，解题的关键是根据截长补短作出辅助线，在AC 上截取一点D ，使AD =AB ，连OD ，证明△ABO≌△ADO ，即可得到答案；【详解】（1）解：∵∠C =32°，∴∠CAB +∠CBA =180°−32°=148°，∵AO 、BO 分别平分∠BAC 、∠ABC ，∴∠CAO +∠CBO =148°2=74°，∴∠AOB =180°−74°=106°；（2）证明：过O 作OD ⊥AC ，OE ⊥AB ，OF ⊥BC ，∵AO 、BO 分别平分∠BAC 、∠ABC ，∴OD =OF ，OD =OE ，∴OC 平分∠ACB ；（3）解：在AC 上截取一点D ，使AD =AB ，连OD ，设∠ACO =∠BCO =α，∵∠ABC =2∠ACB ，∴∠ABC =4α，∵BO 平分∠ABC ，∴∠ABO =∠CBO =2α，∵AO 平分∠BAC ，∴∠BAO =∠DAO ，在△ABO 与△ADO 中，AO =AO ∠BAO =∠DAO AB =AD，∴△ABO≌△ADO(SAS)，∴∠ABO =∠ADO =2α，OB =OD,AB =AD =4，又∵∠ACO =α，∴∠ACO =∠DCO =α，∴OD =OC =AC−AD =7−4=3，∴OB =3．17．证明见解析【分析】本题主要考查了角平分线的定义，三角形外角的性质以及等腰三角形的判定和三角形内角和定理的应用，根据外角的性质求出∠ECD=702，由角平分线的定义得∠ACE=∠ECD=70°，根据三角形内角和定理求出∠CAE=70°，可得∠ACE=∠CAE，从而可得结论．【详解】证明：∠B=30°，∠E=40°，∴∠ECD=∠B+∠E=70°，∵CE平分∠ACD，∴∠ACE=∠ECD=70°，在△ABE中，∠ACE+∠E+∠CAE=180°，∴∠CAE=180°−∠ACE−∠E=180°−70°−40°=70°，∴∠ACE=∠CAE，∴AE=CE．18．(1)见解析(2)14【分析】本题考查角平分线的性质，全等三角形的判定与性质．（1）过点E作EF⊥AD于F，根据角平分线的性质得出CE=EF，再证明△ABE≌△AFE，△CED≌△FED，根据全等三角形的性质得出AB=AF，DC=DF，进而得出结论；（2）由△ABE≌△AFE，△CED≌△FED，推出S△CED=S△FED，S△ABE=S△AFE，据此求解即可．【详解】（1）证明：如图，过点E作EF⊥AD于F，∵∠C=90°，AB∥CD，∴∠B=90°，∵DE平分∠CDA，∴CE=EF，∴Rt△CED≌Rt△FED(HL)，∴DC=DF，∵E是BC的中点，∴BE=CE，∴BE=EF，∵AE=AE，∴Rt△ABE≌Rt△AFE(HL)，∴AD=AF+FD=AB+CD；（2）解：∵△CED≌△FED，△ABE≌△AFE，∴S△CED=S△FED，S△ABE=S△AFE，∵S∴19(2)（（∴∴∴（∴∵∴∴∠BOM=∠ABO，∴BM=OM，同理可得：CN=ON，∴MN=OM+ON=BM+CN，∵AB=7，AC=6，∴△AMN的周长是AM+MN+AN=AM+BM+CN+AN=AB+AC=13．。

（专题三）期中复习专题三：分数篇-2022-2023学年五年级数学下册典型例题系列（原卷版+解析版）苏教版一、【教学目标】1、能够读写简单分数，理解分子与分母的概念；2、掌握分数的基本运算，包括加、减、乘法和除法；3、能够在实际问题中应用分数，如用分数表示比例或比率。

二、【教学重难点】1、理解分子、分母的概念以及读、写、约分等操作；2、学会加、减、乘、除分数的方法和技巧；3、运用分数解决实际问题。

三、【教学过程】1、导入新课从学生平常生活中出发，提问：小李今天吃了几块蛋糕？如果小李吃了单独的一块蛋糕呢？如果小李吃了四分之一个蛋糕呢？从这些问题中可以看出，分数在我们日常生活中已经占有很重要的地位。

2、复习基础知识1）请学生说出下列分数的分子和分母：$\frac{2}{3}$ $\frac{1}{2}$ $\frac{8}{10}$ $\frac{4}{5}$ $\fr ac{15}{21}$2）将下列分数写成阿拉伯数字的形式：$\frac{5}{7}$ $\frac{9}{11}$ $\frac{21}{30}$ $\frac{11}{15} $ $\frac{8}{9}$3）请用最简分数表示：$ \frac{4}{16} $ $ \frac{6}{24}$ $ \frac{7}{28}$ $ \frac{12}{48} $4）简化下列分数：$ \frac{20}{30} $ $ \frac{24}{36} $ $ \frac{16}{24}$ $ \frac{21}{35} $老师可设计多种不同形式的复习题目，让学生巩固基础知识。

3、引入新知1）分数的加法和减法回忆一下小学一年级时候学过的加法和减法，它们是一样的。

只不过现在有些数我们需要用分数来表示。

所以分数的加减法也与整数类似，我们只要把分母相同时，把分子加减就可以了。

具体的，可以用图形来表示。

如下图，三分之二加五分之三。

普及一下“通分”的方法，即找出两个数的公倍数，然后改写成相同的分母即可。

3.2 解三角形基础题命题角度1利用正弦、余弦定理解三角形高考真题体验·对方向1.(2019全国Ⅰ·11)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c.已知a sin A-b sin B=4c sin C ,cosA=-14,则bb =()A.6B.5C.4D.3,得a 2-b 2=4c 2,由余弦定理的推论,得-14=cos A=b 2+b 2-b 22bb, ∴b 2-4b 22bb =-14,∴-3b 2b =-14,∴b b =32×4=6,故选A .2.(2018全国Ⅱ·6)在△ABC 中,cos b2=√55,BC=1,AC=5,则AB=()A.4√2B.√30C.√29D.2√5cos C=2cos 2b 2-1=-35,∴AB 2=BC 2+AC 2-2BC ·AC cos C=1+25+2×1×5×35=32.∴AB=4√2.3.(2018全国Ⅲ·9)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c.若△ABC 的面积为b 2+b 2-b 24,则C=()A.π2B.π3C.π4D.π6S=b2+b2-b24=12ab sin C,得c2=a2+b2-2ab sin C.又由余弦定理c2=a2+b2-2ab cos C,∴sin C=cos C,即C=π4.4.(2017某某·9)在△ABC中,角A,B,C的对边分别为a,b,c,若△ABC为锐角三角形,且满足sin B(1+2cos C)=2sin A cos C+cos A sin C,则下列等式成立的是()A.a=2bB.b=2aC.A=2BD.B=2Asin B(1+2cos C)=2sin A cos C+cos A sin C,∴sin B+2sin B cos C=(sin A cos C+cos A sin C)+sin A cos C,∴sin B+2sin B cos C=sin B+sin A cos C, ∴2sin B cos C=sin A cos C,又△ABC为锐角三角形,∴2sin B=sin A,由正弦定理,得a=2b.故选A.5.(2019全国Ⅱ·15)△ABC的内角A,B,C的对边分别为a,b,c.若b=6,a=2c,B=π3,则△ABC的面积为.√3b2=a2+c2-2ac cos B,∴(2c)2+c2-2×2c×c×12=62,即3c 2=36,解得c=2√3或c=-2√3(舍去).∴a=2c=4√3.∴S △ABC =12ac sin B=12×4√3×2√3×√32=6√3.典题演练提能·刷高分1.在△ABC 中,若原点到直线x sin A+y sin B+sin C=0的距离为1,则此三角形为()A.直角三角形B.锐角三角形C.钝角三角形D.不能确定解析由已知可得√22=1,∴sin 2C=sin 2A+sin 2B ,∴c 2=a 2+b 2,故三角形为直角三角形.选A .2.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若2b cos C+c=2a ,且b=√13,c=3,则a=() A.1 B.√6C.2√2D.42b cos C+c=2a ,由正弦定理可得2sin B cos C+sin C=2sin A=2sin(B+C )=2sin B cos C+2cos B sin C ,∴sin C=2cos B sin C ,∵sin C ≠0,∴cos B=12.由余弦定理可得b 2=a 2+c 2-2ac cos B ,又知b=√13,c=3,解得a=4.故选D .3.(2019某某某某高三质检)已知△ABC 的内角A ,B ,C 的对边分别是a ,b ,c ,若a sin B=2b sinC ,b=3,cos B=14,则△ABC 的面积为()A.9√15B.9√1516C.3√1516D.916a sin B=2b sin C ,结合正弦定理可得ab=2bc ,则a=2c.由余弦定理b 2=a 2+c 2-2ac cos B ,可得9=(2c )2+c 2-2×2c ×c ×14,解得c=32,则a=3.又sin B=√1-cos 2b =√154,所以S △ABC =12ac sin B=12×3×32×√154=9√1516.故选B .4.在△ABC 中,A ,B ,C 的对边分别为a ,b ,c ,若2cos 2b +b2-cos 2C=1,4sin B=3sin A ,a-b=1,则c 的值为()A.√13B.√7C.√37D.6解析∵2cos2b +b2=2cos 2π-b 2=2cos 2π2−b 2=2sin 2b2=1-cos C ,∴1-cos C-cos2C=1.∴cos2C=-cos C.∴2cos 2C+cos C-1=0,解得cos C=12.因为{b -b =1,4b =3b ,故得到{b =3,b =4.根据余弦定理得到12=b 2+b 2-b 22bb,解得c 的值为√13.5.△ABC 内角A ,B ,C 的对边分别为a ,b ,c ,若a=5,B=π3,cos A=1114,则△ABC 的面积S=()A.10√33B.10C.10√3D.20√3cos A=1114,所以sin A=5√314,由正弦定理得到bsin b=bsin b,解得b=7,由正弦定理得到sin C=sin(A+B )=4√37,△ABC 的面积S=12×5×7×4√37=10√3.6.(2019某某某某高三二调)在△ABC 中,角A ,B ,C 成等差数列,且对边分别为a ,b ,c ,若bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =20,b=7,则△ABC 的内切圆的半径为()A.√3B.7√33C.2D.3角A ,B ,C 成等差数列,∴2B=A+C=π-B ,即B=π3,∴bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =ca cos π3=20,即ca=40,由余弦定理b 2=c 2+a 2-2ca cos B ,可得49=a 2+c 2-ac=(a+c )2-3ac=(a+c )2-120,解得a+c=13.故a=5,c=8.设△ABC 的内切圆的半径为r ,则12(a+b+c )r=12ac sin B ,可得12(5+8+7)r=12×5×8×√32,可得△ABC 的内切圆的半径r=√3.故选A .7.如图,平面四边形ABCD 中,AC 与BD 交于点P ,若3bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ +bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =3bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ,AB=AD=√3BC ,∠CAD+∠ACB=56π,则bbbb=() A.√213B.√214C.2√63D.√62BC=1,则AB=AD=√3,延长BC 到E ,使BE=3BC ,所以CE=2,依题意3bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =2bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ +(bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ −bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ )=2bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ +bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ +bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ,所以AC ∥DE ,所以bb bb=bb bb=12,由正弦定理得{bb sin b =bbsin b ,bb sin b=bb sin b,两式相除得2sin b=√3sin b, 所以2sin5π6-α=√3sin α,所以α=π2,β=π3.在△ABC 中,由余弦定理得3=1+AC 2-2AC cos π3,AC=2,在Rt △ACD 中CD=√3+4=√7,故bbbb =√7√3=√213,选A .8.在△ABC 中,AB=2,AC=√7,∠ABC=2π3,则BC=.,根据余弦定理得AC 2=AB 2+BC 2-2AB ·BC ·cos B ,即BC 2+2BC-3=0,解得BC=1,或BC=-3(舍去负值).9.在△ABC 中,a=1,b=√7,且△ABC 的面积为√32,则c=.或2√3△ABC =12ab sin C=12×1×√7×sin C=√32,则sin C=√217,cos C=±2√77, 当cos C=2√77时,c 2=1+7-2×1×√7×2√77=4,c=2;当cos C=-2√77时,c 2=1+7+2×1×√7×2√77=12,c=2√3.10.我国南宋著名数学家秦九韶在他的著作《数书九章》卷五“田域类”里有一个题目:“问有沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里.里法三百步.欲知为田几何.”这道题讲的是有一个三角形沙田,三边长分别为13里,14里,15里,假设1里按500米计算,则该三角形沙田外接圆的半径为米..5由题意画出图象,如图所示,且AB=13里=6500米,BC=14里=7000米,AC=15里=7500米.在△ABC 中,由余弦定理有cos B=bb 2+bb 2-bb 22bb ·bb=132+142-1522×13×14=513,B 为锐角,sin B=√1-cos 2b =1213.设△ABC 外接圆半径为R ,则由正弦定理有bsin b =2R ,R=b2sin b =75002×1213=4062.5(米).命题角度2与三角形有关的最值和X 围问题高考真题体验·对方向1.(2015全国Ⅰ·16)在平面四边形ABCD 中,∠A=∠B=∠C=75°,BC=2,则AB 的取值X 围是.√6−√2,√6+√2).作CE ∥AD 交AB 于E ,则∠CEB=75°,∠ECB=30°.在△CBE中,由正弦定理得,EB=√6−√2.延长CD交BA的延长线于F,则∠F=30°.在△BCF中,由正弦定理得,BF=√6+√2,所以AB的取值X围为(√6−√2,√6+√2).2.(2014全国Ⅰ·16)已知a,b,c分别为△ABC三个内角A,B,C的对边,a=2,且(2+b)(sin A-sinB)=(c-b)sin C,则△ABC面积的最大值为.√3,可得(2+b)(a-b)=(c-b)·c.∵a=2,∴a2-b2=c2-bc,即b2+c2-a2=bc.由余弦定理,得cos A=b2+b2-b22bb =12.∴sin A=√32.由b2+c2-bc=4,得b2+c2=4+bc.∵b2+c2≥2bc,即4+bc≥2bc,∴bc≤4.∴S△ABC=12bc·sin A≤√3,即(S△ABC)max=√3.典题演练提能·刷高分1.(2019某某某某高三一模)在△ABC中,AB=2,C=π6,则AC+√3BC的最大值为() A.4√7 B.3√7C.2√7D.√7ABC 中,AB=2,C=π6,则2R=bbsin b =4,则AC+√3BC=4sin B+4√3sin A=4sin 5π6-A +4√3sin A=2cos A+6√3sin A=4√7sin(A+θ),其中sin θ=√714,cos θ=3√2114,由于0<A<5π6,0<θ<π2,所以0<A+θ<4π3,所以最大值为4√7.故选A .2.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若A=π3,a=2√2,则△ABC 面积的最大值为()A.√2B.2√3C.√6D.√3ABC 中,由余弦定理知a 2=b 2+c 2-2bc cos A ,即8=b 2+c 2-2bc cos π3=b 2+c 2-bc ≥2bc-bc=bc ,即bc ≤8,当且仅当b=c 时,等号成立,所以△ABC 面积的最大值为S=12bc sin A=12×8sin π3=2√3,故选B .3.已知锐角△ABC 中的内角A ,B ,C 的对边分别为a ,b ,c ,若b 2=a (a+c ),则sin 2bsin(b -b )的取值X 围是()A.(0,√22)B.(12,√32) C.(12,√22) D.(0,√32)b 2=a (a+c ),由余弦定理,得a 2+c 2-2ac cos B=a (a+c ), 化简得c-a=2a cos B.由正弦定理,得sin C-sin A=2sin A cos B ,∵C=π-(A+B ),∴sin(A+B )-sin A=2sin A cos B ,化简得sin(B-A )=sin A.∵△ABC 是锐角三角形,∴B-A=A ,即B=2A ,∵{0<b <π2,π2<b +b <π,即{0<2b <π2,π2<3b <π,∴π6<A<π4,∴sin 2bsin(b -b )=sin A ∈(12,√22).4.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知△ABC 的面积为√3,且cos(b +b )cos b=b2b +b ,则c 的最小值是()A.2B.2√2C.2√3D.4∵cos(b +b )cos b=b 2b +b ,∴-cos b cos b =b2b +b ,∴根据正弦定理可得-cos bcos b =sin b2sin b +sin b ,即-2sin A cos C=sin A.∵sin A ≠0,∴cos C=-12.∵C ∈(0,π),∴C=2π3.∵△ABC 的面积为√3,∴S △ABC =12ab sin C=√3,即ab=4.∵cos C=b 2+b 2-b 22bb=-12, ∴c 2=a 2+b 2+ab ≥2ab+ab=3ab=12,当且仅当a=b 时取等号. ∴c min =2√3,故选C .5.在△ABC 中,已知a 2+b 2-c 2=4S (S 为△ABC 的面积),若c=√2,则a-√22b 的取值X 围是()A.0,√2B.-1,0C.-1,√2D.-√2,√2a 2+b 2-c 2=4S ,∴a 2+b 2-c 2=4×12ab sin C=2ab sin C.∴b 2+b 2-b 22bb =sin C ,∴cos C=sin C.∴C=π4. ∵bsin b =bsin b =bsin b =√2√22=2,∴a=2sin A ,b=2sin B ,又a-√22b=2sin A-√22×2sin B=2sin A-√2sin B=2sin A-√2sin3π4-A=sin A-cos A=√2sin A-π4,∵0<A<3π4,∴-π4<A-π4<π2, ∴-1<√2sin A-π4<√2,∴-1<a-√22b<√2,故选C .6.已知平面四边形ABCD 中,AB=AD=2,BC=CD ,∠BCD=90°,则四边形ABCD 面积的最大值为()A.6B.2+2√3C.2+2√2D.4,设∠DAB=θ,BC=CD=x ,则BD=√2x.在△ABD 中,由余弦定理得BD 2=AB 2+AD 2-2AB ·AD ·cos θ,即(√2x )2=4+4-8cos θ=8-8cos θ,∴x 2=4-4cos θ.∴四边形ABCD 的面积为S=12×22×sin θ+12x 2=2sin θ+(2-2cos θ)=2√2sin θ-π4+2.∵0<θ<π,∴-π4<θ-π4<3π4,∴当θ-π4=π2,即θ=3π4时,S 有最大值,且S max =2√2+2.选C .7.已知点O 是△ABC 的内心,∠BAC=60°,BC=1,则△BOC 面积的最大值为.BOC=180°-180°-60°2=120°,在△OBC 中,BC 2=OB 2+OC 2-2OB ·OC ·cos120°,即1=OB 2+OC 2+OB ·OC ≥3OB ·OC ,即OB ·OC ≤13,所以S △OBC =12OB ·OC sin120°≤√312,当OB=OC 时取得最大值.8.在△ABC 中,AB=AC ,D 为AC 的中点,BD=1,则△ABC 面积的最大值为.ABD 中,设AB=AC=b ,由余弦定理得cos A=b 2+b 24-12b ·b 2=54−1b 2,则sin A=√1-(54-1b 2) 2,所以△ABC 的面积为S=12b 2sin A=12b 2·√1-(54-1b2)2=18√-9(b 2-209)2+2569≤23,所以△ABC 的面积的最大值为23.9.在△ABC 中,角A ,B ,C 所对边的边长分别为a ,b ,c ,若|bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ −bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ |=3,bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =6,则△ABC 面积的最大值为.|bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ −bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ |=3,∴|AB|=3.∵bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·bb ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =6,∴ab cos C=6.∴cos C=6bb .由余弦定理得9=a 2+b 2-2ab cos C=a 2+b 2-12≥2ab-12,∴ab ≤212.∴S=12ab sin C=12ab √1-cos 2b=12ab √1-36b 2b 2=12√b 2b 2(1-36b 2b 2 =12√b 2b 2-36≤12√(212) 2-36=3√334.。

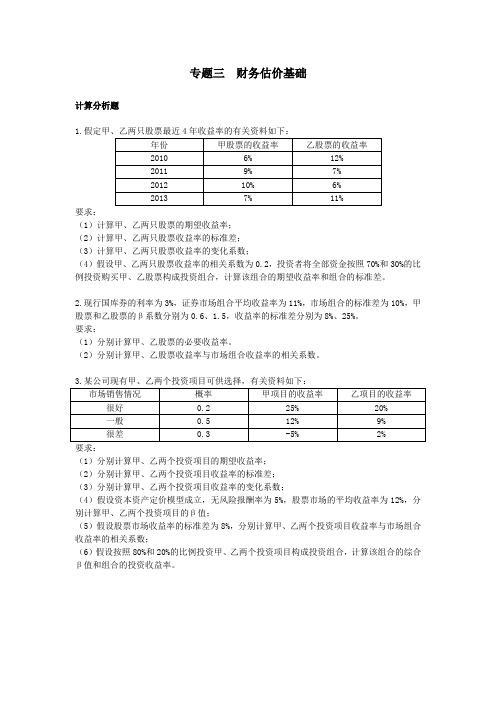
专题三 化学热力学基础学号 姓名 得分1、25℃，KNO 3在水中的溶解度是6mol ·dm -3，若将1 mol 固体KNO 3置于水中，则KNO 3变成盐溶液过程的ΔG 的符号为_____________，ΔS 的符号为_____________。

2、已知下列反映 ：H 2（g ）= 2H （g ） △H = +Q 1 ；1/2O 2（g ）= O （g ） △H = +Q 22H （g ）+ O （g ）= H 2O （g ） △H = －Q 3 ；H 2O （g ）= H 2O （l ） △H = －Q 4 H 2（g ）+ 1/2O 2（g ）= H 2O （l ） △H = －Q 5试指出Q 1、Q 2、Q 3、Q 4、Q 5的关系 。

3、假设反映H 2 (g)−→− 2 H (g) 的内能变化ΔU 与键能ΔH H-H 相等，已知ΔH H-H 为433.2 kJ ·mol -1 ，则键焓ΔH 是 kJ ·mol -1 。

4、298 K 时，生成气态水的Δf G 0m = -228.6 kJ ·mol -1，Δr S 0m = -44.4 J ·mol -1·K -1， 则其Δf H 0m 为_________________________。

5、27℃时，将100g Zn 溶于过量稀硫酸中，反映若分别在开口烧杯和密封容器中进行，哪种情况放热较多？多余多少？6、已知下列反映的焓变为： H 2 (g) +21I 2(s) = HI (g) Δr H 0m = 25.9 kJ ·mol -1 21H 2 (g) = H (g)Δr H 0m = 218 kJ ·mol -1 21I 2(g) = I (g) Δr H 0m = 75.7 kJ ·mol -1 I 2 (s) = I 2 (g)Δr H 0m = 62.3 kJ ·mol -1计算反映 H (g) + I (g) = HI (g) 的焓变Δr H 0m 。