2021复习有方法板块1命题区间教学课件11球与几何体的切接问题
- 格式:ppt
- 大小:5.29 MB
- 文档页数:37



球与几何体的切接问题命题点1外接球求解外接球问题的方法解决多面体外接球问题的关键是确定球心的位置,方法是先选择多面体中的一面,确定此面多边形外接圆的圆心,再过此圆心作垂直此面的垂线,则球心一定在此垂线上,最后根据其他顶点的情况确定球心的准确位置.对于特殊的多面体还可通过补成正方体或长方体的方法找到球心位置.[高考题型全通关]1.直三棱柱ABC-A′B′C′的所有棱长均为23,则此三棱柱的外接球的表面积为()A.12πB.16πC.28πD.36πC[由直三棱柱的底面是边长为23的正三角形,得底面所在平面截外接球所成的圆O的半径r=2,又由直三棱柱的侧棱长为23,得外接球球心到圆O的距离d=3,则外接球半径R满足R2=r2+d2=7,∴外接球的表面积S=4πR2=28π.故选C.]2.(2020·石家庄模拟)已知正三棱锥S-ABC的所有顶点都在球O的球面上,棱锥的底面是边长为23的正三角形,侧棱长为25,则球O的表面积为() A.25πB.20π C.16πD.30πA[如图,延长SO交球O于点D,设△ABC的外心为E,连接AE,AD,由正弦定理得2AE=23=4,∴AE=2,sin 60°易知SE⊥平面ABC,由勾股定理可知,三棱锥S-ABC的高SE=SA2-AE2=(25)2-22=4,由于点A是以SD为直径的球O上一点,∴∠SAD=90°,由射影定理可知,球O 的直径2R =SD =SA 2SE =5, 因此,球O 的表面积为4πR 2=π×(2R )2=25π.] 3.(2020·武汉部分学校质量检测)已知三棱锥P -ABC 的四个顶点均在球O 的球面上,P A =PB =PC =2,且P A ,PB ,PC 两两互相垂直,则球O 的体积为 ( )A .163πB .83πC .43πD .23πC [因为P A ,PB ,PC 两两互相垂直,且P A =PB =PC =2,所以以P A ,PB ,PC 为交于一点的三条棱构造正方体,则球O 即此正方体的外接球,该正方体的体对角线长为球的直径,即球的直径为P A 2+PB 2+PC 2=22+22+22=23,所以球的半径R =3,所以球O 的体积V =43πR 3=43π(3)3=43π,选C .] 4.如图,半径为R 的球的两个内接圆锥有公共的底面.若两个圆锥的体积之和为球的体积的38,则这两个圆锥的高之差的绝对值为( )A .R 2B .2R 3C .4R 3D .RD [设球的球心为O ,半径为R ,体积为V ,上面圆锥的高为h (h <R ),体积为V 1,下面圆锥的高为H (H >R ),体积为V 2,两个圆锥共用的底面的圆心为O 1,半径为r .由球和圆锥的对称性可知h +H =2R ,|OO 1|=H -R .∵V 1+V 2=38V ,∴13πr 2h+13πr 2H =38×43πR 3,∴r 2(h +H )=32R 3.∵h +H =2R ,∴r =32R .∵OO 1垂直于圆锥的底面,∴OO 1垂直于底面的半径,由勾股定理可知R 2=r 2+|OO 1|2,∴R 2=r 2+(H -R )2,∴H =32R ,∴h =12R ,则这两个圆锥的高之差的绝对值为R ,故选D .]命题点2 内切球求解内切球问题的关键点求解多面体的内切球问题的关键是求内切球的半径.求内切球半径的一般方1.已知一圆锥的底面直径与母线长相等,一球体与该圆锥的所有母线和底面都相切,则球的表面积与圆锥的表面积的比值为 ( )A .23B .49C .269D .827B [设圆锥的底面半径为R ,球的半径为r ,由题意知,圆锥的轴截面是边长为2R 的等边三角形,球的大圆是该等边三角形的内切圆,所以r =33R ,S 球=4πr 2=4π·⎝ ⎛⎭⎪⎫33R 2=4π3R 2,S 圆锥=πR ·2R +πR 2=3πR 2,所以球的表面积与圆锥的表面积的比值为4π3R 23πR 2=49,故选B .]2.在封闭的正三棱柱ABC -A 1B 1C 1内有一个体积为V 的球.若AB =6,AA 1=4,则V 的最大值是 ( )A .16πB .32π3C .12πD .43πD [由正三角形ABC 的边长为6,得其内切圆的半径为r =3<2,所以在封闭的正三棱柱ABC -A 1B 1C 1内的球的半径的最大值为3,所以V max =43πr 3=43π,故选D .]3.如图,在三棱锥P -ABC 中,P A =4,AC =27,PB =BC =23,P A ⊥平面PBC ,则三棱锥P -ABC 的内切球的表面积为( )A .32πB .94πC .43πD .163πB [由P A ⊥平面PBC ,且P A =4,PB =23,AC =27,得AB =27,PC =23,所以△PBC 为等边三角形,△ABC 为等腰三角形,V 三棱锥P -ABC =V 三棱锥A -PBC=13S △PBC ×P A =13×34×(23)2×4=43,三棱锥P -ABC 的表面积为S =12×23×4×2+34×(23)2+12×23×5=16 3.设内切球半径为r ,则V 三棱锥P -ABC =13×S ×r ,即43=13×163×r ,所以r =34,所以三棱锥P -ABC 的内切球的表面积为4π×⎝ ⎛⎭⎪⎫342=9π4.] 4.如图,圆柱O 1O 2的底面直径与高都等于球O 的直径,记圆柱O 1O 2的表面积为S 1,球O 的表面积为S 2,则S 1S 2=________. 32 [设球的半径为R ,则圆柱的底面半径为R ,高为2R .所以球的表面积S 2=4πR 2,圆柱的表面积S 1=2πR ×2R +πR 2+πR 2=6πR 2,则S 1S 2=6πR 24πR 2=32.] 命题点3 与球有关的最值问题多面体与球有关的最值问题,主要有三种:一是多面体确定的情况下球的最值问题;二是球的半径确定的情况下与多面体有关的最值问题;三是多面体与球均确定的情况下,截面的最值问题.[高考题型全通关]1.(2020·成都模拟)若矩形ABCD 的对角线交点为O ′,周长为410,四个顶点都在球O 的表面上,且OO ′=3,则球O 的表面积的最小值为( )A .322π3B .642π3C .32πD .48πC [由题意,知矩形ABCD 所在的圆面为球O 的一个截面.因为O ′为矩形ABCD 的对角线的交点,所以OO ′所在直线垂直于矩形ABCD 所在的圆面.因为矩形ABCD 的周长为410,所以BC +CD =210.设BC =x ,则CD =210-x ,所以BD 2=BC 2+CD 2=x 2+(210-x )2,即BD 2=2(x -10)2+20.设球O 的半径为R ,则R 2=⎝ ⎛⎭⎪⎫BD 22+O ′O 2=12(x -10)2+8,所以当x =10时,R 2取得最小值8,所以球O 的表面积的最小值S min =4π(R 2)min =32π,故选C .]2.(2020·洛阳尖子生第一次联考)已知三棱锥P -ABC 的四个顶点均在同一个球面上,底面△ABC 满足BA =BC =6,∠ABC =π2,若该三棱锥体积的最大值为3,则其外接球的体积为( )A .8πB .16πC .163πD .323πD [如图,∵△ABC 是等腰直角三角形,∴AC 为截面圆的直径,外接球的球心O 在截面ABC 上的射影为AC 的中点D ,∴当P ,O ,D 共线且P ,O 位于截面ABC 同一侧时三棱锥的体积最大,高最大,此时三棱锥的高为PD ,由13×12×6×6×PD =3,解得PD =3,设外接球的半径为R ,则OD =3-R ,OC =R ,在△ODC中,CD =12AC =3,由勾股定理得(3-R )2+(3)2=R 2,解得R =2.∴三棱锥P -ABC的外接球的体积V =43π×23=323π.故选D .]3.(2020·惠州第一次调研)在三棱锥A -BCD 中,底面BCD 是直角三角形且BC ⊥CD ,斜边BD 上的高为1,三棱锥A -BCD 的外接球的直径是AB ,若该外接球的表面积为16π,则三棱锥A -BCD 体积的最大值为________.43 [如图,过点C 作CH ⊥BD 于H .由外接球的表面积为16π,可得外接球的半径为2,则AB =4.因为AB 为外接球的直径,所以∠BDA =90°,∠BCA =90°,即BD ⊥AD ,BC ⊥CA ,又BC ⊥CD ,CA ∩CD =C ,所以BC ⊥平面ACD ,所以BC ⊥AD ,又BC ∩BD =B ,所以AD ⊥平面BCD ,所以平面ABD ⊥平面BCD ,又平面ABD ∩平面BCD =BD ,所以CH ⊥平面AB D .设AD =x (0<x <4),则BD =16-x 2.在△BCD 中,BD 边上的高CH =1,所以V 三棱锥A -BCD =V 三棱锥C -ABD =13×12×x ×16-x 2×1=16-x 4+16x 2,当x 2=8时,V 三棱锥-BCD 有最大值,故三棱锥A-BCD体积的最大值为4 3.]4.已知某个机械零件是由两个有公共底面的圆锥组成的,且这两个圆锥有公共点的母线互相垂直,把这个机械零件打磨成球形,该球的半径最大为1,设这两个圆锥的高分别为h1,h2,则h1+h2的最小值为________.22[由题意可知,打磨后所得半径最大的球是由这两个圆锥构成的组合体的内切球,内切球的半径R=1,如图为这个组合体的轴截面示意图,圆O为内切球的轴截面,E,F,G,H分别为切点,连接OA,OB,OC,OD,OE,OF,OG,OH,由题意可知AB⊥BC,AD⊥DC,AC=h1+h2,R=OE=OF=OG=OH=1,则S四边形ABCD=S△AOB+S△BOC+S△COD+S△AOD,即AB×BC=12R×AB+12R×BC+12R×CD+12R×AD=12R(2AB+2BC)=R(AB+BC),所以AB×BC=AB+B C.由基本不等式可得AB×BC=AB+BC≥2AB×BC,则AB×BC≥4,当且仅当AB=BC时等号成立.所以(h1+h2)2=AC2=AB2+BC2≥2AB×BC≥8,当且仅当AB=BC时等号成立,故h1+h2的最小值为2 2.]。





球与各种几何体切、接问题近几年全国高考命题来看,这部分内容以选择题、填空题为主,大题很少见。
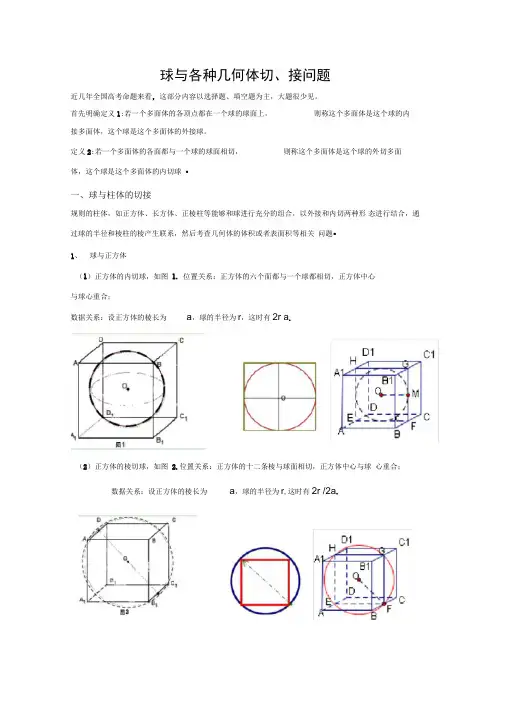
首先明确定义1:若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
定义2:若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球•一、球与柱体的切接规则的柱体,如正方体、长方体、正棱柱等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱柱的棱产生联系,然后考查几何体的体积或者表面积等相关问题•1、球与正方体(1)正方体的内切球,如图1. 位置关系:正方体的六个面都与一个球都相切,正方体中心与球心重合;数据关系:设正方体的棱长为a,球的半径为r,这时有2r a.(2)正方体的棱切球,如图2.位置关系:正方体的十二条棱与球面相切,正方体中心与球心重合;数据关系:设正方体的棱长为a,球的半径为r,这时有2r /2a.(3)正方体的外接球,如图与球心重合;棱长为1的正方体ABCD数据关系:设正方体的棱长为a,球的半径为r,这时有2r 3a.A|B1C1D1的8个顶点都在球0的表面上, E, F分别是棱3. 位置关系:正方体的八个顶点在同一个球面上;正方体中心AA,DD1的中点,则直线EF被球0截得的线段长为( )思路分析:由题意推出,球为正方体的外接球.平面AADD1截面所得圆面的半径R 一- ——,得知直线EF被球0截得的线段就是球的截面圆的直径.2 2【解析】由题意可知]球为正方体的外接琲尸面曲载面所得圆面的半径卫二警二f. •••ETu面九如D巩-直线廿杆止得的线段黄]球的截面厨的直径2—上点评*本题着査球与正方体唏”的间题「闻球的截面性囱转化虛为求球的截面13直径. _____________ 2、球与长方体例2自半径为R的球面上一点M,引球的三条两两垂直的弦MA,MB,MC,求MA2MB2MC2的值.4,体积为16,A. 16B.20 C.24 D.32思路分析:正四棱柱也是长方体 可得长方体的长、宽、高分别为【解析】以谢A/B . MC 为从一个顶点出发的三衆協 将三棱锥3/ -曲C 补应一个长方也 则另外四个 顶点逊在疎面上,故长方体是球的内接民右郎,围按方陳的对星线農是璘的貢径...3A? -M3'十」/C Z = (2A): =点评=此题突出构造法的使用,以反淆觀炜令割补形的方法解诀立体几何中体积计算…结论:长方体的外接球直径是长方体的对角线.例3 (全国卷I 高考题)已知各顶点都在一个球面上的正四棱柱高为球的表面积为()..由长方体的体积16及高4可以求出长方体的底面边长为 2,2, 2,4,长方体内接于球,它的体对角线正好为球的直径【解析】正四粧柱也是长再体.由廉方体的休积応斥高4可刃「出长為悴的底面边扶为2,因此,长肓体的长、宽、鬲分别为囚2, 4,因为长方体內捋于險 所以立药陳对角线正好为瑾能直径.松方体你对角钱故球的表面积沏24 故选G点评*年题考查球与扶帛体^接”的问题,巧勺伕市体■的性质,转化咸対求具体对角餵3、球与正棱柱(1)结论1 :正棱柱的外接球的球心是上下底面中心的连线的中点. (2)结论2 :直三棱柱的外接球的球心是上下底面三角形外心的连线的中点.例1、个兀棱柱的底而足止木边形,面,已知该;;检柱的顶点都&间•个昧而上._!!浚7<检牡的体积为一 •底血周长为3,则这个球的体枳为3已知各厦点都在同一个球面上的正四棱柱的高为4. 休积沟1筋 则这牛嫌的k\ft!袒屋 _______ . 24用例3、 在M 三检柱」EU -蚣EC «P, AB 二 4.AC = 6,ri= !60?rU!H 也-;蛙柱ABC -舛坊G 的外接蟀的表血切二、球与锥体的切接规则的锥体,如正四面体、正棱锥、特殊的一些棱锥等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱锥的棱和高产生联系,然后考查几何体的体积或 者表面积等相关问题. 1、正四面体与球的切接问题(1) 正四面体的内切球,如图 4.位置关系:正四面体的四个面都与一个球相切,正四面体 的中心与球心重合;数据关系:设正四面体的棱长为 a ,高为h ;球的半径为 R ,这时有4R h —6 a ;3【解析】 如图正四面体 A — BCD 的中心为0,即内切球球心,内切球半径 R 即为0到1正四面体各面的距离AB = a,—正四面体的咼h= 丁a,又V A-BCD = 4V o-BCD, ()「. R=[h=12a.(2)正四面体的外接球,位置关系:正四面体的四个顶点都在一个球面上,正四面体的中心与球心重合;数据关系:设正四面体的棱长为a,高为h ;球的半径为R,这时有4R 3h .6a ;(可用正四面体高h 减去内切球的半径得到) 例5求棱长为1的正四面体外接球的半径。