几何体的外接球与内切球讲解学习

如何求解立体几何形的内切球和外接球立体几何形的内切球和外接球是数学和几何学中常见的概念。

内切球是指一个球体正好与该立体几何形相切于内部的球，而外接球则是指一个球体正好与该几何形相切于外部的球。

解决这个问题需要一些几何知识和计算技巧。

一、立方体首先，让我们以立方体为例，来讨论如何求解其内切球和外接球。

立方体是一个六个面都是正方形的立体，所有的边长相等。

立方体的内切球和外接球的半径可以通过简单的计算得到。

1. 内切球内切球的半径等于立方体的半边长。

设立方体的边长为a，则内切球的半径r等于a/2。

这是因为内切球的半径与立方体的棱长之比为1:2。

2. 外接球外接球是一个球体，它与立方体的八个顶点相切。

设立方体的边长为a，则外接球的半径R等于立方体对角线的一半。

根据勾股定理，立方体的对角线的长度d等于a√3。

因此，外接球的半径R等于d/2，即R等于a√3/2。

二、圆柱体对于圆柱体来说，内切球和外接球的求解稍微复杂一些。

1. 内切球内切球的半径等于圆柱体的半径。

设圆柱的半径为r，高度为h，则内切球的半径r'等于r。

2. 外接球外接球是一个球体，它与圆柱体的底面相切。

设圆柱的半径为r，高度为h，则外接球的半径R等于圆柱体的斜高。

根据勾股定理，圆柱体的斜高等于√(h^2 + r^2)。

因此，外接球的半径R等于√(h^2 + r^2)。

三、球体球体的内切球和外接球的求解相对简单。

1. 内切球球体的内切球的半径等于球体的半径。

设球体的半径为R，内切球的半径r等于R。

2. 外接球外接球是一个球体，它与球体的表面相切。

设球体的半径为R，则外接球的半径R'等于2R。

结论：通过以上讨论，我们可以得出以下结论：1. 对于立方体来说，内切球的半径等于边长的一半，外接球的半径等于对角线长的一半。

2. 对于圆柱体来说，内切球的半径等于半径，外接球的半径等于斜高。

3. 对于球体来说，内切球的半径等于半径，外接球的半径等于半径的两倍。

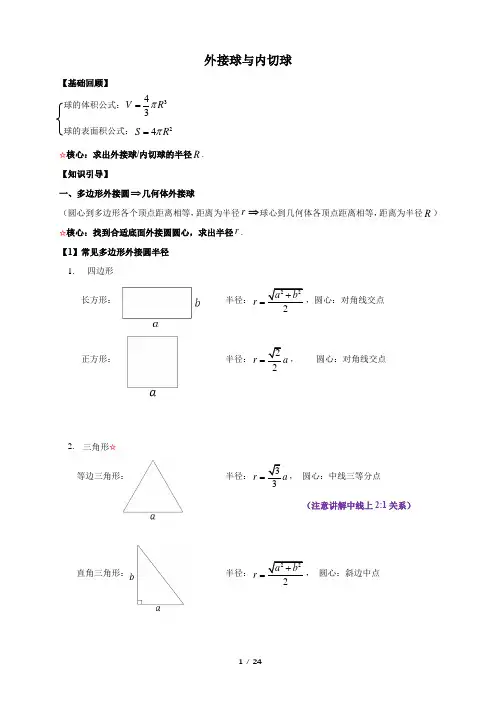
外接球与内切球【基础回顾】 球的体积公式：343V R π=球的表面积公式：24S R π= ☆核心：求出外接球/内切球的半径R . 【知识引导】一、多边形外接圆⇒几何体外接球（圆心到多边形各个顶点距离相等，距离为半径r ⇒球心到几何体各顶点距离相等，距离为半径R ） ☆核心：找到合适底面外接圆圆心，求出半径r . 【1】常见多边形外接圆半径 1. 四边形长方形： 半径：22a br +=，圆心：对角线交点正方形： 半径：22r a =， 圆心：对角线交点2. 三角形☆等边三角形： 半径：3r =， 圆心：中线三等分点 （注意讲解中线上2:1关系）直角三角形： 半径：222a br +=， 圆心：斜边中点120︒等腰三角形： 半径：r a =，圆心：如图，在三角形外部普通三角形： 半径：利用正弦定理2sin ar A= （已知一组对边角） （这里r 即为外接圆半径）【2】常见几何体外接球半径1. 直棱柱：222hR r⎛⎫=+ ⎪⎝⎭，r为底面外接圆半径，h为柱体的高（注：斜棱柱无外接球）长方体：半径：222a b c R++ =正方体：半径：3R=，球心：体对角线交点直三棱柱：半径：222h R r⎛⎫=+ ⎪⎝⎭2. 锥体：正三棱锥：外接球球心在底面的高线上球半径可利用勾股定理列方程求解正四面体：半径：64R=，二、多边形内切圆⇒几何体内切球【解题技巧与步骤】一、求解外接球半径R （☆核心：找到合适底面外接圆圆心，求出半径r ）【1】柱体：R =r 为底面外接圆半径. 【2】锥体步骤：（1）选合适底面，找圆心O '，求出底面外接圆半径r .（底面：长方形，正方形，等边∆，直角∆，120︒等腰∆，已知一组对边角的∆） （2）将圆心向上平移h ，得到球心O☆（3）利用PO AO =（R 相等）列方程求h （OA（4）将h 代入OA =R（三棱锥外接球为重点内容，重点讲解第3步列方程中各长度的求解）二、求解内切球半径R （核心：等体积法）题型一、柱体外接球1. 一个长方体的长、宽、高分别为3,4,5cm cm cm ，则该长方体的外接球的体积是________3cm ．2. 长方体的长宽高分别是 ，，，则其外接球的体积是 ．3.长、宽、高分别为 、 、 的长方体的外接球的表面积为 ．4.一个棱长为2cm 的正方体的外接球的体积是_________3cm ．5.若正方体外接球的体积是 ，则正方体的棱长等于 ．6.已知三棱柱111ABC A B C -的6个顶点都在球O 的球面上，若3AB =，4AC =，AB AC ⊥，112AA =，则球O 的半径为（ ）A . B. C.132D. 7.三棱柱的侧棱垂直于底面，且，，若该三棱柱的所有顶点都在同一球面上，则该球的表面积为A. B. C.D.8.三棱柱 的侧棱垂直于底面，且 ，，若该三棱柱的所有顶点都在同一球面上，则该球的表面积为A.B.C.D.9.已知侧棱与底面垂直的三棱柱满足，，则其外接球的表面积为 ．10.设三棱柱的侧棱垂直于底面，所有棱长都为a ，顶点都在一个球面上，则该球的表面积为（ ） A. 2a π B.273a π C.2113a π D. 25a π11.设正三棱柱中，，，则该正三棱柱外接球的表面积是．12.一个直六棱柱的底面是边长为的正六边形，侧棱长为，则它的外接球的表面积为．题型二：锥体外接球（等边三角形（含正三棱锥））1.在正三棱锥中，，分别是棱，的中点，且，若侧棱，则正三棱锥外接球的表面积是．2.已知三棱锥的所有棱长均为 ，则该三棱锥的外接球的直径为 ．3.一个空心球玩具里面设计一个棱长为4的内接正四面体，过正四面体上某一个顶点所在的三条棱的中点作球的截面，则该截面圆的面积是___________.4.已知球的直径6SC =，,A B 是该球球面上的两点，且3AB SA SB ===，则棱锥S ABC -的体积为A . B.C.D.5.已知三棱锥S ABC -的所有顶点都在球O 的球面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =,则此棱锥的体积为_________________.6.菱形ABCD 边长为6，60BAD ∠=︒，将BCD ∆沿对角线BD 翻折使得二面角C BD A --的大小为120︒，已知,,,A B C D 四点在同一个球面上，则球的表面积等于___________.7.在三棱锥P ABC -中，底面ABC 是等边三角形，侧面PAB 是直角三角形，且2PA PB ==，当三棱锥P ABC -表面积最大时，该三棱锥外接球的表面积为 A. 12π B. 8π C. 43πD.323π8.三棱锥中， 为等边三角形，，，二面角的大小为，则三棱锥 的外接球的表面积为A. B.C.D.9.已知三棱锥A BCD -中，2,2AB AC BD CD BC AD =====，直线AD 与底面BCD 所成角为3π，则此时三棱锥外接球的体积为A. 8πB.C.D.（直角三角形） 1.设，，， 是球面上的四点，，， 两两互相垂直，且 ，，，则球的表面积为A. B. C. D.2.已知 的顶点都在球 的球面上，，，，三棱锥的体积为，则该球的表面积等于 ．3.已知三棱锥 中，，，，，则该三棱锥外接球的体积为 ．4.已知四面体P ABC -的四个顶点都在球O 的球面上，若PB ABC ⊥平面, AB AC ⊥,且AC =2PB AB ==,则球O 的表面积为_______________________.5.某几何体的三视图如图所示，则它的外接球表面积为A. B. C. D.6.一个三棱锥的三视图如图所示，则其外接球的体积是．7.一个几何体的三视图如图所示，则这个几何体的A.外接球的体积为B.外接球的表面积为4πC.体积为D.18.在三棱锥中，，，，，，则三棱锥外接球的表面积是A. B. C. D.9.已知点,,,A B C D 在同一个球的球面上，2AB BC ===,若四面体中球心O 恰好在侧棱DA 上，DC =则这个球的表面积为___________________.10.在体积为43的三棱锥S ABC -中，2,90,AB BC ABC SA SC ==∠=︒=，且平面SAC ⊥平面ABC ，若该三棱锥的四个顶点都在同一球面上，则该球的体积是A.B. 92π C. 272π D. 12π11.如图，三棱锥中S ABC -，,6,12SA ABC AB BC ⊥==平面, AC SB ==则三棱锥S ABC -外接球的表面积为_______________.12.已知三棱锥的外接球的表面积为，该三棱锥的三视图如图所示，三个视图的外轮廓都是直角三角形，则其侧视图面积的最大值为 ．13.在三棱锥 中，， 斜边上的高为 ，三棱锥的外接球的直径是 ，若该外接球的表面积为，则三棱锥体积的最大值为B. C.D.14.如图所示，平面四边形ABCD 中，,,AB AD BD CD BCD ⊥⊥∆BD 折成四面体ABCD ，满足二面角A BD C --为60︒.若四面体ABCD 的顶点在同一个球面上，则该球的表面积的最小值为( )A. 4πB.C. 8πD.（正弦定理）1.如图，三棱锥的所有顶点都在一个球面上，在ABC ∆中，AB =60,90,,ACB BCD AB CD CD ∠=︒∠=︒⊥=则该球的体积为___________.2.三棱锥P ABC -中，PA ⊥底面ABC ，且2,5,6PA AB AC BC ====，则三棱锥P ABC -的外接球表面积为___________.3.三棱锥P ABC -中，6,AB BC AC PC ===⊥平面ABC ，2PC =，则这三棱锥的外接球表面积为A . 253π B.252π C.833π D.832π（120︒等腰∆） 1.已知球的半径为 ，，， 三点在球 的球面上，球心 到平面的距离为，，， 则球的表面积为 A. B.C.D.（四棱锥）1.正四棱锥的顶点都在同一球面上，若该棱锥的高为 ，底面边长为 ，则该球的表面积为 ．2.底面为正方形，顶点投影再底面中心的棱锥P ABCD-的五个顶点在同一球面上，若该棱锥的底面边长为4，侧棱长为，则这个球的表面积为_____________3.如图，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某多面体的三视图，则该多面体外接球的表面积为A. 8πB. 252π C. 12π D.414π4.一个几何体的三视图如图所示，其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则该球体的表面积是A. 12πB. 24πC. 32πD. 48π5.某四棱锥的三视图如图所示，其中网格中的小正方形的边长为1，侧视图是一个边长为2的正三角形，则这个几何体的外接球的表面积是___________.6.已知四棱锥P ABCD -的底面为矩形，PBC ABCD ⊥平面平面，PE BC ⊥于点E ，1EC =，AB =,3,2BC PE ==则四棱锥P ABCD -的外接球半径为________________.7.四棱锥P ABCD -的三视图如下图所示，四棱锥P ABCD -的五个顶点都在一个球面上，,E F 分别是棱,AB CD 的中点，直线EF 被球面所截得的线段长为( )A. 12πB. 24πC. 36πD. 48π8.如图是一个几何体的三视图，则这个几何体的外接球表面积为________________.题型三：内切球1.在正四面体ABCD中，其棱长为a，若正四面体ABCD有一个内切球，则这个球的表面积为．2.已知正四棱锥的底面边长为a，侧棱长为√2a．求它的内切球的表面积．。

内切球和外接球常见解法内切球和外接球是在几何学中常用的概念，它们分别指的是一个几何体内切或外接于另一个几何体的球。

在实际问题中，内切球和外接球常常用于优化问题和几何问题的求解，其解法也有多种。

以下将介绍一些常见的解法。

1. 解法一：利用勾股定理求解。

内切球和外接球都可以利用勾股定理求解。

以内切球为例，我们可以考虑任意三角形ABC，设其内切球的半径为r，以I为内切圆心，则：AB + AC = 2r；AC + BC = 2r；AB + BC = 2r。

整理可得：r = [ABC] / (s + a + b + c)，其中s为半周长，a、b、c为三角形ABC的三边长，[ABC]为三角形ABC的面积。

而外接球的半径r'则可用公式r'=[ABC] / (4S)，其中S为三角形ABC的外接圆半径。

欧拉定理是内切球和外接球求解的另一个重要工具。

欧拉定理有两种形式，分别为：对于任意四面体，其四个顶点、三条棱的中点和六面体质心共九个点在同一球面上。

对于任意三角形ABC，其外接圆心、垂足交点、垂心、重心四点在同一圆上，且圆心为外接球心。

利用欧拉定理可以求得内切球半径：点O为六面体质心，点I为内切圆心，则IO等于内切球半径r。

点O为三角形外心，点H为垂心，点G为重心，则OG等于外接球半径r'。

对于一些优化问题，内切球和外接球也可以通过线性规划求解。

例如，对于一个凸多面体，求其内切球或外接球的半径最大值，可以将问题转化为线性规划问题，即：max rs.t. A_i * x <= b_i, i=1,2,...,mx_i >= 0, i=1,2,...,n其中，A_i是多面体的几何信息，b_i是多面体中某一点到各个面的距离，x是优化变量，r就是所需要求的内切球或外接球半径。

可以使用线性规划求解器求解其最优解。

内切球与外接球常见解法一、内切球内切球是指一个球体恰好能够被另一个球体包围，且两个球体相切于球面上的一个点。

在数学中，内切球经常与三角形、四面体等几何图形相关联。

1. 三角形的内切圆对于一个任意形状的三角形，都存在唯一一个内切圆，该内切圆的圆心与三角形的三条边相切。

下面介绍一种常见的求解方法：以三角形的三个顶点为A、B、C。

1) 求解三个边长a、b、c。

利用两点之间的距离公式可以得到三条边的长度：a = √[(x2 - x1)^2 + (y2 - y1)^2]b = √[(x3 - x2)^2 + (y3 - y2)^2]c = √[(x1 - x3)^2 + (y1 - y3)^2]2) 求解三角形的半周长s。

s = (a + b + c)/23) 求解内切圆的半径r。

r = √[(s - a)(s - b)(s - c)/s]4) 求解内切圆的圆心坐标。

利用三角形面积公式可以求解内切圆的圆心坐标：x = (a*x1 + b*x2 + c*x3)/(a + b + c)y = (a*y1 + b*y2 + c*y3)/(a + b + c)2. 四面体的内切球对于四面体，即由四个平面三角形组成的几何图形，也存在一个内切球。

下面介绍一种常见的求解方法：以四面体的四个顶点为A、B、C、D。

1) 求解四个面的面积S1、S2、S3、S4。

利用三角形面积公式可以求解四个面的面积。

S1 = 1/2 * |(B - A) × (C - A)|S2 = 1/2 * |(C - B) × (D - B)|S3 = 1/2 * |(D - C) × (A - C)|S4 = 1/2 * |(A - D) × (B - D)|2) 求解四面体的体积V。

四面体的体积可以通过以下公式求解：V = 1/6 * |(B - A) · [(C - A) × (D - A)]|3) 求解四面体内切球的半径r。

内切球与外接球常见解法在立体几何的学习中，内切球与外接球问题常常让同学们感到头疼。

其实，只要掌握了常见的解法，这类问题就能迎刃而解。

下面咱们就来详细探讨一下内切球与外接球的常见解法。

首先，咱们得明白什么是内切球和外接球。

内切球就是一个几何体内部恰好能够容纳一个球，并且这个球与几何体的各个面都相切；外接球则是指一个几何体恰好能够被一个球完全包围，并且几何体的各个顶点都在这个球面上。

对于常见的几何体，比如长方体、正方体、正四面体等，都有比较固定的求解方法。

先来说说长方体的外接球。

假设长方体的长、宽、高分别为 a、b、c，那么其外接球的直径就是长方体的体对角线长度。

体对角线长度可以通过勾股定理求出，即\（＼sqrt{a^2 ＋ b^2 ＋ c^2}＼），所以外接球的半径\（R ＝＼frac{＼sqrt{a^2 ＋ b^2 ＋ c^2}｝｛2}＼）。

正方体就更简单啦。

设正方体的棱长为 a，那么其外接球的直径就是正方体的面对角线长度的\（＼sqrt{3}＼）倍，所以外接球的半径\（R ＝＼frac{＼sqrt{3}a}｛2}＼）。

再看看正四面体的外接球。

正四面体比较特殊，我们可以通过一些几何关系来求解。

设正四面体的棱长为 a，先求出正四面体的高\（h ＝＼frac{＼sqrt{6}｝｛3}a\），然后外接球的半径\（R ＝＼frac{＼sqrt{6}｝｛4}a\）。

接下来，咱们说说一般多面体的外接球求解方法。

其中一种常用的方法是补形法。

比如说，如果一个三棱锥的对棱相等，那么我们可以把它补成一个长方体，然后利用长方体的外接球求解方法来解决。

还有一种方法是找球心。

球心到几何体各个顶点的距离都相等，我们可以通过一些已知条件，比如垂直关系、距离关系等来确定球心的位置。

对于内切球的求解，通常会用到体积分割的方法。

比如说，对于一个三棱锥，如果知道了它的表面积和体积，那么内切球的半径 r 就可以通过体积分割来求。

设三棱锥的体积为 V，表面积为 S，那么\（V ＝＼frac{1}｛3}Sr\），从而可以求出内切球的半径 r 。

外接球和内切球问题总结归纳外接球和内切球问题总结归纳在几何学中，外接球和内切球问题是一个重要的概念。

它们不仅在数学领域有着重要的应用，同时也被广泛运用在物理学、工程学以及计算机科学等领域。

本文将对外接球和内切球问题进行深入探讨，从基础概念到应用实例，帮助读者全面理解这一主题。

一、外接球和内切球的定义1. 外接球外接球是指一个球与给定的多边形的所有顶点相切于球面的情况。

在数学中，外接球常常与三角形、四边形等几何图形相关联，其特点是与多边形的各个顶点相切，并且球心通常位于多边形的某个重要位置。

2. 内切球内切球则是指一个球完全被给定的多边形所包围，且球与多边形的边界相切。

在实际应用中，内切球往往能够最大化地利用多边形所包围的空间，因此在工程设计和优化问题中具有重要意义。

二、外接球和内切球的性质1. 外接球的性质外接球的半径通常与多边形的边或者角有着特定的关系。

以三角形为例，外接圆的半径等于三角形三条边的乘积除以其周长的两倍。

这一性质在计算三角形的外接圆时具有重要意义，同时也为几何问题的解决提供了基础。

2. 内切球的性质内切球的半径与多边形的边界有着紧密的联系。

以正方形为例，内切圆的半径等于正方形的边长的一半。

这一性质在优化问题中有着重要的应用，能够帮助设计者最大化地利用空间，提高效率和节约成本。

三、外接球和内切球的应用1. 工程设计外接球和内切球在工程设计中有着广泛的应用。

例如在建筑设计中，内切球可以帮助设计者合理利用建筑空间，提高使用效率；在机械设计中，外接球则可以帮助设计者确定零部件的匹配度和适用性。

2. 计算机科学外接球和内切球也在计算机科学领域有着重要的应用。

例如在计算机图形学中，外接球和内切球经常被用来描述物体的外形和几何特征，同时也可以用于物体的碰撞检测和三维建模。

个人观点和总结外接球和内切球作为一个基础的数学概念，在几何学、工程学和计算机科学等领域有着重要的应用。

通过对外接球和内切球的定义、性质和应用进行深入探讨，我们可以更好地理解其在实际问题中的作用和意义，进一步拓展其在更多领域的应用。

外接球和内切球的方法总结一、前言在数学中，球是一个非常重要的几何概念。

它的应用非常广泛，例如在物理学、工程学和计算机图形学中都有着重要的应用。

其中，外接球和内切球是两种常见的球，本文将对它们的求法进行总结。

二、外接球1. 定义外接球是指一个几何体（如三角形或四面体）最小的球，能够包含住这个几何体。

例如，在三角形ABC中，外接圆就是能够通过三个点A、B、C的圆。

2. 求法（1）对于三角形ABC：a. 首先求出三角形ABC的垂心H（即三条高线交点），并求出AH、BH、CH的长度。

b. 然后根据勾股定理得到$\cos A=\dfrac{b^2+c^2-a^2}{2bc}$等式。

c. 最后根据公式$R=\dfrac{abc}{4\Delta}$计算出外接圆半径R。

（2）对于四面体ABCD：a. 首先求出四面体ABCD所在平面的法向量N。

b. 然后求出四个顶点A、B、C、D到平面N的距离hA, hB, hC, hD。

c. 最后根据公式$R=\dfrac{hA+hB+hC+hD}{4}$计算出外接球半径R。

三、内切球1. 定义内切球是指一个几何体（如三角形或四面体）最大的球，能够被这个几何体所包含。

例如，在三角形ABC中，内切圆就是与三边相切的圆。

2. 求法（1）对于三角形ABC：a. 首先求出三角形ABC的半周长s=$\dfrac{a+b+c}{2}$。

b. 然后根据海伦公式$\Delta=\sqrt{s(s-a)(s-b)(s-c)}$计算出三角形面积$\Delta$。

c. 最后根据公式$r=\dfrac{\Delta}{s}$计算出内切圆半径r。

（2）对于四面体ABCD：a. 首先求出四面体ABCD所在平面的法向量N。

b. 然后求出四个顶点A、B、C、D到平面N的距离hA, hB, hC, hD。

c. 最后根据公式$r=\dfrac{3V}{4\pi(hA+hB+hC+hD)}$计算出内切球半径r，其中V为四面体体积。

空间几何体的外接球与内切球一、有关定义1.球的定义：空间中到定点的距离等于定长的点的集合（轨迹）叫球面，简称球。

2.外接球的定义：若一个多面体的各个顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球。

3.内切球的定义：若一个多面体的各面都与一个球的球面相切，则称这个多面体是这个球的外切多面体，这个球是这个多面体的内切球。

二'外接球的有关知识与方法1.性质:性质1：过球心的平面截球面所得圆是大圆，大圆的半径与球的半径相等；性质2：经过小圆的直径与小圆面垂直的平面必过球心，该平面截球所得圆是大圆；性质3：过球心与小圆圆心的直线垂直于小圆所在的平面（类比：圆的垂径定理）;性质4：球心在大圆面和小圆面上的射影是相应圆的圆心；性质5：在同一球中，过两相交圆的圆心垂直于相应的圆面的直线相交，交点是球心（类比：在同圆中，两相交弦的中垂线交点是圆心）.2.结论：结论1：长方体的外接球的球心在体对角线的交点处，即长方体的体对角线的中点是球心；结论2：若由长方体切得的多面体的所有顶点是原长方体的顶点，则所得多面体与原长方体的外接球相同；结论3：长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心，换言之，就是：底面的一条对角线与一条高（棱）构成的直角三角形的外接圆是大圆；结论4：圆柱体的外接球球心在上下两底面圆的圆心连一段中点处；结论5：圆柱体轴截面矩形的外接圆是大圆，该矩形的对角线（外接圆直径）是球的直径；结论6：直棱柱的外接球与该棱柱外接圆柱体有相同的外接球；结论7：圆锥体的外接球球心在圆锥的高所在的直线上；结论8：圆锥体轴截面等腰三角形的外接圆是大圆，该三角形的外接圆直径是球的直径；结论9：侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.3.终极利器：勾股定理、正弦定理及余弦定理（解三角形求线段长度）；三、内切球的有关知识与方法1.若球与平面相切，则切点与球心连线与切面垂直。

空间几何体的外接球与内切球问题高考分析： 球与几何体的切接问题是近几年高考的高频考点，常以选择题和填空题的形式出现，以中档题和偏难题为主. 一、几种常见几何体的外接与内切球 1.长方体的外接球 (1)球心：体对角线的交点；(2)半径：R ＝a 2＋b 2＋c 22(a ，b ，c 为长方体的长、宽、高)．2.正方体的外接球、内切球及与各条棱相切的球 (1)外接球：球心是正方体的中心；半径R ＝32a(a 为正方体的棱长)； (2)内切球：球心是正方体的中心；半径r ＝2a(a 为正方体的棱长)；(3)与各条棱都相切的球：球心是正方体的中心；半径=2r a (a 为正方体的棱长)． 3.正四面体的外接球与内切球(1)外接球：球心是正四面体的中心；半径R (a 为正四面体的棱长)；(2)内切球：球心是正四面体的中心；半径r (a 为正四面体的棱长)．求外接球问题常用方法：1.补体法。

将几何体补形成长方体正方体等常见模型去求解2.外接球的球心都在过底面外接圆圆心的垂线上（注意球体可以滚动所以可以选择较为方便计算的那一面作为底面）3.利用外接球球心到几何体各顶点距离都等于半径4.球心与截面圆圆心的连线垂直于截面圆求外接球的关键是确定球心位置，进而计算出外接球半径。

题型一：柱体的外接球1.已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为_________．2.已知三棱柱111ABC A B C －的底面是边长为6的正三角形，侧棱垂直于底面，且该三棱柱的外接球的表面积为12 ，则该三棱柱的体积为_________．3.已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是( )A ．16πB ．20πC ．24πD ．32π4.已知圆柱的底面半径为12，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( )A.πB.3π4 C.π2 D.π4题型二：锥体的外接球5.求棱长为1的正四面体外接球的体积为_________．6.已知正四棱锥P －ABCD 内接于一个半径为R 的球，则正四棱锥P －ABCD 体积的最大值是( )A.16R 381B.32R 381C.64R 381 D ．R 3 7.如图，在四棱锥P －ABCD 中，底面ABCD 为菱形，PB ⊥底面ABCD ，O 为对角线AC 与BD 的交点，若PB ＝1，∠APB ＝∠BAD ＝π3，则三棱锥P －AOB 的外接球的体积是_________．8.已知△ABC 是面积为的等边三角形，且其顶点都在球O 的球面上.若球O 的表面积为16π，则O 到平面ABC 的距离为（ ） A.B.C. 1D.9.已知,,A B C 为球O 的球面上的三个点，⊙1O 为ABC 的外接圆，若⊙1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为（ ）A. 64πB. 48πC. 36πD. 32π10.《九章算术》中对一些特殊的几何体有特定的称谓，例如：将底面为直角三角形的直三棱柱称为堑堵．将一堑堵沿其一顶点与相对的棱切开，得到一个阳马(底面是长方形，且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均是直角三角形的四面体)．在如图所示的堑堵ABC －A 1B 1C 1中，AA 1＝AC ＝5，AB ＝3，BC ＝4，则阳马C 1－ABB 1A 1的外接球的表面积是( )A ．25πB ．50πC ．100πD ．200π11.已知三棱锥P −ABC 的四个顶点在球O 的球面上，PA =PB =PC ，△ABC 是边长为2的正三角形，E ，F 分别是PA ，AB 的中点，∠CEF =90°，则球O 的体积为 A ．68πB ．64πC ．62πD ．6π12.已知正三棱锥的所有顶点都在球O 的球面上，其底面边长为3，E,F ,G 分别为为侧棱AB,AC,AD 的中点.若O 在三棱锥A -BCD 内，且三棱锥A -BCD 的体积是三棱锥O -BCD 体积的3倍，则平面EFG 截球O 所得截面的面积为微专题 球与几何体的切接问题——内切球1.半径为R 的球的外切圆柱(球与圆柱的侧面、两底面都相切)的表面积为_________，体积为_________．2.若正四面体的棱长为a ，则其内切球的半径为_________．3.已知正三棱锥的高为6，内切球(与四个面都相切)的表面积为16π，则其底面边长为( ) A ．18 B ．12 C ．6 3 D ．434.将半径为3，圆心角为2π3的扇形围成一个圆锥(接缝处忽略不计)，则该圆锥的内切球的体积为( )A.2π3 B.3π3 C.4π3D ．2π 5.如图，已知球O 是棱长为1的正方体ABCD －A 1B 1C 1D 1的内切球，则平面ACD 1截球O 的截面面积为( )A.66π B.π3 C.π6 D.33π题型三 最值问题6.已知底面是正六边形的六棱锥P －ABCDEF 的七个顶点均在球O 的表面上，底面正六边形的边长为1，若该六棱锥体积的最大值为3，则球O 的表面积为_________．7.四棱锥S －ABCD 的所有顶点都在同一球面上，底面ABCD 是正方形且和球心O 在同一平面内，当此四棱锥的体积取得最大值时，其表面积等于8＋83，则球O 的体积等于( )A.32π3B.322π3 C ．16π D.162π38.已知SAB 是边上为2的等边三角形，045ACB ∠=，则三棱锥体积最大时，CA = ;其外接球的表面积为。

十种求外接球与内切球模型【必备知识点】模型一:墙角模型墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型,用构造法(构造长方体)解决.外接球的直径等于长方体的体对角线长.使用范围:3组或3条棱两两垂直;或可在长方体中画出该图且各顶点与长方体的顶点重合推导过程:长方体的体对角线就是外接球的直径公式:找三条两两垂直的线段,直接用公式(2R)2=a2+b2+c2,即2R=a2+b2+c2,求出R.例1.四面体ABCD的每个顶点都在球O的球面上，AB,AC,AD两两垂直，且AB=3，AC=2，AD= 3，则球O的表面积为( )A.64πB.16πC.4πD.π【答案】B【详解】四面体ABCD的外接球O即为以AB,AC,AD为长、宽、高的长方体的外接球，∴球O的外接球半径R=12AB2+AC2+AD2=2，∴球O的表面积S=4πR2=16π.故选：B.例2.在边长为2的正方形ABCD中，E，F分别为线段AB，BC的中点，连接DE，DF，EF，将△ADE，△CDF，△BEF分别沿DE，DF，EF折起，使A,B,C三点重合，得到三棱锥O-DEF，则该三棱锥外接球的表面积为( )A.3πB.6πC.6πD.24π【答案】C【详解】解：在正方形ABCD中，AD⊥AE，CD⊥CF，BE⊥BF，折起后OD，OE，OF两两垂直，故该三棱锥外接球即以OD，OE，OF为棱的长方体外接球.因为OD=2，OE=1，OF=1，所以2R=OD2+OE2+OF2=6，所以R=62，所以该三棱锥外接球的表面积为S表=4πR2=6π，故选：C.例3.已知P，A，B，C为球O的球面上的四个点，若PA⊥平面ABC，AC⊥BC，PA=1，AC=BC= 2，则球O的表面积为( )A.2πB.3πC.4πD.5π【答案】D【详解】解：在三棱锥P-ABC中，PA⊥平面ABC，AC⊥BC，故可将三棱锥P-ABC补形成如图所示的长方体.若P，A，B，C为球O的球面上的四个点，则该长方体的各顶点亦在球O的球面上.设球O的半经为R，则该长方体的体对角线长为2R，即2R=PA2+AC2+BC2=5，从而有S球O=4πR2=π(2R)2=5π，故选：D.例4.如图，在矩形ABCD中，AB=2,BC=2，E为BC中点，把△ABE和△CDE分别沿AE,DE折起，使点B与点C重合于点P，若三棱锥P-ADE的四个顶点都在球O的球面上，则球O的表面积为( )A.3πB.4πC.5πD.9π【答案】C【详解】依题意，PE⊥PA,PE⊥PD，PA∩PD=P，PA,PD⊂平面PAD，则PE⊥平面PAD，又PA=PD=2,AD=2，即有PA2+PD2=AD2，则PA⊥PD，因此可将三棱锥P-ADE补形成以PE,PA,PD为相邻三条棱的长方体，若三棱锥P-ADE的四个顶点都在球O的球面上，则该长方体的各顶点亦在球O的球面上，设球O的半径为R，则该长方体的体对角线长为2R，即2R=PE2+PA2+PD2=5，所以球O的表面积为S=4πR2=π(2R)2=5π.故选：C例5.在正三棱锥S -ABC 中, 点M 是SC 的中点,且AM ⊥SB ,底面边长AB =22,则正三棱锥S -ABC 的外接球的表面积为()A.6πB.12πC.32πD.36π【答案】B【详解】因为三棱锥S -ABC 为正三棱锥, 所以SB ⊥AC ,又AM ⊥SB ,AC ∩AM =A ,AC ,AM ⊂平面SAC , 所以SB ⊥平面SAC,所以SB ⊥SA ,SB ⊥SC ,同理SA ⊥SC ,即SA ,SB ,SC 三线两两垂直,且AB =22,所以SA =SB =SC =2,所以(2R )2=3×22=12,所以球的表面积S =4πR 2=12π,故选 B .例6.将一个边长为4的正三角形ABC 沿其中线BD 折成一个直二面角，则所得三棱锥A -BCD 的外接球的体积为_________.【答案】2053π【详解】由题意得：AB =BC =4，AD =CD =2，BD ⊥AD ，CD ⊥BD ，即BD ⊥平面ADC ；∵二面角A -BD -C 为直二面角，∴AD ⊥CD ，则三棱锥A -BCD 的外接球即为以BD ,CD ,AD 为长宽高的长方体的外接球，又BD =16-4=23，∴三棱锥A -BCD 的外接球半径R =12AD 2+CD 2+BD 2=124+4+12=5，∴三棱锥A -BCD 的外接球体积V =43πR 3=2053π.故答案为：2053π.例7.在正三棱锥S -ABC 中,M ,N 分别是棱SC ,BC 的中点,且AM ⊥MN , 若侧棱SA =23,则正三棱锥S -ABC 外接球的表面积是_________.【答案】36π【详解】∵AM ⊥MN ,SB ⎳MN ,∴AM ⊥SB ,∵AC ⊥SB ,∴SB ⊥平面SAC,∴SB ⊥SA ,SB ⊥SC ,∵SB ⊥SA ,BC ⊥SA ,∴SA ⊥平面SBC ,∴SA ⊥SC ,故三棱锥S -ABC 的三棱条侧棱两两互相垂直,∴(2R )2=(23)2+(23)2+(23)2=36,即4R 2=36,∴正三棱锥S -ABC 外接球的表面积是36π.例8.在长方体ABCD -A 1B 1C 1D 1中,底面ABCD 是边长为32的正方形,AA 1=3,E 是线段A 1B 1上一点, 若二面角A -BD -E 的正切值为3,则三棱锥A -A 1D 1E 外接球的表面积为_________.【答案】35π【详解】过点E 作EF ⎳AA 1交AB 于F ,过F 作FG ⊥BD 于G ,连接EG ,则∠EGF 为二面角A -BD -E 的平面角,∵tan ∠EGF =3,∴EF FG=3,∵EF =AA 1=3,∴FG =1,则BF =2=B 1E , ∴A 1E =22,则三棱锥A -A 1D 1E 外接球的直径为8+9+18=35,因此三棱锥A -A 1D 1E 外接球的表面积S =35π.模型二:对棱相等模型使用范围:对棱相等的三棱锥推导过程:通过对棱相等,可以将其补全为长方体,补全的长方体体对角线为外接球直径,设长方体的长宽高为别为a ,b ,cAD =BC AB =CD AC =BD ⇒a 2+b 2=BC 2=λ2b 2+c 2=AC 2=μ2c 2+a 2=AB 2=k 2⇒a 2+b 2+c 2=λ2+μ2+k 22⇒R =λ2+μ2+k 28V A -BCD =abc -16abc ×4=13abc 例1.如图，在△ABC 中，AB =25,BC =210,AC=213，D ，E ，F 分别为三边中点，将△BDE,△ADF ,△CEF 分别沿DE ,EF ,DF 向上折起，使A ，B ，C 重合为点P ，则三棱锥P -DEF 的外接球表面积为( )A.72πB.7143πC.14πD.56π【答案】C【详解】由题意可知，PE =DF =10,PF =DE =13,PD =EF =5，即三棱锥P-DEF 的对棱相等，先将该三棱锥补充成长方体，如图所示：设FH =x ,HD =y ,HP =z ，则x 2+y 2=10,y 2+z 2=5,x 2+z 2=13，所以x 2+y 2+z 2=14，于是三棱锥P -DEF 的外接球直径为14，半径为142，所以该三棱锥外接球的表面积为：4π⋅1422=14π.故选：C .例2.在△ABC 中，AB =AC =2，cos A =34，将△ABC 绕BC 旋转至△BCD 的位置，使得AD =2，如图所示，则三棱锥D -ABC 外接球的体积为_____________．【答案】556π【详解】在△ABC 中，由余弦定理得BC 2=22+22-2×2×2×34=2，所以BC =2．在三棱锥D -ABC 中，AB =AC =DB =DC =2，AD =BC =2．将三棱锥D -ABC 放入长方体，设长方体的长、宽、高分别为a ，b ，c ，棱锥D -ABC 外接球的半径为R ，则a 2+b 2=4,b 2+c 2=4,a 2+c 2=2，所以a 2+b 2+c 2=5，所以R =12a 2+b 2+c 2=52，从而三棱锥D -ABC 外接球的体积V =43πR 3=556π.故答案为：556π例3.已知三棱锥P -ABC 的每条侧棱与它所对的底面边长相等，且PA =32，PB =PC =5，则该三棱锥的外接球的表面积为______．【答案】34π【详解】解：根据题意，三棱锥P -ABC 可以嵌入一个长方体内，且三棱锥的每条棱均是长方体的面对角线，设长方体交于一个顶点的三条棱长为a ，b ，c ，如图所示，则a 2+b 2=PA 2=18，a 2+c 2=PB 2=25，b 2+c 2=PC 2=25，解得a =3，b =3，c =4．所以该三棱锥的外接球的半径为R =a 2+b 2+c 22=32+32+422=342，所以该三棱锥的外接球的表面积为S =4πR 2=4π×342 2=34π．故答案为：34π例4.已知四面体ABCD 的棱长满足AB =AC =BD =CD =2，BC =AD =1，现将四面体ABCD 放入一个轴截面为等边三角形的圆锥中，使得四面体ABCD 可以在圆锥中任意转动，则圆锥侧面积的最小值为________．【答案】274π【详解】根据题意，只需四面体ABCD 在圆锥的内切球内，下面求四面体ABCD 的外接球半径．如图所示，将四面体放入长方体中，设长方体的长宽高分别为a ,b ,c ，则a 2+b 2=4，a 2+c 2=4，b 2+c 2=1，故4R 2=a 2+b 2+c 2=92，可得四面体ABCD 的外接球半径为324．当圆锥的侧面积最小时，该圆锥的内切球即四面体ABCD 的外接球，则此时圆锥的内切球的半径为R =324，底面圆的半径为r =324×3=364，母线长为324×2=322，所以侧面积为S =π×364×362=27π4.故答案为：27π4.例5.在三棱锥P -ABC 中，PA =BC =25，PB =AC =13，AB =PC =5，则三棱锥P -ABC 的外接球的表面积是______．【答案】29π【详解】由题意，PA =BC =25，PB =AC =13，PC =AB =5，将三棱锥P -ABC 放到长方体中，可得长方体的三条面对角线分别为25，13，5，设长方体的长宽高分别为a,b ,c ,即a 2+b 2=25，c 2+b 2=13，a 2+c 2=5，解得：a =4，b =2，c =3．长方体的体对角线即为三棱锥和长方体公共外接球的直径2R ，∴(2R )2=a 2+b 2+c 2⇒4R 2=29⇒S 球=4πR 2=29π﹒故答案为：29π．例6.已知三棱锥A -BCD ,三组对棱两两相等,且AB =CD =1,AD =BC =3,若三棱雉A -BCD的外接球表面积为9π2.则AC =______．【答案】5【详解】将四面体A-BCD放置于长方体中, ∵四面体A-BCD的顶点为长方体八个顶点中的四个,∴长方体的外接球就是四面体A-BCD的外接球,∵AB=CD=1,AD=BC=3,且三组对棱两两相等,∴设AC=BD=x,得长方体的对角线长为1212+(3)2+x2=124+x2,可得外接球的直径2R=124+x2,所以 R=24+x24,∵三棱锥A-BCD的外接球表面积为9π2,∴4πR2=9π2,解得 R=32 4, 即24+x24=324,解之得x=5, 因即AC=BD=5.模型三:汉堡模型适用范围:有一条侧棱垂直于底面的柱体推导过程:如图,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形).第一步:确定球心O的位置,O1是ABC的外心,则OO1⊥平面ABC.第二步:算出小圆O1的半径AO1=r,OO1=12AA1=12h AA1=h也是圆柱的高).第三步:勾股定理:OA2=O1A2+O1O2⇒R2=h22+r2⇒R=r2+h2 2,求出R.公式:R=r2+h 22例1.已知某圆柱的高为42，体积为42π，则该圆柱外接球的表面积为( )A.32πB.36πC.40πD.44π【答案】B【详解】设圆柱底面圆的半径为r，则πr2×42=42π，解得r=1．设该圆柱的两底面中心分别为O1、O2，则该圆柱外接球的球心O为线段O1O2的中点，球O 的半径为R =12+422 2=3，故球O 的表面积S =4πR 2=36π．故选：B .例2.已知三棱柱的各个侧面均垂直于底面，底面为正三角形，侧棱长与底面边长之比为3：2，顶点都在一个球面上，若三棱柱的侧面积为162，则该球的表面积为( )A.120πB.129πC.129πD.180π【答案】C【详解】由题意，设球的半径为r ，底面三角形边长为2x ，因为侧棱长与底面边长之比为3：2，所以侧棱长为3x ，因为三棱柱的侧面积为162，即满足3⋅3x ⋅2x =18x 2=162，解得x =3，可知侧棱长为9，底面边长为6，如图所示，设N ，M 分别是上､下底面的中心，MN 的中点O 是三棱柱ABC -A 1B 1C 1外接球的球心，则AM =33×6=23，OM =12MN =12AA 1=92，r =OA =OM 2+AM 2=92 2+23 2=1292，所以S =4πr 2=4π×12922=129π.故选：C .例3.已知三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的表面上，AB =AC =AA 1=2，∠BAC =120∘，则球O 的表面积是( )A.4πB.163πC.16πD.20π【答案】D【详解】由余弦定理得BC 2=AB 2+AC 2-2AB ⋅AC ⋅cos ∠BAC =22+22-2×2×2×-12 =12,∴BC =23,设△ABC 外接圆的圆心为O 1,半径为CO 1，由正弦定理得BC sin ∠BAC =2CO 1 ，即2332=2CO 1，解得CO 1=2，设外接球的半径为R =CO ,∵O 1O =12AA 1=1,∴R =CO =CO 1 2+OO 1 2=22+12=5,球O 的表面积为S =4πR 2=20π,故选：D .例4.直三棱柱ABC -A 1B 1C 1所有顶点都在球O 的表面上，且∠BAC =π6，AA 1=22，AC =3AB =3，则球O 的表面积为________．【答案】20π【详解】解：直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的表面上，且∠BAC =π6,AA 1=22，，AC =3AB =3，∴BC =AB 2+AC 2-2AB ⋅AC cos π6=3+9-2×3×3×32=3，设ΔABC 为外接圆的圆心为E ，2r =3sin π6=23，所以r =3，设外接球的球心为O ，设球的半径为R ，所以R =r 2+12AA 1 2=5，故S 球=4π⋅(5)2=20π．故答案为：20π．例5.在四面体ABCD 中，AB =CD =1，BC =2，且AB ⊥BC ，CD ⊥BC ，异面直线AB ，CD 所成角为π3，则该四面体外接球的表面积为______.【答案】16π3或8π【详解】由题意可以将四面体ABCD 补成一个如图所示的直三棱柱，因为异面直线AB ，CD 所成角为π3，所以∠ABE =π3或2π3，设△ABE 的外接圆半径为r ，当∠ABE =π3时，1sin60∘=2r ,r =33 ，当∠ABE =2π3时，AE =3 ，则3sin120∘=2r ,r =1，设四面体的外接球半径为R ，则R =r 2+BC 2 2=r 2+1 ，所以该四面体外接球的半径R =233或2，则外接球的表面积为.4πR 2=16π3或8π，故答案为：16π3或8π模型四:垂面模型适用范围:有一条棱垂直于底面的椎体推导过程:第一步:将ABC 画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O .第二步:O 1为ABC 的外心,所以OO 1⊥平面ABC ,算出小圆O 1的半径O 1D =r (三角形的外接圆直径算法:利用正弦定理a sin A =b sin B=c sin C =2r ,OO 1=12PA .第三步:利用勾股定理求三棱锥的外接球半径:(1)(2R )2=PA 2+(2r )2⇔2R =PA 2+(2r )2;(2)R 2=r 2+OO 21⇔R =r 2+OO 21.公式:R 2=r 2+h 24例1.已知三棱锥P -ABC ，其中PA ⊥平面ABC ，∠BAC =120°，PA =AB =AC =2，则该三棱锥外接球的表面积为( )A.12πB.16πC.20πD.24π【答案】C【详解】根据题意设底面△ABC 的外心为G ，O 为球心，所以OG ⊥平面ABC ，因为PA ⊥平面ABC ，所以OG ⎳PA ，设D 是PA 中点，因为OP =OA ，所以DO ⊥PA ，因为PA ⊥平面ABC ，AG ⊂平面ABC ，所以AG ⊥PA ，因此OD ⎳AG ，因此四边形ODAG 是平行四边形，故OG =AD =12PA =1，由余弦定理，得BC =AB 2+AC 2-2AB ⋅AC ⋅cos120°=4+4-2×2×2×-12=23，由正弦定理，得2AG =2332⇒AG =2，所以该外接球的半径R 满足R 2=OG 2+AG 2=5⇒S =4πR 2=20π，故选：C ．例2.已知四面体ABCD 的每个顶点都在球O 的球面上，CD ⊥平面ABC ，AC =23，△ABC 是正三角形，△ACD 是等腰三角形，则球O 的体积为( )A.2053πB.86πC.2873πD.36π【答案】C【详解】∵CD ⊥平面ABC ，AC ⊂平面ABC ，∴CD ⊥AC ，又△ACD 是等腰三角形，∴CD =AC ．∵△ABC 是正三角形，∴AB =BC =AC =CD =23．设E 为△ABC 外接圆的圆心，则CE =23×32×23=2，OE =12CD =3，∴OC =OE 2+CE 2=7，∴球O 的体积V =43π×7 3=2873π.故选：C .例3.在三棱锥S -ABC 中, 侧棱SA ⊥底面ABC ,AB =5,BC =8,∠ABC =60°,SA =25, 则该三棱锥的外接球的表面积为()A.643π B.2563π C.4363π D.2048327π【答案】B【详解】 由题意知,AB =5,BC =8,∠ABC =60°,则在△ABC 中, 由余弦定理得 AC 2=AB 2+BC 2-2×AB ×BC ×cos ∠ABC ,解得AC =7,设△ABC 的外接圆半径为 r ,则△ABC 的外接圆直径2r =AC sin ∠ABC =772,∴r =73, 又∵侧棱SA ⊥底面ABC ,∴三棱锥的外接球的球心到平面ABC 的距离 h =12SA =5,则外接球的半径R =732+(5)2=643,则该三棱锥的外接球的表面积为S =4πR 2=2563π.例4.已知四棱锥P -ABCD 的五个顶点在球O 的球面上，PA ⊥底面ABCD ，PA =4，AB =AD ，BC=CD ，∠BAD =120°，且四边形ABCD 的面积为934，则球O 的表面积为___________.【答案】25π【详解】如图所示，在四边形中ABCD ，连结BD ，AC ，由AB =AD ,BC =CD ，所以△ABC ≌△ADC ，所以∠ABC =∠ADC ,∠BAC =∠DAC ，因为A ,B ,C ,D 在同一圆上，所以∠ABC =∠ADC =90°，又因为∠BAD =120°，所以∠BCD =60°，则∠BAC =∠DAC =60°，在Rt △ABC 中，可得BC =3AB ，因为底面ABCD 的面积为934，所以2×12AB ⋅3AB =934，解得AB =32，则BC =332，AC =3322+322=3，所以Rt △ABC 外接圆的半径r =32，将四棱锥P -ABCD 补成直四棱柱PEFG -ABCD ，该直棱柱的所有顶点都在球O 的球面上，设底面四边形ABCD 所在圆的圆心为O 1，连接OO 1，则OO 1⊥平面ABCD ，过OM ⊥PA ，垂足为M ,由球的对称性可知，球心O 到底面ABCD 的距离为d =OO 1=AM =12PA =2，所以球O 的半径R 满足R 2=d 2+r 2=254，所以球O 的表面积S 球O =4πR 2=25π.故答案为：25π.例5.在三棱锥P -ABC 中,PA ⊥平面ABC ,∠BAC =120°,AC =2,AB =1,设D 为BC 中点, 且直线PD 与平面ABC 所成角的余弦值为55, 则该三棱雉外接球的表面积为___________.【答案】 373π【详解】在△ABC 中,∠BAC =120°,AC =2,AB =1,由余弦定理得:BC 2=AC 2+AB 2-2AC ⋅BC ⋅cos ∠BAC ,即BC 2=22+12-2×2×1×cos120°=7,解得:BC =7. 设△ABC 的外接圆半径为r ,由正弦定理得2r =BC sin ∠BAC =7sin120°=273解得:r =73=213;且cos ∠ABC =AB 2+BC 2-AC 22AB ⋅BC =12+(7)2-222×1×7=277,又D 为BC 中点, 在△ABD 中,BD =12BC =72,AB =1,cos ∠ABD =277. 由余弦定理得:AD 2=AB 2+BD 2-2AB ⋅BD cos ∠ABD ,即:AD 2=12+722-2×1×72×277=34,解得AD =32.又因为PA ⊥平面ABC , 所以 ∠PDA 为直线PD 与平面ABC 所成角, 由cos ∠PDA =55,得 sin ∠PDA =255,tan ∠PDA =2所以在Rt △PAD 中, PA =AD ⋅tan ∠PDA =32⋅2=3. 设三棱锥P -ABC 的外接球半径为R , 所以R =PA 22+r 2=322+2132=3712,三棱锥P -ABC 外接球表面积为S =4πR 2=373π.模型五:斗笠模型使用范围:正棱雉或顶点的投影在底面的外心上推导过程:取底面的外心01, 连接顶点与外心,该线为空间几何体的高h ,在h 上取一点作为球心0,根据勾股定理R 2=(h -R )2+r 2⇔R =r 2+h 22h公式:R =r 2+h 22h例1.已知A ,B ,C 为球O 的球面上的三个点,⊙O 1为△ABC 的外接圆.若⊙O 1的面积为4π,AB =BC =AC =OO 1, 则球O 的表面积为()A.64πB.48πC.36πD.32π【答案】A 【详解】设⊙O 1的半径为r ,球的半径为R ,依题意,得πr 2=4π,∴r =2.由正弦定理可得ABsin60°=2r ,∴AB =2r sin60°=2 3.∴OO 1=AB =2 3.根据球的截面性质,得OO 1⊥平面ABC ,∴OO 1⊥O 1A ,R =OA =OO 21+O 1A 2=OO 21+r 2=4,∴球O 的表面积S =4πR 2=64π.故选A .例2.正四棱锥的顶点都在同一球面上, 若该棱锥的高为4 , 底面边长为2 , 则该球的表面积为()A.81π4B.16πC.9πD.27π4【答案】A 【详解】如图所示,设球半径为R ,底面中心为O 且球心为O ,∵正四棱锥P -ABCD 中 AB =2,∴AO =2,∵PO =4,∴在Rt △AOO 中, AO 2=AO ′2+OO ′2,∴R 2=(2)2+(4-R )2,解得R =94,∴该球的表面积为4πR 2=4π×942=81π4.例3.已知一个圆锥的母线长为26，侧面展开图是圆心角为23π3的扇形，则该圆锥的外接球的体积为( )A.36πB.48πC.36D.242【答案】A 【详解】设圆锥的底面半径为r ，由侧面展开图是圆心角为23π3的扇形得：2πr =23π3×26，解得：r =22.作出圆锥的轴截面如图所示：设圆锥的高为h ，则h =26 2-22 2=4.设该圆锥的外接球的球心为O ，半径为R ,则有R =h -R2+r 2，即R =4-R2+22 2，解得：R =3，所以该圆锥的外接球的体积为4πR 33=4π333=36π.故选：A .例4.在三棱锥P -ABC 中，侧棱PA =PB =PC =10，∠BAC =π4，BC =22，则此三棱锥外接球的表面积为_______．【答案】50π3【详解】因为PA =PB =PC =10，所以点P 在底面ABC 的射影为△ABC 的外心O 1，所以球心O 在直线PO 1上，设三棱锥外接球的半径为R ，因为2AO 1=22sin π4，所以AO 1=2，PO 1=6，由AO 2=OO 21+AO 21可得，R 2=6-R 2+4，解得R =56，故此三棱锥外接球的表面积为4πR 2=4π×256=503π．故答案为：50π3．例5.已知正四面体的棱长为4，则此四面体的外接球的表面积是为________.【答案】24π【详解】如图正四面体ABCD 棱长为4，AH ⊥平面BCD 于H ，则H 是△BCD 中心，BH =33×4=433，AH ⊥平面BCD ，BH ⊂平面BCD ，则AH ⊥BH ，AH =42-4332=463，设外接球球心为O ，则O 在AH ，则OA =OB =R 为外接半径，由BH 2+OH 2=BO 2得4332+463-R2=R 2，解得R =6，∴S =4πR 2=24π．故答案为：24π.例6.在三棱雉P -ABC 中,PA =PB =PC =26,AC =AB =4,且AC ⊥AB ,则该三棱锥外接球的表面积为________.【答案】36π【详解】设顶点P 在底面中的射影为O 1,由于PA =PB =PC ,所以O 1A =O 1B =O 1C ,即点O 1 是底面△ABC 的外心,又AC ⊥AB ,所以O 1为BC 的中点,因为PA =PB =PC =26,AC =AB =4,所以BC =42,AO 1=22,PO 1=4,设外接球的球心为O ,半径为R ,则O 必在PO 1上, O 1O =4-R ,在Rt △O 1OA 中, (4-R )2+(22)2=R 2, 解得R =3,所以S 2=4πR 2=36π.例7..一个圆锥恰有三条母线两两夹角为60°, 若该圆雉的侧面积为33π,则该圆雉外接球的表面积为________.【答案】27π2【详解】设∠ASB =∠BSC =∠CSA =60°,则SA =SB =SC =AB =AC =BC .设AB =x ,则底面圆的直径为2r =x sin60°=2x 3,该圆锥的侧面积为12π⋅2x3⋅x =33π,解得x =3,高OS =32-(3)2= 6.∴r =33= 3.设圆锥外接球的半径为R ,所以(6-R )2+r 2=R 2,解得R =364, 则外接球的表面积为4πR 2=27π2.类型六:切瓜模型使用范围:有两个平面互相垂直的棱雉推导过程:分别在两个互相垂直的平面上取外心O 1、O 2过两个外心做两个垂面的垂线, 两条垂线的交点即为球心0,取B C 的中点为E , 连接OO 1、OO 2、O 2E 、O 1E 为矩形由勾股可得|OC |2=|O 2C |2+|OO 2|2=|O 2C |2+|O 1C |2-|CE |2∴R 2=r 21+r 22-l 24公式:R 2=r 21+r 22-l 24例1.已知四棱锥P -ABCD 中，底面ABCD 为边长为4的正方形，侧面PAB ⊥底面ABCD ，且△PAB为等边三角形，则该四棱锥P -ABCD 外接球的表面积为( )A.112π3B.64π3C.64πD.16π【答案】A【详解】如图所示，在四棱锥P -ABCD 中，取侧面△PAB 和底面正方形ABCD 的外接圆的圆心分别为O 1,O 2，分别过O 1，O 2作两个平面的垂线交于点O ，则由外接球的性质知，点O 即为该球的球心，取线段AB 的中点E ，连O 1E ，O 2E ，O 2D ，OD ，则四边形O 1EO 2O 为矩形，在等边△PAB 中，可得PE =23，则O 1E =233，即OO 2=233，在正方形ABCD 中，因为AB =4，可得O 2D =22，在直角△OO 2D 中，可得OD 2=OO 22+O 2D 2，即R 2=OO 22+O 2D 2=283，所以四棱锥P -ABCD 外接球的表面积为S =4πR 2=112π3.故选：A .例2.已知三棱锥A -BCD 中, △ABD 与△BCD 是边长为2的等边三角形且二面角A -BD -C 为直二面角, 则三棱雉A -BCD 的外接球的表面积为()A.10π3B.5πC.6πD.20π3【答案】D 【详解】取BD 的中点M ，连接AM ,CM ,∠AMC =90°,AF :FM =2:1,CE :EM =2:1，OF ⊥AM ，OE ⊥MC ,OE ∩OF =O 连接OC ，点 O 是三棱锥A -BCD 的外接球的球心，因为棱长都是2 ，所以OE =FM =33,EC =233，所以在△OEC 中，R =OC =OE 2+EC 2=153，那么外接球的表面积是S =4πR 2=203π ，故选D .例3.已知四棱锥P -ABCD 的体积是363，底面ABCD 是正方形，△PAB 是等边三角形，平面PAB ⊥平面ABCD ，则四棱锥P -ABCD 的外接球的体积为________.【答案】2821π【详解】设正方形ABCD 的边长为2x ，在等边三角形PAB 中，过P 点作PE ⊥AB 于E ，由于平面PAB ⊥平面ABCD ，∴PE ⊥平面ABCD ．由于△PAB 是等边三角形，则PE =3x ，∴V P -ABCD =13⋅S ABCD ⋅PE =13×2x 2×3x =363，解得x =3．设四棱锥外接球的半径为R ，O 1为正方形ABCD 中心，O 2为等边三角形PAB 中心，O 为四棱锥P -ABCD 外接球球心，则易知OO 2EO 1为矩形，则OO 2=EO 1=12AD =x =3，PO 2=23PE =23⋅33=23，R =OP =OO 22+PO 22=9+12=21，∴外接球体积V =43π×(21)3=2821π．故答案为：2821π．例4.已知四面体ABCD 中，△ABD 和△BDC 是等边三角形，二面角A -BD -C 为直二面角.若AB =43，则四面体ABCD 外接球的表面积为__________________.【答案】80π【详解】如图所示：设O 1为△BCD 的中心，O 为四面体ABCD 的外接球的球心，则OO 1⊥平面BDC ．设M 为线段BD 的中点，外接球的半径为R ，连接AM ,CM ,OA ，过O 作OG ⊥AM 于点G ，易知G 为△ABD 的中心，则OO 1=OG =MO 1=MG ，因为MA =32×43=6，故MG =OG =13×6=2,GA =4，在Rt △AGO 中，GA 2+GO 2=OA 2，故22+42=R 2，则R =25．所以外接球的表面积为S =4πR 2=80π，故答案为：80π.例5.已知在三棱锥A -BCD 中，平面ABD ⊥平面BCD ,△BCD 和△ABD 均是边长为23的正三角形，则该三棱锥的外接球体积为___________.【答案】2053π【详解】依题意，平面ABD ⊥平面BCD ,△BCD 和△ABD 均是边长为23的正三角形，设G 是BD 的中点，则AG ⊥BD ,CG ⊥BD ，由于平面ABD ⊥平面BCD 且交线为BD ，所以AG ⊥平面BCD ，CG ⊥平面ABD .设E ,F 分别是等边三角形ABD 和等边三角形BCD 的中心，则AE =CF =2GE =2GF =23CG =23×3=2,设O 是三棱锥A -BCD 外接球的球心，则OE ⊥平面ABD ，OF ⊥平面BCD .所以外接球的半径R =OF 2+CF 2=12+22=5，所以外接球的体积为4π3×5 3=2053π.故选：2053π模型七:折叠模型使用范围:两个全等三角形或等腰三角形拼在一起,或菱形折叠.推导过程:两个全等的三角形或者等腰拼在一起,或者菱形折叠,设折叠的二面角∠A EC =α,CE =A E =h .如图,作左图的二面角剖面图如右图:H 1和H 2分别为△BCD ,△A BD 外心,CH 1=r =BD2sin∠BCD,EH1=h-r,OH1=(h-r)tan α2故R2=OC2=OH21+CH21=r2+(h-r)2tan2α2.公式:R2=r2+(h-r)2tan2α2例1.已知菱形ABCD中,∠DAB=60°,AB=3,对角线AC与BD的交点为O,把菱形ABCD沿对角线BD折起, 使得∠AOC=90°,则折得的几何体的外接球的表面积为()A.15πB.15π2C.7π2D.7π【答案】A【解析】菱形ABCD中,∠DAB=60°,AB=3,三角形ABD的外接圆的半径为r=32sin60°=3,高h=332,对角线AC与BD的交点为O,使得α=∠AOC=90°,则折得的几何体的外接球的半径为:R=(3)2+332-32tan245°=152,外接球的表面积为S=4π152 2=15π, 故选 A.例2.在三棱雉P-ABC中,PA=PB=AC=BC=2,AB=23,PC=1,则三棱雉P-ABC的外接球的表面积为()A.4π3B.4πC.12πD.52π3【答案】D【解析】取AB中点D,因为PA=PB=AC=BC=2,所以PD=CD=1,又 PD⊥AB,CD⊥AB,则面PDC⊥面ABC,设△ABC的外心为O1,外接圆半径为r,三棱锥P-ABC的外接球的球心为O,则OO1⊥面ABC,∠ACB=120°,由r=AB2sin120°=2,h=1,设∠PDC=α=60°(二面角平面角),外接球的半径为 R,R=r2+(h-r)2tan2α2=(2)2+(1-2)2tan230°=133,所以三棱雉P-ABC的外接球的表面积为4πR2=52π3,故选 D.例3.在边长为23的菱形ABCD中,∠BAD=60°,沿对角线AC折成二面角B-AC-D为120°的四面体ABCD,则此四面体的外接球表面积为________.【答案】84π【解析】如图所示, 典型的全等等腰三角形共底边:ED=h=3,O2D=r=23,∠BED=α=120°,可根据几何性质知道 ∠O 2EO =60°,OO 2=EO 2tan60°=3,R =OO 22+DO 22=(3)2+(23)2=21,或者可以通过公式R =r 2+(h -r )2tan 2α2=(23)2+(3-23)2tan 260°=21,S =4πR 2=84π.模型八:已知球心或球半径模型例1.已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB,SA =AC ,SB =BC ,三棱锥S -ABC 的体积为9,则球O 的表面积为________.【答案】36π【解析】如图, 连接AO ,OB ,∵SC 为球O 的直径,∴点O 为SC 的中点, ∵SA =AC ,SB =BC ,∴AO ⊥SC ,BO ⊥SC ,∵平面SCA ⊥平面SCB , 平面SCA ∩平面SCB =SC ,∴AO ⊥平面SCB , 设球O 的半径为R ,则OA =OB =R ,SC =2R .∴V S ⋅ABC =V A -SBC =13×S △SBC ×AO =13×12×SC ×OB ×AO , 即9=13×12×2R ×R ×R , 解得R =3,∴球O 的表面积为S =4πR 2=4π×32=36π.例2.已知三棱锥A -BCD 的所有顶点都在球O 的球面上,AB 为球O 的直径,若该三棱雉的体积为3,BC =3,BD =3,∠CBD =90°, 则球O 的体积为________.【答案】32π3【解析】设A 到平面BCD 的距离为h∵三棱锥的体积为3,BC =3,BD =3,∠CBD =90°∴13×12×3×3×h =3,∴h =2,∴球心O 到平面BCD 的距离为1.设CD 的中点为E ,连接OE ,则由球的截面性质可得OE ⊥平面CBD ,∵△BCD 外接圆的直径CD =23,∴球O 的半径OD =2,∴球O 的体积为32π3.例3.已知三棱锥S -ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形, SC 为球O的直径, 且SC =2,则此棱锥的体积为()A.26B.36C.23D.22【答案】A【解析】由于三棱锥S -ABC 与三棱锥O -ABC 底面都是△ABC ,O 是SC 的中点, 因此三棱锥S -ABC 的高是三棱锥O -ABC 高的2倍,所以三棱锥S -ABC 的体积也是三棱锥O -ABC 体积的2倍.在三棱锥O -ABC 中,其棱长都是1,S △ABC =34×AB 2=34, 高OD =12-332=63,∴V S -ABC =2V O -ABC =2×13×34×63=26. 故选 A .例4.三棱锥S -ABC 的底面各棱长均为3 , 其外接球半径为2 , 则三棱锥S -ABC 的体积最大时,点S 到平面ABC 的距离为()A.2+3B.2-3C.3D.2【答案】C【解析】如图, 设三棱锥S -ABC 底面三角形ABC 的外心为G , 三棱锥外接球的球心为O , 要使三棱锥 S -ABC 的体积最大, 则O 在SG 上,由底面三角形的边长为3,可得AG =32sin60°=3.连接OA ,在 Rt △OGA 中,由勾股定理求得OG =OA 2-GA 2=22-(3)2=1.∴点S 到平面ABC 的距离为 OS +OG =2+1=3. 故选 C .模型九:最值模型最值问题的解法有两种方法:一种是几何法,即在运动变化过䅣中得到最值,从而转化为定值问题求解.另一种是代数方法,即建立目标函数,从而求目标函数的最值.例1.在边长为6的菱形ABCD 中，∠A =π3，现将△ABD 沿BD 折起，当三棱锥A -BCD 的体积最大时，三棱锥A -BCD 的外接球的表面积为( )A.60πB.30πC.70πD.50π【答案】A 【分析】当三棱锥A -BCD 的体积最大值时，平面ABD ⊥平面BCD ，即可求出外接圆的半径，从而求出面积.【详解】当三棱锥A -BCD 的体积最大值时，平面ABD ⊥平面BCD ，如图，取BD 的中点为H ，连接AH ,CH ，则AH ⊥BD .设O 1,O 2分别为△ABD ，△BCD 外接圆的圆心，O 为三棱锥A -BCD 的外接球的球心，则O 1在AH 上，O 2在CH 上，且AO 1=2O 1H =23AH =23,且O 2H ⊥BD ,OO 1⊥平面ABD ，OO 2⊥平面BCD .∵平面ABD ⊥平面BCD ，平面ABD ∩平面BCD =BD ，AH ⊂平面ABDAH ⊥平面ABD ，AH ⎳O 2O ，同理CH ⎳O 1O ∴四边形O 1OO 2H 为平行四边形∵AH ⊥平面BCD ，O 2H ⊂平面BCD ∴AH ⊥O 2H ，即四边形O 1OO 2H 为矩形.∴OO 2=O 1H =3CO 2=23×32×6=23∴外接球半径R =OO 22+CO 22=3+12=15∴外接球的表面积为4πR 2=60π故选：A .例2.在四棱锥S -ABCD 中，侧面SAD ⊥底面ABCD ，且SA =SD ，∠ASD =90°，底面ABCD 是边长为2的正方形，设P 为该四棱锥外接球表面上的动点，则三棱锥P -SAD 的最大体积为( )A.1+2B.2+223C.2+23D.1+23【答案】D 【详解】连接AC ,BD 交于点O ，取AD 中点为M ，连接SM ,OS ，作图如下：因为AS =DS ,∠ASD =90°，又M 为AD 的中点，故M 为Rt △SAD 的外心，又平面SAD ⊥平面ABCD ，且面SAD ∩面ABCD =AD ，又OM ⊥AD ,OM ⊂面ABCD ，故可得OM ⊥面SAD ，故OA =OS =OD ；又四边形ABCD 为正方形，且O 为对角线交点，故可得OA =OB =OC =OD ，综上所述，OA =OB =OC =OD =OS ，故O 为四棱锥S -ABCD 的外接球的球心.则其外接球半径R =OD =12BD =2.又P 为该四棱锥外接球表面上的动点，若使得三棱锥P -SAD 的体积最大，则此时点P 到平面SAD 的距离h =OM +R =1+2，故其体积的最大值V =13S △SAD ×h =13×12×AD ×SM ×1+2 =13×12×2×1×1+2 =1+23.故选：D .例3.已知P ，A ，B ，C ，D 都在同一个球面上，平面PAB ⊥平面ABCD ，ABCD 是边长为2的正方形，∠APB =60°，当四棱锥P -ABCD 的体积最大时，该球的半径为______．【答案】213【分析】先求出四棱锥P -ABCD 的体积最大时，△PAB 为等边三角形，再找出外接球的球心，通过勾股定理即可求得半径.【详解】如图，过点P 作PQ ⊥AB 于Q ，平面PAB ⊥平面ABCD ，平面PAB ∩平面ABCD =AB ，∴PQ ⊥平面ABCD ，V P -ABCD =13⋅PQ ⋅S ABCD ，故四棱锥P -ABCD 的体积最大，即PQ 最大，∵AB =2，PQ 最大，即△PAB 面积最大，由∠APB =60°,S △PAB =12⋅PA ⋅PB ⋅sin ∠APB =34⋅PA ⋅PB ，得cos ∠APB =AP 2+BP 2-42AP ⋅BP=12，AP 2+BP 2=AP ⋅BP +4≥2AP ⋅BP ，得AP ⋅BP ≤4，当且仅当AP =BP =2时取等号，此时△PAB 面积最大，△PAB 为等边三角形.取△PAB 的外心为O 1，正方形ABCD 的外心为O 2，过O 1,O 2分别作所在平面的垂线，交点为O ，O 即为四棱锥P -ABCD 外接球的球心，四边形OO 2QO 1为矩形，OO 1=O 2Q =1 ，PO 1=23PQ =233，设外接球半径为R ，则R =12+2332=213.故答案为：213.例4.A ，B ，C ，D 四点均在同一球面上，∠BAC =120∘，△BCD 是边长为2的等边三角形，则△ABC 面积的最大值为__________，四面体ABCD 体积最大时球的表面积为___________．【答案】 33 20π3【分析】①由于S △ABC =12AB ⋅AC sin ∠BAC =34AB ⋅AC ，求△ABC 面积的最大值即是求AB ⋅AC 的最大值，利用余弦定理结合重要不等式即可求解②当面ABC⊥面BCD时四面体的体积最大，确定出球心后计算出球的半径即可求解【详解】①因为∠BAC=120∘所以S△ABC=12AB⋅AC sin∠BAC=34AB⋅AC又BC2=AB2+AC2-2AB⋅AC⋅cos120∘即4=AB2+AC2+AB⋅AC≥2AB⋅AC+AB⋅AC=3AB⋅AC所以AB⋅AC≤4 3所以S△ABC=34AB⋅AC≤34×43=33即△ABC面积的最大值为3 3②过A作AH⊥BC，垂足为H, S△ABC=12AH⋅BC=AH则△ABC面积的最大时，AH最大，AH的最大值为3 3，此时△ABC为等腰三角形，H为BC中点S△BCD=12×2×2×32=3，V A-BCD=13S△BCD⋅h=33h则当AH⊥平面BCD时, h最大，此时面ABC⊥面BCD如图,设O为四面体ABCD 外接球的球心, O1，O2分别为△ABC，△BCD的外接圆的圆心. OO1⊥平面ABC，OO2⊥平面BCD,在△ABC中BCsin∠BAC=433=2O2A⇒O2A=33DO1=23DH=23×32×2=233OO1=O2H=O2A-AH=33∴四面体ABCD外接球的半径R=OO21+O1D2=53外接球的表面积为4πR2=20π3模型十:内切球模型以三棱雉P-ABC为例, 求其内切球OE的半径推导过程:等体积法,三棱雉P-ABC体积等于内切球球心与四个面构成的四个三棱雉的体积之和.第一步:先求出四个表面的面积和整个雉体体积;第二步:设内切球的半径为r ,球心为O ,建立等式:V P -ABC =V O -ABC +V O -PAB +V O -PAC +V O -PBC ⇒V P -ABC =13S △ABC ⋅r +13S △PAB ⋅r +13S △PAC ⋅r +13S △PBC ⋅r =13S△ABC+S △PAB +S △PAC +S △PBC ⋅r 第三步:解出r =3V P -ABC S O -ABC +S O -PAB +S O -PAC +S O -PBC =3VS 表.公式:r =3VS 表例1.已知点O 到直三棱柱ABC -A 1B 1C 1各面的距离都相等，球O 是直三棱柱ABC -A 1B 1C 1的内切球，若球O 的表面积为16π，ABC 的周长为4，则三棱锥A 1-ABC 的体积为( )A.43B.163C.833D.1633【答案】B 【详解】解：设直三棱柱ABC -A 1B 1C 1的高为h ，AB =c ，BC =a ，AC =b ，内切球O 的半径为r ，则h =2r ，由题意可知球O 的表面积为16π=4πr 2，解得r =2，∴h =4，又△ABC 的周长为4，即a +b +c =4，∴连接OA ，OB ，OC ，OA 1,OB 1,OC 1可将直三棱柱ABC -A 1B 1C 1分成5个棱锥，即三个以原来三棱柱侧面为底面，内切球球心为顶点的四棱锥，两个以原来三棱柱底面为底面，内切球球心为顶点的的三棱锥，∴由体积相等可得直三棱柱ABC -A 1B 1C 1的体积为S △ABC h =13ahr +13bhr +13chr +2×13S △ABC r ，即4S △ABC =13(a +b +c )hr +43S △ABC ，∴S △ABC =4，∴三棱锥A 1-ABC 的体积为13S △ABC h =13×4×4=163．故选：B ．例2.在《九章算术·商功》中，将四个面都为直角三角形的四面体称为鳖臑，如图在鳖臑ABCD 中，AB ⊥平面BCD ，AB =BC =CD =1，BC ⊥CD ，则鳖臑ABCD 内切球的表面积为( )。

经典三类球：外接球、内切球、棱切球1【考点预测】考点一：正方体、长方体外接球1.正方体的外接球的球心为其体对角线的中点，半径为体对角线长的一半．2.长方体的外接球的球心为其体对角线的中点，半径为体对角线长的一半．3.补成长方体(1)若三棱锥的三条侧棱两两互相垂直，则可将其放入某个长方体内，如图1所示．(2)若三棱锥的四个面均是直角三角形，则此时可构造长方体，如图2所示．(3)正四面体P -ABC 可以补形为正方体且正方体的棱长a =PA2，如图3所示．(4)若三棱锥的对棱两两相等，则可将其放入某个长方体内，如图4所示图1图2图3图4考点二：正四面体外接球如图，设正四面体ABCD 的的棱长为a ，将其放入正方体中，则正方体的棱长为22a ，显然正四面体和正方体有相同的外接球．正方体外接球半径为R =22a ⋅32=64a ，即正四面体外接球半径为R =64a ．考点三：对棱相等的三棱锥外接球四面体ABCD 中，AB =CD =m ，AC =BD =n ，AD =BC =t ，这种四面体叫做对棱相等四面体，可以通过构造长方体来解决这类问题．如图，设长方体的长、宽、高分别为a ,b ,c ，则b 2+c 2=m 2a 2+c 2=n 2a 2+b 2=t2，三式相加可得a 2+b 2+c 2=m 2+n 2+t 22,而显然四面体和长方体有相同的外接球，设外接球半径为R ，则a 2+b 2+c 2=4R 2，所以R =m 2+n 2+t 28．直棱柱外接球如图1，图2，图3，直三棱柱内接于球(同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角形)图1图2图3第一步：确定球心O 的位置，O 1是ΔABC 的外心，则OO 1⊥平面ABC ；第二步：算出小圆O 1的半径AO 1=r ，OO 1=12AA 1=12h (AA 1=h 也是圆柱的高)；第三步：勾股定理：OA 2=O 1A 2+O 1O 2⇒R 2=h 22+r 2⇒R =r 2+h 2 2，解出R考点五：直棱锥外接球如图，PA ⊥平面ABC ，求外接球半径．解题步骤：第一步：将ΔABC 画在小圆面上，A 为小圆直径的一个端点，作小圆的直径AD ，连接PD ，则PD 必过球心O ；第二步：O 1为ΔABC 的外心，所以OO 1⊥平面ABC ，算出小圆O 1的半径O 1D =r (三角形的外接圆直径算法：利用正弦定理，得a sin A=b sin B =c sin C =2r )，OO 1=12PA ；第三步：利用勾股定理求三棱锥的外接球半径：①(2R )2=PA 2+(2r )2⇔2R =PA 2+(2r )2；②R 2=r 2+OO 12⇔R =r 2+OO 12．考点六：正棱锥外接球正棱锥外接球半径：R=r2+h22h．垂面模型如图1所示为四面体P-ABC，已知平面PAB⊥平面ABC，其外接球问题的步骤如下：(1)找出△PAB和△ABC的外接圆圆心，分别记为O1和O2．(2)分别过O1和O2作平面PAB和平面ABC的垂线，其交点为球心，记为O．(3)过O1作AB的垂线，垂足记为D，连接O2D，则O2D⊥AB．(4)在四棱锥A-DO1OO2中，AD垂直于平面DO1OO2，如图2所示，底面四边形DO1OO2的四个顶点共圆且OD为该圆的直径．图1图2考点八：锥体内切球方法：等体积法，即R=3V体积S表面积考点九：棱切球方法：找切点，找球心，构造直角三角形1【典型例题】1(2023春·天津宁河·高一校考期末)在三棱锥P-ABC中，AP=2,AB=3,PA⊥面ABC，且在△ABC中，C=60°，则该三棱锥外接球的表面积为()B.8πC.10πD.12πA.20π3【答案】B【解析】根据题意得出图形如右图：O为球心，N为底面△ABC截面圆的圆心，ON⊥面ABC，∵在三棱锥P-ABC中，AP=2，AB=3，PA⊥面ABC，且在△ABC中，C=60°=2r，解得r=1，∴根据正弦定理得出：3sin60°∵PA⊥面ABC，∴PA⎳ON，∵PA=2，AN=1，ON=d，∴OA=OP=R，∴根据等腰三角形得出：12+d2=(2-d)2+12，解得d=1,∴R=1+1=2∴三棱锥的外接球的表面积为4πR2=8π.故选：B.2(2023·辽宁沈阳·高一东北育才学校校考阶段练习)在正三棱锥S-ABC中，外接球的表面积为36π，M，N分别是SC，BC的中点，且MN⊥AM，则此三棱锥侧棱SA=()A.1B.2C.3D.23【答案】D【解析】取AC的中点E，连结BE、SE，∵三棱锥S-ABC正棱锥，∴SA=SC，BA=BC．又∵E为AC的中点，∴SE⊥AC且BE⊥AC∵SE、BE是平面SBE内的相交直线，∴AC⊥平面SBE，又SB在平面SBE内可得SB⊥AC又∵MN是△SBC的中位线，∴MN∥SB，可得MN⊥AC又∵MN ⊥AM ，又AM ，AC 是平面SAC 内的相交直线，∴MN ⊥平面SAC ，结合MN ∥SB ，可得SB ⊥平面SAC 又∵三棱锥S -ABC 是正三棱锥，∴∠ASB =∠BSC =∠ASC =90°，因此将此三棱锥补成正方体，则它们有相同的外接球，设球的半径为R ，可得4πR 2=36π，解得R =3，∴SA 2+SA 2+SA 2=2R =6，解之得SA =23故选：D3(2023春·河南南阳·高一校联考期末)《九章算术》是我国古代著名的数学著作，书中记载有几何体“刍甍”.现有一个刍甍如图所示，底面ABCD 为正方形，EF ∥平面ABCD ，四边形ABFE ,CDEF为两个全等的等腰梯形，EF =12AB =2,AE =23则该刍甍的外接球的体积为()A.642π3B.3πC.643π3D.642π【答案】A【解析】取AD ，BC 中点N ，M ，正方形ABCD 中心O ，EF 中点O 2，连接EN ，MN ，FM ，OO 2，如图，依题意，OO2⊥平面ABCD，EF⎳AB⎳MN，点O是MN的中点，MN=AB=4，等腰△AED中，AD⊥EN，EN=AE2-AN2=22，同理FM=22，因此，等腰梯形EFMN的高OO2=EN2-MN-EF22=7，由几何体的结构特征知，刍甍的外接球球心O1在直线OO2上，连O1E，O1A，OA，正方形ABCD外接圆半径OA= 22，则有O1A2=OA2+OO21O1E2=O2E2+O2O21，而O1A=O1E,O2E=12EF=1，当点O1在线段O2O的延长线(含点O)时，视OO1为非负数，若点O1在线段O2O(不含点O)上，视OO1为负数，即有O2O1=O2O+OO1=7+OO1，即(22)2+OO21=1+(7+OO1)2，解得OO1=0，因此刍甍的外接球球心为O，半径为OA=22，所以刍甍的外接球的体积为4π3×223=642π3．故选：A．4(2023·高一课时练习)已知圆台的上下底面半径分别为1和2，侧面积为35π，则该圆台的外接球半径为()A.1055B.654C.1854D.1054【答案】B【解析】设圆台的高和母线分别为h,l，球心到圆台上底面的距离为x，根据圆台的侧面积公式可得π1+2l=35π⇒l=5，因此圆台的高h=l2-2-12=2，当球心在圆台内部时，则12+x2=22+h-x2，解得x=74，故此时外接球半径为1+x2=65 16=65 4，当球心在圆台外部时，则12+x2=22+x-h2，x>h，解得x=74不符合要求，舍去，故球半径为65 4故选：B5(2023·高一课时练习)已知圆锥的底面半径为2，高为42，则该圆锥的内切球表面积为()A.4πB.42πC.82πD.8π【答案】D【解析】如图，圆锥与内切球的轴截面图，点O为球心，内切球的半径为r，D,E为切点，设OD=OE=r，即BE=BD=2由条件可知，AB=422+22=6，△ADO中，AO2=AD2+DO2，即42-r2=6-22+r2，解得：r=2，所以圆锥内切球的表面积S=4πr2=8π.故选：D6(2023·高一课时练习)一个正四棱柱的每个顶点都在球O的球面上，且该四棱柱的底面面积为3，高为10，则球O的体积为()A.16πB.32π3C.10π D.28π3【答案】B【解析】设该正四棱柱的底面边长为a，高为h，则a2=3,h=10，解得a=3，所以该正四棱柱的体对角线为球O的直径，设球O的半径为R，所以，2R=a2+a2+h2=3+3+10=4，即R=2，所以，球O的体积为4π3×23=32π3．故选：B7(2023·高一课时练习)正八面体是每个面都是正三角形的八面体．如图所示，若此正八面体的棱长为2，则它的内切球的表面积为()A.423π B.8327π C.83π D.163π【答案】C【解析】以内切球的球心为顶点、正八面体的八个面为底面，可将正八面体分为8个全等的正三棱锥，设内切球的半径为r ，则8V 三棱锥=V 正八面体=2V 正四棱锥，且正四棱锥的高为图中CO ，易得CO =2，即：8×13×12×2×2×32 ⋅r =2×13×2×2 ×2解得：r =63，所以，内切球的表面积为8π3.故选：C ．8(2023·高一课时练习)已知A ，B ，C 三点均在球O 的表面上，AB =BC =CA =2，且球心O 到平面ABC 的距离等于球半径的13，则下列结论正确的为()A.球O 的外切正方体的棱长为6B.球O 的表面积为8πC.球O 的内接正方体的棱长为3D.球O 的半径为32【答案】A【解析】设球O 的半径为R ，△ABC 的外接圆半径为r ，则r =233，因为球心O 到平面ABC 的距离等于球O 半径的13，所以R 2-19R 2=43，得R 2=32，即R =62，故D 错误；球O 的外切正方体的棱长b 满足b =2R =6，故A 正确；所以球O 的表面积S =4πR 2=4π×32=6π，故B 错误；球O 的内接正方体的棱长a 满足3a =2R =6，即a =2，故C 错误.故选：A .9(2023·河南开封·开封高中校考模拟预测)已知某棱长为22的正四面体的各条棱都与同一球面相切，则该球与此正四面体的体积之比为()A.π2B.π3C.3π3D.2π2【答案】A【解析】如图，正方体ABCD -A 1B 1C 1D 1中，棱长为2，所以，四面体A 1BDC 1是棱长为22的正四面体，当正四面体的各条棱都与同一球面相切时，该球为正方体的内切球，半径为1，所以，该球的体积为4π3，因为正四面体的体积为8-4×13×12×2×2×2=8-163=83，所以，该球与此正四面体的体积之比为4π383=π2.故选：A10(2023·高一课时练习)正四面体ABCD 的棱长为a ，O 是棱AB 的中点，以O 为球心的球面与平面BCD 的交线和CD 相切，则球O 的体积是()A.16πa 3B.26πa 3 C.36πa 3 D.23πa 3【答案】D【解析】设点A 在平面BCD 内的射影为点E ，则E 为△BCD 的中心，取CD 的中点M ，连接BM ，则E ∈BM ，取线段BE 的中点F ，连接OF ，因为O 、F 分别为AB 、BE 的中点，则OF ⎳AE 且OF =12AE ，因为AE ⊥平面BCD ，则OF ⊥平面BCD ，因为BE ⊂平面BCD ，则AE ⊥BE ，正△BCD的外接圆半径为BE=a2sinπ3=33a，∴AE=AB2-BE2=63a，所以，OF=12AE=66a，易知球O被平面BCD所截的截面圆圆心为点F，且BF=EF=EM，故FM=BE=33a，因为△BCD为等边三角形，M为CD的中点，则BM⊥CD，因为以O为球心的球面与平面BCD的交线和CD相切，则切点为点M，则球O的半径为OM=OF2+FM2=22a，因此，球O的体积是V=43π×22a3=23πa3.故选：D.11(2023·高一课时练习)已知直三棱柱ABC-A1B1C1的底面为直角三角形，如图所示，∠BAC= 90°，AB=1，AC=2，AA1=3，则四面体A-A1BC的体积为，四棱锥A1-BCC1B1的外接球的表面积为．【答案】 1 14π【解析】由题意可得S△ABC=12×AB⋅AC=12×2×1=1，且h=AA1，则V A-A1BC=13S△ABC⋅h=13×1×3=1因为△ABC 外接圆的圆心即为BC 中点，设为O ，△A 1B 1C 1外接圆的圆心即为B 1C 1中点，设为O 1，则OO 1的中点到六个顶点的距离相等，则OO 1的中点M 为外接球的球心，即CM 为半径，OC =12BC =12AC 2+AB 2=52，OM =12AA 1 =32所以CM =OC 2+OM 2=54+94=142，即外接球的表面积为4πR 2=4π×144=14π故答案为:1，14π2【过关测试】一、单选题1(2023·高一课时练习)若正四面体的表面积为83，则其外接球的体积为()A.43πB.12πC.86πD.323π【答案】A【解析】设正四面体的棱长为a ，由题意可知：4×34a 2=83，解得：a =22，所以正四面体的棱长为22，将正四面体补成一个正方体，则正方体的棱长为2，正方体的体对角线长为23，因为正四面体的外接球的直径为正方体的体对角线长，所以外接球半径R =3，则外接球的体积为V =43πR 3=43π，故选：A .2(2023·陕西渭南·高一统考期末)在直三棱柱ABC -A 1B 1C 1中，AB =BC =2，AA 1=22，∠ABC =π2，则此三棱柱外接球的表面积为()A.4πB.8πC.16πD.24π【答案】C 【解析】因为AB=BC=2，∠ABC=π2，所以△ABC为等腰直角三角形，将直三棱柱ABC-A1B1C1补全为如图长方体ABCD-A1B1C1D1，则长方体的外接球即直三棱柱的外接球，因为AB=BC=2，AA1=22，所以外接球直径2R=AC1=22+22+222=4，所以外接球半径R=2，表面积S=4πR2=16π.故选：C.3(2023春·河北衡水·高一校考阶段练习)在正四棱锥P-ABCD中，AB=4，PA=26，则平面PAB截四棱锥P-ABCD外接球的截面面积是()A.65π5B.36π5C.12πD.36π【答案】B【解析】如图，作PO ⊥平面ABCD，垂足为O ，则O 是正方形ABCD外接圆的圆心，从而正四棱锥P-ABCD外接球的球心O在PO 上，取棱AB的中点E，连接O D,O E,OD,PE，作OH⊥PE，垂足为H.由题中数据可得O D=22,O E=2,PE=25,O P=4，设四棱锥P-ABCD外接球的半径为R，则R2=O D2+O O2=OP2=O P-O O2，即R2=8+O O2=4-O O2，解得R=3.由题意易证△OPH∽△EPO ，则PHO P=OPPE，故PH=65 5.故所求截面圆的面积是π⋅PH2=36π5.故选：B4(2023春·山西太原·高一校考阶段练习)在三棱锥P -ABC 中，PA =PB =PC =3，侧棱PA与底面ABC 所成的角为60°，则该三棱锥外接球的体积为()A.πB.π3C.4πD.4π3【答案】D【解析】设点P 在平面ABC 内的射影点为E ，如下图所示：由线面角的定义可知，直线PA 与底面ABC 所成的角为∠PAE =60°，所以，PE =3sin60°=32，AE =3cos60°=32，因为PE ⊥平面ABC ，BE 、CE ⊂平面ABC ，∴PE ⊥BE ，PE ⊥CE ，∴BE =PB 2-PE 2=32=PC 2-PE 2=CE ，所以，△ABC 的外接圆圆心为点E ，且其外接圆半径为32，所以，三棱锥P -ABC 的外接球球心O 在直线PE 上，设球O 的半径为r ，由几何关系可得OE 2+AE 2=OA 2，即32-r 2+322=r 2，解得r =1，因此，三棱锥P -ABC 外接球的体积为V =43πr 3=43π.故选：D .5(2023春·河南鹤壁·高一河南省浚县第一中学校考阶段练习)已知三棱锥P -ABC 的四个顶点均在同一个球面上，底面ABC 满足BA =BC =6，∠ABC =π2，若该三棱锥体积的最大值为3，则其外接球的体积为()A.323π B.32π C.16π D.823π【答案】A【解析】在△ABC中，BA=BC=6，∠ABC=π2，因此三棱锥P-ABC的外接球被平面ABC截得的截面小圆圆心是AC的中点O1，令三棱锥P-ABC的外接球球心为O，则OO1⊥平面ABC，而S△ABC=12AB⋅BC=3，O1A=3，因三棱锥P-ABC体积的最大值为3，则三棱锥P-ABC底面ABC上的高最大，设此最大高为h，由13×3h=3得h=3，要三棱锥P-ABC的体积最大，当且仅当球O上的点P到平面ABC的距离最大，则点P在线段O1O的延长线上，设球O半径为R，则有(h-R)2+O1A2=R2，即(3-R)2+(3)2=R2，解得R=2，所以三棱锥P-ABC的外接球体积为V=43πR3=323π.故选：A6(2023·高一课时练习)《九章算术》是我国古代数学名著，它在几何学中的研究比西方早1000多年．在《九章算术》中，将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马．如图P-ABCD 是阳马，PA⊥平面ABCD，PA=5，AB=3，BC=4．则该阳马的外接球的表面积为()A.1252π3B.50π C.100π D.500π3【答案】B【解析】因PA⊥平面ABCD，AB⊂平面ABCD，AD⊂平面ABCD，则PA⊥AB，PA⊥AD，又因四边形ABCD为矩形，则AB⊥AD.则阳马的外接球与以PA，AB，AD为长宽高的长方体的外接球相同.又PA=5，AB=3，AD=BC=4．则外接球的直径为长方体体对角线，故外接球半径为：R=PA2+AB2+AD22=32+42+522=522，则外接球的表面积为：S=4πR2=4π⋅504=50π.故选：B7(2023·吉林·高一吉林一中校考阶段练习)如图，在△ABC中，AB=25,BC=210,AC=213，D ，E ，F 分别为三边中点，将△BDE ,△ADF ,△CEF 分别沿DE ,EF ,DF 向上折起，使A ，B ，C 重合为点P ，则三棱锥P -DEF 的外接球表面积为()A.72π B.7143π C.14π D.56π【答案】C【解析】由题意可知，PE =DF =10,PF =DE =13,PD =EF =5，即三棱锥P -DEF 的对棱相等，先将该三棱锥补充成长方体，如图所示：设FH =x ,HD =y ,HP =z ，则x 2+y 2=10,y 2+z 2=5,x 2+z 2=13，所以x 2+y 2+z 2=14，于是三棱锥P -DEF 的外接球直径为14，半径为142，所以该三棱锥外接球的表面积为：4π⋅142 2=14π.故选：C .8(2023·高一课时练习)如图，在等腰梯形ABCD 中，AB =2DC =2,∠DAB =60°,E 为AB 中点.将ΔADE 与ΔBEC 分别沿ED 、EC 折起，使A 、B 重合于点P ，则三棱锥P -DCE 的外接球的体积为()A.43π27B.6π2C.6π8D.6π24【答案】C【解析】易证所得三棱锥为正四面体，它的棱长为1，故其外接球与棱长为22的正方体的外接球一直，又正方体外接球半径为R=12+12+122=64故外接球的体积为43π633=68π故选C．9(2023·高一课时练习)边长为1的正四面体内切球的体积为()A.6π8B.212C.π6D.6π216【答案】D【解析】将棱长为1的正四面体ABCD补成正方体AECF-GBHD，则该正方体的棱长为22，V A-BCD=223-4V B-ACE=24-4×13×12×22 3=212，设正四面体ABCD的内切球半径为r，正四面体ABCD每个面的面积均为34×12=34，由等体积法可得V A-BCD=212=13r S△ABC+S△ACD+S△ABD+S△BCD=33r，解得r=612，因此，该正四面体的内切球的体积为V=43π×6123=6216π.故选：D.10(2023·高一课时练习)已知三棱锥S-ABC的所有顶点都在球O的球面上，SC是球O的直径.若平面SAC⊥平面SBC，SA=AC，SB=BC，球O的体积为36π，则三棱锥S-ABC的体积为()A.9B.18C.27D.36【答案】A【解析】如图，三棱锥S-ABC的所有顶点都在球O的球面上，SC是球O的直径O为SC中点，SA=AC,SB=BC∴AO⊥SC，BO⊥SC，∵平面SAC⊥平面SBC，平面SAC∩平面SBC=SC，BO⊂平面SBC，∴BO⊥平面SCA，设BO=r，由球O的体积为36π，可得43πr3=36π,∴r=3，则V S-ABC=V B-SCA=13S△SCA⋅BO=13×12×2r×r×r=13r3=9，∴三棱锥S-ABC的体积为9，故选∶A．11(2023·高一课时练习)如下图是一个正八面体，其每一个面都是正三角形，六个顶点都在球O 的球面上，则球O与正八面体的体积之比是()A.πB.4π3C.3π2D.2π【答案】A【解析】由题意得正方形ABCD的中心O即为外接球球心，设AB=a，则R=OA=22a，球O的体积为V1=43π×22a3=2π3a3，而h=OE=22a，故正八面体的体积V2=2×13×a2×22a=23a3，得V1V2=π，故选：A12(2023·高一课时练习)已知三棱柱ABC-A1B1C1所有的顶点都在球O的球面上，球O的体积是500π3，∠ABC =60°，AC =43，则AA 1=()A.3B.6C.4D.8【答案】B【解析】设球O 的半径为R ，△ABC 外接圆的半径为r ，则43πR 3=500π3，解得R =5，因为∠ABC =60°，AC =43，由正弦定理得，△ABC 外接圆的半径r =432sin60°=4，则AA 1=2R 2-r 2=2×3=6．故选：B二、多选题13(2023春·湖北襄阳·高一襄阳四中校考阶段练习)如图，线段AB 为圆O 的直径，点E ，F 在圆O 上，EF ⎳AB ，矩形ABCD 所在平面和圆O 所在平面垂直，且AB =2，EF =AD =1，则下列说法正确的是()A.OF ⎳平面BCEB.BF ⊥平面ADFC.三棱锥C -BEF 外接球的体积为5πD.三棱锥C -BEF 外接球的表面积为5π【答案】ABD【解析】选项A ：由EF ⎳AB ，AB =2，EF =1，可得EF // OB 则四边形OBEF 为平行四边形，则OF ⎳BE又OF ⊄平面BCE ，BE ⊂平面BCE ，则OF ⎳平面BCE .判断正确；选项B ：连接BF ，线段AB 为圆O 的直径，则BF ⊥AF 由平面ABCD ⊥平面ABEF ，平面ABCD ∩平面ABEF =AB AD ⊂平面ABCD ，AD ⊥AB ，则AD ⊥平面ABEF则AD ⊥BF ，又AF ∩AD =A ，AF ⊂平面ADF ，AD ⊂平面ADF 则BF ⊥平面ADF .判断正确；选项C ：取CD 中点H ，连接OH由平面ABCD ⊥平面ABEF ，平面ABCD ∩平面ABEF =ABOH ⊥AB ,OH ⊂平面ABEF ，可得OH ⊥平面ABEF又点E ，F ，B 在圆O 上，则三棱锥C -BEF 外接球球心在直线OH 上，由OH ⎳BC ，OH ⊄平面BCE ，BC ⊂平面BCE可得OH ⎳平面BCE ，则三棱锥C -BEF 外接球球心到平面BCE 的距离为点O 到平面BCE 的距离由BC ⊥平面ABEF ，BC ⊂平面BCE ，可得平面BCE ⊥平面ABEF ，则点O 到平面BCE 的距离即点O 到直线BE 的距离，又点O 到直线BE 的距离为32，则三棱锥C -BEF 外接球球心到平面BCE 的距离为32在△BCE 中，BC ⊥BE ，BC =BE =1，则CE =2，则△BCE 外接圆半径为22则三棱锥C -BEF 外接球的半径R =22 2+32 2=52则三棱锥C -BEF 外接球的体积为43π⋅52 3=556π.判断错误；选项D ：由三棱锥C -BEF 外接球的半径R =52则三棱锥C -BEF 外接球的表面积为4πR 2=4π⋅522=5π.判断正确.故选：ABD14(2023春·江苏无锡·高一江苏省江阴市第一中学校考阶段练习)我们把所有棱长都相等的正棱柱(锥)叫“等长正棱柱(锥)”，而与其所有棱都相切的称为棱切球，设下列“等长正棱柱(锥)”的棱长都为1，则下列说法中正确的有()A.正方体的棱切球的半径为2B.正四面体的棱切球的表面积为π2C.等长正六棱柱的棱切球的体积为4π3D.等长正四棱锥的棱切球被棱锥5个面(侧面和底面)截得的截面面积之和为7π12【答案】BCD 【解析】正方体的棱切球的直径为正方体的面对角线，正方体的棱切球的半径为面对角线的一半，即为22，选项A 错误；如图，四面体ABCD 为棱长为1的正四面体，把正四面体ABCD 放到正方体中，则正方体的棱长即为正四面体的棱切球的直径，所以正四面体的棱切球的半径为24，即正四面体的棱切球的表面积为π2，选项B 正确；如图，等长正六棱柱的棱切球的直径为AB ，即直径为2，半径为1，所以等长正六棱柱的棱切球的体积为4π3，选项C 正确；由棱切球的定义可知，棱切球被每一个面所截，截面为该面的内切圆，则等长正四棱锥的底面内切圆的面积为π×12 2=π4，每个侧面正三角形的内切圆的半径为正三角形高的13，即36，所以四个侧面正三角形的内切圆的面积为4×π×36 2=π3，所以等长正四棱锥的棱切球被棱锥5个面截得的截面面积之和为π4+π3=7π12，选项D 正确.故选：BCD .15(2023春·湖南邵阳·高一湖南省邵东市第三中学校考期中)已知正方体ABCD -A 1B 1C 1D 1的各棱长均为2，下列结论正确的是()A.该正方体外接球的直径为23B.该正方体内切球的表面积为4πC.若球O 与正方体的各棱相切，则该球的半径为2D.该正方体外接球的体积为43【答案】ABC【解析】若正方体的棱长为2，则：①若球为正方体的外接球，则外接球直径等于正方体体对角线，即2R =22+22+22=23，故A 正确，外接球体积为43πR 3=43π，故D 错误；②若球为正方体的内切球，则内切球半径为棱长的一半，故R =1，球的表面积为4πR 2=4π，故B 正确；③若球与正方体的各棱相切，则球的直径等于正方形对角线长，即R =22+22=22，球的半径为R =2，故C 正确．故本题选：ABC .三、填空题16(2023春·陕西汉中·高一校考期中)已知球O 是四棱锥P -ABCD 的外接球，四边形ABCD 是边长为1的正方形，点P 在球面上运动且PA =2，则当四棱锥P -ABCD 的体积最大时，球O 的表面积是.【答案】6π【解析】设PA 与平面ABCD 夹角为θ，则四棱锥P -ABCD 的体积为V =13S ABCD ⋅h =13×1×h =13×PA ×sin θ=23sin θ，当sin θ=1时，四棱锥P -ABCD 的体积最大，即θ=90°，此时PA ⊥平面ABCD ，将四棱锥P -ABCD 补成一个正四棱柱，如图所示，此时四棱锥P -ABCD 和该正四棱柱有相同的外接球O ，设球O 的半径为R ，则2R =PC =12+12+22=6，可得R =62，所以球O 的表面积为S =4πR 2=4π×622=6π.故答案为：6π17(2023·高一课时练习)、已知正方体外接球的体积是323π，那么正方体的棱长等于【答案】433【解析】设正方体的棱长为a ，则外接球的半径为3a 2，外接球的体积V =4π3R 3=4π3×3a 2 3=3πa 32=32π3，解得a =433，即正方体的棱长等于433．18(2023春·浙江宁波·高一余姚中学校考阶段练习)已知某圆锥的内切球的体积为32π3，则该圆锥的表面积的最小值为．【答案】32π【解析】设圆锥的内切球半径为r ，则43πr 3=32π3，解得r =2，设圆锥顶点为A ，底面圆周上一点为B ，底面圆心为C ，内切球球心为D ，内切球切母线AB 于E ，底面半径BC =R >2,∠BDC =θ，则tan θ=R 2，又∠ADE =π-2θ，由已知△BDE ,△BDC 为直角三角形，又DC =DE ，BD =BD ，所以△BDE ≅△BDC ，所以BE =BC =R ,∠BDE =∠BDC =θ，所以∠ADE =π-2θ，故AB=BE +AE =R +2tan π-2θ =R -2tan2θ，又tan2θ=2tan θ1-tan 2θ=R 1-R 24=4R 4-R 2，故AB =R -8R 4-R 2=R R 2+4 R 2-4，故该圆锥的表面积为S =πR 2R 2+4 R 2-4+πR 2=2πR 4R 2-4，令t =R 2-4>0,则S =2π(t +4)2t =2πt +16t +8 ≥2π2t ×16t +8 =32π，当且仅当t =16t，即t =4,R =22时取等号．故答案为：32π.19(2023·高一课时练习)如果圆柱、圆锥的底面直径和高都等于一个球的直径，则圆柱、球、圆锥的体积的比是.【答案】3:2:1【解析】设球的半径为r ，则球的体积为V 球=43πr 3，圆柱的体积为V 圆柱=πr 2⋅2r =2πr 3，圆锥的体积为V 圆锥=13πr 2⋅2r =2πr 33，因此，V 圆柱:V 球:V 圆锥=2:43:23=3:2:1.故答案为：3:2:1.20(2023·高一课时练习)已知A 、B 、C 是球面上三点，且AB =AC =4，∠BAC =90°，若球心O 到平面ABC 的距离为22，则该球表面积为.【答案】64π【解析】因为AB =AC =4，∠BAC =90°，所以BC 为平面ABC 截球所得小圆的直径，如图，设小圆的半径为r ，得2r =AB 2+AC 2=42，解得r =22，又球心O 到平面ABC 的距离d =22，根据球的截面圆性质，得球的半径R =r 2+d 2=4，所以球的表面积为S =4πR 2=64π.故答案为：64π.21(2023春·河南商丘·高一商丘市第一高级中学校考期中)已知正三棱锥S -ABC ,SA =SB =SC =23,AB =3，球O 与三棱锥S -ABC 的所有棱相切，则球O 的表面积为．【答案】(19-83)π【解析】取等边△ABC 的中心E ，连接SE ，则SE ⊥平面ABC ，连接AE 并延长，交BC 于点D ，则D 为BC 中点，且AD ⊥BC ，在SE 上找到棱切球的球心O ，连接OD ，则OD 即为棱切球的半径，过点O 作OF ⊥SA 于点F ，则OF 也是棱切球的半径，设OD =OF =R ，因为SA =SB =SC =23,AB =3，所以求得AD =332,AE =3,DE =32，由勾股定理得：SE =12-3=3，且∠ASE =30°，设OE =h ，OD =OE 2+ED 2=h 2+34，SO =3-h ，OF =123-h ，由题意得：h 2+34=123-h ，解得：h =3-1或-1-3，当h=3-1时，R2=h2+34=194-23，此时球O的表面积为(19-83)π；当棱切球的半径最大时，切点为A，B，C，由于∠ASE=30°，SA=SB=SC=23，可求得最大半径R=23tan30°=2，而当h=-3-1时，R2=h2+34=194+23>4，显然不成立，故h=-3-1舍去，综上：球O的表面积为(19-83)π故答案为：(19-83)π22(2023春·山东德州·高一德州市第一中学校考阶段练习)边长为2的正四面体内有一个球，当球与正四面体的棱均相切时，球的体积为．【答案】2 3π【解析】结合正四面体的性质：球心在正四面体的体高上，且为外接球的球心，如下图：取球心O，若OD⊥PA，则OD即为球的半径，而O 为底面中心，∴PO ⊥面ABC，若E为BC中点，则AE=PE=3，∴PO =263，PO=62，AO=233，由Rt△PDO∼Rt△PO A，则POPA=ODAO，故OD=22，∴球的体积为43π⋅OD3=23π.故答案为：23π23(2023春·广东江门·高一江门市培英高级中学校考期中)已知正方体的棱长为2，则与正方体的各棱都相切的球的表面积是．【答案】8π【解析】过正方体的对角面作截面如图，故球的半径r=2，∴其表面积S=4π×(2)2=8π．故答案为：8π.24(2023春·江苏苏州·高一江苏省苏州实验中学校考阶段练习)一个球被平面截下的一部分叫做球缺，截面叫做球缺的底面，垂直于截面的直径被截下的线段长叫做球缺的高，球缺的体积公式为V =π3(3R-h)h2，其中R为球的半径，h为球缺的高.若一球与一棱长为2的正方体的各棱均相切，则该球与正方体的公共部分的体积为.【答案】10-162 3π【解析】由题可得该球与正方体的公共部分球去掉6个球缺，则球的半径为R=22+222=2，球缺高h=2-1，则一个球缺的体积为π332-2-12-12=π342-5，则该球与正方体的公共部分的体积为4π3×23-6×π342-5=10-1623π.故答案为：10-162 3π.四、解答题25(2023·全国·高一专题练习)已知球与正四面体的六条棱都相切，求球与正四面体的体积之比．【解析】如图，设正四面体棱长为a，球半径为R，取AB的中点为E，CD中点F，连接AF,BF,EF，则AF=BF=32a，∴EF⊥AB，同理EF⊥CD，∴EF是AB,CD的公垂线，则EF的长是AB,CD的距离，EF=AF2-AE2=34a2-14a2=22a，又由球与正四面体的六棱都相切，得EF是该球的直径，即2R=22a，∴R3=232a3，V 球=43πR3=43π⋅232a3=224πa3，又V正四面体=13×S×h=13×12×a×a×sin60°×63a=212a3,故V球V正四面体=π226(2023·高一课时练习)有三个球，已知球O1内切于正方体，球O2与这个正方体各棱都相切，球O3过这个正方体的各个顶点，求球O1、球O2、球O3的表面积之比.【解析】设正方体的棱长为a.①球O1为正方体的内切球，球心O1是正方体的中心，切点是正方体六个面的中心，经过四个切点及球心作截面，如图1所示，设球O1的半径为r1，表面积为S1，则2r1=a，r1=a2，所以S1=4πr21=πa2.②球O2与正方体各棱的切点为各棱的中点，过正方体的两个相对面的面对角线作截面，如图2所示，设球O2的半径为r2，表面积为S2，则2r2=2a，r2=22a，所以S2=4πr22=2πa2.③球O3过正方体的各个顶点，即正方体的各个顶点都在球面上，过正方体的体对角线作截面，如图3所示，设球O3的半径为r3，表面积为S3，则2r3=3a，r3=32a，所以S3=4πr23=3πa2.故这三个球的表面积之比S1:S2:S3=πa2:2πa2:3πa2=1:2:3.图1 图2 图3。

内切球与外接球常见解法内切球与外接球是数学里经典的概念，许多数学问题都涉及到了这两类球的概念，比如说圆锥曲线，并且内切球与外接球的解法也十分经典。

本文将会介绍内切球与外接球的常见解法。

一、内切球的解法1. 欧拉公式法欧拉公式告诉我们，对于任意一个凸多面体，其顶点数、棱数、面数之和等于2加上该凸多面体的亏格数。

因此，对于一个球体，其亏格数为2。

设内切球半径为r，球心到多面体某一个面的距离为d，则可以得到以下公式：r=(d1+d2+...+dn-nr)/(n-2)其中，d1、d2、...、dn为该面到球心的距离。

该公式适用于多面体的任何一个面。

2. 套路法对于任意一个多面体，在球心到多面体顶点的连线上，肯定会存在一个最小的球，使得该球完全包含了多面体的所有面。

这个球就是内切球。

通过套路法可求出内切球的半径。

首先取一个多面体面的中心点作为初始点，然后每次将该点沿着与之相邻的面的法线方向平移，并使点到多面体的距离为内切球半径。

当所有点到多面体距离之和最小时的内切球半径即为所求。

3. 向量法对于一个三角形，其内切球圆心为三角形的角平分线交点。

我们可以求出三角形的边向量和平面法向量，从而得到角平分线向量。

由角平分线乘以内切球半径即可得到内切球圆心坐标。

同理，对于多面体，内切球圆心为多面体一个面的平面角平分线交点。

二、外接球的解法1. 向量法对于一个三角形，其外接圆圆心为三角形的垂心和三边的交点。

由于垂心很难求得，我们通常使用法向量法求出外接球圆心。

首先求出三角形的边向量和平面法向量，然后将平面法向量沿着垂直三角形所在平面的方向延长，得到一个点P。

将点P连线到三角形三个顶点分别得到三个垂足，并将三个垂足连线求出其交点，即为外接圆圆心。

同理，对于多面体，通过面的法向量求得平面，然后将平面法向量沿着垂直多面体所在平面的方向延长，得到一个点P。

将点P连线到多面体任一面的一个顶点分别得到各个垂足，并将各个垂足连线求出其交点，即为外接球圆心。

空间几何体的外接球与内切球九大模型模型一墙角模型【方法总结】墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型，用构造法(构造长方体)解决．外接球的直径等于长方体的体对角线长(在长方体的同一顶点的三条棱长分别为a，b，c，外接球的半径为R，则2R＝a2＋b2＋c2．)，秒杀公式：R2＝a2＋b2＋c24．可求出球的半径从而解决问题．有以下四种类型：【例题选讲】[例](1)已知三棱锥A－BCD的四个顶点A，B，C，D都在球O的表面上，AC⊥平面BCD，BC⊥CD，且AC＝3，BC＝2，CD＝5，则球O的表面积为()A．12πB．7πC．9πD．8π答案A解析由AC⊥平面BCD，BC⊥CD知三棱锥A－BCD可构造以AC，BC，CD为三条棱的长方体，设球O的半径为R，则有(2R)2＝AC2＋BC2＋CD2＝3＋4＋5＝12，所以S球＝4πR2＝12π，故选A．(2)若三棱锥ABCS-的三条侧棱两两垂直，且2=SA，4==SCSB，则该三棱锥的外接球半径为()．A．3B．6C．36D．9答案A解析616164)2(2=++=R，3=R，故选A．(3)已知S，A，B，C，是球O表面上的点，SA⊥平面ABC，AB⊥BC，SA＝AB＝1，BC＝2，则球O的表面积等于()．A．4πB．3πC．2πD．π答案解析由已知，222211(2)2R=++=，244S Rπ∴==球π．(4)在正三棱锥S－ABC中，M，N分别是棱SC，BC的中点，且AM MN⊥，若侧棱SA=S－ABC外接球的表面积是________．答案π36解析 MNAM⊥，MNSB//，∴SBAM⊥， SBAC⊥，∴⊥SB平面SAC ，∴SA SB ⊥，SC SB ⊥， SA SB ⊥，SA BC ⊥，∴⊥SA 平面SBC ，∴SC SA ⊥，故三棱锥ABC S -的三棱条侧棱两两互相垂直，222(2)(2R ∴=+2+36=，即3642=R ，∴正三棱锥ABC S -外接球的表面积是π36．(5)(2019全国Ⅰ)已知三棱锥P －ABC 的四个顶点在球O 的球面上，PA ＝PB ＝PC ，△ABC 是边长为2的正三角形，E ，F 分别是PA ，AB 的中点，∠CEF =90°，则球O 的体积为()．A ．68πB ．64πC ．6πD ．6π答案D 解析解法一：, PA PB PC ABC == △为边长为2的等边三角形，P ABC ∴-为正三棱锥，PB AC ∴⊥，又E ，F 分别为PA ，AB 的中点，EF PB ∴∥，EF AC ∴⊥，又EF CE ⊥，,CE AC C EF =∴⊥ 平面PAC ，∴PB ⊥平面PAC ，APB PA PB PC ∴∠=90︒,∴===P ABC ∴-为正方体的一部分，2R =，即344π2338R V R π=∴==⨯=，故选D ．解法二：设2PA PB PC x ===，, E F 分别为, PA AB 的中点，EF PB ∴∥，且12EF PB x ==，ABC △为边长为2的等边三角形，CF ∴=，又90CEF ∠=︒，1 2CE AE PA x ∴===，AEC △中，由余弦定理可得()2243cos 22x x EAC x+--∠=⨯⨯作PD AC ⊥于D ，PA PC = ，D ∴为AC 的中点，cos E ∠12AD AC PA x==，2243142x x x x +-+∴=，221212 2x x x ∴+=∴==，，PA PB PC ∴===，又2AB BC AC ===，, , PA PB PC ∴两两垂直，2R ∴==，R ∴=，34433V R ππ∴==⨯8=，故选D ．(6)已知二面角α－l －β的大小为π3，点P ∈α，点P 在β内的正投影为点A ，过点A 作AB ⊥l ，垂足为点B ，点C ∈l ，BC ＝22，PA ＝23，点D ∈β，且四边形ABCD 满足∠BCD ＋∠DAB ＝π．若四面体PACD 的四个顶点都在同一球面上，则该球的体积为________．答案86π解析∵∠BCD ＋∠DAB ＝π，∴A ，B ，C ，D 四点共圆，直径为AC ，∵PA ⊥平面β，AB ⊥l ，∴易得PB ⊥l ，即∠PBA 为二面角α－l －β的平面角，即∠PBA ＝π3，∵PA ＝23，∴BA ＝2，∵BC ＝22，∴AC＝23．设球的半径为R ，则23－R 2－(3)2＝R 2－(3)2，∴R ＝6，V ＝4π3(6)3＝86π．模型二对棱相等模型【方法总结】对棱相等模型是三棱锥的三组对棱长分别相等模型，用构造法(构造长方体)解决．外接球的直径等于长方体的体对角线长，即2R =(长方体的长、宽、高分别为a 、b 、c )．秒杀公式：R 2＝x 2＋y 2＋z 28(三棱锥的三组对棱长分别为x 、y 、z )．可求出球的半径从而解决问题．【例题选讲】[例](1)正四面体的各条棱长都为，则该正面体外接球的体积为________．答案解析这是特殊情况，但也是对棱相等的模式，放入长方体中，32=R ，23=R ，ππ2383334=⋅=V ．(2)在三棱锥A －BCD 中，AB ＝CD ＝2，AD ＝BC ＝3，AC ＝BD ＝4，则三棱锥BCD A -外接球的表面积为__．答案292π解析构造长方体，三个长度为三对面的对角线长，设长宽高分别为c b a ,,，则922=+b a ，422=+c b ，1622=+a c ∴291649)(2222=++=++c b a ，291649)(2222=++=++c b a ，229222=++c b a ，22942=R ，π229=S ．(3)在三棱锥A －BCD 中，AB ＝CD ＝6，AC ＝BD ＝AD ＝BC ＝5，则该三棱锥的外接球的体积为____．答案6解析依题意得，该三棱锥的三组对棱分别相等，因此可将该三棱锥补形成一个长方体，设该长方体的长、宽、高分别为a 、b 、c ，且其外接球的半径为R ，2＋b 2＝62，2＋c 2＝52，2＋a 2＝52，得a 2＋b 2＋c 2＝43，即(2R )2＝a 2＋b 2＋c 2＝43，易知2R =，即为该三棱锥的外接球的半径，所以该三棱锥的外接球的表面积为3436R π=．(4)在正四面体A BCD -中，E 是棱AD 的中点，P 是棱AC 上一动点，BP PE +，则该正四面体的外接球的体积是()A B ．6πC D ．32π答案A解析将侧面ABC ∆和ACD ∆展成平面图形，如图所示：设正四面体的棱长为a ，则BP PE +的最小值为2BE ==，2a ∴=．在正四面体A BCD -的边长为2，外接球的半径42R ==，外接球的体积343V R π==．(5)已知三棱锥A BCD -，三组对棱两两相等，且1AB CD ==，AD BC ==，若三棱锥A BCD -的外接球表面积为92π．则AC =________．答案解析将四面体A BCD -放置于长方体中， 四面体A BCD -的顶点为长方体八个顶点中的四个，∴长方体的外接球就是四面体A BCD -的外接球，1AB CD == ，AD BC ==，且三组对棱两两相等，∴设AC BD x ==，得长方体的对角线长为=，可得外接球的直径2R =以R =， 三棱锥A BCD -的外接球表面积为92π，2942R ππ∴=，解得4R =，324=，解之得x =AC BD ==模型三汉堡模型【方法总结】汉堡模型是直棱柱的外接球、圆柱的外接球模型，用找球心法(多面体的外接球的球心是过多面体的两个面的外心且分别垂直这两个面的直线的交点．一般情况下只作出一个面的垂线，然后设出球心用算术方法或代数方法即可解决问题．有时也作出两条垂线，交点即为球心．)解决．以直三棱柱为例，模型如下图，由对称性可知球心O 的位置是△ABC 的外心O 1与△A 1B 1C 1的外心O 2连线的中点，算出小圆O 1的半径AO 1＝r ，OO 1＝2h ，2224h R r ∴=+．【例题选讲】[例](1)(2013辽宁)已知直三棱柱ABC －A 1B 1C 1的6个顶点都在球O 的球面上．若AB ＝3，AC ＝4，AB ⊥AC ，AA 1＝12，则球O 的半径为()．A ．3172B ．210C ．132D ．310答案C 解析如图所示，由球心作平面ABC 的垂线，则垂足为BC 的中点M ．又AM ＝12BC ＝52，OM ＝12AA 1＝6，所以球O 的半径R ＝OA ＝522＋62＝132．另解过C 点作AB 的平行线，过B 点作AC 的平行线，交点为D ，同理过C 1作A 1B 1的平行线，过B 1作A 1C 1的平行线，交点为D 1，连接DD 1，则ABCD －A 1B 1C 1D 1恰好成为球的一个内接长方体，故球的半径r 132=．故选C ．(2)设三棱柱的侧棱垂直于底面，所有棱长都为a ，顶点都在一个球面上，则该球的表面积为()．A ．2a πB ．273a πC ．2113a πD ．237a π答案B 解析222222274312a a R OB OE BE a ==+=+=，22743S a a ππ∴==．故选B ．(3)(2009全国Ⅰ)直三棱柱ABC －A 1B 1C 1的各顶点都在同一球面上，若AB ＝AC ＝AA 1＝2，∠BAC ＝120°，则此球的表面积等于()．A ．10πB ．20πC ．30πD ．40π答案B解析如图，先由余弦定理求出BC ＝23，再由正弦定理求出r ＝AO 1＝2，外接球的直径R ＝12＋22＝5，所以该球的表面积为4πR 2＝20π．故选B ．(4)已知圆柱的高为2，底面半径为3，若该圆柱的两个底面的圆周都在同一个球面上，则这个球的表面积等于()A ．4πB ．16π3C ．32π3D ．16π答案D解析由题意知圆柱的中心O 为这个球的球心，于是，球的半径r ＝OB ＝OA 2＋AB 2＝12＋（3）2＝2．故这个球的表面积S ＝4πr 2＝16π．故选D ．(5)若一个圆柱的表面积为12π，则该圆柱的外接球的表面积的最小值为()A ．12)π-B ．C ．3)πD ．16π答案A解析设圆柱的底面半径为r ，高为h ，则22212r rh πππ+=，则6h r r=-．设该圆柱的外接球的半径为R ，则22222221659()()333244h R r r r r r r =+=+-=+--=- ，当且仅当22594r r =，即4365r =时，等号成立．故该圆柱的外接球的表面积的最小值为43)12)ππ-=．模型四垂面模型【方法总结】垂面模型是有一条侧棱垂直底面的棱锥模型，可补为直棱柱内接于球，由对称性可知球心O 的位置是△CBD的外心O 1与△AB 2D 2的外心O 2连线的中点，算出小圆O 1的半径AO 1＝r ，OO 1＝2h ，2224h R r ∴=+．【例题选讲】[例](1)已知在三棱锥S －ABC 中，SA ⊥平面ABC ，且∠ACB ＝30°，AC ＝2AB ＝23，SA ＝1．则该三棱锥的外接球的体积为()A ．13813πB ．13πC ．136πD ．13136π答案D解析∵∠ACB ＝30°，AC ＝2AB ＝23，∴△ABC 是以AC 为斜边的直角三角形，其外接圆半径r ＝AC2＝3，则三棱锥外接球即为以△ABC 为底面，以SA 为高的三棱柱的外接球，∴三棱锥外接球的半径R 满足R ＝132，故三棱锥外接球的体积V ＝43πR 3＝13136π．故选D ．第(1)小题图第(2)小题图1第(2)小题图2(2)三棱锥P －ABC 中，平面PAC ⊥平面ABC ，AB ⊥AC ，PA ＝PC ＝AC ＝2，AB ＝4，则三棱锥P －ABC 的外接球的表面积为()A ．23πB ．234πC ．64πD ．643π答案D解析如图1，设O 为三棱锥外接球的球心，O 1为正△PAC 的中心，则OO 1＝12AB ＝2．2AO 1＝2sinπ3＝433，AO 1＝233，R 2＝OA 2＝O 1A 2＋O 1O 2＝43＋4＝163，故几何体外接球的表面积S ＝4πR 2＝643．另解：如图2，设O ′为正△PAC 的中心，D 为Rt △ABC 斜边的中点，H 为AC 中点．由平面PAC ⊥平面ABC ，则O ′H ⊥平面ABC ．作O ′O ∥HD ，OD ∥O ′H ，则交点O 为三棱锥外接球的球心，连接OP ，又O ′P ＝23＝23×32×2＝233，OO ′＝DH ＝12AB ＝2．∴R 2＝OP 2＝O ′P 2＋O ′O 2＝43＋4＝163．故几何体外接球的表面积S ＝4πR 2＝643π．(3)在三棱锥S －ABC 中，侧棱SA ⊥底面ABC ，AB ＝5，BC ＝8，∠ABC ＝60°，SA ＝25，则该三棱锥的外接球的表面积为()A ．643πB ．256πC ．4363πD ．2048327π答案B解析由题意知，AB ＝5，BC ＝8，∠ABC ＝60°，则在△ABC 中，由余弦定理得AC 2＝AB 2＋BC 2－2×AB ×BC ×cos ∠ABC ，解得AC ＝7，设△ABC 的外接圆半径为r ，则△ABC 的外接圆直径2r ＝ACsin ∠ABC ＝732，∴r ＝73，又∵侧棱SA ⊥底面ABC ，∴三棱锥的外接球的球心到平面ABC 的距离h ＝12SA ＝5，则外接球的半径R ＝732＋(5)2＝643，则该三棱锥的外接球的表面积为S ＝4πR 2＝2563π.(4)在三棱锥P －ABC 中，已知PA ⊥底面ABC ，∠BAC ＝120˚，PA ＝AB ＝AC ＝2，若该三棱锥的顶点都在同一个球面上，则该球的表面积为()A ．103πB ．18πC ．20πD ．93π答案C解析如图1，先由余弦定理求出BC ＝23，再由正弦定理求出r ＝AO 1＝2，外接球的直径R ＝12＋22＝5，所以该球的表面积为4πR 2＝20π．第(3)小题图第(4)小题图1第(4)小题图2另解如图2，该三棱锥为图中正六棱柱内的三棱锥P －ABC ，PA ＝AB ＝AC ＝2，所以该三棱锥的外接球即该六棱柱的外接球，所以外接球的直径2R ＝42＋22＝25⇒R ＝5，所以该球的表面积为4πR 2＝20π．(5)在三棱锥P ABC -中，PA ⊥平面ABC ，120BAC ∠=︒，2AC =，1AB =，设D 为BC 中点，且直线PD与平面ABC 所成角的余弦值为5，则该三棱锥外接球的表面积为________．答案373π解析在ABC ∆中，120BAC ∠=︒，2AC =，1AB =，由余弦定理得：22BC AC =+22cos AB AC BC BAC -⋅⋅∠，即22221221cos1207BC =+-⨯⨯⨯︒=，解得：BC =．设ABC ∆的外接圆半径为r ，由正弦定理得2sin BC r BAC ===∠解得：r ==；且222cos 2AB BC AC ABC AB BC +-∠==，又D 为BC 中点，在ABD ∆中，122BD BC ==，1AB =，cos 7ABD ∠=．由余弦定理得：2222cos AD AB BD AB BD ABD =+-∠ ，即：22231()212274AD =+-⨯⨯=，解得2AD =．又因为PA ⊥平面ABC ，所以PDA ∠为直线PD 与平面ABC 所成角，由cos 5PDA ∠=，得sin 5PDA ∠=，tan 2PDA ∠=，所以在Rt PAD ∆中，tan 22PA AD PDA =∠== ．设三棱锥P ABC -的外接球半径为R ，所以R =，三棱锥P ABC -外接球表面积为23743S R ππ==．模型五切瓜模型【方法总结】切瓜模型是有一侧面垂直底面的棱锥型，常见的是两个互相垂直的面都是特殊三角形且平面ABC ⊥平面BCD ，如类型Ⅰ，△ABC 与△BCD 都是直角三角形，类型Ⅱ，△ABC 是等边三角形，△BCD 是直角三角形，类型Ⅲ，△ABC 与△BCD 都是等边三角形，解决方法是分别过△ABC 与△BCD 的外心作该三角形所在平面的垂线，交点O 即为球心．类型Ⅳ，△ABC 与△BCD 都一般三角形，解决方法是过△BCD 的外心O 1作该三角形所在平面的垂线，用代数方法即可解决问题．设三棱锥A －BCD 的高为h ，外接球的半径为R ，球心为O ．△BCD 的外心为O 1，O 1到BD 的距离为d ，O 与O 1的距离为m 2＝r 2＋m 2，2＝d 2＋(h －m )2，解得R ．可用秒杀公式：R 2＝r 12＋r 22－l 24(其中r 1、r 2为两个面的外接圆的半径，l 为两个面的交线的长)【例题选讲】[例](1)已知在三棱锥P －ABC 中，V P ­ABC ＝433，∠APC ＝π4，∠BPC ＝π3，PA ⊥AC ，PB ⊥BC ，且平面PAC ⊥平面PBC ，那么三棱锥P －ABC 外接球的体积为________．答案32π3解析如图，取PC 的中点O ，连接AO ，BO ，设PC ＝2R ，则OA ＝OB＝OC ＝OP ＝R ，∴O 是三棱锥P －ABC 外接球的球心，易知，PB ＝R ，BC ＝3R ，∵∠APC ＝π4，PA ⊥AC ，O 为PC 的中点，∴AO ⊥PC ，又平面PAC ⊥平面PBC ，且平面PAC ∩平面PBC ＝PC ，∴AO ⊥平面PBC ，∴V P ­ABC ＝V A ­PBC ＝13×12×PB ×BC ×AO ＝13×12×R ×3R ×R＝433，解得R ＝2，∴三棱锥P －ABC 外接球的体积V ＝43πR 3＝32π3．(2)如图，已知平面四边形ABCD 满足AB ＝AD ＝2，∠A ＝60˚，∠C ＝90˚，将△ABD 沿对角线BD 翻折，使平面ABD ⊥平面CBD ，则四面体ABCD 外接球的体积为__．答案323π27解析在四面体ABCD 中，∵AB ＝AD ＝2，∠BAD ＝60˚，∴△ABD为正三角形，设BD 的中点为M ，连接AM ，则AM ⊥BD ，又平面ABD ⊥平面CBD ，平面ABD ∩平面CBD ＝BD ，∴AM ⊥平面CBD ．∵△CBD 为直角三角形，∴其外接圆的圆心是斜边BD 的中点M ，由球的性质知，四面体ABCD 外接球的球心必在线段AM 上，又△ABD 为正三角形，∴球心是△ABD 的中心，则外接球的半径为23×2×32＝233，∴四面体ABCD 外接球的体积为43×π×(233)3＝323π27．(3)已知三棱锥A －BCD 中，△ABD 与△BCD 是边长为2的等边三角形且二面角A －BD －C 为直二面角，则三棱锥A －BCD 的外接球的表面积为()A ．10π3B ．5πC ．6πD ．20π3答案D解析如图，取BD 中点M ，连接AM ，CM ，取△ABD ，△CBD 的中心即AM ，CM 的三等分点P ，Q ，过P 作平面ABD 的垂线，过Q 作平面CBD 的垂线，两垂线相交于点O ，则点O 为外接球的球心，如图，其中OQ ＝33，CQ ＝233，连接OC ，则外接球的半径R ＝OC ＝153，表面积为4πR 2＝20π3，故选D ．(4)已知ABC ∆是以BC 为斜边的直角三角形，P 为平面ABC 外一点，且平面PBC ⊥平面ABC ，3BC =，PB =PC =，则三棱锥P ABC -外接球的表面积为________．答案10π解析由题意知BC 的中点O 为ABC ∆外接圆的圆心，且平面PBC ⊥平面ABC ，过O 作面ABC 的垂线l ，则垂线l 一定在面ABC 内．根据球的性质，球心一定在垂线l 上， 球心1O 一定在平面PBC 内，且球心1O 也是PBC ∆外接圆的圆心．在PBC ∆中，由余弦定理得222cos 22PB BC PC PBC PB BC +-∠==，sin 2PBC ∴∠=，由正弦定理得：2sin PCR PBC=∠，解得2R =，∴三棱锥的外接球的表面积2410R ππ==．(5)已知等腰直角三角形ABC 中，AB ＝AC ＝2，D ，E 分别为AB ，AC 的中点，沿DE 将△ABC 折成直二面角(如图)，则四棱锥A －DECB 的外接球的表面积为________．答案10π解析取DE 的中点M ，BC 的中点N ，连接MN (图略)，由题意知，MN ⊥平面ADE ，因为△ADE是等腰直角三角形，所以△ADE 的外接圆的圆心是点M ，四棱锥A －DECB 的外接球的球心在直线MN 上，又等腰梯形DECB 的外接圆的圆心在MN 上，所以四棱锥A －DECB 的外接球的球心就是等腰梯形DECB 的外接圆的圆心．连接BE ，易知△BEC 是钝角三角形，所以等腰梯形DECB 的外接圆的圆心在等腰梯形DECB 的外部．设四棱锥A －DECB 的外接球的半径为R ，球心到BC 的距离为d 2＝d 2＋(2)2，2＝(d ＋222＋(22)2，解得R 2＝52，故四棱锥A －DECB 的外接球的表面积S ＝4πR 2＝10π．模型六斗笠模型【方法总结】圆锥、顶点在底面的射影是底面外心的棱锥．秒杀公式：R ＝h 2＋r 22h(其中h 为几何体的高，r 为几何体的底面半径或底面外接圆的圆心)【例题选讲】[例](1)一个圆锥恰有三条母线两两夹角为60︒，若该圆锥的侧面积为，则该圆锥外接球的表面积为________．答案272π解析设60ASB BSC CSA ∠=∠=∠=︒，则SA SB SC AB AC BC =====．设AB x =，则底面圆的直径为2sin 60x r ==︒，该圆锥的侧面积为12x π=，解得3x =，高OS =．r ∴=．设圆锥外接球的半径为R ，所以222)R r R -+=，解得R =，则外接球的表面积为22742R ππ=．(2)(2020·全国Ⅰ)已知A ，B ，C 为球O 的球面上的三个点，⊙O 1为△ABC 的外接圆．若⊙O 1的面积为4π，AB ＝BC ＝AC ＝OO 1，则球O 的表面积为()A ．64πB ．48πC ．36πD ．32π答案A解析设⊙O 1的半径为r ，球的半径为R ，依题意，得πr 2＝4π，∴r ＝2．由正弦定理可得ABsin 60°＝2r ，∴AB ＝2r sin 60°＝23．∴OO 1＝AB ＝23．根据球的截面性质，得OO 1⊥平面ABC ，∴OO 1⊥O 1A ，R ＝OA ＝OO 21＋O 1A 2＝OO 21＋r2＝4，∴球O 的表面积S ＝4πR 2＝64π．故选A ．(3)在三棱锥P ABC -中，PA PB =26, 4PC AC AB ====，且AC AB ⊥，则该三棱锥外接球的表面积为________．答案36π解析设顶点P 在底面中的射影为1O ，由于PA PB PC ==，所以111O A O B O C ==，即点1O 是底面ABC ∆的外心，又AC AB ⊥，所以1O 为BC 的中点，因为PA PB = 4PC AC AB ====，所以11 4BC AO PO ===，设外接球的球心为O ，半径为R ，则O 必在1PO 上，=-14O O R ，在∆1Rt O OA中，()(2224R R -+=，解得3R =，所以22436S R ππ==．(4)正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为()A ．81π4B ．16πC ．9πD ．27π4答案A解析如图所示，设球半径为R ，底面中心为O ′且球心为O ，∵正四棱锥P ­ABCD 中AB ＝2，∴AO ′＝2，∵PO ′＝4，∴在Rt △AOO ′中，AO 2＝AO ′2＋OO ′2，∴R 2＝(2)2＋(4－R )2，解得R ＝94，∴该球的表面积为4πR 2＝4π×942＝81π4.(5)如图所示，在正四棱锥P －ABCD 中，底面ABCD 是边长为4的正方形，E ，F 分别是AB ，CD 的中点，cos ∠PEF ＝22，若A ，B ，C ，D ，P 在同一球面上，则此球的体积为________．答案36π解析由题意，得底面ABCD 是边长为4的正方形，cos ∠PEF ＝22，故高PO 1为2．易知正四棱锥P －ABCD 的外接球的球心在它的高PO 1上，记球心为O ，则AO 1＝22，PO ＝AO ＝R ，PO 1＝2，OO 1＝2－R 或OO 1＝R －2(此时O 在PO 1的延长线上)，在直角△AO 1O 中，R 2＝AO 21＋OO 21＝(22)2＋(2－R )2，解得R ＝3，所以球的体积为V ＝43πR 3＝4π3×33＝36π．(6)在三棱锥P ABC -中，2PA PB PC ===，1AB AC ==，3BC =棱锥外接球的体积为()A ．43πB ．823πC ．3πD ．323π答案A解析由PA PB PC ===P 作PG ⊥平面ABC ，垂足为G ，则G 为三角形ABC 的外心，在ABC ∆中，由1AB AC ==，BC =，可得120BAC ∠=︒，则由正弦定理可得：2AG =，即1AG =．1PG ∴==．取PA 中点H ，作HO PA ⊥交PG 于O ，则O 为该三棱锥外接球的球心．由PHO PGA ∆∆∽，可得PH PG PO PA =，则211PH PA PO PG === ．可知O 与G 重合，即该棱锥外接球半径为1．∴该三棱锥外接球的体积为43π．模型七已知球心或球半径模型【例题选讲】[例](1)(2017·全国Ⅰ)已知三棱锥S －ABC 的所有顶点都在球O 的球面上，SC 是球O 的直径．若平面SCA ⊥平面SCB ，SA ＝AC ，SB ＝BC ，三棱锥S －ABC 的体积为9，则球O 的表面积为________．答案36π解析如图，连接AO ，OB ，∵SC 为球O 的直径，∴点O 为SC 的中点，∵SA ＝AC ，SB ＝BC ，∴AO ⊥SC ，BO ⊥SC ，∵平面SCA ⊥平面SCB ，平面SCA ∩平面SCB ＝SC ，∴AO ⊥平面SCB ，设球O 的半径为R ，则OA ＝OB ＝R ，SC ＝2R ．∴V S ­ABC ＝V A ­SBC ＝13×S △SBC ×AO ＝13×SC ×AO ，即9＝13×R ×R ，解得R ＝3，∴球O 的表面积为S ＝4πR 2＝4π×32＝36π．(2)已知三棱锥A －BCD 的所有顶点都在球O 的球面上，AB 为球O 的直径，若该三棱锥的体积为3，BC ＝3，BD ＝3，∠CBD ＝90˚，则球O 的体积为________．答案32π3解析设A 到平面BCD 的距离为h ，∵三棱锥的体积为3，BC ＝3，BD ＝3，∠CBD ＝90˚，∴13×12×3×3×h ＝3，∴h ＝2，∴球心O 到平面BCD 的距离为1．设CD 的中点为E ，连接OE ，则由球的截面性质可得OE ⊥平面CBD ，∵△BCD 外接圆的直径CD ＝23，∴球O 的半径OD ＝2，∴球O 的体积为32π3．(3)(2012全国Ⅰ)已知三棱锥S －ABC 的所有顶点都在球O 的球面上，△ABC 是边长为1的正三角形，SC 为球O 的直径，且SC ＝2，则此棱锥的体积为()A ．26B ．36C ．23D ．22答案A解析由于三棱锥S －ABC 与三棱锥O －ABC 底面都是△ABC ，O 是SC 的中点，因此三棱锥S －ABC 的高是三棱锥O －ABC 高的2倍，所以三棱锥S －ABC 的体积也是三棱锥O －ABC 体积的2倍．在三棱锥O －ABC 中，其棱长都是1，如图所示，S △ABC ＝34×AB 2＝34，高OD ＝12－332＝63，∴V S －ABC ＝2V O －ABC ＝2×13×34×63＝26．故选A ．(4)(2020·新高考全国Ⅰ)已知直四棱柱ABCD －A 1B 1C 1D 1的棱长均为2，∠BAD ＝60°．以D 1为球心，5为半径的球面与侧面BCC 1B 1的交线长为________．答案2π2解析如图，设B 1C1的中点为E ，球面与棱BB 1，CC 1的交点分别为P ，Q ，连接DB ，D 1B 1，D 1P ，D 1E ，EP ，EQ ，由∠BAD ＝60°，AB ＝AD ，知△ABD 为等边三角形，∴D 1B 1＝DB ＝2，∴△D 1B 1C 1为等边三角形，则D 1E ＝3且D 1E ⊥平面BCC 1B 1，∴E 为球面截侧面BCC 1B 1所得截面圆的圆心，设截面圆的半径为r ，则r ＝R 2球－D 1E 2＝5－3＝2．又由题意可得EP ＝EQ ＝2，∴球面与侧面BCC 1B 1的交线为以E 为圆心的圆弧PQ ．又D 1P ＝5，∴B 1P ＝D 1P 2－D 1B 21＝1，同理C 1Q ＝1，∴P ，Q 分别为BB 1，CC 1的中点，∴∠PEQ ＝π2，知 PQ的长为π2×2＝2π2，即交线长为2π2．(5)三棱锥S －ABC 的底面各棱长均为3，其外接球半径为2，则三棱锥S －ABC 的体积最大时，点S 到平面ABC 的距离为()A ．2＋3B ．2－3C ．3D ．2答案C 解析如图，设三棱锥S －ABC 底面三角形ABC 的外心为G ，三棱锥外接球的球心为O ，要使三棱锥S －ABC 的体积最大，则O 在SG 上，由底面三角形的边长为3，可得AG ＝32sin60°＝3．连接OA ，在Rt △OGA 中，由勾股定理求得OG ＝OA 2－GA 2＝22－（3）2＝1．∴点S 到平面ABC 的距离为OS ＋OG ＝2＋1＝3．故选C ．模型八最值模型【方法总结】最值问题的解法有两种方法：一种是几何法，即在运动变化过程中得到最值，从而转化为定值问题求解．另一种是代数方法，即建立目标函数，从而求目标函数的最值．【例题选讲】[例](1)已知三棱锥P －ABC 的顶点P ，A ，B ，C 在球O 的球面上，△ABC 是边长为3的等边三角形，如果球O 的表面积为36π，那么P 到平面ABC 距离的最大值为________．答案3＋22解析依题意，边长是3的等边△ABC 的外接圆半径r ＝12·3sin 60°＝1.∵球O 的表面积为36π＝4πR 2，∴球O 的半径R ＝3，∴球心O 到平面ABC 的距离d ＝R 2－r 2＝22，∴球面上的点P 到平面ABC 距离的最大值为R ＋d ＝3＋22．(2)在四面体ABCD 中，AB ＝1，BC ＝CD ＝3，AC ＝2，当四面体ABCD 的体积最大时，其外接球的表面积为()A ．2πB ．3πC ．6πD ．8π答案C 解析∵AB ＝1，BC ＝3，AC ＝2，由勾股定理可得AB 2＋AC 2＝BC 2，所以△ABC 是以BC 为斜边的直角三角形，且该三角形的外接圆直径为BC ＝3，当CD ⊥平面ABC 时，四面体ABCD 的体积取最大值，此时，其外接球的直径为2R ＝BC 2＋CD 2＝6，因此，四面体ABCD 的外接球的表面积为4πR 2＝π×(2R )2＝6π．故选C ．(3)已知四棱锥S －ABCD 的所有顶点在同一球面上，底面ABCD 是正方形且球心O 在此平面内，当四棱锥的体积取得最大值时，其表面积等于16＋163，则球O 的体积等于()A ．42π3B ．162π3C ．322π3D ．642π3答案D解析由题意得，当四棱锥的体积取得最大值时，该四棱锥为正四棱锥．因为该四棱锥的表面积等于16＋163，设球O 的半径为R ，则AC ＝2R ，SO ＝R ，如图，所以该四棱锥的底面边长AB ＝2R ，则有(2R )2＋4×12×2R ×16＋163，解得R ＝22，所以球O 的体积是43πR 3＝6423π．故选D ．(4)三棱锥A －BCD 内接于半径为5的球O 中，AB ＝CD ＝4，则三棱锥A －BCD 的体积的最大值为()A ．43B ．83C ．163D ．323答案C解析如图，过CD 作平面ECD ，使AB ⊥平面ECD ，交AB 于点E ，设点E 到CD 的距离为EF ，当球心在EF 上时，EF 最大，此时E ，F 分别为AB ，CD 的中点，且球心O 为EF 的中点，所以EF ＝2，所以V max ＝13×12×4×2×4＝163，故选C ．(5)已知正四棱柱的顶点在同一个球面上，且球的表面积为12π，当正四棱柱的体积最大时，正四棱柱的高为_．答案8解析设正四棱柱的底面边长为a ，高为h ，球的半径为r ，由题意知4πr 2＝12π，所以r 2＝3，又2a 2＋h 2＝(2r )2＝12，所以a 2＝6－h 22，所以正四棱柱的体积V ＝a 2h ，则V ′＝6－32h 2，由V ′>0，得0<h <2，由V ′<0，得h >2，所以当h ＝2时，正四棱柱的体积最大，V max ＝8．模型九内切球模型【方法总结】以三棱锥P －ABC 为例，求其内切球的半径．方法：等体积法，三棱锥P －ABC 体积等于内切球球心与四个面构成的四个三棱锥的体积之和；第一步：先求出四个表面的面积和整个锥体体积；第二步：设内切球的半径为r ，球心为O ，建立等式：V P －ABC ＝V O －ABC ＋V O －P AB ＋V O －P AC ＋V O －PBC ⇒V P －ABC ＝13S △ABC ·r ＋13S △P AB ·r ＋13S △P AC ·r ＋13S △r ＝13S △ABC ＋S △P AB ＋S △P AC ＋S △PBC )·r ；第三步：解出r ＝3V P －ABC S O －ABC ＋S O －P AB ＋S O －P AC ＋S O －PBC ＝3VS 表．秒杀公式(万能公式)：r ＝3VS 表【例题选讲】[例](1)已知一个三棱锥的所有棱长均为2，则该三棱锥的内切球的体积为________．答案354π解析由题意可知，该三棱锥为正四面体，如图所示．AE ＝AB ·sin 60°＝62，AO ＝23AE ＝63，DO ＝AD 2－AO 2＝233，三棱锥的体积V D ­ABC ＝13S △ABC ·DO ＝13，设内切球的半径为r ，则V D ­ABC ＝13r (S △ABC ＋S △ABD ＋S △BCD ＋S △ACD )＝13，r ＝36，V 内切球＝43πr 3＝354π．(2)(2020·全国Ⅲ)已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为________．答案23π解析圆锥内半径最大的球即为圆锥的内切球，设其半径为r ．作出圆锥的轴截面PAB ，如图所示，则△PAB 的内切圆为圆锥的内切球的大圆．在△PAB 中，PA ＝PB ＝3，D 为AB 的中点，AB ＝2，E 为切点，则PD ＝22，△PEO ∽△PDB ，故PO PB ＝OEDB ，即22－r 3＝r 1，解得r ＝22，故内切球的体积为43π223＝23π．(3)阿基米德(公元前287年～公元前212年)是古希腊伟大的哲学家、数学家和物理学家，他和高斯、牛顿并列被称为世界三大数学家．据说，他自己觉得最为满意的一个数学发现就是“圆柱内切球体的体积是圆柱体积的三分之二，并且球的表面积也是圆柱表面积的三分之二”．他特别喜欢这个结论．要求后人在他的墓碑上刻着一个圆柱容器里放了一个球，如图，该球顶天立地，四周碰边．若表面积为54π的圆柱的底面直径与高都等于球的直径，则该球的体积为()A ．4πB ．16πC ．36πD ．64π3答案C解析设该圆柱的底面半径为R ，则圆柱的高为2R ，则圆柱的表面积S ＝S 底＋S 侧＝2×πR 2＋2·π·R ·2R ＝54π，解得R 2＝9，即R ＝3．∴圆柱的体积为V ＝πR 2×2R ＝54π，∴该圆柱的内切球的体积为23×54π＝36π．故选C ．(4)已知三棱锥P －ABC 的三条侧棱PA ，PB ，PC 两两互相垂直，且PA ＝PB ＝PC ＝2，则三棱锥P －ABC 的外接球与内切球的半径比为________．答案33＋32解析以PA ，PB ，PC 为过同一顶点的三条棱，作长方体，由PA ＝PB ＝PC ＝2，可知此长方体即为正方体．设外接球的半径为R ，则R ＝4＋4＋42＝3，设内切球的半径为r ，则内切球的球心到四个面的距离均为r ，由13(S △ACP ＋S △APB＋S △PCB ＋S △ABC )·r ＝13·S △PCB ·AP ，解得r ＝23＋3，所以Rr ＝323＋3＝33＋32．(5)正四面体的外接球和内切球上各有一个动点P 、Q ，若线段PQ ，则这个四面体的棱长为________．答案4解析设这个四面体的棱长为a ，则它的外接球与内切球的球心重合，且半径R =外，r =内，依题意得4123a a +=，4a ∴=．。