参数估计教程

ˆ (a , , a ), j j 1 k
其中
1 n j a j xi n i1
j 1, , k ,
25 November 2018
华东师范大学
第六章 参数估计
第7页
例6.1.2 设总体服从指数分布，由于EX=1/， 即 =1/ EX，故 的矩法估计为
ˆ 1/ x
华东师范大学
第六章 参数估计
第8页
例 6.1.3 x1, x2, …, xn 是来自 (a,b) 上的均匀分布 U(a,b) 的样本， a 与 b 均是未知参数，这里 k=2 ， 由于
ab EX , 2 (b a ) 2 Var( X ) , 12
不难推出
a EX 3Var( X ), b EX 3Var( X ),
L( ) ( ) [2 (1 )] [(1 ) ]
2 n1 n2 2 n3
2
n2
2 n1 n 2
(1 )
2 n3 n2
其对数似然函数为
ln L( ) (2n1 n2 ) ln (2n3 n2 ) ln(1 ) n2 ln 2
1 n n n 2 2 ln L( , ) 2 ( xi ) ln ln(2) 2 i 1 2 2
2
25 November 2018
华东师范大学
第六章 参数估计
第14页
将 lnL(, 2) 分别关于两个分量求偏导并令 其为0, 即得到似然方程组
ln L( , 2 ) 1 n 2 ( xi ) 0 i 1 ln L( , 2 ) 1 n n 2 4 ( xi ) 2 0 2 2 i 1 2

参数估计步骤
参数估计是统计学中的一个关键任务，用于从收集到的数据中推断未知的参数值。

以下是一般的参数估计步骤：
1.明确问题和目标：
确定需要估计的参数是什么。

明确估计的目标，例如点估计还是区间估计。

2.选择合适的概率分布：
基于问题的性质和数据的特征，选择一个合适的概率分布，如正态分布、泊松分布等。

3.建立统计模型：
建立描述数据生成过程的统计模型，包括参数和概率分布。

4.收集数据：
收集与问题相关的数据样本。

5.选择估计方法：
选择合适的估计方法，如最大似然估计、最小二乘法、贝叶斯估计等，取决于问题和模型。

6.构建估计统计量：
基于所选的估计方法，构建相应的估计统计量。

7.计算估计值：
使用收集到的数据计算估计统计量的具体值。

8.评估估计的性能：
评估估计的精确性和效果，考虑估计的方差、置信区间等。

9.进行假设检验（可选）：
如果需要，进行假设检验以验证估计的显著性。

10.解释和报告结果：
将估计结果进行解释，并报告估计的点值或区间。

11.敏感性分析：
进行敏感性分析，考虑不同假设和参数值对估计的影响。

12.持续监测和更新：
定期监测估计的性能，如果有新数据可用，可以更新估计。

这些步骤的具体实施取决于问题的性质、数据的特点以及所选择的统计方法。

在实际应用中，研究人员需要根据具体情况灵活运用这些步骤。

从一批灌装产品中，随机抽取20灌，得样本方差为0.0025。试以95%的置 信度，估计总体方差的存在区间。
n 1 s2 2 n 1 s2
2 2
2 1 2
n 1 s2
2 0.025
2
n 1 s2
2 0.975
19 0.0025 2 19 0.0025
32.8523
8.90655
自正态总体抽样时，总体均值与总体中位数相同，而中位数的 标准误差大约比均值的标准误差大25%。因此，样本均值更有效。
x 的抽样分布
M e的抽样分布
____
X
有效性
一致性
如果 lim
P
1(为任意小数，n
为样本容量）
n
则称 为的满足一致性标准的点估计量
ˆ1的抽样分布 ˆ2的抽样分布
x s 2 p 均为一致性估计量
X～N， 2
x__
～
N
， 2 n
__
Z x ～N 0,1
n
P Z
Z Z
1
2
2
P Z
2
__
x n
Z
1
2
显著性水平
22
2
Z 2
置信度
1
0
P_x_ Z
2
n
__
x Z 2
1
n
2
Z 2
显著性水平α下，μ在1- α置信水平下的置信区间：
__
x
Z
2
__
n , x Z 2
f x
x
n
x 2
f x
1
e 2 2 x
2
x
抽样分布
E(x)

参数估计的一般步骤引言：参数估计是统计学中一项重要的任务，它用于根据样本数据来推断总体参数的值。

参数估计的一般步骤包括确定估计方法、选择样本、计算估计值和进行推断。

本文将详细介绍参数估计的一般步骤，并以人类的视角进行描述，使读者更好地理解和应用这些步骤。

一、确定估计方法在参数估计中，首先需要确定合适的估计方法。

估计方法可以分为点估计和区间估计两种。

点估计方法通过单个数值来估计参数的值，例如最大似然估计和矩估计。

区间估计方法则通过一个区间来估计参数的范围，例如置信区间估计。

选择合适的估计方法是参数估计的第一步。

二、选择样本在确定了估计方法后，接下来需要选择合适的样本进行参数估计。

样本应当具有代表性，能够反映总体的特征。

为了保证样本的代表性，可以使用随机抽样方法来选择样本。

通过合理选择样本，可以减小估计误差，提高参数估计的准确性。

三、计算估计值在选择好样本后，需要计算参数的估计值。

对于点估计方法，可以使用最大似然估计或矩估计等方法来计算参数的估计值。

对于区间估计方法，可以使用置信区间估计来计算参数的范围。

计算估计值时，需要根据样本数据和估计方法进行相应的计算，确保估计结果的准确性。

四、进行推断在计算得到估计值后，需要进行推断，即根据估计值对总体参数进行推断。

对于点估计方法，可以直接使用估计值作为总体参数的估计值。

对于区间估计方法，可以使用置信区间来表示总体参数的范围。

通过推断可以了解总体参数的可能取值范围，帮助做出正确的决策和预测。

总结：参数估计的一般步骤包括确定估计方法、选择样本、计算估计值和进行推断。

在进行参数估计时，需要选择合适的估计方法和样本，计算出估计值，并进行相应的推断。

参数估计在统计学中扮演着重要的角色，它帮助我们根据样本数据来推断总体参数的值，从而更好地了解和应用统计学。

通过本文的介绍，希望读者能够更好地理解和应用参数估计的一般步骤。

《参数估计方法》ppt 课件
目录
• 参数估计方法概述 • 点估计 • 区间估计 • 最大似然估计法 • 最小二乘估计法 • 贝叶斯估计法
01
参数估计方法概述
参数估计方法的定义
参数估计方法的定
义
参数估计方法是一种统计学中的 方法，它通过分析样本数据来估 计未知的参数值。这些参数可以 描述总体特性的程度，如平均值 、方差等。
使得它容易进行统计推断。
最小二乘估计法的应用场景
线性回归分析
最小二乘估计法是线性回归分析中最常用的 参数估计方法，用于预测一个因变量与一个 或多个自变量之间的关系。
时间序列分析
在时间序列分析中，最小二乘估计法可用于拟合和 预测时间序列数据，例如ARIMA模型。
质量控制
在质量控制中，最小二乘估计法可用于拟合 控制图，以监测过程的稳定性和预测异常情 况。
区间估计
区间估计是一种更精确的参数估计方法，它给出未知参数的一个置信区间，即有较大的把握认为未知参数落在这个区 间内。例如，用样本均值和标准差来估计总体均值的置信区间。
贝叶斯估计
贝叶斯估计是一种基于贝叶斯定理的参数估计方法，它根据先验信息和样本数据来推断未知参数的后验 概率分布。贝叶斯估计能够综合考虑先验信息和样本数据，给出更加准确的参数估计结果。
贝叶斯估计法的性质
01
02
03
贝叶斯估计法是一种主观概率估 计方法，因为它依赖于先验信息 的可信度和准确性。
先验信息的不确定性可以通过引 入一个先验分布来表达，该分布 描述了先验信息中未知参数的可 能取值及其概率。
贝叶斯估计法的后验概率分布可 以用于推断未知参数的估计值和 不确定性程度。
贝叶斯估计法的应用场景
3

[muratio,sgmratio]=fugailv(0,1,1000,200,0.05) [muratio,sgmratio]=fugailv(10,2,2000,500,0.01) [muratio,sgmratio]=fugailv(4,6,5000,400,0.025)
2、其它分布的参数估计
要依据该g( ).
参数估计

点估计 区间估计
点估计 —— 估计未知参数的值。 区间估计—— 根据样本构造出适当的区间， 使它以一定的概率包含未知参数或未知参 数的已知函数的真值。
（一）点估计的求法 1、矩估计法 基本思想是用样本矩估计总体矩 .
(1). 取容量充分大的样本（n>50），按中心极限定理， 它近似地服从正态分布； (2).使用Matlab工具箱中具有特定分布总体的估计命令. 10[muhat, muci] = expfit(X,alpha)----- 在显著性水平 alpha下，求指数分布的数据X的均值的点估计及其区间 估计. 20 [lambdahat, lambdaci] = poissfit(X,alpha)----- 在显 著性水平alpha下，求泊松分布的数据X 的参数的点估 计及其区间估计. 30[phat, pci] = weibfit(X,alpha)----- 在显著性水平alpha 下，求Weibull分布的数据X 的参数的点估计及其区间 估计.
的无约束最优化问题。
方法： ①最速下降法 ②Newton(牛顿）法及其修正的方法。 ③共轭方向法和共轭梯度法 ④变尺度法（拟牛顿法） 等等 详见北京大学出版社 高惠璇编著《统计计算》 P359------P379
二、假设检验
统计推断的另一类重要问题是假设检验问题。 在总体的分布函数完全未知或只知其形式，但 不知其参数的情况，为了推断总体的某些未知 特性，提出某些关于总体的假设。 对总体X的分布律或分布参数作某种假设，根据 抽取的样本观察值，运用数理统计的分析方法， 检验这种假设是否正确，从而决定接受假设或拒 绝假设.

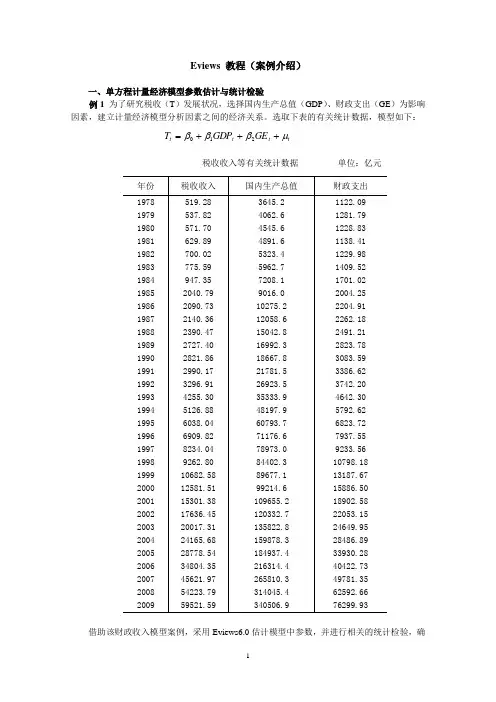
Eviews 教程（案例介绍）一、单方程计量经济模型参数估计与统计检验例1 为了研究税收（T ）发展状况，选择国内生产总值（GDP ）、财政支出（GE ）为影响因素，建立计量经济模型分析因素之间的经济关系。

选取下表的有关统计数据，模型如下：t t t t GE GDP T μβββ+++=210税收收入等有关统计数据 单位：亿元借助该财政收入模型案例，采用Eviews6.0估计模型中参数，并进行相关的统计检验，确定最终模型。

Eviews软件模型分析过程如下：1.创建工作文件启动Eviews软件，在主菜单上依次单击File→New→Workfile，选择数据类型（时间序列或非时间序列），并输入样本区间和工作文件名，创建工作文件的子窗口如图1-1所示。

图1-1 创建工作文件2.建立变量组Eviews软件建立变量组可采用三种途径：（1）在主菜单上依次单击Quick→Empty Group，在数据编辑窗口中单击Edit+/-，并按上行健↑，这样可依次输入变量名；（2）在主菜单上依次单击Objects→New Objects，在对话框中选择“Group”并定义文件名，在数据编辑窗口中首先按上行健↑，这样可依次输入变量名；（3）在主菜单上Eviews命令框中直接输入命令：Data T GDP GT CPI（命令及变量名之间用空格分隔），将直接出现已定义变量名称的数据编辑窗口。

图1-2 数据编辑窗口3.输入经济变量的样本数据在图1-2所示的数据编辑窗口中，在“NA”的位置可输入各经济变量的样本数据，输入样本数据后及时予以保存。

样本数据也可以从有关Office软件的各类表格中进行数据的复制；也可以通过Eviews 软件本身生产新的变量数据序列，如在主菜单上依次单击Quick→Generate Series、或者在工作文件（Workfile）窗口中单击Generate，在弹出窗口中输入方程式，如图1-3所示。

图1-3 生产新变量数据序列4.估计模型参数在主菜单上依次单击Quick→Estimate Equation，弹出对话框，在“Specification”选项卡中输入模型中被解释变量、常数项、解释变量序列，并选择估计方法及样本区间，如图1-4所示，估计结果如图1-5。

§5.3 区间估计
• 1. 样本中的支持率为 90% ， 即用样本 样本中的支持率为90 90% 比例作为对总体比例的点估计 • 2. 估计范围为 90%±3%(±3% 的误差 ) ， 估计范围为90 90% 的误差) 即区间(93% 87% 即区间(93%，87%)。 • 3. 如用类似的方式 ， 重复抽取大量 如用类似的方式， 样本量相同的）样本时， （样本量相同的）样本时，产生的大 量类似区间中有些会覆盖真正的 p ， 而有些不会； 但其中大约有95 95% 而有些不会 ； 但其中大约有 95% 会覆 盖真正的总体比例。 盖真正的总体比例。
§5.3 区间估计
• 这样得到的区间被称为总体比例 的 这样得到的区间被称为总体比例p的 置信度(confidence level)为 95%的 置信度 为 的 置信区间(confidence interval)。这 置信区间 。 置信水平或 里的置信度又称置信水平 里的置信度又称 置信水平 或 置信系 数。 • 显然置信度的概念又是大量重复抽 样时的一个渐近概念。 样时的一个渐近概念。
• 如果我们想知道桂林人认可某饮料 的比例， 的比例，人们只有在桂林人中进行 抽样调查以得到样本， 抽样调查以得到样本，并用样本中 认可该饮料的比例来估计真实的比 例。 • 从不同的样本得到的结论也不会完 全一样。 全一样。虽然真实的比例在这种抽 样过程中永远也不知道； 样过程中永远也不知道；但可以知 道估计出来的比例和真实的比例大 致差多少。 致差多少。
描描描统
449.0104 447.4124 450.6084 448.9500 30.287 5.50339 439.60 461.10 21.50 8.18
§5.2 点估计
• 那么，什么是好估计量的标准呢？ 那么，什么是好估计量的标准呢？ • 一种统计量称为无偏估计量 estimator)。 (unbiased estimator)。 • 所谓的 无偏性 (unbiasedness) 就是 ： 所谓的无偏性 (unbiasedness)就是 无偏性(unbiasedness) 就是： 虽然每个样本产生的估计量的取值 不一定等于参数， 不一定等于参数 ， 但当抽取大量样 本时， 本时 ， 那些样本产生的估计量的均 值会接近真正要估计的参数。 值会接近真正要估计的参数。

参数估计的一般步骤
参数估计是统计学中的一种方法，用于根据样本数据估计总体参数的值。

它是一个重要的统计推断技术，可以帮助我们了解和描述总体的特征。

参数估计的一般步骤如下：
1. 确定研究对象和目标参数：首先，我们需要明确研究对象是什么，需要估计的是哪个参数。

例如，我们可能希望估计某个产品的平均寿命，那么研究对象是产品，目标参数是平均寿命。

2. 收集样本数据：为了进行参数估计，我们需要收集一定数量的样本数据。

样本应该能够代表总体，并且必须是随机选择的，以避免抽样偏差。

3. 选择合适的估计方法：根据研究对象和目标参数的不同，我们可以选择不同的估计方法。

常见的估计方法包括点估计和区间估计。

点估计给出一个单一的数值作为参数的估计值，而区间估计给出一个范围，以表明参数估计值的不确定性。

4. 计算估计值：根据选择的估计方法，我们可以使用样本数据计算出参数的估计值。

例如，对于平均寿命的估计，我们可以计算样本的平均值作为总体平均寿命的估计值。

5. 评估估计的准确性：估计值的准确性可以通过计算估计的标准误
差或置信区间来评估。

标准误差反映了估计值与真实参数值之间的差异，而置信区间提供了参数估计值的不确定性范围。

6. 解释和应用估计结果：最后，我们需要解释估计结果并应用于实际问题中。

根据估计结果，我们可以得出结论，做出决策或提出建议。

参数估计是一种重要的统计推断方法，可以帮助我们了解总体特征并做出准确的推断。

通过正确的步骤和方法，我们可以获得可靠的参数估计结果，并将其应用于实际问题中。

目录参数估计 ________________________________________________________________________________ 3第一节抽样推断的基本概念与原理 ________________________________________________________ 3一、抽样推断的特点和作用 _____________________________________________________________ 3二、重复抽样与不重复抽样 _____________________________________________________________ 4三、抽样误差与抽样平均误差 ___________________________________________________________ 4四、抽样推断的理论基础 _______________________________________________________________ 6五、参数估计的基本步骤 _______________________________________________________________ 7第二节参数估计中的点估计 ______________________________________________________________ 7一、总体参数的点估计 _________________________________________________________________ 7二、点估计量的优良标准 _______________________________________________________________ 7第三节参数估计中的区间估计 ____________________________________________________________ 8一、参数估计的精度与抽样平均误差计算 _________________________________________________ 8二、参数估计的误差范围与概率度 _______________________________________________________11三、总体参数的区间估计 ______________________________________________________________ 12第四节抽样组织方式及其参数估计 _______________________________________________________ 13一、简单随机抽样 ____________________________________________________________________ 13二、分层抽样 ________________________________________________________________________ 14三、机械抽样 ________________________________________________________________________ 16四、整群抽样 ________________________________________________________________________ 16第五节必要样本容量的确定 _____________________________________________________________ 17一、平均数的必要样本容量 ____________________________________________________________ 17二、成数的必要样本容量 ______________________________________________________________ 18三、影响必要样本容量的因素 __________________________________________________________ 19 习题 ___________________________________________________________________ 错误!未定义书签。

1

例5. 设X服从[0,λ]区间上的均匀分布,参数
λ>0,求λ的最大似然估计. 1 解:由题意得: X ~ f ( x; )
1 L( x1 , x 2 ,..., x n ; ) n 0
0 x
0 其它 0 x1 , x 2 ,..., x n
dL n n1 0 d
其它
无解.
应用最大似然估计基本思想: L越大,样本观察值越可能出现 取 max( x1 , x 2 ,..., x n ) 此时,L取值最大, 所以,所求最大似然估计为 max( x1 , x 2 ,..., x n )
考虑L的取值,要使L取值最大,λ应最小, 0 x1 , x 2 ,..., x n


例2 设总体 X ~ N ( , 2 ) ,其中 及 2 都是未知参数，如
果取得样本观测值为 x1 ,, x n , 求 及 2 的矩估计值。
解： 因为总体X的分布中有两个未知参数，所以应考虑一、二阶 原点矩，我们有 v1 ( X ) E ( X )
v 2 ( X ) E( X 2 ) D( X ) [ E( X )]2 2 2
e

e
1 2
2
2
( x )2 2 2
e
L( x1 , x 2 ,..., x n ; , )
2
i 1
1 2
2
( xi )2
(
2
1 2
2

1 2 2
) e
n

i 1
n
( xi )2

1 n 2 n 1 n 2 2 ) 2 ( x i ) ln 2 ln L n ln( ( xi ) 2 i 1 2 2 2 n 2 2 i 1 1 ln L 1 n Xi X 2 ( xi ) 0 n i 1 i 1 1 n 2 1 n n ln L n 1 ( xi )2 ( xi X )2 2 2 4 ( x i ) 0 n i 1 n i 1 2 2 2 i 1

参数估计的一般步骤参数估计是统计学中的一种方法，用于根据样本数据估计总体参数的取值。

它在各个领域都有广泛的应用，例如经济学、医学、社会学等。

本文将介绍参数估计的一般步骤，帮助读者了解如何进行参数估计。

一、确定参数类型在进行参数估计之前，首先需要确定要估计的参数类型。

参数可以是总体均值、总体比例、总体方差等，根据具体问题来确定。

二、选择抽样方法接下来，需要选择合适的抽样方法来获取样本数据。

常用的抽样方法有简单随机抽样、系统抽样、分层抽样等。

选择合适的抽样方法可以保证样本的代表性，从而提高参数估计的准确性。

三、收集样本数据在进行参数估计之前，需要收集样本数据。

收集样本数据时要注意数据的准确性和完整性，避免数据采集过程中的偏差。

四、计算点估计量得到样本数据后，可以计算点估计量来估计总体参数的取值。

点估计量是根据样本数据计算得出的一个具体数值，用来估计总体参数的未知值。

常见的点估计量有样本均值、样本比例等。

五、构建置信区间除了点估计量，还可以构建置信区间来估计总体参数的取值范围。

置信区间是一个区间估计，表示总体参数的真值有一定的概率落在该区间内。

置信区间的计算方法与具体的参数类型有关，可以利用统计学中的分布理论或抽样分布来计算。

六、进行假设检验除了估计总体参数的取值，参数估计还可以用于假设检验。

假设检验是根据样本数据来判断总体参数是否符合某个特定的假设。

在假设检验中，需要先提出原假设和备择假设，然后计算检验统计量，最后根据统计显著性水平来判断是否拒绝原假设。

七、解释结果需要对参数估计的结果进行解释和说明。

解释结果时要清楚、简洁，避免使用过于专业的术语，以便读者能够理解和接受。

参数估计是统计学中重要的内容之一，它可以帮助我们从有限的样本数据中推断总体的特征。

通过合理选择抽样方法、收集准确的样本数据，并运用适当的统计方法，我们可以得到准确可靠的参数估计结果，为实际问题的决策提供科学依据。

注:由于 θ ( x1 ,L, xn ) 是实数域上的一个点,现用它来
估计 θ ,故称这种估计为点估计.
5 6
,σ 2未知,
… 随机抽查100个婴儿 得100个体重数据 10,7,6,6.5,5,5.2, …
而全部信息就由这100个数组成. 据此,我们应如何估计 和 σ 呢?
我们知道,服从正态分布N ( , σ 2 )的r.v. X , E ( X ) = , 由大数定律, 样本体重的平均值 1 → ∑ X i P n i =1 自然想到把样本体重的平均值作为总体平均 体重的一个估计. X= 用样本体重的均值 X估计 , 类似地,用样本体重的方差 S 2估计 σ 2 . 1 n 1 n 2 X = ∑ Xi, S = ∑ ( X i X )2 n 1 i =1 n i =1
(一)矩估计法
基本思想:用样本矩估计总体矩
(二)最大似然估计法
基本思想:
15
16
最大似然估计法 (最大似然法)
它首先是由德国数学家 高斯在1821年提出的 , 然而,这个方法常归功于 英国统计学家费希尔(Fisher) . 费希尔在1922年重新发现了 这一方法,并首先研究了这 种 方法的一些性质 . Fisher
1. 矩估计法 2. 最大似然法 3. 最小二乘法 4. 贝叶斯方法 ……
(一) 矩估计法(简称"矩法")
它是基于一种简单的"替换"思想 建立起来的一种估计方法 . 英国统计学家 K. 皮尔逊 最早提出的 . 基本思想: 用样本矩估计总体矩 . 理论依据: 大数定律
Ak = 1 n k P ∑ X i → k = E ( X k ) n i =1
4
在参数估计问题中,假定总体分布 形式已知,未知的仅仅是一个或几个 参数.

第6章　参数估计一、点估计的概念与无偏性1．设x 1，x 2，x 3是取自某总体的容量为3的样本，试证下列统计量都是该总体均值μ的无偏估计，在方差存在时指出哪一个估计的有效性最差？（1）1123111=236x x x μ∧++（2）2123111=333x x x μ∧++（3）3123112=663x x x μ∧++解：先求三个统计量的数学期望，1123111111()=()()()236222E E x E x E x μμμμμ∧++=++=2123111111()=()()()333333E E x E x E x μμμμμ∧++=++=3123112112()=()()()663663E E x E x E x μμμμμ∧++=++=这说明它们都是总体均值μ的无偏估计，下面求它们的方差，不妨设总体的方差为σ2，则222211231111117()=()()()4936493618Var Var x Var x Var x μσσσσ∧++=++=222221231111111()=()()()9999993Var Var x Var x Var x μσσσσ∧++=++=222231231141141()=()()()36369363692Var Var x Var x Var x μσσσσ∧++=++=不难看出，从而的有效性最差．123()<()<()Var Var Var μμμ∧∧∧3μ∧由此可推测。

当用样本的凸组合估计总体均值时，样本均值是最有效的。

1ni ii a x =∑x 2．x 1，x 2，…，x n 是来自Exp(λ)的样本，已知为1/λ的无偏估计，试说明1/是x x 否为λ的无偏估计．解：因为x 1，x 2，…，x n 服从Exp(λ)，所以y ＝~Ga （n ，λ），相应的密度函数1ni i x =∑为1()exp()y 0()n n p y n y y n λλλ-=->Γ，，，于是20(1/)e y ()n n y E y yn λλ∞--=Γ⎰d所以，．即不是λ的无偏估计，但它是λ的渐近无偏估计，经修偏，是λ的无偏估计．3．设是参数θ的无偏估计，且有，试证不是θ2的无偏估计．证：由方差的定义可知，由于是参数θ的无偏估计，即．因而所以不是θ2的无偏估计．4．设总体，是来自该总体的一个样本．试确定常数c 使为σ2的无偏估计．解：由于总体，这给出，于是若要使为σ2的无偏估计，即，这给出5．设总体为，为样本，证明样本均值和样本中程都是θ的无偏估计，并比较它们的有效性．解：由总体，得，，因而，这首先说明样本均值是θ的无偏估计，且为求样本中程的均值与方差，注意到，令则由于，故，从而这就证明了样本中程是θ的无偏估计．又注意到（参见第五章5.3节习题33）所以从而于是在n＞2时，，这说明作为0的无偏估计，在n＞2时，样本中程比样本均值有效．6．设x 1，x2，x3服从均匀分布，试证及都是θ的无偏估计量，哪个更有效？证：由可知x（1），x（3）的密度函数分别为从而故，由知两者均为θ的无偏估计．又可算得，从而故，即更有效．事实上，这里x（3）是充分统计量，这个结果与充分性原则是一致的．7．设从均值为μ，方差为的总体中，分别抽取容量为n1和n2的两独立样本，和分别是这两个样本的均值．试证，对于任意常数a，b（a＋b＝1），都是μ的无偏估计，并确定常数a，b使Var（Y）达到最小．证：由于和是容量分别为n1和n2的两独立样本的均值，故，，，因而这证明了是μ的无偏估计．又由a＋b＝1知，，从而由求导知，当时，Var（Y）达到最小，此时这个结果表明，来自同一总体的两个容量为n1和n2的样本的合样本（样本量为n1＋n2）的均值是线性无偏估计类中方差最小的．8．设总体X的均值为μ，方差为σ2，是来自该总体的一个样本，为μ的任一凸线性无偏估计量．证明：与T的相关系数为．证：由于为μ的线性无偏估计量，故，其中，于是而，故有，从而9．设有k台仪器，已知用第i台仪器测量时，测定值总体的标准差为σi（i＝1，2，…，k）．用这些仪器独立地对某一物理量θ各观察一次，分别得到设仪器都没有系统误差．问应取何值，方能使成为θ的无偏估计，且方差达到最小？解：若要使为θ的无偏估计，即则必须有，此时，。

参数估计的方法
1 参数估计的概念
参数估计（Parameter Estimation）是指基于样本观测数据，构
建统计模型，用来估计未观测总体参数得出最有效的模型解释参数结
果的过程。

参数估计是统计学里研究重要问题的一个根本步骤，它先
假设一个统计模型，然后求解模型的参数，从而最能满足观测数据的
条件。

2 参数估计的方法
1.参数最大似然估计（Maximum Likelihood Estimation）：最大
似然估计的基础是独立，同分布的随机变量的概率密度函数或概率分
布函数必须可知。

该方法下只需估计一个参数，则把样本数据的似然
函数定义为θ；如果需要估计多个参数，则把样本数据的似然函数定
义为$L(θ)=\prod\limits_i^nf(x_i;θ)$，其中f(x;θ)是关于未知
参数θ 的概率密度函数。

2.方差最小估计（Minimum Variance Estimation）：该方法的基
本思想是选择一种损失函数，把参数估计估计结果误差的.期望最小化，从而得出最优参数估计结果。

3.贝叶斯估计（Bayesian Estimation）：基于先验知识，建模到
后验知识的过程，利用样本信息改进模型参数和变量之间关系的方法。

3 参数估计的作用
参数估计是统计学里研究重要问题的一个根本步骤，它可以帮助我们识别变量之间的相互影响，从而更好的预测未来的发展趋势，决定合适的策略。

在企业战略决策，市场营销，生产服务运筹控制，经济营商模型分析决策管理，投资事前风险分析，社会环境分析等方面都有重要的作用。

参数估计的一般步骤
参数估计是通过从总体中抽取一个样本，利用样本数据对总体未知参数进行估计的过程。

参数估计的一般步骤如下：
1. 确定总体参数：首先需要明确要估计的总体参数，例如总体均值、总体比例、总体方差等。

2. 选择样本：从总体中抽取一个合适的样本。

样本的选择应该具有代表性，能够反映总体的特征。

3. 收集样本数据：对选择的样本进行观测或测量，收集样本数据。

4. 选择估计方法：根据所收集的样本数据和要估计的总体参数，选择合适的估计方法。

常见的估计方法包括点估计和区间估计。

5. 计算估计量：使用所选择的估计方法，根据样本数据计算出估计量。

估计量是用于估计总体参数的统计量。

6. 评估估计量的性质：评估所计算出的估计量的性质，如无偏性、有效性、一致性等。

这些性质可以帮助判断估计量的优劣。

7. 计算置信区间或置信水平：如果进行的是区间估计，根据估计量和置信水平，计算出总体参数的置信区间。

8. 解释估计结果：根据估计量或置信区间，对总体参数进行推断和解释。

同时，需要考虑估计结果的统计显著性和实际意义。

9. 分析误差和不确定性：考虑样本大小、抽样方法等因素对估计结果的影响，分析可能存在的误差和不确定性。

10. 结论和应用：根据参数估计的结果，得出结论并将其应用于实际问题中，例如进行决策、预测或进一步的研究。

需要注意的是，参数估计的具体步骤和方法会根据不同的统计问题和数据类型而有所差异。

在进行参数估计时，应根据实际情况选择合适的方法，并结合统计学原理和专业知识进行分析和解释。

2 a n u ,
2
2 b (2nX u ) ,
2
总体服从指数分布 未知参数 的置信水平为1 的置信区间是 1 1 1 1 ˆ ˆ ( 1 , 2 ) ( (1 u ) , (1 u ) ).
X n
2
c nX 2 .
X
n
2
概率论与数理统计教程（第四版）
[例2] 从一批电子元件中，抽取 50个样品，测得它们 设电子元件的使用寿命 的使用寿命的均值为1200小时， 服从指数分布e( ) , 求未知参数 的置信水平为 0.99 的置信区间.
解:由题设有 n 50 , x 1200. 已给置信水平1 0.99 ,
0.01 , 查附表得 u2 u0.005 t0.005 () 2.58. 由此得
目录
上一页
下一页
返回
结束
[例1]从一批产品中抽取 200个样品， 发现其中 9 个次品， 求这批产品的次品率 p 的置信水平为90%的置信区间. 解: 设随机变量 0 , 若取得正品； X 1 , 若取得次品. p ( x ; p ) p x (1 p )1 x , 概率函数为 则 X 服从 "0 1" 分布， x 0或1, 其中 p 是这批产品的次品率. 按题意， 样本容量 n 200 ,样本观测值 x1 , x2 ,, x200 中恰有 9 个 1 与 191个 0 , 所以 1 200 9 x xi 200 0.045. 200 i 1
则未知参数 p 的置信水平为1 的置信区间是
b b 2 4ac b b 2 4ac ( p1 , p2 ) ( ˆ ˆ , ). 2a 2a