电源设计中的小信号分析

开关电源的建模和环路补偿设计(1)：小信号建模的基本概念和方法(二)用电压模式控制闭合反馈环路输出电压可以由闭合的反馈环路系统调节。

例如，在图12 中，当输出电压VOUT 上升时，反馈电压VFB 上升，负反馈误差放大器的输出下降，因此占空比 d 下降。

结果，VOUT 被拉低，以使VFB = VREF。

误差运算放大器的补偿网络可以是I 型、II 型或III 型反馈放大器网络。

只有一个控制环路调节VOUT。

这种控制方法称为电压模式控制。

凌力尔特公司的LTC3861 和LTC3882 就是典型的电压模式降压型控制器。

图12：具闭合电压反馈环路的电压模式降压型转换器方框图为了优化电压模式PWM 转换器，如图13 所示，通常需要一种复杂的III 型补偿网络，以凭借充足的相位裕度设计一个快速环路。

如等式7 和图14 所示，这种补偿网络在频率域有 3 个极点和两个零点：低频积分极点(1/s) 提供高的DC 增益，以最大限度减小DC 调节误差，两个零点放置在系统谐振频率f0 附近，以补偿由功率级的L 和 C 引起的–180° 相位延迟，在fESR 处放置第一个高频极点，以消除COUT ESR 零点，第二个高频极点放置在想要的带宽fC 以外，以衰减反馈环路中的开关噪声。

III 型补偿相当复杂，因为这种补偿需要 6 个R/C 值。

找到这些值的最佳组合是个非常耗时的任务。

图13：用于电压模式转换器的III 型反馈补偿网络图14：III 型补偿A(s) 提供3 个极点和两个零点，以实现最佳的总体环路增益TV(s)为了简化和自动化开关模式电源设计，凌力尔特开发了LTpowerCAD 设计。

小信号放大电路图详解小 信号放大一直是电子设计竞赛经久不衰的题目，也是工程师们设计电路时经常遇到的问题。

作者历经小信号放大的血泪史，介绍了小信号放大中的集成芯片放大电 路、滤波器电路和分立元件放大器，有详细的电路图讲解哦！其中LC无源滤波器的软件设计、仿真以及硬件制作流程也合适很多其他电路设计。

第一部分：集成芯片放大器电路图讲解不知有多少童鞋知道TI公司的LHM6624。

这个芯片对于作者来说那是福星一枚。

其主要技术指标如下：Single/Dual Ultra Low Noise Wideband Operational Amplifier（单/双电源低噪声宽带小信号放大器）；其增益带宽积在单电源供电时可达1.5GHz，双电源供电时可达1.3GHz；供电电压双电源 （± 2.5V to ± 6V）单电源（+5V to +12V）；摆率（Slew rate） 350V/μs增益为10dB(AV = 10)时摆率400V/μs；输入噪声0.92nV/；输入失调电压典型值700uV 。

应用电路图如下：其中双电源供电±5V，C12，C13作用是电源滤波，即稳压；输入阻抗为50W；输出信号峰峰值可至8V（最好不要超过3V，因为大信号会出现非线性放 大）。

这是一个典型的同相放大器，放大倍数计算公式为AV=R14/R12，图中参数放大倍数20倍，即26dB。

值得注意的一点是电阻R16的作用：调 节零漂~如果对低频放大没什么特别需要的话，此处电阻R13，R16以及C11都可省略，但是如果想要放大直流信号的话，此处调节电路就十分有必要了。

模拟放大电路的电源滤波处理是十分有必要的，目的是防止高频模拟信号影响污染整个电源系统。

图中C12，C13在pcb中的位置要尽量靠近IC的电源入 口。

另外也可选择把磁珠（要求严格时可用电感，要求不高时可用100W电阻）和两个电容组成p形滤波电路， 这样可以把电源中的噪音滤得干干净净~2：滤波器滤波器分为有源滤波器和无源滤波器两种，区别在于有没有外接电源。

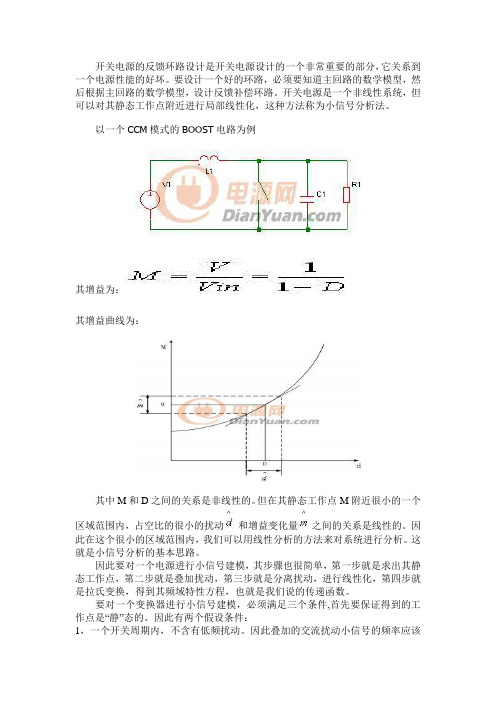
开关电源的反馈环路设计是开关电源设计的一个非常重要的部分，它关系到一个电源性能的好坏。

要设计一个好的环路，必须要知道主回路的数学模型，然后根据主回路的数学模型，设计反馈补偿环路。

开关电源是一个非线性系统，但可以对其静态工作点附近进行局部线性化，这种方法称为小信号分析法。

以一个CCM模式的BOOST电路为例其增益为：其增益曲线为：其中M和D之间的关系是非线性的。

但在其静态工作点M附近很小的一个区域范围内，占空比的很小的扰动和增益变化量之间的关系是线性的。

因此在这个很小的区域范围内，我们可以用线性分析的方法来对系统进行分析。

这就是小信号分析的基本思路。

因此要对一个电源进行小信号建模，其步骤也很简单，第一步就是求出其静态工作点，第二步就是叠加扰动，第三步就是分离扰动，进行线性化，第四步就是拉氏变换，得到其频域特性方程，也就是我们说的传递函数。

要对一个变换器进行小信号建模，必须满足三个条件,首先要保证得到的工作点是“静”态的。

因此有两个假设条件：1，一个开关周期内，不含有低频扰动。

因此叠加的交流扰动小信号的频率应该远远小于开关频率。

这个假设称为低频假设2，电路中的状态变量不含有高频开关纹波分量。

也就是系统的转折频率要远远小于开关频率。

这个假设称为小纹波假设。

其次为了保证这个扰动是在静态工作点附近，因此有第三个假设条件：3，交流小信号的幅值必须远远小于直流分量的幅值。

这个称为小信号假设。

对于PWM模式下的开关电源，通常都能满足以上三个假设条件，因此可以使用小信号分析法进行建模。

对于谐振变换器来说，由于谐振变换器含有一个谐振槽路。

在一个开关时区或多个开关时区内，谐振槽路中各电量为正弦量，或者其有效成分是正弦量。

正弦量的幅值是在大范围变化的，因此在研究PWM型变换器所使用的“小纹波假设”在谐振槽路的小信号建模中不再适用。

对于谐振变换器，通常采用数据采样法或者扩展描述函数法进行建模。

以一个CCM模式下的BUCK电路为例，应用上面的四个步骤，来建立一个小信号模型。

河北工业大学学报JOURNAL OF HEBEI UNIVERSITY OF TECHNOLOGY第42卷第2期V ol.42No.22013年4月April 2013文章编号：1007-2373(2013)02-0001-05基于小信号分析的反激电源反馈补偿网络的设计孙英，曹长春，严晓娜，王志华（河北工业大学电磁场与电器可靠性省部共建重点实验室，天津300130）摘要基于小信号传递函数的网络分析理论，对60W 反激电源进行反馈补偿网络设计．为使补偿后电源系统达到较好的系统动态响应、负载调整率及更好的稳定性，补偿前对各网络进行分析，得出各网络的传递函数．按照补偿后系统伯德图应满足的3个特性，对电压反馈补偿网络进行设计．使用Matlab 软件提供的伯德图分析工具对反馈网络传递函数进行分析，优化得到最佳参数．最后验证了该补偿网络可以使电源达到较好的静态与动态响应．关键词反激电源；小信号分析；反馈补偿；Matlab中图分类号TN86文献标志码AFeedback compensation network design of the flyback powersupply based on small-singal analysisSUN Ying ，CAO Chang-chun ，Y AN Xiao-na ，WANG Zhi-hua(Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability ,HebeiUniversity o f Technology ,Tianjin 300130,Ch ina )Abstract This paper designs 60W flyback powe r supply compensation networ k based on the network analysis theory ofsmall-signal transfer function.In or der to make the power supply system to achieve the best dynamic response,load re gu-lation and stability ,the network before compensation is analyzed and obtains each network transfer function.According to the three characteristics which the compensation system Bode diagram need to have,this paper designs the feedback compensation network.In this proc ess,the Bode tools in Matlab are used to get the best parameters.Finally,this com-pensation network allows the power supply to achieve good static and dynamic response.Key wordsflyback power supply ；small signal analysis ；feedback compensation ；matlab单端反激式开关电源凭借外围电路简单、宽电压输入、输入/输出电气隔离强度高等优点，在150W 以下的小功率开关电源中应用广泛[1]．在反激式开关电源使用过程中，有时会出现负载突变、输出电压突然升高或降低的情况，为了保持电源的输出电压稳定，防止出现振荡的情况，需要设计良好的反馈补偿网络，以满足电源系统的静态和动态指标的要求[2]．另外，反激电源控制回路的关键器件，如输出滤波器、TL431、光耦等都引入了额外的零点和极点，因此需要引入零极点对反馈环路进行补偿，完成系统的零极点配置，以得到期望的静态和动态响应特性[3-4]．为此，本文对补偿前的电源网络进行小信号传递函数分析，按照反馈补偿的特性要求，设计了60W 反激电源的反馈补偿回路，确定了反馈补偿参数，并用Matlab 软件进行频域仿真，优化设计参数，使电源达到设计和使用要求．1电流型反激电源环路设计常用的补偿方法电流型反激电源环路中常用的3种动态补偿的方法如图1~图3所示[5]．图1所示为单极点补偿，适用于电流型控制反激式电源和工作模式在不连续电流模式（DCM ）[6]的电源．此种补偿方式的小信号传递函数为=111(1)收稿日期：5基金项目：国家自然科学基金（53）；河北省自然科学基金（）；河北省自然科学基金基地专项（B 3）作者简介：孙英（），女（汉族），副教授，博士．2012-10-0110700E201020207008001970-2河北工业大学学报第42卷图2所示为极零点补偿，此种补偿方式的小信号传递函数为=1+2111(2)图3所示为双极点单零点补偿，适用于功率部分只有1个极点的补偿，例如，电流型控制和非连续方式的电压型控制可以采用这种补偿方式[7]．此种补偿方式的小信号传递函数为=1+2111+2+212(3)2补偿前网络的小信号分析反激电源的控制环路分为4个主要部分：电阻分压、输出滤波、PWM 电路和反馈补偿，其控制环路方框图如图4所示．1为输出滤波部分的传递函数，2为PWM电路部分的传递函数，为电阻分压部分的传递函数，3为反馈补偿部分的传递函数．反激电源的设计参数如下：输入交流电压为176~264V ，整流后的直流输入电压为228.9~375V ，输出为12V/5A ，初级电感量为722.7H ，初级匝数为51匝，次级匝数为5匝，匝比为10.2，次级滤波电容为1000F ×2=2000F ，电源的开关频率为60kHz ，电流采样电阻=0.5，电压采样电阻分别为13=38k和14=10k ．反激电源反馈网络如图5所示．在低输入电压和重输出负载的情况下，设计环路补偿时能留有一定的相位裕量和增益裕量，则电源在任何模式下都能正常工作．反激式开关电源的工作模式为DCM 模式，反馈补偿不存在右半面零点的问题，所以负载电流突变引起的瞬态响应更快，过冲不会太高．1）电阻分压部分的传递函数电阻分压把输出电压降低到TL431的参考电压水平，其传递函数按简单的电阻分压式可以得到：=1413+14=524(4)2）输出滤波部分的传递函数1[8]输出滤波部分简单框图如图6所示．其中，为滤波电容的等效串联电阻．在电流模式的控制系统中，调节输出电流以达到要求的输出电压，小信号分析得到：=13+14(5)OUT=OUT//1+(6)1=OUT OUT=1+++1=48000*1+15384.696+1(7)传递函数1给出的初始低频增益，这个增益在POLE=1+=0.0017Hz 处开始降低，并在Z RO==z 处变为图5反激电源反馈网络F 5F f f y 图1单极点补偿Fig.1Single-pole comp ensation图2极零点补偿Fig.2Th e pole-zero compensation图3双极点单零点补偿Fig.3Double pole-single zero compensation图4控制环路方框图Fig.4Block diagram of controlloop1111221211011141213增益相位0°90°频率增益相位0°90°频率增益相位0°90°频率121112111221122212212E 12244.8H ig .e edba ck n etwor k o l ba ck po wer3孙英，等：基于小信号分析的反激电源反馈补偿网络的设计第2期水平．利用Matlab软件画出1的伯德图如图7所示．3）PWM电路部分的传递函数2从误差放大器的输出到UC3842的COMP脚的传输关系是COMP CA TH O DE=10C OMP(8)COMP是1脚的输出阻抗，实验时测得为1.6k，是光耦的电流传输比．当误差信号传递到补偿脚以后，将其与电流检测信号比较，从而调节PWM 波的占空比，以稳定输出电压．电流检测比较器和开关部分的简单框图如图8所示．在闭环系统中，系统维持稳定，所以小信号分析可得：=S EC=COMP S E NC E=OUT(9)COMP OU T=S E NCE(10)综合上式可得PWM部分的传递函数为：2=OU T CAT H ODE=SE NCE*10*COMP=10.20.5* 2.72000*1600=44.064(11)传递函数2仅包含增益没有相移．所以，除补偿部分外，开环传递函数为：KH=12=440640*1+15374.696+1(12)其Bode 图如图9所示．3反馈补偿网络的设计反激式电压补偿回路的设计目标就是使系统达到较好的动态响应，负载调整率及更好的稳定性．补偿后的系统的伯德图应满足3个特性[9]：1）在带宽频率（增益0dB 处的频率）处，相位裕量至少有45°；2）较高的增益以保证好的线性和电源的负载调整率；3）在带宽频率处的增益斜率为20dB/dec ．在开关电源系统中，通常取带宽频率为开关频率的1/5[10]，所以取带宽频率=12kHz ．ZE RO处的零点（引起相位超前）和POLE处的极点（引起相位滞后）引起的相位滞后为=arctan 0P O L Earctan0Z ER O=arctan120000.00165arctan 120002448.511.53°(13)分析图9可以看出，在12kHz 处，KH 的频域曲线为水平，且相位滞后较小，为了使超出带宽频率的部分信号迅速衰减，可以直接采用单极点补偿．在带宽频率处补偿电路的传递函数的增益应该等于KH在该频率处增益的负数，KH在带宽频率处的增益为=6565=55B()图6输出滤波部分简单框图Fig.6Simp lified block diagram o f the output filter section图71的伯德图Fig.7The Bode diagram of1图8比较器与开关管简单框图Fig.8Simplified block diagram of the comparator and MOS图的伯德图F T Bfoutout20lo g4404020lo g 2448.0.00110.d 149ig.9he ode d ia gra m o4河北工业大学学报第42卷所以补偿电路在12kHz 处的增益为10.55dB ，则10.55=20log 1120002*38000*12，可得12≈103.5pF ．相位裕量为=180°90°11.53°=78.47°(15)补偿后系统总的开环传递函数为：=123=440640*1+15384.61.686*10596+1(16)系统传递函数伯德图如图10所示．从图10中可以看出，反馈补偿网络使系统在增益为0dB 时，频率约为12.4kHz ，此时的相位值约为101°，故在带宽频率处系统的相位裕量为=180°101°=79°，得出的结论与上述理论分析基本一致，满足稳定性和动态特性的要求．对补偿后的反激电源，调节负载，测试得到如图11所示输出波形．由波形可知，当负载突变时，电源输出不会发生振荡现象，说明电源的反馈补偿网络参数合理．4结束语反馈补偿环节是整个反激式开关电源设计的重点和难点，本文结合实例分析了各个环节的传递函数，结合Matlab 的伯德图分析工具得到合理的补偿参数．按照以上分析设计的反馈补偿网络，使所设计的反激电源动态响应良好，能够在负载突变的情况下保证电源输出的稳定性．参考文献：[1]李海龙．基于UC384*系列芯片的反激稳压电源的设计和分析[J ]．低压电器，2009（19）：42-44．[2]张占松，蔡宣三．开关电源的原理与设计[M ]．北京：电子工业出版社，2005：109-116．[3]王斌．基于DP A426R 的开关电源环路补偿设计[J ]．电源技术，2012，36（11）：108-110．[4]Vladimir A Katic ，Dus an Graovac ．A method for PWM rectifier lin e side filter optimization in tran s ient and steady states [J ]．IEEE Tran s action onPo wer Electronics ，2002，17（5）：1219-1224．[5]韩林华，吴迺陵，史小军，等．反激开关电源中基于PC817A 与TL431配合的环路动态补偿设计[J ]．电子工程师，2005（11）：29-32．[6]徐勇，金辛海．多路输出反激式开关电源的反馈环路设计[J ]．电源技术应用，2009，12（1）：23-27．[7]管晓磊，刘富利，迟爽，等．基于UC3844的反激式开关电源控制环路设计实例[J ]．通信电源技术，2010，27（5）：53-55．[8]Kazimierczuk M K ．Tran s fer fu n ction of current modulator in PWM converters with current-mode con trol [J ]．Circuits and Systems I ：FundamentalTheory an d Applications ．IEEE Trans actions on ，2000，47（9）：1407-1412．[9]闫福军．宽电压输入反激式开关电源的研究[D ]．成都：成都电子科技大学，2010．[10]Erickson R W ，Dragan M ．Fu n d amentals of Power Electronics [M ]．Second Edition ．New York ：Klu wer Acdemic Publishers ，2000：300-376．[责任编辑代俊秋]图10传递函数的伯德图Fig.10Bode d iagram of the transferfunction图11电源输出波形Fig.11Output waveform of p o wer。

基于buck电路开关电源的小信号模型及环路设计作者：孙凯博来源：《数码设计》2018年第15期电压模式和电流模式控制下的环路设计问题。

关键词：开关电源;小信号模型;电流模式控制;电压模式控制中图分类号：TN86 ; 文献标识码：A ; 文章编号：1672-9129（2018）15-0076-02Abstract： The small-signal mathematical model of buck circuit in continuous current mode is established. The loop design problem under voltage mode and current mode control is analyzed according to the stability principle.Keywords： switching power supply; small signal model; current mode control; voltage mode control1 Buck电路电感电流连续时的小信号模型下图是一个具有典型意义的Buck电路图。

为了使得分析更为直观、简单，假设整个电路的理想开关为S与D，那么其对应的理想电感则为滤波电感（对应感受电阻为零）。

在此工作模式之下，整个电路处于连续工作状态。

那么R则为电容C串联的电阻，R为负载电阻。

性详细的变量如下图所示。

在整个环路的传递函数表达式一致的情况下，那么就可以进行对电压误差放大器的设计了。

已经具有了一个零点与两个谐振极点，所以，可以将PI调节器即为，。

在这一方程式中，主要是为了消除误差，取值一般为零极点的十分之一以下。

VMC主要存在以下兩方面的弊端：1）由于并不存在电压前馈机制，无法对输入电压的影响进行预测与判断，因而当电压发生变化的时候，其反应较慢，而且所需增益较高。

2）对于电路当中产生的二阶极点并没有对应的补偿，因而其动态响应也存在一定程度的缺失。

电源反馈设计速成篇之八: 建模篇(Peak Current Mode) 图1为Peak Current Mode 等效小信号模型. Vg为输入电压, Vo为输出电压, io 为输出电流, iL 为电感电流, d为占空比, Vc为反馈控制电压. Gvg为Vg到Vo的传递函数, Gvd为d 到Vo的传递函数, Gig, Gio, Gid分别为Vg, io, d到iL的传递函数, Zo为开环输出阻抗, Fm为等效调制比(Voltage Mode就是三角波幅度倒数, Current Mode是电压和电流的综合),Kf和Kr是考虑了Vg和Vo的扰动影响, 其值很小, 一般忽略没有大的影响. Hv是电压反馈环, Hi是电流采样系数, 负号表示负反馈. 如果是采样电阻的CIC(Current Injection Control)法, Hi就是采样电阻,如果是电感电压的SCM(Standard Current Mode)法, Hi要根据具体电路求得. Current Mode的精髓是要知道电感的di/dt.Gvg, Gvd, Zo, Gig, Gid, Gio这些传递函数都可以由Voltage Mode得到. 不再赘述.图1. Peak Current Mode等效小信号模型He 是等效采样保持传递函数1)(−⋅=⋅sT s se e T s s HTs 为开关周期.如下表:: Ri 为电流取样电阻, 即Hi.可以证明, 不论Ri 去多大, 电流内环都一样, 因为Fm 可以和Ri 对消．一般Ri 由功耗等决定．定义s e n s n c m T S S T S m F )(11+==, ne cS S m +=1Ts 为开关周期, Se 为外加斜坡补偿三角波幅值, Sn 为电感电流采样等效三角波幅值. mc 为衡量斜坡补偿效果系数, mc=1即Se=0, 为纯电流控制，mc>>1既外加斜坡补偿>>电感电流采样等效三角波幅值, 退化为Voltage Mode.一般mc=1.5-2.Hv 为设计参数，一般用Type2补偿，零点决定响应快慢，极点补偿ESR 零点，ＲＨＰ零点，或1/2开关频率，三者取其低的值.以上为CCM Mode, 如果为DCM mode, 则开环参数为DCM mode 下的各个参数, 如下表:图1为整个系统的信号流图, 在推导小信号公式时有很多变量为零, 可大大简化. 以控制到输出传递函数为例, 图2为buck 电路, 图3为buck 小信号模型和控制到输出信号流图.V in图2. Buckd*Vap/Dvc图3. Buck 小信号模型和控制到输出信号流图可以求得电流内环开环回路增益Ti 为)()(s G s H H F T id e i m i ⋅⋅⋅=,电阻取样Hi=Ri, 否则要另行计算, 和具体电路有关. 当电流内环闭环时, 控制到输出传递函数Goc 为)(1)(s G F K T s G F G vd m r i vd m oc ⋅⋅−+⋅=电压回路增益Tv 为)()(s G s H F T vd v m v ⋅⋅=, Hv(s)为要设计的反馈部分.电压外环回路增益T2为ivT T T +=12, 根据T2来看相位和幅值裕量. 电流环闭合后输出阻抗Zoicl 为gi vd m e i vd o oicl V T s G F s H H s G s Z Z ⋅+⋅⋅⋅⋅+=)1()()()()(, Zo(s)为开环输出阻抗.电流环和电压环都闭合后输出阻抗Zovcl 为ivd m r vd m v oiclovcl T s G F K s G F s H Z Z +⋅⋅−⋅⋅+=1)()()(1 例子 Buck 电路:Vg 11:=L 37.5106−⋅:= Rc 0.02:= C 400106−⋅:= Fs 50103⋅:= Vo 5:= R 1:=Ri 0.33:=Sn Vg Vo −L Hi ⋅:= Sn 5.28104×=Fm mc ()1mc Sn ⋅Ts ⋅:=mc 设为变量, 对Hv 零点和极点的选取:选择 wzc 使Settling time 为 0.5ms,wzc 10.5103−⋅:=wzc 2103×=选择wpc 为 ESR 零点, RHP 零点, 1/2 开关频率, 三者的低频:w ZESR 1.25105×=ws 2π⋅Fs ⋅:= 0.5ws 1.571105×= 因没有RHP 零点, ESR 零点比1/2 开关频率低, 取wpc w ZESR :=wpc 1.25105×= Rx 103:=Ry 103:=Hv s wi ,()Ry Rx Ry +wis1swzc +1s wpc+⋅:=Kr Ts Ri⋅2L ⋅:=Kr 0.088=Kf D −Ts ⋅Ri⋅L1D 2−⎛⎜⎝⎞⎟⎠⋅:=Kf 0.062−=图4为电流内环闭环时, 控制到输出传递函数Goc, 参变量mc 为1,1.2,1.5,2,4. Mc=1.5 –2时系统相位和幅值变化平稳. 选取mc=1.5.变化wi 不会改变Hv 相位, 选取 wi 以满足相位和幅值裕量要求. 图5给出了T2和wi 关系. 选取 wi = 40000, 剪切频率fc=13253 Hz, 相位和幅值裕量 55 degree, 6 dB.图6为求得反馈部分电阻,电容值后电流内环闭环时, 控制到输出传递函数Goc, mc=1为纯电流控制, mc=1.5为外加斜坡补偿的优化设计.图7为电流环闭合后输出阻抗Zoicl, mc=1为纯电流控制, mc=1.5为外加斜坡补偿的优化设计.图8为电流环和电压环都闭合后输出阻抗Zoicl, mc=1为纯电流控制, mc=1.5为外加斜坡补偿的优化设计.图9-11分别为mc=1时的PSPICE 仿真结果, 用来验证公式的正确.101001.1031.1041.1051.10660402020gain Goc 2i π⋅f n ⋅1,()()gain Goc 2i π⋅f n ⋅ 1.2,()()gain Goc 2i π⋅f n ⋅ 1.5,()()gain Goc 2i π⋅f n ⋅2,()()gain Goc 2i π⋅f n ⋅4,()()f n101001.1031.1041.1051.10620015010050180−phase Goc 2i π⋅f n ⋅1,()()phase Goc 2i π⋅f n ⋅ 1.2,()()phase Goc 2i π⋅f n ⋅ 1.5,()()phase Goc 2i π⋅f n ⋅2,()()phase Goc 2i π⋅f n ⋅4,()()f n图4. 电流内环闭环控制到输出传递函数Goc101001.1031.1041.1051.10660303060gain T22i π⋅f n ⋅ 1.5,10000,()()gain T22i π⋅f n ⋅ 1.5,20000,()()gain T22i π⋅f n ⋅ 1.5,40000,()()gain T22i π⋅f n ⋅ 1.5,100000,()()gain T22i π⋅f n ⋅ 1.5,200000,()()f n101001.1031.1041.1051.10630025020015010050180−phase T22i π⋅f n ⋅ 1.5,10000,()()phase T22i π⋅f n ⋅ 1.5,20000,()()phase T22i π⋅f n ⋅ 1.5,40000,()()phase T22i π⋅f n ⋅ 1.5,100000,()()phase T22i π⋅f n ⋅ 1.5,200000,()()f n图5. 电压外环回路增益T2 和wi 关系1101001.1031.1041.1051.1068060402020gain Goc 2i π⋅f n ⋅1,()()gain Goc 2i π⋅f n ⋅mc,()()f n1101001.1031.1041.1051.10620015010050180−phase Goc 2i π⋅f n ⋅1,()()phase Goc 2i π⋅f n ⋅mc,()()f n图6. 电流内环闭环控制到输出传递函数Goc (mc=1, 1.5)1101001.1031.1041.1051.10640302010gain Zoicl 2i π⋅f n ⋅1,()()gain Zoicl 2i π⋅f n ⋅mc ,()()f n1101001.1031.1041.1051.10680604020phase Zoicl 2i π⋅f n ⋅1,()()phase Zoicl 2i π⋅f n ⋅mc,()()f n图7.电流环闭合后输出阻抗Zoicl (mc=1, 1.5)1101001.1031.1041.1051.10680604020gain Zovcl 2i π⋅f n ⋅1,wi,()()gain Zovcl 2i π⋅f n ⋅mc ,wi,()()f n1101001.1031.1041.1051.106200100100180−phase Zovcl 2i π⋅f n ⋅1,wi ,()()phase Zovcl 2i π⋅f n ⋅mc ,wi ,()()f n图8. 电流环和电压环都闭合后输出阻抗Zovcl (mc=1, 1.5)图9. Pspice 结果:电流内环闭环控制到输出传递函数Goc (mc=1)图10. Pspice 结果: 电流环闭合后输出阻抗Zoicl (mc=1)图11. Pspice 结果: 电流环和电压环都闭合后输出阻抗Zovcl (mc=1)。