各国大跨径悬索桥建设风格及成桥线形计算方法
- 格式:ppt
- 大小:7.64 MB
- 文档页数:77
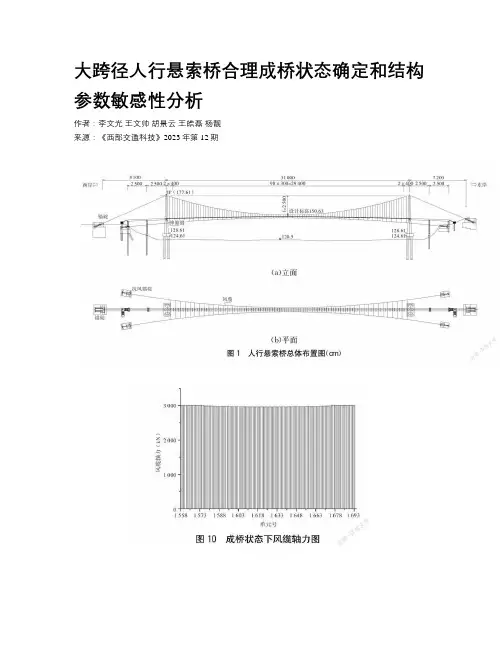
大跨径人行悬索桥合理成桥状态确定和结构参数敏感性分析作者:李文光王文帅胡景云王皓磊杨靓来源:《西部交通科技》2023年第12期摘要:为优化大跨径人行悬索桥设计方法,文章以一座双塔地锚式人行悬索桥为工程背景,采用Midas Civil软件建立全桥模型,通过改变跨度比、主缆矢跨比、塔梁约束形式、索塔约束形式等参数,对大跨径人行悬索桥结构参数进行敏感性分析,研究其改变对结构静力性能的影响,同时分析抗风缆对大跨径人行悬索桥动力特性的影响。
结果表明:合理增大主缆矢跨比对减小主缆应力和主塔内力起明显作用;索塔滑移的约束形式能够极大降低塔底弯矩;塔梁铰接的约束形式更适合此类大跨径人行悬索桥;合理增大跨度比可以减小锚碇锚固端的拉力与主塔内力;架设抗风缆大幅度提高了结构刚度,也提高了结构整体稳定性。
关键词:人行悬索桥;结构参数;静力性能;动力特性;敏感性分析中图分类号:U448.25 A 40 128 60 引言目前国内人行悬索桥设计尚未形成行业规范,设计者多参考公路悬索桥,但由于人行悬索桥更加纤细、轻柔[1],因此不一定适用《公路悬索桥设计规范》(JGT/D65-05-2015)[2]中的结构参数。
此外,合理的结构参数能够很大程度地减少工程造价、降低施工难度,故对大跨径人行悬索桥结构参数进行敏感性分析具有十分重要的工程意义。
近几年,国内学者对悬索桥结构参数敏感性分析的研究逐渐增多。
苏龙等[3]分析了结构参数变化对主缆跨中垂度的影响,为主缆线形调整提供了参考;张翼等[4]对主梁采用板桁结构的悬索桥进行参数分析,研究发现改变下平联斜腹杆尺寸和弦杆截面尺寸对一阶振型影响显著;陈伟华等[5]研究了不同结构参数对悬索桥动力特性的影响,结果表明,随着矢跨比的减小,主缆侧动频率减小,适当增大主缆刚度和主塔刚度分别对减小主缆侧动频率和侧弯频率有显著作用;彭益华等[6]研究了中央扣对大跨径悬索桥结构动力特性的影响,结果表明,设置中央扣对提高结构反对称扭转频率、增大结构的整体刚度、提高静风稳定性有显著作用;郭小权[7]研究了自锚式悬索桥缆索系统和塔梁系统参数的改变对成桥状态确定的影响;黄明金[8]研究了小矢跨比人行悬索桥的力学性能,结果表明,小矢跨比设计增大了悬索桥整体的结构刚度,进而提高了结构横向静风稳定性。

悬索桥的计算方法及其发展悬索桥是一种古老的桥梁结构形式,也是目前大跨度桥梁的主要结构型式之一。
悬索桥主要是由缆索、吊杆、加劲梁、主塔、锚碇等构成。
从结构形式上看,它是一种由索和梁所构成的组合体系,在受力本质上它是一种以柔性索为主要承重构件的悬挂结构。
悬索桥随着跨度的增大,柔性加大,在荷载作用下会呈现出较强的非线性,所以悬索桥宜采用非线性方法来进行结构分析。
考虑悬索桥非线性因素的结构分析方法主要有挠度理论和有限位移理论。
挠度理论考虑了悬索桥几何非线性的主要因素,可用比较简便的数值方法来分析,又有影响线可资利用,故很适用于初步设计阶段的结构设计计算。
有限位移理论则全面地考虑了悬索桥几何非线性因素,计算结果较挠度理论精确,但计算过程复杂,直接用于设计计算有诸多不便和困难。
悬索桥挠度理论是一种古典的悬索桥结构分析理论。
这种理论主要考虑悬索和加劲梁变形对结构内力的影响,在中小跨度范围内其计算结果比较接近结构的实际受力情况,具有较好的精度。
悬索桥挠度理论主要分为多塔悬索桥挠度理论和自锚式悬索桥挠度理论。
最初的悬索桥分析理论是弹性理论。
弹性理论认为缆索完全柔性,缆索曲线形状及坐标取决于满跨均布荷载而不随外荷载的加载而变化,吊杆受力后也不伸长,加劲梁在无活载时处于无应力状态。
弹性理论用普通结构力学方法即可求解,计算简便,至今仍在跨径小于200米的悬索桥设计中应用[1]。
但弹性理论假定缆索形状在加载前后不发生变化,显然与悬索桥的可挠性不符,因此发展出计入变形影响的悬索桥挠度理论。
古典的挠度理论称为“膜理论”。
它是将悬索桥的全部近视看成是一种连续的不变形的膜,当缆索产生挠度时,加劲梁也随之产生相同的挠度。
由于根据作用于缆索单元上吊杆力与缆索拉力的垂直分力平衡以及作用于加劲梁单元上的外荷载及吊杆力与加劲梁弹性抗力平衡的条件建立力的平衡微分方程而求解。
挠度理论和弹性理论的最大区别是摒弃了弹性理论中关于缆索形状不因外荷载介入而改变的假设,相应建立缆索在恒载下取得平衡的几何形状将因外荷载介入而改变及同时计入缆索因外荷载所增索力引起的伸长量的假设,极大的接近悬索桥主索的实际工作状态,对悬索桥的发展起到了很大的推动作用。


大跨径悬索桥主缆成桥线形计算方法研究及应用大跨径悬索桥是一种建筑结构工程中常见的桥梁形式,它的主要特点是利用悬索的拉力来支撑桥梁的自重和荷载。
而主缆则是悬索桥中起到主要承载作用的部分。
本文将研究大跨径悬索桥主缆的成桥线形计算方法,并探讨其在实际应用中的相应应用。
在进行大跨径悬索桥主缆成桥线形计算方法研究之前,首先需要了解大跨径悬索桥的基本概念和构造。
大跨径悬索桥由悬索、主缆、主塔等组成。
其中,主缆被悬挂在主塔上,作为悬索的延伸,并用于支撑桥面板。
主缆的成桥线形是指主缆在自重和荷载的情况下所形成的曲线形状。
大跨径悬索桥主缆成桥线形计算方法的研究是基于力学原理和结构力学的分析。
首先,需要确定主缆的初始线形,通常可以假设为一定的曲线形状,如悬链线形。
然后,根据桥面板的自重和荷载情况,通过数值计算或解析计算的方法,确定主缆的悬挂点位置以及推力大小。
对于大跨径悬索桥主缆成桥线形计算方法的应用,可以分为以下几个方面。
首先,主缆成桥线形的计算可以用于确定主缆的几何参数,包括主缆的长度、形状和初始线形等。
这些参数的确定对于设计和施工是非常重要的。
其次,主缆成桥线形的计算可以用于确定主缆的受力情况,包括主缆的张力和弯矩等。
这些受力情况的计算可以用于判断主缆是否满足设计要求,以及确定主缆的安全性和可靠性。
最后,主缆成桥线形的计算也可以用于对已建成的大跨径悬索桥进行检测和监测,以保证桥梁的正常使用和运行。
在实际应用中,大跨径悬索桥主缆成桥线形的计算涉及到多种计算工具和方法。
其中,常用的方法包括有限元方法、近似解法和经验公式等。
这些方法各有优缺点,在具体应用中需要综合考虑工程的实际情况和计算精度的要求,选择合适的计算方法。
综上所述,大跨径悬索桥主缆成桥线形计算方法的研究及应用是一项重要的工作。
通过对主缆成桥线形计算方法的研究,可以为大跨径悬索桥的设计、施工和监测提供重要的理论依据和技术支持。
在实际应用中,需要综合考虑多种计算方法和工具,以确保计算结果的准确性和可靠性。

悬索桥的计算方法及其发展悬索桥是一种古老的桥梁结构形式,也是目前大跨度桥梁的主要结构型式之一。
悬索桥主要是由缆索、吊杆、加劲梁、主塔、锚碇等构成。
从结构形式上看,它是一种由索和梁所构成的组合体系在受力本质上它是一种以柔性索为主要承重构件的悬挂结构。
悬索桥随着跨度的增大,柔性加大,在荷载作用下会呈现出较强的非线性,所以悬索桥宜采用非线性方法来进行结构分析。
考虑悬索桥非线性因素的结构分析方法主要有挠度理论和有限位移理论。
挠度理论考虑了悬索桥几何非线性的主要因素,可用比较简便的数值方法来分析,又有影响线可资利用,故很适用于初步设计阶段的结构设计计算。
有限位移理论则全面地考虑了悬索桥几何非线性因素,计算结果较挠度理论精确,但计算过程复杂,直接用于设计计算有诸多不便和困难。
悬索桥挠度理论是一种古典的悬索桥结构分析理论。
这种理论主要考虑悬索和加劲梁变形对结构内力的影响,在中小跨度范围内其计算结果比较接近结构的实际受力情况,具有较好的精度。
悬索桥挠度理论主要分为多塔悬索桥挠度理论和自锚式悬索桥挠度理论最初的悬索桥分析理论是弹性理论。
弹性理论认为缆索完全柔性,缆索曲线形状及坐标取决于满跨均布荷载而不随外荷载的加载而变化,吊杆受力后也不伸长,加劲梁在无活载时处于无应力状态弹性理论用普通结构力学方法即可求解,计算简便,至今仍在跨径小于200米的悬索桥设计中应用[1]。
但弹性理论假定缆索形状在加载前后不发生变化,显然与悬索桥的可挠性不符,因此发展出计入变形影响的悬索桥挠度理论。
古典的挠度理论称为“膜理论”。
它是将悬索桥的全部近视看成是一种连续的不变形的膜,当缆索产生挠度时,加劲梁也随之产生相同的挠度。
由于根据作用于缆索单元上吊杆力与缆索拉力的垂直分力平衡以及作用于加劲梁单元上的外荷载及吊杆力与加劲梁弹性抗力平衡的条件建立力的平衡微分方程而求解。
挠度理论和弹性理论的最大区别是摒弃了弹性理论中关于缆索形状不因外荷载介入而改变的假设,相应建立缆索在恒载下取得平衡的几何形状将因外荷载介入而改变及同时计入缆索因外荷载所增索力引起的伸长量的假设,极大的接近悬索桥主索的实际工作状态,对悬索桥的发展起到了很大的推动作用。



大跨径悬索桥施工及成桥阶段抗风措施研究大跨径悬索桥是一种特殊的桥梁结构,在施工期间和成桥阶段需要进行一系列的抗风措施研究,以确保桥梁的安全和稳定。
本文将对大跨径悬索桥施工及成桥阶段的抗风措施进行研究,并提出相关建议。
1. 风场评估:在进行大跨径悬索桥施工前,需要对施工区域的风场进行评估。
通过风速和风向的实时监测,可以选择适合施工的时间和条件,减少风对施工的影响。
2. 悬索索塔设计:悬索桥的悬索索塔是承受悬索和桥面荷载的主要结构,需要进行合理的设计。
在考虑风荷载的情况下,悬索索塔的设计需要考虑风的影响,采取加固措施,确保其稳定性和安全性。
3. 施工设备固定:在施工过程中,需要使用吊车、起重机等大型设备进行吊装作业。
在风大的情况下,这些设备容易受到风的影响,影响施工的进行。
在施工前需要对这些设备进行固定,防止风对其的影响。
4. 施工进度安排:在制定施工计划时,需要考虑风的影响因素,合理安排施工进度。
在风速较大的情况下,可以暂停高空作业,待风速减小后再进行施工。
5. 安全防护设施:为了保障施工人员的安全,在施工现场需要设置安全防护设施。
对于高空作业人员,需要配备安全带等装备,防止风对其的影响。
1. 成桥阶段的抗风措施比施工阶段更为重要,因为大跨径悬索桥的结构稳定性和安全性对成桥环境的要求更高。
2. 成桥过程中需要采取的抗风措施包括:(1) 钢缆索塔固定:成桥过程中,悬索索塔的固定非常重要。
特别是在吊装悬索的过程中,需要对钢缆索塔进行加固,以抵抗风荷载对其的影响。
(2) 桥面荷载均衡:在成桥过程中,需要平衡桥面的荷载,以减小风对桥面的影响。
对桥面荷载进行调整和均衡,可以有效减小风的影响。
(3) 连接件固定:在成桥过程中,需要对各个连接件进行固定,防止其在风大的情况下产生位移或变形,影响整个桥梁的稳定性。
3. 成桥阶段的抗风措施需要经过详细的工程计算和实验验证,确保其有效性和可靠性。
在成桥过程中,需要对整个桥梁结构进行综合考虑和分析,针对风的影响因素进行相应的抗风措施设计。


悬索桥的结构原理、力学性能及建造方法一、原理悬索桥中最大的力是悬索中的张力和塔架中的压力。
由于塔架基本上不受侧向的力,它的结构可以做得相当纤细,此外悬索对塔架还有一定的稳定作用。
假如在计算时忽视悬索的重量的话,那么悬索形成一个双曲线。
这样计算悬索桥的过程就变得非常简单了。
老的悬索桥的悬索一般是铁链或联在一起的铁棍。
现代的悬索一般是多股的高强钢丝。
二、结构悬索桥的构造方式是19世纪初被发明的,许多桥梁使用这种结构方式。
现代悬索桥,是由索桥演变而来。
适用范围以大跨度及特大跨度公路桥为主,当今大跨度桥梁全采用此结构。
是大跨径桥梁的主要形式。
悬索桥是以承受拉力的缆索或链索作为主要承重构件的桥梁,由悬索、索塔、锚碇、吊杆、桥面系等部分组成。
悬索桥的主要承重构件是悬索,它主要承受拉力,一般用抗拉强度高的钢材(钢丝、钢缆等)制作。
由于悬索桥可以充分利用材料的强度,并具有用料省、自重轻的特点,因此悬索桥在各种体系桥梁中的跨越能力最大,跨径可以达到1000米以上。
1998年建成的日本明石海峡桥的跨径为1991米,是目前世界上跨径最大的桥梁。
悬索桥的主要缺点是刚度小,在荷载作用下容易产生较大的挠度和振动,需注意采取相应的措施。
三、性能按照桥面系的刚度大小,悬索桥可分为柔性悬索桥和刚性悬索桥。
柔性悬索桥的桥面系一般不设加劲梁,因而刚度较小,在车辆荷载作用下,桥面将随悬索形状的改变而产生S 形的变形,对行车不利,但它的构造简单,一般用作临时性桥梁。
刚性悬索桥的桥面用加劲梁加强,刚度较大。
加劲梁能同桥梁整体结构承受竖向荷载。
除以上形式外,为增强悬索桥刚度,还可采用双链式悬索桥和斜吊杆式悬索桥等形式,但构造较复杂。
桥面支承在悬索(通常称大揽)上的桥称为悬索桥。
英文为Suspension Bridge,是“悬挂的桥梁”之意,故也有译作“吊桥”的。
“吊桥”的悬挂系统大部分情况下用“索”做成,故译作“悬索桥”,但个别情况下,“索”也有用刚性杆或键杆做成的,故译作“悬索桥”不能涵盖这一类用桥。

悬索桥主缆线形解析方程解及应用第22卷第3期2005年 6 月文章编号工程力学ENGINEERING MECHANICS Vol.22 No.3 June 2005邹振祝1,2(1. 哈尔滨工业大学航天工程与力学系陈伟22.石家庄铁道学院土木分院, 河北石家庄050043) 摘要弹性伸长对主缆线比重影响的计算模型óé±ì??t?μ?a?¼?a3?¸??μ线形坐标都可以用于悬索桥设计与施工计算悬索桥中图分类号解析方程A有应力索长加劲梁按考虑和不考虑主缆通过引入一个参数u(shu=dy/dx)ò??×àí??¶?o¼º¨1y??±?2?¸yu来确定主缆算例结果表明两种计算模型收敛速度较快SOLUTION OF MAIN CABLE SHAPE EQUATIONS OF A SUSPENSIONBRIDGE AND ITS APPLICATION*ZHANG Zhi-guo1,2 , ZOU Zhen-zhu1,2 , ZHAO Yu-cheng2 , CHEN Wei2(1. Department of Astronautics and Mechanics, Harbin Institute of Technology, Harbin 150001, China;2. School of Civil Engineering, Shijiazhuang Railway Institute, Shijiazhuang 050043, China)Abstract: Analytic parameter equations for the main cable curve of a suspension bridge are derived. Calculation models taking into account the influence of its elastic elongation due to its weight and neglecting the elongation are established. A set of non-linear equations result after incorporating boundary conditions. The equations are solved with quasi-Newton method. A formula is derived for the main cable length of a suspension bridge in free stress or stressed state with integration method. The calculation result shows that the two calculation models enjoy rapid convergence and high precision, and are applicable to the design and construction control of suspension bridges.Key words: suspension bridge; main cable; analytic equation;stress-free cable length; stressed cable length1 引言悬索桥是由主缆等构成的组合结构体系[1]锚碇吊索à??Tó|á|3¤?è°°?¤??µ?oº±¸??μ??¾′???à?°2×°?÷目前抛物线法[1~4]?×·¨?ù?¨?÷à?×?è·è·?¨??3é??11D?ê?·òa?÷àD??±?¼¼°?¹3·??³′¹??µ11¹??μμ¹?¸Àµ|²1??μDü?÷??3éD?ê?è·?¨?÷2003-07-11作者简介男男男陈伟(1971)2003-12-11副教授教授副教授o¼′??¶?′¼¸µo1¤3¹μ??D??.从事断裂力学和桥梁计算理论的研究(E-mail:******************.cn)从事固体力学的研究梁得到的索形是抛物线但精度不高悬链线索元递推法[6~9]是将加劲梁吊点间索段由于只受沿弧长方向均布的主缆自重荷载而呈悬链线可以建立相邻索段间的递推关系该法精度较高本文将主缆自重看作是沿弧长均布吊索并分别按考虑和不考虑主缆弹性伸长对主缆线比重影响然后给出了确定主缆水平张力和线形坐标的计算方法该法由微元力学平衡关系推得收敛快为悬索桥主缆线形和索长计算提供了一种实用的求解方法(1) 主缆索绝对柔性不能承受弯矩即主缆材料的应力应变关系是线弹性的其它恒载(用W表示)μ??½°?à°???÷éèê?μè??·??ò?ù?è·?2?óéóú??3?1??μ³?±¸?μxoy的原点定在主缆对称中心由竖直方向的平衡可得主缆曲线微分方程为H为主缆拉力的水平分量其在主缆内各处均相等令b=W/H (2)式(1)改写成y′(x)=shu (4) 将式(4)代入式(3)dx=chu1chuachu+bdu=b?1+mchudu (5)式中代表主缆自重与除主缆自重外的其它恒载之比积分式(5)Φ(u,m)=u1mexp(u)+1??m2m?lnm?m2mexp(u)+1+?m2由式(4)得dy=shudx=shu?chub(1+mchu)du (7)积分式(7)D?éóé±ì??tè·?¨è?í?1f)»??aμ?¸?L(跨长之半)待求的是HD1ò??aO点边界条件x=0分别代入方程(6)和(8)D1x=1b*Φ(u,m)?Φ(0,m)] (9a) y=111+ma(chu?1+mln1+mchu ) (9b) 支点B处有边界条件x=L代入式(9)得174 工程力学Φ(uL,m)?Φ(0,m)=bL (10a) chuL?1+1mln1+m1+mchu=af (10b) L联立以上两式其中仅含H和uL两个未知数(H隐含于a因而解是唯一的迭代初值取抛物线理论的近似计算值求出了Hb已知比如要确定成桥状态吊点的纵坐标得到一个非线性方程再将ut代入式(9b)重复这一过程这里的非线性方程可以采用对分法[10]求解uL]?òê?á2?ù?èoü?ì?éò?·D??2??è??DDμ?±???¸??¿»??aH的条件下D1和端点未知参数u0然后再按上述方法求出主缆吊点坐标已知H?aà?2??ù?êê?Dü?÷??3éD??íò?íêè?è·?¨??á?oíê?1¤?Dμ?ò÷òa2?êy?ùòê?·òa?ú?÷àá|H和端点参数u确定后下面仅按中跨推导计算公式可知弧微分公式为得ds=1b?ch2u1+mchudu (12) 对于中跨对应x=0和x=L的参数u分别为u0=0和uL(注意边跨u0≠0)得中跨主缆有应力长的一半为E为索材弹性模量T为主缆张力万方数据得dss0=d1+T/(EA)(14)由于悬索只承受拉力可得T=H+(y′)2=Hchu (15)将式(12)和式(15)代入式(14)得dsch2udu0=b(1+mchu)(1+εchu)(16)积分式(16)s10=b(m?ε),*Φ(uL,ε)?Φ(u0,ε)+(17) ?*Φ(uL,m)?Φ(u0,m)+-由于u0和uL已在前面求出注意这里的无应力索长是精确值即将式(14)按级数展开ds0=[1?T/(EA)]ds则索段伸长量为得εch3d(?s)=b?u1+mchudu积分上式?s=εauL?u02+sh2uL?sh2u04(19) ?1m(shu1L?shu0)+m[Φ(uL,m)?Φ(u0,m)]}则中跨主缆无应力半长的一阶近似为一阶近似的无应力索长较精确值小有u0=0μ?2?ê§ò?°?D?3 考虑主缆弹性伸长对主缆线比重的影响3.1 主缆线形解析方程解上述推导中但实际中一般已知的是主缆无应力状态下的自重荷载集度q0?½´·¹3¤?¾»?o·ˉ?¶??¼·q0减小到q´′º?μ?DÀ?½½´D?2?¸y²?3¹沿弧长的自重荷载集度为q0?½´y±??aA假设图1中有应力索微段长为ds设E为主缆索弹性模量则由虎克定律有受力前后主缆微段质量保持不变q0ds0=qds (22)由式(21)得q=q0/[1+T/(EA0)] (23) 取主缆微段分析所以由水平平衡仍得主缆水平张力H处处相等但此时主缆自重荷载集度q应由式(23)表示得Hd2yq0dsd2x=1+T/(EA?+W (24) 0)dx采用与前面相似的变换整理得dx=(1+εchu)chub(1+nchu)du (25)式中bε=H/(EA0)积分式(25)得dy=(1+εchu)shuchub(1+nchu)du (27)积分式(27)得y=1εmmbn[2ch2u+nchu?n2ln(1+nchu)+D1] (28)式(26)和式(28)就是考虑主缆弹性伸长时的线形方程D1为积分常数3.2 主缆线形求解方法求解过程同前节边界条件与前节相同可确定积分常数D代回后u=uLy=f¶?¼·?a?£?¾²¨[10]求解可由方程(29)依前节过程确定主缆吊点坐标3.3 主缆长度计算将式(4)和(25)代入式(11)得s=1u?u0sh2uLbn,ε(L2+?sh2u04 (31) +mn*shuL?shu0+Φ(u0,n)?Φ(uL,n)]}将式(30)和式(15)代入式(14)得s10=bn[shuL?shu0+Φ(u0,n)?Φ(uL,n)] (33) 同理?s=εsh3uLbn,ε(shu?sh3uL?shu0+03)+mu?u0sh2uL?sh2u0nL2+4) (34) +mn2[shu0?shuL+Φ(uL,n)?Φ(u0,n)]} 将式(31)和式(34)代入式(20)¸?(31)和式(33)计算结果的2倍从以上推导可以看出这里列出这些公式只是为了比较说明4 算例某两支点等高悬索桥[6]吊索间距12m加劲梁等其余恒载集度W=200kN/m索材弹性模量E=2.0跨中矢高f=6080100m2·¼¶主缆有应力长结果分别列于表1和表2176 工程力学表1 水平张力H和y值比较Table 1 Comparison of horizontal component of cable tension and y-coordinate矢高f/m不考虑q变化60 70 80 90 100417807.1 358284.5 313663.7 278977.1 251244.1水平张力H/kN 考虑q变化417495.8 358054.5 313486.6 278836.3 251129.2文献[6] 417801.2 358282.3 313663.4 278978.8 251245.7抛物线法417271.2 357661.0 312953.4 278180.8 250362.7不考虑q变化15.8068 18.4351 21.0606 23.6829 26.3017x=228m处y值/m 考虑q变化15.8069 18.4352 21.0608 23.6831 26.3020文献[6] 15.8063 18.4349 21.0606 23.6834 26.3023抛物线法15.8218 18.4587 21.0957 23.7327 26.3696表2 索长值比较Table 2 Comparison of cable length矢高f/m有应力索长s/m不考虑q变化60 70 80 90 100898.7006 902.5123 906.8772 911.7824 917.2136考虑q变化898.7006 902.5123 906.8772 911.7822 917.2135精确无应力索长s0/m 不考虑q变化895.5447 899.7814 904.4620 909.6099 915.2328考虑q变化895.5470 899.7831 904.4633 909.6109 915.2335不考虑q变化895.5335 899.7731 904.4556 909.6047 915.2285 一阶近似无应力索长s0/m 考虑q变化895.5359 899.7748 904.4569 909.6057 915.2293文献[6] 895.5321 899.7708 904.4525 909.6005 915.2234抛物线法895.5324 899.7683 904.4451 909.5859 915.1984比较表1和表2的计算结果可见说明计算精度较高抛物线法与其它方法相比误差较大考虑和不考虑主缆弹性伸长对主缆线比重的影响水平张力相差稍大误差随垂度增加而减小主缆张力精度对于强度设计已足够但对采用新型索材的超大跨悬索桥建议按考虑主缆线比重变化的公式计算主缆参考文献中(3) 在一般跨度悬索桥的设计与施工控制分析对于超大跨悬索桥主缆有应力和无应力长在其设计施工中十分重要(2) 本文计算公式由主缆微元力学平衡关系推得求解容易算例结果与文献[6]非常吻合剪力墙多垂直杆单元模型的改进及应用189为接近限制单元模型的高宽比(3) 剪力墙的拉压滞变模型和剪切滞变模型并不多见给出了多垂直杆单元的受压极限变形算例分析表明计算值与试验结果吻合较好本文方法适用于高层建筑结构的弹塑性静力和动力分析[1] 李国强, 周向明, 丁翔. 钢筋混凝土剪力墙非线性动力分析模型[J]. 世界地震工程, 2000, 2: 13-18.Li Guoqiang, Zhou Xiangming, Ding Xiang. Models of reinforced concrete shear walls for nonlinear dynamic analysis [J]. WorldInformation on Earthquake Engineering, 2000, 2: 13-18. (in Chinese)[2] 孙景江, 江近仁. 高层建筑抗震墙非线性分析的扩展铁木辛哥分层梁单元[J]. 地震工程与工程振动, 2001, 21(2):78-83.Sun Jingjiang, Jiang Jinren. Extended layered Timoshenko beam element for nonlinear analysis of RC high-rise buildings with structural walls [J]. Earthquake Engineering And Engineering Vibration, 2001, 21(2): 78-83. (in Chinese)[3] 蒋欢军, 吕西林. 用一种墙体单元模型分析剪力墙结构[J]. 地震工程与工程振动, 1998, 18(3): 40-48.Jiang Huanjun, Lu Xilin. Analysis of shear wall structures using a type of wall element [J]. Earthquake Engineering And Engineering Vibration, 1998, 18(3): 40-48. (in Chinese)[4] 汪梦甫, 周锡元. 钢筋混凝土剪力墙多垂直杆非线性单元模型的改进及其应用[J]. 建筑结构学报, 2002, 23(1): 38-42, 57.Wang Mengfu, Zhou Xiyuan. The improved parallelmulti-component model for the nonlinear seismic response analysis of RC walls and its application [J]. Journal of Building Structures, 2002, 23(1): 38-42, 57. (in Chinese)[5] 汪梦甫, 周锡元. 钢筋混凝土框架-剪力墙结构非线性地震反应实用分析方法的研究[J]. 土木工程学报, 2002, 35(6):32-38.Wang Mengfu, Zhou Xiyuan. A practical method for nonlinear seismic responses of RC frame-wall structure [J]. China Civil Engineering Journal, 2002, 35(6): 32-38. (in Chinese)[6] 沈蒲生, 王海波. 剪力墙结构的非线性地震反应分析[J]. 土木工程学报, 2003, 36(5): 11-16.Shen Pusheng, Wang Haibo. Nonlinear seismic response to shear wall structures [J]. China Civil Engineering Journal, 2003, 36(5): 11-16. (in Chinese)[7] 江近仁, 孙景江, 丁世文. 轴向循环荷载下钢筋混凝土柱的试验研究[J]. 世界地震工程, 1998, 14(4): 12-16. Jiang Jinren, Sun Jingjiang, Ding Shiwen. Experimental study of RC columns subjected to axial cyclic loads [J]. World Information on Earthquake Engineering, 1998, 14(4): 12-16. (in Chinese)[8] 吕西林, 金国芳, 吴晓涵. 钢筋混凝土结构非线性有限元理论与应用[M]. 上海: 同济大学出版社, 1997. Lu Xilin, Jin Guofang, Wu Xiaohan. Theory and application of nonlinear finite element of reinforced concrete [M]. Shanghai: Tongji University Press, 1997. (in Chinese)[9] Oesterle R G. Web crushing of reinforced concretestructural walls [J]. ACI Structural Journal, Proceedings, 1984, 81(3): 231-241.[10] F J Vecchio. Towards cyclic load modeling of reinforcedconcrete [J]. ACI Structural Journal, Technical, 1999, 96(2): 193-202.(上接)[5] 肖汝诚, 贾丽君, 王小同. 确定大跨悬索桥主缆成桥线形的虚拟梁法[J]. 计算力学学报学报, 1999, 16(1): 108-113.Xiao Rucheng, Jia Lijun, Wang Xiaotong. Fictitious beam method for determination of main cable shape of long-span suspension bridge[J]. Chinese Journal of Computational Mechanics, 1999, 16(1): 108-113. (in Chinese)[6] 沈锐利. 悬索桥主缆系统设计及架设计算方法研究[J].土木工程学报, 1996, 29(2): 3-9.Shen Ruili. Calculation methods for design and erection of cables of suspension bridge[J]. Journal of Civil Engineering, 1996, 29(2): 3-9.(in Chines)[7] 唐茂林, 强士中, 沈锐利. 悬索桥成桥主缆线形计算的分段悬链线法[J]. 铁道学报, 2003, 25(1): 87-91.Tang Maolin, Qiang Shizhong, Shen Ruili. Segmental catenary method of calculating the cable curve ofsuspension bridge [J]. Journal of the China Railway Society, 2003, 25(1): 87-91. (in Chinese)[8] 肖汝诚. 确定大跨径桥梁结构合理设计状态的理论与方法研究[D]. 上海: 同济大学, 1996. Xiao Rucheng. Theoriesand methods for determinationof reasonable design state of long span bridges [D]. Shanghai: Tongji University, 1996. (in Chinese)[9] 罗喜恒. 复杂悬索桥施工过程精细化分析研究[D]. 上海: 同济大学, 2004. Luo Xiheng. Fine analysis of construction process ofcomplex suspension bridges [D]. Shanghai: Tongji University, 2004. (in Chinese)[10] 徐士良. FORTRAN常用算法程序集[M]. 北京: 清华大学出版社, 1992. 98-127.Xu Shiliang. A library of common FORTRAN routines [M]. Beijing: Tsinghua University Press, 1992. 98-127. (in Chinese)万方数据作者:作者单位:张志国,邹振祝,赵玉成,陈伟,ZHANG Zhi-guo,ZOU Zhen-zhu,ZHAO Yu-cheng,CHEN Wei张志国,ZHANG Zhi-guo(哈尔滨工业大学航天工程与力学系,黑龙江,哈尔滨,150001),邹振祝,ZOU Zhen-zhu(哈尔滨工业大学航天工程与力学系,黑龙江,哈尔滨,150001;石家庄铁道学院土木分院,河北,石家庄,050043),赵玉成,陈伟,ZHAO Yu-cheng,CHEN Wei(石家庄铁道学院土木分院,河北,石家庄,050043)工程力学ENGINEERING MECHANICS2005,22(3)1次刊名:英文刊名:年,卷(期):被引用次数:参考文献(10条)1.钱冬生.陈仁福大跨悬索桥的设计与施工19972.N J Gimsing Cable supported bridges-concept and design 19973.H M Irvine Cable structures 19814.史建三悬索桥大缆架设计算的索长分析法[期刊论文]-桥梁建设1993(04)5.肖汝诚.贾丽君.王小同确定大跨悬索桥主缆成桥线形的虚拟梁法[期刊论文]-计算力学学报1999(01)6.沈锐利悬索桥主缆系统设计及架设计算方法研究1996(02)7.唐茂林.强士中.沈锐利悬索桥成桥主缆线形计算的分段悬链线法[期刊论文]-铁道学报2003(01)8.肖汝诚确定大跨径桥梁结构合理设计状态的理论与方法研究[学位论文] 19969.罗喜恒复杂悬索桥施工过程精细化分析研究[学位论文] 200410.徐士良FORTRAN常用算法程序集1992引证文献(1条)1.赵文婷空间缆索悬索桥主缆线形的分析方法[期刊论文]-黑龙江交通科技2008(4)本文链接:/Periodical_gclx200503030.aspx。
斜拉桥与悬索桥计算理论简析斜拉桥与悬索桥是桥梁结构中跨越能力最大的两种桥型,随着桥梁建造向大跨径方向发展,它们越来越成为人们研究的热点。
通过大跨径桥梁理论的学习,我对斜拉桥与悬索桥的计算理论有了较为系统的了解。
在本文中,我想从一个设计者的角度,在概念层次上,对斜拉桥与悬索桥的计算理论做个总结,以加深自己对这些计算理论的理解。
一、斜拉桥的计算理论斜拉桥诞生于十七世纪,在最近的五十年间,斜拉桥有了飞速的发展,成为200米到800米跨径范围内最具竞争力的桥梁结构形式之一。
有理由相信,在大江河口的软土地基上或不适合建造悬索桥的地区,有可能修建超过1200米的斜拉桥。
斜拉桥是塔、梁、索三种基本结构组成的缆索承重结构体系,一般表现为柔性的受力特性。
(一)、斜拉桥的静力设计过程1、方案设计阶段此阶段也称为概念设计。
本阶段的主要任务是凭借设计者的经验,参考别的斜拉桥的设计,结合自己的分析计算,来完成结构的总体布置,初拟构件尺寸。
根据此设计文件,设计者或甲方(有些地方领导说了算)进行方案比选。
2、初步设计阶段本阶段在前一阶段工作的基础上进一步细化。
主要任务是:通过反复计算比较以确定恒活载集度、恒载分析、调索初定恒载索力、修正斜拉索截面积、活载及附加荷载计算、荷载组合及梁体配索、索力优化以及强度刚度验算等。
3、施工图设计阶段此阶段要对斜拉桥的每一部位以及每一施工阶段进行计算,确保结构安全。
主要计算内容有:构件无应力尺寸计算、对施工阶段循环倒退分析、计算斜拉索初张力、预拱度计算、强度刚度稳定性验算以及前进分析验算等。
(二)、斜拉桥的计算模式1、平面杆系加横分系数此模式用在概念设计阶段研究结构的设计参数,以求获得理想的结构布置。
还可用于技术设计阶段,仅仅计算恒载作用下的内力。
2、空间杆系计算模式此模式用在空间荷载(风载、地震荷载以及局部温差等)作用下的静力响应分析。
此模式按照主梁可分为三种:“鱼骨”模式、双梁式模式与三梁式模型。