数字电路第4章(4数据选择器及数值比较器)_2..

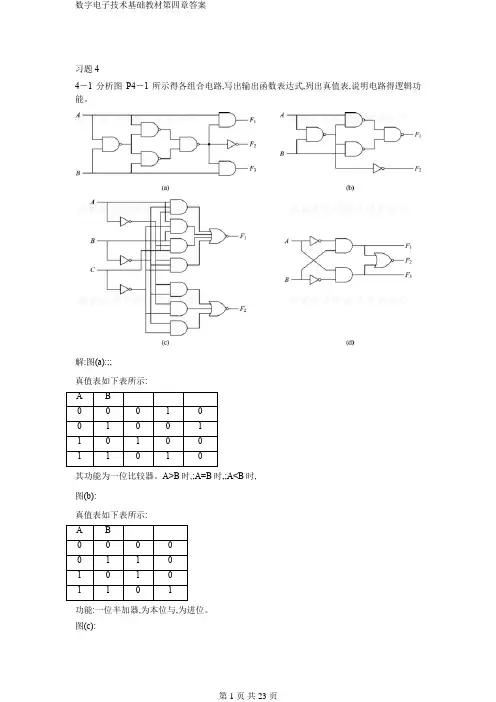
习题44－1 分析图P4－1所示得各组合电路,写出输出函数表达式,列出真值表,说明电路得逻辑功能。

解:图(a):;;真值表如下表所示:其功能为一位比较器。

A>B时,;A=B时,;A<B时,图(b):真值表如下表所示:功能:一位半加器,为本位与,为进位。

图(c):真值表如下表所示:功能:一位全加器,为本位与,为本位向高位得进位。

图(d):;;功能:为一位比较器,A<B时,＝1;A=B时,＝1;A>B时,＝14－2 分析图P4－2所示得组合电路,写出输出函数表达式,列出真值表,指出该电路完成得逻辑功能。

解:该电路得输出逻辑函数表达式为:因此该电路就是一个四选一数据选择器,其真值表如下表所示:,当M＝1时,完成4为二进制码至格雷码得转换;当M＝0时,完成4为格雷码至二进制得转换。

试分别写出,,,得逻辑函数得表达式,并列出真值表,说明该电路得工作原理。

解:该电路得输入为,输出为。

真值表如下:由此可得:完成二进制至格雷码得转换。

完成格雷码至二进制得转换。

4－4 图P4－4就是一个多功能逻辑运算电路,图中,,,为控制输入端。

试列表说明电路在,,,得各种取值组合下F与A,B得逻辑关系。

解:,功能如下表所示,两个变量有四个最小项,最多可构造种不同得组合,因此该电路就是一个能产生十六种函数得多功能逻辑运算器电路。

4－5 已知某组合电路得输出波形如图P4－5所示,试用最少得或非门实现之。

解:电路图如下:4－6 用逻辑门设计一个受光,声与触摸控制得电灯开关逻辑电路,分别用A,B,C表示光,声与触摸信号,用F表示电灯。

灯亮得条件就是:无论有无光,声信号,只要有人触摸开关,灯就亮;当无人触摸开关时,只有当无关,有声音时灯才亮。

试列出真值表,写出输出函数表达式,并画出最简逻辑电路图。

解:根据题意,列出真值表如下:由真值表可以作出卡诺图,如下图:C AB 00 10 11 100 1由卡诺图得到它得逻辑表达式为: 由此得到逻辑电路为:4－7 用逻辑门设计一个多输出逻辑电路,输入为8421BCD 码,输出为3个检测信号。

第一章信号表述数字信号----时间和数值均离散的电信号模拟信号----时间和数值均连续变化的电信号，如正弦波、三角波等数字信号的描述方法1、二值数字逻辑和逻辑电平（逻辑0和逻辑1）2、数字波形非归零形归零形数制进制下表进位基数数码符号十进制 D 10 0、1、2、3、4、5、6、7、8、9二进制 B 2 0、1八进制O 8 0、1、2、3、4、5、6、7十六进制H 16 0、1、2、3、4、5、6、7、8、9 、A、B、C、D、E、F 十进制一般表达式∞K i∗10i K i∈[0~9](N)10=i=―∞二进制一般表达式∞(N)2=K i∗2i K i∈[0，1]i=―∞进制转换1、二进制数→十进制数将二进制的数按权展成多项式，按十进制求和.2、十进制数→二进制数整数部分转换方法：除2取余，直到商为0。

（短除法）拆分法凑数法小数部分转换方法：乘2取整直到积的小数为零或满足误差要求。

（连乘法）3、十六←→二进制之间转换4、八←→二进制之间转换二进制代码BCD码有权码：8421码、2421码、5421码无权码：余3码、余3循环码格雷码ASCII码逻辑运算逻辑函数的表示方法真值表逻辑函数表达式逻辑图波形图逻辑函数表示方法之间的转换1.真值表到逻辑图的转换(1)根据真值表写出逻辑表达式(2) 化简逻辑表达式(3) 根据与或逻辑表达式画逻辑图2. 逻辑图到真值表的转换根据逻辑图逐级写出表达式；化简变换求最简与或式；将输入变量的所有取值逐一代入表达式得真值表第二章逻辑代数的基本定律和恒等式=A=1=A=1B+AA+(B+C)A∙B+A∙CB=A+B+C+⋯=A+BC=A∙B+A∙C等式证明①.采用代数的方法②.采用真值表的方法逻辑代数的基本规则1. 代入规则：⑴规则：任何一个含有某变量的等式，如果等式中所有出现此变量的位置均代之以一个逻辑函数式，则此等式依然成立。

⑵作用：扩大基本公式的应用范围。

2. 反演规则⑴规则：对于任意一个逻辑函数式F，做如下处理：* 若把式中的运算符“ · ”换成“ + ”，“ + ” 换成“ · ”* 常量“0”换成“1”，“1”换成“0”* 原变量换成反变量，反变量换成原变量* 保持原函数的运算次序不变那么得到的新函数式称为原函数式F的反函数式。

第1章 数制和码制 一、填空题1．数制转换：（011010）2 =（ ）10 =（ ）8 =（ ）16。

2．数制转换：（35）10 =（ ）2 =（ ）8 =（ ）16。

3．数制转换：（251）8 =（ ）2 =（ ）16 =（ ）10。

4．数制转换：（4B ）16 =（ ）2 =（ ）8 =（ ）10。

5．数制转换：（69）10 =（ ）2 =（ ）16 =（ ）8。

6．将二进制数转换为等值的八进制和十六进制数 （10011011001）2 =（ ）8 =（ ）16。

7．将二进制数转换为等值的八进制和十六进制数 （1001010.011001）2 =（ ）8 =（ ）16。

一、填空题答案： 1．26、32、1A ； 2．100011、43、 23； 3．10101001、A9、169； 4．1001011、113、75； 5．1000101、45、105； 6．2331、4D9； 7．112.31、4A.64。

第2章 逻辑代数基础 一、填空题1．逻辑函数Y AB A B ''=+，将其变换为与非-与非形式为 。

2．逻辑函数Y A B AB C ''=+，将其变换为与非-与非形式为 。

3. 将逻辑函数AC BC AB Y ++=化为与非-与非的形式，为 。

4．逻辑函数Y A A BC '''=+，化简后的最简表达式为 。

5．逻辑函数Y A B A B ''=++，化简后的最简表达式为 。

6．逻辑函数()()Y A BC AB ''''=+，化简后的最简表达式为 。

7. 逻辑函数Y AB AB A B ''=++，化简后的最简表达式为 。

一、填空题答案1．()()()Y AB A B '''''= ； 2．()()()Y A B AB C '''''=； 3． ()()()()Y AB BC AC ''''=； 4． Y A '=； 5．1Y =； 6．1Y =； 7．Y A B =+。

第4章习题及解答用门电路设计一个4线—2线二进制优先编码器。

编码器输入为3210A A A A ，3A 优先级最高，0A 优先级最低，输入信号低电平有效。

输出为10Y Y ，反码输出。

电路要求加一G 输出端，以指示最低优先级信号0A 输入有效。

题 解：根据题意，可列出真值表，求表达式，画出电路图。

其真值表、表达式和电路图如图题解所示。

由真值表可知3210G A A A A =。

(a)0 0 0 00 0 0 10 0 1 00 0 1 10 1 0 00 1 0 10 1 1 00 1 1 11 0 0 0 1 0 0 11 0 1 01 0 1 11 1 0 01 1 0 11 1 1 01 1 1 10000000000000000000000000010100011111010110000103A 2A 1A 0A 1Y 0Y G真值表≥1&1Y 3A 2A 1&&1A 0Y &1GA 00 01 11 100010001111000000001101113A 2A 1A 0A 03231Y A A A A =+00 01 11 1000000011110001000011103A 2A 1A 0A 132Y A A =(b) 求输出表达式(c) 编码器电路图图 题解4.1试用3线—8线译码器74138扩展为5线—32线译码器。

译码器74138逻辑符号如图（a ）所示。

题 解：5线—32线译码器电路如图题解所示。

&&&&11EN01234567BIN/OCTENY 0&G 1G 2AG 2B42101234567BIN/OCTEN&G 1G 2A G 2B42101234567BIN/OCT EN&G 1G 2A G 2B42101234567BIN/OCT EN&G 1G 2A G 2B421A 0A 1A 2A 3A 4Y 7Y 8Y 15Y 16Y 23Y 24Y 31图 题解4.3写出图所示电路输出1F 和2F 的最简逻辑表达式。

习题答案第一章数制和码制1．数字信号和模拟信号各有什么特点?答：模拟信号——量值的大小随时间变化是连续的。

数字信号——量值的大小随时间变化是离散的、突变的（存在一个最小数量单位△）。

2．在数字系统中为什么要采用二进制?它有何优点?答：简单、状态数少，可以用二极管、三极管的开关状态来对应二进制的两个数。

3.二进制：0、1；四进制：0、1、2、3；八进制：0、1、2、3、4、5、6、7；十六进制：0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。

4.(30.25)10=( 11110.01)2=( 1E.4)16。

(3AB6)16=( 0011101010110110)2=(35266)8。

(136.27)10=( 10001000.0100)2=( 88.4)16。

5.B E6.ABCD7.(432.B7)16=( 010*********. 10110111)2=(2062. 556)8。

8.二进制数的1和0代表一个事物的两种不同逻辑状态。

9.在二进制数的前面增加一位符号位。

符号位为0表示正数；符号位为1表示负数。

这种表示法称为原码。

10.正数的反码与原码相同，负数的反码即为它的正数原码连同符号位按位取反。

11.正数的补码与原码相同，负数的补码即为它的反码在最低位加1形成。

12.在二进制数的前面增加一位符号位。

符号位为0表示正数；符号位为1表示负数。

正数的反码、补码与原码相同，负数的反码即为它的正数原码连同符号位按位取反。

负数的补码即为它的反码在最低位加1形成。

补码再补是原码。

13.A:(+1011)2的反码、补码与原码均相同：01011；B: (-1101)2的原码为11101，反码为10010，补码为10011.14.A: (111011)2 的符号位为1，该数为负数，反码为100100，补码为100101. B: (001010)2 的符号位为0，该数为正，故反码、补码与原码均相同：001010.15.两个用补码表示的二进制数相加时，和的符号位是将两个加数的符号位和来自最高有效数字位的进位相加，舍弃产生的进位得到的结果就是和的符号。

第1章 数字电路基础知识1 电子电路主要分为两类：一类是电子电路主要分为两类：一类是 模拟电路 ，另一类是，另一类是 数字电路 。

2 模拟电路处理的是模拟电路处理的是 模拟信号 ，而数字电路处理的是，而数字电路处理的是 数字信号 。

3 晶体管（即半导体三极管）的工作状态有三种：晶体管（即半导体三极管）的工作状态有三种：截止截止、 放大和 饱和。

在模拟电路中，晶体管主要工作在体管主要工作在 放大状态 。

4 在数字电路中，晶体管工作在在数字电路中，晶体管工作在 截止与 饱和状态，也称为状态，也称为 “开关”状态。

状态。

5 模拟信号是一种模拟信号是一种大小随时间连续变化大小随时间连续变化的电压或电流，数字信号是一种的电压或电流，数字信号是一种突变突变的电压和电流。

6 模拟信号的电压或电流的大小是模拟信号的电压或电流的大小是随时间连续缓慢变化的随时间连续缓慢变化的，而数字信号的特点是“保持”（一段时间内维持低电压或高电压）和“段时间内维持低电压或高电压）和“突变突变”（低电压与高电压的转换瞬间完成）。

7 在数字电路中常将0~1v 范围的电压称为范围的电压称为低电平低电平，用，用““0”来表示；将3~5v 范围的电压称为高电平，用，用““1”来表示。

来表示。

介绍了数字电路的发展状况和数字电路的一些应用领域，并将数字电路和模拟电路进行了比较，让读者了解两者的区别，以利于后面数字电路的学习。

以利于后面数字电路的学习。

第2章 门电路1 基本门电路有基本门电路有与门与门、或门、非门三种。

三种。

2 与门电路的特点是：只有输入端都为只有输入端都为 高电平 时，输出端才会输出高电平；只要有一个输入端为“0”，输出端就会输出输出端就会输出 低电平 。

与门的逻辑表达式是与门的逻辑表达式是 Y A B =· 。

3 或门电路的特点是：只要有一个输入端为只要有一个输入端为 高电平 ，输出端就会输出高电平。

只有输入端都为 低电平 时，输出端才会输出低电平。

数字电路第四章答案【篇一：数字电路答案第四章时序逻辑电路2】p=1，输入信号d被封锁，锁存器的输出状态保持不变；当锁存命令cp=0，锁存器输出q?d，q=d；当锁存命令cp出现上升沿，输入信号d被封锁。

根据上述分析，画出锁存器输出q及 q的波形如习题4.3图（c）所示。

习题4.4 习题图4.4是作用于某主从jk触发器cp、j、k、 rd及 sd 端的信号波形图，试绘出q端的波形图。

解：主从jk触发器的 rd、且为低有效。

只有当rd?sd?1 sd端为异步清零和复位端，时，在cp下降沿的作用下，j、k决定输出q状态的变化。

q端的波形如习题4.4图所示。

习题4.5 习题4.5图（a）是由一个主从jk触发器及三个非门构成的“冲息电路”，习题4.5图（b）是时钟cp的波形，假定触发器及各个门的平均延迟时间都是10ns，试绘出输出f的波形。

cpf cp100ns10nsq（a）f30ns10ns（b）（c）习题4.5图解：由习题4.5图（a）所示的电路连接可知：sd?j?k?1，rd?f。

当rd?1时，在cp下降沿的作用下，且经过10 ns，状态q发生翻转，再经过30ns，f发生状态的改变，f?q。

rd?0时，经过10ns，状态q=0。

根据上述对电路功能的分析，得到q和f的波形如习题4.5图（c）所示。

习题4.6 习题4.6图（a）是一个1检出电路，图（b）是cp及j端的输入波形图，试绘出 rd端及q端的波形图（注：触发器是主从触发器，分析时序逻辑图时，要注意cp=1时主触发器的存储作用）。

cpj（a）qd（c）cp j（b）习题图解：分析习题4.6图（a）的电路连接：sd?1,k?0,rd?cp?q；分段分析习题4.6图（b）所示cp及j端信号波形。

（1）cp=1时，设q端初态为0，则rd?1。

j信号出现一次1信号，即一次变化的干扰，且k=0，此时q端状态不会改变；（2）cp下降沿到来，q端状态变为1，rd?cp，此时cp=0，异步清零信号无效；（3）cp出现上升沿，产生异步清零信号，使q由1变为0，在很短的时间里 rd又恢复到1；（4）同理，在第2个cp=1期间，由于j信号出现1信号，在cp下降沿以及上升沿到来后，电路q端和 rd端的变化与（2）、（3）过程的分析相同，其波形如习题4.6图（c）所示。

第1章数字电路基础知识1 电子电路主要分为两类：一类是模拟电路，另一类是数字电路。

2 模拟电路处理的是模拟信号，而数字电路处理的是数字信号。

3 晶体管（即半导体三极管）的工作状态有三种：截止、放大和饱和。

在模拟电路中，晶体管主要工作在放大状态。

4 在数字电路中，晶体管工作在截止与饱和状态，也称为“开关”状态。

5 模拟信号是一种大小随时间连续变化的电压或电流，数字信号是一种突变的电压和电流。

6 模拟信号的电压或电流的大小是随时间连续缓慢变化的，而数字信号的特点是“保持”（一段时间内维持低电压或高电压）和“突变”（低电压与高电压的转换瞬间完成）。

7 在数字电路中常将0~1v范围的电压称为低电平，用“0”来表示；将3~5v范围的电压称为高电平，用“1”来表示。

第2章 门电路1 基本门电路有与门、或门、非门三种。

2 与门电路的特点是：只有输入端都为 高电平 时，输出端才会输出高电平；只要有一个输入端为“0”，输出端就会输出 低电平 。

与门的逻辑表达式是 Y A B =∙ 。

3 或门电路的特点是：只要有一个输入端为 高电平 ，输出端就会输出高电平。

只有输入端都为 低电平 时，输出端才会输出低电平。

或门的逻辑表达式是Y A B =+ 。

4 非门电路的特点是：输入与输出状态总是 相反 。

非门的逻辑表达式是 Y A -= 。

5 与非门的特点是：只有输入全为“1”，输出为 0 ，只要有一个输入端为“0”，输出端就会输出 1 。

与非门的逻辑表达式是 。

6 或非门的特点是：只有输入全为“0”时，才输出 1 ，只要输入有“1”，输出就为 0 。

或非门的逻辑表达式是 。

7 与或非的特点是：A 、B 或C 、D 两组中有一组全为“1”，输出就为 0 ，否则输出就为 1 。

与或非门的逻辑表达式是 。

8 异或门的特点是：当两个输入端一个为“0”，另一个为“1”，输出为 1 ，当两个输入端均为“1”或“0”时，输出为 0 。

异或门的逻辑表达式是 。