求直导线中的感应电动势解

习题十三13-1 如题图13-1所示，两条平行长直导线和一个矩形导线框共面，且导线框的一个边与长直导线平行，到两长直导线的距离分别为1r ，2r 。

已知两导线中电流都为0sin I I t ω=，其中I 0和ω为常数，t 为时间。

导线框长为a ，宽为b ，求导线框中的感应电动势。

解：无限长直电流激发的磁感应强度为02IB rμ=π。

取坐标Ox 垂直于直导线，坐标原点取在矩形导线框的左边框上，坐标正方向为水平向右。

取回路的绕行正方向为顺时针。

由场强的叠加原理可得x 处的磁感应强度大小00122()2()IIB r x r x μμ=+π+π+方向垂直纸面向里。

通过微分面积d d S a x =的磁通量为00m 12d d d d 2()2()I I B S B S a x r x r x μμΦππ⎡⎤=⋅==+⎢⎥++⎣⎦通过矩形线圈的磁通量为00m 012d 2()2()b I I a x r x r x μμΦ⎡⎤=+⎢⎥π+π+⎣⎦⎰012012ln ln sin 2a r b r b I t r r μω⎛⎫++=+ ⎪π⎝⎭ 感生电动势0m 12012d ln ln cos d 2i a r b r b I t t r r μωΦεω⎛⎫++=-=-+ ⎪π⎝⎭ 012012()()ln cos 2ar b r b I t r r μωω⎡⎤++=-⎢⎥π⎣⎦0i ε>时，回路中感应电动势的实际方向为顺时针；0i ε<时，回路中感应电动势的实际方向为逆时针。

13-2 如题图13-2所示，有一半径为r =10cm 的多匝圆形线圈，匝数N =100，置于均匀磁场B 中（B =0.5T ）。

圆形线圈可绕通过圆心的轴O 1O 2转动，转速1600r min n -=⋅。

求圆线圈自图示的初始位置转过题图13-1题图13-2解图13-1/2π时，(1) 线圈中的瞬时电流值（线圈的电阻为R =100Ω，不计自感）； (2) 圆心处磁感应强度。

电磁感应部分基本要求：1、掌握法拉第电磁感应定律，会用法拉第电磁感应定律求电动势；2、掌握动生电动势计算公式并会用该公式求相关习题；3、掌握感生电动势计算公式，会求两种类型的感生电动势；4、掌握自感、互感的定义，会求自感、互感系数以及自感、互感电动势；5、掌握通电线圈的储能公式，磁场能量计算公式，会计算无限长载流圆柱面、体限定区域内的能量；6、了解真空中麦克斯韦方程组中每个方程的物理意义；7、掌握平面电磁波的性质、能量密度及能流密度公式。

相关习题：一、计算题1．如图所示，一根很长的直导线载有交变电流0i I sin t ω=，它旁边有一长方形线圈ABCD ，长为l ，宽为b a -，线圈和导线在同一平面内，求：(1)穿过回路ABCD 的磁通量m Φ；（2）互感系数；(3)回路ABCD 中的感应电动势。

2．一长直载充导线，电流强度I=10A ，有另一变长L=0.2m 金属棒AB ，在载流导线的平面内以2m ·5-1的速度平行于导线运动。

如图所示：棒的一端离导线a=0.1m ，求运动导线中的电动势εAB ，哪点电势高？ACDlbia3.如图，长度为R 的均匀导体棒OA 绕O 点以角速度ω转动，均匀磁场B 的方向与转动平面垂直。

试求棒中动生电动势的大小并说明方向。

⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯A O ωB4．长直导线与矩形单匝线圈共面放置，导线与线圈的长边平行，矩形线圈的边长分别为a 、b ，它到直导线的距离为c （如图所示），当矩形线圈中通有电流t I I ωsin 0=时，求直导线中的感应电动势。

5．一圆环形线圈a 由1N 匝细线绕成，截面积半径为r ，放在另一个匝数为2N ，半径为R 的圆环形线圈b的中心，其中R r >>，两线圈同轴，求（1）两线圈的互感系数M ；（2）当线圈a 中的电流以dI dt变化时，求线圈b 中的感生电动势（习题16.13）。

6.一无限长直导线，截面各处的电流密度相等，电流为I 。

电磁感应专题复习（重要）基础回顾（一）法拉弟电磁感应定律1、内容：电路中感应电动势的大小，跟穿过这一电路的磁通量的变化率成正比E＝nΔΦ/Δt（普适公式）当导体切割磁感线运动时，其感应电动势计算公式为E＝BLVsinα2、E＝nΔΦ/Δt与E＝BLVsinα的选用①E＝nΔΦ/Δt计算的是Δt时间内的平均电动势，一般有两种特殊求法ΔΦ/Δt=BΔS/Δt即B不变ΔΦ/Δt=SΔB/Δt即S不变② E＝BLVsinα可计算平均动势，也可计算瞬时电动势。

③直导线在磁场中转动时，导体上各点速度不一样，可用V平=ω（R1+R2）/2代入也可用E＝nΔΦ/Δt 间接求得出 E＝BL2ω/2（L为导体长度，ω为角速度。

）（二）电磁感应的综合问题一般思路：先电后力即：先作“源”的分析--------找出电路中由电磁感应所产生的电源，求出电源参数E和r。

再进行“路”的分析-------分析电路结构，弄清串、并联关系，求出相应部分的电流大小，以便安培力的求解。

然后进行“力”的分析--------要分析力学研究对象（如金属杆、导体线圈等）的受力情况尤其注意其所受的安培力。

按着进行“运动”状态的分析---------根据力和运动的关系，判断出正确的运动模型。

最后是“能量”的分析-------寻找电磁感应过程和力学研究对象的运动过程中能量转化和守恒的关系。

【常见题型分析】题型一楞次定律、右手定则的简单应用例题（2006、广东）如图所示，用一根长为L、质量不计的细杆与一个上弧长为L0 、下弧长为d0的金属线框的中点连接并悬挂于o点，悬点正下方存在一个弧长为2 L0、下弧长为2 d0、方向垂直纸面向里的匀强磁场，且d0 远小于L先将线框拉开到图示位置，松手后让线框进入磁场，忽略空气阻力和摩擦，下列说法中正确的是A、金属线框进入磁场时感应电流的方向为a→b→c→d→B、金属线框离开磁场时感应电流的方向a→d→c→b→C、金属线框d c边进入磁场与ab边离开磁场的速度大小总是相等D、金属线框最终将在磁场内做简谐运动。

9-1两个半径分别为R 和r 的同轴圆形线圈相距x ，且R >>r ，x >>R ．若大线圈通有电流I 而小线圈沿x 轴方向以速率v 运动，试求小线圈回路中产生的感应电动势的大小． 解：在轴线上的磁场()()22003322222IR IR B x R x R xμμ=≈>>+32202xr IR BS πμφ==v xr IR dt dx x r IR dt d 422042202332πμπμφε=--=-=9-2如图所示，有一弯成θ 角的金属架COD 放在磁场中，磁感强度B ϖ的方向垂直于金属架COD 所在平面．一导体杆MN 垂直于OD 边，并在金属架上以恒定速度v ϖ向右滑动，v ϖ与MN 垂直．设t =0时，x = 0．求当磁场分布均匀，且B ϖ不随时间改变，框架内的感应电动势i ε．解：12m B S B xy Φ=⋅=⋅,θtg x y ⋅=,vt x =22212/()/i d dt d Bv t tg dt Bv t tg εϕθθ=-=-=⋅，电动势方向：由M 指向N9-3 真空中，一无限长直导线，通有电流I ，一个与之共面的直角三角形线圈ABC 放置在此长直导线右侧。

已知AC 边长为b ，且与长直导线平行，BC 边长为a ，如图所示。

若线圈以垂直于导线方向的速度v 向右平移，当B 点与直导线的距离为d 时，求线圈ABC 内的感应电动势的大小和方向。

解：当线圈ABC 向右平移时，AB 和AC 边中会产生动生电动势。

当C 点与长直导线的距离为d 时，AC 边所在位置磁感应强度大小为：02()IB a d μπ=+AC 中产生的动生电动势大小为：xr IRx vC DOxMθBϖv ϖ02()AC AC IbvBl v a d μεπ==+，方向沿CA 方向如图所示，在AB 边上取微分元dl ，微分元dl 中的动生电动势为，()AB d v B dl ε=⨯⋅v v v其方向沿BA 方向。

高中物理中关于感应电动势的计算公式有两个：E=△φ/△t和E= BLvsinθ。

对于这两个公式的真正物理含义及适用范围，有些学生模糊不清。

现就这一知识点做如下阐述。

（一）关于E=△φ/△t严格地说，E=△φ/△t不能确切反映法拉第电磁感应定律的物理含义。

教材中关于法拉第电磁感应定律是这样阐述的：电路中感应电动势的大小跟穿过这一电路的磁通量的变化率成正比。

而表达式△φ/△t所表示的物理意义应为：磁通变化量与发生此变化所用时间的比值，这与磁通变化率是不能等同的，只有在△t →0时，△φ/△t的物理意义才是磁通量的变化率。

由于中学阶段没有涉及微积分，故教材用E=△φ/△t 来表示法拉第电磁感应定律是完全可以的。

但必须清楚：用公式E=△φ/△t求得的感应电动势只能是一个平均值，而不是瞬时值。

因为△和△t 都是某一时间段内的对应量而不是某一时刻的对应量，所以直接用此公式求得的E为△t时间内产生的感应电动势的平均值。

（二）关于E=BLvsinθ公式E=BLvsinθ是由公式E=Δφ/Δt推导而来。

此公式适用于导体在匀强磁场中切割磁力线而产生感应电动势的情况，实质是由于导体的相对磁力线运动（切割磁力线），使回路所围面积发生变化，使得通过回路的磁通量发生变化从而产生感应电动势。

可以认为公式E=BLvsinθ 所表示的物理意义是法拉第电磁感应定律的一种特殊情况。

用此公式求得的E可为平均值也可为瞬时值：若v为某时间段内的平均速度，则求得的E为相应时间段内的平均感应电动势；若v为某时刻的瞬时速度，则求得的E为相应时刻的瞬时感应电动势。

一般用此公式来计算瞬时感应电动势。

（三）例题分析如图1，两根平行金属导轨固定在水平桌面上，每根导轨每米的电阻为r, 导轨的端点P、Q用电阻可忽略的导线相连，两道轨间距为L。

有随时间变化的匀强磁场垂直于桌面，已知磁感应强度B与时间t的关系为B=kt ( k为常数，且k＞0)，一电阻不计的金属杆可在导轨上无摩擦地滑动，在滑动过程中保持与导轨垂直。

第六章 电磁感应与暂态过程一、判断题1、若感应电流的方向与楞次定律所确定的方向相反，将违反能量守恒定律。

√2、楞次定律实质上是能量守恒定律的反映。

√3、涡电流的电流线与感应电场的电场线重合。

×4、设想在无限大区域内存在均匀的磁场，想象在这磁场中作一闭合路径，使路径的平面与磁场垂直，当磁场随时间变化时，由于通过这闭合路径所围面积的磁感通量发生变化，则此闭合路径存在感生电动势。

×5、如果电子感应加速器的激励电流是正弦交流电，只能在第一个四分之一周期才能加速电子。

√6、自感系数I L ψ=,说明通过线圈的电流强度越小，自感系数越大。

×7、自感磁能和互感磁能可以有负值。

×8、存在位移电流，必存在位移电流的磁场。

×9、对一定的点，电磁波中的电能密度和磁能密度总相等。

√ 10、在电子感应加速器中，轨道平面上的磁场的平均磁感强度必须是轨道上的磁感强度的两倍。

√11、一根长直导线载有电流I ，I 均匀分布在它的横截面上，导线内部单位长度的磁场能量为：πμ1620I 。

√12、在真空中，只有当电荷作加速运动时，它才可能发射电磁波。

√13、振动偶极子辐射的电磁波，具有一定方向性，在沿振动偶极子轴线方向辐射最强，而与偶极子轴线垂直的方向没有辐射。

×14、一个正在充电的圆形平板电容器，若不计边缘效应，电磁场输入的功率是⎪⎪⎭⎫⎝⎛=∙=⎰⎰C q dt d A d S P 22 。

(式中C 是电容，q 是极板上的电量，dA 是柱例面上取的面元)。

√二、选择题1、一导体棒AB 在均匀磁场中绕中点O 作切割磁感线的转动AB 两点间的电势差为： （A ）0（B ）1/2OA ωB （C ）-1/2AB ωB （D ）OA ωB A2、如图所示，a 和b 是两块金属板，用绝缘物隔开，仅有一点C 是导通的，金属板两端接在一电流计上，整个回路处于均匀磁场中，磁场垂直板面，现设想用某种方法让C 点绝缘，而同时让C 点导通，在此过程中（A ）电路周围的面积有变化。

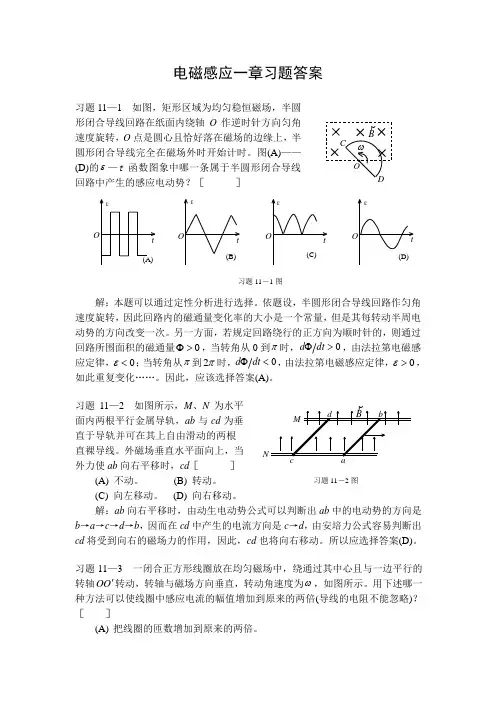
电磁感应一章习题答案习题11—1 如图，矩形区域为均匀稳恒磁场，半圆形闭合导线回路在纸面内绕轴O 作逆时针方向匀角速度旋转，O 点是圆心且恰好落在磁场的边缘上，半圆形闭合导线完全在磁场外时开始计时。

图(A)——(D)的ε—t 函数图象中哪一条属于半圆形闭合导线回路中产生的感应电动势？［ ］解：本题可以通过定性分析进行选择。

依题设，半圆形闭合导线回路作匀角速度旋转，因此回路内的磁通量变化率的大小是一个常量，但是其每转动半周电动势的方向改变一次。

另一方面，若规定回路绕行的正方向为顺时针的，则通过回路所围面积的磁通量0>Φ，当转角从0到π时，0>Φdt d ，由法拉第电磁感应定律，0<ε；当转角从π到π2时，0<Φdt d ，由法拉第电磁感应定律，0>ε，如此重复变化……。

因此，应该选择答案(A)。

习题11—2 如图所示，M 、N 为水平面内两根平行金属导轨，ab 与cd 为垂直于导轨并可在其上自由滑动的两根直裸导线。

外磁场垂直水平面向上，当外力使ab 向右平移时，cd ［ ］(A) 不动。

(B) 转动。

(C) 向左移动。

(D) 向右移动。

解：ab 向右平移时，由动生电动势公式可以判断出ab 中的电动势的方向是b →a →c →d →b ，因而在cd 中产生的电流方向是c →d ，由安培力公式容易判断出cd 将受到向右的磁场力的作用，因此，cd 也将向右移动。

所以应选择答案(D)。

习题11—3 一闭合正方形线圈放在均匀磁场中，绕通过其中心且与一边平行的转轴O O '转动，转轴与磁场方向垂直，转动角速度为ω，如图所示。

用下述哪一种方法可以使线圈中感应电流的幅值增加到原来的两倍(导线的电阻不能忽略)？［ ］(A) 把线圈的匝数增加到原来的两倍。

习题11―1图t εO(A)tεO(B)tεO(C)tεO(D)abc d M NB ρ 习题11―2图(B) 把线圈的面积增加到原来的两倍，而形状不变。

无限长直导线感生电动势的简便推导作者：姚关心贾华锋来源：《物理教学探讨》2018年第02期摘要：利用了初等数学和法拉第电磁感应定律，推导出无限长直导线在穿过磁场和不穿过磁场两种情况下的感生电动势的统一表达式，并指明了感生电动势方向的判断方法。

推导过程简单，避免了高等数学中微积分的复杂运算。

关键词：无限长直导线；电磁感应定律；感生电动势中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2018）2-0056-21 引言根据麦克斯韦电磁场理论，当空间的磁场发生变化时，将在其周围区域产生涡旋电场，该电场对放入其中的电荷有力的作用。

因此，将导体放入该场中，导体中的电子会在涡旋电场的作用下定向移动，从而在导体的两端产生感生电动势。

导体两端的感生电动势的求解是大学物理和中学物理教学中一项重要的研究内容。

由于产生感生电动势的磁场通常分布在某一个特定区域，给我们计算导体两端的感生电动势带来了困难。

目前，对有限长的导体在一些规则的几何外形的磁场中的感生电动势的研究较多[1-5]，而对无限长的导体两端电动势的研究相对较少，其采用的是高等数学中微积分的方法[4]。

论文将利用初等数学和法拉第电磁感应定律方法，讨论无限长直导线在任意形状的磁场区域所产生的感生电动势。

2 模型如图1所示。

磁感应强度的方向保持不变，大小以常数、大于零变化，无限长直导线垂直于磁场方向，求图1中两根无限长直导线的感生电动势的大小。

3 解答过程3.1 无限长直导线 l1 感生电动势的推导在图1中无限长直导线l1的下方放置一根无限长直导线l3，l3∥l1，如图2所示。

由初等数学可知，两条平行线在无穷远处相交。

设交点分别为a、b两点，则两根相互平行的无限长直导线可以看成一个闭合回路L1。

在回路L1区域内没有磁场，则磁通量的变化率为零。

用ε表示回路的感生电动势，ε、ε分别表示无限长直导线l1、无限长直导线l3的感生电动势，由法拉第电磁感应定律，各个部分的电动势之间的关系可写为ε=ε+ε=0（1）由（1）式可得|ε|=|ε|（2）（2）式说明，在磁场外任何无线长直导线的感生电动势的大小相等，与无限长直导线到磁场区域的距离无关。

电磁学_北京大学中国大学mooc课后章节答案期末考试题库2023年1.如图为一均匀带电半球壳，关于其大圆截面S上电场和电势说法正确的是：【图片】参考答案:S面上电力线处处垂直于表面_S面为等势面2.关于静电场，以下说法正确的是参考答案:场强处处为零的区域一定是等势区域。

_等势区域一定是场强处处为零的区域。

3.已知一个气球上的正电荷均匀分布，假定皮球膨胀过程中保持球形，则当气球膨胀时参考答案:球外某点电场强度不变，电势不变_球内某点电场强度不变，电势变小4.图中两个互相垂直的圆电流环公共中心处的磁感应强度的大小和方向为【图片】参考答案:，平行于xz平面，与正x轴成夹角。

5.图示两根长直导线通有电流I，图中四种环路的环流正确的是：【图片】参考答案:，，，。

6.以下关于安培的四个示零实验说法正确的是参考答案:载流对折导线对无定向秤作用力为零，该实验说明：当电流反向时，它产生的作用力也反向。

_载流对折导线中一条为载流曲折线时对无定向秤作用力为零，该实验说明：电流元具有矢量的性质，即许多电流元的合作用是各个电流元产生作用的矢量叠加。

_A、B、C三个圆线圈，线度之比为1/n:1:n，A和C放在B两侧，AB距离与BC距离之比为1:n时，A和C对B的作用力为零，该实验说明：所有几何线度（电流元长度、相互距离）增加同一倍数时，作用力不变。

7.两个正电荷分别带电量q和Q，相对于确定的参考系以不为零的速度运动，某一时刻，两者相距为【图片】时，由电荷Q施加在电荷q上的磁力参考答案:方向垂直于电荷q的速度，大小取决于电荷Q的速度和电荷q的速度。

8.下面哪个叙述是不正确的？参考答案:电场线发自正电荷，收于负电荷。

_空间存在多个电荷时，同一电荷处既可以发出电场线，也可以接受电场线。

9.无穷大平面1的面电荷密度为+σ，无穷大平面2的面电荷密度为-σ。

当这两个无穷大平面平行放置时，电场强度的大小是：参考答案:两平面内部是σ/ε0，外部是010.设氢原子中的电子沿半径为r的圆轨道绕原子核运动，原子核中心位置固定不变。

《大学物理CII 》作业 No.04 电磁感应与电磁理论班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、选择题： 一、选择题1．如图，长度为l 的直导线ab 在均匀磁场B中以速度v移动，直导线ab 中的电动势为[ ] (A) Bl v (B) Bl v sin α(C) Bl v cosα(D) 0解：直导线ab 中的感应电动势为动生电动势，如图有ααεsin d 90cos sin d )(0Blv l vB l B v l ==⨯=⎰⎰⋅选B2．一矩形线框长为a 宽为b ，置于均匀磁场中，线框绕OO ′ 轴以匀角速度ω旋转（如图所示）。

设0=t 时，线框平面处于纸面内，则任一时刻感应电动势的大小为： [ ](A) t abB ωcos 2 (B) abB ω(C) t abB ωωcos 21(D) t abB ωωcos(E) t abB ωωsin解：因矩形线框绕OO ′ 轴在均匀磁场中以匀角速度ω旋转，则由图示有任一时刻穿过线框的磁通量为⎰=-=⋅=)sin()90cos(d t Bab t Bab S B ωωΦ，则由法拉第电磁感应定律得线框内的感应电动势大小：t abB t i ωωΦcos /d d =-=选D3．圆铜盘水平放置在均匀磁场中，B的方向垂直盘面向上。

当铜盘绕通过中心垂直于盘面的轴沿图示方向转动时， [ ](A) 铜盘上有感应电流产生，沿着铜盘转动的相反方向流动 (B) 铜盘上有感应电流产生，沿着铜盘转动的方向流动 (C) 铜盘上产生涡流 (D) 铜盘上有感应电动势产生，铜盘边缘处电势最高 (E) 铜盘上有感应电动势产生，铜盘中心处电势最高解：铜盘旋转时，可以视为是沿半径方向的铜导线在做切割磁力线的运动，铜盘上有感应电动势产生（动生电动势），且由⎰⋅⨯=ε沿半径l B vd )(知铜盘边缘处电势最高。

故选D4．两根无限长平行直导线载有大小相等方向相反的电流I ，I 以t ω-ItId d 的变化率增长，一矩形线圈位于导线平面内（如图），则：[ ](A)线圈中无感应电流 (B)线圈中感应电流为顺时针方向(C)线圈中感应电流为逆时针方向 (D)线圈中感应电流方向不确定解：因0d d >tI ，在回路产生的垂直于纸面向外的磁场⊗增强，根据愣次定律，回路中产生的感应电流应为顺时针方向，用以反抗原来磁通量的增加。

求解感应电动势的几种方法一 根据tE ∆∆Φ=求解 根据法拉第电磁感应定律计算感应电动势是最基本的方法，特别是对由于磁场变化而产生的感应电动势的计算，一般都采用此法。

例1 如图1所示，用同种材料、同样粗细的导线制成的两个单匝圆形线圈同心共面放置，大线圈的半径是小线圈半径的两倍，即r 1 = 2r 2。

只有小线圈内存在垂直于小线圈平面的磁场，当磁感应强度随时间而均匀变大时，大线圈与小线圈的电流大小之比为________，电流的热功率之比为_______。

解析 根据法拉电磁感应定律t n E ∆∆Φ=，有E 1 = E 2； 根据电阻定律Sl R ρ=，可知两线圈的电阻之比2121r r R R == 2； 根据欧姆定律RU I =，可得211221==R R I I ； 根据电流的热功率P = I 2R ，可知大线圈与小线圈的热功率之比为2122212121==R I R I P P 。

二 根据E = BLv 求解感应电动势导体平动切割磁感线产生电动势E = BLv sin θ，其中v ⊥ L ，L 为导体切割磁感线的有效长度，θ为磁场方向与速度方向之间的夹角。

例2 如图2所示，平行金属轨道间距为d ，一端跨接在阻值为R 的电阻，匀强磁场的磁感应强度为B ，方向垂直平行轨道所在的平面。

一根长直金属棒与轨道成30°角放置，金属棒每单位长度的电阻为r ，a 、b 两点分别为棒与轨道的接触点。

当金属棒以垂直于棒的恒定速度v 在金属轨道上滑行时，电路中的电流方向为_______，a 、b 两点间的电压为______。

解析 根据右手定则可知，电路中感应电流方向为逆时针方向。

金属棒切割磁感线的有效长度为d d 230sin 0=，则感应电动势为E = B · 2d · v ，则a 、b 两点间的电压为U ab =drR BdvR R drR E 222+=⋅+。

三 根据ω221BL E = 求解感应电动势 导体棒以某一点为轴，在垂直于磁场方向的匀强磁场中以角速度ω匀速转动，所产生的感应电动势为ω221BL E =。