偏振光和双折射相关概念详解共50页

第五章 光的偏振和晶体的双折射§ 5.1光的偏振态偏振：振动方向相对于传播方向的不对称性。

一．光是横波1、 光是电磁波——横波2、 用二向色性晶体（电气石晶体、硫酸碘奎宁晶体）检验——横波。

最初的器件是用细导线做成的密排线栅（金质线栅，d=5.08×10-4mm ），光通过时，由于与导线同方向的电场被吸收，留下与其垂直的振动。

1928年，Harvaed 大学的Land （19岁）发明了人造偏振片，用聚乙烯醇膜浸碘制得。

到1938年，出现了H 型偏振片，原理相同。

3、名词起偏：使光变为具有偏振特性。

检偏：检验光的偏振特性。

透振方向：通过偏振仪器光的电矢量的振动方向。

二．光的偏振态偏振：振动方向相对于传播方向的不对称性。

对可见光，只考虑其电矢量。

1．自然光振动方向随机，相对于波矢对称。

光的叠加是按强度相加。

可沿任意方向正交分解，在任一方向的强度为总强度之半。

021I I自然光是大量原子同时发出的光波的集合。

其中的每一列是由一个原子发出的，有一个偏振方向和相位，但光波之间是没有任何关系的。

所以，他们的集合，就是在各个方向振动相等、相位差随机的自然光。

在直角坐标系中，一列沿z 向传播、振动方向与X 轴夹角为θ的光，在X 方向的振幅为θθcos A A x =，由于各个光波在X 方向的总强度是光强相加，故有22022220cos )(A d A d A I x x πθθθππθ===⎰⎰同理2A I y π= 而总光强22022A d A I πθπ==⎰，故021I I I y x == 2．平面偏振光（线偏振光）只包含单一振动方向的电矢量。

在任一方向的光强θθ20cos I I =，马吕斯定律。

用偏振片可以获得平面偏振光。

偏振仪器（起偏器）的消光比=最小透射光强/最大透射光强 3．部分偏振光 介于自然光和线偏光之间。

偏振度=（I MAX -I MIN ）/（I MAX +I MIN ） 4．圆偏振光电矢量端点轨迹的投影为圆。

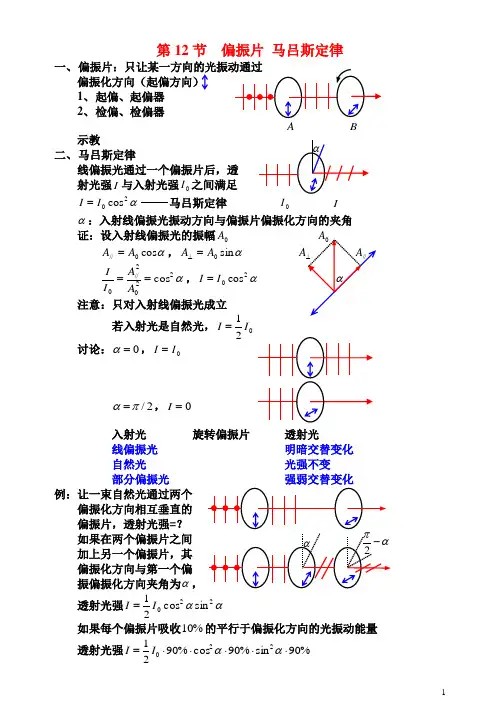
第12节 偏振片 马吕斯定律一、 偏偏振化方向（起偏方向）1、 起偏、起偏器2、 检偏、检偏器A B 示教二、 马吕斯定律 线偏振光通过一个偏振片后，透射光强I 与入射光强0I 之间满足α20cos I I = 马吕斯定律 0I Iα：入射线偏振光振动方向与偏振片偏振化方向的夹角证：设入射线偏振光的振幅0A αcos 0//A A =，αsin 0A A =⊥ α2202//0cos ==A A I I，α20cos I I = 注意：只对入射线偏振光成立若入射光是自然光，021I I =讨论：0=α，0I I =2/πα=，0=I入射光 旋转偏振片 透射光线偏振光 明暗交替变化自然光 光强不变部分偏振光 强弱交替变化 例：让一束自然光通过两个偏振化方向相互垂直的偏振片，透射光强=？如果在两个偏振片之间 加上另一个偏振片，其 偏振化方向与第一个偏振偏振化方向夹角为α，透射光强αα220sin cos 21I I =如果每个偏振片吸收%10的平行于偏振化方向的光振动能量 透射光强%90sin %90cos %9021220⋅⋅⋅⋅⋅=ααI I第13节 反射和折射光的偏振入射面：∏（入射线，法线）反射定律i i ='折射定律γsin sin 21n i n = MM '反射光和折射光都是部分偏振光反射光中，⊥振动多于//振动 折射光中，//振动多于⊥振动120n n arctg i i ==时 反射光为完全偏振光，只包含⊥0i ：布儒斯特角（起偏角） 120n n tgi =：布儒斯特定律 注意：（1）0i i =时，只反射部分⊥振动，不反射//振动折射光中包含其余的⊥振动和全部的//振动折射光仍是部分偏振光（2）0i i =时，反射光线⊥折射光线 证明：γsin sin 201n i n =，120n n tgi ==00cos sin i i ，0201cos sin i n i n = γs i n 2n =02cos i n ，γsin =0cos i =)sin(0i -π，20πγ=+i （3）自然光以布儒斯特角 照射玻璃片堆，可使折射光成为完全偏振光折射光中只剩下//振动例：一束自然光以布儒斯特角从空气照射玻璃片，界面2上的反射光是（A ）自然光 （B ）完全偏振光，光矢量振动方向⊥ （C ）完全偏振光，光矢量振动方向// （D ）部分偏振光 解：对界面1，0i 是布儒斯特角，对界面2，γ是布儒斯特角 120n n t g i =，20πγ=+i ，210n n c t g i tg ==γ 例：第14节 晶体的双折射现象一、晶体的双折射现象用自然光照射某些晶体（方解石）表面 产生两束折射光 示教特点：（1） 寻常光线（o 光），遵守折射定律非常光线（e 光），不遵守折射定律（2） 两条光线都是线偏振光，振向不同（3） 光轴（光线沿该方向入射不产生双折射）p253，单轴晶体，双轴晶体某条光线与光轴构成的平面：该光线的主平面 ∏（o 光，光轴）：o 光主平面 ∏（e 光，光轴）：e 光主平面（4）o 光振向⊥o 光主平面e 光振向//e 光主平面二、 对双折射的解释产生双折射的原因： o 光、e 光在晶体中的传播速度不同o 光波面是球面，e 光波面是旋转椭球面沿光轴方向o 光、e 光速度相同垂直光轴方向o 光、e 光速度相差最大o V ：o e 光速度o V e Vo V e e oo o n V c =/，e e n V c =/o n 、e n ：晶体的主折射率1、 平行光斜入射（光轴位于2、平行光垂直入射（光轴位于 入射面内，光轴与界面斜交） 入射面内，光轴与界面斜交）3、 平行光垂直入射（光轴平行4、平行光垂直入射（光轴位于 界面，光轴位于入射面内） 入射面内，光轴垂直界面）光轴 e o ,光同传播方向，但速度不同 e o ,光同传播方向，速度相同 仍属于双折射 不属于双折射5、 平行光斜入射（光轴//界面，光轴垂直入射面）o 光、e 光都遵守折射定律，e e o o n n i n γγsin sin sin 1==三、 偏振棱镜1、 尼科耳（棱镜）用加拿大树胶粘在一起加拿大树胶对o 2、 渥拉斯顿镜两块方解石直角棱镜构成两者光轴相垂直负晶体，e V >o V ，e n n <e 垂直板面振动的光线： 对第一块棱镜是o 光对第二块棱镜是e 光平行板面振动的光线： 对第一块棱镜是e 光对第二块棱镜是o 光垂直板面振动的光线由o →e 光，光密→光疏，折射光偏离法线 平行板面振动的光线由e →o 光，光疏→光密，折射光靠近法线 两条光线分开，都是线偏振光四、 偏振片某些双折射晶体对o 光和e 光的吸收率不同：二向色性 偏振片 获得偏振光的方法：（1）偏振片（2）偏振棱镜（3）以布儒斯特角照射玻璃片例：两块偏振片叠放在一起，其偏振化方向夹角 30，用强度相同的自然光和线偏振光混合而成的光束垂直入射，已知两成分的入 射光透射后强度相等求：（1）入射光中线偏振光振向与第一块偏振片偏振化方向夹角（2）透射光强与入射光强之比（3）若每个偏振片对透射光吸收率为%5，再求透射光强与入射光强之比解：（1）设入射线偏振光强为I ，入射自然光强为I30cos 2130cos cos 222I I =α，21c o s 2=α， 45=α（2）375.083230cos 2130cos cos 222==+=I I Iα入射光强透射光强（3）=入射光强透射光强=I I I 2%9530cos %9521%9530cos %95cos 222⋅⋅+⋅⋅⋅α=338.0%)95(832=⨯。

第五章 光的偏振和晶体的双折射§ 5.1光的偏振态偏振：振动方向相对于传播方向的不对称性。

一．光是横波1、 光是电磁波——横波2、 用二向色性晶体（电气石晶体、硫酸碘奎宁晶体）检验——横波。

最初的器件是用细导线做成的密排线栅（金质线栅，d=5.08×10-4mm ），光通过时，由于与导线同方向的电场被吸收，留下与其垂直的振动。

1928年，Harvaed 大学的Land （19岁）发明了人造偏振片，用聚乙烯醇膜浸碘制得。

到1938年，出现了H 型偏振片，原理相同。

3、名词起偏：使光变为具有偏振特性。

检偏：检验光的偏振特性。

透振方向：通过偏振仪器光的电矢量的振动方向。

二．光的偏振态偏振：振动方向相对于传播方向的不对称性。

对可见光，只考虑其电矢量。

1．自然光振动方向随机，相对于波矢对称。

光的叠加是按强度相加。

可沿任意方向正交分解，在任一方向的强度为总强度之半。

021I I自然光是大量原子同时发出的光波的集合。

其中的每一列是由一个原子发出的，有一个偏振方向和相位，但光波之间是没有任何关系的。

所以，他们的集合，就是在各个方向振动相等、相位差随机的自然光。

在直角坐标系中，一列沿z 向传播、振动方向与X 轴夹角为θ的光，在X 方向的振幅为θθcos A A x =，由于各个光波在X 方向的总强度是光强相加，故有22022220cos )(A d A d A I x x πθθθππθ===⎰⎰同理2A I y π= 而总光强22022A d A I πθπ==⎰，故021I I I y x == 2．平面偏振光（线偏振光）只包含单一振动方向的电矢量。

在任一方向的光强θθ20cos I I =，马吕斯定律。

用偏振片可以获得平面偏振光。

偏振仪器（起偏器）的消光比=最小透射光强/最大透射光强 3．部分偏振光 介于自然光和线偏光之间。

偏振度=（I MAX -I MIN ）/（I MAX +I MIN ） 4．圆偏振光电矢量端点轨迹的投影为圆。