鲁棒控制大作业

鲁棒控制理论第六章本章将介绍鲁棒控制理论的基本概念和重要性。

鲁棒控制是一种能够在面对各种不确定性和扰动时保持系统稳定性和性能的控制方法。

在实际工程中，由于各种外部因素的存在，系统常常会面临不确定性和扰动，这导致传统控制方法的性能下降或失效。

鲁棒控制理论的提出旨在解决这些问题，使得控制系统能够在不确定环境下保持稳定并具备良好的性能。

鲁棒控制理论的基本概念包括：鲁棒稳定性和鲁棒性能。

鲁棒稳定性指的是控制系统在面对各种不确定性时能够保持稳定，即使系统参数发生变化或外部干扰存在，仍能使受控系统收敛到期望状态。

鲁棒性能则是指控制系统在鲁棒稳定的前提下，仍能保持良好的控制性能，如快速响应、抑制干扰等。

___控制在工程领域具有广泛的应用价值。

它能够有效应对各种不确定性因素，如参数变化、外部扰动、测量误差等，保证系统稳定和性能优良。

鲁棒控制不仅能够应用于传统的电气和机械系统中，还可以应用于复杂的多变量和非线性系统中，如控制网络、飞行器、汽车等。

因此，掌握鲁棒控制理论对于工程领域的研究和实践具有重要意义。

在接下来的章节中，我们将进一步探讨___控制理论的原理和方法，以及其在实际工程中的应用案例。

通过深入了解和研究鲁棒控制理论，我们将能够更好地设计和实现稳定可靠的控制系统，提高工程领域的控制技术水平。

鲁棒控制理论是一种应用于控制系统设计的理论框架，旨在解决系统不确定性和外部干扰对系统性能造成的影响。

该理论的主要目标是设计出对参数变化、模型不准确性和外部扰动具有强鲁棒性的控制器。

鲁棒控制理论的主要原理是通过在控制系统中引入设计参数的变化范围，并使用鲁棒性准则来评估控制系统的性能。

这样设计的控制器能够在不确定性条件下保持系统的稳定性和性能。

在鲁棒控制理论中，主要采用了一些常见的数学工具和方法，如线性矩阵不等式、H∞控制、μ合成等。

这些方法能够有效地处理系统不确定性和外部干扰，并提供了一种灵活且可行的控制系统设计方案。

总而言之，鲁棒控制理论是一种应对系统不确定性和外部干扰的有效工具。

四轮汽车液压转向系统鲁棒H2/H∞控制1.引言传统汽车是由驾驶员控制前轮或者后轮进行转向的。

两个车轮的转向系统的不足之处在于转向直径大，而且不容易满足在狭窄的空间要求下转向，这便限制了它的应用，特别是对大型和重型施工车辆。

为了提高方向的可操作性和驱动期间的稳定性，此外还要提高安全性和舒适性，四个轮子“转向（4WS）系统最近正在被研究。

汽车四轮转向系统已积极研究改善车辆在低速的操纵性和增强在高速的稳定性。

许多汽车公司开发的概念车四轮转向系统，例如，本田，日产尼桑，马自达。

从汽车行业借鉴这个idea，四轮转向已应用于工程车辆，例如CMI Terex公司生产的混凝土摊铺机“SF-3004“和Case公司生产的挖沟机“560”。

工程车辆的不确定性比汽车更严重，因为工程车辆有一个大功率液压系统工作在脏乱差的环境。

四轮转向系统的控制是复杂的，有时由于非线性特性的和未知的环境参数可能不是有效的。

在过去的20年中，许多不同的控制方法已被应用于四轮转向系统。

早期的四轮转向汽车，一个简单的前轮和后轮之间的速度依赖性比率已经被用在开环控制器中实现方向操纵零恒定的侧滑角。

Ackermann 和 Sienel 在他们的非线性3自由度模型中用比例控制器，同时Ji等人在他们的控制策略中运用比例控制器和补偿控制器。

Lv 等人以及 You 和 Chai用模糊逻辑方法来研究关于车轮转角的控制性能，但是他们没有给出实验的验证。

随着滑动模型控制的发展，它已经应用于四轮汽车的控制。

然而，应该指出的是，上述制器是基于相当简洁的模型，其中没有考虑不确定性。

工程汽车的参数容易受到一个广阔的不确定性影响，比如外部扰动，未建模动态，路面不平度，阵风，负荷波动，制动或加速力。

因此，一个严重的四轮转向车辆控制的鲁棒稳定性问题已经被提出；即，车辆控制器要应对这些不确定性保持操纵稳定和保证系统性能不恶化的太多。

由于不确定性的线性设计模型不能表达通常控制器设计要求的准确行为，因此经典控制方法对于保证控制性能是无效的。

鲁棒控制原理及应用举例摘要：本文简述了鲁棒控制的由来及其发展历史，强调了鲁棒控制在现代控制系统中的重要性,解释了鲁棒控制、鲁棒性、鲁棒控制系统、鲁棒控制器的意义，介绍了鲁棒控制系统的分类以及其常用的设计方法，并对鲁棒控制的应用领域作了简单介绍，并举出实例。

关键词：鲁棒控制鲁棒性不确定性设计方法现代控制系统经典的控制系统设计方法要求有一个确定的数学模型。

在建立数学模型的过程中，往往要忽略许多不确定因素：如对同步轨道卫星的姿态进行控制时不考虑轨道运动的影响，对一个振动系统的控制过程中不考虑高阶模态的影响等。

但经过以上处理后得到的数学模型已经不能完全描述原来的物理系统，而仅仅是原系统的一种近似。

对许多要求不高的系统，这样的数学模型已经能够满足工程要求。

然而，对于一些精度和可靠性要求较高的系统，如导弹控制系统设计，若采用这种设计方法，就会浪费了大量的人力物力在反复计算数弹道、调整控制器参数以及反复试射上。

因此，为了解决不确定控制系统的设计问题，科学家们提出了鲁棒控制理论。

由于鲁棒控制器是针对系统工作的最坏情况而设计的，因此能适应所有其它工况，所以它是解决这类不确定系统控制问题的有力工具。

鲁棒控制（Robust Control）方面的研究始于20世纪50年代。

上世纪60年代，状态空间结构理论的形成，与最优控制、卡尔曼滤波以及分离性理论一起，使现代控制理论成了一个严密完整的体系。

随着现代控制理论的发展，从上世纪80年代以来，对控制系统的鲁棒性研究引起了众多学者的高度重视。

在过去的20年中，鲁棒控制一直是国际自控界的研究热点。

通常说一个反馈控制系统是鲁棒的，或者说一个反馈控制系统具有鲁棒性，就是指这个反馈控制系统在某一类特定的不确定性条件下具有使稳定性、渐进调节和动态特性保持不变的特性，即这一反馈控制系统具有承受这一类不确定性影响的能力。

设被控系统的数学模型属于集合D，如果系统的某些特性对于集合U中的每一对象都保持不变，则称系统具有鲁棒性。

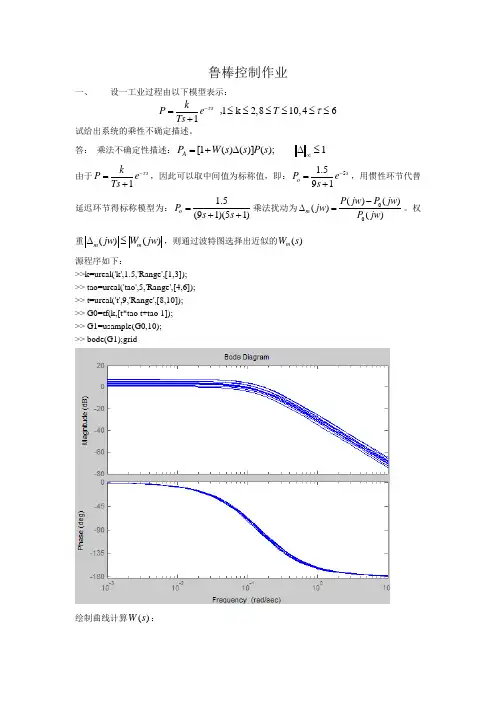
鲁棒控制作业一、设一工业过程由以下模型表示：1k 2,810,461s kP e T Ts ττ-=≤≤≤≤≤≤+ , 试给出系统的乘性不确定描述。

答： 乘法不确定性描述：1);()]()(1[≤∆∆+=∞s P s s W P A由于1s k P e Ts τ-=+，因此可以取中间值为标称值，即：51.591so P e s -=+，用惯性环节代替延迟环节得标称模型为： 1.5(91)(51)o P s s =++乘法扰动为00()()()()m P jw P jw jw P jw -∆=。

权重()()m m jw W jw ∆≤，则通过波特图选择出近似的()m W s 源程序如下：>>k=ureal('k',1.5,'Range',[1,3]); >> tao=ureal('tao',5,'Range',[4,6]); >> t=ureal('t',9,'Range',[8,10]); >> G0=tf(k,[t*tao t+tao 1]); >> G1=usample(G0,10);>> bode(G1);grid绘制曲线计算()W s ：乘法不确定函数)(s W 的频率增益线必须覆盖住它所有频率线，选择红色曲线对应的函数为()W s ，由上图可以计算得到，所选的Bode 图所对应的开环传递函数为12()10(1)(1)(101)(1)3k kW s T s T s s s ==++++ 有比较的程序如下：k=ureal('k',1.5,'Range',[1,2]); tao=ureal('tao',5,'Range',[4,6]); t=ureal('t',9,'Range',[8,10]); G0=tf(k,[t*tao t+tao 1]); G1=usample(G0,20); bode(G1); grid; hold on;W=tf(0.1,[100/3 40/3 1]); bode(W); hold on;W=tf(10/3,[100/3 40/3 1]); bode(W); hold on;W=tf(10,[100/3 40/3 1]); bode(W); hold on;一般说来，在对控制性能影响大的中低频段内应当尽量使()W s 不过分超过摄动的增益。

鲁棒控制当今的自动控制技术都是基于反馈的概念。

反馈理论的要素包括三个部分：测量、比较和执行。

测量关心的变量，与期望值相比较，用这个误差纠正调节控制系统的响应。

这个理论和应用自动控制的关键是，做出正确的测量和比较后，如何才能更好地纠正系统。

鲁棒控制（Robust Control）方面的研究始于20世纪50年代。

在过去的20年中，鲁棒控制一直是国际自控界的研究热点。

所谓“鲁棒性”，是指控制系统在一定（结构，大小）的参数摄动下，维持某些性能的特性。

根据对性能的不同定义，可分为稳定鲁棒性和性能鲁棒性。

以闭环系统的鲁棒性作为目标设计得到的固定控制器称为鲁棒控制器。

由于工作状况变动、外部干扰以及建模误差的缘故，实际工业过程的精确模型很难得到，而系统的各种故障也将导致模型的不确定性，因此可以说模型的不确定性在控制系统中广泛存在。

如何设计一个固定的控制器，使具有不确定性的对象满足控制品质，也就是鲁棒控制，成为国内外科研人员的研究课题。

鲁棒控制的早期研究，主要针对单变量系统（SISO）的在微小摄动下的不确定性，具有代表性的是Zames提出的微分灵敏度分析。

然而，实际工业过程中故障导致系统中参数的变化，这种变化是有界摄动而不是无穷小摄动。

因此产生了以讨论参数在有界摄动下系统性能保持和控制为内容的现代鲁棒控制。

现代鲁棒控制是一个着重控制算法可靠性研究的控制器设计方法。

其设计目标是找到在实际环境中为保证安全要求控制系统最小必须满足的要求。

一旦设计好这个控制器，它的参数不能改变而且控制性能能够保证。

鲁棒控制方法，是对时间域或频率域来说，一般要假设过程动态特性的信息和它的变化范围。

一些算法不需要精确的过程模型，但需要一些离线辨识。

一般鲁棒控制系统的设计是以一些最差的情况为基础，因此一般系统并不工作在最优状态。

常用的设计方法有：INA方法，同时镇定，完整性控制器设计，鲁棒控制，鲁棒PID控制以及鲁棒极点配置，鲁棒观测器等。

鲁棒控制方法适用于稳定性和可靠性作为首要目标的应用，同时过程的动态特性已知且不确定因素的变化范围可以预估。

渤海大学硕士研究生鲁棒控制课程考核论文院（系、部）：工学院年级： 2013 级专业：控制理论与控制工程姓名：郑晓龙学号： 2013080030 密封线任课教师：邰治新一、命题部分写一篇和鲁棒控制相关的论文。

二、评分标准1、论文排版格式（20分）；2、问题的提出（10分）；3、模型的建立（20分）4、问题的分析与求解（40分）；5、总结（10分）。

三、教师评语____________________________注1：本页由学生填写卷头和“任课教师”部分，其余由教师填写。

其中蓝色字体部分请教师在命题时删除。

提交试卷时含本页。

学生从第二页开始写作，要求见蓝色字体部分。

注2：“阅卷教师评语”部分请教师用红色或黑色碳素笔填写，不可用电子版。

无“评语”视为不合规范。

注3：试题、评分标准、评语尽量控制在本页。

注4：不符合规范试卷需修改规范后提交。

密 封 线基于T-S 模糊模型的多轴转向车辆∞H 鲁棒控制郑晓龙提要 为了解决多轴转向车辆模型非线性和各种干扰影响下的控制问题，分析了轮胎非线性和外界干扰建立多轴转向车的二自由度非线性模型，应用T-S 模糊理论，将其转换为局部线性的T-S 模糊模型。

基于并行分配补偿法（PDC ）和∞H 鲁棒控制理论，设计了转向系统的模糊∞PDCH 鲁棒控制器，并利用线性矩阵不等式和模糊逻辑控制工具求解控制器。

在正弦波和阶跃信号干扰下，车速为 801-⋅h km 时，进行前轮转向回正和前轮角阶跃输入转向的仿真试验。

仿真结果表明：侧偏角和横摆角速度动态响应的超调均为0，且均在0.06ｓ内达稳态值；前轮转向回正试验的侧偏角和横摆角速度稳态值均为0，前轮角阶跃输入转向试验的相应值分别为0和1.2，且稳态横摆角速度增益为0.24，这说明了多轴转向车辆在模糊∞PDCH 鲁棒控制下的高速转向平稳迅速，T-S 模糊建模和鲁棒控制器设计算法对解决轮胎非线性和外界干扰影响是有效的。

关键词 多轴转向 T-S 模糊 鲁棒控制一、引言多轴转向技术逐渐应用于大型公路运输车辆和工程车辆中，其操纵稳定性控制问题引起了国内外专家学者们的普遍关注。

E x e rc i s e1. Derive the classical feedback control transfer matrix and draw LTI block diagram 典型闭环系统方框图解：定义如下的双端口结构：由闭环系统的框图可知控制输入为 u = u，系统测量输岀为y = -(y p ■ n sensor )根据公式 H =(PL P Zu K(1 - P yu K)」P y.)，可得: 通过上面传递函数，我们可以得到如下的双端口网络：典型闭环系统二端口网络结构图one-degree feedback control transfer matrix and drawLTI block diagram由闭环系统的框图可知控制器的输入y 二r - (y p • n sensor )，其输岀u = u其中 y p — (u n proc )* F 0 ， y — r _(u n proc )* P 0 _ n sensor 综上可得:nproc I；①=|，z 二nsensor |IL u定义:由框图得 y p =(u - n prQ * P 0 ,y= -(U n proc ) R) - n sensor2. Derive the classical 解：定义nprocnsen sor，Z =u L -_ r一综上可得:根据公式H 二(巳■巳u K(1-P yu K)」P y. )，可得:通过以上分析，现绘制二端口网络结构图，如下图所示。

伺服系统二端口网络结构图two-degree feedback control transfer matrix and drawLTI block diagram双自由度控制系统结构方框图综上可得:= (2. P zu K(1 - P yu K)'P y.)，可得:通过以上分析，现绘制二端口网络结构图，如下图所示。

双自由度控制系统二端口网络结构图Con sider a disturba nee process described by:In this problem, the disturba nee rejectio n is an importa nt objective in additi on to comma nd tracking.Solutio n:nproc"sen sor ，z ='u 」r一解：定义■-=O0 0 ； P Q 0 0 0 j 1 00 1! 0 -1 0 -P c其中P =[空網-电P y O \ P yu _巳时［巳U]・・■■■■■'・・■ nailer ■ ■ r ■ vn0 0 \ P Q ~\-PO3. Derive the classical 由闭环系统的框图可知控制器的输入y =〔r 「I y out1-(yp + n s en sor)，其输岀u = u其中yp-(u nproc )* F Q , y-1—(U * 门卩讥)F Q _ H sensor4. Program ming to syn thesize an卄 con troller in 卩-toolbox and LMI-toolbox.(1) Programming to synthesize an con troller in 卩-toolbox其中P(%********************************************************************%* file : [i _toolbox.m%* function : Programming to synthesize an H g controller in[i _toolbox (%********************************************************************clear all ;clc;G=n d2sys(1,c on v([10 1],co nv([0.05 1],[0.05 1])),200); m=1.5;wb=10;A=1.e-4;wu=1;wp=nd2sys([1/m wb],[1 wb*A]);syste mn ames= 'G wp wu' ;in putvar= '[r(1);u ⑴]' ;outputvar= '[wp;wu;r-G]' ;in put_to_G= '[u]';in put_to_wp= '[r-G]' ;in put_to_wu= '[u]' ;sysout name= 'p';clea nupsysic= 'yes' ;sysic;[khi nf,gh in f,gopt]=h infsyn (p,1,1,0.5,20,0.001);运行结果为:Resett ing value of Gamma min based on D_11, D_12, D_21 termsTest bou nds: 0.6667 < gamma <= 20.0000hamy_eig yi nf_eig n rho_xy p/fgamma hamx_eig xinf_eig20.000 9.6e+000 1.3e-005 1.0e-003 -1.8e-012 0.0000 p10.333 9.6e+000 1.3e-005 1.0e-003 0.0e+000 0.0000 p5.500 9.5e+000 1.3e-005 1.0e-003 0.0e+000 0.0000 p3.083 9.5e+000 1.4e-005 1.0e-003 -1.8e-012 0.0000 p1.875 9.4e+000 1.5e-005 1.0e-003 0.0e+000 0.0000 p1.271 9.1e+000 -2.1e+001# 1.0e-003 -1.8e-012 0.0000 f1.573 9.3e+000 1.5e-005 1.0e-003 0.0e+000 0.0000 p1.422 9.2e+000 1.6e-005 1.0e-003 0.0e+000 0.0000 p1.346 9.2e+000 -1.1e+002# 1.0e-003 0.0e+000 0.0000 f1.384 9.2e+000 1.6e-005 1.0e-003 0.0e+000 0.0000 p1.365 9.2e+000 -3.3e+003# 1.0e-003 -1.8e-012 0.0000 f1.375 9.2e+000 1.6e-005 1.0e-003 0.0e+000 0.0000 p1.370 9.2e+000 1.6e-005 1.0e-003 0.0e+000 0.0000 p1.368 9.2e+000 1.6e-005 1.0e-003 0.0e+000 0.0000 p1.366 9.2e+000 1.6e-005 1.0e-003 0.0e+000 0.0000 p1.366 9.2e+000 -2.2e+004# 1.0e-003 1 0.0e+000 0.0000 fGamma value achieved: 1.3664(2) Programming to synthesize an controller in LMI -toolbox :图1 Shaping 前后的Bode 图比较图2无扰动时Shaping 前后的阶跃响应图的比较图3有扰动时系统的输岀比较其中图中红色的线表示 Loop-shap ing 后的系统响应曲线，而系统的干扰为单位阶跃信号。

车载液压机械臂轨迹的鲁棒跟踪控制学院：通信工程学院专业：控制理论与控制工程姓名：王蒙学号：2011522080一、申明本人郑重申明：所呈交的车载液压机械臂的鲁棒控制，是本人经查阅相关文献，结合自己研究课题，独立进行研究所取得的成果。

1、本研究选取了车载液压机械臂前两个连杆，比实际的少了一个伸缩的连杆（子系统）。

2、没有考虑负载情况下机械臂的变形以及振动，即只考虑机械臂为刚性机械臂情况。

3、只考虑车在静态搬运负载过程中的轨迹跟踪问题。

4、采用鲁棒控制和PD 控制相结合控制方法，并设计框图。

5、新选取广义控制力矩、状态变量、并对模型进行线性化；6、选取李雅普诺夫函数、控制量，并证明了稳定性。

7、仿真并分析结果。

结果分析方面：在相同输入情况下，PD 控制器参数不变，改变鲁棒控制率二、研究背景、控制要求以及控制策略车载机械臂是一种装配在汽车上，用来实现对货物的抓取、回转、搬运的自动化装置。

它具有严重的非线性、以及连杆与关节之间的强比控制效果的一个参数，)(中的)(~~t t BP x Px B u T Tψψρρ+-=耦合作用，此外由于负载变化、外部扰动以及大量不确定量（参数不确定量和非线性模型不确定量）的存在，增大了控制器的设计难度，特别是外部扰动、不确定参数以及不确定模型都将对系统的动态特性和稳定性产生较大影响。

针对此问题本研究提出了鲁棒控制设计方法，控制力矩τ由两部分组成，前馈控制部分只与自身结构有关，本质上是一种PD 控制，其作用是使系统沿标称轨迹运动所需要的控制力矩；反馈控制部分包含外界控制输入量u ，本质上是鲁棒控制，作用是消除外界不确定性干扰。

总之本文是基于车载液压机械臂系统，针对系统的不确定量和外部干扰，设计了PD 控制器和鲁棒控制器使机械臂达到轨迹跟踪控制。

三、车载液压机械臂模型车载机械臂装载在车辆尾部，主要用于吊装大载荷物体，完成物体在该车和运输车之间的转载任务。

本研究中车载机械臂是由一个回转关节、一个转动关节以及连杆组成，其简化模型如图1所示。

12 H 鲁棒控制12．1鲁棒控制的概念20世纪末，现代控制的理论与方法已日趋完善，然而，在工程实际中的应用依然困难.其中一个重要原因是，现代控制理论在很大程度上要依赖于有一个描述被控对象动态特性的精确数学模型、或者要求对象的不确定性和外界干扰满足某种特殊的假定。

而且，利用这种理论设计的系统只对数学模型保证预期的性能指标。

然而，控制系统设计中一个不可避免的问题是系统的数学模型与实际系统总难免会有些不同。

这是由于在控制系统设计时对实际物理系统进行数学模型化时不可避免地会遇到权衡数学模型的简单性和与实际系统吻合程度的真实性的问题。

数学模型与实际系统之间的差异可能通过许多途径产生，例如：线性化、参数估计等等。

而且，在实际物理系统中，某些参数可能并不是确定的，例如：液压系统中的油液粘度将随油温而变化。

为了弥补现代控制理论的这种不足，最有效的手段是在系统的分析和设计时充分考虑被控对象中所存在的各种不确定因素，即基于含不确定因素的非精确模型来分析系统和设计控制器，使所设计的控制系统能在某一类特定的不确定性条件下具有使系统稳定性、渐近调节和动态特性保持不变的特性。

系统的这种承受不确定性影响的能力即系统的鲁棒性。

20世纪80年代以来，关于控制系统的鲁棒性研究得到了很大的发展。

现代鲁棒控制理论继承了以往的鲁棒性研究方法，以基于使用状态空间模型的频率设计方法为主要特征，提出从根本上解决控制对象模型不确定性和外界扰动不确定性问题的有效方法，主要方法有H ∞控制方法，u 解析方法，LQG/LTR 方法等。

其中最为重要的是H ∞控制方法。

12．2 H ∞鲁棒控制问题的基本知识 1．H ∞范数（H ∞ norm ）对于一个连续时间状态变量系统.x （t ）=Ax(t)+Bu(t)y(t)=Cx(t)+Du(t) (12.2-1) 其相应的传递函数矩阵为：G （s ）=C(sI-A)-1B+D (12.2-2) 则G （s ）的H ∞范数为‖G ‖∞=Sup w -σ（G(j ω)） (12.2-3) 这里，)(∙-σ表示最大奇异值。

鲁棒控制理论在飞行器自动控制中的应用在现代工业化社会，飞行器自动控制系统早已成为不可或缺的一部分，尤其是在军事和航空领域，飞机和无人机等载具的自动控制系统倍受关注。

控制系统的可靠性和稳定性对运输的安全和效率有着至关重要的作用。

但是，飞行器自动控制系统也面临着各种稳定性和可靠性方面的挑战，如飞行器在恶劣环境下的处理能力、机械故障和外力干扰等问题。

因此，鲁棒控制理论成为自动控制系统中广泛实用的领域之一。

本文将探讨鲁棒控制理论在飞行器自动控制系统中的应用。

一、鲁棒控制理论的介绍鲁棒控制理论是一种在系统存在不确定性和干扰时，可以保证系统稳定和鲁棒性的控制方法。

可以抵御来自外界的不确定性和干扰，减少控制系统的风险，在工业、制造、军事等领域得到广泛应用。

鲁棒控制理论的核心思想是基于系统内部模型和外部信号干扰的不确定性，实现系统的鲁棒控制。

鲁棒控制理论把控制系统分成主控制和辅助控制两部分，主控制实现控制系统的基本功能，而辅助控制则提供了一种抵御不确定性和干扰的保护机制。

鲁棒控制理论的优势在于其能够处理系统内部和来自外界的各种不确定因素，使得系统能够具有更加稳定和可靠的控制能力。

二、飞行器自动控制系统的挑战控制飞行器自动控制系统主要是为了保证平稳的飞行和航线的稳定。

由于飞行器需要在恶劣的条件下运行，如风、动态干扰、引擎燃烧不完全等会导致飞行器出现偏差，进而影响飞行的稳定性和可靠性。

由于不同的飞行器在设计和制造过程中需要考虑到各种因素，如电磁干扰、机械故障、油料耗尽等，因此，这些不确定性和干扰性因素都会影响到飞行器自动控制系统的稳定和控制精度。

三、鲁棒控制在飞行器自动控制系统中的应用鲁棒控制在飞行器自动控制系统中的应用有着很广泛的潜在价值。

鲁棒控制理论可以解决飞行器自动控制系统中的稳定性和可靠性问题，从而提高控制精度和稳定性，并且可以有效地处理飞行器受到的干扰和非线性因素，使得控制系统具有更好的适应性和鲁棒性能。

目录一、鲁棒控制理论概述 (3)1.1 鲁棒性的定义及分类 (3)1.2 鲁棒控制的概念 (3)1.3 系统的不确定性类型 (4)1.4 鲁棒控制研究的问题和所用方法 (5)1.4.1 鲁棒控制研究的问题 (5)1.4.2 鲁棒控制所采用的方法 (5)1.4.3 求解控制问题方法的比较 (5)1.4.4 MATLAB中鲁棒控制工具箱 (6)二、建立飞机线性化模型 (8)2.1基准运动的配平 (8)2.2 纵向线性化数值状态方程 (8)2.3 横侧向线性化数值状态方程 (9)三、H∞控制理论 (9)3.1 标准H∞控制问题 (9)3.2 状态反馈H∞的控制 (10)3.3 输出反馈H∞的控制 (12)四、控制器设计 (12)4.1 PID控制器设计 (12)4.1.1 俯仰姿态控制律设计 (12)4.1.2 滚转姿态控制律设计 (15)4.2 H∞控制器设计 (17)4.2.1 俯仰角控制律设计 (17)4.2.2 滚转角控制律设计 (22)五、GUI界面设计 (27)六、保性能控制理论 (29)6.1保性能控制问题 (29)6.2保性能控制存在的一般条件 (30)6.3保性能控制设计方法 (31)6.4保性能控制器设计实例 (31)七、小结与展望 (34)八、总结 (35)一、鲁棒控制理论概述一个反馈控制系统的设计问题就是根据给定的控制对象模型，寻找一个控制器，以保证反馈控制系统的稳定性，使反馈控制系统达到期望的性能指标，并对模型不确定性和干扰不确定性具有鲁棒性。

控制系统性能的好坏很大程度上取决于对象模型的精确程度。

在实际的控制问题中，不确定性是普遍存在的，它可能来自对所描述控制对象的模型化误差，也可能来自外界扰动的多样性，所以，控制系统的设计必须考虑不确定性带来的影响。

1.1鲁棒性的定义及分类所谓鲁棒性是指控制对象在一定范围内变化时，它能在某种程度上保持系统的稳定性和动态性能的能力。

一个反馈控制系统是鲁棒的，或者说一个反馈控制系统具有鲁棒性，就是指这个反馈控制系统具有在某一类特定的不确定性条件下具有使系统的稳定性和动态特性保持不变的能力，即这一反馈控制系统具备承受这一类不确定性影响的能力。

认识鲁棒控制认识鲁棒控制（转载）鲁棒控制课程要写⼤作业了，顺便总结⼀下，鲁棒控制已经⾮常成熟了，也就⼏个概念。

⼀般步骤是把⽅框图转化为标准形式，然后把性能指标转换为权函数，权函数最后都能弄到⼴义控制对象中，然后⽤H⽆穷求出控制器。

⼴义控制系统所谓鲁棒控制，从应⽤的⾓度讲，就是设计⼀个控制器，满⾜⼀些性能指标。

⽽⼏乎所有的控制问题都可以转化为下图表⽰图 1最⼀般的控制系统其中：W：所有外部输⼊，如参考输⼊、扰动、传感器噪声等Z：被控输出Y：被测量输出（也就是所有传感器的输出）U：控制器输出，⽤于控制⼴义控制对象⼴义控制对象P：除了控制器以外的部分，包括实际控制对象，执⾏机构，传感器，A/D,D/A等对于图1所⽰的情形，有由w到z闭环传函矩阵为即为G和K的下线性分式变换系统G的范数：对于平⽅可积的输⼊信号w和输出z，其能量分别定义为这样就得到G的范数：次优控制问题：使得闭环传函矩阵的范数⼩于⼀个给定的常数，即最优控制问题：就是最⼩化闭环传函矩阵的范数：应⽤中，都是次优控制问题。

例如：混合S/KS问题可⽤下图来说明从w到z的闭环传递函数可以表⽰为转换为下图的标准形式：灵敏度函数S就是灵敏度函数了，d（⼲扰）为0时，r到e的传函，或者，输⼊r为0时，⼲扰d到输出y的传函W S和W KS为调整参数。

⼀种选择⽅法为：其中A<1为允许的最⼤稳态误差，为期望带宽，M为灵敏度峰值（⼀般情况下A=0.01，M=2）。

⼀般权函数是为了保证各个性能指标的⼴义过程模型P(s)（见图2）可以表⽰为得到P的状态⽅程形式以后，就可以根据论⽂提出的状态⽅程解法进⾏求解了。

控制器设计设计问题是寻找⼀控制器K，使之稳定系统G，并使下列的H∞范数最⼩：有很多种得到H∞控制器的⽅法，例如hinfsyn，hinfric，hinflmi，这些函数将P作为输⼊，并以系统矩阵（mu-tools）⽅式表达。

结果分析当控制器设计好后，需要对结果进⾏分析，这时可以利⽤Control System Toolbox提供的函数，例如利⽤lsim，step（阶跃响应），bode（伯德图），sigma（奇异值），freqresp（频域响应）等函数对传递函数S，KS，T，K，GK进⾏分析。