12-6麦克斯韦气体分子速率分布律

麦克斯韦速率分布定律的说明说明：1> 条件：理想气体、平衡态2> 下式意义：对于曲线1，dv v v N dN dv v f +→=~)(这个区间内分子数dN 占总分子数N 的百分比。

对上式两端求积分v v f NN dv Ndv dN dv v f v v v v ∆≈∆==⎰⎰)()(2121，其物理意义是v 1到v 2这个速率区间内所含的分子数。

若取速率0~∞的积分归一化条件→===⎰⎰∞1)(0NN N dN dv v f N （曲线下的面积为1） 通过归一化条件可知，分布曲线并不一定是只有曲线1这一种分布，还可以有类似于曲线2这种分布，通过对比可知曲线峰值高的，速率区间宽度肯定会较窄，其原因就是两个曲线下的总面积都为1 。

三种特征速率1. 最可几速率p υ：由0)(=dv v df 、)(v f 最大值对应的v ，MRT M RT m kT v p 41.122≈==，其中m 为分子质量，M 为摩尔质量。

其物理意义：若把速率区间分成许多相等的区间，p υ所在的区间内分子数占总数的百分比最大。

需要注意：p υ不是最大速率，而是与分布曲线峰值对应的速率。

2. 平均速率v ：M RT M RT dv v vf N dN v N N v N N v N v v Niii 60.18)(02211≈===∆=+∆+∆=⎰⎰∑∞π ， 物理意义：在平衡状态下，气体分子速率的算术平均值，注意：平均速率不是平均速度。

因为分子都是作物规则的运动，所以其平均速度0=v 。

3. 方均根速率2v ：MRT M RT v 73.132≈=，物理意义：在平衡状态下，气体分子热运动速率的另一种统计平均值。

注意：22v v v v =∙≠，方均根速率是每个分子的速率平方后再累加求平均值。

4. 说明：1> 三种速率均由麦氏速率 分布率求得（理想气体 平衡态），2> 具有统计意义——属于大量分子整体，均正比与MRT ，且2v v v p <<。

麦克斯韦气体速率分布律推导麦克斯韦-玻尔兹曼速率分布律描述了理想气体中分子速度的统计分布。

以下是该分布律的推导过程。

首先，考虑一个由大量相同分子组成的理想气体，这些分子在容器中随机、无序地运动。

由于分子间的碰撞非常频繁，我们可以假定每个分子的运动是相互独立的。

我们的目标是求出分子速率的分布函数。

1. 假设分子的运动是三维的随机运动，并且分子间无相互作用力。

2. 假设分子的运动是各向同性的，即在任何方向上运动的概率都是相等的。

3. 假设分子的运动是稳定的，即分子的速率分布不随时间改变。

4. 引入分子速度的微分元素d³v，表示速度在v到v+dv之间的分子数。

5. 引入微元体积元素dV和微元时间元素dt。

接下来，我们将使用微元分析法来推导速率分布律。

对于一个具有速率v的分子，在时间dt内，它将沿着速度方向移动的距离为v·dt。

因此，它所扫过的体积元素为dV = v²·cos²(θ)·sin(θ)·dv·dt，其中θ是速度方向与某一选定方向（通常是x轴）的夹角。

现在，考虑在dt时间内所有具有速率v的分子所扫过的体积总和，即所有可能的方向θ的贡献。

由于θ的取值范围是0到π，我们可以将上述体积元素乘以角度元素dθ（从0到π）并积分，以得到总的体积元素dV_total：dV_total = ∫(v²·cos²(θ)·sin(θ)·dv)·dθ·dt由于cos²(θ)·sin(θ)是关于θ的偶函数，而在0到π的范围内积分，它的积分结果为零。

为了解决这个问题，我们需要考虑在速度方向上的微小位移。

在速度方向上的微小位移为v·cos(θ)·dt，因此，在dt时间内，具有速率v的分子在速度方向上的微小体积元素为dV_v = v·cos(θ)·dv·dt。

教案适用对象批准人<附讲稿：页）教研室教员年月日课目：第十八讲气体分子速率分布目的：理解速率分布函数及麦克斯韦速率分布律的意义。

了解三种速率，了解自由程的概念。

重点：一、麦克斯韦气体分子速率分布率1、测定气体分子速率分布的实验2、麦克斯韦气体分子速率分布定律3、三种统计定律二、分子平均碰撞次数和平均自由程三、气体迁移现象1、粘滞现象2、热传导现象3、扩散现象难点：理解速率分布函数及麦克斯韦速率分布律的意义，了解三种速率，了解自由程的概念。

主要方法：讲授讨论练习基本要求：理解速率分布函数及麦克斯韦速率分布律的意义。

了解3中速率，了解验证速率分布律的实验依据。

了解玻耳兹曼能量分布律的意义及在重力场中粒子数密度公式。

了解分子平均碰撞频率及平均自由程的概念。

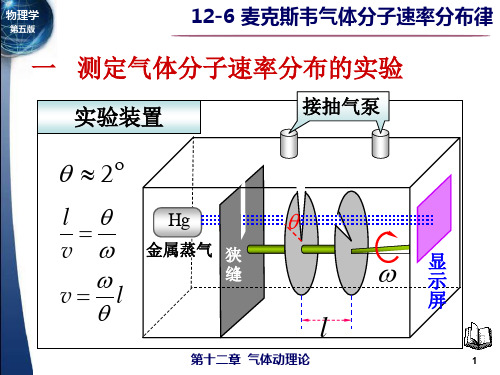
b5E2RGbCAP教案内容：6.6 麦克斯韦速率分布律6.6.1实验小孔充分小，改变w，测D上的沉积厚度，图6-7 测定分子速率的实验装置示意图就可测气体速率分布。

给定w。

粒子速率分布实验曲线如图6-8所示。

6.6.2气体分子速率分布律<函数）由于分子数目巨大且碰撞频繁，故单个分子速率取值任意偶然。

但又由分子平均平动动能公式知：温度T一定时，大量分子的方均根速率却又是确定的。

p1EanqFDPw 说明：平衡态时，虽然单个分子的速率取值偶然，但大量分子的速率满足一定的统计规律。

麦克斯韦从理论上得出如下规律：DXDiTa9E3d图6－8 分子速率分布实验曲线满足归一化条件：1. 速率分布的概念分子可能的速率值：速率区间：使得：内的分子数为，表示第i个速图6-9 不同温度下的速率分布曲线率间隔中的分子数占总分子数的百分比或表示单个分子速率值落在区间内的概率。

实验证明：平衡态时,分布在不同区间的不同,但却是确定的。

2. 气体分子速率分布律由实验知：与速率区间有关。

当时，与无关，仅是的连续函数，即速率分布函数物理意义：速率在v附近单位速率间隔内的分子数占总分子数的百分比,或某分子速率出现在v 附近的单位速率间隔内的概率。

麦克斯韦速率分布律的推导
麦克斯韦速率分布律是一种有用的概念，其可以帮助我们对问题的复杂性进行评估，
包括对问题的解决方案的可行性进行评估。

通常，当我们正在设计一个程序，并面临着复
杂和不可预测的问题时，麦克斯韦速率分布律就可以派上用场了。

麦克斯韦速率分布律是由美国数学家麦可·斯韦尔博士提出的。

斯韦尔提出了一套基
于序列分析法的分析工具，以对 inerconnected events 的速率进行统计分析。

他认为，
复杂系统中的事件有若干 nested stages：这些阶段之前的事件可能会影响后续的事件，
产生一种 cascade effect。

因此，他提出了一种分布式的统计模型，来描述这种指数级
跌落的现象，即 ------------->
麦克斯韦速率分布律。

该模型指出，问题的复杂性在问题维度上是以指数方式递增的，这一模型可以以下形式表达： problem complexity = C * z ^ n , 其中C 为一个常数，
z 为问题的附加复杂维度， n 为问题的基础复杂度等级。

这种模型可以帮助我们评估问题的复杂性是否可控、可维护，以及是否满足事件驱动
的应用通用性要求。

例如，如果一个系统的维度太多，其复杂程度就会指数级增长，那么
就需要对这一系统进行重构，以简化其复杂性并可持续维护。

此外，它也可以帮助我们推
断出某些系统是否有效解决会议解决方案。

总而言之，麦克斯韦速率分布律有助于识别可能会遇到的问题，并给出比较有效的解
决方案。

这种概念可以为我们设计可持续高性能系统提供一定的指导作用，进而有助于实
现系统的稳定和可靠性。