下载文档原格式
1.十几乘十几：口诀：头乘头，尾加尾，尾乘尾。
例：12×14=？解: 1×1=1２＋４＝６２×４＝８12×14=168注：个位相乘，不够两位数要用0占位。
２.头相同，尾互补(尾相加等于10)：口诀：一个头加１后，头乘头，尾乘尾。
例：23×27=？解：２＋１＝３２×３＝６３×７＝2123×27=621注：个位相乘，不够两位数要用0占位。
３.第一个乘数互补，另一个乘数数字相同：口诀：一个头加１后，头乘头，尾乘尾。
例：37×44=？解：3+1=44×4=167×4=2837×44=1628注：个位相乘，不够两位数要用0占位。
４.几十一乘几十一：口诀：头乘头，头加头，尾乘尾。
例：21×41=？解：2×4=82+4=61×1=121×41=861５.11乘任意数：口诀：首尾不动下落，中间之和下拉。
例：11×23125=？解：2+3=53+1=41+2=32+5=72和5分别在首尾11×23125=254375注：和满十要进一。
６.十几乘任意数：口诀：第二乘数首位不动向下落，第一因数的个位乘以第二因数后面每一个数字，加下一位数，再向下落。
例：13×326=？解：13个位是33×3+2=113×2+6=123×6=1813×326=4238注：和满十要进一。
1
乘法巧算
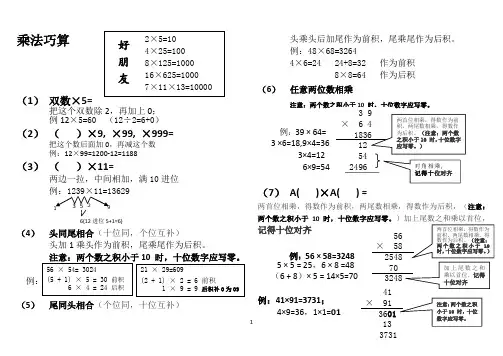
（1） 双数×5=
把这个双数除2，再加上0；
例12×5=60 （12÷2=6+0）
（2） （ ）×9, ×99,
×999=
把这个数后面加0，再减这个数 例：12×99=1200-12=1188
（3）
（ ）×11=
两边一拉，中间相加，满10进位 （4）
头加1乘头作为前积，尾乘尾作为后积。
注意：两个数之积小于10 时，十位数字应写零。
（5） 尾同头相合（个位同，十位互补）
头乘头后加尾作为前积，尾乘尾作为后积。
例：48×68=3264
4×6=24 24+8=32 作为前积
8×8=64 作为后积
（6） 任意两位数相乘
例：39 × 64= 3×4=12
（7） A(
)×A( ) =
两首位相乘，得数作为前积，两尾数相乘，得数作为后积，（注意：
两个数之积小于10 时，十位数字应写零。
）加上尾数之和乘以首位，
记得十位对齐
例：5 × 5 = 25，（6 + 8） 例：41×91=3731； 4×9=36，1×1=01
（4+9）×1=13
（8）两个接近100的数相乘
×
2。
数学巧算速算方法
以下是一些常见的数学巧算速算方法：
1. 乘法速算：
- 相邻两位数相乘：如72 × 74 = 5376，先计算7 × 7 = 49，再计算2 × 4 = 8，最后将结果连接起来，得到5376。
- 一位数乘以11的倍数：如4 × 44 = 176，将原数首尾加起来得到第一位数（4 + 4 = 8），再将原数的个位数放在中间，得到结果176。
2. 除法速算：
- 除以10的倍数：如240 ÷ 30 = 8，将被除数末尾的0去掉，再将结果与被除数的个位数相乘，得到最终结果8。
- 除以2的倍数：如468 ÷ 12 = 39，将被除数每一位数相加得到和（4 + 6 + 8 = 18），再判断和是否能被12整除，如果可以，则商为和除以12，否则商加1。
3. 平方速算：
- 以5为基准的平方：如65² = 4225，将原数去掉个位数后乘以（原数加1），再在末尾加上25，得到结果4225。
- 以50为基准的平方：如57² = 3249，将原数去掉个位数后乘以（原数加1），再在末尾加上49，得到结果3249。
这些巧算速算方法可以帮助简化数学运算，提高计算速度。
但需要注意的是，速算方法适用于简单的计算，对于复杂的计算仍然需要使用正常的计算方法。
三年级乘法巧算题目经典题
一、乘法交换律和结合律的巧算题目
1. 题目
- 公式
2. 解析
- 根据乘法交换律公式，我们可以交换公式和公式的位置，得到公式。
- 因为公式，再乘以公式，结果为公式。
3. 题目
- 公式
4. 解析
- 根据乘法结合律公式，先计算公式
，再乘以公式，得到公式。
4. 题目
- 公式
5. 解析
- 利用乘法交换律和结合律，将式子变为公式。
- 先算公式，公式，最后公式。
二、乘法分配律的巧算题目
1. 题目
- 公式
2. 解析
- 根据乘法分配律公式，这里公式，公式，公式。
- 所以公式。
3. 题目
- 公式
4. 解析
- 按照乘法分配律公式，公式，公式，公式。
- 则公式。
- 因为公式，公式，所以结果为公式。
5. 题目
- 公式
6. 解析
- 把公式写成公式，那么公式。
- 根据乘法分配律得到公式。
乘法的巧算（一）知识要点：1、牢记：5×2=10， 25×4=100， 125×8=10002、熟练运用乘法分配律和结合律。
3、观察特点，找共同因数，没有共同因的找倍数。
例1、 125×16 25×8= 125×8×2 = 25×4×2= 1000×2 = 100×2= 2000 = 200☆☆开心一练：你最棒！！！！25×16 125×32 25×28125×64 25×36 125×24例2： 125×25×32 1、 125×25×64= 125×25×8×4= （125×8）×（25×4）= 1000×100= 1000002、 125×25×483、 25×8×54、 25×5×565、 125×25×128例3、 82×15＋18×15 63×27－23×27= （82＋18）×15 = （63－23）×27= 100×15 = 40×27= 1500 = 1080提示：找共同因数，看有多少个相同因数相加减。
开心一练：你最棒！！！！！1、 83×13＋17×132、59×25＋41×253、 37×16＋63×164、 78×61－58×615、43×26－43×166、29×65－29×35例4、32×44－11×18 62×33＋11×14= 32×4×11－11×18 = 62×3×11＋11×14= 128×11－11×18 = 186×11＋11×14= （128－18）×11 = （186＋14）×11= 1210 = 2200提示：没有共同因数，先找倍数，再找共同因数。
一、一个数乘以一个特殊数的简便方法1、一个数乘以11。
其算理是：（a·10 ＋b）×11= a·100＋（a＋b）·10＋b[注：其中字母（如这里的a、b）皆表示0～9这十个数字，且表示最高位数字的字母（如这里的a）不能为0，下同]因此，一个数乘以11的简便计算方法，可以概括为：“首尾不变；两边相加，放在中间”。
例如：35×11=385其中，积385的构成为：首（3）尾（5）未变；两边3，5相加得8，放在中间。
2、一个数乘以15。
一个数乘以15的计算方法，可以概括为：“添零加半”。
例如：27×15=405其算理是，添零（27后添零为270）相当于乘以10，加半（270的一半是135）相当于乘以5，合起来是405。
3、一个数乘以5（或25或125）。
一个数乘以5（或25或125），可以在其后添一个（或两个或三个）零，再除以2（或4或8），例如：123×5=615123×25=3075123×125=15375二、两位数乘以两位数，两数中有部分数字相加得十的简便方法为了便于说明算法，我们把相加得十的两个数称作互为补数，即1与9，2与8，3与7，4与6，5与5互为补数。
4、首同尾补的两个两位数相乘。
其算理是：当a＋b＝10时，（A·10＋a）(A·10＋b)=A·(A＋１)·100＋ab即，两位数乘两位数，如果首同（十位数相同）尾补（个位数字相加得十），其积可分两段直接写出：首段（千位、百位）可用十位数字乘以十位数字加１的和得到，末段（十位、个位）可由个位数字相乘得到。
（注意：十位数字可能为零）例如：23×27=621 (积的首段6=2×(2＋1),末段21=3×7)62×68=4216 (积的首段42=6×(6＋1),末段16=2×8)41×49=2009 (积的首段20=4×(4＋1),末段09=1×9)5、尾同首补的两个两位数相乘。
乘法巧算速算技巧嘿，你问乘法巧算速算技巧啊？那可多了去啦！咱先说说凑整法吧。
比如说你要算25×32，这时候你就可以把 32 拆成4×8，那式子就变成了25×4×8。
25×4 多好算呀，等于 100，100 再乘 8 就是 800。
这就轻松多了吧？就像你玩拼图，把一个大难题拆成几个小部分，一下子就好解决了。
再说说乘法分配律。
比如45×98，你可以把 98 看成100 - 2，那式子就变成了45×（100 - 2）。
然后用乘法分配律，45×100 等于 4500，45×2 等于 90，最后一减，4500 - 90 就是 4410。
这就像你分糖果，把一大把糖果分成两堆，分别算好再合起来。
还有啊，十几乘十几也有窍门。
比如13×14，你先把十位数相乘，1×1 等于 1，再把个位数相加，3+4 等于 7，最后把个位数相乘，3×4 等于 12。
把这三个数组合起来就是 182。
这就像变魔术一样，一下子就得出答案啦。
咱再说说特殊数字的乘法。
比如 11 乘一个数，就很有规律。
比如34×11，把 34 拉开，中间填上 3+4 的和，就是 374。
如果中间的和大于 10，就往前进一位。
这多好玩呀，就像在玩数字游戏。
我给你举个例子哈。
我表弟上小学的时候，一开始做乘法题可慢了，老出错。
后来我教了他这些巧算速算技巧，嘿，那做题速度蹭蹭往上涨。
有一次考试，他用这些方法很快就做完了题，还得了个高分呢。
从那以后，他可喜欢做乘法题了，觉得自己像个小数学家。
所以啊，这些乘法巧算速算技巧真的很有用，能让你在做数学题的时候又快又准。
咱就把做数学题当成玩游戏，用这些小技巧轻松打败难题。
乘法中的巧算1.乘11，101，1001的速算法一个数乘以11，101，1001时，因为11，101，1001分别比10，100，1000大1，利用乘法分配律可得a×11=a×(10＋1)=10a＋a，a×101=a×(101＋1)=100a＋a，a×1001=a×(1000＋1)=1000a＋a。
例如，38×101=38×100＋38=3838。
2.乘9，99，999的速算法一个数乘以9，99，999时，因为9，99，999分别比10，100，1000小1，利用乘法分配律可得a×9=a×(10-1)=10a-a，a×99=a×(100-1)=100a- a，a×999=a×(1000-1)=1000a-a。
例如，18×99=18×100-18=1782。
上面讲的两类速算法，实际就是乘法的凑整速算。
凑整速算是当乘数接近整十、整百、整千……的数时，将乘数表示成上述整十、整百、整千……与一个较小的自然数的和或差的形式，然后利用乘法分配律进行速算的方法。
例1 计算：(1) 356×1001＝356×(1000＋1)＝356×1000＋356＝356000＋356＝356356；(2) 38×102＝38×(100＋2)＝38×100＋38×2＝3800＋76＝3876；(3)526×99＝526×(100-1)＝526×100-526＝52600-526＝52074；(4)1234×9998＝1234×(10000-2)＝1234×10000-1234×2＝12340000-2468＝12337532。
3.乘5，25，125的速算法一个数乘以5，25，125时，因为5×2＝10，25×4＝100，125×8＝1000，所以可以利用“乘一个数再除以同一个数，数值不变”及乘法结合律，得到例如，76×25＝7600÷4＝1900。
乘法速算
一、知识要点
我们已经学会了整数乘法的计算方法，但计算多位数乘法要一位一位地乘，运算起来比较麻烦。
其实，多位数与一些特殊的数相乘，也可以用简便的方法来计算。
计算乘法时，如果一个因数是25，另一个因数考虑可拆成4×几，这样可“先拆数再扩整”。
两位数、三位数及更高位数乘以11，可采用“两头一拉，中间相加”的办法，但要注意相邻两位相加作积的中间数时，哪一位上满十要向前一位进一。
比如两位数乘以11，我们有“两位数与11相乘，首尾不变中间变，左右相加放中间，满十进一头就变。
”
二、精讲精练
【例题1】试着计算下列各题，你发现了什么规律？
（1）26×11 （2）57×11 （3）253×11 （4）467×11
【思路导航】通过计算、观察可以发现，一个数与11相乘，所得的结果就是将这个数的首位和末位拉开分别作为积的最高位和最低位，再依次将这个数相邻两位由个位加起，和写在十位、百位……，哪一位上满十就向前一位进一。
（1）26×11=286 （2）57×11=627 （3）253×11=2783 （4）247×11=2717 练习1：很快算出下面各题的结果。
（1）12×11 （2）34×11 （3）25×11 （4）11×44
（5）48×11 （6）65×11 （7）11×75 （8）87×11
【例题2】下面的乘法计算有规律吗？
（1）25×24 （2）21×25 （3）25×427 （4）1998×25
【思路导航】因为25×4=100，因此，一个数与25相乘，我们就看这个数里有几个4，有几个4就有几个100，余1就加25，余2就加50，余3就加75。
（1）25×24=100×6=600 （2）21×25=100×5+25=525
（3）25×427=100×106+75=10600+75=10675
（4）1998×25=100×499+50=49900+50=49950
练习2：速算。
（1）12×25 （2）34×25 （3）25×121 （4）25×46
（5）148×25 （6）643×25
【例题3】很快算出下面各题的结果。
（1）24×15 （2）248×15 （3）5678×15
【思路导航】因为15=10+5，那么24×15就可以写成24×（10+5），也就是用24加上它的一半再乘以10，24+12=36，再用36×10=360。
一个因数乘以15，也就是用这个数加上它的一半再乘以10。
具体过程如下：
（1）24×15 （2）248×15 （3）5678×15
=（24+12）×10 =（248+124）×10 =（5678+2839）×10
=36×10 =360 =372×10 =3720 =8517×10 =85170 练习3：很快算出下面各题的结果。
（1）34×15 （2）436×15
【例题4】很快算出下面各题的结果。
（1）45×9 （2）32×99 （3）78×999
【思路导航】（1）我们可以先用45×10=450，这样就多加了一个45，因此我们还要从450中减去1个45，即450-45=405。
（2）我们可以先用32×100=3200，这样就多加了一个32，因此我们还要从3200中减去1个32，即3200-32=3168。
（3）我们可以先用78×1000=78000，这样就多加了一个78，因此我们还要从78000中减去1个78，即78000-78=77922。
从上面几题可以看出，一个数与9相乘，就用这个数乘以10，再减去这个数；一个数与99相乘，就用这个数乘以100，再减去这个数；一个数与999相乘，就用这个数乘以1000，再减去这个数。
（1）45×9 （2）32×99 （3）78×999
=45×10-45 =32×100-32 =78×1000-78
=450-45 =405 =3200-32 =3168 =78000-78 =77922
练习4：计算。
（1）32×9 （2）461×9 （3）1234×9
（4）45×99 （5）85×99 （6）728×99
【例题5】下面的乘法计算有规律吗？
（1）15×15 （2）25×25 （3）35×35
（4）45×45 （5）65×65 （6）95×95
【思路导航】通过计算我们发现，个位是5的两个相同的两位数相乘，积的末尾两位都是25，25前面的数是这个两位数首位数与首位数加1的积，例如：
我们还可以发现，这种方法还适用于个位是5的两个相同的多位数相乘的计算。
练习5：速算。
（1）55×55 （2）75×75
（4）105×105 （5）125×125
课后作业：
（1）124×11 （2）305×11 （3）439×11 （4）872×11 （5）25×7252 （6）5678×25 （7）8472×15 （8）24×999 （9）3×999 （10）56×999 （11）85×85 （12）995×995。
