第四章有限状态机

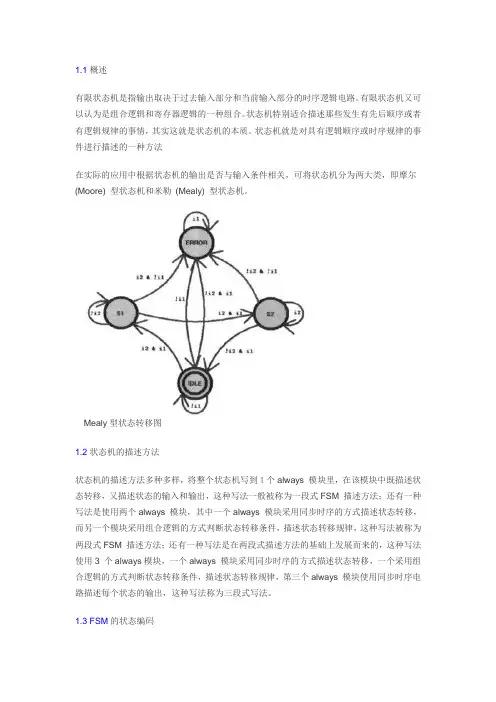
1.1概述有限状态机是指输出取决于过去输入部分和当前输入部分的时序逻辑电路。

有限状态机又可以认为是组合逻辑和寄存器逻辑的一种组合。

状态机特别适合描述那些发生有先后顺序或者有逻辑规律的事情，其实这就是状态机的本质。

状态机就是对具有逻辑顺序或时序规律的事件进行描述的一种方法在实际的应用中根据状态机的输出是否与输入条件相关，可将状态机分为两大类，即摩尔(Moore) 型状态机和米勒(Mealy) 型状态机。

Mealy型状态转移图1.2状态机的描述方法状态机的描述方法多种多样，将整个状态机写到１个always 模块里，在该模块中既描述状态转移，又描述状态的输入和输出，这种写法一般被称为一段式FSM 描述方法；还有一种写法是使用两个always 模块，其中一个always 模块采用同步时序的方式描述状态转移，而另一个模块采用组合逻辑的方式判断状态转移条件，描述状态转移规律，这种写法被称为两段式FSM 描述方法；还有一种写法是在两段式描述方法的基础上发展而来的，这种写法使用3 个always模块，一个always 模块采用同步时序的方式描述状态转移，一个采用组合逻辑的方式判断状态转移条件，描述状态转移规律，第三个always 模块使用同步时序电路描述每个状态的输出，这种写法称为三段式写法。

1.3 FSM的状态编码二进制码（Binary）和格雷码（Gray）属于压缩状态编码，这种编码的优点是使用的状态向量最少，但是需要较多的逻辑资源用来状态译码。

二进制码从一个状态转换到相邻状态时，可能有多个比特位发生变化，易产生中间状态转移问题，状态机的速度也要比采用其它编码方式慢。

格雷码两个相邻的码值仅有一位就可区分，这将会减少电路中相邻物理信号线同时变化的情况，因而可以减少电路中的电噪声。

Johnson码也有同样的特点，但是要用较多的位数。

独热码（One-hot）指对任意给定的状态，状态寄存器中只有l位为1，其余位都为0。

程序设计之有限状态机程序设计之有限状态机状态机？以前听说过，忘了是老师说的，还是老大说得了。

当时的认识也就是字面的意思，无非是和状态以及状态转换有关系。

也许在写过或者读过的一些代码中有遇到过有限状态机的程序，但是当时是一定没有想到这就是状态机吧。

最近在学习一些东西的时候竟然多次遇到，觉得还是有必要写点关于程序设计中有限状态机的东西。

，这里是一篇对状态机从定义到实现都有很好解释的文章，摘录部分如下：*************************************************************** ************************依据状态之间是否有包含关系，分以下两种（1）常规状态机。

状态机中的所有状态是不相交的、互斥的。

（2）层次状态机。

状态机中的状态之间要么是互斥的，要么是真包含的，可以用树性结构来描述这些状态集，包含其它状态的状态称为枝节点，不包含其它状态的状态称为叶节点，为方便单树描述，总是设计一个状态包含所有的状态节点，称为根节点。

状态机的状态只能停留在叶节点，而不能停留在枝节点，每个枝节点需要指定一个子节点为它的默认子节点，以便状态机进入枝节点的时候能够停留到叶节点。

一般都用switch/case if/else方式实现。

在少量状态（3个及其以下）的时候，不需要引入专门的状态机模块。

常规状态机模块实现涉及到的结构由上而下为：顶层结构是状态机：当前状态id，缺省操作，状态表，状态表：状态数组状态结构：状态id，状态名，进入操作，退出操作，缺省操作，状态事件表（数组）状态事件结构：操作，事件，下一状态的id*************************************************************** ************************从代码易读及美观角度来说，建议用switch/case来实现。

从经验来看，在一些稍大的程序设计中一般都会有状态机的实现，特别是在分层实现，协议栈实现，编解码方面。

实验四有限状态机设计(2学时)实验内容一：状态机是指用输入信号和电路状态（状态变量）的逻辑函数去描述时序逻辑电路功能的方法，也叫时序机。

有限状态机是指在设计电路中加入一定的限制条件，一般用来实现数字系统设计中的控制部分。

根据时序电路输出信号的特点可将时序电路划为Mealy 型和Moore 型两种。

Moore型电路中，输出信号仅仅取决于存储电路的状态。

Mealy型电路中，输出信号不仅取决于存储电路的状态，而且还取决于输入变量。

图1是某Mealy型电路的状态转换图，图中圆圈内的S0、S1等代表电路的状态，状态转换箭头旁斜杠“/”上边的数字代表输入信号，斜杠“/”下边的数字代表输出信号。

假设电路的当前状态为S0，当输入信号为0时，电路的下一个状态仍为S0，输出信号为0；当输入信号为1时，电路的下一个状态为S1，输出为1。

图1 Mealy状态机下面的程序中使用两个进程来描述该状态机。

第一个进程负责状态转化，在CP上升沿到达时，当前状态（PresetState）向下一个状态（NextState）的转换；第二个进程负责检测输入信号（DIN）和当前状态（PresetState）的值，并由CASE-WHEN 语句决定输出信号（OP）和下一个状态值（NextState）的值。

请补充下图中虚线“…”部分省略掉的程序，然后对完整程序进行编译，并用Tools->Netlist Views->State Machine Viewer和RTL Viewer工具查看该状态机的状态图和RTL顶层图。

……实验内容二：论文《基于VHDL的一个简单Mealy状态机》中设计了一个Mealy状态机用来检测数据流“1101010”，用以验证状态机在数据检测上的应用。

请在读懂文中程序的基础上，在Quartus Ⅱ软件中通过编译仿真得到状态图和波形图，仿真中输入波形的设置应能体现该状态机的用途。

实验报告：本次实验占用两个学时，请于12周周四(5月12日)上课时交实验报告。

有限状态机原理
有限状态机原理是一种计算模型，它包含一组有限个状态及其之间的转移规则。

它可以被用来描述不同对象或者系统在不同状态下的行为和变化。

有限状态机由三个主要部分组成：状态集合、转移规则和起始状态。

状态集合是有限的，每个状态代表系统的一个特定状态。

转移规则定义了状态之间的转移条件，根据当前的输入确定下一个状态。

起始状态是系统的初始状态，从这个状态开始执行转移规则。

有限状态机可以描述不同的行为和变化情况，通过根据输入选择对应的转移规则来改变状态。

在执行过程中，有限状态机会根据输入和当前状态确定下一个状态，并在转移后更新当前状态。

有限状态机可以根据实际需求进行设计和实现，可以是确定性的（每个输入对应唯一的转移规则）或者非确定性的（一个输入可以对应多个转移规则）。

有限状态机广泛应用于各个领域，例如计算机科学、计算机网络、自动化控制等。

它可以用于设计和实现各种系统和算法，如编译器、路由器、电梯控制和游戏引擎等。

总之，有限状态机原理是一种描述对象或系统不同状态和行为变化的模型，通过状态集合、转移规则和起始状态来描述系统的行为。

它在计算机科学和其他领域有着广泛的应用。

1.什么是有限状态机，Moore机和Mealy机的各自特点和他们之间的区别是什么？答：有限状态机是指输出取决于过去输入部分和当前输入部分的时序逻辑电路。

Mealy机属于同步输出状态机，他的输出是当前状态和所有输入信号的的函数，其输出会在输出仅为当前状态的函数，与当前输入信号无关。

当然，当前状态是和上一时刻时输入信号相关的，当前输入的变化必须等待下一时钟到来使状态发生变化时才能导致输出的变化。

因此，Moore机比Mealy机多等待一个时钟周期才会引起输出的变化，由于Mealy机的输出不与时钟同步，当状态译码比较复杂时，易在输出端产生不可避免的毛刺。

********************************************************************* 2.一个复杂的电路可以划分为几个不同的抽象级别：系统级，算法级，寄存器传输级，逻辑门级，晶体管开关级。

********************************************************************* 3.reg和wire的区别Reg型变量需要被明确赋值，并且在重新赋值前，一直保持原值，wire对应于连续赋值，如assign,reg对应于过程赋值，如always，initial。

********************************************************************* 4.阻塞和非阻塞的区别非阻塞赋值在整个过程块结束后才能完成赋值操作，阻塞赋值在该语句结束时就立即完成赋值操作，阻塞语句是顺序执行的，而非阻塞语句是同时执行的。

********************************************************************* 5.举例说明触发器在什么情况下会在综合过程中生成锁存器在写组合逻辑电路的always块中，， always块中要使用的输入信号在always 后面的敏感信号表中有遗漏，组合逻辑电路设计时不能有反馈。

有限状态机原理
有限状态机（Finite State Machine, FSM）是一种计算模型，用于描述系统或算法的行为。

它由一组有限个状态、一组可能的输入信号和一组定义状态转换规则的状态转换函数组成。

在任意时刻，FSM都处于一个特定的状态，等待输入信号触发状态转换。

有限状态机具有以下基本特点：
1. 状态：有限状态机有一组预定义的状态，每个状态表示系统或算法的一种行为或状态。

2. 输入信号：系统或算法接收一组可能的输入信号，每个输入信号可能触发状态的转换或执行某种操作。

3. 状态转换：有限状态机通过状态转换函数定义可能的状态转换规则，以及在特定输入信号下从一个状态转换到另一个状态的动作或操作。

4. 动作：状态转换可以伴随着执行特定的动作或操作，用于改变系统的状态或执行一些其他的操作。

有限状态机应用广泛，可以用于描述各种系统的行为，如计算机中的指令执行、网络通信协议、自动控制系统等。

它可以帮助开发者理清系统的行为逻辑，简化复杂系统的设计和实现。

有限状态机还可以通过组合、嵌套等方式进行组合和扩展，以应对更加复杂的问题。

有限状态机算法
有限状态机（Finite State Machine，FSM）是一种计算模型，用于描述一个系统的行为。

它由一组状态、一组输入和一组转移函数组成，通过状态转移来响应输入。

有限状态机算法是指通过有限状态机模型来解决特定问题的一种算法。

下面是有限状态机算法的基本原理：
1. 确定状态：根据问题的需求，确定有限状态机的状态集合。

每个状态代表着问题的一个特定情况或阶段。

2. 定义输入：确定有限状态机在每个状态下接受的输入集合。

输入可以是来自外部环境的事件或信号。

3. 定义转移函数：对每个状态和输入定义状态转移函数。

状态转移函数指定了在特定状态下接收到某个输入后，有限状态机应该转移到哪个新的状态。

4. 定义输出：根据问题的需求，确定有限状态机在每个状态下的输出。

输出可以是对外部环境的操作或者内部状态的变化。

5. 执行状态转移：根据问题的实际情况，通过执行状态转移函数，将有限状态机从一个状态转移到另一个状态。

有限状态机算法通常用于解决一些需要跟踪状态和处理不同输入的问题。

例如，网络协议中的数据包处理、编译器中的词法分析等都可以使用有限状态机算法进行实现。

什么是有限状态机FSM简介有限状态机（以下用FSM指代）是一种算法思想，简单而言，有限状态机由一组状态、一个初始状态、输入和根据输入及现有状态转换为下一个状态的转换函数组成。

在Gof的23种设计模式里的state模式是一种面向对象的状态机思想，可以适应非常复杂的状态管理。

现在，FSM被普遍用于搜索引擎的分词、编译器实现和我们普遍关注的游戏开发中。

游戏开发中，通常用FSM实现NPC控制，如当NPC受到攻击时根据健康、力量等选择逃跑还是反攻的行为，一般是用FSM实现的。

FSM的实现方法有很多种，不能简单地说孰优孰劣，但现代开发中，一般都比较推荐面向对象的实现方式：因为可重用性和健壮性更高，而且当需求变更的时候，也有很好的适应性。

实践理论从实践中来，也要回到实践中去。

我们现在通过实例来探索一下FSM的实现吧。

首先假设有这样一个世界（World），世界里只有一台永不缺乏动力的汽车（Car），汽车是次世代的，没有油门方向盘之类的落后设备，只有两个互斥的按钮——停止（Stop）和行进（Run），随着时间的流逝，汽车根据驾驶员的操作走走停停。

下面的代码可以实现这种功能：while True:key = get_key() # 按下什么键if key == "stop":stop(car)elif key == "run":go(car)keep(car) # 保持原态完成了功能而且直观、简洁的程序员万岁！但这时候客户（策划或者玩家）觉得走走停停太没意思了，他们想要掉头、左转和右转的功能，我们就要在while 循环里增加更多的if...else分支；他们想要更多的车，我们就要要在每一个分枝里增加循环；他们不仅仅想要Car了，他们还要要玩Truck，这时我们就需要在分枝的循环里判断当前的车是否支持这个操作（如Truck的装卸货物Car 就不支持）；他们……这个while循环终于无限地庞大起来，我们认识到这样的设计的确是有点问题的，所以我们尝试用另一种方法去实现FSM。

有限状态机是由寄存器组和组合逻辑构成的硬件时序电路，其状态（即由寄存器组的1和0的组合状态所构成的有限个状态）只可能在同一时钟跳变沿的情况下才能从一个状态转向另一个状态，究竟转向哪一状态还是留在原状态不但取决于各个输入值，还取决于当前所在状态。

状态机特别适合描述那些有发生有先后顺序，或者有逻辑规律的事情——其实这就是状态机的本质。

状态机的本质就是对具有逻辑顺序或时序规律事件的一种描述方法。

这个论断的最重要的两个词就是“逻辑顺序”和“时序规律”，这两点就是状态机所要描述的核心和强项，换言之，所有具有逻辑顺序和时序规律的事情都适合用状态机描述。

很多初学者不知道何时应用状态机。

这里介绍两种应用思路：第一种思路，从状态变量入手。

如果一个电路具有时序规律或者逻辑顺序，我们就可以自然而然地规划出状态，从这些状态入手，分析每个状态的输入，状态转移和输出，从而完成电路功能；第二种思路是首先明确电路的输出的关系，这些输出相当于状态的输出，回溯规划每个状态，和状态转移条件与状态输入。

无论那种思路，使用状态机的目的都是要控制某部分电路，完成某种具有逻辑顺序或时序规律的电路设计。

其实对于逻辑电路而言，小到一个简单的时序逻辑，大到复杂的微处理器，都适合用状态机方法进行描述。

请读者打开思路，不要仅仅局限于时序逻辑，发现电路的内在规律，确认电路的“状态变量”，大胆使用状态机描述电路模型。

由于状态机不仅仅是一种电路描述工具，它更是一种思想方法，而且状态机的HDL 语言表达方式比较规范，有章可循，所以很多有经验的设计者习惯用状态机思想进行逻辑设计，对各种复杂设计都套用状态机的设计理念，从而提高设计的效率和稳定性。

//1-paragraph method to decribe FSM//Describe state transition, state output, state input condition in only 1 always block //Westor Wang, Dec. 2006//Verilog Training -- How to write FSM bettermodule state1 ( nrst,clk,i1,i2,o1,o2,err);input nrst,clk;input i1,i2;output o1,o2,err;reg o1,o2,err;reg [2:0] NS; //NextStateparameter [2:0] //one hot with zero idleIDLE = 3'b000,S1 = 3'b001,S2 = 3'b010,ERROR = 3'b100;//1 always block to describe state transition, state output, state input condition always @ (posedge clk or negedge nrst)if (!nrst)beginNS <= IDLE;{o1,o2,err} <= 3'b000;endelsebeginNS <= 3'bx;{o1,o2,err} <= 3'b000;case (NS)IDLE: beginif (~i1) begin{o1,o2,err}<=3'b000;NS <= IDLE; endif (i1 && i2) begin{o1,o2,err}<=3'b100;NS <= S1; endif (i1 && ~i2) begin{o1,o2,err}<=3'b111;NS <= ERROR;endendS1: beginif (~i2) begin{o1,o2,err}<=3'b100;NS <= S1; endif (i2 && i1) begin{o1,o2,err}<=3'b010;NS <= S2; endif (i2 && (~i1)) begin{o1,o2,err}<=3'b111;NS <= ERROR;endendS2: beginif (i2) begin{o1,o2,err}<=3'b010;NS <= S2; endif (~i2 && i1) begin{o1,o2,err}<=3'b000;NS <= IDLE; endif (~i2 && (~i1))begin{o1,o2,err}<=3'b111;NS <= ERROR;end endERROR: beginif (i1) begin{o1,o2,err}<=3'b111;NS <= ERROR;endif (~i1) begin{o1,o2,err}<=3'b000;NS <= IDLE; endendendcaseendendmodule//2-paragraph method to describe FSM//Describe sequential state transition in 1 sequential always block//State transition conditions in the other combinational always block//Package state output by task. Then register the output//Westor Wang, Dec. 2006//Verilog Training -- How to write FSM bettermodule state2 ( nrst,clk,i1,i2,o1,o2,err);input nrst,clk;input i1,i2;output o1,o2,err;reg o1,o2,err;reg [2:0] NS,CS;parameter [2:0] //one hot with zero idleIDLE = 3'b000,S1 = 3'b001,S2 = 3'b010,ERROR = 3'b100;//sequential state transitionalways @ (posedge clk or negedge nrst)if (!nrst)CS <= IDLE;elseCS <=NS;//combinational condition judgmentalways @ (nrst or CS or i1 or i2)beginNS = 3'bx;ERROR_out;case (CS)IDLE: beginIDLE_out;if (~i1) NS = IDLE;if (i1 && i2) NS = S1;if (i1 && ~i2) NS = ERROR; endS1: beginS1_out;if (~i2) NS = S1;if (i2 && i1) NS = S2;if (i2 && (~i1)) NS = ERROR; endS2: beginS2_out;if (i2) NS = S2;if (~i2 && i1) NS = IDLE;if (~i2 && (~i1)) NS = ERROR; endERROR: beginERROR_out;if (i1) NS = ERROR;if (~i1) NS = IDLE;endendcaseend//output tasktask IDLE_out;{o1,o2,err} = 3'b000;endtasktask S1_out;{o1,o2,err} = 3'b100;endtasktask S2_out;{o1,o2,err} = 3'b010;endtasktask ERROR_out;{o1,o2,err} = 3'b111;endtaskendmodule//3-paragraph method to describe FSM//Describe sequential state transition in the 1st sequential always block //State transition conditions in the 2nd combinational always block//Describe the FSM out in the 3rd sequential always block//Westor Wang, Dec. 2006//Verilog Training -- How to write FSM bettermodule state3 ( nrst,clk,i1,i2,o1,o2,err);input nrst,clk;input i1,i2;output o1,o2,err;reg o1,o2,err;reg [2:0] NS,CS;parameter [2:0] //one hot with zero idleIDLE = 3'b000,S1 = 3'b001,S2 = 3'b010,ERROR = 3'b100;//1st always block, sequential state transitionalways @ (posedge clk or negedge nrst)if (!nrst)CS <= IDLE;elseCS <=NS;//2nd always block, combinational condition judgment always @ (nrst or CS or i1 or i2)beginNS = 3'bx;case (CS)IDLE: beginif (~i1) NS = IDLE;if (i1 && i2) NS = S1;if (i1 && ~i2) NS = ERROR; endS1: beginif (~i2) NS = S1;if (i2 && i1) NS = S2;if (i2 && (~i1)) NS = ERROR; endS2: beginif (i2) NS = S2;if (~i2 && i1) NS = IDLE;if (~i2 && (~i1)) NS = ERROR; endERROR: beginif (i1) NS = ERROR;if (~i1) NS = IDLE;endendcaseend//3rd always block, the sequential FSM outputalways @ (posedge clk or negedge nrst)if (!nrst){o1,o2,err} <= 3'b000;elsebegin{o1,o2,err} <= 3'b000;case (NS)IDLE: {o1,o2,err}<=3'b000;S1: {o1,o2,err}<=3'b100;S2: {o1,o2,err}<=3'b010;ERROR: {o1,o2,err}<=3'b111;endcase endendmodule。

编译原理有限状态机及化简编译原理是计算机科学中的一门重要课程，它研究的是如何将高级语言程序转化为可执行的低级机器语言。

在编译原理中，有限状态机是一种重要的工具，它能够帮助我们理解和设计编程语言的词法结构。

而化简则是在设计有限状态机时的一项重要技巧，能够简化状态机的复杂度，提高编译器的效率。

有限状态机（Finite State Machine，FSM）是一种用于描述系统行为的数学模型。

在编译原理中，有限状态机被广泛应用于词法分析阶段，用于识别和解析程序中的各类词法单元。

有限状态机由一组状态和一组转移函数组成。

状态表示系统所处的某个特定状态，转移函数表示状态之间的转移条件和动作。

通过不断地进行状态转移，有限状态机可以识别和解析输入的程序。

在编译过程中，我们需要将源代码中的字符序列转化为一系列词法单元，如关键字、标识符、运算符等。

有限状态机可以帮助我们识别这些词法单元。

例如，我们可以设计一个有限状态机来识别整数常量。

该状态机的状态可以分为初始状态、扫描状态和接受状态。

初始状态表示状态机的起始状态，扫描状态表示状态机正在扫描数字字符，接受状态表示状态机已经扫描完整个整数常量。

通过定义合适的转移函数，我们可以使状态机按照预定的规则进行状态转移，最终得到正确的整数常量词法单元。

在设计有限状态机时，我们常常需要考虑状态的合并和化简。

化简是指将状态机中的一些状态合并为一个等价的状态，从而减少状态的数量。

通过化简可以使状态机更加简洁，提高编译器的效率。

化简的过程中，我们需要考虑状态之间的等价性。

两个状态是等价的，当且仅当它们在任何输入条件下都具有相同的转移行为。

通过判断状态的等价性，我们可以将等价的状态合并为一个新的状态，从而化简状态机。

化简状态机的过程可以使用等价类划分算法来实现。

该算法首先将状态划分为两个互不相交的等价类：接受状态和非接受状态。

然后，对每个等价类进行划分，直到无法再进行划分为止。

最终，我们可以得到一个化简后的状态机，其状态数量更少，但仍能正确识别和解析程序中的词法单元。