清华大学2011年保送生考试试题

2011年清华等高校联合自主招生试题一、选择题(本题共10小题，每小题3分，共30分．在每小题给出的四个选项中，有一个或多个选项符合题目要求，把符合题目要求的选项前的字母填在题后括号内)1．根据玻尔原子理论，当一个氢原子吸收一个光子后 ( B )A ．氢原子所处的能级下降B ．氢原子的电势能增大C ．电子绕核运动的轨道半径减小D ．电子绕核运动的动能增加2．如图所示，AB 杆以恒定角速度ω绕A 点转动，并带动套在水平杆OC 上小环M 运动．运动开始时，AB 杆在竖直位置，则运动中小环M 的加速度将（A ） A ．逐渐增大 B ．先减小后增大 C ．先增加后减小D ．逐渐减小3．在杨氏双缝干涉实验中，如果单色光源S 从图所示的中轴位置沿垂直SO 的方向向上移动一段微小的距离，则中心干涉条纹向何方向移动?相邻明条纹间的间距如何变化? ( C )A ．相邻明条纹间的间距不变中心干涉明条纹向上移动B ．相邻明条纹间的间距变大中心干涉明条纹向下移动C ．相邻明条纹间的间距不变中心干涉明条纹向下移动Ｄ．相邻明条纹间的间距变小中心干涉明条纹向上移动上移动4．一质点沿直线做简谐运动，相继通过距离为16cm 的两点A和B ，历时ls ，并且在A 、B两点处具有相同的速率；再经过ls ，质点第二次通过B 点，该质点运动的周期和振幅分别为( D)A ．3s ，83cmB ．3s ，82cmC ．4 s ，83cmD ．4s ，82cm5．水流以与水平方向成角度θ的速度冲入到水平放置的水槽中，则从左面流出水量的和从右面流出的水量的比值可能为 (D )A ．l 十2sin 2θB ．l 十2cos 2θC ．l+2tan 2θD ．l 十2cot 2θ6．如图所示，带电质点P 1固定在光滑的水平绝缘桌面上，在桌面上距P 1一定距离处有另一个带电质点P 2，P 2在桌面上运动，某一时刻质点P 2的速度沿垂直于P 1P 2的连线方向，则 ( ACD) A ．若P 1、P 2为同种电荷，以后P 2一定做速度变大的曲线运动B ．若P 1、P 2为同种电荷，以后P 2一定做加速度变大的曲线运动2 PC ．若P 1、P 2为异种电荷，以后P 2的速度大小和加速度大小可能都不变D ．若P 1、P 2为异种电荷，以后P 2可能做加速度、速度都变小的曲线运动7．空间某区域内存在匀强磁场，磁场的上下边界水平，方向向和竖直平面（纸面）垂直，两个由完全相同的导线制成的刚性线框a 和b ，其形状分别是周长为4l 的正方形和周长为6l 的矩形，线框a 和b 在竖直平面内从图示位置开始自由下落，若从开始下落到线框完全离开磁场的过程中安培力对两线框的冲量分别为I a 、I b ，则I a ∶I b为 ( A ) A ．3:8 B ．1:2 C ．1:1 D ．3:2二、实验题(共12分，根据题目要求作答)11．当压强不变且温度变化量T 不太大时，液体或固体在某一温度下的体膨胀系数α可以表示为T V V ∆∆=α，式中为该温度时的体积，△V 为体积的变化量．一般来说，在常温下液体的体膨胀系数分别在10-3/K 量级和10-6~10-5/K 量级．如图所示的装置，可以用来测量控温箱中圆筒形玻璃控温箱容器内液体的体膨胀系数，实验步骤如下：①拿掉浮标，将液体的温度调为接近室温的某一温度T 0，测量液柱的高度化h ．②放入浮标，保持压强不变，将液体的温度升高一个不太大的量△T ，用精密的位置传感器确定指针高度的变化量△h ．③利用步骤①和②中测得的数据，计算液体在T 0时的体膨胀系数α．回答下列问题：(1)不考虑温度变化导致的液体密度变化，写出用测量量表示的α的表达式；(2)步骤②在温度升高过程中，液体密度变化会对用上面的表达式计算出的结果有什么影响?为什么?(3)当所用的浮标为直立圆柱体时，某同学对如何减少这一影响提出以下条几建议，其中有效的是 ．(填大入正确选项前的字母)A ．选用轻质材料制成的浮标B ．选用底面积较大的浮标C ．选用高度较小的浮标D ．尽量增大液柱的高度hE ．尽量选用底面积大的玻璃容器解析 (1)不考虑温度变化导致的液体密度变化，由于液体质量不变，则液体的体积V 不变.设圆筒形玻璃容器内液体的底面积为S ，则Th h T Sh h S T V V ∆∆=∆∆=∆∆=α (2) α会偏大．因为温度升高，导致液体体积变大，故液体密度ρ液会变小，根据阿基米德定× × × × × × B a b l 2l律可得ρ液V 排g=ρ物V 物g ，则V 物变大，即浮标进入液体的深度会更深，测得的△h 会偏大，α会偏大．(3)由ρ液V 排g=mg 可知，浮标质量越小，对V 物的影响就越小，即对△h 的影响减少，故A 选项正确．从ρ液V 排g=ρ物V 物g 可知，浮标底面积的大小及浮标的高度都不影响V 物，即△h 不变，则B 、C 选项错误；增大液柱的高度h 、选用底面积较大的玻璃容器，浮标进入液体的深度变化对液柱高度的变化量△h 影响减小，则D 、E 选项正确三、推理、论证题(共32分．解答时应写出必要的文字说明和推理过程)14．我们知道，在压强不太大、温度不太低的情况下，气体分子本身的大小比分子间的距离要小很多，因而，在理想气体模型中通常会忽略分子的大小．己知液氮的密度ρ=810kg/m 3，氮气的摩尔质量M mol =28×10-3kg/mol ．假设液氮可看作是由立方体分子堆积而成的，根据所给数据对标准状态下的氮气做出估算，说明上述结论的合理性．解析 1个氮分子自身的体积为3293232mol 0m 108.5m 1002.68101028--⨯=⨯⨯⨯==A N M V ρ 1个氮分子的边长为m 104m 108.51032930--⨯≈⨯==V l1个氮气分子占据的体积为 AN V V m ol =氮气分子间的距离为 m 193m 1002.6104.22932333mol 3--⨯≈⨯⨯===A N V V d 比较可知，气体分子本身的大小比分子间的距离要小很多，因此可以忽略分子的大小．四、计算题(共26分·解答时应写出必要的文字说明、方程式和主要演算步骤，只写出最后结果不能得分)15．(12分)竖直墙面和水平地面均光滑，质量分别为m A =m ，m B =3m 的A 、B 两物体如图所示放置，其中物体A 紧靠墙壁，A 、B 之间由质量不计的轻弹簧相连，现对物体B 缓慢施加一个向左的力，该力做功为W ，使A 、B 之间轻弹簧被压缩且保持系统静止，然后突然撤去向左的推力解除压缩，求： （1）从撤去外到物块A 开始运动，墙对A 冲量多大?（2）A 、B 都运动后，A 、B 两物体的最小速度各为多少？解析 (1)压缩弹簧时，外力做的功全部转化为弹性势能；撤去外力后，物体B 在弹力作用下做加速运动；在弹簧恢复原长的过程中，系统的机械能守恒．设弹簧恢复原长时，物体B 的速度为v B0．，则有 20321B mv W ⋅= 得 mW v B 320= 此过程中墙壁对A 的冲量大小等于弹簧对A 的冲量大小，也等于弹簧对B 的冲量大小，则有mW mv I B 630==(2)当弹簧恢复原长后，A 离开墙壁开始运动，因开始时B 的速度比A 的速度大，弹簧伸长，A 在弹簧弹力作用下做加速运动，B 做减速运动，弹簧伸长量增大，当A 、B 速度相等时弹簧伸长到最长，之后A 的速度比B 的速度大，弹簧的形变量减小，过程中A 仍做加速运动，B 仍做减速运动当弹簧恢复到原长时，物体A 的速度为最大，B 的速度最小，此时A 的速度比B 的速度大，弹簧开始压缩，A 做减速运动，B 做加速运动，当弹簧再次恢复到原长时A 的速度最小，B 的速度为最大．设弹簧恢复到原长时A 的速度为为v A ，B 的速度为v B ，在此过程中系统的动量守恒、机械能守恒．则有3mv B0=mv A +3mv B222032121321B A B mv mv mv ⋅+=⋅ 联立解得v A1=0， v B1=v B00223B A v v =，0221B B v v = 所以，物体A 的最小速度为0，B 的最小速度为m W v v B B 62102==． 16.(14分)在xOy 平面内，x ＞0，y ＞0的空间区域内存在匀强电场，场强大小为100V/m ；x ＞0，y ＜3m 的区域内存在垂直于xOy 平面的磁场．现有一带负电的粒子，电量为q =2×10-7C ，质量为m =1×10-6 k g ，从坐标原点O 以一定的初动能射出，经过点P (4，3)时，其动能变为初动能的0.2倍，速度方向平行于y 轴正方向．最后，粒子从y 轴上点M (0，5)射出电场，此时动能变为过O 点时初动能的0.52倍．粒子重力不计．(1)写出在线段OP 上与M 点等电势点Q 的坐标；(2)求粒子由P 点运动到M 点所需的时间．解析 (1)设粒子在O 点时的动能为E k0，则在M 点的动能为0.52E k0，由于洛伦兹力不做功，粒子从O 点到P 点和从P 点到M 点的过程中，电场力做的功分别为―0.8 E k0、―0.48 E k0，O 、P 及O 、M 间的电势差分别为q E U k OP 08.0=、q E U k OM 048.0= 点及M 点的电势差分别为 如图所示，由几何关系知OP 的长度为5m ，沿OP 方向电势均匀降落，电势每米下降qE k 016.0，则OQ =3m ． 设OP 与x 轴的夹角为α，则sin α=3/5，cos α=4/5，Q 点的坐标为x Q =OQ cos α=3×0.8m=2.4my Q =OQ sin α=3×0.6m=1.8m(2)M 、Q 是等势点，MQ 是电场的一条等势线，等势线与电场垂直，可知电场方向沿OP 方向．电场强度的x 分量为E x =E cos α=100×0.8V/m=80 V/m粒子由P 点运动到M 点，在x 方向上作初速度为0的匀加速直线运动，则221t mqE x x P = s 22s 8010241012276=⨯⨯⨯⨯⨯==--x P qE mx t。

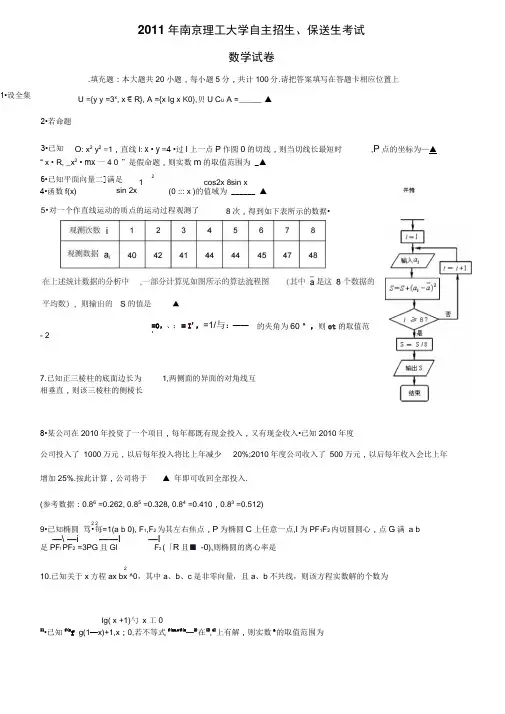
1•设全集2•若命题3•已知圆O: x2 y2=1，直线l: x • y =4 •过l上一点P作圆0的切线，则当切线长最短时,P点的坐标为—▲开赭sin 2x2011年南京理工大学自主招生、保送生考试数学试卷.填充题：本大题共20小题，每小题5分，共计100分.请把答案填写在答题卡相应位置上U ={y y =3x, x € R}, A ={x Ig x K0},贝U C U A = _____ ▲“ x • R, _x2• mx 一4 0 ”是假命题，则实数m的取值范围为 _▲21 cos2x 8sin x4•函数f(x) (0 ::: x )的值域为______ ▲- 27.已知正三棱柱的底面边长为1,两侧面的异面的对角线互相垂直，则该三棱柱的侧棱长8•某公司在2010年投资了一个项目，每年都既有现金投入，又有现金收入•已知2010年度公司投入了1000万元，以后每年投入将比上年减少20%;2010年度公司收入了500万元，以后每年收入会比上年增加25%.按此计算，公司将于▲ 年即可收回全部投入.(参考数据：0.86=0.262, 0.85=0.328, 0.84=0.410，0.83=0.512)2 29•已知椭圆笃•每=1(a b 0), F1,F2为其左右焦点，P为椭圆C上任意一点,I为PF1F2内切圆圆心，点G满a b —\ —i ——I —I足PF! PF2 =3PG且Gl F2 (「R且■ -0),则椭圆的离心率是210.已知关于x方程ax bx ^0，其中a、b、c是非零向量，且a、b不共线，则该方程实数解的个数为lg( x +1)勺x 工011•已知f(x f g(1—x)+1,x；0,若不等式f(ax"f(x—2)在[3,4]上有解，则实数a的取值范围为5•对一个作直线运动的质点的运动过程观测了8次，得到如下表所示的数据•=1/与：——=0，、；= I'，16•已知平面向量二]满足的夹角为60 °，则ot的取值范围12.已知m・N，若函数f(x)=2x「m 4-x-m存在整数零点，则m的取值范围为_______ 13•设】表示不超过x的最大整数，例如：[-1.3] =-2,[2] =2,[2.5] =2等.则方程〔tan J - 2si n2x在[0,2二)内的解a + a —114. 已知数列佝？满足：』n n (n • N ”),且a4=28,则何？的通项公式为a. = ▲____an+ —a n +115. 已知ax - y =2a 3 (a为正常数，x _0,y _0)，若x2 y2的最大值为S,且S・［49,121］,则a的取值范围为▲1 116. 已知函数f(x)=sin x--x,x三［0, n • cosx o =-( x°w［0, n )，那么下面命题中真命题的序号是▲:3 3① f(x)的最大值为f(X o)；②f(X)的最小值为f(x o)；③f(x)在［O,x o］上是减函数；④f(X)在［X o, n上是减函数•317. 已知函数f(x)二xx—a 1 ,若a，(0,3)且f(x)在区间［1,2］上的最小值为，则a二▲___________________18. 设函数f(x)是定义在R上的奇函数，且对任意的［1,a］,当X2必时，总有f^) • f(xj .0,则下列不等式一定成立的是▲(填上你认为正确的结论的序号):1 +a 一 1 _3a 1 _3a① f (a) f (0)；② f (- 一) f( a);③ f (一―) f (-3);④ f (- 一)f(—a)2 1+a 1+a19. 在平面直角坐标系xOy中，0为坐标原点.定义卩(为,％)、Qg’y?)两点之间的“直角距离”为d(P,Q)= X1- X2 + y1- y2若点Q在直线l上运动，定义d(P,l) = d(P,Q)min.已知点B(1,0)，直线M的方程为kx- y+ k+ 3= 0(k> 0)，贝U d(B,M )的最大值为▲ _______20. 已知函数f(x) / 3bX sinx bxcosx^b R),若f(x)在R上既有最大值，又有最小值，且最大值与最小3 +cosx值的和为6,则a b=▲.二•解答题：本大题共6小题，共计100分•解答时应写出文字说明、证明过程或演算步骤21 .(本小题满分14分)在锐角ABC中，角A,B,C的对边分别为a,b,c,已知b二■一 sinc .2(I)若tanA =3,求tanB 的值；(n)求tanB的最大值.22. (本小题满分14分)如图，在三棱锥P-ABC中，AC= BC= 2 , ?ACB 90°，侧面PAB为等边三角形，侧棱PC = 2 • 2 , E为PB中点•(I)求证：PC丄AB ;(n)求证：平面PAB A平面ABC; (川)求点E到平面PAC的距离.23. (本小题满分14分)某商场以100元/件的价格购进一批衬衣，以高于进货价的价格出售，销售期有淡季与旺季之分，通过市场调查发现：①销售量r(x)(件)与衬衣标价x(元/件)在销售旺季近似地符合函数关系：r(x)=kx+b，在销售淡季近似地符合函数关系：r(x) =kx ，其中k ：：：0,bp b, . 0且k、b P b2为常数；②在销售旺季，商场以140元/件的价格销售能获得最大销售利润；③若称①中r(x)=0时的标价x为衬衣的临界价格”则销售旺季的临界价格”是销售淡季的临界价格的1.5倍.请根据上述信息，完成下面问题：(I )分别写出销售旺季和销售淡季销售总利润y (元)与标价x(元/件)的函数关系式(含k、bi或b2);(n)在销售淡季，该商场要获得最大销售利润，衬衣的标价应定为多少元/件？24. (本小题满分18分)已知点M(1,y)在抛物线C:y2=：2px (p .0)上，M点到抛物线C的焦点F的距离为2,直线1l : y x b与抛物线交于A, B两点.2(I)求抛物线C的方程；(n)若以AB为直径的圆与x轴相切，求该圆的方程；(川)若直线l与y轴负半轴相交，求AOB面积的最大值25. (本小题满分20分)如图,殆1,%),巳亿』?)，…,Pngy.) , (0 ：： % ：：y?：：川：:：y n, n N )是曲线C:y2=3x(y_0)上的n个点，点A(a ,0)( i =1,2,3,|l| , n)在x轴的正半轴上，AA」AP是正三角形(A是坐标原点).(I)求a1,a2,a3;(n)求出点A n (a n,0)( n • N*)的横坐标务关于n的表达式；1 1 1 1(川)设b n，若对任意正整数n及an十a n七a n七a2n1 3 7xu(0,2］，不等式-x -ax兰------- b n恒成立，求实数a的取值范围.2 626. (本小题满分20分)16.①④已知实数 a 满足 0 :- a ：：:2,a =1，设函数 f (x) -1 x ? - a - x-^ax .3 2 (I )当a =2，求f (x)的极小值；2 2(n )若函数g(x) =ax bx -(2b 4)x ln x(b • R)的极小值点与f (x)的极小值点相同.求g(x)的极大值的最大值，并求取到最大值时a,b 的值.数学自主招生、保送生考试数学试卷参考答案1亠917.—或— 18.①②④19. 520. 82 4.填充题：本大题共20小题,每小题5分,共计100分.请把答案填写在答题卡相应位置上 2.6. (0,^^]31. (0,1) — 552. W3. (2,2) ° [4，；) 5. §8. 2014 1 9.-210. 0 或 1 11. 1,0)U (|, ；)12.恥“ 13.0書,二214. 2n —n15.冷[2,4].解答题：本大题共6小题，共计100分.解答时应写出文字说明、证明过程或演算步骤2sin AcosC 2cosAsinC = sin AcosC ,2 2------ + -------- tan A tan C =1.tan B 二 tan(二-(A C))2（n ）由（i ）知，tan A tan C1 - tan AtanC 211,即 tan A tanC tan AtanC.--tan (A C)二 __9-1710分21 .(本小题满分14分)a b 」a sin B解：(i) ,. b .sin A sin B sin A a 2asin Bi b = — sinC,. ------------ = asinC.. 2sin B = sinAsinC .2 sin A7 A B C -si n B =si n( A C) = sin AcosC cos Asin C ,又 tan A =3,得 tanC =6tan A tan C2ABC 为锐角三角形” tan A,tanC 均为正数，_______ 1.tan A tanC_2 .tanAtanC ,当且仅当 tan A = tanC 时等号成立.4.〔tanAtanC_2、、tanAtanC,. tanAtanC_16 当且仅当tanA=tanC时等号成立.21 -° tanA + tanC 尹n AtanC 1.八 f tanB2 (1). 1 -ta nAta nC tan Ata nC-1 2 tan Ata nC-18 8.tanB ，即tanB 的最大值的最大值为 一 15 15 22.(本小题满分14分) 解：(I)设AB 中点为D ，连结PD , CD ,因为 AP= BP ，所以 PD A AB . ......... 又 AC = BC ，所以 CD A AB . .......... 因为PD I CD = D ，所以ABA 平面PCD . 因为PC i 平面PCD ，所以PC A AB. •- 14分(n)由已知？ACB 90o , AC = BC= 2 , 所以 AD = BD = CD = 2, AB = 2.2 . B6分又DPAB 为正三角形，且 PD AAB ，所以 PD = .6.因为 PC = 2.2，所以 PC 2= CD 2+ PD 2. 所以CD A PD . ................................................................. 8分又 CD A AB , AB 平面 PAB , PD 平面 PAB , AB" PD = D 所以CD _平面PAB . \*CD 平面ABC ,平面PAB A 平面ABC . （川）设B 到平面平面PAC 的距离为h ，: E 为PB 的中点， -E 到平面平面PAC 的距离为一. 2 10分11分 由 V P~ACB 二 V B~PAC ,1 ^42 一 S PACh ——37.E到平面平面h / /IOPAC的距离为一二一 ......................... 14分2 723.(本小题满分14分)2 2解：(I)旺季y=kx -(100k -bjx-100b,,淡季y = kx -(100k-b2)x-100b2 ................................................... 5分2(n)在(I)的表达式y=kx -(100k-b i)x-100b i 中，由k . 0 可知，在销售旺季，当“号严=50 - 2k时利润y取得最大值;在销售淡季，当x = ------ —- 50 - -2时，利润y取得最大值 .................. 7分2k 2k下面分销售旺季和淡季进行讨论：由②知，在销售旺季，商场以140元/件的价格出售时，能获得最大利润•因此在销售旺季，当标价x =50-邑=140时，利润y取得最大值。

T1#include <stdio.h>#include <math.h>#include <string.h>void main(){int a[200],i,m,n,s=0;floatb,t,min,max,p;for(i=0;i<200;i++)scanf("%d",&a[i]);for(i=0,s=0;i<200;i++)s=s+a[i];b=s/200.0;min=fabs(a[0]-b);for(i=0;i<200;i++){t=fabs(a[i]-b);if(t<min){min=t;m=i;}}max=fabs(a[0]-b);for(i=0;i<200;i++){p=fabs(a[i]-b);if(p>max){max=p;n=i;}}printf("the average is %f\n",b);printf("the fraest is a[%d],%d\n",n,a[n]);printf("the nearst is a[%d],%d\n",m,a[m]); }T2void main(){int a[101],m,k,i,j,r;double q;do{printf("Please input m=");scanf("%d",&m);printf("Please input k=");scanf("%d",&k);if(m==0||k==0)break;for(i=0;i<k;){j=2;if(m==1)m=m+1;q=sqrt(m);while(j<q+1){r=fmod(m,j);if(r==0)break;elsej++;}if(j>q){a[i]=m;i++;}m=m+1;}for(i=k-1;i>=0;i--)printf("%d ",a[i]);printf("\n");}while(m!=0&&k!=0);}T3#include <stdio.h>#include <math.h>#include <string.h>#include <ctype.h>void main(){char c;intnuma[100],p=0,s,d,n,t,i,j;for(i=0;;){c=getchar();if(c=='\n'){if(p==1)numa[i]=s;break;}if(c>47&&c<58){d=c-48;if(p==0)s=d;elses=s*10+d;p=1;}else{if(p==1){numa[i]=s;i++;}p=0;}}n=i-1;for(j=0;j<n;j++){for(i=0;i<n-j;i++){if(numa[i]>numa[i+1]){t=numa[i];numa[i]=numa[i+1];numa[i+1]=t;}}}n++;for(i=0;i<n;i++)printf("%d\n",numa[i]);}T4#include <stdio.h>#include <math.h>#include <string.h>#include <ctype.h>void main(){charmi[26][5]={{'.','-'},{'-','.','.','.'},{'-','.','-','.'},{'-','.','.'},{'.'},{'.','.','-','.'},{'-','-','.'},{'.','.','.','.'},{'.','.'},{'.','-','-', '-'},{'-','.','-'},{'.','-','.','.'},{'-','-'},{'-','.'},{'-','-','-'},{'.','-','-'},{'-','-','.','-'},{'.','-','.'},{'.','.','.'},{'-'},{'.','.','-'},{'.' ,'.','.','-'},{'.','-','-'},{'-','.','.','-'},{'-','.','-','-'},{'-','-','.','.'}};charstr[100][5],newstr[100][5],c[100];inta,n,i,j,r;gets(c);n=strlen(c);for(i=0;i<n;i++){if(isupper(c[i]))c[i]=tolower(c[i]);a=c[i]-97;for(r=0;r<5;r++)str[i][r]=mi[a][r];if(i==0){j=n-4;for(r=0;r<5;r++)newstr[j][r]=str[i][r];}if(i==1){j=n-3;for(r=0;r<5;r++)newstr[j][r]=str[i][r];}if(i==2){j=n-2;for(r=0;r<5;r++)newstr[j][r]=str[i][r];}if(i==3){j=n-1;for(r=0;r<5;r++)newstr[j][r]=str[i][r];}if(i>3){j=i-4;for(r=0;r<5;r++)newstr[j][r]=str[i][r];}}for(i=0;i<n;i++){for(j=0;j<5;j++)printf("%c",newstr[i][j]);printf(" ");}printf("\n");}。

2011年清华金秋营数学试题及解答1.求sinn πsin Λn π2sin nn π)1(-的值。

解：设ni n ππεsin cos +=（i 为虚数单位）,则1,)1(22,,-n εεεΛ为012=-nx 的根。

kk k k i i n k εεεεπ212sin 2-=-=-，sin n πsin Λn π2sin nn π)1(-=)1(2111)1(2422)1()1)(1(-------n n n n n i εεεεΛ =211)1(2421)(2)1()1)(1()1(--------n n n n i εεεΛ=1)1(2422)1()1)(1(-----n n εεεΛ,而)())(()1(224222----n x x x εεεΛ=12)2(2)1(2+++--x x x n n Λ,n n =---∴-)1()1)(1()1(242εεεΛ12)1(sin 2sinsin-=-∴n n n n n nπππΛ 2.定义符号Ord p (n)(其中n 为整数，p 为素数）满足：若Ord p (n)= m ，则表示p m|n,并且p1+m ҂n ,定义S p (n)表示n 在p 进制表示下各位数字之和.（1)求证：Ord p (n!)=1)(--P n S n P（2)利用（1）的结论证明：)!1(!)!2(+n n n 为整数.（3)利用（1）的结论证明：)!1()!())!1((++n mn m n 为整数.证明：（1）设n=a k p k+11--k k pa +Λ+a 0,a i ∈{0,1,Λ,p-1}则Ord p （n!)=⎥⎦⎤⎢⎣⎡∑∞+=i p n i 1=a k p1-k +21--k k pa +Λ+a 2p+a 1 +a k p2-k +31--k k pa +Λ+a 2+Λ+a k=11--p p a k k +1111----p p a k k +Λ+1122--p p a +1111--p p a=1)()(0110111-+++-+++---p a a a a a p a p a p a k k k k k k ΛΛ=1)(--P n S n P(2)设p α||(n+1) (P 为n+1的任一素 因子) 即n+1=a k p k+ a 1-k p 1-k +Λa αp α(0≤a i ≤p-1,且1≤a α≤p-1)则n=a k p k+a 1-k p1-k +Λ+(a α-1)p α+(p-1)p1-α+(p-1)p2-α+Λ+(p-1)2n=2a k p k +2a 1-k p1-k +Λ+2(a α-1)p α+2(p-1)p1-α+2(p-1)p2-α+Λ+2(p-1)显然*∈+=+N C n C n n n n n n n 22,1)!1(!)!2(S p (n)=a k +a 1-k +Λ+(a α-1)+α(p-1)S p (2n)=2(a k +a 1-k +Λ+(a α-1))-α(p-1)-t(p-1) (t ≥0)Ord p （C nn 2)=Ord p （2n!)-2Ord p （n!)=1)2()(2--p n S n S p p =1)1()1(--+-p p t p α=αα≥+tnn C p 2|α∴, 即)!1(!)!2(+n n n *∈N .(3).由题知：若p 为n+1的素因子，且)1(||+n p α,则（p,m)=(1,(p,n))=1, 设n+1=a k p k+ a 1-k p1-k +Λa αp α(a α)1≥mn=b k p k + b 1-k p1-k +Λb 0(b 0)1≥ 则，n=a k p k+ a 1-k p1-k +Λ(a α-1)p α+(p-1)p1-α+Λ+(p-1)mn+n=(a k +b k )p k+(a 1-k +b 1-k )p1-k +Λ(a α+b α-1)p α+(b 1-α+p-1)p1-α+Λ(b 0+p-1)S p (n)=a k + a 1-k +Λ(a α-1)+α(p-1)S p (mn)=b k + b 1-k +Λb 0,10≥b Θ,S p (mn+n)=(a k +b k )+(a 1-k +b 1-k )+Λ(a α+b α-1)-)1()1(---p t p α (其中a k +b k ,a 1-k +b 1-k ,+Λa α+b α,共有t 次进位）显然1)!1()!())!1((+=+++n C n mn m n n n mn ，=∴+)(nn mn p C Ord Ord p （（mn+n)!)-Ord p （n!)-Ord p （(mn)!) =1)()()(-+-+p n mn S n S mn S p p p=αα≥+tnn mn C p +∴|α,即)!1()!())!1((++n mn m n *∈N 。

2011年南京理工大学自主招生、保送生考试数学试卷一. 填充题:本大题共20小题,每小题5分,共计100分.请把答案填写在答题卡相应位置上. 1.设全集{}{}3,,lg 0x U y y x R A x x ==∈=≥,则U C A = ▲2.若命题“2,40x R x mx ∃∈-+->”是假命题,则实数m 的取值范围为 ▲ .3.已知圆O :221x y +=,直线:4l x y +=.过l 上一点P 作圆O 的切线,则当切线长最短时,P 点的坐标为 ▲4.函数21cos28sin ()(0)sin 22x x f x x x π++=<<的值域为 ▲5．对一个作直线运动的质点的运动过程观测了8次,得到如下表所示的数据.观测次数i 1 2 3 4 5 6 7 8 观测数据i a4042414444454748在上述统计数据的分析中,一部分计算见如图所示的算法流程图（其中a 是这8个数据的平均数），则输出的S 的值是 ▲6.已知平面向量,αβu r u r 满足:0,,1,ααββα≠≠=u r r u r u r u r u r 与αβ-u r u r 的夹角为60︒,则αu r的取值范围为 ▲7. 已知正三棱柱的底面边长为1,两侧面的异面的对角线互相垂直,则该三棱柱的侧棱长为 ▲8.某公司在2010年投资了一个项目,每年都既有现金投入,又有现金收入.已知2010年度公司投入了1000万元,以后每年投入将比上年减少20%;2010年度公司收入了500万元,以后每年收入会比上年增加25%.按此计算,公司将于 ▲ 年即可收回全部投入. (参考数据:65430.80.262,0.80.328,0.80.410,0.80.512====)9.已知椭圆2212221(0),,x y a b F F a b+=>>为其左右焦点,P 为椭圆C 上任意一点,I 为12PF F ∆内切圆圆心,点G 满足123PF PF PG +=u u u r u u u u r u u u r 且12GI F F λ=u u r u u u u r(R λ∈且0λ≠),则椭圆的离心率是 ▲10.已知关于x 方程20ax bx c ++=r r r r ，其中a r 、b r 、c r 是非零向量，且a r 、b r不共线，则该方程实数解的个数为▲ 个11.已知lg(1)1,0,()lg(1)1,0,x x f x x x ++≥⎧=⎨-+<⎩若不等式(1)(2)f ax f x ->-在[3,4]上有解,则实数a 的取值范围为 ▲12.已知m ∈N ，若函数()24f x x m x m =--存在整数零点，则m 的取值范围为 ▲13.设[]x 表示不超过x 的最大整数,例如:[ 1.3]2,[2]2,[2.5]2-=-==等.则方程[]2tan 2sin x x =在[0,2)π内的解组成的集合为 ▲ 14.已知数列{}n a 满足:111()1n n n n a a n n N a a *+++-=∈-+,且428a =,则{}n a 的通项公式为n a = ▲15. 已知23(ax y a a +=+为正常数,0,0)x y ≥≥,若22x y +的最大值为S ,且[49,121]S ∈,则a 的取值范围为 ▲16.已知函数1()sin ,[0,π]3f x x x x =-∈.01cos 3x =（0[0,π]x ∈），那么下面命题中真命题的序号是 ▲ :①()f x 的最大值为0()f x ;②()f x 的最小值为0()f x ; ③()f x 在0[0,]x 上是减函数; ④()f x 在0[,π]x 上是减函数.17.已知函数()1f x x x a =-+,若(0,3)a ∈且()f x 在区间[1,2]上的最小值为32,则a = ▲ 18.设函数()f x 是定义在R 上的奇函数,且对任意的12,[1,]x x a ∈,当21x x >时,总有2()f x >1()0f x >,则下列不等式一定成立的是 ▲ (填上你认为正确的结论的序号):①()(0)f a f >;②1()2a f f +>; ③13()(3)1a f f a ->-+; ④13()()1af f a a->-+19.在平面直角坐标系xOy 中,O 为坐标原点.定义()11,P x y 、()22,Q x y 两点之间的“直角距离”为1212(,)d P Q x x y y =-+-,若点Q 在直线l 上运动,定义min (,)(,)d P l d P Q =.已知点()1,0B ，直线M 的方程为30(0)kx y k k -++=>，则(,)d B M 的最大值为 ▲20.已知函数3sin cos ()(,)3cos a bx x bx xf x a b R x+++=∈+,若()f x 在R 上既有最大值,又有最小值,且最大值与最小值的和为6,则a b += ▲ .二.解答题:本大题共6小题,共计100分.解答时应写出文字说明、证明过程或演算步骤. 21．（本小题满分14分）在锐角ABC ∆中,角,,A B C 的对边分别为,,a b c ,已知sin 2ab C =.（Ⅰ）若tan 3A =,求tan B 的值; （Ⅱ）求tan B 的最大值.22.（本小题满分14分）如图，在三棱锥P ABC -中，2AC BC ==，90ACB ?o，侧面PAB 为等边三角形，侧棱PC =E 为PB 中点. （Ⅰ）求证：PC ⊥AB ；（Ⅱ）求证：平面PAB ^平面ABC ； （Ⅲ）求点E 到平面PAC 的距离.BA23.（本小题满分14分）某商场以100元/件的价格购进一批衬衣，以高于进货价的价格出售，销售期有淡季与旺季之分，通过市场调查发现：①销售量()r x (件)与衬衣标价x (元/件)在销售旺季近似地符合函数关系：1()r x kx b =+，在销售淡季近似地符合函数关系：2()r x kx b =+，其中12120,0k b b k b b <>、且、、为常数； ②在销售旺季，商场以140元/件的价格销售能获得最大销售利润；③若称①中()0r x =时的标价x 为衬衣的“临界价格”，则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍．请根据上述信息，完成下面问题：(Ⅰ)分别写出销售旺季和销售淡季销售总利润y (元)与标价x (元/件)的函数关系式(含k 、1b 或2b ); (Ⅱ)在销售淡季，该商场要获得最大销售利润，衬衣的标价应定为多少元/件？24.（本小题满分18分）已知点(1,)M y 在抛物线2:2C y px =(0)p >上，M 点到抛物线C 的焦点F 的距离为2，直线:l 12y x b =-+与抛物线交于,A B 两点.（Ⅰ）求抛物线C 的方程；（Ⅱ）若以AB 为直径的圆与x 轴相切，求该圆的方程； （Ⅲ）若直线l 与y 轴负半轴相交，求AOB ∆面积的最大值. 25．（本小题满分20分）如图,111(,)P x y ，222(,)P x y ，L ，(,)n n n P x y ，12(0,)n y y y n N *<<<<∈L 是曲线2:3(0)C y x y =≥上的n个点，点(,0)(1,2,3,,)i A a i n =L 在x 轴的正半轴上，1i i i A A P -∆是正三角形(0A 是坐标原点) .（Ⅰ）求123,,a a a ；（Ⅱ）求出点n A (,0)(*)n a n N ∈的横坐标n a 关于n 的表达式； （Ⅲ）设12321111n n n n nb a a a a +++=++++L ，若对任意正整数n 及 (0,2]x ∈,不等式31726n x ax b -≤-恒成立,求实数a 的取值范围.26．（本小题满分20分）已知实数a 满足02,1a a <≤≠,设函数3211()32a f x x x ax +=-+．(Ⅰ) 当2a =，求()f x 的极小值；(Ⅱ) 若函数22()(24)ln ()g x ax bx b x x b R =+-++∈的极小值点与()f x 的极小值点相同．求()g x 的极大值的最大值,并求取到最大值时,a b 的值．数学自主招生、保送生考试数学试卷参考答案一.填充题:本大题共20小题,每小题5分,共计100分.请把答案填写在答题卡相应位置上.1. (0,1)2. [4,4]-3. (2,2)4. [4,)+∞5.558 6. 7.2 8. 2014 9. 1210. 0或1 11. 2(,0)(,)3-∞+∞U 12. {}0,3,8 13. 50,,,44πππ⎧⎫⎨⎬⎩⎭ 14. 22n n - 15. 13[,][2,4]35U16. ①④ 17.12或9418. ①②④ 19. 5 20. 8 二.解答题:本大题共6小题,共计100分.解答时应写出文字说明、证明过程或演算步骤.21．（本小题满分14分）解: （Ⅰ）sin ,sin sin sin a b a Bb A B A =∴=Q. 2sin sin ,sin .2sin sin sin 2sin a a B b C a C B A C A=∴=∴=Q .………………… 2分,sin sin()sin cos cos sin A B C B A C A C A C π++=∴=+=+Q ,2sin cos 2cos sin sin cos A C A C A C ∴+=,221tan tan A C∴+=………………… 4分 又tan 3A =,得tan 6C =tan tan 9tan tan(())tan()1tan tan 17A CB AC A C A C π+∴=-+=-+=-=-………………… 7分（Ⅱ）由（Ⅰ）知, 221tan tan A C ∴+=,即1tan tan tan tan .2A C A C +=ABC ∆Q 为锐角三角形,tan ,tan A C ∴均为正数,tan tan A C ∴+≥当且仅当1tan tan 4A C ==时等号成立. ………………… 10分1tan tan tan tan 162A C A C ∴≥∴≥ 当且仅当1tan tan 4A C ==时等号成立. 1tan tan tan tan 112tan (1)1tan tan tan tan 12tan tan 1A CA CB AC A C A C +=-==+---Q . 8tan 15B ∴≤,即tan B 的最大值的最大值为815.………………… 14分22.（本小题满分14分）解: （Ⅰ）设AB 中点为D ，连结PD ，CD ， 因为AP BP =，所以PD AB ^.………… 1分又AC BC =，所以CD AB ^. ………………… 2分 因为PD CD D =I ，所以AB ^平面PCD .因为PC Ì平面PCD ，所以PC AB ^. ……… 5分 （Ⅱ）由已知90ACB?o ，2AC BC ==，所以AD BD CD ===AB =.又PAB D 为正三角形，且PD AB ^，所以PD =…………………… 6分因为PC =222PC CD PD =+.所以CD PD ^. …………………………………………… 8分 又CD AB ^,AB ⊂平面PAB ,PD ⊂平面PAB ,AB PD D =I所以CD ⊥平面PAB .CD ⊂Q 平面ABC ,∴平面PAB ^平面ABC . …………………………… 10分 （Ⅲ）设B 到平面平面PAC 的距离为h ,E Q 为PB 的中点,E ∴到平面平面PAC 的距离为2h.…………………………… 11分由P ACB B PAC V V --=,得11337ABC PAC S PD S h h ∆∆⋅=⋅⇒= CABPEDE ∴到平面平面PAC 的距离为2h…………………………… 14分 23.（本小题满分14分）解：（Ⅰ）旺季112100)100(b x b k kx y ---=,淡季222100)100(b x b k kx y ---=………………… 5分 （Ⅱ）在（Ⅰ）的表达式112100)100(b x b k kx y ---=中，由0<k 可知， 在销售旺季，当kbk b k x 250210011-=-=时，利润y 取得最大值；在销售淡季，当kbk b k x 250210022-=-=时，利润y 取得最大值………………… 7分下面分销售旺季和淡季进行讨论：由②知，在销售旺季，商场以140元/件的价格出售时，能获得最大利润. 因此在销售旺季，当标价1402501=-=kb x 时，利润y 取得最大值。

北大清华自主招生面试考题(完整版)北大清华自主招生面试考题(完整版)梧桐夜雨1.马克思在《资本论》中论述机器夺走了工人的饭碗时写道：“蒸汽机一开始就是人力的对头”。

请谈谈你的看法。

2.近期房产税、车船税、“馒头税”等均引发社会热议，请谈谈你对纳税与公民权利关系的理解。

3.哈佛大学图书馆墙上写有这样一句话：“请享受无法回避的痛苦”，谈谈你的理解。

4.假如用一种植物比喻中国人的国民性，你会选择什么？为什么？5.有人说：“智慧比体力更重要，成功的关键在于如何使用智慧”，请谈谈你的看法。

6.现在很多家长在高中阶段就把孩子送到国外学习，谈谈你的看法。

7.国家最近规定，中央和省级机构录用公务员，一般情况下都须具有两年以上基层工作经历，不再招收应届毕业生，你对此有何评论。

8.“穷则独善其身，达则兼济天下”，在今天是否还适用？9.目前一些人富裕了但并没感到幸福，谈谈你的看法。

10.有人认为“三纲”(君臣、父子、夫妻)无益，“五常”(仁义礼智信)可取。

试述你的观点。

11.近来续写《红楼梦》又成为社会热点话题。

你认为后人可以续写、仿写、改写经典名著吗？12.古人云“诗画同源”，“诗是无形画，画是有形诗”。

请谈谈你的见解。

13.请从世界历史和国际政治的角度，分析“只有永远的利益，没有永远的朋友”这句话的含义。

14.今年是辛亥革命100周年，海峡两岸将共同举行隆重庆典。

你认为大陆和台湾看待辛亥革命的角度和意义会有什么不同？15.网络带来丰富的信息，但也存在着许多虚假报道和伪装成民意的倾向性意见，你认为政府如何才能从网络上获取真实的社情民意？16.日本政府最近称，由于中国的GDP已经超过日本，所以要大幅削减对华援助，你如何看待此事？17.在鲁迅的小说《祝福》中，“我”作为一个现代知识分子，为什么不告诉祥林嫂“人死后是没有灵魂的”？18.牛顿第一定律可以被实验验证吗？19.“火”被古人当成一种物质元素，今天我们如何认识“火”？20.诗曰：“我看青山多妩媚，料青山看我应如是”，说说你的理解。

2012年北京大学保送生考试数学试题1.已知数列{a}为正项等比数列，且a₃+a₄-α-a₂=5,求as+a₆的最小值.2.已知/(x)为二次函数，且a,f(a),f(f(a)).ʃ(ʃ(ʃ(a))成正项等比数列，求证：f(a)=a.3. 称四个顶点都落在三角形三边上的正方形叫三角形的内接正方形.若锐角三角形ABC 的三边满足a>b>c,证明：这个三角形的内接正方形边长的最小值为4.从O 点发出两条射线A,3, 已知直线/交4,L2于A,B 两点，且Saa=c(c 为定值),记AB 中点为X, 求证：X 的轨迹为双曲线.5. 已知a(i=1,2, …,10)满足a+a₂+ …+ao=30,aa₂…o<21,求证：3a,(i=1,2,…,10),使a,<1.2012年清华大学保送生考试数学试题一 、填空题1.若复数=为虚数，且 |= |=1,Re(=(1-2i))=1,2.在数列{a} 中，α=1,a*₁=an+2.则 = =若数列的 前 n 项 和 为,则11=。

3.现有6人会英语，4人会日语，2人都会(共12人),从其中选出3人做翻译，要求两种语言都有人做翻译，则符合条件的选法种数为 .4.有一人进行投篮训练，投篮5次，失误一次扣1分，进一次得1分，连进2次得3分，连进3次得5分.若投篮的命中率为 ,则投篮3次恰好得2分的概率为厦门一中2011级自主招生辅导讲义一数学一黄昌毅5.不定方程≤=)的解(r,y,z)的组数为。

6.某几何体的三视图如右图所示，用α,β,γ分别表示主视图、左视图、俯视图，设Sa,Sg,S,是实际几何体中能看到的面积，则 Sa,Sg,S, 从小到大的顺序为二、解答题7.抛物线与直线l:y=x+4 所围成区域中有一个矩形ABCD, 且点A,B 在抛物线上，点D 在直线/上，其中点B 在y 轴右侧，且|AB |=2t(t>0).(1)当AB 与x轴平行时，求矩形ABCD 面积S(t) 的函数关系式；(2)当边CD 在直线/上时，求矩形ABCD 面积的最大值.8.已知函数,且.x∈[0,2π].(1)求函数f(x) 的最大值和最小值；(2)求方程ʃ(x)= √3的解.9.已知函数,且数列{a} 满足：α=1,am₁=f(an).(1)求证：r ·e'-e'+1≥0恒成立；(2)求函数f(x) 的单调区间；(3)求证：数列{a₁} 单调递减，且ax>0 恒成立.10.在△OAB内(含边界),其中O 为坐标原点，点A,B 分别在在x轴，y 轴的正半轴上，且OA= OB=2(1)用方程或不等式表示△OAB围成的区域；(2)求证：在△OA B 内的任意11个点，总可以分成两组，一组中各点的横坐标之和不大于6,另一组中各点的纵坐标之和不大于62013年北京大学保送生考试数学试题【第1题】△ABC 内点M 满足∠CMB=100°,线段BM 的中垂线交边AB 于P, 线段CM 的中垂线交边AC 于Q, 已知：P 、M 、Q 三点共线，求∠CAB.【第2题】正数a,b,c 满足a<b+c, 求证：【第3 题】是否存在两两不同的实数a,b,c,使直角坐标系中的三条直线y=ax+b,y=br+c,y=cx+a 共点.【第4题】对{1,2, …9}的某非空子集，若其中所有元素的和为奇数，则称为奇子集，问奇子集的个数.【第5题】在一个2013×2013的正数数表中，每行都成等差数列，每列平方后都成等差，求证：左上角的数和右下角的数之积等于左下角的数和右上角的数之积.2013年清华大学保送生考试数学试题【第1题】求证：【第2题】求证：为关于x的整系数多项式. 【第3题】已知,求αb⁵+bc⁵+cd 的值.【第4题】求证：平面内间跟为d 的一组平行直线，任意放一长为(I<d) 的针与直线相交的概率为【第5题】求证：2013年北京大学保送生考试数学试题详解【第1题】△ABC 内点M 满足∠CMB=100°,线段BM 的中垂线交边AB 于P, 线段CM 的中垂线交边AC 于Q, 已知：P 、M 、Q 三点共线，求∠CAB.解：如图.∠PBM+ ∠QCM= ∠PMB+ ∠QMC=180°- ∠BMC=80°∠MBC+ ∠MCB=180°- ∠BMC=80°于是∠ABC+ ∠ACB=( ∠PBM+ ∠QCM)+)( ∠MBC+ ∠MCB)=160°, ∠BAC'=20°【第2题】正数a,b,c 满足a<b+c, 求证：解：因此原不等式得证.【第3题】是否存在两两不同的实数a,b,c , 使直角坐标系中的三条直线y=ax+b,y=br+c,y=cr+a 共点.解：原问题即方程组ax+b=br+c=cx+a 有解(a,b,c,x), 其中a,b,c 两两不同.整理, 得d²+b²+c²=ab+bc+ca, 与a,b,c 两两不同矛盾.于是不存在符合题意的实数对(a,b,c).【第4题】对{1,2,…9}的某非空子集，若其中所有元素的和为奇数，则称为奇子集，问奇子集的个数.解：设M={1,3,5,7,9},N={2,4,6,8}, 则奇子集由M 中的1个、3个或5个元素以及N 中的任意个元素组成.因此奇子集共有.2⁴=256个.【第5 题】在一个2013×2013的正数数表中，每行都成等差数列，每列平方后都成等差，求证：左上角的数和右下角的数之积等于左下角的数和右上角的数之积.解：下面证明对nxn 的数表，n≥3,n∈N,n 是奇数，命题均成立.当n=2k+1时，不妨设数表如图baa …………………………·……·…···……………dC ….…于是→(a+b)²+(c+d²=α+c²+b+d+2√(α+c)+(F+d)→(ab+cd)²=(d+c²)(b²+d)→2abcd=b²c²+ad→ ad=bc因此命题成立.2013年清华大学保送生考试数学试题详解【第1题】求证：证明：用数学归纳法证明.当n=1,2,3,4,5,6 时，命题显然成立.假设当n=k 当时命题成立，即,则n=k+6时(由归纳假设)厦门一中2011级自主招生辅导讲义一数学一黄昌毅下面证明Vk ∈N,当 k =6m 时 ，当k=6m+1时 左边以下略.【第2题】求证：为关于x 的整系数多项式 .证明：只需要证明 为关于x 的整系数多项式 ., 则φ:(x)是在实数范围内不可分的φ(k)次整系数多项式因式(因分分圆多项式必然为整系数多项式，其中φ为欧拉函数 ) , 如q(x)=x- 1,9₂(x)=x+1,9₃(x)=x²+x+1,4₄(x)=x²+1, ….于是,如x⁶-1= g(r) ·φ₂(x) ·甲₃ (x):₆(x)., 其中表示对取整.因此问题即对于任意正整数p,分子所含因式φ。

2011高考试题及答案2011年普通高等学校招生全国统一考试语文试卷及答案解析一、现代文阅读（9分，每小题3分）阅读下面的文字，完成1-3题。

《中国建筑的特征》中国建筑，具有悠久的历史传统和光辉的成就。

从陕西半坡村遗址发掘的方形或圆形浅穴式房屋发展到现在，已有六七千年的历史。

历代政治中心，随着社会生产力的发展，建筑技术和建筑艺术也随之不断提高，规模宏大而平面变化丰富的中国古代建筑，已成为中国古代文化的重要组成部分。

1. 下列关于“中国古代建筑”的表述，不正确的一项是（）A. 中国古代建筑具有悠久的历史传统和光辉的成就。

B. 中国古代建筑从陕西半坡村遗址发掘的房屋发展到现在，已有六七千年的历史。

C. 中国古代建筑技术和建筑艺术随着社会生产力的发展而不断提高。

D. 中国古代建筑是中国古代文化的重要组成部分，规模宏大而平面变化丰富。

答案：D解析：选项D中“规模宏大而平面变化丰富”是对中国古代建筑的描述，但原文中并没有提到这一点，因此选项D不正确。

2. 下列理解，不符合原文意思的一项是（）A. 中国古代建筑的发展与社会生产力的发展密切相关。

B. 中国古代建筑技术和建筑艺术随着政治中心的转移而不断提高。

C. 中国古代建筑已成为中国古代文化的重要组成部分。

D. 中国古代建筑的发展是一个漫长的历史过程。

答案：B解析：原文中提到“历代政治中心，随着社会生产力的发展，建筑技术和建筑艺术也随之不断提高”，并没有提到“政治中心的转移”，因此选项B不符合原文意思。

3. 根据原文内容，下列推断不正确的一项是（）A. 中国古代建筑的发展是一个不断进步的过程。

B. 中国古代建筑的发展与社会生产力的发展是同步的。

C. 中国古代建筑的发展与中国古代文化的发展是同步的。

D. 中国古代建筑的发展是一个独立于社会生产力发展之外的过程。

答案：D解析：原文中明确提到中国古代建筑的发展与社会生产力的发展密切相关，因此选项D“独立于社会生产力发展之外”的推断是不正确的。