第十二章轴向拉压详解
- 格式:pdf
- 大小:537.04 KB
- 文档页数:55


12-1 强度计算与刚度计算1)构件的失效模式若载荷过大,超出了构件的承载能力,构件将失去某些功能而不能正常工作,称为构件失效。
工程中,构件的失效模式主要有:•强度失效——构件的材料断裂或屈服。
•刚度失效——构件的弹性变形过大,超出规定范围。
•疲劳失效——构件在交变应力作用下的强度失效。
•稳定失效——构件丧失了原有的平衡形态。
本章只研究杆件强度失效与刚度失效的计算问题。
12-1 强度计算与刚度计算首先根据内力分析方法,对受力杆件进行内力分析(画出内力图),确定可能最先发生强度失效的横截面(危险截面)。
[]()4 , 3 , 2 , 1 之一=≤i ri σσ根据强度条件,即上面不等式,强度计算可解决三类问题:•校核强度•设计截面•计算许可载荷1)构件的失效模式2)杆件的强度计算其次根据杆件横截面上应力分析方法,确定危险截面上可能最先发生强度失效的点(危险点),并确定出危险点的应力状态。
最后根据材料性能(脆性或塑性)和应力状态,判断危险点的强度失效形式(断裂或屈服),选择相应的强度理论,建立强度条件:12-1 强度计算与刚度计算3)杆件的刚度计算除了要求满足强度条件之外,对其刚度也要有一定要求。
即要求工作时杆件的变形或某一截面的位移(最大位移或指定截面处的位移)不能超过规定的数值,即∆为计算得到的变形或位移;[∆]为许用(即人为规定的)变形或位移。
对轴向拉压杆,∆是指轴向变形或位移u ;对受扭的杆件,∆是指两指定截面的相对扭转角φ或单位长度扭转角ϕ;对于梁,∆是指挠度v 或转角θ。
根据刚度条件,即上面不等式,刚度计算可解决三类问题:•校核刚度•设计截面•计算许可载荷][ΔΔ≤刚度条件1)构件的失效模式2)杆件的强度计算12-2 轴向拉压杆件的强度计算轴向拉压杆横截面上正应力是均匀分布的,各点均处于单向应力状态。
因此,无论选用哪个强度理论,强度条件表达式均演化为][m axσσ≤例1螺旋压力机的立柱如图所示。

04、基本知识 怎样推导轴向拉压和扭转的应力公式、变形公式(供参考)同学们学习下面内容后,一定要向老师回信(****************),说出你对本资料的看法(收获、不懂的地方、资料有错的地方),以便考核你的平时成绩和改进我的工作。
回信请注明班级和学号的后面三位数。
1 * 问题的提出 ........................................................................................................................... 1 2 下面就用统一的步骤,研究轴向拉压和扭转的应力公式和变形公式。
........................... 2 3 1.1 轴向拉压杆的应力公式推导 ............................................................................................ 2 4 1.2 轴向拉压杆的变形公式推导 ............................................................................................ 4 5 1.3 轴向拉压杆应力公式和变形公式的简要推导 ................................................................ 4 6 1.4 轴向拉压杆的强度条件、刚度条件的建立 .................................................................... 4 7 2.1 扭转轴的应力公式推导 .................................................................................................... 5 8 2.2 扭转轴的变形公式推导 .................................................................................................... 7 9 2.3 扭转轴应力公式和变形公式的简要推导 ........................................................................ 7 10 2.4 扭转的强度条件、刚度条件的建立 ............................................................................ 8 11 3. 轴向拉压、扭转、梁的弯曲剪切,应力公式和变形公式推导汇总表 .. (9)1* 问题的提出在材料力学里,分析杆件的强度和刚度是十分重要的,它们是材料力学的核心内容。

材料力学各章重点内容总结第一章 绪论一、材料力学中工程构件应满足的3方面要求是:强度要求、刚度要求和稳定性要求。
二、强度要求是指构件应有足够的抵抗破坏的能力;刚度要求是指构件应有足够的抵抗变形的能力;稳定性要求是指构件应有足够的保持原有平衡形态的能力。
三、材料力学中对可变形固体进行的3个的基本假设是:连续性假设、均匀性假设和各向同性假设。
第二章 轴向拉压一、轴力图:注意要标明轴力的大小、单位和正负号。
二、轴力正负号的规定:拉伸时的轴力为正,压缩时的轴力为负。
注意此规定只适用于轴力,轴力是内力,不适用于外力。
三、轴向拉压时横截面上正应力的计算公式:N FAσ= 注意正应力有正负号,拉伸时的正应力为正,压缩时的正应力为负。
四、斜截面上的正应力及切应力的计算公式:2cos ασσα=,sin 22αστα=注意角度α是指斜截面与横截面的夹角。
五、轴向拉压时横截面上正应力的强度条件[],maxmax N F Aσσ=≤六、利用正应力强度条件可解决的三种问题:1.强度校核[],maxmax N F Aσσ=≤一定要有结论 2.设计截面[],maxN F A σ≥3.确定许可荷载[],maxN F A σ≤七、线应变ll ε∆=没有量纲、泊松比'εμε=没有量纲且只与材料有关、 胡克定律的两种表达形式:E σε=,N F ll EA∆=注意当杆件伸长时l ∆为正,缩短时l ∆为负。
八、低碳钢的轴向拉伸实验:会画过程的应力-应变曲线,知道四个阶段及相应的四个极限应力:弹性阶段(比例极限p σ,弹性极限e σ)、屈服阶段(屈服极限s σ)、强化阶段(强度极限b σ)和局部变形阶段。
会画低碳钢轴向压缩、铸铁轴向拉伸和压缩时的应力-应变曲线。
九、衡量材料塑性的两个指标:伸长率1100l llδ-︒=⨯︒及断面收缩率1100A A Aϕ-︒=⨯︒,工程上把5δ︒≥︒的材料称为塑性材料。
十、卸载定律及冷作硬化:课本第23页。




第十二章组合变形【学时】4内容:组合变形的概念及工程实例;斜弯曲时的应力和强度计算;拉(压)与弯曲组合时应力和强度计算;偏心压缩(拉伸);截面核心;弯曲与扭转组合时的强度计算。
基本要求:【基本要求】1.理解组合变形的概念[2]。
2.掌握斜弯曲时的应力和强度计算[1]。
3.掌握拉(压)与弯曲组合时应力和强度计算[1]。
4.理解偏心压缩(拉伸)[2]。
5.了解截面核心的概念[3]。
6.掌握弯曲与扭转组合时的强度计算[1]。
重点:【重点】斜弯曲,弯扭组合时的强度计算难点:【难点】截面核心§12–1 概 述一、组合变形 :在复杂外载作用下,构件的变形会包含几种简单变形,当几种变形所对应的应力属同一量级时,不能忽略之,这类构件的变形称为组合变形。
二、组合变形的研究方法 —— 叠加原理① 外力分析:外力向形心(后弯心)简化并沿主惯性轴分解③ 内力分析:求每个外力分量对应的内力方程和内力图,确定危险面 ③应力分析:画危险面应力分布图,叠加,建立危险点的强度条件。
§12–2 斜弯曲一、斜弯曲:挠曲线与外力(横向力)不共面。
二、斜弯曲的研究方法 :1.分解:将外载沿横截面的两个形心主轴分解,于是得到两个正交的平面弯曲。
2.叠加:对两个平面弯曲进行研究;然后将计算结果叠加起来。
解:1.将外载沿横截面的形心主轴分解ϕsin P P y =ϕcos P P z =2.研究两个平面弯曲 ①内力ϕϕϕcos sin sin )()(M M M x L P x L P M y y z ==-=-=(2)应力M y 引起的应力:ϕσcos I M I z M yyy z-=-='M z引起的应力:ϕσsin I M I y M zz z y -=-=''合应力:)sin I y cos I z (M z y ϕϕσσσ+-=''+'=(3)中性轴方程000=+-=)sin I ycos I z (M z y ϕϕσϕαctg tg 00yz I Iz y ==可见:仅当Iy = Iz ,中性轴与外力才垂直(4)最大正应力距中性轴的两侧最远点为拉压最大正应力点 (5)变形计算当ϕ = β 时,即为平面弯曲【例】 矩形截面木檩条,简支在屋架上,跨度l=4m,荷载及截面尺寸(图中单位:mm)如图所示,材料许用应力[σ]=10MPa ,试校核檩条强度,并求最大挠度。

刚体:在力的作用下不会发生形变的物体。
合力投影定理:合力在任一轴上的投影,等于各分力在该轴上投影的代数和。
力矩M 0(F)=±Fh(逆时针为正),点O 为矩心,垂直距离h 为力臂,力使物体逆时针转动为正。
合力矩定理:平面汇交力系的合力对平面内任一点的矩,等于所有各分力对同一点的矩的代数和。
力偶:大小相等、方向相反,作用线平行且不共线的两个力组成的力系称为力偶; 平面力偶系:作用在刚体上同一平面内的多个力偶,称为平面力偶系。
力的平移定理:作用于刚体上的力可以平行移动到刚体内的任意一点,但必须附加一个力偶,该附加力偶的力偶矩等于原力对指定点的矩。
平面任意力系中各力的矢量和F R `称为该力系的主矢量,简称主矢;力系各力对简化中心O 的矩的代数和Mo 称为该力系对简化中心O 的主矩。
平面任意力系平衡的必要和充分条件是:力系的主矢和对任意一点的主矩都等于零。
地心对物体的吸引力称为物体的重力,其大小就是物体的重量。
物体重力的作用点称为物体的重心。
由物体的几何形状和尺寸所决定的点是物体的几何中心,称为物体的形心。
强度(构件抵抗破坏的能力刚度(构件抵抗变形的能力稳定性(构件保持原有平衡形式的能力连续性假设(认为组成变形固体的物质毫无间隙地充满了它的整个几何空间,而且变形后仍保持这种连续性。
)、均匀性假设(认为整个物体是由同一材料组成。
)、 各向同性假设(认为物体在各个方向具有相同的物理性质)、内力:因外力作用而引起构件内各部分之间相互作用力的改变量,称为附加内力,简称内力。
全应力:dAdF=P ,通常把全应力p 分解为垂直于截面的分量σ(正应力)和与截面相切的分量τ(切应力)。
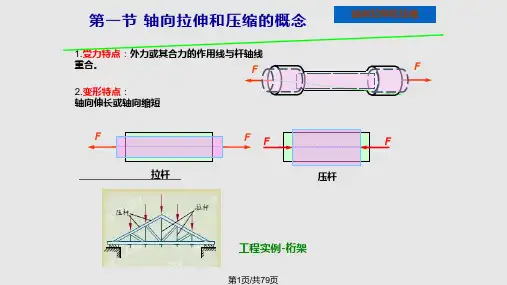
第十二章 轴向拉伸与压缩一、拉伸与压缩的概念:杆件所受外力(或外力的合力)作用线与杆轴线重合;杆件的变形为轴线方向的伸长或缩短。
这种变形形式称为轴向拉伸或轴向压缩。
线应变:l l∆=ε,胡克定律εσE =或EAl F l N =∆,E 是材料拉压弹性模量,E A 是材料抗拉压刚度横向线应变μεε-=`,μ是泊松比1、低碳钢在拉伸时四个阶段(1)弹性阶段(2)屈服阶段(3)强化阶段(4)局部变形阶段%1001⨯-=lll δ,衡量材料塑性的另一指标是断面收缩率ψ,%1001⨯-=AA A ψ塑性材料(如低碳钢)通常以屈服极限为其极限应力。