下载文档原格式
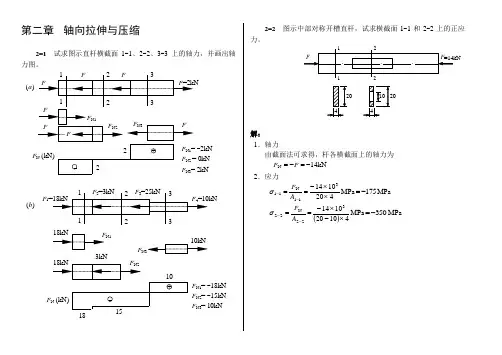
第二章 拉伸、压缩与剪切第二章答案2.1 求图示各杆指定截面的轴力，并作轴力图。
40kN 50kN 25kN（a）44F RF N440kN 3F N325kN 2F N220kN11F N1解：F R =5kN F N 4=F R =5 kNF N 3=F R +40=45 kNF N 2=-25+20=-5 kNF N 1=20kN45kN 5kN20kN5kN（b ）110kN6kNF N 1=10 kN F N 2=10-10=0F N 3=6 kN1—1截面：2—2截面：3—3截面：10kNF N 11110kN10kN22F N 26kN33F N 32.2 图示一面积为100mm ⨯200mm 的矩形截面杆，受拉力F = 20kN 的作用，试求：（1）6π=θ的斜截面m-m 上的应力；（2）最大正应力max σ和最大剪应力max τ的大小及其作用面的方位角。
解：320101MPa0.10.2P A σ⨯===⨯2303cos 14σσα==⨯=3013sin600.433MPa222στ==⨯=max 1MPaσσ==max 0.5MPa2στ==F2.3 图示一正方形截面的阶梯形混凝土柱。
设重力加速度g = 9.8m/s 2, 混凝土的密度为33m /kg 1004.2⨯=ρ，F = 100kN ，许用应力[]MPa 2=σ。
试根据强度条件选择截面宽度a和b 。
ba解：24,a ρ⋅3422.0410ρ=⨯⨯11[]aσσ=0.228ma ≥==22342424431001021040.2282104a b b ρρ=⋅+⋅=⨯⨯+⨯⨯⨯+⨯⨯⨯2[],bσσ≥0.398m 398mmb≥==2.4 在图示杆系中，AC 和BC 两杆的材料相同，且抗拉和抗压许用应力相等，同为[]σ。
BC 杆保持水平，长度为l ，AC 杆的长度可随θ角的大小而变。
为使杆系使用的材料最省，试求夹角θ的值。
第二章轴向拉压一、选择题1．图1所示拉杆的外表面上有一斜线，当拉杆变形时，斜线将( D)A．平动B．转动C．不动D．平动加转动2．轴向拉伸细长杆件如图2所示，其中1-1面靠近集中力作用的左端面，则正确的说法应是( C)A．1-1、2-2面上应力皆均匀分布B．1-1、2-2面上应力皆非均匀分布C．1-1面上应力非均匀分布，2-2面上应力均匀分布D．1-1面上应力均匀分布，2-2面上应力非均匀分布（图1）（图2）3．有A、B、C三种材料，其拉伸应力—应变实验曲线如图3所示，曲线( B)材料的弹性模量E大，曲线( A )材料的强度高，曲线( C)材料的塑性好。
4．材料经过冷作硬化后，其( D)。
A．弹性模量提高，塑性降低B．弹性模量降低，塑性提高C．比例极限提高，塑性提高D．比例极限提高，塑性降低5．现有钢、铸铁两种杆材，其直径相同。
从承载能力与经济效益两个方面考虑，图4所示结构中两种合理选择方案是( A)。
A．1杆为钢，2杆为铸铁B．1杆为铸铁，2杆为钢C．2杆均为钢D．2杆均为铸铁（图3）（图4）（图5）6．在低碳钢的拉伸试验中，材料的应力变化不大而变形显著增加的是（B）。
A. 弹性阶段；B.屈服阶段；C.强化阶段；D.局部变形阶段。
7．铸铁试件压缩破坏（B）。
A. 断口与轴线垂直；B. 断口为与轴线大致呈450~550倾角的斜面；C. 断口呈螺旋面；D. 以上皆有可能。
8．为使材料有一定的强度储备，安全系数取值应（ A ）。
A .大于1； B. 等于1； C.小于1； D. 都有可能。
9. 等截面直杆在两个外力的作用下发生轴向压缩变形时，这对外力所具备的特点一定是等值、( C )。
A 反向、共线B 反向，过截面形心C 方向相对，作用线与杆轴线重合D 方向相对，沿同一直线作用10. 图6所示一阶梯形杆件受拉力Ｐ的作用，其截面1-1，2-2，3-3上的内力分别为N 1，N 2和N 3，三者的关系为( B )。
材料力学第二章的习题答案材料力学第二章的习题答案材料力学是一门研究物质的力学性质和变形行为的学科，其内容涉及广泛且深奥。
在学习材料力学的过程中，习题是不可或缺的一部分，通过解答习题可以加深对理论知识的理解，提高解决实际问题的能力。
本文将为大家提供材料力学第二章的习题答案，希望能对大家的学习有所帮助。
第一题：一个长为L、截面为A的均匀杆件，其杨氏模量为E，受到拉力F。
求杆件的伸长量。
解答：根据胡克定律，应力与应变成正比。
应力σ等于拉力F除以截面积A，应变ε等于伸长量ΔL除以杆件的原始长度L。
根据胡克定律的表达式σ=Eε，我们可以得到伸长量的计算公式：ΔL = FL / (AE)其中，ΔL为伸长量，F为拉力，L为杆件的原始长度，A为截面积，E为杨氏模量。
第二题：一个长为L、截面为A的均匀杆件，其杨氏模量为E，受到弯矩M。
求杆件的弯曲角度。
解答：根据弯曲理论，弯矩M等于杆件截面上的应力σ乘以截面的转动惯量I。
弯曲角度θ等于弯矩M乘以杆件的长度L除以杨氏模量E乘以截面的转动惯量I。
因此，弯曲角度的计算公式为：θ = ML / (EI)其中，θ为弯曲角度，M为弯矩，L为杆件的长度，E为杨氏模量，I为截面的转动惯量。
第三题：一个长为L、截面为A的均匀杆件，其杨氏模量为E，受到剪力V。
求杆件的剪切变形。
解答：根据剪切变形的定义，剪切变形γ等于剪力V乘以杆件的长度L除以杨氏模量E乘以截面的剪切模量G。
因此，剪切变形的计算公式为：γ = VL / (EG)其中，γ为剪切变形，V为剪力，L为杆件的长度，E为杨氏模量，G为截面的剪切模量。
通过解答以上三个习题，我们可以看到材料力学第二章主要涉及杆件的拉伸、弯曲和剪切变形问题。
通过掌握这些基本的计算公式，我们能够准确地计算杆件在不同受力情况下的变形量。
这对于工程实践中的结构设计和材料选用具有重要的指导意义。
除了以上习题，材料力学第二章还包括其他一些重要的内容，如应力、应变、弹性模量、截面形状对杆件变形的影响等。
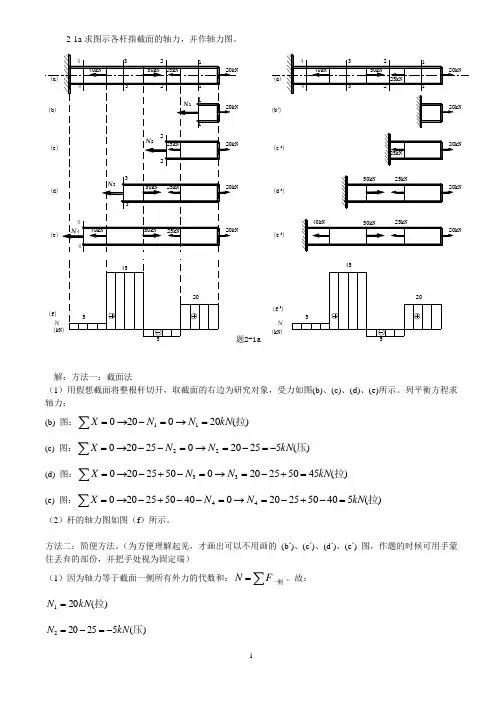
2-1a 求图示各杆指截面的轴力，并作轴力图。
(c ')(e ')(d ')N (kN)205455(f ')解：方法一：截面法（1）用假想截面将整根杆切开，取截面的右边为研究对象，受力如图(b)、(c)、(d)、(e)所示。
列平衡方程求轴力： (b) 图：)(20020011拉kN N NX =→=-→=∑(c) 图：)(5252002520022压kN N NX -=-=→=--→=∑(d) 图：)(455025200502520033拉kN N NX =+-=→=-+-→=∑(e) 图：)(540502520040502520044拉kN N NX =-+-=→=--+-→=∑（2）杆的轴力图如图（f ）所示。
方法二：简便方法。
（为方便理解起见，才画出可以不用画的 (b ‘)、(c ‘)、(d ‘)、(e ‘) 图，作题的时候可用手蒙住丢弃的部份，并把手处视为固定端）（1）因为轴力等于截面一侧所有外力的代数和：∑=一侧FN 。
故：)(201拉kN N =)(525202压kN N -=-=)(455025203拉kN N =+-=)(5405025204拉kN N =-+-=（2）杆的轴力图如图（f ‘）所示。
2-2b 作图示杆的轴力图。
(c)图：(b)图：（3）杆的轴力图如图（d ）所示。
2-5 图示两根截面为100mm ⅹ100mm 的木柱，分别受到由横梁传来的外力作用。
试计算两柱上、中、下三段的应力。
(b)(c)(d)(f)题2-5-N图（kN）6108.5N图（kN）326.5-解：（1）梁与柱之间通过中间铰，可视中间铰为理想的光滑约束。
将各梁视为简支梁或外伸梁，柱可视为悬臂梁，受力如图所示。
列各梁、柱的平衡方程，可求中间铰对各梁、柱的约束反力，计算结果见上图。
（2）作柱的轴力图，如(e)、(f)所示。
（3）求柱各段的应力。
解：（1）用1-1截面将整个杆切开，取左边部分为研究对象；再用x -x 截面整个杆切开，取右边部分为研究对象，两脱离体受力如图(b)、(c)，建立图示坐标。
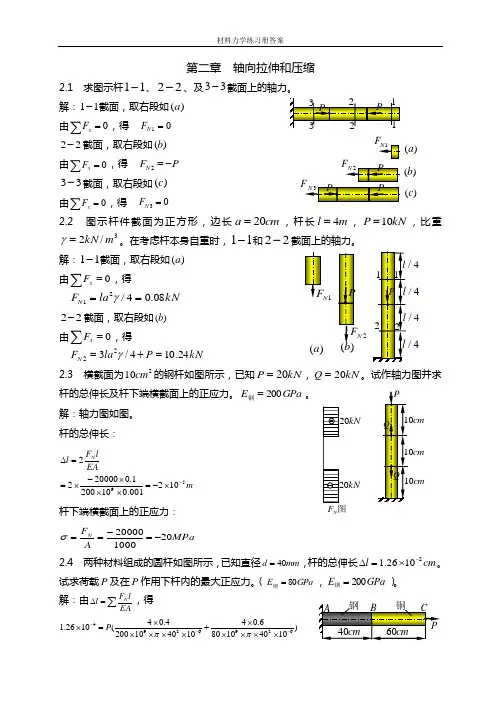
第二章 轴向拉伸和压缩2.1 求图示杆11-、22-、及33-截面上的轴力。
解：11-截面，取右段如)(a 由0=∑x F ，得 01=N F22-截面，取右段如)(b由0=∑x F ，得 P F N -=233-截面，取右段如)(c由0=∑x F ，得 03=N F2.2 图示杆件截面为正方形，边长cm a 20=，杆长m l 4=，kN P 10=，比重3/2m kN =γ。
在考虑杆本身自重时，11-和22-截面上的轴力。
解：11-截面，取右段如)(a 由0=∑xF，得kN la F N 08.04/21==γ22-截面，取右段如)(b由0=∑xF，得kN P la F N 24.104/322=+=γ2.3 横截面为210cm 的钢杆如图所示，已知kN P 20=，kN Q 20=。
试作轴力图并求杆的总伸长及杆下端横截面上的正应力。
GPa E 200=钢。
解：轴力图如图。
杆的总伸长：m EA l F l N59102001.0102001.02000022-⨯-=⨯⨯⨯-⨯==∆ 杆下端横截面上的正应力：MPa A F N 20100020000-=-==σ 2.4 两种材料组成的圆杆如图所示，已知直径mm d 40=，杆的总伸长cm l 21026.1-⨯=∆。
试求荷载P 及在P 作用下杆内的最大正应力。
（GPa E 80=铜，GPa E 200=钢）。
解：由∑=∆EAl F l N ，得)104010806.0410********.04(1026.16296294---⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯=⨯ππP4/4/4/4/)(a )(b )(c 2N1N )(a kNkN 图NF cm cmcm解得： kN P 7.16= 杆内的最大正应力：MPa A F N 3.13401670042=⨯⨯==πσ 2.5 在作轴向压缩试验时，在试件的某处分别安装两个杆件变形仪，其放大倍数各为1200=A k ，1000=B k ，标距长为cm s 20=，受压后变形仪的读数增量为mm n A 36-=∆，mm n B 10=∆，试求此材料的横向变形系数ν（即泊松比）。
第二章轴向拉(压变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。
（a）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。
（b）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。
（c）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。
（d）解：（1）求指定截面上的轴力（2）作轴力图中间段的轴力方程为：轴力图如图所示。
[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。
若横截面面积，试求各横截面上的应力。
解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。
（3）计算各截面上的应力[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。
若横截面面积，，，并求各横截面上的应力。
解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。
（3）计算各截面上的应力[习题2-4] 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EC横截面上的应力。
解：（1）求支座反力由结构的对称性可知：（2）求AE和EG杆的轴力①用假想的垂直截面把C铰和EG杆同时切断，取左部分为研究对象，其受力图如图所示。
由平衡条件可知：②以C节点为研究对象，其受力图如图所示。
由平平衡条件可得：（3）求拉杆AE和EG横截面上的应力查型钢表得单个等边角钢的面积为：[习题2-5] 石砌桥墩的墩身高，其横截面面尺寸如图所示。
荷载，材料的密度，试求墩身底部横截面上的压应力。
解：墩身底面的轴力为：墩身底面积：因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。
[习题2-6]图示拉杆承受轴向拉力，杆的横截面面积。
如以表示斜截面与横截面的夹角，试求当时各斜截面上的正应力和切应力，并用图表示其方向。
解：斜截面上的正应力与切应力的公式为：式中，，把的数值代入以上二式得：轴向拉/压杆斜截面上的应力计算题目编号10000 100 0 100 100.0 0.0 习题2-6100 30 100 75.0 43.310000100 45 100 50.0 50.010000100 60 100 25.0 43.310000100 90 100 0.0 0.010000[习题2-7]一根等直杆受力如图所示。
习题2-1一木柱受力如图示，柱的横截面为边长20cm 的正方形，材料服从虎克定律，其弹性模量MPa ．如不计柱自重，试求：51010.0×=E （1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形．解：（1）轴力图（2）AC 段应力a a ΜΡΡσ5.2105.22.010100623−=×−=×−=CB 段应力aa ΜΡΡσ5.6105.62.010260623−=×−=×−=（3）AC 段线应变45105.2101.05.2−×−=×−==ΕσεN-图CB 段线应变45105.6101.05.6−×−=×−==Εσε（4）总变形m 3441035.15.1105.65.1105.2−−−×=××−××−=ΑΒ∆2-2图(a)所示铆接件，板件的受力情况如图（ｂ）所示．已知：P ＝7kN ，t ＝0.15cm ，b 1＝0.4cm ，b 2=0.5cm ，b 3=0.6cml 。
试绘板件的轴力图，并计算板内的最大拉应力。
解:（2）aΜΡσ4.194101024.015.0767311=×××××=−a ΜΡσ1.311101025.015.0767322=×××××=−a ΜΡσ9.388101026.015.07673=××××=−最大拉应力aΜΡσσ9.3883max ==2-3直径为１cm 的圆杆，在拉力P ＝10kN 的作用下，试求杆内最大剪应力，以及与横截面夹角为＝30o 的斜截面上的正应力与剪应力。
α解:（1）最大剪应力a d ΜΡππΡστ66.6310101102212672241max =××××===−（2）界面上的应力°=30α()a ΜΡασσα49.952366.632cos 12=×=+=a ΜΡαστα13.5530sin 66.632sin 2=×=×=°2-4图示结构中ABC 与CD 均为刚性梁，C 与D 均为铰接，铅垂力P ＝20kN 作用在C 铰，若（1）杆的直径d 1=1cm ，（2）杆的直径d 2=2cm ，两杆的材料相同，E ＝200Gpa ，其他尺寸如图示，试求（1）两杆的应力；（2）C 点的位移。
解（1）1杆的应力ad ΜΡππΡσ6.254101012046722141)1(=××××=−2杆的应力ad ΜΡππΡσ3.1271010220226722241)2(=××××=−（2）C 点的位移cm m l l 2546.010546.22102006.254331)1(1=×=××==−Εσ∆cmm l l 1273.010273.12102003.127332)2(2=×=××==−Εσ∆cm c 509.0212=+=∆∆∆2-5某铣床工作台进给油缸如图示，缸内工作油压，油缸内径D ＝7.5cm ，活塞杆直径d MPa p 2=＝1.8cm.，已知活塞杆材料的许用应力Mpa 。
试校核活塞杆的强度。
[]50=σ解()[]σΜΡππσ<=−×=−×=a d d D p 7.328.1)8.15.7(22222412241max 故安全2-6钢拉杆受轴向拉力P ＝４０kN ，杆材料的许用应力MPa ，杆的横截面为矩形，并且b []100=σ＝2a ，试确定a 与b 的尺寸。
解[]241010040cm =×=≥σΡΑ22a ab ==Αcm a 414.12=≥Αcmb 828.2≥2-7大功率低速柴油机的气缸盖螺栓如图示，螺栓承受预紧力P ＝390kN ，材料的弹性模量E ＝210Gpa ，求螺栓的伸长变形。
解:mm l l l 376.076802679021039022412211=⎟⎠⎞⎜⎝⎛+=+=πΕΑΡΕΑΡ∆2-8常用仓库搁架前后面用两根圆钢杆AB 支持，其平面投影图如图示，估计搁架上的最大载重量为P ＝10kN ，假定合力P 作用在搁板BC 的中线上。
已知，杆材料的许用应力[]＝160Mpa ，试o 45=ασ求所需圆钢杆的直径。
解杆轴力ΑΒΚΝΡ536.32121=×=N 杆直径ΑΒ[]cm N D 53.04=≥σπ2-9图示吊钩的上端为T110x2梯形螺纹，它的外径d ＝110mm ，内径d 1=97mm ，其材料为20号钢，许用应力[]=50Mpa 。
试根据吊钩的直杆部分确定吊构所容许的最大起吊重量P 。
σ解:[]ΚΝπσπΡ5.36910450110422=×××=≤d 2-10吊架结构的尺寸及受力情况如图示。
水平梁AB 为变形可忽略的粗刚梁，CA 是钢杆，长＝2m ，1l 横截面面积A 1=2cm 2，弹性模量E １＝200Gpa ；DB 是钢杆，长＝１m ，横截面面积A 2=8cm 2，弹性模量2l E 2=100Gpa ，试求：（1）使刚性梁AB 仍保持水平时，载荷P 离DB 杆的距离x ；（2）如使水平梁的竖向位移不超过0.2cm ，则最大的P 力应为多少?解（1）111311ΑΕΡ∆xl l =()2223123ΑΕΡ∆l x l −=21l l ∆∆=m x 6.0=(2)ΚΝΑΕΡ2001026.022********=××××=≤−xl 2-11铰接的正方形结构如图所示，各杆材料皆为铸铁，许用拉应力[+]=400kg/cm 2，许用压应力σ[]=600kg/cm 2，各杆的截面积均等于25cm 2。
试求结构的许用载荷P 。
−σ解:AC 、CB 、BD 、DA 杆受拉力，大小为21Ρ=ΤDC 杆受压力，大小为Ρ=Τ2得[]ΑΤ≥+1σkg 141422540021=××≤Ρ得[]ΑΤ≥−2σkg150********=×≤Ρ故kg14142≤Ρ2-12图示拉杆沿斜截面m －n 由两部分胶合而成，设在胶合面上许用拉应力[]＝100MPa ，许用剪σ应力=50MPa ，胶合面的强度控制杆件的拉力，试求：为使杆件承受最大拉力P ，角的值应为多少？][τα若横截面面积为4cm 2，并规定，试确定许可载荷P 。
060≤α解:（1）5.010050===αασταtg 时杆件承受最大拉力。
°=5.26α（2）[]ΚΝ=××=Α≤Ρ−°16010460cos 100cos 122ασ[]ΚΝ=×××=Α≤Ρ−°1.46104120sin 5022sin 21ατ故许可载荷为46.1ΡΚΝ2-13油缸盖与缸体采用６个螺栓连接．已知油缸内径D ＝350mrn ，油压p ＝１Mpa 。
若螺栓材料的许用应力[]=40MPa ，求螺栓的内径d ．σ解24pD π=Ρ[]246d σπ×≤Ρ[]mm pD d 59.22406350622=×=≥∴σ2-14试确定轧钢机承压装置安全螺栓的直径d ，当P ＝6000kN 时，螺径即行断裂，其材料的强度极限＝600Mpa 。
各接触面间的摩擦力可不计。
b σ解:螺栓所受的拉力为2Ρ=R []24d R πσ≥[]cm R d 98.710600600024=×××=≤πσπ2-15木材试件（立方体cm ）在手压机内进行压缩。
作用力P ＝400N ，其方向垂直于杠222××杆OA ，此杠杆可绕固定心轴o 转动，在某一时刻，拉杆BC 垂直于OB 且平分ECD 角，∠CED ＝。
杠杆长度OA ＝lm ，OB ＝5cm ，拉杆BC 的直径d l ＝1.0cm ，CE 杆与CD 杆的直径相0211)2.0arctan(′=�同d 2＝2.0cm 。
试求（1）此时拉杆BC ，以及杆CD 与CE 内的应力；（2）木材的弹性模量E=10GPa ，计算被压试件的缩短变形。
解:（1）Ν=×=Ν800005.01400BC Ν−=−=Ν−=Ν=Ν°°2039631.11sin 400031.11sin 21BC CE CDΜΡ=××=ΑΝ=−9.101104800021πσBC BC ΜΡ−=××−=ΑΝ==−9.64102420396222πσσCD CE CD （2）被压试件的缩短量cm l l 01.01041022.0/80007=×××=ΕΑΝ=∆−2-16设水平刚性杆AB 不变形，拉杆CD 的直径d=2cm ，许用应力[]=160MPa ，材料的弹性模量E σ＝200GPa ，在B 端作用载荷P ＝12kN ．试校核CD 杆的强度并计算B 点的位移．解:ΚΝ=×=Ν64.342/35.212CD 故安全[]σπσ≤=××=ΑΝ=3.11010464.3441CD CD mm l l CD CD 635.060sin 2003.110°=Ε=∆σB 点的位移，方向向下。
mm l CD B 833.15.232=××∆=∆2-17设压入机体中的钢销子所受的连结力是沿着它的长度平均分布的，为了拔出这个销子，在它l 的一端施加P ＝20kN 的力。
已知销子截面积A ＝2cm 2,长度=40cm ，a=15cm ，E ＝200GPa ，试绘出杆的l 应力图和计算杆的伸长。
解:部分应力沿分布：l x a x x l x ΜΡ=××=ΑΡ=25010402203σ)0(l x ≤≤当时，a l ≥aΜΡ=×=1004.0250*σ应力图为mm l a 175.010)2015(200100212**=×+=Ε+Ε=∆−σσ2-18试求下列各简单结构中节点A 的位移，设各杆的抗拉压刚度均为EA 。
解:（a ）AC 杆受力为零，BA 杆伸长为αcos ΕΑΡ=∆ll AB A 点沿BA 方向移动αα2sin 2sin ΕΑΡ=∆=∆l l AB A （b ）AB 杆受拉力为P ，BC 杆受拉力为P ，BD 杆受压力为P2EA PLAB =∆EA PLBC =∆EAPL EA L P BD 222=×=∆由几何关系，得B 点位移水平位移EA PL BD BC B )21(211+=∆+∆=∆垂直位移EA PL BD B B )221(2112+=∆+∆=∆故A 点位移水平位移EA PL B A )21(11+=∆=∆垂直位移EAPLAB B A )21(212+=∆+∆=∆2-19水平刚性梁ABCD 在B 、D 两点用钢丝绳悬挂，尺寸及悬挂方式如图示，E 、F 两处均为无摩阻力的小滑轮。
