利用三边关系判定三角形相似

相似直角三角形三边比例关系相似直角三角形是指具有相同形状但尺寸不同的直角三角形。

在相似直角三角形中，三条边的比例关系是一个重要的性质。

在本文中，我们将探讨相似直角三角形的三边比例关系，并解释其几何意义。

在直角三角形中，两条边与直角的夹角为90度，而第三条边则是斜边。

我们可以用a、b、c来表示直角三角形的三边，其中a和b 分别为直角的两条边，c为斜边。

在相似直角三角形中，如果两个直角三角形的对应边长之比相等，那么这两个三角形就是相似的。

假设有两个相似直角三角形，它们的边长分别为a₁、b₁、c₁和a₂、b₂、c₂。

根据相似三角形的性质，我们可以得出以下关系：a₁/a₂ = b₁/b₂ = c₁/c₂其中a₁/a₂表示a₁与a₂的比值，b₁/b₂表示b₁与b₂的比值，c₁/c₂表示c₁与c₂的比值。

这个比值可以用任意单位来表示，如厘米、米等，因为比值是一个无量纲的数。

可以看出，相似直角三角形的三边比例关系是固定的，在同一个相似直角三角形中，任意两边之比都等于另一对相似直角三角形相应边之比。

这个比例关系可以帮助我们计算未知边长或角度。

例如，已知一个直角三角形的两条边长分别为3cm和4cm，我们可以根据三边比例关系计算出斜边的长度。

设斜边的长度为c，则根据三边比例关系有：3/c = 4/3通过交叉相乘得到：3 * 3 =4 * c化简得到：9 = 4c解方程得到：c = 9/4 = 2.25cm因此，斜边的长度为2.25cm。

除了计算边长，三边比例关系还可以帮助我们计算角度。

在相似直角三角形中，两个角度之比等于两个对边之比。

例如，已知一个直角三角形的两条边长分别为3cm和4cm，我们可以通过三边比例关系计算出斜边与直角的夹角。

设直角的两边分别为a和b，斜边为c，直角的两个角分别为A和B。

根据三边比例关系有：a/b = A/B代入已知边长得到：3/4 = A/B通过交叉相乘得到：3B = 4A通过解方程得到：B = (3/4)A因此，斜边与直角的夹角B等于直角的夹角A的三分之四。

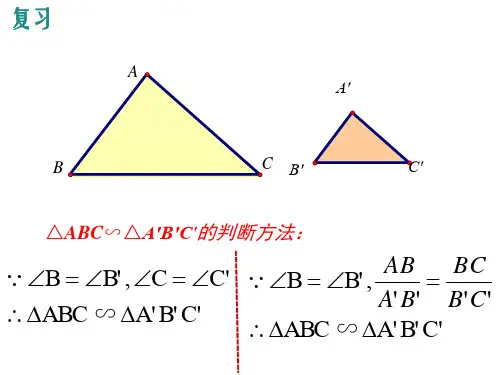
三角形的相似性质及证明三角形是基础的几何图形之一，它具有多种性质和特点。

其中之一便是相似性质。

本文将会介绍三角形的相似性质，以及其证明过程。

一、相似性质的定义在几何学中，当两个三角形的对应角度相等，而对应边的比值相等时，我们称这两个三角形为相似三角形。

记作∆ABC∼∆DEF。

二、相似性质的判定1. AAA判定法：如果两个三角形的三个内角相等，则这两个三角形是相似的。

例如，已知∠A=∠D，∠B=∠E，∠C=∠F，在此条件下可以判定∆ABC∼∆DEF。

证明过程：由已知∠A=∠D，∠B=∠E，∠C=∠F，可以得到三角形ABC与DEF中的角度对应关系相等。

因此，根据AAA判定法，可以判定∆ABC∼∆DEF。

2. AA判定法：若两个三角形的两个角度对应相等，则这两个三角形是相似的。

例如，已知∠A=∠D，∠B=∠E，在此条件下可以判定∆ABC∼∆DEF。

证明过程：由已知∠A=∠D，∠B=∠E，可以得到三角形ABC与DEF中的角度对应关系相等。

因此，根据AA判定法，可以判定∆ABC∼∆DEF。

3. SAS判定法：如果两个三角形的一个角和两边分别相等，则这两个三角形是相似的。

例如，已知∠A=∠D，AB/DE=BC/EF，在此条件下可以判定∆ABC∼∆DEF。

证明过程：由已知∠A=∠D，AB/DE=BC/EF，可以得到三角形ABC与DEF中的角度和边长对应关系相等。

因此，根据SAS判定法，可以判定∆ABC∼∆DEF。

4. SSS判定法：若两个三角形的三边对应相等，则这两个三角形是相似的。

例如，已知AB/DE=BC/EF=AC/DF，在此条件下可以判定∆ABC∼∆DEF。

证明过程：由已知AB/DE=BC/EF=AC/DF，可以得到三角形ABC与DEF中的边长对应关系相等。

因此，根据SSS判定法，可以判定∆ABC∼∆DEF。

三、相似性质的应用相似性质在几何学中有广泛的应用，以下列举几个例子。

1. 相似三角形的比例关系：根据相似三角形的定义，可以得到相似三角形的对应边长之间的比例关系。

三角形相似的判定条件：三角形相似的条件：两角分别对应相等的两个三角形相似；两边对应成比例且夹角相等，两个三角形相似；三边对应成比例，两个三角形相似；三边对应平行，两个三角形相似；斜边与直角边对应成比例，两个直角三角形相似；全等三角形相似。

一、相似三角形的判定定理：1.平行于三角形一边的直线和其他两边和两边的延长线相交，所构成的三角形与原三角形相似。

2.如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似。

3.如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似。

4.如果两个三角形的两个角分别对应相等（或三个角分别对应相等），则有两个三角形相似。

二、相似三角形介绍三角分别相等，三边成比例的两个三角形叫作相似三角形。

相似三角形是几何中重要的证明模型之一，是全等三角形的推广。

全等三角形可以被理解为相似比为1的相似三角形。

相似三角形其实是一套定理的集合，它主要描述了在相似三角形是几何中两个三角形中，边、角的关系。

三、相似三角形的性质1.性质1：相似三角形对应边上的高、中线和它们周长的比都等于相似比；性质2：相似三角形的面积比等于相似比的平方．结论：相似三角形外接圆的直径比、周长比等于相似比，外接圆的面积比等于相似比的平方2.性质：三条平行线截两条直线，所得的对应线段成比例推论：平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例。

3.如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等．推论1：经过三角形一边的中点与另一边平行的直线必平分第三边。

推论2：经过梯形一腰的中点，且与底边平行的直线平分另一腰。

四、特殊情况1.凡是全等的三角形都相似。

全等三角形是特殊的相似三角形，相似比为1。

反之，当相似比为1时，相似三角形为全等三角形。

2. 有一个顶角或底角相等的两个等腰三角形都相似。

由此，所有的等边三角形都相似。

相似三角形找对应边关系的诀窍主要有以下三种：
1.如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这
两个三角形相似。

这种方法下，顶点之间的对应关系比较好找，只需将两个角的顶点写在对应的位置上，第三个顶点就自然确定了。

2.如果两个三角形的两组对应边成比例，并且对应的夹角相等，那么这
两个三角形相似。

此时可以用三点定型法：确定三角形和夹角的思路。

先根据两边所在的三角形和两边夹角来确定一个顶点，然后结合数据将短边对应短边写在相应位置，长边对长边写在相应位置即可确定另外两个顶点。

3.如果两个三角形的三组对应边成比例，那么这两个三角形相似。

这种
情况下，可以随意找三个顶点作为起始点，然后按照边的比例关系找到另外三个顶点。