世界数学大事年表(1900年以前)

中外数学史年表008-06-03 115:5约前4000 (中)西安半坡出土陶器上有许多刻符，其中包括一些数字刻符。

约前3000 古埃及用象形字记数。

约前2400 古巴比伦采用六十进制位值制记数法。

约前2100 (中)大禹主持治水工程时已使用规、矩、准、绳四种几何测量工具。

约前2000 (中)山东省城子崖遗址出土的陶器上有数字刻划符号。

前2100-前1600 在美索不达米亚地区发现大量刻写有文字的古巴比伦泥书板。

据考证，其中有些是载有数表和数学问题的书板。

书板上出现简单的乘法、平方和立方的数表及简单的二次方程等许多内容。

前1900-前1600 现存属于这段时期的埃及纸草书记载了很多数学问题。

古埃及人已能求三角形、梯形面积和棱柱体体积，而且也能解简单的二次方程。

约前1400 (中)殷商时代甲骨文中已有十进数字的记录，其中最大的数字为三万。

约前1000 (中)开始用筹进行计算。

约前800-前500 (印)在一类宗教典籍《吠陀》中，包含古印度修筑祭坛的法典，其中涉及某些几何知识。

约前600 (希)泰勒斯将埃及的实用几何知识带入希腊，开始证明几何命题。

约前585 (希)毕达哥拉斯学派对数和图形进行比较广泛的探讨和研究。

约前462 (希)芝诺等人提出有关时空及数学方面的悖论。

约前440-前430 (希)希波克拉茨研究化圆为方及立方倍积问题。

(希)安提芬采用穷竭法。

约前425 (希)希比亚斯应用他发现的“割圆曲线”解决三等分角的问题。

约前400 (中)《墨经》中有许多几何学的义理。

约前398 (希)德谟克利特发现圆锥与棱锥体积分别是同底同高圆柱和棱柱体积的1/3。

他在数学中应用了原子论观点，认为线段、面积和体积由不可分的原子构成。

约前370 (希)欧多克斯创立比例论并将其应用于不可通约量上，开始对数做出以公理为依据的演绎整理。

前350 (希)密内凯莫斯发现三种圆锥曲线，并用圆锥曲线求解立方倍积问题。

约前335 (希)亚里士多德确立形式逻辑学，把演绎逻辑系统化。

数学大事年表数学发展至今，不知道经历了多少人的呕心沥血，现在把数学历史上发生的大事的年表列出：约公元前3000年埃及象形数字。

公元前2400～前1600年早期巴比伦泥版楔形文字，采用60进位值制记数法。

已知勾股定理。

公元前1850～前1650年埃及纸草书（莫斯科纸草书与莱茵德纸草书），使用10进非位值制记数法。

公元前1400～前1100年中国殷墟甲骨文，已有10进制记数法。

周公(公元前11世纪)、商高时代已知勾三、股四、弦五。

约公元前600年希腊泰勒斯开始了命题的证明。

约公元前540年希腊毕达哥拉斯学派，发现勾股定理，并导致不可通约量的发现。

约公元前500年印度《绳法经》中给出√2相当精确的值，并知勾股定理。

约公元前460年希腊智人学派提出几何作图三大问题：化圆为方、三等分角和二倍立方。

约公元前450年希腊埃利亚学派的芝诺提出悖论。

公元前430年希腊安提丰提出穷竭法。

约公元前380年希腊柏拉图在雅典创办“学园”，主张通过几何的学习培养逻辑思维能力。

公元前370年希腊欧多克索斯创立比例论。

约公元前335年欧多莫斯著《几何学史》。

中国筹算记数，采用十进位值制。

约公元前300年希腊欧几里得著《几何原本》，是用公理法建立演绎数学体系的最早典范。

公元前287～前212年希腊阿基米德，确定了大量复杂几何图形的面积与体积；给出圆周率的上下界；提出用力学方法推测问题答案，隐含近代积分论思想。

公元前230年希腊埃拉托塞尼发明“筛法”。

公元前225年希腊阿波罗尼奥斯著《圆锥曲线论》。

约公元前150年中国现存最早的数学书《算数书》成书（1983～1984年间在湖北江陵出土）。

约公元前100年中国《周髀算经》成书，记述了勾股定理。

中国古代最重要的数学著作《九章算术》经历代增补修订基本定形（一说成书年代为公元50～100年间），其中正负数运算法则、分数四则运算、线性方程组解法、比例计算与线性插值法盈不足术等都是世界数学史上的重要贡献。

世界数学大事记——1800～1900年1801-1850年*1801年, 出版《算术研究》，开创近代数论（德国高斯）。

*1809年，出版了微分几何学的第一本书《分析在几何学上的应用》（法国蒙日）。

*1812年，《分析概率论》一书出版，是近代概率论的先驱（法国拉普拉斯）。

*1816年，发现非欧几何，但未发表（德国高斯）。

*1821年，《分析教程》出版，用极限严格地定义了函数的连续、导数和积分，研究了无穷级数的收敛性等（法国柯西）。

*1822年,系统研究几何图形在投影变换下的不变性质，建立了射影几何学（法国彭色列）。

1822年，研究热传导问题，发明用傅立叶级数求解偏微分方程的边值问题，在理论和应用上都有重大影响（法国傅立叶）。

*1824年，证明用根式求解五次方程的不可能性（挪威阿贝尔）。

*1825年，发明关于复变函数的柯西积分定理，并用来求物理数学上常用的一些定积分值（法国柯西）。

*1826年，发现连续函数级数之和并非连续函数（挪威阿贝尔）。

1826年，改变欧几理得几何学中的平行公理，提出非欧几何学的理论（俄国罗巴切夫斯基，匈牙利波约）。

*1827-1829年，确立了椭圆积分与椭圆函数的理论，在物理、力学中都有应用（德国雅可比，挪威阿贝尔，法国勒让德尔）。

*1827年，建立微分几何中关于曲面的系统理论（德国高斯）。

1827年，出版《重心演算》，第一次引进齐次坐标（德国梅比武斯）。

*1830年，给出一个连续而没有导数的所谓“病态”函数的例子（捷克波尔查诺）。

1830年，在代数方程可否用根式求解的研究中建立群论（法国伽罗华）。

*1831年，发现解析函数的幂级数收敛定理（法国柯西）。

1831年，建立了复数的代数学，用平面上的点来表示复数，破除了复数的神秘性（德国高斯）。

*1835年，提出确定代数方程式实根位置的方法（法国斯特姆）。

*1836年，证明解析系数微分方程式解的存在性（法国柯西）。

1836年，证明具有已知周长的一切封闭曲线中包围最大面积的图形必定是圆（瑞士史坦纳）。

数学大事年表约公元前3000年埃及象形数字公元前2400~前1600年早期巴比伦泥版楔形文字,采用60进位值制记数法。

已知勾股定理公元前1850~前1650年埃及纸草书(莫斯科纸草书与莱茵德纸草书),使用10进非位值制记数法公元前1400~前1100年中国殷墟甲骨文,已有10进制记数法周公(公元前11世纪)、商高时代已知勾三、股四、弦五约公元前600年希腊泰勒斯开始了命题的证明约公元前540年希腊毕达哥拉斯学派,发现勾股定理,并导致不可通约量的发现约公元前500年印度《绳法经》中给出√2相当精确的值,并知勾股定理约公元前460年希腊智人学派提出几何作图三大问题:化圆为方、三等分角和二倍立方约公元前450年希腊埃利亚学派的芝诺提出悖论公元前430年希腊安提丰提出穷竭法约公元前380年希腊柏拉图在雅典创办“学园”,主张通过几何的学习培养逻辑思维能力公元前370年希腊欧多克索斯创立比例论约公元前335年欧多莫斯著《几何学史》中国筹算记数,采用十进位值制约公元前300年希腊欧几里得著《几何原本》,是用公理法建立演绎数学体系的最早典范公元前287~前212年希腊阿基米德,确定了大量复杂几何图形的面积与体积;给出圆周率的上下界;提出用力学方法推测问题答案,隐含近代积分论思想公元前230年希腊埃拉托塞尼发明“筛法”公元前225年希腊阿波罗尼奥斯著《圆锥曲线论》约公元前150年中国现存最早的数学书《算数书》成书(1983~1984年间在湖北江陵出土)约公元前100年中国《周髀算经》成书,记述了勾股定理中国古代最重要的数学著作《九章算术》经历代增补修订基本定形(一说成书年代为公元50~100年间),其中正负数运算法则、分数四则运算、线性方程组解法、比例计算与线性插值法盈不足术等都是世界数学史上的重要贡献约公元62年希腊海伦给出用三角形三边长表示面积的公式(海伦公式)约公元150年希腊托勒密著《天文学》,发展了三角学约公元250年希腊丢番图著《算术》,处理了大量不定方程问题,并引入一系列缩写符号,是古希腊代数的代表作约公元263年中国刘徽注解《九章算术》,创割圆术,计算圆周率,证明圆面积公式,推导四面体及四棱锥体积等,包含有极限思想约公元300年中国《孙子算经》成书,系统记述了筹算记数制,卷下“物不知数”题是孙子剩余定理的起源公元320年希腊帕普斯著《数学汇编》,总结古希腊各家的研究成果,并记述了“帕普斯定理”和旋转体体积计算法公元410年希腊许帕提娅,历史上第一位女数学家,曾注释欧几里得、丢番图等人的著作公元462年中国祖冲之算出圆周率在 3.1415926与3.1415927之间,并以22/7为约率,355/113为密率(现称祖率)中国祖冲之和他的儿子祖暅提出“幂势既同则积不容异”的原理,现称祖暅原理,相当于西方的卡瓦列里原理(1635)公元499年印度阿耶波多著《阿耶波多文集》,总结了当时印度的天文、算术、代数与三角学知识。

数学发展史时间轴
数学发展史可以追溯到人类文明的起源，几乎与人类思维和社会发展同步进行。

下面是一个简要的数学发展史时间轴：
1. 古代数学（约公元前3000年-公元5世纪）：
古代数学主要集中在古巴比伦、古埃及、古希腊、古印度和古中国等地。

这个时期的数学主要涉及算术、几何和代数等基本概念和方法的发展。

2. 中世纪数学（公元5世纪-15世纪）：
中世纪数学主要由阿拉伯数学家和欧洲学者推动。

阿拉伯人引入了印度-阿拉伯数字系统和代数的进一步发展。

欧洲学者则致力于恢复和传播古代数学知识，推动了几何学的发展。

3. 文艺复兴时期（15世纪-17世纪）：
文艺复兴时期是数学发展的黄金时期，涌现出许多伟大的数学家。

代表性的有勒内·笛卡尔和伽利略·伽利雷，他们为代数和几何学的发展做出了重要贡献。

4. 近代数学（17世纪-19世纪）：
近代数学的突破主要来自于微积分学的发展。

牛顿和莱布尼茨同
时独立发现了微积分的基本原理。

这一时期还涌现出许多其他重要的数学家，如欧拉、高斯和拉格朗日等。

5. 现代数学（20世纪至今）：
现代数学涉及的领域非常广泛，包括数学分析、代数学、几何学、概率论、统计学、拓扑学等。

数学家们不断提出新的理论、方法和应用，推动着数学的不断发展和应用的扩展。

这只是一个简要的数学发展史时间轴，数学的发展一直在不断演进，影响着我们的生活和科学技术的进步。

数学的发展历史概述
数学的发展历史可以追溯到古代文明时期。

以下是数学发展的一些重要阶段和
里程碑：
古代数学（约公元前3000年-公元前500年）：古代数学主要发展在古埃及、
古巴比伦、古印度和古希腊等地。

这个时期的数学主要集中在计数、测量和几何等方面。

古巴比伦人发明了基于60进制的数制系统和计算法则，古希腊人则在几何
学方面作出了重要贡献。

中世纪数学（公元500年-公元1500年）：在中世纪，数学的发展主要由阿拉
伯数学家推动。

阿拉伯数学家将印度的十进制数制和零的概念引入欧洲，这对于现代数学的发展起到了重要作用。

同时，他们还对代数学和三角学等领域做出了贡献。

近代数学（公元1500年-1900年）：在这个时期，数学经历了重大的变革和发展。

文艺复兴时期的欧洲浮现了许多重要的数学家，如勒内·笛卡尔、伽利略·伽利
雷和爱尔兰的威廉·罗万等人。

他们对代数学、几何学和力学等领域做出了重要贡献。

此外，牛顿和莱布尼茨的微积分的发明也是这个时期的重要成就。

现代数学（20世纪至今）：20世纪以来，数学的发展取得了巨大的发展。

在
这个时期，数学分支日益细分，如数理逻辑、抽象代数、拓扑学、数论、概率论和统计学等。

数学在物理学、工程学、计算机科学和经济学等领域的应用也日益广泛。

总的来说，数学的发展历史是一个不断积累和演化的过程，每一个时代都有其
独特的贡献和突破。

数学的发展不仅为人类认识世界提供了工具和方法，也为其他学科的发展提供了基础和支持。

数学大事年表，涨知识了！1901年·德国希尔伯特证明了狄利克雷原理，开创变分法的直接解法。

·意大利里奇、列维-齐维塔创立绝对微分法，是微分几何学的一个重要理论。

1902年·法国勒贝格发表论文《积分、长度与面积》，建立了“勒贝格测度”和“勒贝格积分”的概念，开创现代积分理论。

·英国伯恩塞德提出伯恩塞德猜想：每一个非交换的单群都是偶数阶的 (1963年由汤普森等人证明)。

1903年·英国罗素提出“罗素悖论”，促进了数学基础研究。

1904年·德国策梅罗提出选择公理，并证明“良序定理”：任何集合都能良序化。

·法国勒贝格证明了有界函数黎曼可积的充要条件是其不连续点构成一个零测度集，完全解决了黎曼可积性的问题。

·法国庞加莱提出“庞加莱猜想”。

1905年·德国舒尔重建群的特征理论，同年爱因斯坦发表了他的物理学发现。

1906年·法国弗雷歇引入函数空间的一般概念，定义“度量空间”；引入“泛函”概念，并给出泛函的连续性和可微性的定义。

·俄国马尔可夫提出“马尔可夫链”的概念，用以研究自然过程。

·美国维尔钦斯基发表《曲线和直纹曲面的射影微分几何》，这是现代射影微分几何学的开端之一。

1907年·匈牙利里斯证明矩阵力学与波动力学等价的数学基本定理。

·荷兰布劳威尔提出直觉主义数学，是构造性数学的开端。

·法国庞加莱证明了复变函数论的一个基本定理-黎曼共形映射定理。

·德国E．施密特定义了以复数无穷序列为元素的函数空间，确定了范数等概念，推动了泛函分析的发展。

1908年·德国策梅罗发表《集合论基础研究》，建立第一个公理集合论理论系统。

·德国亨泽尔出版《代数数论》。

·英国戈塞特（W. S. Gossett,1876-1937）提出精确样本理论（数理统计）。

数学发展史时间轴及事件1.古埃及数学（公元前3000年-公元前1000年）数学在古埃及有着悠久的历史。

古埃及人发展出了一套完整的计数系统，以及用于计算和测量的一系列实用技术和工具。

例如，他们使用了“象形数字”来表达数值，同时发明了一种称为“祭坛测量的土地”的算法，用于计算矩形或金字塔的面积。

2.古希腊数学（公元前600年-公元500年）古希腊数学在西方数学史上占据了重要的地位。

在这个时期，出现了许多杰出的数学家，如毕达哥拉斯、欧几里得和阿基米德等。

他们为数学界的发展做出了巨大的贡献，如毕达哥拉斯提出了著名的勾股定理，欧几里得写下了著名的《几何原本》，阿基米德则发明了微积分的基本原理。

3.中世纪欧洲数学（公元500年-1500年）在中世纪欧洲，数学得到了进一步的发展。

在这个时期，出现了许多修道士和学者，如奥尔本修道士和尼科马科斯等。

他们对数学进行了深入的研究，并在代数、几何和三角学等领域取得了一些重要成果。

同时，中世纪欧洲的数学教育也变得日益重要，一些大学纷纷开设数学课程。

4.文艺复兴时期数学（公元1500年-1700年）在文艺复兴时期，数学经历了巨大的变革和发展。

人们重新审视古希腊数学，并在此基础上进行创新。

代数学逐渐成为数学的主流，同时平面几何和立体几何也得到了极大的发展。

一些重要的数学思想和方法开始形成，如极限、导数和微积分等。

在这个时期，一些重要的数学家如雷科德、韦达和牛顿等为数学界的发展做出了巨大贡献。

雷科德在其著作《大术》中系统地阐述了代数符号和算术方法，韦达则发展出了符号代数，为现代代数奠定了基础。

牛顿则在微积分和物理学等领域做出了杰出的贡献。

5.近现代数学（公元1800年至今）近现代数学的发展可以说是日新月异。

在19世纪，数学家们开始研究更抽象的问题，如数论、抽象代数和拓扑学等。

同时，概率论和统计学也得到了迅速的发展。

20世纪初，数学开始与物理学、工程学等领域紧密联系，出现了许多应用数学分支，如量子力学、计算机科学、经济学等。

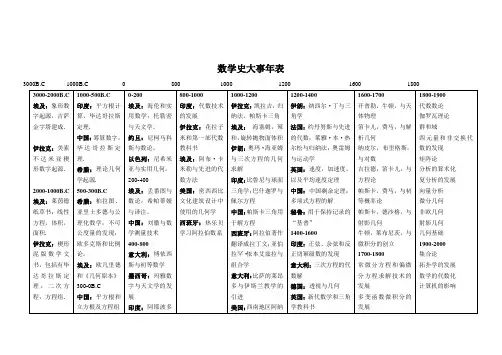
极客数学帮数学文化大事记，盘点历史上数学发展过程中的重大事件，一起来看看吧。

401-1000年五世纪，算出了π的近似值到七位小数，比西方早一千多年(中国祖冲之)。

五世纪，著书研究数学和天文学，其中讨论了一次不定方程式的解法、度量术和三角学等(印度阿耶波多)。

六世纪中国六朝时，提出祖氏定律：若二立体等高处的截面积相等，则二者体积相等。

西方直到十七世纪才发现同一定律，称为卡瓦列利原理(中国祖暅)。

七世纪，研究了定方程和不定方程、四边形、圆周率、梯形和序列。

给出了ax+by=c(a ,b,c,是整数)的第一个一般解(印度婆罗摩笈多)。

九世纪，发表《印度计数算法》，使西欧熟悉了十进位制(阿拉伯阿尔·花刺子模)。

1001-1500年十一世纪，第一次解出x2n+axn=b型方程的根(阿拉伯阿尔·卡尔希)。

十一世纪，完成了一部系统研究三次方程的书《代数学》(阿拉伯卡牙姆)。

十一世纪，解决了“海赛姆”问题，即要在圆的平面上两点作两条线相交于圆周上一点，并与在该点的法线成等角(埃及阿尔·海赛姆)。

十二世纪，《立剌瓦提》一书是东方算术和计算方面的重要著作(印度拜斯迦罗)。

1202年，发表《计算之书》，把印度-阿拉伯记数法介绍到西方(意大利费婆拿契)。

1464年，在《论各种三角形》(1533年出版)中，系统地总结了三角学(德国约·米勒)。

1 494年，发表《算术集成》，反映了当时所知道的关于算术、代数和三角学的知识(意大利帕奇欧里)。

1501-1600年1545年，卡尔达诺在《大法》中发表了非尔洛求三次方程的一般代数解的公式(意大利卡尔达诺、非尔洛)。

1550─1572年，出版《代数学》，其中引入了虚数，完全解决了三次方程的代数解问题(意大利邦别利)。

1591年左右，在《美妙的代数》中出现了用字母表示数字系数的一般符号，推进了代数问题的一般讨论(德国韦达)。

1596─1613年，完成了六个三角函数的间隔10秒的十五位小数表(德国奥脱、皮提斯库斯)。

二年级数学历史事件年表整理历史事件年表公元前3000年-公元前2000年- 古代数学：古巴比伦人使用基数十进制系统进行计数，并解决了一元二次方程和立方方程。

- 古代数学：古埃及人使用基数十进制系统计算土地面积，掌握了分数的运算。

- 古代数学：古印度人发展了一种称为维达斯的计数系统，其中包括使用等差数列和等差数列求和的方法。

公元前500年-公元500年- 古希腊数学：毕达哥拉斯学派提出并证明了毕氏定理，其理论奠定了几何学的基础。

- 古希腊数学：欧几里得的《几何原本》成为后世几何学的主要教材，为数学建立了严密的证明体系。

- 古罗马数学：罗马人引入罗马数字系统，使数字的记数方式更为简洁方便。

公元800年-公元1500年- 中世纪数学：阿拉伯数学家将印度数字系统引入欧洲，这成为现代十进制系统的基础。

- 中世纪数学：费尔马研究数论，并提出了费尔马大定理，该定理直到近350年后才被证明。

- 文艺复兴时期：数学家斯皮格尔首次使用代数符号来表示未知数，为代数学的发展开辟了新的途径。

公元1600年-公元1800年- 微积分的发展：牛顿和莱布尼茨独立地发明了微积分学，并解决了许多与运动与变化有关的问题。

- 概率与统计学：帕斯卡与费马在赌博问题上的合作研究奠定了概率论的基础，这也是统计学的起源。

- 复数的引入：数学家欧拉引入了虚数单位i，并建立了复数的代数体系。

公元1800年-现代- 非欧几何学：黎曼和庞加莱等数学家推动了非欧几何学的发展，打破了传统欧几里得几何学的限制。

- 数学逻辑学：直到19世纪末，哥德尔、罗素和维特根斯坦等数学家对数学的基础进行了深入的研究。

- 离散数学：在这个时期，数学家开始系统研究离散数学的各个分支，如图论、代数结构等。

总结：数学历史发展了几千年，从古代的基础计数方法到现代的高等数学，每个时期都有重要的数学发现和突破。

这些历史事件不仅推动了数学的发展，也深刻地影响了其他科学领域。

数学年表帮助我们了解数学在各个时期的演变和重要里程碑，为今后的研究和应用奠定了基础。

数学⼤事年表（2）数学⼤事年表(2)公元1750年 瑞⼠g.克莱姆给出解线性⽅程组的克莱姆法则瑞⼠l.欧拉发表多⾯体公式:v-e+f =2公元1770年 法国j.－l.拉格朗⽇深⼊探讨代数⽅程根式求解问题，考虑有理函数当变量发⽣置换时所取值的个数，成为置换群论的先导德国j.h.朗伯开创双曲函数的全⾯研究公元1777年 法国g.-l.l.de布丰提出投针问题,是⼏何概率理论的早期研究公元1779年 法国□.贝祖著《代数⽅程的⼀般理论》，系统论述消元法理论公元1788年 法国j.－l.拉格朗⽇的《分析⼒学》出版，使⼒学分析化，并总结了变分法的成果公元1794年 法国a.－m.勒让德的《⼏何学基础》出版，是当时标准的⼏何教科书法国建⽴巴黎综合⼯科学校和巴黎⾼等师范学校公元1795年 法国g.蒙⽇发表《关于把分析应⽤于⼏何的活页论⽂》，成为微分⼏何学先驱公元1797年 法国j.-l.拉格朗⽇著《解析函数论》，主张以函数的幂级数展开为基础建⽴微积分理论挪威c.韦塞尔最早给出复数的⼏何表⽰公元1799年法国g.蒙⽇出版《画法⼏何学》，使画法⼏何成为⼏何学的⼀个专门分⽀德国c.f.⾼斯给出代数基本定理的第⼀个证明公元1799～1825年　法国p.-s.拉普拉斯的5卷巨著《天体⼒学》出版，其中包含了许多重要的数学贡献，如拉普拉斯⽅程、位势函数等公元1801年 德国c.f.⾼斯的《算术研究》出版，标志着近代数论的起点公元1802年 法国j.e.蒙蒂克拉与j.de拉朗德合撰的《数学史》共4卷全部出版,成为最早的较系统的数学史著作公元1807年 法国j.－b.－j.傅⾥叶在热传导研究中提出任意函数的三⾓级数表⽰法（傅⾥叶级数），他的思想总结在1822年发表的《热的解析理论》中公元1810年 法国j.－d.热尔岗创办《纯粹与应⽤数学年刊》，这是最早的专门数学期刊公元1812年 英国剑桥分析学会成⽴法国 p.-s.拉普拉斯著《概率的解析理论》,提出概率的古典定义,将分析⼯具引⼊概率论公元1814年 法国 a.-l.柯西宣读复变函数论第⼀篇重要论⽂《关于定积分理论的报告》（1827年正式发表），开创了复变函数论的研究公元1817年 捷克b.波尔查诺著《纯粹分析的证明》，⾸次给出连续性、导数的恰当定义，提出⼀般级数收敛性的判别准则公元1818年 法国s.-d.泊松导出波动⽅程解的“泊松公式”公元1821年 法国a.-l.柯西出版《代数分析教程》，引进不⼀定具有解析表达式的函数概念；独⽴于b.波尔查诺提出极限、连续、导数等定义和级数收敛判别准则，是分析严密化运动中第⼀部影响深远的著作公元1822年 法国j.－v.彭赛列著《论图形的射影性质》，奠定了射影⼏何学基础公元1826年 挪威n.h.阿贝尔著《关于很⼴⼀类超越函数的⼀个⼀般性质》，开创了椭圆函数论研究德国a.l.克雷尔创办《纯粹与应⽤数学杂志》法国j.-d.热尔岗与j.-v.彭赛列各⾃建⽴对偶原理公元1827年 德国c.f.⾼斯著《关于曲⾯的⼀般研究》，开创曲⾯内蕴⼏何学德国a.f.麦⽐乌斯著《重⼼演算》，引进齐次坐标，与j.普吕克等开辟了射影⼏何的代数⽅向公元1828年 英国g.格林著《数学分析在电磁理论中的应⽤》，发展位势理论公元1829年德国c.g.j.雅可⽐著《椭圆函数论新基础》，是椭圆函数理论的奠基性著作俄国н.и.罗巴切夫斯基发表最早的⾮欧⼏何论著《论⼏何基础》公元1829～1832年　法国e.伽罗⽡彻底解决代数⽅程根式可解性问题，确⽴了群论的基本概念公元1830年英国g.⽪科克著《代数通论》，⾸创以演绎⽅式建⽴代数学，为代数中更抽象的思想铺平了道路公元1832年 匈⽛利j.波尔约发表《绝对空间的科学》，独⽴于н.и.罗巴切夫斯基提出了⾮欧⼏何思想瑞⼠j.施泰纳著《⼏何形的相互依赖性的系统发展》公元1836年 法国j.刘维尔创办法⽂的《纯粹与应⽤数学杂志》公元1837年 德国p.g.l.狄利克雷提出现今通⽤的函数定义(变量之间的对应关系)公元1840年 法国 a.-l柯西证明了微分⽅程初值问题解的存在性公元1841～1856年　德国k.（t.w.）外尔斯特拉斯关于分析严密化的⼯作，主张将分析建⽴在算术概念的基础之上，给出极限的ε－δ说法和级数⼀致收敛性概念；同时在幂级数基础上建⽴复变函数论公元1843年 英国w.r.哈密顿发现四元数公元1844年 德国e.e.库默尔创⽴理想数的概念德国h.g.格拉斯曼出版《线性扩张论》。

数学年谱之公元1800公元１８００～１８９９年1801年，德国的高斯出版《算术研究》，开创近代数论。

1809年，法国的蒙日出版了微分几何学的第一本书《分析在几何学上的应用》。

1812年，法国的拉普拉斯出版《分析概率论》一书，这是近代概率论的先驱。

1816年，德国的高斯发现非欧几何，但未发表。

1821年，法国的柯西出版《分析教程》，用极限严格地定义了函数的连续、导数和积分，研究了无穷级数的收敛性等。

1822年，法国的彭色列系统研究了几何图形在投影变换下的不变性质，建立了射影几何学。

法国的傅立叶研究了热传导问题，发明用傅立叶级数求解偏微分方程的边值问题，在理论和应用上都有重大影响。

1824年，挪威的阿贝尔证明用根式求解五次方程的不可能性。

1826年，挪威的阿贝尔发现连续函数的级数之和并非连续函数。

俄国的罗巴切夫斯基和匈牙利的波约改变欧几里得几何学中的平行公理，提出非欧几何学的理论。

1827～1829年，德国的雅可比、挪威的阿贝尔和法国的勒阿德尔共同确立了椭圆积分与椭圆函数的理论，在物理、力学中都有应用。

1827年，德国的高斯建立了微分几何中关于曲面的系统理论。

德国的莫比乌斯出版《重心演算》，第一次引进齐次坐标。

1830年，捷克的波尔查诺给出一个连续而没有导数的所谓“病态”函数的例子。

法国的伽罗华在代数方程可否用根式求解的研究中建立群论。

1831年，法国的柯西发现解析函数的幂级数收敛定理。

德国的高斯建立了复数的代数学，用平面上的点来表示复数，破除了复数的神秘性。

1835年，法国的斯特姆提出确定代数方程式实根位置的方法。

1836年，法国的柯西证明解析系数微分方程解的存在性。

瑞士的史坦纳证明具有已知周长的一切封闭曲线中包围最大面积的图形一定是圆。

1837年，德国的狄利克莱第一次给出了三角级数的一个收敛性定理。

1840年，德国的狄利克莱把解析函数用于数论，并且引入了“狄利克莱”级数。

1841年，德国的雅可比建立了行列式的系统理论。

数学文化大事记——来看看数学发展史上的重大事件
数学文化大事记——来看看数学发展史上的重大事件
极客数学帮数学文化大事记，盘点历史上数学发展过程中的重大事件，一起来看看吧。

401-1000年
五世纪，算出了π的近似值到七位小数，比西方早一千多年(中国祖冲之)。

五世纪，着书研究数学和天文学，其中讨论了一次不定方程式的解法、度量术和三角学等(印度阿耶波多)。

六世纪中国六朝时，提出祖氏定律：若二立体等高处的截面积相等，则二者体积相等。

西方直到十七世纪才发现同一定律，称为卡瓦列利原理(中国祖暅)。

数学大事年表约公元前3000年埃及象形数字公元前2400～前1600年早期巴比伦泥版楔形文字，采用60进位值制记数法。

已知勾股定理公元前1850～前1650年埃及纸草书（莫斯科纸草书与莱茵德纸草书），使用10进非位值制记数法公元前1400～前1100年中国殷墟甲骨文，已有10进制记数法周公(公元前11世纪)、商高时代已知勾三、股四、弦五约公元前600年希腊泰勒斯开始了命题的证明约公元前540年希腊毕达哥拉斯学派，发现勾股定理，并导致不可通约量的发现约公元前500年印度《绳法经》中给出√2相当精确的值，并知勾股定理约公元前460年希腊智人学派提出几何作图三大问题：化圆为方、三等分角和二倍立方约公元前450年希腊埃利亚学派的芝诺提出悖论公元前430年希腊安提丰提出穷竭法约公元前380年希腊柏拉图在雅典创办"学园"，主张通过几何的学习培养逻辑思维能力公元前370年希腊欧多克索斯创立比例论约公元前335年欧多莫斯著《几何学史、中国筹算记数，采用十进位值制约公元前300年希腊欧几里得著《几何原本》，是用公理法建立演绎数学体系的最早典范公元前287～前212年希腊阿基米德，确定了大量复杂几何图形的面积与体积；给出圆周率的上下界；提出用力学方法推测问题答案，隐含近代积分论思想公元前230年希腊埃拉托塞尼发明"筛法"公元前225年希腊阿波罗尼奥斯著《圆锥曲线论》约公元前150年中国现存最早的数学书《算数书》成书（1983～1984年间在湖北江陵出土）约公元前100年中国《周髀算经》成书，记述了勾股定理中国古代最重要的数学著作《九章算术》经历代增补修订基本定形（一说成书年代为公元50～100年间），其中正负数运算法则、分数四则运算、线性方程组解法、比例计算与线性插值法盈不足术等都是世界数学史上的重要贡献约公元62年希腊海伦给出用三角形三边长表示面积的公式（海伦公式）约公元150年希腊托勒密著《天文学》，发展了三角学约公元250年希腊丢番图著《算术》，处理了大量不定方程问题，并引入一系列缩写符号，是古希腊代数的代表作约公元263年中国刘徽注解《九章算术》，创割圆术，计算圆周率,证明圆面积公式,推导四面体及四棱锥体积等，包含有极限思想约公元300年中国《孙子算经》成书，系统记述了筹算记数制，卷下"物不知数"题是孙子剩余定理的起源公元320年希腊帕普斯著《数学汇编》，总结古希腊各家的研究成果,并记述了"帕普斯定理"和旋转体体积计算法公元410年希腊许帕提娅，历史上第一位女数学家，曾注释欧几里得、丢番图等人的著作公元462年中国祖冲之算出圆周率在3.1415926与3.1415927之间,并以22/7为约率，355/113为密率（现称祖率）中国祖冲之和他的儿子祖暅提出"幂势既同则积不容异"的原理，现称祖暅原理，相当于西方的卡瓦列里原理(1635)公元499年印度阿耶波多著《阿耶波多文集》，总结了当时印度的天文、算术、代数与三角学知识。