Minimum Cost Routing Robustness through Randomization

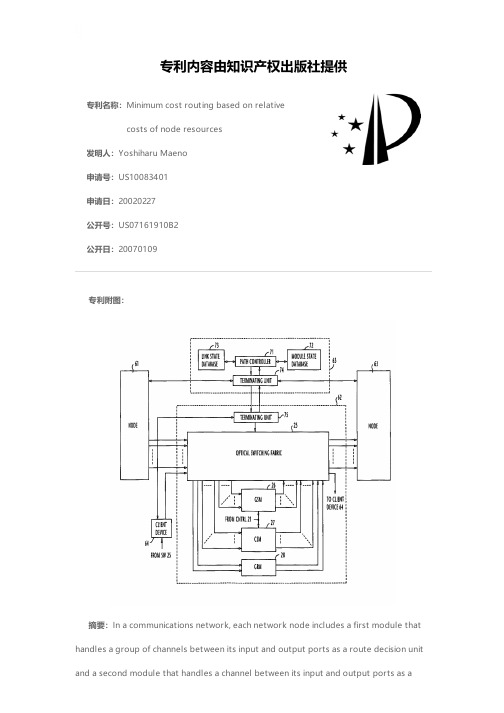
专利名称：Minimum cost routing based on relativecosts of node resources发明人：Yoshiharu Maeno申请号：US10083401申请日：20020227公开号：US07161910B2公开日：20070109专利内容由知识产权出版社提供专利附图：摘要：In a communications network, each network node includes a first module that handles a group of channels between its input and output ports as a route decision unit and a second module that handles a channel between its input and output ports as aroute decision unit. A module state database stores module cost data of the first and second modules and a link state database stores link cost data of the links. Using the module and link state databases a route of minimum cost is determined and a connection is established between an incoming link and one of the input ports of the first and second modules and a connection is established between one of the output ports of the first and second modules and an outgoing link. The contents of the module and state databases are broadcast to the network.申请人：Yoshiharu Maeno地址：Tokyo JP国籍：JP代理机构：Dickstein Shapiro LLP更多信息请下载全文后查看。

2015年3月Journal on Communications March 2015 第36卷第3期通信学报V ol.36No.3 IP网络时延敏感型业务流自适应负载均衡算法杨洋1,2,3，杨家海1,2，王会1,2，李晨曦1,2，王于丁1,2（1. 清华大学网络科学与网络空间研究院，北京100084;2. 清华信息科学与技术国家实验室（筹），北京100084；3. 西安通信学院信息管理中心，陕西西安710106）摘 要：互联网对时延敏感的业务数据流，要求具有较低的端到端时延，但是网络拥塞的发生，将会使服务质量无法保证。

基于链路关键度提出了一种新的自适应负载均衡路由算法(LARA，load adaptive routing algorithm)，能最大限度地避开拥塞链路从而减少端到端延迟。

该算法通过得到一个优化目标函数，并利用凸优化理论将优化目标函数分解为若干个子函数，最终得到一个简单的分布式协议。

利用NS2仿真器在基于CERNET2真实的拓扑结构上进行仿真实验，同时与网络中能普遍部署的等开销多路径（ECMP，equal-cost multi-path）算法相比较，通过测试反馈时延、分组丢失率、流量负载，结果表明LARA具有更好的自适应性和健壮性，性能相比更优。

关键词：网络拥塞；关键链路；链路关键度；多路径路由；负载均衡中图分类号：TP393.1 文献标识码：ATowards load adaptive routing based on link criticaldegree for delay-sensitive traffic in IP networksYANG Yang1,2,3, YANG Jia-hai1,2, WANG Hui1,2, LI Chen-xi1,2, WANG Yu-ding1,2(1. Institute for the Network Sciences and Cyberspace, Tsinghua University, Beijing 100084, China;2. Tsinghua National Laboratory for Information Science and Technology (TNList), Beijing 100084, China;3. Information Management Center, Xi’an Communication Institute, Xi’an 710106, China )Abstract: Delay-sensitive traffic requires lower end-to-end delay in IP networks, such as online video, VoIP, video con-ference. Based on the criticality degree of link. A load adaptive routing algorithm (LARA) was presented which could avoid the link to be congested to reduce the end-to-end delay. Firstly, an optimization objective function has been put forward; and then decomposed into several sub-functions by using convex optimization theory; finally, the optimization objective function and sub-functions were transformed into a simple distributed protocol. LARA with ECMP (equal-cost multipath) routing strategy was compared which was widely deployed in the network by using NS2 simulation under CERNET2 topology. By evaluating the feedback delay, packet loss rate and traffic load, the results show that LARA can exhibit good performance and achieve excellent load balance, and meanwhile improve the robustness of the link when using multipath routing technology.Key words: network congestion; critical link; criticality degree of link; multipath routing; load balance1引言伴随着宽带互联网增值业务进入消费者市场，交互式应用程序变得越来越流行，如视频直播、VoIP、多媒体会议、在线游戏等。

Recent Advances in Robust Optimization and Robustness:An OverviewVirginie Gabrel∗and C´e cile Murat†and Aur´e lie Thiele‡July2012AbstractThis paper provides an overview of developments in robust optimization and robustness published in the aca-demic literature over the pastfive years.1IntroductionThis review focuses on papers identified by Web of Science as having been published since2007(included),be-longing to the area of Operations Research and Management Science,and having‘robust’and‘optimization’in their title.There were exactly100such papers as of June20,2012.We have completed this list by considering 726works indexed by Web of Science that had either robustness(for80of them)or robust(for646)in their title and belonged to the Operations Research and Management Science topic area.We also identified34PhD disserta-tions dated from the lastfive years with‘robust’in their title and belonging to the areas of operations research or management.Among those we have chosen to focus on the works with a primary focus on management science rather than system design or optimal control,which are broadfields that would deserve a review paper of their own, and papers that could be of interest to a large segment of the robust optimization research community.We feel it is important to include PhD dissertations to identify these recent graduates as the new generation trained in robust optimization and robustness analysis,whether they have remained in academia or joined industry.We have also added a few not-yet-published preprints to capture ongoing research efforts.While many additional works would have deserved inclusion,we feel that the works selected give an informative and comprehensive view of the state of robustness and robust optimization to date in the context of operations research and management science.∗Universit´e Paris-Dauphine,LAMSADE,Place du Mar´e chal de Lattre de Tassigny,F-75775Paris Cedex16,France gabrel@lamsade.dauphine.fr Corresponding author†Universit´e Paris-Dauphine,LAMSADE,Place du Mar´e chal de Lattre de Tassigny,F-75775Paris Cedex16,France mu-rat@lamsade.dauphine.fr‡Lehigh University,Industrial and Systems Engineering Department,200W Packer Ave Bethlehem PA18015,USA aure-lie.thiele@2Theory of Robust Optimization and Robustness2.1Definitions and BasicsThe term“robust optimization”has come to encompass several approaches to protecting the decision-maker against parameter ambiguity and stochastic uncertainty.At a high level,the manager must determine what it means for him to have a robust solution:is it a solution whose feasibility must be guaranteed for any realization of the uncertain parameters?or whose objective value must be guaranteed?or whose distance to optimality must be guaranteed? The main paradigm relies on worst-case analysis:a solution is evaluated using the realization of the uncertainty that is most unfavorable.The way to compute the worst case is also open to debate:should it use afinite number of scenarios,such as historical data,or continuous,convex uncertainty sets,such as polyhedra or ellipsoids?The answers to these questions will determine the formulation and the type of the robust counterpart.Issues of over-conservatism are paramount in robust optimization,where the uncertain parameter set over which the worst case is computed should be chosen to achieve a trade-off between system performance and protection against uncertainty,i.e.,neither too small nor too large.2.2Static Robust OptimizationIn this framework,the manager must take a decision in the presence of uncertainty and no recourse action will be possible once uncertainty has been realized.It is then necessary to distinguish between two types of uncertainty: uncertainty on the feasibility of the solution and uncertainty on its objective value.Indeed,the decision maker generally has different attitudes with respect to infeasibility and sub-optimality,which justifies analyzing these two settings separately.2.2.1Uncertainty on feasibilityWhen uncertainty affects the feasibility of a solution,robust optimization seeks to obtain a solution that will be feasible for any realization taken by the unknown coefficients;however,complete protection from adverse realiza-tions often comes at the expense of a severe deterioration in the objective.This extreme approach can be justified in some engineering applications of robustness,such as robust control theory,but is less advisable in operations research,where adverse events such as low customer demand do not produce the high-profile repercussions that engineering failures–such as a doomed satellite launch or a destroyed unmanned robot–can have.To make the robust methodology appealing to business practitioners,robust optimization thus focuses on obtaining a solution that will be feasible for any realization taken by the unknown coefficients within a smaller,“realistic”set,called the uncertainty set,which is centered around the nominal values of the uncertain parameters.The goal becomes to optimize the objective,over the set of solutions that are feasible for all coefficient values in the uncertainty set.The specific choice of the set plays an important role in ensuring computational tractability of the robust problem and limiting deterioration of the objective at optimality,and must be thought through carefully by the decision maker.A large branch of robust optimization focuses on worst-case optimization over a convex uncertainty set.The reader is referred to Bertsimas et al.(2011a)and Ben-Tal and Nemirovski(2008)for comprehensive surveys of robust optimization and to Ben-Tal et al.(2009)for a book treatment of the topic.2.2.2Uncertainty on objective valueWhen uncertainty affects the optimality of a solution,robust optimization seeks to obtain a solution that performs well for any realization taken by the unknown coefficients.While a common criterion is to optimize the worst-case objective,some studies have investigated other robustness measures.Roy(2010)proposes a new robustness criterion that holds great appeal for the manager due to its simplicity of use and practical relevance.This framework,called bw-robustness,allows the decision-maker to identify a solution which guarantees an objective value,in a maximization problem,of at least w in all scenarios,and maximizes the probability of reaching a target value of b(b>w).Gabrel et al.(2011)extend this criterion from afinite set of scenarios to the case of an uncertainty set modeled using intervals.Kalai et al.(2012)suggest another criterion called lexicographicα-robustness,also defined over afinite set of scenarios for the uncertain parameters,which mitigates the primary role of the worst-case scenario in defining the solution.Thiele(2010)discusses over-conservatism in robust linear optimization with cost uncertainty.Gancarova and Todd(2012)studies the loss in objective value when an inaccurate objective is optimized instead of the true one, and shows that on average this loss is very small,for an arbitrary compact feasible region.In combinatorial optimization,Morrison(2010)develops a framework of robustness based on persistence(of decisions)using the Dempster-Shafer theory as an evidence of robustness and applies it to portfolio tracking and sensor placement.2.2.3DualitySince duality has been shown to play a key role in the tractability of robust optimization(see for instance Bertsimas et al.(2011a)),it is natural to ask how duality and robust optimization are connected.Beck and Ben-Tal(2009) shows that primal worst is equal to dual best.The relationship between robustness and duality is also explored in Gabrel and Murat(2010)when the right-hand sides of the constraints are uncertain and the uncertainty sets are represented using intervals,with a focus on establishing the relationships between linear programs with uncertain right hand sides and linear programs with uncertain objective coefficients using duality theory.This avenue of research is further explored in Gabrel et al.(2010)and Remli(2011).2.3Multi-Stage Decision-MakingMost early work on robust optimization focused on static decision-making:the manager decided at once of the values taken by all decision variables and,if the problem allowed for multiple decision stages as uncertainty was realized,the stages were incorporated by re-solving the multi-stage problem as time went by and implementing only the decisions related to the current stage.As thefield of static robust optimization matured,incorporating–ina tractable manner–the information revealed over time directly into the modeling framework became a major area of research.2.3.1Optimal and Approximate PoliciesA work going in that direction is Bertsimas et al.(2010a),which establishes the optimality of policies affine in the uncertainty for one-dimensional robust optimization problems with convex state costs and linear control costs.Chen et al.(2007)also suggests a tractable approximation for a class of multistage chance-constrained linear program-ming problems,which converts the original formulation into a second-order cone programming problem.Chen and Zhang(2009)propose an extension of the Affinely Adjustable Robust Counterpart framework described in Ben-Tal et al.(2009)and argue that its potential is well beyond what has been in the literature so far.2.3.2Two stagesBecause of the difficulty in incorporating multiple stages in robust optimization,many theoretical works have focused on two stages.Regarding two-stage problems,Thiele et al.(2009)presents a cutting-plane method based on Kelley’s algorithm for solving convex adjustable robust optimization problems,while Terry(2009)provides in addition preliminary results on the conditioning of a robust linear program and of an equivalent second-order cone program.Assavapokee et al.(2008a)and Assavapokee et al.(2008b)develop tractable algorithms in the case of robust two-stage problems where the worst-case regret is minimized,in the case of interval-based uncertainty and scenario-based uncertainty,respectively,while Minoux(2011)provides complexity results for the two-stage robust linear problem with right-hand-side uncertainty.2.4Connection with Stochastic OptimizationAn early stream in robust optimization modeled stochastic variables as uncertain parameters belonging to a known uncertainty set,to which robust optimization techniques were then applied.An advantage of this method was to yield approaches to decision-making under uncertainty that were of a level of complexity similar to that of their deterministic counterparts,and did not suffer from the curse of dimensionality that afflicts stochastic and dynamic programming.Researchers are now making renewed efforts to connect the robust optimization and stochastic opti-mization paradigms,for instance quantifying the performance of the robust optimization solution in the stochastic world.The topic of robust optimization in the context of uncertain probability distributions,i.e.,in the stochastic framework itself,is also being revisited.2.4.1Bridging the Robust and Stochastic WorldsBertsimas and Goyal(2010)investigates the performance of static robust solutions in two-stage stochastic and adaptive optimization problems.The authors show that static robust solutions are good-quality solutions to the adaptive problem under a broad set of assumptions.They provide bounds on the ratio of the cost of the optimal static robust solution to the optimal expected cost in the stochastic problem,called the stochasticity gap,and onthe ratio of the cost of the optimal static robust solution to the optimal cost in the two-stage adaptable problem, called the adaptability gap.Chen et al.(2007),mentioned earlier,also provides a robust optimization perspective to stochastic programming.Bertsimas et al.(2011a)investigates the role of geometric properties of uncertainty sets, such as symmetry,in the power offinite adaptability in multistage stochastic and adaptive optimization.Duzgun(2012)bridges descriptions of uncertainty based on stochastic and robust optimization by considering multiple ranges for each uncertain parameter and setting the maximum number of parameters that can fall within each range.The corresponding optimization problem can be reformulated in a tractable manner using the total unimodularity of the feasible set and allows for afiner description of uncertainty while preserving tractability.It also studies the formulations that arise in robust binary optimization with uncertain objective coefficients using the Bernstein approximation to chance constraints described in Ben-Tal et al.(2009),and shows that the robust optimization problems are deterministic problems for modified values of the coefficients.While many results bridging the robust and stochastic worlds focus on giving probabilistic guarantees for the solutions generated by the robust optimization models,Manuja(2008)proposes a formulation for robust linear programming problems that allows the decision-maker to control both the probability and the expected value of constraint violation.Bandi and Bertsimas(2012)propose a new approach to analyze stochastic systems based on robust optimiza-tion.The key idea is to replace the Kolmogorov axioms and the concept of random variables as primitives of probability theory,with uncertainty sets that are derived from some of the asymptotic implications of probability theory like the central limit theorem.The authors show that the performance analysis questions become highly structured optimization problems for which there exist efficient algorithms that are capable of solving problems in high dimensions.They also demonstrate that the proposed approach achieves computationally tractable methods for(a)analyzing queueing networks,(b)designing multi-item,multi-bidder auctions with budget constraints,and (c)pricing multi-dimensional options.2.4.2Distributionally Robust OptimizationBen-Tal et al.(2010)considers the optimization of a worst-case expected-value criterion,where the worst case is computed over all probability distributions within a set.The contribution of the work is to define a notion of robustness that allows for different guarantees for different subsets of probability measures.The concept of distributional robustness is also explored in Goh and Sim(2010),with an emphasis on linear and piecewise-linear decision rules to reformulate the original problem in aflexible manner using expected-value terms.Xu et al.(2012) also investigates probabilistic interpretations of robust optimization.A related area of study is worst-case optimization with partial information on the moments of distributions.In particular,Popescu(2007)analyzes robust solutions to a certain class of stochastic optimization problems,using mean-covariance information about the distributions underlying the uncertain parameters.The author connects the problem for a broad class of objective functions to a univariate mean-variance robust objective and,subsequently, to a(deterministic)parametric quadratic programming problem.The reader is referred to Doan(2010)for a moment-based uncertainty model for stochastic optimization prob-lems,which addresses the ambiguity of probability distributions of random parameters with a minimax decision rule,and a comparison with data-driven approaches.Distributionally robust optimization in the context of data-driven problems is the focus of Delage(2009),which uses observed data to define a”well structured”set of dis-tributions that is guaranteed with high probability to contain the distribution from which the samples were drawn. Zymler et al.(2012a)develop tractable semidefinite programming(SDP)based approximations for distributionally robust individual and joint chance constraints,assuming that only thefirst-and second-order moments as well as the support of the uncertain parameters are given.Becker(2011)studies the distributionally robust optimization problem with known mean,covariance and support and develops a decomposition method for this family of prob-lems which recursively derives sub-policies along projected dimensions of uncertainty while providing a sequence of bounds on the value of the derived policy.Robust linear optimization using distributional information is further studied in Kang(2008).Further,Delage and Ye(2010)investigates distributional robustness with moment uncertainty.Specifically,uncertainty affects the problem both in terms of the distribution and of its moments.The authors show that the resulting problems can be solved efficiently and prove that the solutions exhibit,with high probability,best worst-case performance over a set of distributions.Bertsimas et al.(2010)proposes a semidefinite optimization model to address minimax two-stage stochastic linear problems with risk aversion,when the distribution of the second-stage random variables belongs to a set of multivariate distributions with knownfirst and second moments.The minimax solutions provide a natural distribu-tion to stress-test stochastic optimization problems under distributional ambiguity.Cromvik and Patriksson(2010a) show that,under certain assumptions,global optima and stationary solutions of stochastic mathematical programs with equilibrium constraints are robust with respect to changes in the underlying probability distribution.Works such as Zhu and Fukushima(2009)and Zymler(2010)also study distributional robustness in the context of specific applications,such as portfolio management.2.5Connection with Risk TheoryBertsimas and Brown(2009)describe how to connect uncertainty sets in robust linear optimization to coherent risk measures,an example of which is Conditional Value-at-Risk.In particular,the authors show the link between polyhedral uncertainty sets of a special structure and a subclass of coherent risk measures called distortion risk measures.Independently,Chen et al.(2007)present an approach for constructing uncertainty sets for robust opti-mization using new deviation measures that capture the asymmetry of the distributions.These deviation measures lead to improved approximations of chance constraints.Dentcheva and Ruszczynski(2010)proposes the concept of robust stochastic dominance and shows its applica-tion to risk-averse optimization.They consider stochastic optimization problems where risk-aversion is expressed by a robust stochastic dominance constraint and develop necessary and sufficient conditions of optimality for such optimization problems in the convex case.In the nonconvex case,they derive necessary conditions of optimality under additional smoothness assumptions of some mappings involved in the problem.2.6Nonlinear OptimizationRobust nonlinear optimization remains much less widely studied to date than its linear counterpart.Bertsimas et al.(2010c)presents a robust optimization approach for unconstrained non-convex problems and problems based on simulations.Such problems arise for instance in the partial differential equations literature and in engineering applications such as nanophotonic design.An appealing feature of the approach is that it does not assume any specific structure for the problem.The case of robust nonlinear optimization with constraints is investigated in Bertsimas et al.(2010b)with an application to radiation therapy for cancer treatment.Bertsimas and Nohadani (2010)further explore robust nonconvex optimization in contexts where solutions are not known explicitly,e.g., have to be found using simulation.They present a robust simulated annealing algorithm that improves performance and robustness of the solution.Further,Boni et al.(2008)analyzes problems with uncertain conic quadratic constraints,formulating an approx-imate robust counterpart,and Zhang(2007)provide formulations to nonlinear programming problems that are valid in the neighborhood of the nominal parameters and robust to thefirst order.Hsiung et al.(2008)present tractable approximations to robust geometric programming,by using piecewise-linear convex approximations of each non-linear constraint.Geometric programming is also investigated in Shen et al.(2008),where the robustness is injected at the level of the algorithm and seeks to avoid obtaining infeasible solutions because of the approximations used in the traditional approach.Interval uncertainty-based robust optimization for convex and non-convex quadratic programs are considered in Li et al.(2011).Takeda et al.(2010)studies robustness for uncertain convex quadratic programming problems with ellipsoidal uncertainties and proposes a relaxation technique based on random sampling for robust deviation optimization sserre(2011)considers minimax and robust models of polynomial optimization.A special case of nonlinear problems that are linear in the decision variables but convex in the uncertainty when the worst-case objective is to be maximized is investigated in Kawas and Thiele(2011a).In that setting,exact and tractable robust counterparts can be derived.A special class of nonconvex robust optimization is examined in Kawas and Thiele(2011b).Robust nonconvex optimization is examined in detail in Teo(2007),which presents a method that is applicable to arbitrary objective functions by iteratively moving along descent directions and terminates at a robust local minimum.3Applications of Robust OptimizationWe describe below examples to which robust optimization has been applied.While an appealing feature of robust optimization is that it leads to models that can be solved using off-the-shelf software,it is worth pointing the existence of algebraic modeling tools that facilitate the formulation and subsequent analysis of robust optimization problems on the computer(Goh and Sim,2011).3.1Production,Inventory and Logistics3.1.1Classical logistics problemsThe capacitated vehicle routing problem with demand uncertainty is studied in Sungur et al.(2008),with a more extensive treatment in Sungur(2007),and the robust traveling salesman problem with interval data in Montemanni et al.(2007).Remli and Rekik(2012)considers the problem of combinatorial auctions in transportation services when shipment volumes are uncertain and proposes a two-stage robust formulation solved using a constraint gener-ation algorithm.Zhang(2011)investigates two-stage minimax regret robust uncapacitated lot-sizing problems with demand uncertainty,in particular showing that it is polynomially solvable under the interval uncertain demand set.3.1.2SchedulingGoren and Sabuncuoglu(2008)analyzes robustness and stability measures for scheduling in a single-machine environment subject to machine breakdowns and embeds them in a tabu-search-based scheduling algorithm.Mittal (2011)investigates efficient algorithms that give optimal or near-optimal solutions for problems with non-linear objective functions,with a focus on robust scheduling and service operations.Examples considered include parallel machine scheduling problems with the makespan objective,appointment scheduling and assortment optimization problems with logit choice models.Hazir et al.(2010)considers robust scheduling and robustness measures for the discrete time/cost trade-off problem.3.1.3Facility locationAn important question in logistics is not only how to operate a system most efficiently but also how to design it. Baron et al.(2011)applies robust optimization to the problem of locating facilities in a network facing uncertain demand over multiple periods.They consider a multi-periodfixed-charge network location problem for which they find the number of facilities,their location and capacities,the production in each period,and allocation of demand to facilities.The authors show that different models of uncertainty lead to very different solution network topologies, with the model with box uncertainty set opening fewer,larger facilities.?investigate a robust version of the location transportation problem with an uncertain demand using a2-stage formulation.The resulting robust formulation is a convex(nonlinear)program,and the authors apply a cutting plane algorithm to solve the problem exactly.Atamt¨u rk and Zhang(2007)study the networkflow and design problem under uncertainty from a complexity standpoint,with applications to lot-sizing and location-transportation problems,while Bardossy(2011)presents a dual-based local search approach for deterministic,stochastic,and robust variants of the connected facility location problem.The robust capacity expansion problem of networkflows is investigated in Ordonez and Zhao(2007),which provides tractable reformulations under a broad set of assumptions.Mudchanatongsuk et al.(2008)analyze the network design problem under transportation cost and demand uncertainty.They present a tractable approximation when each commodity only has a single origin and destination,and an efficient column generation for networks with path constraints.Atamt¨u rk and Zhang(2007)provides complexity results for the two-stage networkflow anddesign plexity results for the robust networkflow and network design problem are also provided in Minoux(2009)and Minoux(2010).The problem of designing an uncapacitated network in the presence of link failures and a competing mode is investigated in Laporte et al.(2010)in a railway application using a game theoretic perspective.Torres Soto(2009)also takes a comprehensive view of the facility location problem by determining not only the optimal location but also the optimal time for establishing capacitated facilities when demand and cost parameters are time varying.The models are solved using Benders’decomposition or heuristics such as local search and simulated annealing.In addition,the robust networkflow problem is also analyzed in Boyko(2010),which proposes a stochastic formulation of minimum costflow problem aimed atfinding network design andflow assignments subject to uncertain factors,such as network component disruptions/failures when the risk measure is Conditional Value at Risk.Nagurney and Qiang(2009)suggests a relative total cost index for the evaluation of transportation network robustness in the presence of degradable links and alternative travel behavior.Further,the problem of locating a competitive facility in the plane is studied in Blanquero et al.(2011)with a robustness criterion.Supply chain design problems are also studied in Pan and Nagi(2010)and Poojari et al.(2008).3.1.4Inventory managementThe topic of robust multi-stage inventory management has been investigated in detail in Bienstock and Ozbay (2008)through the computation of robust basestock levels and Ben-Tal et al.(2009)through an extension of the Affinely Adjustable Robust Counterpart framework to control inventories under demand uncertainty.See and Sim (2010)studies a multi-period inventory control problem under ambiguous demand for which only mean,support and some measures of deviations are known,using a factor-based model.The parameters of the replenishment policies are obtained using a second-order conic programming problem.Song(2010)considers stochastic inventory control in robust supply chain systems.The work proposes an inte-grated approach that combines in a single step datafitting and inventory optimization–using histograms directly as the inputs for the optimization model–for the single-item multi-period periodic-review stochastic lot-sizing problem.Operation and planning issues for dynamic supply chain and transportation networks in uncertain envi-ronments are considered in Chung(2010),with examples drawn from emergency logistics planning,network design and congestion pricing problems.3.1.5Industry-specific applicationsAng et al.(2012)proposes a robust storage assignment approach in unit-load warehouses facing variable supply and uncertain demand in a multi-period setting.The authors assume a factor-based demand model and minimize the worst-case expected total travel in the warehouse with distributional ambiguity of demand.A related problem is considered in Werners and Wuelfing(2010),which optimizes internal transports at a parcel sorting center.Galli(2011)describes the models and algorithms that arise from implementing recoverable robust optimization to train platforming and rolling stock planning,where the concept of recoverable robustness has been defined in。

Securing OT Networks With MicrosegmentationExecutive SummaryTraditionally, operational technology (OT) networks have used local-area network(LAN) solutions, such as virtual LAN (VLAN) on switches, to protect against lateralmovement of malware throughout the network. While VLAN solutions can providesegmentation with a greater degree of flexibility, this level of segmentation isinsufficient to secure these networks.With Fortinet microsegmentation, it is possible to implement a zero-trust securitypolicy and to scan all traffic within a VLAN using a next-generation firewall (NGFW),dramatically decreasing the ability of malware to move laterally throughout thenetwork. Microsegmentation provides the OT network with the level of security thatit needs without sacrificing network performance.Introduction to ICS/OT NetworksThe communications network within an industrial control system (ICS)/operationaltechnology (OT) realm is known as a process control network (PCN). It enablescommunication between the various automation processes residing on discretecomponents of the ICS, including the programmable logic controller (PLC), remoteterminal unit (RTU), distributed control system (DCS), and supervisory control anddata acquisition (SCADA) systems.A VLAN operates at Layer 2 of the communications network and divides a single communications network into multiple virtual networks. This partitions a single broadcast domain into multiple smaller domains, improving network performance. VLANs also enable logical grouping of network elements that are physically dispersed within acommunications network.SOLUTION BRIEF The PCN transmits instructions and data between control and measurement units and interconnects various components within an ICS/OT environment. They are high-performance, robust, and deterministic LANs. A PCN must maintain constant availability, rapid response, robust error checking, and correction to ensure zero downtime and enable the deterministic, error-free, and continuous operations of an ICS.To achieve the determinism and robustness requirements of an ICS, PCNs are often configured in flat network structures with little or no boundary limits between the different components of an ICS, as shown in Figure 1. This inherently flat network structure of the PCN makes it faster and easier to maintain.Figure 1: Example of flat PCN topology.HMISCADA historianSingle PLCHowever, it also makes it prone to numerous security threats, such as lateralmovement of malware within the PCN and network floods. These threats can potentially disrupt the PCN communications and stall the entire ICS. Moreover,the flat network structure makes it difficult to integrate a PCN with other communications networks outside of the ICS boundary.Traditionally, the automation industry has utilized LAN solutions, such as network bridges and gateways, to separate the various components and restrict network broadcasts or floods within the PCN. The implementation of VLANs can add flexibility to this segmentation process, allowing network separation regardlessof physical layout. However, VLANs alone do not address the security issues that could still cause significant damage to the PCN. Furthermore, the adoption of VLAN-based segmentation within PCNs is slow compared to enterprise networks. Zones and Conduits in ICS/OT NetworksTo address the security challenges within ICS/OT networks, the automation industry introduced the concept of zones and conduits to segment the PCN into multiple zones, isolating the various components in an ICS. Within an ICS, a zone groups logical or physical assets that share common security requirements and defines the security boundaries for information entering and leaving a zone. Conduits are introduced between different zones to control communication between zones and to implement security controls. Conduits act as control mechanisms (gatekeepers) between the different zone boundaries.The Purdue EnterpriseReference Architecture, originally developed in the 1990s for computer integrated manufacturing, provides guidance to system integrators and owners on how to segmenta large-scale system into multiple levels. This enables better control over integration of various components and subsystems. ISA-99 adopted this model for segmenting ICS into multiple levels and implementing security controls. ISA-99 later became an IECstandard, ISA/IEC 62443.The zone and conduit model is introduced in International Society of Automation (ISA)/International Electrotechnical Commission (IEC) 62443-1-1 and IEC 62443-3-2 and provides detailed guidance on how to define zones and conduits. Additionally, the Purdue Enterprise Reference Architecture (PERA) framework can be used to segment the various zones and conduits within an ICS into multiple levels.ConduitZone A Zone BFigure 2: Concept of zones and conduits.Industrial Disruption—OT, IIoT, IT, IoT, and ConvergenceThe evolution of Industry 4.0 and disruptive technologies, like the Internet of Things (IoT) and Industrial IoT (IIoT), transformed ICS/OT networks into more converged networks. ICS/OT are no longer operating in an isolated environment. Instead, they are connected to enterprise IT networks and the external internet and are being used to collect business intelligence and derive business decisions.In a converged ICS/OT and IT infrastructure, communication is no longer based on proprietary network communication protocols or even simply ICS/OT-specific communication protocols. Instead, the converged ICS/OT and IT network relies on a combination of complex proprietary and open standard communication protocols that are inherently vulnerable to various attacks. Thisexpands the network’s attack surface and makes traditional security controls, suchas VLANs, insufficient for ICS, especially as OT and IT networks converge. Although defining zones and conduits and segmenting networks into levels are essential for ICS/OT and IT convergence, it doesn’t entirely address network security challenges within a converged infrastructure. VLANs are not sufficient to prevent sophisticated network attacks.VLANs freely forward network packets to devices that are part of the same broadcast domain. Every packet that needs to travel beyond the broadcast domain boundary requires a network routing mechanism. Typically, the routing mechanism acts as a virtual or physical conduit and is sometimes used to implement security controls, such as network traffic inspection, to control communication between the two broadcast domains. While VLAN routing mechanisms offer some security benefits, they are insufficient in modern ICS/OT and IT converged infrastructure. VLANs also fail to inspect the network communication within the same broadcast domain. Within a broadcast domain, the devices that are part of a VLAN can unrestrictedly communicate with one another without these communications being inspected or controlled.The zero-trust securitymodel states that all attempted connections to an organization’s system should be verified before granting access, whether they come from inside or outside the organization’s network. The same zero-trust securityconcept is followed inICS/OT infrastructureto whitelist the network communication between different ICS components.In a typical ICS/OT network deployment, there are dozens of components grouped together in a single VLAN, and these components can freely communicate with one another without going through a routing conduit. This enables any anomalous network communication to move laterally within the PCN.Once these networks are converged with other networks, usually outside the ICS/OT boundaries, it becomes critical to inspect each and every communication channel. Otherwise, attacks on the network could remain undetected due to complex network integrations. Moreover, the use of open communication protocols for exchanging information between the ICS/OT and IT networks introduces additional risk, where weakness in the communication protocol design and the availability of exploits can provide a vector to attack ICS/OT environments.Microsegmenting ICS/OT NetworksVLAN provides logical segmentation flexibility; however, microsegmentation provides more granular control over network traffic by further partitioning the VLAN and implementing security policies for each partition. Further, these security policies can be tailored to different types of network traffic to limit network and application flows between various components of an ICS. With microsegmentation, ICS owners can implement a zero-trust security model, ensuring that a particular PLC cannot communicate with another PLC unless explicitly permitted by the security policy, even when both PLCs are part of the same VLAN.Firewall FortiGateVLAN 1VLAN 1FortiSwitchFortiSwitchVLAN 1VLAN 1PLC PLCPLC PLCFigure 3: Normal VLAN routing vs. microsegmentation using Fortinet FortiSwitch and FortiGate.Typically, in a microsegmented network, NGFWs are used in conjunction with VLANsto implement security policies and to inspect and filter network communications.Fortinet FortiSwitch and FortiGate NGFW offer an integrated approach tomicrosegmentation. This integrated solution expands VLAN capabilities from Layer2 network communication to Layer3 (routing) and Layer 7 (visibility), enablingnetwork traffic inspection. The FortiSwitch acts at Layer 2, defining VLANs, andthe FortiGate NGFW acts at Layer 3, routing all communications between VLANsand within the same VLAN. This enables network traffic inspection using granularsecurity policies, and the NGFWs enable Layer 7 inspection for the networkprotocols and information passing through the firewall.The Fortinet integrated solution for microsegmenting the ICS/OT networks providesnumerous benefits to ICS owners.n n Host/device isolation. Isolating each device within the ICS network providesgranular control over the network communication. The network traffic enteringand exiting a device is forced to flow through the FortiGate NGFW, enablingsecurity policy enforcement, traffic inspection, application control, and intrusiondetection and prevention.n n ICS protocol deep packet inspection (DPI). The FortiGate NGFW provides support for DPI for over 32 ICS/OT protocols with 1,500+ out-of-the-boxapplication control signatures.The FortiGate NGFW runs on Fortinet’s proprietary operating system, FortiOS, which provides industry-leading network security features, such as DPI for ICS/OT protocols, support for ICS/OT specific network protocols, such as the Parallel Redundancy Protocol (PRP), advanced malware protection, an intrusion prevention system (IPS), and software-defined wide-area networking (SD-WAN) capabilities.n n Lateral movement prevention. Isolation of each component of ICS makes it difficult for malware to spread laterally within the ICS network. All traffic within the ICS network is subject to inspection and policing.n n High performance. FortiGate NGFWs are high-performance firewalls with low latency, which makes them an ideal choice for network traffic inspection within a microsegmented ICS network.n n Seamless integration. Logical and physical network connections remain unchanged.n n Single-pane-of-glass management. The entire solution is managed through an integrated management console, assisting ICS owners with security automation.The Fortinet integrated solution for microsegmentation also uses PERA guidance for solution deployment. Themicrosegmentation can be implemented at any level within the ICS/OT network as long as there is network connectivity between the various components of the ICS.Level 2SupervisoryControl Network Engineering workstation VLAN 100VLAN 100PLC #1PLC #2PLC #3Operator PCLevel 1Process ControlLocal-area Network Level 0Physical Plant FloorInstrumentationBus NetworkFortinet traffic flow with NGFW inspectionNormal VLAN traffic blocked Figure 4: Sample Fortinet FortiSwitch and FortiGate microsegmentation PERA deployment architecture.ConclusionICS/OT networks are largely composed of long life-cycle devices with unique operating requirements. They require an OT-specific approach to security.Fortinet has demonstrated that it has a unique perspective on ICS/OT network security, which enables Fortinet to combine insights with OT-specific threats tracked by FortiGuard Labs into OT-specific security threat reports and to develop solutions that uniquely meet the needs of OT environments.VLAN-based microsegmentation enables ICS to control business risk while benefiting from a logically segmented network. The Fortinet Security Fabric is essential to tying these solutions together and providing the security team with full, centralized visibility and control over all of their security infrastructure. Copyright © 2021 Fortinet, Inc. All rights reserved. Fortinet, FortiGate, FortiCare and FortiGuard, and certain other marks are registered trademarks of Fortinet, Inc., and other Fortinet names herein may also be registered and/or common law trademarks of Fortinet. All other product or company names may be trademarks of their respective owners. Performance and other metrics contained herein were attained in internal lab tests under ideal conditions, and actual performance and other results may vary. Network variables, different network environments and other conditions may affect performance results. Nothing herein represents any binding commitment by Fortinet, and Fortinet disclaims all warranties, whether express or implied, except to the extent Fortinet enters a binding written contract, signed by Fortinet’s General Counsel, with a purchaser that expressly warrants that the identified product will perform according to certain expressly-identified performance metrics and, in such event, only the specific performance metrics expressly identified in such binding written contract shall be binding on Fortinet. For absolute clarity, any such warranty will be limited to performance in the same ideal conditions as in Fortinet’s internal lab tests. Fortinet disclaims in full any covenants, representations, and guarantees pursuant hereto, whether express or implied. Fortinet reserves the right to change, modify, transfer, or otherwise revise this publication without notice, and the most current version of the publication shall be applicable.August 27, 2021 6:09 AM562135-A-0-EN。

A Leading Provider of Smart, Connected and Secure Embedded Control SolutionsdsPIC33C Digital Signal ControllerDesign GuidelinesdsPIC33C Digital Signal ControllersGeneric Robust GuidelineRobustness features on dsPIC33C DSCs•Internal regulator is Capacitor-less design•No need of an external capacitor, no noise injection from the board•Saves space on the board for routing•Lower component count, lower cost•One extra I/O pin•Virtual Pins for Redundancy and Monitoring : Dual core device feature to cross check/monitor •Flash ECC (Error Correcting Code):Flash Error check with 1-bit detection/correction & 2-bit detection •DMT (Deadman Timer) : Instruction cycle counting and could be used as a SW checkpoint•WDT (Watchdog Timer) : For system recovery•CodeGuard™Security : For code protection schemes•CRC (Cyclic Redundancy Check) : For code validation•Two-Speed Start-up : For slow start up from power on, reduce inrush current•Fail-Safe Clock Monitoring : Clock monitor and switch•Backup FRC (BFRC) : Backup for the FRC clock•AEC-Q100 REVG (Grade 0: -40°C to +150°C) Compliant : Automotive QualDecoupling Capacitor•For wide frequency noise filtering, provide multiple decoupling capacitors (e.g.0.01uF,0.1uF) across supply pins of dsPIC33C DSC •When multiple capacitors are provided, place them in ascending order of their value with lowest value capacitor closest to the dsPIC33C pin •Provide decoupling capacitors between each VDD/GND pair of the dsPIC33C DSC •Place decoupling capacitors close to VDD and GND pin pairs of the dsPIC33C DSC•Connect dsPIC33C DSC pin and capacitor pads using shorter directtraces without any vias between them•Also connect decoupling capacitor between AVDD and AGNDusing shorter tracesDecoupling Caps :AVDD -AGND Decoupling Caps : DVDD -DGNDOscillator and MCLR•Place crystal oscillator close to OSCI/OSCO pins ofthe dsPIC33C DSC and connect it using short directtraces avoiding vias•Provide isolated ground plane under the crystal,connect this ground Isle to Board Ground•Avoid any high-speed signals running near theoscillator circuit•Add series resistor between reset pushbutton andMCLR pin of the dsPIC33C DSCsCurrent feedbacksFrom shunt to amplifier inputs•Use Kelvin sensing –take separate tracesfrom pads of the shunt resistor forconnecting to amplifier input resistors•Take the current feedbacks traces fromshunt resistor as differential pair runningparallel across the board until it isconnected to amplifier input resistors(which are placed closer to amplifierpositive and negative input pins)Ground Connection Analog and Digital Ground•Separate the ground of digital circuits, analog circuits ,high speed circuit, high current circuit etc.•The separated ground must be connected only at supply start point which is closer to the 3.3V LDO (dsPIC33C DSC Supply)•In case of multilayer board, dedicate at least one internal layer for grounds. Try to provide solid ground plane avoiding any cuts •To do this , it is necessary to identify the components that connect to specific ground and place them close to each other in specific area of the boardExample :Solid internal AnalogGround(AGND) planejoining at LDO ground.Digital Ground (DGND) trace Analog Ground (AGND) traceAGND and DGND are joined at one point near the source using net tie.Low Noise GuidelineWeak Spot ADCAnalog-To-Digital Converter Circuit•Increasing CPU speed with shrinking structure sizes result in an increased sensitivity to noise•CPU load transient frequencies stimulate passive/reactive circuits formed by parasitic RLC resonators (PCB)•Digital high-speed peripherals add to noise level•In control applications, the ADC is the most sensitive element and provides the guiding value for noise budget estimations •Power Electronics Control Applications are most sensitive to ADC accuracy•Limited Resolution limits dynamic range of control loop •Noise on feedback signal reproduces on ADC results •Noise on supply lines influences internal references •Faster ADCs generate more noise within the internal, analog circuit DIGITIZEDBLOCK ADC Power Stage(Plant)Error Amplifier +–PWM (Modulator)VoltageDividerREF V ERROR REF OUT V V K V =−⋅EA V D K OUTV INVNoise BudgetHow much noise is acceptable?•Determine maximum acceptable voltage deviation •The most system element influencing the most sensitive parameter of the product determines the acceptance level •In power conversion, this is output voltage / output current accuracy and response characteristic •Both highly depend on reliable ADC results Power ConverterCircuitV IN V OUTADC REF V FBerror+-H C z(Compensator)outputinput Anti-WindupPWMNoise Budget –Potential Noise SourcesHow much noise is acceptable?•Noise can influence the ADC through 3 major ports•(A) Feedback Noise via Input Pin •(B) Ground Noise / Bouncing•(C) Reference Voltage derived from Supply Voltage•Noise can inject•Alias frequencies•Random, erroneous samples•Decrease effective ADC resolution•Maximum acceptable noise levels are application dependent and need to be derived individuallyV FBV F B (t ) ± VTimeFeedbackV o u t [n ]n →InputCLOCKAVSSAVDDV REFABCThree Major Noise PortsADCAlias Frequencies•Random noise on feedback signals are relatively uncritical•Periodic noise components exceeding the minimum ADC granularity may influence ADC results •If these are at around or higher than f SAM /2, alias-frequencies may be injected•High-speed ADCs with very small Sample & Hold (S&H)•Capacitance and short sampling times are getting increasingly sensitive to periodic noise on feedback signals •Once alias frequencies have been injected in the data stream, they may influence the control system.•Recommended to add anti-alias filters to input pins, tuned for the effective sampling frequency of the application while still allowing relevant transients to pass.-1.5-1-0.500.511.504590135180225270315360Waveform Sampled at f NFeedback Sampled InputM a g n i t u d ef SAM 2f SAM70k H z40k H z30k H z 25k H z 10k H z160k H z510k H zI n p u t F r e q u e n c yI n p u t F r e q u e n c yI n p u t F r e q u e n c yAnti-Alias Filter DesignAdjustment of anti-alias cut-off frequencies need to consider the internal ADC architecture to prevent excessive ADC result deviations•Shared ADC CoresADC cores with multiple analog input pins (ANx) connect the single S&H capacitor to the pin via multiplexers. To prevent cross-talkbetween input channels, the S&H capacitor needs to be discharged before connection. When connected, the S&H capacitor needsenough time to charge up to the feedback voltage level to achievean accurate result.•Dedicated ADC CoresDedicated cores continuously keep their S&H connected to the pin, tracking the feedback voltage. The connection is only opened during conversion and closed when conversion has completedADCV FB*V FBCAnti-Alias Filter Design / Shared ADC Core•Step 1: Decoupling Capacity•During sampling using the shared ADC core, the discharged S&H capacitor C HOLD is connected to the feedback circuit. C HOLD is charged through R SS and R IC (~350 W ). The high charging current right after SW SS is closed injects a fast transient into the feedback line. Depending on the distance between the voltage divider and the device input pin, the parasitic trace inductance might prevent to bias this inrush current. Hence, this current is exclusively biased by decoupling capacitor C , eventually forming a capacitive voltage divider with C HOLD . As a result, the final sampling voltage will always settle below the real feedback voltage V FB introducing a measurement error ofError = 1−C HOLD C(first assessment of the static offset)•Software adjustable sampling times allow accounting for and thus minimizing these effects which, however , increases the data acquisitionlatency. For high-speed designs it is therefore recommended to minimize the static error by placing enough capacitance as close as possible at the ADC input pin (recommended value = 30…50 x C HOLD ).V FB *V FBCRV OUTC PINC HOLDV DDR ICR SSSampling Switch I LEAKAGESL TRACEParasitic Trace InductanceC DR BSW SSAnti-Alias Filter Design / Shared ADC Core•Step 2: Filter Resistor•Peak-to-Peak voltage levels of periodic noise should be limited to the voltage equivalent of approx. 3 LSB. At V REF = 3.3V and 12-bit resolution the ADC has a total granularity of 806 µV/tick. 3 LSB therefore have a voltage equivalent of 6.44 mV . The total acceptable level,however , depends on the total feedback signal range and needs to be calculated for every application individually.Example:•A signal is sampled at f SAM = 500 kHz (Nyquist-Shannon limit at f N = 250 kHz). A dominant, periodic noise component f Noise = 1000 kHz with a max. deviation of V Noise pk-pk = 60mV is observed. To prevent alias frequencies being injected into the ADC data stream, this noise needs to be damped to less than 6.44 V @ f N .(-20dB @ f N = 6 mV). The pole introduced by the RC filter therefore needs to be placed one magnitude below f N (=25 kHz) to effectively damp the noise magnitude at f N by factor 10.V FB *V FBCRV OUTC PINC HOLDV DDDistance XR ICR SSSampling SwitchI LEAKAGESL TRACEParasitic Trace InductanceC DR AR BSW SSAnti-Alias Filter Design / Shared ADC Core•Step 3: Recharging Decoupling Capacitor C•After the sampling transient has passed, decoupling capacitor C needs to be recharged up to the feedback level for the next sample. With high resistive voltage divider networks, it is recommended to place an additionaldecoupling capacitor in parallel to the lower voltage divider resistor. This capacitor also helps to compensate the parasitic trace inductance L TRACE . At high sampling frequencies hand high resistive voltage dividers an operational amplifier might be required to recharge C in time for the next sample.V FB *V FBCRV OUTC PINC HOLDV DDDistance XR ICR SSSampling Switch I LEAKAGESL TRACEParasitic Trace Inductance C DR AR BSW SSAnti-Alias Filter Design / Shared ADC Core•Design Tip:•Power electronics designs are commonly noisy as the circuit itself produces noise over a very wide frequency range up to manyGHz. Dominant noise bands in the range of 8-15 MHz caused by Diode ringing as well as harmonics of the switching frequency are sometimes difficult to contain and might be induced in feedback lines. The magnitude of the induced noise is independent from the voltage level present.•Hence, it is recommended to place the voltage divider close to the device, minimizing Distance X as well as the parasitic trace inductance L TRACE . Especially, however, preventing noise from being induced in low voltage signals. Noise induced on high voltage signals will get divided with the feedback signal and will therefore have lower amplitudes requiring less damping and thus expanding the maximum bandwidth of the feedback signal.V FB *V FBCRV OUTC PINC HOLDV DDR ICR SSSampling Switch I LEAKAGESL TRACEParasitic Trace Inductance C DR AR BSW SSNoise Budget –Potential Noise SourcesHow much noise is acceptable?•In addition to adjust noise filtering on feedback signals, it is required to analyze the noise floor on supply and ground lines•The ADC uses a reference voltage, which is derived from the supply voltage•Noise on this supply rail can influence the reference level during a conversion process, equally perturbing ADC results as sampling noisy signals.•Supply rain noise can enter the system through VDD as well as through VSSV FBB (t ) ± VFeedbackV o u t [n ]n →InputCLOCKAVSSAVDDV REFABCADCSymmetrical Layout•The CPU itself is a potential noise hub in the system. Each instruction executed by the CPU will create a load step with low amplitude but high edge speed. These high frequency current pulses are exclusively biased by the decoupling capacitors. The generated AC noise inevitably migrates into supply and ground traces, forward into the device as well as backwards to the voltage regulator (VRM).•Insufficient decoupling can stimulate passive/reactive elements along the way, which, if stimulated in the right frequency, may start to resonate, increasing the noise level.FBVDD/VSSANALOG INPUTSCDLOADVoltage Regulator Module (VRM)Passive/Reactive NetworkActive NetworkVREFC DAB dsPIC33C DSCCCCDigital GroundAnalog GroundOESRC ESLL O A DI LI ESLV DDV SSSymmetrical LayoutFour resonant peaks were found withinthe relevant frequency bandVDD Impedance profile measured at every decoupling capacitor(unpowered and powered)dsPIC33 Target ImpedanceHighly reactive resonance valleysI m p e d a n c e M a g n i t u d eSymmetrical Layout dsPIC33TargetImpedancewindow of interest Stimulus windowTotal VDD Impedance profile measured at PDN Port BCPU Clock Frequencies f CY2f CY f OSCKey Takeaways•Key Takeaways•Sharp valleys in an impedance profile indicate the presence of resonance/anti-resonance frequencies of passive/reactive network elements•The CPU load profile is determined by instruction execution and peripheral activity, which are both software dependent to a high degree•The faster the CPU, the wider the frequency range across potential stimuli can be injected into the passive/reactive network segment•If one or more resonators are stimulated simultaneously, the noise level may inflationary increase (Rouge Wave)•Remedy: Flat Impedance Design•Output impedance of voltage regulator must match target impedance•Decoupling capacitors must be selected to match/cancel excess inductance (traces)•Symmetrical design (equal trace length and width of VDD lines reduce number of resonant peaks)•Using ground planes instead of traces reduce VSS trace impedance, shifting potential resonant peaks into high frequency range beyond the Window Of InterestPlease note:Although passive/reactive network components may still be stimulated by higherfrequencies within the Stimulus Window, the CPU won’t be able to pick them up.Noise Budget –Target ImpedanceFlat Impedance Design•Determining Target Impedance Z TARGET•Determine max. acceptable voltage deviation for the application•ADC being the most sensitive element (ADC sample tolerance, e.g.10mV)•Determine minimum and maximum load current, depending on CPU speed and peripheral usage (e.g.I min= 40mA, I max= 80mA)Example:minmaxarg IIToleranceVZ DDetT−⨯=Z T arg et=3.3V×0.010V0.080A−0.040A=0.825WExcess Impedance Cancellation •Positive supply traces (V DD ) between PDN port (B) anddecoupling ports (C) should be as symmetrical as possible toprevent potential resonant frequencies spreading intomultiple peaks concentrated in a narrow frequency range.•Decoupling capacitance need to be selected to cancel the excess inductance of the supply traces. Too much or less capacitance will inevitably result in resonant tank becomingreactive to stimuli. A symmetrical design will allow to use thesame capacitance at every decoupling point (C)•Analog supply voltage is best taken from the nearest decoupling point (C) being filtered through a ferrite bead (E)FB VDD/VSS ANALOG INPUTSCD C C C D O EExcess Impedance Cancellation •Using ground planes instead of traces lowers the excess inductance, effectively moving potential resonant frequencies to higher ranges and eventually out of the Window Of Interest •Digital and analog ground should always be separated preventing noise produced by the CPU entering sensitive analog circuits •Prevent ground planes from overlapping and accidentally coupling noise between planes •Ground decoupling can be done by•Plane gaps, introducing a slightly increased resistance and inductance between both planes limiting noise from migrating•Putting 0 W resistors in between planes introducing the package inductance as a filter barrier•Replacing 0 W resistors by ferrite beads for a more specific filter characteristicFB VDD/VSS ANALOG INPUTS C D CC C Digital GroundAnalog Ground E 0R 0RAnalog Rail DecouplingVDD-2-AVDD Filtering •Digital noise generated by the CPU on V DD gets contained within the network segment by putting up a barrier between V DD and AV DD :•Ferrite Beads allow selective filtering of frequency bands while ensuring proper balancing of decoupling capacitors on V DD and AV DD (recommended)•Low Resistance Resistors also introduce some small package inductance as well provide resistance adding to lowering the Q resp. increase damping (e.g.4.7 W ) •Gapping of layout traces will have similar effects like the options above, but their effectiveness is questionable (not recommended in general) FB VDD/VSSANALOG INPUTS CD CC C Digital GroundAnalog Ground EV SS AV SSFBV DD AV DD 0RAdditional Design GuidanceDesign Example & DocumentsdsPIC33C DSC Design Reference:dsPIC33CH512MP506 Digital Power Plug-In Module (DP-PIM),Part-No. MA330049Anti-Alias Filter Design Guidance:dsPIC33CH512MP506 DP-PIM User Guide /Appendix C. Characterization Data。

J g-J i-多重心法选址案例研究：XIANDAIYINGXIAO牛东来武佳(首都经济贸易大学管理工程学院北京100070)摘要：配送中心是现代物流系统重要组成部分，在规划设计配送中心时，合理的配送中心选址可以大大降低其运营成本。

本文对解决多设施选址问题中的多重心法进行了实例计算，在手工Excel迭代计算过程中，发现每次的计算结果都只是局部最优 解。

经过分析，是由于初始分组情况不同导致最终的计算结果不同，为解决此问题，采用计算机程序遍历分组情况，计算每种情 况的选址结果与运费，最后通过比较，得到总运费最小的全局最优解。

关键词：多重心法；选址；迭代；计算机程序中图分类号：F文献识别码：A DOI：10.19932/ki.22-1256/F.2021.01.152A Case Study of Multiple Gravity Method Site SelectionNIU Donglai WU Jia(Capital University of Economics and Business,School of Management and Engineering.Beijing , 100070) Abstract：Distribution centers are an important part of m odern logistics systems.When planning and designing distribution centers, reasonable distribution center location can greatly reduce their operating costs.In this paper,the multiple gravity methods to solve the problem of multi—facility site selection is calculated by an example.In the process of manual Excel iterative calculation,it is found that each calculation result is only a local optimal solution.A fter analysis,it is because of d ifferent initial grouping conditions that the final calculation results are different.In order to solve this problem,a computer program was used to traverse the grouping cases,calculate the location result and freight cost of each case,and finally get the global optimal solution with the minimum total freight cost through comparison.Key words rmultiple gravity methods,Site selection,iterative method,computer programs1.引言设施选址的方法有很多，重心法是其中之一。

未来汽车的利与弊英语作文The Pros and Cons of Future Cars。

In the ever-evolving landscape of technology, the automotive industry stands as a testament to human ingenuity and innovation. With the rapid advancement of technology, the future of automobiles holds both promises and challenges. In this essay, we will delve into the advantages and disadvantages of future cars.Advantages:1. Environmental Benefits: One of the most significant advantages of future cars lies in their potential to reduce environmental impact. Electric and hybrid vehicles are becoming increasingly popular, offering lower emissions and decreased reliance on fossil fuels. This shift towards cleaner energy sources can help mitigate air pollution and combat climate change.2. Fuel Efficiency: Future cars are expected to be more fuel-efficient than their predecessors. With advancements in engine technology and lightweight materials, these vehicles can travel longer distances on less fuel, ultimately saving consumers money and reducing carbon emissions.3. Autonomous Driving: The emergence of autonomous driving technology promises to revolutionize the way we commute. Self-driving cars have the potential to improve road safety by eliminating human error, reduce traffic congestion, and provide greater mobility for individuals with disabilities or limited access to transportation.4. Innovative Features: Future cars are equipped with a myriad of innovative features designed to enhance the driving experience. From augmented reality dashboards to advanced driver-assistance systems, these technologies aim to improve safety, convenience, and entertainment for passengers.5. Integration with Smart Infrastructure: As citiesbecome more interconnected, future cars will seamlessly integrate with smart infrastructure systems. Thisintegration can lead to smoother traffic flow, optimized routing, and enhanced communication between vehicles and traffic signals, ultimately improving overall efficiencyand safety on the roads.Disadvantages:1. Cost: Despite their many benefits, future cars can come with a hefty price tag. Electric and autonomousvehicles tend to be more expensive than traditionalgasoline-powered cars, making them inaccessible to some consumers. Additionally, the high cost of maintenance and repair for advanced technologies may deter potential buyers.2. Infrastructure Challenges: The widespread adoptionof electric and autonomous vehicles hinges on theavailability of adequate infrastructure. Charging stations for electric cars are still relatively sparse in many regions, and the development of autonomous vehicle infrastructure, such as dedicated lanes and trafficmanagement systems, poses logistical and financial challenges.3. Privacy Concerns: The integration of advanced technology in future cars raises concerns about privacy and data security. Autonomous vehicles collect vast amounts of data about passengers' whereabouts, driving habits, and personal preferences, raising questions about who has access to this information and how it is used.4. Job Displacement: The rise of autonomous vehicles could potentially lead to job displacement in industries reliant on manual labor, such as transportation and logistics. Truck drivers, taxi drivers, and delivery workers may find themselves out of work as self-driving vehicles become more prevalent, posing economic challenges for affected individuals and communities.5. Reliability and Safety: While autonomous driving technology holds the promise of safer roads, it is not without its challenges. Concerns about the reliability and safety of self-driving cars persist, particularly inunpredictable driving conditions or emergency situations where human intervention may be required. Ensuring the robustness of these systems through rigorous testing and regulation is paramount to their widespread adoption.In conclusion, future cars offer a plethora of advantages, from environmental benefits to innovative features that enhance the driving experience. However, they also present challenges such as cost, infrastructure limitations, and concerns about privacy and safety. Addressing these challenges will be crucial in harnessing the full potential of future cars and creating a transportation system that is sustainable, efficient, and equitable for all.。