2014届高三数学一轮复习专讲专练(基础知识+小题全取+考点通关)：1.3全称量词与存在量词、逻辑联结词

课时跟踪检测(八) 函数的图像1．y ＝x ＋cos x 的大致图像是( )2.(2012·威海质检)函数y ＝f (x )(x ∈R)的图像如图所示，下列说法正确的是( )①函数y ＝f (x )满足f (－x )＝－f (x )； ②函数y ＝f (x )满足f (x ＋2)＝f (－x )； ③函数y ＝f (x )满足f (－x )＝f (x )； ④函数y ＝f (x )满足f (x ＋2)＝f (x )．A ．①③B ．②④C ．①②D ．③④3．函数y ＝log 22－x 2＋x 的图像( )A ．关于原点对称B ．关于直线y ＝－x 对称C ．关于y 轴对称D ．关于直线y ＝x 对称4．(2012·山东高考)函数y ＝cos 6x2x －2－x的图像大致为( )5．(2012·新课标全国卷)已知函数f (x )＝1ln (x ＋1)－x，则y ＝f (x )的图像大致为( )6．给出四个函数，分别满足①f (x ＋y )＝f (x )＋f (y )， ②g (x ＋y )＝g (x )·g (y )，③h (x ·y )＝h (x )＋h (y )，④m (x ·y )＝m (x )·m (y )．又给出四个函数的图像，那么正确的匹配方案可以是( )A ．①甲，②乙，③丙，④丁B ．①乙，②丙，③甲，④丁C ．①丙，②甲，③乙，④丁D ．①丁，②甲，③乙，④丙7．(2011·北京高考)已知函数f (x )＝⎩⎪⎨⎪⎧2x ，x ≥2，(x －1)3，x ＜2.若关于x 的方程f (x )＝k 有两个不同的实根，则实数k 的取值范围是________．8．函数f (x )＝x ＋1x图像的对称中心为________．9．(2012·潍坊模拟)为了得到函数f (x )＝log 2x 的图像，只需将函数g (x )＝log 2x8的图像________．10．已知函数f (x )＝⎩⎪⎨⎪⎧3－x 2，x ∈[－1，2]，x －3，x ∈(2，5].(1)在如图所示给定的直角坐标系内画出f (x )的图像； (2)写出f (x )的单调递增区间；(3)由图像指出当x 取什么值时f (x )有最值．11．当x∈(1,2)时，不等式(x－1)2<log a x恒成立，求a的取值范围．12．若直线y＝2a与函数y＝|a x－1|(a＞0且a≠1)的图像有两个公共点，求a的取值范围．1．若函数f (x )的图像经过变换T 后所得图像对应函数的值域与函数f (x )的值域相同，则称变换T 是函数f (x )的同值变换．下面给出四个函数及其对应的变换T ，其中变换T 不属于函数f (x )的同值变换的是( )A ．f (x )＝(x －1)2，变换T 将函数f (x )的图像关于y 轴对称B ．f (x )＝2x －1－1，变换T 将函数f (x )的图像关于x 轴对称C ．f (x )＝2x ＋3，变换T 将函数f (x )的图像关于点(－1,1)对称D ．f (x )＝sin ⎝⎛⎭⎫x ＋π3，变换T 将函数f (x )的图像关于点(－1,0)对称 2．(2011·天津高考)对实数a 和b ，定义运算“⊗”：a ⊗b ＝⎩⎪⎨⎪⎧a ，a －b ≤1，b ，a －b >1.设函数f (x )＝(x 2－2)⊗(x －x 2)，x ∈R.若函数y ＝f (x )－c 的图像与x 轴恰有两个公共点，则实数c 的取值范围是( )A.(]－∞，－2∪⎝⎛⎭⎫－1，32 B.(]－∞，－2∪⎝⎛⎭⎫－1，－34 C.⎝⎛⎭⎫－1，14∪⎝⎛⎭⎫14，＋∞ D.⎝⎛⎭⎫－1，－34∪⎣⎡⎭⎫14，＋∞ 3．已知函数y ＝f (x )的定义域为R ，并对一切实数x ，都满足f (2＋x )＝f (2－x )． (1)证明：函数y ＝f (x )的图像关于直线x ＝2对称；(2)若f (x )是偶函数，且x ∈[0,2]时，f (x )＝2x －1，求x ∈[－4,0]时的f (x )的表达式．答 案 课时跟踪检测(八)A 级1．选B 当x ＝0时，y ＝1，排除A ；当x ＝π2时，y ＝π2，排除D ；当x ＝－π2时，y ＝－π2，排除C ，可知B 正确．2．选C 由图像可知，函数f (x )为奇函数且关于直线x ＝1对称；对于②，因为f (1＋x )＝f (1－x )，所以f [1＋(x ＋1)]＝f [1－(x ＋1)]，即f (x ＋2)＝f (－x )．故①②正确．3．选A ∵函数y ＝log 22－x2＋x∴2－x2＋x>0即－2<x <2. 又f (－x )＝－f (x )，∴f (x )是奇函数，故图像关于原点对称．4．选D 函数y ＝cos 6x2x －2－x是奇函数，图像关于坐标原点对称，排除选项A 中的图像；当x >0时，2x－2－x＝22x －12x >0，故函数值的符号取决于cos 6x 的符号，x ∈⎝⎛⎦⎤0，π12时cos 6x >0，排除选项B 中的图像；在后续区间上函数值取正负的区间长度都是π6，排除选项C 中的图像，只能是选项D 中的图像．5．选B 函数的定义域是(－1,0)∪(0，＋∞)，值域是(－∞，0)，所以其图像为B. 6．选D 图像甲是一个指数函数的图像，它应满足②；图像乙是一个对数函数的图像，它应满足③；图像丁是y ＝2x 的图像，满足①.结合选项可知D 正确．7．解析：作出函数f (x )的图像，如图，由图像可知，当0＜k ＜1时，函数f (x )与y ＝k 的图像有两个不同的交点，所以所求实数k 的取值范围是(0,1)．答案：(0,1)8．解析：f (x )＝x ＋1x ＝1＋1x ，把函数y ＝1x 的图像向上平移1个单位，即得函数f (x )的图像．由y ＝1x的对称中心为(0,0)，可得平移后的f (x )图像的对称中心为(0,1)．答案：(0,1)9．解析：g (x )＝log 2x8＝log 2x －3＝f (x )－3，因此只需将函数g (x )的图像向上平移3个单位即可得到函数f (x )＝log 2x 的图像．答案：向上平移3个单位10．解：(1)函数f (x )的图像如图所示．(2)由图像可知，函数f (x )的单调递增区间为[－1,0]，[2,5]． (3)由图像知当x ＝2时，f (x )min ＝f (2)＝－1， 当x ＝0时，f (x )max ＝f (0)＝3.11．解：设f 1(x )＝(x －1)2，f 2(x )＝log a x ，要使当x ∈(1,2)时，不等式(x －1)2<log a x 恒成立， 只需f 1(x )＝(x －1)2在(1,2)上的图像在f 2(x )＝log a x 的下方即可．当0<a <1时，综合函数图像知显然不成立．当a >1时，如图，要使在(1,2)上，f 1(x )＝(x －1)2的图像在f 2(x )＝log a x 的下方， 只需f 1(2)≤f 2(2)，即(2－1)2≤log a 2，log a 2≥1， ∴1＜a ≤2.∴a 的取值范围是(1,2]．12．解：当0＜a ＜1时，y ＝|a x －1|的图像如图1所示，由已知得0＜2a ＜1，即0＜a ＜12.当a ＞1时，y ＝|a x －1|的图像如图2所示， 由已知可得0＜2a ＜1， 即0＜a ＜12，但a ＞1，故a ∈∅.综上可知，a 的取值范围为⎝⎛⎭⎫0，12. B 级1．选B 对于A ，与f (x )＝(x －1)2的图像关于y 轴对称的图像对应的函数解析式为g (x )＝(－x －1)2＝(x ＋1)2，易知两者的值域都为[0，＋∞)；对于B ，函数f (x )＝2x －1－1的值域为(－1，＋∞)，与函数f (x )的图像关于x 轴对称的图像对应的函数解析式为g (x )＝－2x －1＋1，其值域为(－∞，1)；对于C ，与f (x )＝2x ＋3的图像关于点(－1,1)对称的图像对应的函数解析式为2－g (x )＝2(－2－x )＋3，即g (x )＝2x ＋3，易知值域相同；对于D ，与f (x )＝sin ⎝⎛⎭⎫x ＋π3的图像关于点(－1,0)对称的图像对应的函数解析式为g (x )＝sin ⎝⎛⎭⎫x －π3＋2，其值域为[－1,1]，易知两函数的值域相同．2．选B 由题意可知f (x )＝⎩⎪⎨⎪⎧x 2－2，x 2－2－x ＋x 2≤1x －x 2，x 2－2－x ＋x 2>1＝⎩⎨⎧x 2－2，－1≤x ≤32，x －x 2，x <－1或x >32作出图像，由图像可知y ＝f (x )与y ＝c 有两个交点时，c ≤－2或－1<c <－34，即函数y ＝f (x )－c 的图像与x 轴恰有两个公共点时实数c 的取值范围是(－∞，－2]∪⎝⎛⎭⎫－1，－34.3．解：(1)证明：设P (x 0，y 0)是函数y ＝f (x )图像上任一点，则y 0＝f (x 0)，点P 关于直线x ＝2的对称点为P ′(4－x 0，y 0)．因为f (4－x 0)＝f [2＋(2－x 0)]＝f [2－(2－x 0)]＝f (x 0)＝y 0，所以P ′也在y ＝f (x )的图像上，所以函数y ＝f (x )的图像关于直线x ＝2对称．(2)因为当x ∈[－2,0]时，－x ∈[0,2]， 所以f (－x )＝－2x －1. 又因为f (x )为偶函数，所以f (x )＝f (－x )＝－2x －1，x ∈[－2,0]． 当x ∈[－4，－2]时，4＋x ∈[0,2]， 所以f (4＋x )＝2(4＋x )－1＝2x ＋7. 而f (4＋x )＝f (－x )＝f (x )， 所以f (x )＝2x ＋7，x ∈[－4，－2]．所以f (x )＝⎩⎪⎨⎪⎧2x ＋7，x ∈[－4，－2]，－2x －1，x ∈[－2，0].。

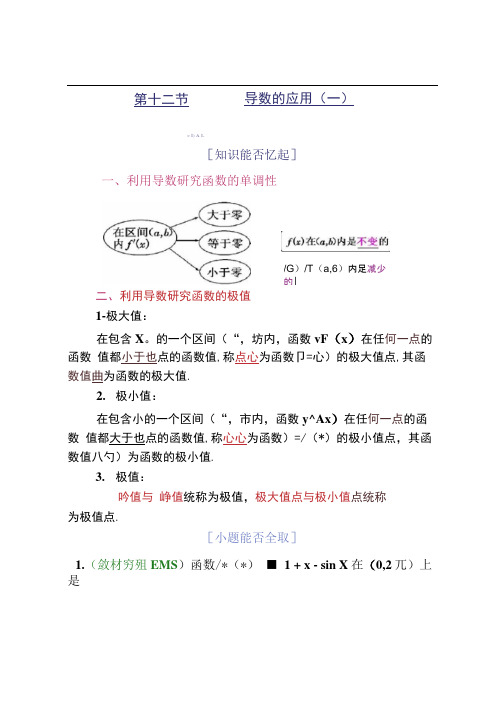
第十二节导数的应用（一）> I) A L［知识能否忆起］一、利用导数研究函数的单调性/G）/T（a,6）内足减少的|二、利用导数研究函数的极值1-极大值：在包含X。

的一个区间（“，坊内，函数vF（x）在任何一点的函数值都小于也点的函数值,称点心为函数卩=心）的极大值点,其函数值曲为函数的极大值.2.极小值：在包含小的一个区间（“，市内，函数y^Ax）在任何一点的函数值都大于也点的函数值,称心心为函数）=/（*）的极小值点，其函数值八勺）为函数的极小值.3.极值：吟值与峥值统称为极值，极大值点与极小值点统称为极值点.［小题能否全取］1.（敛材穷殂EMS）函数/*（*）■ 1 + x - sin X在（0,2兀）上是A.增加的B.减少的C.在（0,兀）上增，在（兀，2兀）上减D.在（0,兀）上减，在（兀，2兀）上增解析：当xW（02r）时，fix）- 1 - cosx>0,・・JU）在（0,2?r）上递增.答案：A2•函数/（x）的定义域为开区间（“，〃），导,函数f 3）在（“，知内的图像如图所示，则函数/U）在开区间S,小内有极小值点（）A・1个 B. 2个C・3个 D. 4个解析：极小值点应有先减后增的特点，即f （x）vO-f （x）=（x）>0.由图像可知只有1个极小值点.答案：A3. （2012-辽宁离考屈数^=屮2—Inx的单调递减区间为A. (-1,1]B. «),1]C・[1, +«>) D・(0, +«>)解析：函数y=^x2—lnx的定义域为(0, +°°), y' =x—?= —[x+‘),令尸WO,则可得0<rWl・答案：B4. （2012•陕西高冷）设函数几r）=xeS则【大值点B.x=l为/（x）的极小值点C.x=-l^jf（x）的极大值点D. x= —1为/（X）的极小值点解析：求导得广令广（工）=疔仗+ 1）=0,解得兀=一1,易知兀=一1是函数/'（X）的极小值点.5.已知d>0,函数/'（x）=0—or在［1, +QO）上是单调增函数, 则"的最大值是解析：—3x2 G [ 1, +oo)±t f(x)>0, wir(i)>o=>«<3.答案:3------------------------------ I名师叮瞩要牢记］------------------ If 仗）>0与/B为增函数的关系：/'仗）>0能推出/U）为增函数，但反之不一定.如国数心）=，在（-8, +8）上单调递增，但r（对工仇所以r（x）x）是/=）为增函数的充分不必要条件.2.可导函数的极值点必须是导数为U的点，但导数为0的点不一定是极值点，&QT （勺）=0是可导国数几上血=心处取得极值的必要不充分条件•例如函数y="在” =u处的导数为<>,但兀=0不是极值点.此外，国数不可导的点也可能是因数的极值点.闿■頻■点关［考点一」运用导数解决函数的单调性问题盂典题导入[例1] （2012•山欢髙考改缭）已知函数伙为常数,e=2・718 2"…是自然对数的底数），曲线y =/<x ）在点（1, /（I ））处的切线与x 轴平行.（1）求去的值；⑵求几r ）的单调区间.r . 、 一一、 In x + Ar［自主解答］（1）由/（X ） 厂由于曲线j ，・/（工）在（I, /（!））处的切线与兀轴平行，所以V (1)-0,因此*・1・(2)由(1)得(x)-^(l -x-xlnx), x € (0, +8),令〃(x) n 1 - JT 一 xln x, x 6 (0, + °°),得厂（X ）・ \-kx -x\nxxe x当x€ (0,1)时，7i(x)>0;当x € (i, + 8)时，//(x)<0. 又e x>(),所以x € (0,1)时，/' (x)>0;x € (1, +8)时，f (x)<0.因此/(x)的单调递增区间为(0,1),单调递减区间为(1， +8).2由题悟法求可导函数单调区间的一般步骤和方法⑴确定函数心)的定义域；(2)求厂仗)，令『(x)=u,求出它在定义域内的一切实数根；⑶把函数心)的间断点(即/(Q的无定义点)的横坐标和上面的各实数根按由小到大的顺序排列起来，然后用这些点把函数/d)的定义区间分成若干个小区间；(4)确定广(x)在各个开区间内的符号，根据广⑴的符号判定函数/仗)在每个相应小开区间内的增减性.3以题试法已知“ER,e为自然对数的底数).(1)当“=2时，求函数/仗)的单调递增区间；(2)是否存在“使函数/匕)为R上的单调递减函数，若存在，求出“的取值范围；若不存在，请说明理由. 解：(1)当a-2 0t, /[x)-(-x2 + 2r)e x,•••f (*)■(- 2x + 2)e” + (-宀2r)e x■(-宀2)e x. 令f (x)>0,即(一工 + 2府>U,Ve x>0,・*. -x2 + 2>0,解得一、，2<x< \2・••函数/(x)的单调递增区间是(-^2, A/2).(2)若函数/(x)在R上单调递减，则f(x)9对xWR都成立，即[—0+(a — 2)x+“即？对x e R都成立.Te^X), .\x2—(a—2)x—«>OX^x E R都成立.:.d=(a-2)2+4a<09即a2+4<0,这是不可能的. 故不存在“使函数/U)在R上单调递减.1考点二运用导数解决函数的极值问题1典题导入［例2］(2012 •江苏离令)若函数y =/(x)在x =丸处取得极大值或极小值，则称心为函数y=/(x)的极值点.己知"，〃是实数，1和一1是函^［,f(x)=x5+ax2+hx的两个极值点.(1)求a和〃的值；(2)设函数g(x)的导函数0(x)=/lr) + 2,求g(x)的极值点.［自主解答］⑴由题设知f(x)=3x2十2^+亿且、［\—1)=3—2«十〃=0,f(1)=3+加+於=0,解W«=0, b=—3・⑵由(1)知/仗)=0—3x ・因为/仗)十2=仗一1)2仗十2),所以g'(")=0的根为x l=x2=l, x,= —2,于是函数^(兀)的极值点只可能是1或一2・当x<-2时，g%r)V0；当一2V*V1 时，g%r)>0, 故一2是^(兀)的极值点.当一2VxV丄或x>l时，g r(x)>0,故丄不是g(x)的极值点.所以g(x)的极值点为一2・。

2014届高三数学一轮复习专讲(基础知识+小题全取+考点通关+课时检测)：1.3全称量词与存在量词、逻辑联结词课时跟踪检测(三)全称量词与存在量词、逻辑联结词1．命题a2＋b2＋2ab＝(a＋b)2的否定是()A．存在a，b∈R，a2＋b2＋2ab≠(a＋b)2B．存在a<0，b>0，a2＋b2＋2ab＝(a＋b)2C．任意a>0，b>0，a2＋b2＋2ab＝(a＋b)2D．任意a，b∈R，a2＋b2＋2ab＝(a＋b)22．(2012·山东高考改编)设命题p：函数y＝sin 2x的最小正周期为π2；命题q：函数y＝cosx的图像关于直线x＝π2对称．则下列判断正确的是()A．p为真 B．q为真C．p且q为假D．p或q为真3．下列命题中，真命题是()A．存在m∈R，使函数f(x)＝x2＋mx(x∈R)是偶函数B．存在m∈R，使函数f(x)＝x2＋mx(x∈R)是奇函数C．对任意m∈R，函数f(x)＝x2＋mx(x∈R)`都是偶函数D．对任意m∈R，函数f(x)＝x2＋mx(x∈R)都是奇函数4．(2012·长沙模拟)设p、q是两个命题，则“命题p或q为真，p且q为假”的充要条件是()A．p、q中至少有一个为真B．p、q中至少有一个为假C．p、q中有且只有一个为真D．p为真，q为假5．(2012·揭阳模拟)已知命题p：存在x∈R，cos x＝54；命题q：任意x∈R，x2－x＋2>0，则下列结论正确的是()题为真命题．其中所有真命题的序号是( ) A ．①②③ B ．②④ C ．②D ．④8．(2012·石家庄模拟)已知命题p ：任意x ∈[1,2]，x 2－a ≥0，命题q ：存在x ∈R ，x 2＋2ax ＋2－a ＝0，若“p 且q ”为真命题，则实数a 的取值范围是( )A ．a ＝1或a ≤－2B ．a ≤－2或1≤a ≤2C ．a ≥1D ．－2≤a ≤19．命题“存在实数x ，使sin x ＝x ”的否定是________．10．已知命题p ：“存在正数x ，使x >1x ”，命题p 的否定为命题q ，则q 是“________”；q 的真假为________(填“真”或“假”)．11．若命题“存在实数x ，使x 2＋ax ＋1<0”的否定是假命题，则实数a 的取值范围为________．12．若存在θ∈R ，使sin θ≥1成立，则cos ⎝⎛⎭⎪⎪⎫θ－π6的值为________．13．已知命题p ：存在a ∈R ，曲线x 2＋y2a ＝1为双曲线；命题q ：x －1x －2≤0的解集是{x |1<x <2}．给出下列结论：①命题“p 且q ”是真命题；②命题“p 且(綈q )”是真命题；③命题“(綈p )或q ”为真命题；④命题“(綈p )或(綈q )”是真命题．其中正确的是________．14．下列结论：①若命题p ：存在x ∈R ，tan x ＝2；命题q ：任意x ∈R ，x 2－x ＋12>0.则命题“p 且(綈q )”是假命题；②已知直线l 1：ax ＋3y －1＝0，l 2：x ＋by ＋1＝0，则l 1⊥l 2的充要条件是ab ＝－3；③“设a 、b ∈R ，若ab ≥2，则a 2＋b 2>4”的否命题为：“设a 、b ∈R ，若ab <2，则a 2＋b 2≤4”．其中正确结论的序号为________．(把你认为正确结论的序号都填上)1．下列说法错误的是( )A ．如果命题“綈p ”与命题“p 或q ”都是真命题，那么命题q 一定是真命题B ．命题“若a ＝0，则ab ＝0”的否命题是：若“a ≠0，则ab ≠0”C ．若命题p ：存在x ∈R ，ln(x 2＋1)<0，则綈p ：任意x ∈R ，ln(x 2＋1)≥0D ．“sin θ＝12”是“θ＝30°”的充分不必要条件2．(2013·“江南十校”联考)命题p ：若a·b>0，则a与b的夹角为锐角；命题q：若函数f(x)在(－∞，0]及(0，＋∞)上都是减函数，则f(x)在(－∞，＋∞)上是减函数．下列说法中正确的是()A．“p或q”是真命题B．“p或q”是假命题C．綈p为假命题D．綈q为假命题3．已知命题p：“任意x∈R，存在m∈R,4x －2x＋1＋m＝0”，若命题綈p是假命题，则实数m的取值范围是________．4．下列四个命题：①存在x∈R，使sin x＋cos x＝2；②对任意x∈R，sin x＋1sin x≥2；③对任意x∈⎝⎛⎭⎪⎪⎫0，π2，tan x＋1tan x≥2；④存在x∈R，使sin x＋cos x＝ 2.其中正确命题的序号为________．5．设命题p：实数x满足x2－4ax＋3a2<0，其中a >0，命题q ：实数x 满足⎩⎨⎧x 2－x －6≤0，x 2＋2x －8>0.(1)若a ＝1，且p 且q 为真，求实数x 的取值范围；(2)綈p 是綈q 的充分不必要条件，求实数a 的取值范围．6．已知命题p：方程2x2＋ax－a2＝0在[－1,1]上有解；命题q：只有一个实数x0满足不等式x20＋2ax0＋2a≤0，若命题“p或q”是假命题，求a的取值范围．答案课时跟踪检测(三)A级1．选A该命题是全称命题，即对任意a，b∈R，a2＋b2＋2ab＝(a＋b)2，其否定为：存在a，b∈R，a2＋b2＋2ab≠(a＋b)2.2．选C命题p，q均为假命题，故p且q 为假命题．3．选A由于当m＝0时，函数f(x)＝x2＋mx＝x2为偶函数，故“存在m∈R，使函数f(x)＝x2＋mx(x∈R)为偶函数”是真命题．4．解析：选C∵p或q为真⇔p、q中至少有一个为真；p且q为假⇔p、q中至少有一个为假，∴“命题p或q为真，p且q为假”⇔p 与q一真一假．5．选C命题p是假命题，命题q是真命题，∴p且q是假命题，p且(綈q)是假命题，(綈p)且q是真命题，(綈p)或(綈q)是真命题．6．选D因为对任意x∈R，e x＞0，故排除A；取x＝2，则22＝22，故排除B；a＋b＝0，＝－1，故排除C.取a＝b＝0，则不能推出ab7．选C命题“存在x∈R，x2＋1>3x”的否定是“任意x∈R，x2＋1≤3x”，故①错；“p 或q”为假命题说明p和q都假，则綈p且綈q 为真命题，故②对；a>5⇒a>2，但a>2⇒/a>5，故“a>2”是“a>5”的必要不充分条件，故③错；“若xy＝0，则x＝0且y＝0”为假命题，故其逆否命题也为假命题，故④错．8．选A若命题p：任意x∈[1,2]，x2－a≥0真，则a≤1.若命题q：存在x∈R，x2＋2ax＋2－a＝0真，则Δ＝4a2－4(2－a)≥0，a≥1或a≤－2，又p且q为真命题所以a＝1或a≤－2.9．对任意实数x，都有sin x≠x.10．解析：命题q为“对任意正数x，x≤1 x”是假命题．答案：对任意正数x，x≤1x假11．解析：由于命题的否定是假命题，所以原命题为真命题，结合图像知Δ＝a 2－4>0，解得a >2或a <－2.答案：(－∞，－2)∪(2，＋∞) 12．解析：∵存在θ∈R 使sin θ－1≥0. 又－1≤sin θ≤1，∴sin θ＝1. ∴θ＝2k π＋π2(k ∈Z)．故cos ⎝⎛⎭⎪⎪⎫θ－π6＝12.答案：1213．解析：因为命题p 是真命题，q 为假命题，所以命题“p 且q ”是假命题，命题“p 且(綈q )”是真命题，命题“(綈p )或q ”是假命题，命题“(綈p )或(綈q )”是真命题．答案：②④14．解析：在①中，命题p 是真命题，命题q 也是真命题，故“p 且(綈q )”是假命题是正确的．在②中l 1⊥l 2⇔a ＋3b ＝0，所以②不正确．在③中“设a 、b ∈R ，若ab ≥2，则a 2＋b 2>4”的否命题为：“设a 、b ∈R ，若ab <2，则a 2＋b 2≤4”正确．答案：①③B 级1．选D sin θ＝12是θ＝30°的必要不充分条件．2．选B ∵当a ·b >0时，a 与b 的夹角为锐角或零度角，∴命题p 是假命题；命题q 是假命题，例如f (x )＝⎩⎨⎧－x ＋1，x ≤0，－x ＋2，x >0，综上可知，“p或q ”是假命题．3．解析：若綈p 是假命题，则p 是真命题，即关于x 的方程4x －2·2x ＋m ＝0有实数解，由于m ＝－(4x －2·2x )＝－(2x －1)2＋1≤1，∴m ≤1.答案：(－∞，1]4．解析：∵sin x ＋cos x ＝2sin ⎝⎛⎭⎪⎪⎫x ＋π4∈[－2， 2 ]；故①存在x ∈R ，使sin x ＋cos x ＝2错误； ④存在x ∈R ，使sin x ＋cos x ＝2正确； ∵sin x ＋1sin x ≥2或sin x ＋1sin x ≤－2，故②对任意x ∈R ，sin x ＋1sin x ≥2错误；③对任意x ∈⎝⎛⎭⎪⎪⎫0，π2，tan x >0，1tan x >0，由基本不等式可得tan x ＋1tan x≥2正确．答案：③④5．解：(1)由x 2－4ax ＋3a 2<0， 得(x －3a )(x －a )<0. 又a >0，所以a <x <3a ， 当a ＝1时，1<x <3， 即p 为真命题时，1<x <3.由⎩⎨⎧ x 2－x －6≤0，x 2＋2x －8>0，解得⎩⎨⎧－2≤x ≤3，x <－4或x >2，即2<x ≤3.所以q 为真时，2<x ≤3.若p 且q 为真，则⎩⎨⎧1<x <3，2<x ≤3，⇔2<x <3，所以实数x 的取值范围是(2,3)．(2)设A ＝{x |x ≤a ，或x ≥3a }，B ＝{x |x ≤2，或x >3}，因为綈p 是綈q 的充分不必要条件，所以A B .所以0<a ≤2且3a >3，即1<a ≤2. 所以实数a 的取值范围是(1,2]． 6．解：由2x 2＋ax －a 2＝0， 得(2x －a )(x ＋a )＝0， ∴x ＝a2或x ＝－a ，∴当命题p 为真命题时，⎪⎪⎪⎪⎪⎪⎪⎪a 2≤1或|－a |≤1， ∴|a |≤2.又“只有一个实数x 0满足不等式x 20＋2ax 0＋2a ≤0”，即抛物线y ＝x 2＋2ax ＋2a 与x 轴只有一个交点，∴Δ＝4a 2－8a ＝0，∴a ＝0或a ＝2. ∴当命题q 为真命题时，a ＝0或a ＝2. ∴命题“p 或q ”为真命题时，|a |≤2. ∵命题“p 或q ”为假命题， ∴a >2或a <－2.即a 的取值范围为⎩⎨⎧a ⎪⎪⎪⎭⎬⎫a >2，或a <－2.。