计量经济学 第二章 简单线性回归模型案例分析
- 格式:ppt
- 大小:1.74 MB
- 文档页数:17

计量经济学教学案例案例一 简单线性回归模型一、主题与背景用真实数据进行简单线性回归分析,应用Eviews6.0分析软件进行操作,与课本内容相对应,分析模型的截距、斜率以及可决系数,引导学生熟悉Eviews6.0的基本操作,能够解读分析报告,并尝试进行被解释变量的预测,体会变量测度单位的改变和函数形式变化给OLS 估计结果和统计特征的影响。
二、情景描述对于由CEO 构成的总体,令y 代表年薪(salary),单位为千美元。
令x 表示某个CEO 所在公司在过去三年的平均股本回报率(roe ,股本回报率定义为净收入占普通股价的百分比)。
为研究该公司业绩指标和CEO 薪水之间的关系,可以定义以下模型:Salary=0β+1βroe + u . 斜率参数1β衡量当股本回报率增长一个单位(一个百分点)时CEO 年薪的变化量,由于更高的股本回报率预示更高的CEO 年薪,所以,1β>0。
三、教学过程设计(一)数据说明数据集CEOSAL1.RAW 包含1990年209位CEO 的相关信息,该数据来自《商业周刊》(5/6/91),该样本中CEO 年薪的平均值为$1,281,120,最低值和最高值分别为$223,000和$14,822,000,1988、1989和1990年的平均股本回报率是17.18%。
(二)操作建议1:在 eviews6.0命令输入窗口定义变量:data salary roe2、用 edit+/- 编辑数据3、描述统计分析过程:view---descriptive stats---common sample4、画散点图:Scat roe salary5、在eviews6.0命令输入窗口运行简单线性回归 Ls salary c roe6、用resids 观测残差7、产生新序列:S eries lsalary =log(salary)8、改变函数形式:Ls lsalary c lsales9、改变变量测度单位:Ls salary*1000 c roe四、教学研究(一)案例结论1、回归结果估计出的回归线为:salˆary = 963.191 + 18.501 roe(1)截距和斜率保留了3位小数,回归结果显示,如果股本回报率为0,年薪的预测值为截距963.191千美元,可以把年薪的预测变化看做股本回报率变化的函数:∆salˆary = 18.501 (∆roe),这意味着当股本回报率增加1个百分点,即∆roe =1,则年薪的预测变化就是18.5千美元,在线性方程中,估计的变化与初始年薪无关。


计量经济学作业姓名:***班级:08级数学一班学号:***********简单线性回归模型一、建立模型为了研究四川省城镇具名消费支出以及可支配收入之间的关系,又经济理论分析可知,收入是影响居民消费支出的主要因素,居民消费支出Y与可支配收入X之间存在密切的关系,消费支出随着收入的增加而增加,但变动的幅度相比较低,即边际消费倾向MPC有0<MPC<1。
因此可设定居民消费支出Yi与Xi的关系为:Yi=ß1+ß2Xi+ui,其中ß1表示四川省城镇居民家庭平均每人年生活性消费支出(元);Xi为城镇居民家丁平均没人年可支配收入(元)。
变量采用年度数据,样本期为1978-1998年。
这里的ß1为居民没有收入来源时的最低消费。
二、估计模型中的位置参数假设模型中的随机误差项ui满足古典假定,运用OLS方法估计模型的参数,利用计量经济学计算机软件EViews计算过程如下:简历文档,输入数据首先点击EViews图标,进入EViews主页。
点击File后,在File菜单的New选项中点击Workfile,这时屏幕上出现Workfile Range对话框,在Srart Date里键入1978,在End Date里键入1998,点击OK后屏幕出现Workfile工作框。
在Object菜单栏,点击New Object对话框里选Group并在Name for Object上定义文件名,点击OK,屏幕出现数据编辑框。
也可在光标出直接输入Data Y X,回车后即可出现数据编辑框。
此时可录入数据,首先按上行键,这时对应“obs”字样的空格会自动上跳,在对应第二个“obs”字样,有边框的空格里键入变量名,再按下行键,这时对应变量名下的这一列出现“NA”字样,便可依时间顺序键入相应的数据。
其他变量的数据类似输入。
可以几个变量同时录入数据。
在主页上选Quick菜单,点击Eatimate Equation项,屏幕上出现估计对话框(Equation Spacification),在Easmation Setting中选OLS估计,即Least Squares,键入Y C X或Y X C(C为EViews固定的截距系数)。
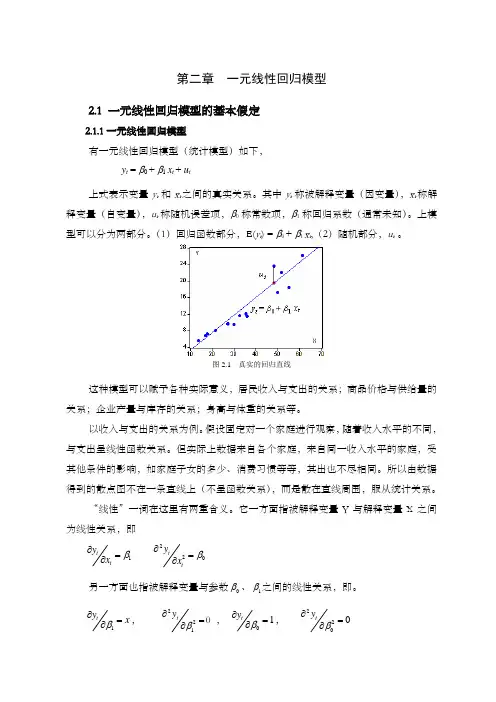
第二章 一元线性回归模型2.1 一元线性回归模型的基本假定2.1.1一元线性回归模型有一元线性回归模型(统计模型)如下, y t = β0 + β1 x t + u t上式表示变量y t 和x t 之间的真实关系。
其中y t 称被解释变量(因变量),x t 称解释变量(自变量),u t 称随机误差项,β0称常数项,β1称回归系数(通常未知)。
上模型可以分为两部分。
(1)回归函数部分,E(y t ) = β0 + β1 x t ,(2)随机部分,u t 。
图2.1 真实的回归直线这种模型可以赋予各种实际意义,居民收入与支出的关系;商品价格与供给量的关系;企业产量与库存的关系;身高与体重的关系等。
以收入与支出的关系为例。
假设固定对一个家庭进行观察,随着收入水平的不同,与支出呈线性函数关系。
但实际上数据来自各个家庭,来自同一收入水平的家庭,受其他条件的影响,如家庭子女的多少、消费习惯等等,其出也不尽相同。
所以由数据得到的散点图不在一条直线上(不呈函数关系),而是散在直线周围,服从统计关系。
“线性”一词在这里有两重含义。
它一方面指被解释变量Y 与解释变量X 之间为线性关系,即1tty x β∂=∂220tt y x β∂=∂另一方面也指被解释变量与参数0β、1β之间的线性关系,即。
1ty x β∂=∂,221ty β∂=∂0 ,1ty β∂=∂,2200ty β∂=∂2.1.2 随机误差项的性质随机误差项u t 中可能包括家庭人口数不同,消费习惯不同,不同地域的消费指数不同,不同家庭的外来收入不同等因素。
所以在经济问题上“控制其他因素不变”是不可能的。
随机误差项u t 正是计量模型与其它模型的区别所在,也是其优势所在,今后咱们的很多内容,都是围绕随机误差项u t 进行了。
回归模型的随机误差项中一般包括如下几项内容: (1)非重要解释变量的省略, (2)数学模型形式欠妥, (3)测量误差等,(4)随机误差(自然灾害、经济危机、人的偶然行为等)。







《计量经济学》实验报告实验课题:各章节案列分析姓名:茆汉成班级:会计学12-2班学号:指导老师:蒋翠侠报告日期:目录第二章简单线性回归模型案例 (1)1 问题引入 (2)2 模型设定 (2)3 估计参数 (2)4 模型检验 (2)第三章多元线性回归模型案例 (3)1 问题引入 (3)2 模型设定 (3)3 估计参数 (4)4 模型检验 (4)第四章多重线性案例 (4)1 问题引入 (4)2 模型设定 (5)3 参数估计 (5)4 对多重共线性的处理 (5)第五章异方差性案例 (6)1 问题引入 (6)2 模型设定 (6)3 参数估计 (6)4 异方差检验 (7)5 异方差性的修正 (7)第六章自相关案例 (8)1 问题引入 (8)2 模型设定 (8)3 用OLS估计 (8)4 自相关其他检验 (8)5 消除自相关 (9)第七章分布滞后模型与自回归模型案例 (9)案例1 (9)1 问题引入 (9)2 模型设定 (10)3 参数估计 (10)案例2 (10)1 问题引入 (10)2 模型设定 (10)3、回归分析 (10)4 模型检验 (11)第八章虚拟变量回归案例 (11)1 问题引入 (11)2 模型设定 (11)3 参数估计 (12)4 模型检验 (12)第二章简单线性回归模型案例1、问题引入居民消费在社会经济的持续发展中有着重要的作用。
适度的居民消费规模和合理的消费模型是人民生活水平的具体体现,有利于经济持续健康的增长。
随着社会信息化程度和居民的收入水平的提高,计算机的运用越来越普及,作为居民耐用消费品重要代表的计算机已经为众多的城镇居民家庭所拥有。
研究中国各地区城镇居民计算机拥有量与居民收入水平的数量关系。
影响居民计算机拥有量的因素有多种,但从理论和经验分析,最主要的影响因素应是居民收入水平。
从理论上说居民收入水平越高,居民计算机拥有量越多。
所以我们设定“城镇居民家庭平均每百户计算机拥有量(台)”为被解释变量,“城镇居民平均每人全年家庭总收入(元)”为解释变量。
时间地点实验题目简单线性回归模型分析一、实验目的与要求:目的:影响财政收入的因素可能有很多,比如国内生产总值,经济增长,零售物价指数,居民收入,消费等。
为研究国内生产总值对财政收入是否有影响,二者有何关系。
要求:为研究国内生产总值变动与财政收入关系,需要做具体分析。
二、实验内容根据1978-1997年中国国内生产总值X和财政收入Y数据,运用EV软件,做简单线性回归分析,包括模型设定,估计参数,模型检验,模型应用,得出回归结果。
三、实验过程:(实践过程、实践所有参数与指标、理论依据说明等)简单线性回归分析,包括模型设定,估计参数,模型检验,模型应用。
(一)模型设定为研究中国国内生产总值对财政收入是否有影响,根据1978-1997年中国国内生产总值X 和财政收入Y,如图1:1978-1997年中国国内生产总值和财政收入(单位:亿元)根据以上数据,作财政收入Y 和国内生产总值X 的散点图,如图2:从散点图可以看出,财政收入Y 和国内生产总值X 大体呈现为线性关系,所以建立的计量经济模型为以下线性模型:01i i i Y X u ββ=++(二)估计参数1、双击“Eviews ”,进入主页。
输入数据:点击主菜单中的File/Open /EV Workfile —Excel —GDP.xls;2、在EV 主页界面点击“Quick ”菜单,点击“Estimate Equation ”,出现“Equation Specification ”对话框,选择OLS 估计,输入“y c x ”,点击“OK ”。
即出现回归结果图3:图3. 回归结果Dependent Variable: Y Method: Least Squares Date: 10/10/10 Time: 02:02 Sample: 1978 1997 Included observations: 20Variable Coefficient Std. Error t-Statistic Prob. C 857.8375 67.12578 12.77955 0.0000 X0.1000360.00217246.049100.0000R-squared 0.991583 Mean dependent var 3081.158 Adjusted R-squared 0.991115 S.D. dependent var 2212.591 S.E. of regression 208.5553 Akaike info criterion 13.61293 Sum squared resid 782915.7 Schwarz criterion 13.71250 Log likelihood -134.1293 F-statistic 2120.520 Durbin-Watson stat0.864032 Prob(F-statistic)0.000000参数估计结果为:i Y = 857.8375 + 0.100036i X(67.12578) (0.002172)t =(12.77955) (46.04910)2r =0.991583 F=2120.520 S.E.=208.5553 DW=0.8640323、在“Equation ”框中,点击“Resids ”,出现回归结果的图形(图4):剩余值(Residual )、实际值(Actual )、拟合值(Fitted ).(三)模型检验1、 经济意义检验回归模型为:Y = 857.8375 + 0.100036*X (其中Y 为财政收入,i X 为国内生产总值;)所估计的参数2ˆ =0.100036,说明国内生产总值每增加1亿元,财政收入平均增加0.100036亿元。
《计量经济学》实验报告实验课题:各章节案列分析姓名:茆汉成班级:会计学12-2班学号: **********指导老师:***报告日期: 2015.06.18目录第二章简单线性回归模型案例 (1)1 问题引入 (1)2 模型设定 (1)3 估计参数 (3)4 模型检验 (3)第三章多元线性回归模型案例 (5)1 问题引入 (5)2 模型设定 (5)3 估计参数 (6)4 模型检验 (6)第四章多重线性案例 (8)1 问题引入 (8)2 模型设定 (8)3 参数估计 (8)4 对多重共线性的处理 (9)第五章异方差性案例 (11)1 问题引入 (11)2 模型设定 (11)3 参数估计 (11)4 异方差检验 (12)5 异方差性的修正 (14)第六章自相关案例 (15)1 问题引入 (15)2 模型设定 (15)3 用OLS估计 (15)4 自相关其他检验 (16)5 消除自相关 (17)第七章分布滞后模型与自回归模型案例 (19)7.2案例1 (19)1 问题引入 (19)2 模型设定 (19)3 参数估计 (19)7.3案例2 (21)1 问题引入 (21)2 模型设定 (21)3、回归分析 (21)4模型检验 (23)第八章虚拟变量回归案例 (24)1 问题引入 (24)2 模型设定 (24)3 参数估计 (26)4 模型检验 (27)第二章简单线性回归模型案例1、问题引入居民消费在社会经济的持续发展中有着重要的作用。
适度的居民消费规模和合理的消费模型是人民生活水平的具体体现,有利于经济持续健康的增长。
随着社会信息化程度和居民的收入水平的提高,计算机的运用越来越普及,作为居民耐用消费品重要代表的计算机已经为众多的城镇居民家庭所拥有。
研究中国各地区城镇居民计算机拥有量与居民收入水平的数量关系。
影响居民计算机拥有量的因素有多种,但从理论和经验分析,最主要的影响因素应是居民收入水平。
从理论上说居民收入水平越高,居民计算机拥有量越多。
计量经济学实验简单线性回归模型引言计量经济学是经济学中的一个分支,致力于通过经验分析和实证方法来研究经济问题。
实验是计量经济学中的重要方法之一,能够帮助我们理解和解释经济现象。
简单线性回归模型是实验中常用的工具之一,它能够通过建立两个变量之间的数学关系,预测一个变量对另一个变量的影响。
本文将介绍计量经济学实验中的简单线性回归模型及其应用。
简单线性回归模型模型定义简单线性回归模型是一种用于描述自变量(X)与因变量(Y)之间关系的线性模型。
其数学表达式为:Y = β0 + β1X + ε其中,Y表示因变量,X表示自变量,β0和β1为未知参数,ε表示误差项。
参数估计在实际应用中,我们需要通过数据来估计模型中的参数。
最常用的估计方法是最小二乘法(OLS)。
最小二乘法的目标是通过最小化观测值与拟合值之间的平方差来估计参数。
具体而言,我们需要求解以下两个方程来得到参数的估计值:∂(Y - β0 - β1X)^2 / ∂β0 = 0∂(Y - β0 - β1X)^2 / ∂β1 = 0解释变量与被解释变量在简单线性回归模型中,解释变量(X)用来解释或预测被解释变量(Y)。
例如,我们可以使用房屋的面积(X)来预测房屋的价格(Y)。
在实验中,我们可以根据收集到的数据来建立回归模型,并利用该模型进行预测和分析。
应用实例数据收集为了说明简单线性回归模型的应用,我们假设收集了一些关于学生学习时间与考试成绩的数据。
下面是收集到的数据:学习时间(小时)考试成绩(百分制)2 723 784 805 856 88模型建立根据收集到的数据,我们可以建立简单线性回归模型来分析学生学习时间与考试成绩之间的关系。
首先,我们需要确定自变量和因变量的符号。
在这个例子中,我们可以将学习时间作为自变量(X),考试成绩作为因变量(Y)。
然后,我们使用最小二乘法来估计模型中的参数。
通过计算,可以得到如下参数估计值:β0 = 69.85β1 = 2.95最终的回归方程为:Y = 69.85 + 2.95X预测与分析通过建立的回归模型,我们可以进行预测和分析。
计量经济学模型案例计量经济学是经济学的一个重要分支,它运用数理统计和数学工具来分析经济现象。
计量经济学模型是对经济现象进行定量分析的重要工具,通过建立数学模型来揭示经济现象的内在规律。
在本文中,我们将通过几个实际案例来介绍计量经济学模型的应用。
首先,我们来看一个简单的线性回归模型。
假设我们想要分析收入对消费支出的影响,我们可以建立一个线性回归模型来探讨二者之间的关系。
通过收集一定时间内的个体数据,我们可以利用最小二乘法来估计模型参数,从而得到收入对消费支出的影响程度。
这个模型可以帮助我们更好地理解收入和消费之间的关系,为政府制定经济政策提供参考依据。
其次,我们可以考虑一个面板数据模型的案例。
面板数据是指在一定时间内对多个个体进行观测得到的数据,它能够更好地反映出个体间的异质性。
比如,我们可以建立一个面板数据模型来分析不同城市房价与人口密度、经济发展水平等因素的关系。
通过面板数据模型,我们可以更准确地把握不同城市房价受到各种因素影响的情况,为房地产市场的监管和预测提供支持。
最后,让我们来看一个时间序列模型的案例。
时间序列数据是指在一段时间内对同一变量进行观测得到的数据,它能够更好地反映出变量随时间的变化规律。
比如,我们可以建立一个时间序列模型来预测未来某个经济指标的变化趋势。
通过对历史数据的分析和建模,我们可以利用时间序列模型来进行未来经济趋势的预测,为政府和企业的决策提供参考。
综上所述,计量经济学模型在实际应用中具有重要的意义。
通过建立合适的模型,我们可以更好地分析和解释经济现象,为经济政策的制定和实施提供科学依据。
当然,在实际应用中,我们需要根据具体问题选择合适的模型,并结合实际数据进行估计和预测。
希望本文介绍的几个案例能够帮助读者更好地理解计量经济学模型的应用。