坐标系中两点间公式和中点公式

两点间的距离及中点公式在空间几何中，我们经常会遇到计算两点之间的距离以及求取两点之间的中点的问题。

无论是平面几何还是立体几何，两点之间的距离和中点都是非常基础且常见的问题。

1.两点之间的距离在平面几何中，两点A(x₁,y₁)和B(x₂,y₂)之间的距离可以通过勾股定理来计算。

根据勾股定理，两点的距离等于两个坐标差的平方和的平方根，即：d=√((x₂-x₁)²+(y₂-y₁)²)2.中点公式在平面几何中，两点的中点可以通过横坐标和纵坐标分别取平均值来得到中点的坐标。

即：中点的横坐标=(x₁+x₂)/2中点的纵坐标=(y₁+y₂)/2接下来，我们将分别对上述两点之间的距离和中点公式进行详细说明，以及举例验证其正确性。

一、两点之间的距离在平面几何中，我们常常需要计算两点之间的距离。

如何计算两点之间的距离呢？根据勾股定理，我们可以利用两个点的横坐标和纵坐标的差的平方和开方来得到两点之间的距离。

假设有两个点A(3,4)和B(8,10)，我们可以计算点A到点B的距离。

按照勾股定理的公式，我们有：d=√((8-3)²+(10-4)²)=√((5)²+(6)²)=√(25+36)=√61≈7.81因此，点A到点B的距离约为7.81二、中点公式在平面几何中，我们常常需要求取两点之间的中点，即两个点的坐标的平均值。

在平面几何中，两点的中点可以通过横坐标和纵坐标分别取平均值来得到中点的坐标。

假设有两个点A(3,4)和B(8,10)，我们可以计算点A和点B之间的中点。

中点的横坐标=(3+8)/2=11/2=5.5中点的纵坐标=(4+10)/2=14/2=7因此，点A和点B之间的中点为M(5.5,7)。

通过上述两个例子，我们可以验证两点之间的距离和中点公式的正确性。

总结：在空间几何中，两点之间的距离及中点是非常基础且常见的问题。

根据勾股定理，我们可以计算两点之间的距离，而中点可以通过横坐标和纵坐标分别取平均值来求得。

两点之间中点坐标公式
两点之间的中点坐标可以通过以下公式求解：
假设已知点A的坐标为(x1,y1)，点B的坐标为(x2,y2)，我们要求的中点坐标为(x,y)。

可以通过以下公式来求解中点坐标：
x=(x1+x2)/2
y=(y1+y2)/2
这个公式的原理是将两个点的x坐标分别相加并除以2，得到中点的x坐标；将两个点的y坐标分别相加并除以2，得到中点的y坐标。

下面我们通过一个具体的例子来说明这个公式的应用：
假设点A的坐标为(3,5)，点B的坐标为(9,11)。

我们要求这两个点的中点坐标。

根据上述公式，可以得到中点的x坐标为(3+9)/2=12/2=6，中点的y 坐标为(5+11)/2=16/2=8
因此，点A和点B的中点坐标为(6,8)。

这个公式的原理其实很简单，通过将两个点的x坐标和y坐标分别相加并除以2，就可以得到这两个坐标的中点。

这个公式的应用非常广泛，可以用于求解多个点之间的中点坐标，无论多少个点，只需要将其坐标相加并除以点的数量即可。

另外，还可以通过这个公式进行一些变形，例如，将x坐标和y坐标
的加法变成减法，可以求得两个点之间的中点连线与x轴和y轴的交点坐标。

总之，两点之间的中点坐标公式是一个非常简单而实用的公式，可以
用于解决各种与两点相关的问题。

无论是在几何学中，还是在其他学科中，都可以使用这个公式来求解两点之间的中点坐标。

两点间的距离公式及中点公式在我们学习数学的旅程中，有两个非常实用的宝贝，那就是两点间的距离公式和中点公式。

这两个公式就像是我们探索数学世界的秘密武器，能帮助我们解决好多有趣又有点小挑战的问题。

先来说说两点间的距离公式。

想象一下，在一个大大的平面上，有两个点 A(x1, y1) 和 B(x2, y2)，就好像是两个小伙伴在操场上站着。

那怎么算出这两个小伙伴之间的距离呢？这时候两点间的距离公式就派上用场啦，它就像是一把神奇的尺子，能告诉我们答案。

公式是：d = √[(x2 - x1)² + (y2 - y1)²] 。

给大家举个例子吧。

有一次我去公园散步，看到两个花坛，一个在坐标（3，5）的位置，另一个在（7，9）的位置。

我就想啊，这两个花坛之间的距离到底是多少呢？我马上就想到了两点间的距离公式，把数字代进去，算出来距离是√[(7 - 3)² + (9 - 5)²] = √[4² + 4²] = √32 =4√2 。

哇，一下子就知道了它们之间的距离，感觉自己就像个数学小侦探，特有成就感！再来说说中点公式。

假如还是这两个点 A(x1, y1) 和 B(x2, y2)，那它们连线的中点坐标是啥呢？中点公式告诉我们：中点坐标为（(x1 + x2) / 2, (y1 + y2) / 2）。

我想起有一次帮小朋友们分糖果。

有两个小朋友分别站在不同的位置，我想把糖果公平地放在他们中间的位置，让他们过来拿都差不多远。

这时候中点公式就帮了大忙，我算出了中点的位置，把糖果放在那里，两个小朋友都很开心，觉得特别公平。

在实际生活中，这两个公式的用处可多啦。

比如在建筑设计中，工程师要确定两个建筑物之间的距离和中间的位置；在地图导航里，计算两个地点之间的距离和中间的参考点。

所以啊，同学们可别小看这两个公式，它们虽然看起来简单，但是作用大大的。

只要我们认真掌握，就能在数学的世界里畅行无阻，解决更多的难题，发现更多的乐趣！总之，两点间的距离公式和中点公式是我们数学学习中的好帮手，让我们继续努力，用它们去探索更多未知的数学奥秘吧！。

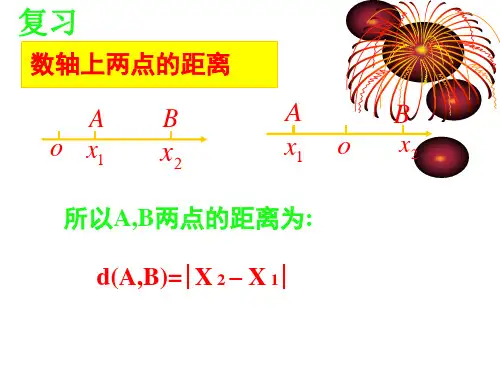
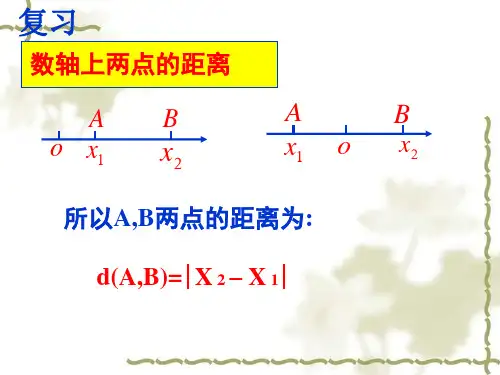
直角坐标系中两点间的中点公式在直角坐标系中，计算两点之间的中点是一项常见的算术操作。

通过使用中点公式，我们可以轻松地找到给定两点的中点坐标。

假设我们有两个点A和B，它们的坐标分别为(x₁, y₁)和(x₂, y₂)。

中点公式的推导过程很简单。

我们知道，中点M的坐标可以表示为：M = ((x₁ + x₂) / 2, (y₁ + y₂) / 2)这个公式实际上是将两个点在x轴和y轴上的坐标分别相加，然后除以2得出中点M的坐标。

这是因为在直角坐标系中，中点的横坐标是两个点横坐标的平均值，纵坐标是两个点纵坐标的平均值。

让我们通过一个具体的例子来演示中点公式的应用。

假设点A的坐标为(3, 4)，点B的坐标为(7, 2)。

我们可以将这些值代入中点公式中：x₁ = 3, y₁ = 4, x₂ = 7, y₂ = 2将它们代入中点公式，我们得到：M = ((3 + 7) / 2, (4 + 2) / 2)计算后，我们可以得出中心点M的坐标为：M = (5, 3)因此，点A(3, 4)和点B(7, 2)之间的中点坐标为(5, 3)。

这个例子展示了中点公式的实际应用，让我们能够快速准确地找到两点之间的中点。

在实际问题中，中点公式可以广泛应用，例如在计算机图形学中确定线段的中点、在几何学中确定多边形的中心等。

掌握中点公式不仅可以帮助我们解决数学问题，还可以让我们更好地理解直角坐标系中点的性质和关系。

总之，中点公式是一个简单但实用的数学工具，在直角坐标系中计算两点之间的中点时起到了关键作用。

通过这个公式，我们能够快速求解中点坐标，为更复杂的数学问题和几何问题奠定基础。

希望通过这篇文档的介绍，读者能更加深入了解直角坐标系中两点间的中点公式的应用和意义。

两点间距离公式与线段中点的坐标一、二维空间中两点间的距离公式在二维空间中有两点A(x1,y1)和B(x2,y2)。

我们可以通过勾股定理来计算AB之间的距离。

勾股定理表示直角三角形的斜边的平方等于两直角边平方和。

根据勾股定理，AB的距离公式为：AB=√((x2-x1)²+(y2-y1)²)这个公式可以通过计算两点的横纵坐标之差，并且将结果平方和开根号来得到两点之间的距离。

示例：假设有两点A(1,2)和B(4,6)，计算AB之间的距离。

AB=√((4-1)²+(6-2)²)=√(3²+4²)=√(9+16)=√25=5所以，点A和点B之间的距离为5个单位。

二、三维空间中两点间的距离公式在三维空间中有两点A(x1,y1,z1)和B(x2,y2,z2)。

对应的两点之间的距离可以通过三个坐标轴上的坐标之差来计算。

根据勾股定理，AB的距离公式为：AB=√((x2-x1)²+(y2-y1)²+(z2-z1)²)这个公式可以通过计算两点在横纵纵坐标轴上的差，并且将结果平方和开根号来得到两点之间的距离。

示例：假设有两点A(1,2,3)和B(4,6,8)，计算AB之间的距离。

AB=√((4-1)²+(6-2)²+(8-3)²)=√(3²+4²+5²)=√(9+16+25)=√50所以，点A和点B之间的距离为√50个单位。

线段的中点是指线段上距离两个端点等距离的点。

在二维空间中，通过计算线段的横纵坐标之和的一半来获得中点的横纵坐标。

假设有两个端点A(x1, y1)和B(x2, y2)，线段的中点坐标为M(xm, ym)。

中点的横坐标为两个端点横坐标之和的一半，纵坐标为两个端点纵坐标之和的一半，即：xm = (x1 + x2) / 2ym = (y1 + y2) / 2示例：假设有两个端点A(1,2)和B(4,6)，计算线段AB的中点坐标。

两点之间中点公式两点之间中点公式是初中数学中比较基础的知识点，也是几何上的常用公式之一。

在二维或三维空间中，两个点之间的中点是通过它们的坐标计算出来的，这个公式可以轻松地帮助我们确定图形的中心位置、两点之间的距离等相关计算。

一、两点之间的中点在二维直角坐标系中，两个点A(x1,y1)和B(x2,y2)之间的中点M(x,y)的坐标可以通过以下公式计算：x = (x1+x2)/2y = (y1+y2)/2我们可以简单地解释一下这个公式的意义：两点之间的中点的x坐标等于这两个点的x坐标之和的一半，y坐标同理。

下面我们用一个简单的例子来说明如何应用中点公式：例：已知线段AB的两个端点A(-1,2)和B(5,-6)，求线段AB的中点C坐标。

解：根据中点公式，通过简单的计算得到：x = (-1+5)/2 = 2y = (2+(-6))/2 = -2因此，线段AB的中点C的坐标为(2,-2)。

从这个例子中，我们可以看出中点公式具有简单、直观、易懂的特点。

无论是在求解几何问题还是实际应用中，都具有很高的实用价值。

二、两点之间的距离另外，通过两点之间的中点，我们还可以轻松地求解它们之间的距离。

在二维直角坐标系中，两个点A(x1,y1)和B(x2,y2)之间的距离公式可以由勾股定理推导而来：AB = √[(x2-x1)²+(y2-y1)²]在这个公式中，我们可以看到x2-x1和y2-y1这两个数代表了线段AB在x和y轴上的长度差。

接着我们可以计算这两个数的平方和，再对它们进行开方，从而得到两点之间的距离。

根据勾股定理，我们不难发现，在直角三角形中，它的斜边长度就是两边长度平方和的平方根。

因此，两点之间的距离公式是继承并拓展了勾股定理的一种应用形式。

接下来我们再来看一个实际的例子。

例：已知点A(2,1)和点B(8,5)，求线段AB的长度。

解：通过两点间的距离公式，我们可以直接进行计算：AB = √[(8-2)²+(5-1)²]= √[(6)²+(4)²]= √(36+16)= √52因此，线段AB的长度为√52，约等于7.211。