坐标系中的基本公式

2.1.2平面直角坐标系中的基本公式课程学习目标目标重点：平面上两点间的距离公式和中点公式；目标难点：两点间距离公式的推导；［学法关键］1．领会从特殊到一般的过程来研究两点间的距离公式及中点坐标公式；2．距离公式的实质是将二维空间的长度计算问题转化为一维空间的长度计算问题。

研习点1. 两点间的距离公式1． 两点 A (x 1，y 1)，B (x 2,y 2)间的距离公式表示为d (A ，B2． 当AB 平行于x 轴时，d (A ，B )=|x 2－x 1|；当AB 平行于y 轴时，d (A ，B )=|y 2－y 1|；当B 为原点时，d (A ，B求两点距离的步骤已知两点的坐标，为了运用两点距离公式正确地计算两点之间的距离，我们可分步骤计算：（1）给两点的坐标赋值：(x 1，y 1)，(x 2，y 2).（2）计算两个坐标的差，并赋值给另外两个变量，即△x =x 2－x 1，△y =y 2－y 1.（3）计算d 22x y +.（4）给出两点的距离d .通过以上步骤，对任意的两点，只要给出两点的坐标，就可一步步地求值，最后算出两点的距离研习点2. 坐标法坐标法：就是通过建立坐标系（直线坐标系或者是直角坐标系），将几何问题转化为代数问题，再通过一步步地计算来解决问题的方法.用坐标法证题的步骤（1）根据题设条件，在适当位置建立坐标系（直线坐标系或者是直角坐标系）；（2）设出未知坐标；（3）根据题设条件推导出所需未知点的坐标，进而推导结论.研习点3. 中点坐标公式已知A (x 1，y 1),B (x 2，y 2)两点，M (x ，y )是线段AB 的中点，则有121222x x x y y y +⎧=⎪⎪⎨+⎪=⎪⎩（1）两点间线段的中点坐标是常遇到的问题，中点法也是数形结合中常考察的知识点，这一思想常借助于图象的线段中点特征加以研究，确定解题策略。

（2）若已知点P (x ，y )，则点P 关于点M (x 0，y 0)对称的点坐标为P ’(2x 0－x ，2y 0－y ).（3）利用中点坐标可以求得△ABC （A (x 1，y 1)，B (x 2，y 2)，C (x 3，y 3)）的重心坐标为12312333x x x x y y y y ++⎧=⎪⎪⎨++⎪=⎪⎩题型1. 公式的基本应用例1.求下列两点的距离及线段中点的坐标，（1）A (－1，－2)，B (－3，－4)；（2）C (－2，1)，D (5，2).解：（1）设AB 的中点为M (x ，y )，得线段AB 的中点坐标为M (－2，－3)， AB 两点的距离d (A ，B=。

直角坐标系中的基本公式
一、坐标极限
在直角坐标系中，每个坐标轴的极限均为正无穷大、负无穷大，若设坐标轴为x轴和y轴，则有：
x→±∞，y→±∞
二、坐标点
坐标系中的任意一点通过其与坐标轴的交点定义出来，若该点与坐标轴上的点非常接近，则坐标系中的任意一点可以用坐标点(x,y)表示，其中x和y分别表示该点到x轴和y轴的距离，正数表示向右向上距离，负数表示向左向下距离。

三、坐标轴
在直角坐标系中，一般有两个相互垂直的坐标轴，一般称为x轴和y 轴，x轴垂直于y轴，x轴向右为正方向，y轴向上为正方向，称为坐标轴正方向。

四、坐标原点
在直角坐标系中，由x轴和y轴交点定义的点称为坐标原点，符号为O，x轴上该点的坐标为(0,0)，即x=0，y=0。

五、坐标轴上的点
在直角坐标系中，任何一点，其到坐标轴的距离均为常数，若该点在x轴上的坐标为a，在y轴上的坐标为b，则该点的坐标可表示为(a,0)（在x轴上）或(0,b)（在y轴上），其中a和b均为实数。

六、基本公式
1、点到坐标轴的距离
设点P(x,y)与x轴和y轴的距离为a和b，则有：a=，x，b=，y
2、点到坐标原点的距离。

直角坐标系的8大公式直角坐标系是数学中常用的坐标系之一，广泛应用于几何、物理和工程等领域。

在直角坐标系中，我们通过坐标对点进行唯一标识和定位。

本文将介绍直角坐标系中的8大公式，这些公式在解决几何和代数问题时非常有用。

一、坐标距离公式在直角坐标系中，我们可以通过两点的坐标计算它们之间的距离。

假设点A的坐标为(x₁, y₁)，点B的坐标为(x₂, y₂)，那么点A和点B之间的距离可以由以下公式求得：d = √((x₂ - x₁)² + (y₂ - y₁)²)这个公式被称为坐标距离公式，可以通过计算两点之间的直线距离来确定它们之间的距离。

二、中点公式在直角坐标系中，我们可以通过两点的坐标计算它们的中点坐标。

假设点A的坐标为(x₁, y₁)，点B的坐标为(x₂, y₂)，那么这两点的中点坐标可以由以下公式求得：M = ((x₁ + x₂) / 2, (y₁ + y₂) / 2)这个公式被称为中点公式，可以通过计算两点坐标的平均值来确定它们的中点坐标。

三、斜率公式在直角坐标系中，我们可以通过两点的坐标计算它们之间的斜率。

假设点A的坐标为(x₁, y₁)，点B的坐标为(x₂, y₂)，那么这两点之间的斜率可以由以下公式求得：m = (y₂ - y₁) / (x₂ - x₁)这个公式被称为斜率公式，可以用于计算两点之间直线的斜率。

斜率表示直线的倾斜程度。

四、线性方程公式在直角坐标系中，我们可以通过直线的斜率和一点的坐标来确定直线的方程。

假设直线的斜率为m，一点的坐标为(x₁, y₁)，那么直线的方程可以由以下公式给出：y - y₁ = m(x - x₁)这个公式被称为线性方程公式，可以用于描述直线在直角坐标系中的方程。

五、平行线公式在直角坐标系中，我们可以通过两条平行线的斜率来确定它们之间的关系。

假设平行线L₁的斜率为m₁，平行线L₂的斜率为m₂，那么这两条平行线之间的关系可以由以下公式给出：m₁ = m₂这个公式表示两条平行线的斜率相等。

张喜林制2.1.2 平面直角坐标系中的基本公式教材知识检索考点知识清单1．两点间的距离公式：设),(),(2211y x B y x A 、是平面上的两点，则=||AB2．中点公式：已知),,(),(2211y x B y x A 、设M(x ，y)是线段AB 的中点，则=x =y ,3．平行四边形的两条对角线的平方和等于它的四边的要点核心解读1．两点间的距离公式(1)平面上的点),(y x P 到原点)0,0(O 的距离=),(P O d .22y x +(2)平面上任意两点间的距离公式：设,(),211x B y x A 、（),2y 则.)()(),(212212y y x x B A d -+-=(3)求两点间距离的步骤：①给两点坐标赋值：?,,,,2121====y y x x ？？？②计算两个坐标的差，并赋值给另外两个变量，即;,1212y y y x x x -=∆-=∆ ③计算;)()(22y x d ∆+∆=④给出两点的距离．2．中点公式已知),,(),(2211y x B y x A 、设点),(y x M 是线段AB 的中点(如图2-1 -2 -1)，过点A 、B 、M 分别向x 轴、y 轴作垂线、、21AA AA ,2121MM MM BB BB 、、、垂足分别为、、、)0,((B )(0,)0,(211211x y A x A )0,(),,0(122x M y B ).,0(2y M 因为M 是线段AB 的中点，所以点1M 和点2M 分别是11B A 和22B A 的中点，即⋅==22221111,B M M A B M M A所以⋅-=--=-y y y y x x x x 2121,即 2,22121y y y x x x +=+= 这就是线段中点坐标的计算公式，简称中点公式．3．解析法的应用解析法是解决解析几何、立体几何等的重要方法，它是把几何问题转化成代数问题，通过建立适当的坐标系加以分析研究解决问题的方法．用解析法解决几何问题的基本步骤如下：(1)选择坐标系：坐标系选择是否恰当，直接关系到以后的论证是否简捷．原则是：选择坐标系要使得问题所涉及的坐标中尽可能多地出现零．为此，常常有以下规律：①将图形一边所在的直线或定直线作为x 轴；②若为对称图形则取对称轴为x 轴或y 轴；③若有直角，则取直角边所在的直线为坐标轴；④可将图形的一个定点或两个定点连线的中点作为原点．(2)标出图形上有关点的坐标，按已知条件用坐标表示图形中的等量关系．(3)通过以上两个程序，把几何问题转化为代数问题来求解．典例分类剖析考点1 平面上两点闻距离的求法及应用命题规律主要强调两点间距离公式的应用，两点间的距离公式作为解析几何的重点之一，常会考查．[例1] (1)已知),3,1()3,6()1,2(C B A 、、求证：△ABC 为直角三角形．(2)已知点A(3，6)，在x 轴上的点P 与点A 的距离为10，求点P 的坐标．[解析] (1)要判断三角形是否为直角三角形，其中一种方法是考虑各边长之间是否满足勾股定理，即需求出三条边长．[答案] 由两点间的距离公式得;20)13()26(),(=-+-=B A d;5)13()21(),(=-+-=C A d;25)33()61(),(22=-+-=C B d,||||||222BC AC AB =+∴∴ △ABC 为直角三角形．(2)设点P 的坐标为（x ，O ），由,10),(=P A d 得,10)60()3(22=-+-x解得11=x 或,5-=x∴ 点P 的坐标为(-5，0)或(11，0)．母题迁移 1．已知等边△ABC 的两个顶点、的坐标为),0,2()0,4(B A 、-试求：(1) C 点的坐标；(2)△ABC 的面积．考点2 中点坐标公式及其应用命题规律考查中点坐标公式及其应用．[例2] △ABC 三个顶点的坐标分别为,2)4,4(（、B A --),2,4()2-C 、求三边中线的长．[答案] 设AB 的中点D 的坐标为D （x,y ）,由中点公式得,1224,1224-=+-=-=+-=y x 即 ⋅--)1,1(D同理，BC 的中点E(3，0)，AC 的中点F(O ，-3)．),(||D C d CD =∴22)]2(1[)41(---+--=;26=),(||E A d AE =)40()43(+++=;65=),(||F B d BF =)23()20(-⋅-+-=.29=母题迁移 2．△ABC 三个顶点的坐标为),1,0(-A ),2,2(),3,1(-C B 求中线AD 的长．考点3 两点问距离公式的几何意义命题规律利用两点间距离公式的几何意义求某些函数的最值．[例3] 求函数++-=3712)(2x x x f 134+-x x 的最小值．[答案] ,1)6(3722+-=+-x x r x ∴+-=+-,9)2(1342x x x 可设,6（A 、、)3,2()1B )0,P(x 则.||||)(PB PA x f +=要求)(x f 的最小值，只需在x 轴上找一点P ，使||||PB PA +最小即可．设B 关于x 轴的对称点为,/B 则)3,2(/-B （如图2 -1 -2-2所示）． |,|||||||||//AB PB PA PB PA ≥+=+,24)13()62(||22/=--+-=AB∴ 当A P B 、、/三点共线时取等号，即||||PB PA +的最小值为,24也就是)(x f 的最小值为.24[点拨] (1)涉及无理式，尤其是含平方的算式，我们可联想到两点间的距离，故构造两点间的距离来解题．(2)本题切忌将两个无理函数最小值的和当作f(x)的最小值．母题迁移 3．求函数1342222+-++-=x x x x y 的最小值．优化分层测讯学业水平测试1．已知),15,2().5,3(B A -则=),(B A d （ ）25.A 135.B 175.C 55.D2．已知两点),,(),(d c B b a A 、且,02222=+-+d c b a 则( )．A ．原点一定是线段AB 的中点 B.A 、B 一定都与原点重合C ．原点一定在线段AB 上但不是中点D ．以上结论都不正确3．点P(2，-1)关于点(3，4)的对称点是( )．)5,1.(A )9,4.(B )3,5(⋅C )4,9.(D4．已知点A(3，6)，在x 轴上的点P 与点A 的距离等于10，则点P 的坐标为5．在△ABC 中，设),5,2()7,3(-B A 、若AC 、BC 的中点都在坐标轴上，则点C 的坐标为6．已知，平面内平行四边形的三个顶点).3,1()1,2(--B A 、),4,3(C 求第四个顶点D 的坐标．高考能力测试（测试时间：45分钟测试满分：100分）一、选择题（5分x8 =40分）1．以A(5，5)、B(1，4)、C(4，1)为顶点的三角形是( )．A.直角三角形 B ．等腰三角形 C ．等边三角形 D ．等腰直角三角形2．已知△ABC 的三个顶点是)0,()0,(a B a A 、-和),23,2(a aC 则△ABC 的形状是( )． A ．等腰三角形 B ．等边三角形 C ．直角三角形D ．斜三角形3．已知点),2,4()0,2(B A 、若|,|2||BC AC =则C 点的坐标为( )．)1,1(-⋅A ），或（15)1,1(--⋅B )3,1()1,1(或-⋅C D ．无数个 4．已知点A （x ，5）关于点C(l ，y)的对称点是),3,2(--B 则点),(y x P 到原点的距离是( )．4.A 13.B 15.C 17.D5．已知菱形的三个顶点为),0,0(),(),(、、a b b a -则它的第四个顶点是( )．),2(b a A ⋅ ),(b a b a B +-⋅ ),.(a b b a C -+ ),(a b b a D --⋅6．光线从点A （-3，5）射到x 轴上，经过反射后经过点B(2，10)，则光线从A 到B 的距离为( )．25.A 52.B 105.C 510.D7．某县位于山区，居民的居住区域大致呈如图2 -1-2 -3所示的五边形，近似由一个正方形和两个等腰直角三角形组成，若,30,60km CD AE km AB ===为了解决当地人民看电视难的问题，准备建一个电视转播台，理想方案是转播台距五边形各顶点距离的平方和最小，图中4321P P P P 、、、是AC 的五等分点，则转播台应建在( )．1.P A 处2.P B 处3.P C 处4.P D 处8．（2006年福建）对于直角坐标平面内的任意两点).,(11y x A ),,(22y x B 定义它们之间的一种“距离”：+-=||||12x x AB .||12y y -给出下列三个命题：①若点C 在线段AB 上，则|;|||||AB CB AC =+②在△ABC 中，若,90 =∠C 则;||||||222AB CB AC =+③在△ABC 中，.||||||AB CB AC >+其中真命题的个数为( )．0.A 1.B 2.C 3.D二、填空题（5分x4 =20分）9．已知),,2()6,(b B a A -、点P(2，3)平分线段AB ，则=+b a10．已知),3,0()3,5()1,1(C B A 、、则△ABC 的形状为11．已知),3().2,1(b B A -两点间的距离为,24则=b12.已知两点),2,3()4,1(A P 、-则点A 关于点P 的对称点的坐标为三、解答题（10分x4 =40分）13.求函数84122+-++=x x x y 的最小值．14.已知△ABC 三顶点的坐标为,8)3,11()8,3(--（、、C B A ),2-求BC 边上的高AD 的长度．15.若a 、b 、c 、d 都是实数，试证明≥+++2222db c a .)()(22d c b a +++16.在△ABC 所在平面上求一点P ，使222||||||PC PB PA ++取得最小值.。

平面直角坐标系八大公式
在平面直角坐标系中，常用的八大公式如下：
1. 距离公式：两点P1(x1, y1)和P2(x2, y2)之间的距离为：d = √((x2 - x1)² + (y2
- y1)²)。

2. 中点公式：两点P1(x1, y1)和P2(x2, y2)的中点坐标为：M((x1 + x2)/2, (y1 +
y2)/2)。

3. 斜率公式：两点P1(x1, y1)和P2(x2, y2)之间的斜率为：m = (y2 - y1)/(x2 - x1)，其中x2不等于x1。

4. 判别式公式：对于一次函数的方程y = ax + b，其判别式为：Δ = b² - 4ac，其中a、
b、c为方程的系数。

5. 点到直线的距离公式：对于一条直线的方程Ax + By + C = 0，点P(x0, y0)到该直线
的距离为：d = |Ax0 + By0 + C|/√(A² + B²)。

6. 直线的倾斜角公式：对于一条直线的斜率为m，则该直线与x轴的夹角θ满足：
tan(θ) = m。

7. 两条直线的夹角公式：设两条直线的斜率分别为m1和m2，则两条直线的夹角θ满足：tan(θ) = |(m2 - m1)/(1 + m1m2)|。

8. 直线的方程公式：已知一条直线通过点P(x1, y1)且斜率为m，则该直线的方程为：y
- y1 = m(x - x1)。

以上是平面直角坐标系中常用的八大公式，它们在求解点、直线、距离等问题时非常有用。

坐标计算公式范文坐标计算是一种在数学和几何学中广泛使用的方法，用于确定点在一个指定坐标系中的位置。

在平面坐标系中，点的位置通常由两个坐标值表示，即水平方向的x坐标和垂直方向的y坐标。

在三维坐标系中，点的位置由三个坐标值表示，即水平方向的x坐标、垂直方向的y坐标和垂直方向的z坐标。

下面将介绍几种常见的坐标计算公式。

1.距离公式：距离公式用于计算两个点之间的距离，可以根据点的坐标使用勾股定理计算：d=√[(x2-x1)²+(y2-y1)²](二维空间)d=√[(x2-x1)²+(y2-y1)²+(z2-z1)²](三维空间)2.中点公式：中点公式用于计算连接两个点的线段的中点的坐标，可以通过两个点的坐标值的平均值来计算：(x,y)=((x1+x2)/2,(y1+y2)/2)(二维空间)(x,y,z)=((x1+x2)/2,(y1+y2)/2,(z1+z2)/2)(三维空间)3.倾斜角度公式：倾斜角度公式用于计算连接两个点的线段与水平轴之间的夹角，可以使用反三角函数计算：θ = arctan[(y2 - y1) / (x2 - x1)] (二维空间)θ = arccos[(v1 · v2) / (，v1，· ，v2，)] (三维空间)其中，v1=(x2-x1,y2-y1,z2-z1)，v2为水平向量4.坐标旋转公式：坐标旋转公式用于计算将一个点绕另一个点旋转后的新坐标，可以使用三角函数和矩阵运算计算：x' = x1 + (x - x1) * cos(θ) - (y - y1) * sin(θ)y' = y1 + (x - x1) * sin(θ) + (y - y1) * cos(θ)其中，(x,y)为旋转前的点的坐标，(x',y')为旋转后的点的坐标，(x1,y1)为旋转中心，θ为旋转角度。

5.坐标缩放公式：坐标缩放公式用于计算将一个点缩放到另一个点的比例后的新坐标，可以使用比例关系计算：x'=x1+(x-x1)*ry'=y1+(y-y1)*r其中，(x,y)为原始点的坐标，(x',y')为缩放后的点的坐标，(x1,y1)为参考点的坐标，r为缩放比例。

坐标计算的基本公式坐标计算是一个常见的数学问题，用于确定物体在一个特定坐标系中的位置。

这个问题可以在平面坐标系上或者在三维坐标系上进行。

在这篇文章中，我们将讨论一些常见的坐标计算的基本公式。

1.点到点的距离：点到点的距离可以通过勾股定理计算得到。

在平面坐标系中，点A和点B的距离可以使用以下公式计算：AB = sqrt((x2 - x1)^2 + (y2 - y1)^2)在三维坐标系中，点A和点B的距离可以使用以下公式计算：AB = sqrt((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2)2.点的中点：在平面坐标系中，两个点的中点可以使用以下公式计算：M=((x1+x2)/2,(y1+y2)/2)在三维坐标系中，两个点的中点可以使用以下公式计算：M=((x1+x2)/2,(y1+y2)/2,(z1+z2)/2)3.点的向量方向：点A到点B的向量方向可以使用以下公式计算：AB=(x2-x1,y2-y1)在三维坐标系中，点A到点B的向量方向可以使用以下公式计算：AB=(x2-x1,y2-y1,z2-z1)该向量方向可以用来表示从点A到点B的方向和距离。

4.点的旋转：点P绕点O逆时针旋转θ角度后的位置可以使用以下公式计算：P' = (cosθ * (P.x - O.x) - sinθ * (P.y - O.y) + O.x, sinθ * (P.x - O.x) + cosθ * (P.y - O.y) + O.y)在三维坐标系中，点P绕点O逆时针旋转θ角度后的位置可以使用以下公式计算：P' = (cosθ * (P.x - O.x) - sinθ * (P.y - O.y) + O.x, sinθ * (P.x - O.x) + cosθ * (P.y - O.y) + O.y, P.z)这个公式可以用来计算点在旋转后的位置。

这些公式是坐标计算中的基本公式，它们可以帮助我们计算物体在一个特定坐标系中的位置、方向和距离。

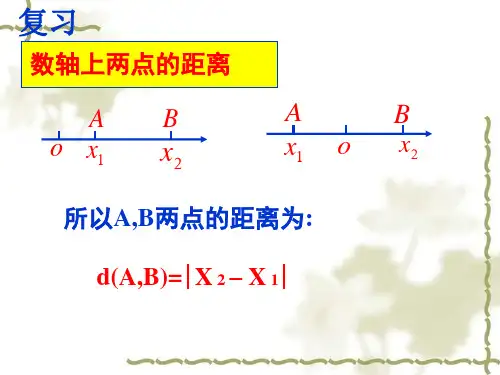
平面直角坐标系中的基本公式【知识梳理】要点一：直线坐标系(1)定义：一条给出了原点、度量单位和正方向的直线叫做数轴，或者说在这条直线上建立了直线坐标系． 要点诠释：一般地，我们约定数轴水平放置，正方向为从左到右．(2)数轴上的点与实数的对应法则：P ←−−−−→一一对应实数x ． (3)记法：如果点P 与实数x 对应，则称点P 的坐标为x ，记作P (x )．当x ＞0时，点P 位于原点右侧，且点P 与原点O 的距离|OP |＝x ；当x ＜0时，点P 位于原点左侧，且点P 与原点的距离|OP |＝-x要点二：向量及数轴上两点间的距离公式(1)定义：位移是一个既有大小又有方向的量，通常叫做位移向量，本书简称为向量．从点A 到点B 的向量，记作AB ．点A 、B 分别叫做向量AB 的起点、终点．向量的长度：线段AB 的长叫做向量AB 的长度，记作|AB |．相等的向量：数轴上同向且等长的向量叫做相等的向量．数量：我们可用实数表示数轴上的一个向量AB ，这个实数叫做向量AB 的坐标或数量．要点诠释：要正确区分向量、向量的长度、向量的坐标（数量）这几个概念，它们分别用AB 、||AB 、AB 来表示；两个向量相等，必须长度和方向都相同；零向量是起点和终点重合的向量，它的长度为0，方向不确定．(2)位移向量的和：在数轴上，如果点A 作一次位移到点B ，接着由点B 再作一次位移到点C ，则位移AC 叫做位移AB 与位移BC 的和，记作AC AB BC =+．要点诠释：作和向量的规律特点：前一个向量的终点是下一个向量的起点(尾首相接)，而和向量是第一个向量的起点指向最后一个向量的终点(首尾相连)．(3)数量和：数轴上任意三点A 、B ，C ，都具有关系AC ＝AB+BC ．要点诠释：①这个公式反映了数轴上向量加法的坐标运算法则，是解析几何的基本公式．②数轴上任意三点．A 、B 、C 都有关系AC ＝AB+BC ，但不一定有|AC |＝|AB |+|BC |，它与A 、B 、C 三个点的相对位置有关．(4)数轴上两点间的距离公式：向量的坐标计算公式：设AB 是数轴上的任意一个向量，点A 的坐标为1x ，点B 的坐标为2x ，则21AB x x =-．一般地，数轴上的任意一个向量的坐标等于它的终点坐标减去起点坐标．用d (A ，B )表示A ，B 两点的距离，可得数轴上两点A ，B 的距离公式是21()||||d A B AB x x ==-，．要点三：平面直角坐标系中两点间的距离公式平面上有两点A (1x ，1y )，B (2x ，2y ) ，则两点间的距离为d (A ，B )＝|AB |＝222121()()x x y y -+-．要点诠释：两点间的距离公式是一个很重要的公式，要熟练地掌握，记住公式的形式，对于两点的横坐标或纵坐标相等的情况，可以直接利用距离公式的特殊情况求解．要点四：中点坐标公式若A (1x ，1y )、B (2x ，2y )，则线段AB 的中点M (x ，y )的坐标计算公式为122x x x +=，122y y y +=． 要点诠释：此公式的推导过程中注意把问题向数轴上转化，体现了数学上的转化思想．要点五：坐标法1．通过建立平面直角坐标系，用代数方法来解决几何问题的方法叫做坐标法，其体现的基本思想是数形结合思想．2．用解析法解决几何问题的基本步骤如下：(1)选择坐标系．坐标系的选择是否恰当，直接关系到以后的论证是否简洁．原则：选择坐标系要使得问题所涉及的坐标中尽可能多地出现零．为此，常常有以下约定：①将图形一边所在的直线或定直线作为x 轴．②对称图形，则取对称轴为x 轴或y 轴．③若有直角，则取直角边所在的直线为坐标轴．④可将图形的一个定点或两个定点连线的中点作为原点．(2)标出图形上有关点的坐标，按已知条件用坐标表示等量关系．(3)通过以上两个程序，把几何问题等价转化为代数式来计算．【典型例题】类型一：向量及数轴上点的距离公式例1．已知A 、B 、C 是数轴上任意三点．(1)若AB ＝5，CB ＝3，求AC ；(2)证明：AC+CB ＝AB ；(3)若|AB |＝5，|CB |＝3，求|AC |．【答案】（1）2（2）略（3）2或8【解析】 (1)AC ＝AB+BC ＝AB -CB ＝5-3＝2．(2)证明：设数轴上A 、B 、C 三点的坐标分别为A x 、B x 、C x ，则AC+CB ＝(C A x x -)+(B C x x -)＝B A x x AB -=，故AC+CB ＝AB ．(3)当点C 在A 、B 两点之间时，由下图①可知|AC |＝|AB |-|BC |＝5-3＝2；当点C 在A 、B 两点之外时，由上图②可知|AC |＝|AB |+|BC |＝5+3＝8．综上所述，|AC |＝2或8．【总结升华】 向量及向量长度的计算应熟练地运用公式AB ＝B A x x -，及|AB |＝||||B A A B x x x x -=-进行求解．对于(3)要注意点B (或点C )的位置，若不确定应分类讨论．举一反三：【变式1】已知数轴上A 、B 两点的坐标分别为1x a b =+，2x a b =-．求AB 、BA 、d (A ，B )、d (B ，A )．【答案】2b - 2b 2||b 2||b【解析】 21AB x x =-=()()2a b a b b --+=-，12()()2BA x x a b a b b =-=+--=，d (A ，B )＝21||2||x x b -=，d (B ，A )＝12||2||x x b -=．【变式2】 关于位移向量，下列说法正确的是 ( )A ．数轴上任意一个点的坐标有正负和大小，它是一个位移向量B ．两个相等的向量的起点可以不同C ．每一个实数都对应数轴上的唯一的一个位移向量D ．AB 的大小是数轴上A 、B 两点到原点距离之差的绝对值【答案】 B【解析】 一个点的坐标没有大小，每个实数对应着无数个位移向量。

坐标系中点到直线距离公式在坐标系中，求点到直线的距离是一个常见的几何问题。

在本文中，我们将介绍两种常用的点到直线距离的计算方法，分别为点到直线的公式和点到直线的投影方法。

一、点到直线的公式：设直线的方程为ax+by+c=0，点的坐标为(x0, y0)。

步骤1：求直线的斜率k。

由于直线的一般式为ax+by+c=0，我们可以观察到a和b的比值即为直线的斜率。

步骤2：求直线上一点P(x1,y1)的直线方程。

由于点P和直线上其他任意一点在直线上，所以可以使用点坐标代入直线方程得到一直线上的点。

步骤3：求点P到直线的距离。

我们可以使用点P到直线的距离公式，即点P到直线l的距离为:d = ，ax0 + by0 + c，/ √(a^2 + b^2)其中，.，代表绝对值符号，√代表开平方，^代表幂运算。

计算该距离的过程如下：1. 确定直线的斜率k。

由直线的一般式ax + by + c = 0可知，斜率为-k，即k = -a/b。

2. 由于直线上的任意一点(x1, y1)满足直线方程ax1 + by1 + c = 0，代入y = kx + b可得y1 = kx1 - c/b。

因此任意一点为(x1, kx1 -c/b)。

3.计算点P到直线的距离。

d = ，(ax0 + by0 + c) / √(a^2 + b^2)这就是点到直线距离的公式。

例如，对于直线2x+3y-6=0和点(1,2)：直线的斜率为k=-a/b=-2/3任意一点为(x1, kx1 - c/b) = (x1, 2x1 - 2)。

代入点(1,2)计算得直线上一点为(1,0)。

计算点到直线的距离：d=，(2×1+3×2-6)/√(2^2+3^2)d=，(2+6-6)/√(4+9)d=，2/√13所以点(1,2)到直线2x+3y-6=0的距离为，2/√13二、点到直线的投影方法：投影方法是通过点到直线上的投影点来计算点到直线的距离。

步骤1：求直线的单位法向量。