架空输电线路档距折算
- 格式:xls
- 大小:33.00 KB
- 文档页数:2
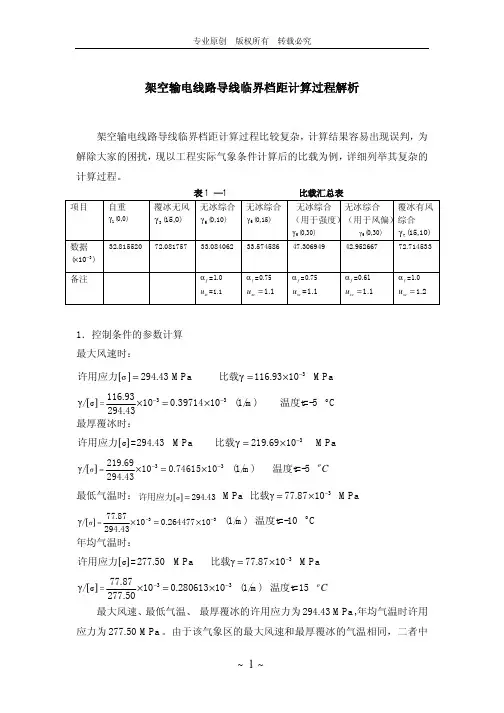
架空输电线路导线临界档距计算过程解析架空输电线路导线临界档距计算过程比较复杂,计算结果容易出现误判,为解除大家的困扰,现以工程实际气象条件计算后的比载为例,详细列举其复杂的计算过程。
表1 —1 比载汇总表项目自重1(0,0)γ覆冰无风 3(15,0)γ 无冰综合 6(0,10)γ 无冰综合 6(0,15)γ 无冰综合 (用于强度)6(0,30)γ 无冰综合 (用于风偏)6γ(0,30) 覆冰有风综合7(15,10)γ数据3(10)−×32.815520 72.081757 33.084062 33.574586 47.30694942.95266772.714533备注=1.0f α =1.1sc u =0.75f α 1.1sc u = =0.75f α =1.1sc u =0.61f α 1.1sc u = =1.0f α1.2sc u =1.控制条件的参数计算 最大风速时:[]294.43σ=许用应力MPa 3116.9310γ−=×比载 MPa []33σ116.93γ/100.3971410294.43−−=×=× (1/m) t=-5温度 o C 最厚覆冰时: []σ=294.43许用应力 MPa 3219.6910γ−=×比载 MPa[]33σ219.69γ/100.7461510294.43−−=×=× (1/m) t=-5温度 oC 最低气温时:[]σ294.43=许用应力 MPa 3γ77.8710−=×比载 MPa[]33σ77.87γ/100.26447710294.43−−=×=× (1/m) t=-10温度 oC 年均气温时:[]σ=277.50许用应力 MPa 3γ77.8710−=×比载 MPa []33σ77.87γ/100.28061310277.50−−=×=× (1/m) t=15温度 o C 最大风速、最低气温、 最厚覆冰的许用应力为294.43MPa ,年均气温时许用应力为277.50MPa 。

高压输电线路水平档距和垂直档距计算一、水平档距和水平荷载在线路设计中,对导线进行力学计算的目的主要有两个:一是确定导线应力大小,以保证导线受力不超过允许值;二是确定杆塔受到导线及避雷线的作用力,以验算其强度是否满足要求。
杆塔的荷载主要包括导线和避雷线的作用结果,以及还有风速、覆冰和绝缘子串的作用。
就作用方向讲,这些荷载又分为垂直荷载、横向水平荷载和纵向水平荷载三种。
为了搞清每基杆塔会承受多长导线及避雷线上的荷载,则引出了水平档距和垂直档距的概念。
悬挂于杆塔上的一档导线,由于风压作用而引起的水平荷载将由两侧杆塔承担。
风压水平荷载是沿线长均布的荷载,在平抛物线近似计算中,我们假定一档导线长等于档距,若设每米长导线上的风压荷载为P,则AB档导线上风压荷载,如图2-10所示:则为,由AB两杆塔平均承担;AC档导线上的风压荷载为,由AC两杆塔平均承担。
图2-10水平档距和垂直档距如上图所示:此时对A杆塔来说,所要承担的总风压荷载为因此我们可知,某杆塔的水平档距就是该杆两侧档距之和的算术平均值。
它表示有多长导线的水平荷载作用在某杆塔上。
水平档距是用来计算导线传递给杆塔的水平荷载的。
严格说来,悬挂点不等高时杆塔的水平档距计算式为只是悬挂点接近等高时,一般用式其中单位长度导线上的风压荷载p,根据比载的定义可按下述方法确定,当计算气象条件为有风无冰时,比载取g4,则p=g4S;当计算气象条件为有风有冰时,比载取g5,则p=g5S,因此导线传递给杆塔的水平荷载为:无冰时(2-48)有冰时(2-49)式中S—导线截面积,mm2。
二、垂直档距和垂直荷载如图2-10所示,O1、O2分别为档和档内导线的最低点,档内导线的垂直荷载(自重、冰重荷载)由B、A两杆塔承担,且以O1点划分,即BO1段导线上的垂直荷载由B杆承担,O1A段导线上的垂直荷载由A杆承担。
同理,AO2段导线上的垂直荷载由A杆承担,O2C段导线上的垂直荷载由C杆承担。

架空线常用计算公式和应用举例前言在基层电力部门从事输电线路专业工作的技术人员,需要掌握导线的基本的计算方法。
这些方法可以从教材或手册中找到。
但是,教材一般从原理开始叙述,用于实际计算的公式夹在大量的文字和推导公式中,手册的计算实例较少,给应用带来一些不便。
本书根据个人在实际工作中的经验,摘取了一些常用公式,并主要应用Excel工作表编制了一些例子,以供相关人员参考。
本书的基本内容主要取材于参考文献,部分取材于网络。
所用参考文献如下:1. GB50545 -2010《110~750kV架空输电线路设计规程》。
2. GB50061-97 《66kV及以下架空电力线路设计规范》。
3. DL/T5220-2005 《10kV及以下架空配电线路设计技术规程》。
4. 邵天晓著,架空送电线路的电线力学计算,中国电力出版社,2003。
5. 刘增良、杨泽江主编,输配电线路设计, 中国水利水电出版社,2004。
6.李瑞祥编,高压输电线路设计基础,水利电力出版社,1994。
7.电机工程手册编辑委员会,电机工程手册,机械工业出版社,1982。
8.张殿生主编,电力工程高压送电线路设计手册,中国电力出版社,2003。
9.浙西电力技工学校主编,输电线路设计基础,水利电力出版社,1988。
10.建筑电气设计手册编写组,建筑电气设计手册,中国建筑工业出版社,1998。
11.许建安主编,35-110kV输电线路设计,中国水利水电出版社,2003。
由于个人水平所限,书中难免出现错误,请识者不吝指正。
四川安岳供电公司李荣久2015-9-16目录第一章电力线路的导线和设计气象条件第一节导线和地线的型式和截面的选择一、导线型式二、导线截面选择与校验的方法三、地线的选择第二节架空电力线路的设计气象条件一、设计气象条件的选用二、气象条件的换算第二章导线(地线)张力(应力)弧垂计算第一节导线和地线的机械物理特性与单位荷载一、导线的机械物理特性二、导线的单位荷载第二节导线的最大使用张力和平均运行张力一、导线的最大使用张力二、导线的平均运行张力第三节导线张力弧垂的精确计算一、导线的悬链线解析方程式二、导线的张力、弧垂与线长三、导线的允许档距和允许高差四、导线悬挂点等高时的张力弧垂计算五、架空线的等效张力(平均张力)第四节导线张力弧垂的近似计算一、导线的抛物线解析方程式二、导线的张力、弧垂与线长第五节水平档距和垂直档距一、水平档距和水平荷载二、垂直档距和垂直荷载第六节导线的状态方程式一、孤立档的状态方程式二、连续档的状态方程式和代表档距第七节临界档距一、用斜抛物线状态方程式求临界档二、用临界档距判别控制条件所控制的档距范围第八节导线张力弧垂计算步骤第九节导线应力弧垂分析一、导线和地线的破坏应力与比载二、导线的悬链线公式三、导线应力弧垂的近似计算四、水平档距和垂直档距五、导线的斜抛物线状态方程式六、临界档距第三章特殊情况导线张力弧垂的计算第一节档距中有一个集中荷载时导线张力弧垂的计算一、档距中有一个集中荷载的弧垂和张力二、导线强度及对地或交叉跨越物距离的校验第二节孤立档导线的计算一、耐张绝缘子串的单位荷载二、孤立档导线的张力和弧垂三、孤立档的临界档距第三节导线紧线时的过牵引计算一、紧线施工方法与过牵引长度二、过牵引引起的伸长和变形三、不考虑耐张绝缘子串的导线过牵引计算四、孤立档考虑耐张绝缘子串的导线过牵引计算第四节连续倾斜档的安装计算一、连续倾斜档导线安装时的受力分析二、连续倾斜档观测弧垂的确定三、悬垂线夹安装位置的调整四、地线的安装第五节耐张绝缘子串倒挂的校验第六节悬垂线夹悬垂角的计算第四章导线和地线的防振计算第一节防振锤和阻尼线一、防振锤的安装二、阻尼线的安装第二节分裂导线的防振第五章架空线的不平衡张力计算第一节刚性杆塔固定横担线路不平衡张力的计算一、线路产生不平衡张力时的几种关系二、不均匀覆冰或不同时脱冰时的不平衡张力求解方法三、断线张力求解方法四、导线从悬垂线夹松落时的不平衡张力第二节固定横担线路考虑杆塔挠度时不平衡张力的计算一、线路产生不平衡张力时的几种关系二、不均匀覆冰或不同时脱冰时考虑杆塔挠度的不平衡张力求解方法三、考虑杆塔挠度时的断线张力求解方法第三节转动型横担线路断线张力的计算一、断线张力的求解方程二、断线张力的计算机试凑求解方法第四节相分裂导线不平衡张力的计算一、计算分裂导线的不平衡张力的公式二、计算公式中几个参数的取值与计算三、不平衡张力的求解方法四、用Excel工作表进行计算的方法第五节地线支持力的计算一、电杆的刚度和刚度系数二、电杆的挠度三、地线支持力的计算四、地线支持力的计算机试凑求解方法第六章架空线弧垂观测计算第一节弧垂观测概述一、观测档的选择二、导线初伸长的处理三、弧垂的观测方法四、弧垂的调整与检查五、观测弧垂时应该注意的问题第二节均布荷载下的弧垂的观测参数计算一、用悬链线法求弧垂观测参数二、弧垂观测角的近似计算公式三、用异长法和等长法观测弧垂时a、b与弧垂f的关系第三节观测档内联有耐张绝缘子串时弧垂的观测参数计算一、观测档弧垂的计算公式二、用等长法和异长法观测弧垂三、用角度法观测弧垂架空线常用计算公式和应用举例安岳供电公司李荣久第一章电力线路的导线和设计气象条件第一节导线和地线的型式和截面的选择一、导线型式常用导线的型号和名称如表1-1-1。
![[国网]关于一般档距的档距中央、导线与地线间距离标准差异的问题](https://uimg.taocdn.com/90b5271152ea551810a687cf.webp)
[国网]关于一般档距的档距中央、导线与地线间距离标准差
异的问题
1.条款原文(1 )GB/T 50064 ‐2014 《交流电气装置的过电压保护和绝缘配合设计规范》5.3.1 第8 款要求:1 )范围Ⅰ的输电线路,15 ℃无风时档距中央导线与地线间的最小距离宜按下式计算:S1=0.012L+1 ;2 )范围Ⅱ的输电线路,15 ℃无风时档距中央导线与地线间的最小距离宜按下式计算:S2=0.015L+1 (2 )GB50545 ‐2010 《110kV ‐750kV 架空输电线路设计规范》第7.0.15 条要求:在一般档距的档距中央,导线与地线间的距离,应按下式计算:S ≥0.012L+1
2.主要差异GB50064 ‐2014 《交流电气装置的过电压保护和绝缘配合设计规范》按范围Ⅰ及范围Ⅱ给出了两种计算方式,而GB 50545 ‐2010 《110kV ‐750kV 架空输电线路设计规范》未区分范围Ⅰ及范围Ⅱ,仅给出一种算法。
3.分析解释GB50064 ‐2014 《交流电气装置的过电压保护和绝缘配合设计规范》中按范围Ⅰ
及范围Ⅱ两种情况考虑,范围Ⅱ(电压等级在220kV 以上),范围Ⅰ(电压等级在220kV 及以下)两种情况电压等级差异较大,因此针对性地给出了两种不同的
具体算法,要求比GB50545 ‐2010 《交流电气装置的过
电压保护和绝缘配合设计规范》更严格。
4.条款统一意见按GB 50064 ‐2014 《交流电气装置的过电压保护和绝缘配合设计规范》的规定执行。
以上摘录于《国家电网公司关于印发电网设备技术标准差异条款统一意见的通知》(国家电网科〔2017〕549号)电网设备技术标准差异条款进行了统一意见。
------------E N D------------。

输电线路的常用档距及影响因素[摘要]导线对地或跨越物物如果距离较小,往往会造成导线放电事故。
同时电磁波还会对通讯线路产生干扰。
本文主要分析输电线路的常用档距及影响因素。
【关键词】输电线路;常用档距;影响因素一、前言架空输电线路对地安全距离有时小于规程规定值,需在事后采取补救措施。
究其原因,除了勘测时的测了误差以外,也有设计工作上的误差的影响引起图形与实际有较大的相差。
相邻两基耐张杆塔间的距离称为输电线路耐张段;耐张段中仅包括一个线档的叫孤立档;若包含多个线档的叫连续档;在连续档中,使各线档架空线的张力趋近稳定于一个基本档间的数值上等值档距叫代表档距。
输电线路为何要设耐张段呢?正常情况下,输电线路是由直线杆塔和耐张杆塔所组成,直线杆塔在输电线路中是主要杆塔,占杆塔总数的80%左右。
直线杆塔主要承受导地线、绝缘子和金具等的垂直荷载以及横线路方向的水平风荷载,而不承受顺线路的张力荷载。
耐张杆塔除具有承受直线杆塔同样的荷载外,更重要的是要承受输电线路顺线路方向的张力荷载、事故断线时产生的纵向不平衡张力、线路转角产生的不平衡张力以及因线路施工、检修时附加张力等。
保证在线路施工、检修及事故断线时,导线悬挂点不产生位移,以限制事故断线的影响范围。
二、输电线路常用档距输电线路相邻两基杆塔中心线的水平距离叫输电线路的档距。
1.代表档距只有在连续档中存在。
对耐张段间具有若干悬垂绝缘子串的直线杆塔的连续档中,各档电线的水平应力σ0是按同一值设计架设的。
但当气象条件变化时,由于各档的档距线长及高差不一定相同,各档的应力变化也就不完全相同,从而使直线杆塔出现不平衡张力差,使悬垂绝缘子串产生偏斜,偏斜结果则又使各档应力趋于基本相同的某个数值上,这个应力称为耐张段内的代表应力。
代表应力值是用耐张段的“代表档距”代入电线状态方程式中求出的。
综上所述,代表档距不一定是线路的实际档距。
它的主要作用是使耐张段中各线挡架空线的张力趋近稳定于一个基本相同的数值,从而使整个耐张段的水平应力基本一致。

高压输电线路常用的几种档距1.档距:两相邻杆塔导线悬挂点间的水平距离。
常用L表示。
2.水平档距:相邻两档档距之和的一半。
常用Lh表示。
3.垂直档距:相邻两档档距间导线最低点之间的水平距离,称为垂直档距,常用Lv表示。
4.极大档距:弧垂最低点和高悬挂点应力都为最大值时的档距。
即高悬挂点应力[σm]=1.1倍许用应力[σ]时的最大档距。
5.允许档距:放松悬挂点应力使最低点的应力和高悬挂点应力达到允许值的档距。
6.极限档距:允许档距的上限值称极限档距。
当随悬挂点应力放松,允许档距增大道一定值后,若继续放松架空线,则由于弧垂的增大使架空线重量迅速增大,超过最低点应力的减少对高悬挂点应力的影响,而起主要作用,允许档距不在增大反而减小。
极限档距是允许档距的上限值,极大档距是允许档距的下限值。
7.连续档:两基耐张杆塔之间的若干基直线杆塔构成的档距。
8.代表档距:由于荷载或温度变化引起张力变化的规律与耐张段实际变化规律几乎相同的假设档距。
即耐张段内,当直线杆塔上出现不平均张力差,悬垂绝缘子串发生偏斜,而趋于平衡时,导线的应力(称代表应力)在状态方程式中所对应的档距。
在排杆塔位时,只要该转角塔两侧代表档距相差不是特别悬殊,那么,只要校核一下该塔的水平档距和垂直档距即可。
代表档距是反映一个连续耐张段的代表应力的一个参数。
在杆塔选用时,所选的设计代表档距应尽量与实际相符合.在实际设计中,设计代表档距选定以后,在一个耐张段里各种工况下的导线张力就选定,那么杆塔设计中的代表档距绝对要大于选定的耐张段的代表档距(导线截面\设计工况与杆塔设计的参数相同)。
如果导线截面小于杆塔设计的限定的导线截面,设计代表档距可以加大到多大需具体计算.铁塔图中给出的代表档距是铁塔设计校验时的参考代表档距。
代表档距不作为排杆塔位的依据,对于直线杆塔而言,只要水平、垂直档距满足要求即可,对于耐张杆塔,只要其两侧档距相差不是特别的悬殊,不考虑代表档距的问题。

10千伏架空线路是电力输配系统中常见的一种电力输送方式,其安全可靠性关系到人民生命财产安全以及电力系统的稳定运行。
在10千伏架空线路的设计和施工中,档距的允许误差是一个重要的技术指标,对于保障线路安全运行和提高电网的供电质量具有重要意义。
一、10千伏架空线路的档距定义及作用1.档距定义10千伏架空线路的档距是指两个相邻的绝缘子串之间的垂直距离。
一般来说,档距与线路的电气参数、绝缘子串的型号、导线的材质和风载荷等因素有关,是线路设计中的重要参数之一。
2.档距的作用档距的大小直接关系到线路的运行安全和电气性能。
合理的档距能够保证线路的绝缘水平,减少线路的跳闸故障,降低线路的绝缘串中的电场强度,减小绝缘子串受到的风荷载,从而提高线路的可靠性和安全性。
档距的允许误差是需要严格控制的。
二、10千伏架空线路的档距允许误差标准根据《电力工程电气设备安装工程施工及验收规范》GB xxx-96的规定,10千伏架空线路的档距允许误差标准如下:- 水平档距误差≤±150mm- 垂直档距误差≤±100mm根据具体情况,对于一些特殊线路,还可以在设计文件中明确规定其档距允许误差范围。
三、档距允许误差的影响1.对电气性能的影响当档距偏大或偏小时,都会对线路的电气性能产生影响。
档距偏大会增大线路的电容,导致电压梯度过大,影响线路的绝缘水平;而档距偏小会造成线路的相间短路和跃闸故障。
档距允许误差需要在设计和施工中严格控制,确保线路的电气性能符合要求。
2.对结构安全的影响档距的偏差会直接影响到线路的结构安全。
当档距偏大时,会增加线路的悬挂点受力,加剧线路的挠度,增大线路对支柱、吊塔的侧向压力,从而影响线路的整体稳定;而档距偏小时会使线路绝缘子串受到过大的风压,影响绝缘子串的安全性。
要严格控制档距允许误差,确保线路的结构安全。
3.对供电质量的影响适当的档距能够减少线路的电场强度,减小绝缘子串受到的风压,提高线路的供电质量。

高压输电线路水平档距和垂直档距计算一、水平档距和水平荷载在线路设计中,对导线进行力学计算的目的主要有两个:一是确定导线应力大小,以保证导线受力不超过允许值;二是确定杆塔受到导线及避雷线的作用力,以验算其强度是否满足要求。
杆塔的荷载主要包括导线和避雷线的作用结果,以及还有风速、覆冰和绝缘子串的作用。
就作用方向讲,这些荷载又分为垂直荷载、横向水平荷载和纵向水平荷载三种。
为了搞清每基杆塔会承受多长导线及避雷线上的荷载,则引出了水平档距和垂直档距的概念。
悬挂于杆塔上的一档导线,由于风压作用而引起的水平荷载将由两侧杆塔承担。
风压水平荷载是沿线长均布的荷载,在平抛物线近似计算中,我们假定一档导线长等于档距,若设每米长导线上的风压荷载为P,则AB档导线上风压荷载,如图2-10所示:则为,由AB两杆塔平均承担;AC档导线上的风压荷载为,由AC两杆塔平均承担。
图2-10水平档距和垂直档距如上图所示:此时对A杆塔来说,所要承担的总风压荷载为因此我们可知,某杆塔的水平档距就是该杆两侧档距之和的算术平均值。
它表示有多长导线的水平荷载作用在某杆塔上。
水平档距是用来计算导线传递给杆塔的水平荷载的。
严格说来,悬挂点不等高时杆塔的水平档距计算式为只是悬挂点接近等高时,一般用式其中单位长度导线上的风压荷载p,根据比载的定义可按下述方法确定,当计算气象条件为有风无冰时,比载取g4,则p=g4S;当计算气象条件为有风有冰时,比载取g5,则p=g5S,因此导线传递给杆塔的水平荷载为:无冰时(2-48)有冰时(2-49)式中S—导线截面积,mm2。
二、垂直档距和垂直荷载如图2-10所示,O1、O2分别为档和档内导线的最低点,档内导线的垂直荷载(自重、冰重荷载)由B、A两杆塔承担,且以O1点划分,即BO1段导线上的垂直荷载由B杆承担,O1A段导线上的垂直荷载由A杆承担。
同理,AO2段导线上的垂直荷载由A杆承担,O2C段导线上的垂直荷载由C杆承担。

浅谈输电线路铁塔档距超限处理方法摘要:水平档距、垂直档距和转角度数是控制铁塔承受荷载的基本约束。
为保证输电线路工程安全运行,定型塔型必须在设计条件范围内应用。
若超出设计条件使用,必须对所用杆塔进行档距折算和应力校核。
本文针对工程实践中输电线路铁塔超限使用的情况,提出了处理方法。
关键词:水平档距;垂直档距;档距折算;应力校核引言输电线路工程中所用铁塔通常为某一典型设计模块相关塔型,典型设计塔型具有适用的水平档距、垂直档距和转角度数等设计参数。
在排塔设计中,线路转角一定时,水平档距和垂直档距是限制铁塔使用的约束条件。
在工程实践中,部分铁塔的使用档距超出相应设计档距,为保证输电线路安全运行,需对超限铁塔进行处理,以适应实际工程使用条件。
1 水平档距超限水平档距为杆塔两侧档距之和的平均值,可以反映导、地线承受风压荷载的大小。
导、地线风压荷载的大小,通常被近似的认为导、地线单位长度的风压与杆塔两侧档距平均值的乘积。
杆塔所承受的水平荷载包括导、地线风荷载、塔身风荷载及角度荷载。
导、地线风荷载标准值表达式为由式(1)可知,铁塔水平档距超限,直接影响导、地线风荷载,进而影响铁塔所承受的水平荷载。
2 垂直档距超限垂直档距为杆塔两侧导、地线弧垂最低点之间的水平距离。
导、地线传递给铁塔的垂直荷载有导、地线自重和覆冰重。
垂直荷载与垂直档距成正比关系,铁塔垂直档距越大,所承受的垂直荷载越大。
铁塔垂直档距超限,也就意味着铁塔所承受的垂直荷载超限。
通常同一模块的耐张铁塔垂直档距设计值是一样的,若J1型耐张铁塔不满足垂直档距要求,J2或J3型铁塔的垂直档距同样不满足垂直档距要求,在此情况下,可采用应力分析法,对所采用铁塔进行建模并做应力分析,增大应力比或长细比超限杆件规格型号,对其进行加固处理,使其满足实际垂直档距要求。
3 工程实例以某水电站110kV送出线路工程为例,工程设计风速为25m/s,设计覆冰厚度为10mm。
T9#杆塔为J2-24塔型,设计转角为20°~40°,设计水平档距为400m,设计垂直档距为600m。


架空输电线路电线拉力&弧垂理论基础李叔昆编2012年3月目录一、电线上的荷载二、悬链线方程式三、档距中的弧垂与线长四、大气条件变化时电线中的应力与弧垂的变化――状态方程式五、临界档距六、临界温度七、状态方程式的求解八、电线力学特性表及安装表的计算九、悬点不等高时档距中的应力、弧垂与线长十、孤立档导线的应力和弧垂架空线路的电线悬于大自然界空气中,要遭受外加荷载的作用,如冰雪、风,使电线的拉力发生变化。
外加荷载的作用是不均匀的,一般在计算中假定荷载的分布是均匀的。
在计算中,表明荷载的方式是比载(或单重)。
即单位长度(1m),单位截面(1mm2),电线上的负荷(kg)。
或采用单位长度上的荷载kg/m 。
比载的分类及计算公式:1) 电线自重比载g1g1=W/S kg/m· mm2式中W-电线单重,(kg/m);S-电线截面,(mm2)。
2) 冰层比载g2(当冰层比重为0.0009kg/cm3时)g2=0.00283b(d+b)/S kg/m· mm2式中b-电线上冰层厚度,(mm);d-电线直径,(mm)。
或g2=Πb(d+b)γ0/1000S kg/m· mm2式中γ0-电线上冰比重,(kg/cm3);Π-3.1416。
3 )电线自重加冰重比载g3g3=g1+g2 kg/m· mm2 4) 作用于电线上风压的比载g4g4=0.0000636dV2/S kg/m· mm2式中V-风速,(m/S)。
5) 有冰时作用于电线上风压的比载g5g5=0.0000636V2(d+2b)/S kg/m· mm2 6) 电线自重与风压综合比载g6g6=√(g12+g42) kg/m· mm2 7) 电线自重与冰、风压综合比载g7g7=√(g32+g52) kg/m· mm2◎如图,沿线荷载均匀分布,比载为g 的电线,悬挂于A B 两点之间,所形成的曲线称为悬链线。
架空输电线路基础知识概述输电线路是联系发电⼚、变电所与⽤电设备的⼀种传送电能的装置,它分架空线路和电缆线路两种。
⾼压输电线路是电⼒⼯业的⼤动脉,是电⼒系统的重要组成部分。
本次主要介绍架空输电线路。
电⼒线路有输(送)电线路和配电线路之分。
由发电⼚向电⼒负荷中⼼输送电能的线路以及电⼒系统之间的联络线路称为输(送)电线路,由电⼒负荷中⼼向各个电⼒⽤户分配电能的线路称为配电线路。
电⼒线路按电压等级分为低压、⾼压、超⾼压和特超⾼压线路。
电压等级在1kV以下的是低压线路,10kV及以上的是⾼压线路,500kV及以上的是超⾼压线路,750kV 及以上的是特⾼压线路。
输电线路按线路架设材料不同分为架空输电线路和电缆输电线路。
输电线路按电流的性质分为交流和直流线路。
架空输电线路按杆塔上的回路数⽬分为单回路、双回路和多回路线路。
1. 架空输电线路的主要设备架空输电线路主要由导线、避雷线、绝缘⼦、⾦具、杆塔、基础以及接地装置等部分组成。
1.1导线其功能主要是输送电能。
线路导线应具有良好的导电性能,导线是架设在杆塔上,长期处于野外,承受各种⽓象条件和各种荷载,因此对导线除要求导电性能好外,还要求具有较⾼的机械强度、耐震性能,⼀定的耐化学腐蚀能⼒,且价格经济合理。
任何导线故障,均能引起或发展为断线事故。
线路导线⽬前常采⽤钢芯铝绞线、铝包钢芯铝绞线、钢芯铝合⾦绞线、防腐钢芯铝绞线。
1.1.1 钢芯铝绞线国产钢芯铝绞线的标准先后有(D)57-1962、JB·649-1965、GB1179-1974、GB1179-1983《铝绞线及钢芯铝绞线》、GB/T1179-1999《圆线同⼼绞架空导线》(等同于IEC6089-1991)和GB/T1179-2008《圆线同⼼绞架空导线》五种。
⽬前后三种应⽤较为⼴泛。
1.1.2 常⽤架空导地线的型号及其意义L—铝;G—钢;J—绞;Q—轻型;J—加强;F—防腐;X—稀⼟;LJ—硬铝绞线LGJ—钢芯铝绞线LGJQ—轻型钢芯铝绞线LGJJ—加强型钢芯铝绞线LGJF—防腐型钢芯铝绞线GJ—钢绞线注:以上为GB1179-1983标准JL/G1A、JL/G1B、JL/G2A、JL/G2B、JL/G3A--钢芯铝绞线JL/G1AF、JL/G2AF、JL/G3AF--防腐性钢芯铝绞线G1A、G1B--普通强度钢线(单线⾦属的电阻率为191.57nΩ·m,对应于9%IACS)G2A、G2B--⾼强度钢线(单线⾦属的电阻率为191.57nΩ·m,对应于9%IACS)G3A--特⾼强度钢线(单线⾦属的电阻率为191.57nΩ·m,对应于9%IACS)注:以上为GB1179-2008标准1.2.3 钢芯铝绞线型号常⽤的GB 1179-83标准现⽤⽤的GB 1179-2008标准防腐钢芯铝绞线。
一、填空题1、输电线路任务是输送电能,电力系统联网。
2、小高差(1.0/≤l h )档距采用平抛物线公式,大高差(25.0/1.0≤≤l h )档距采用斜抛物线公式,其他采用悬链线公式3、目前我国输电线路的电压等级有35kV 、66kV 、110kV 、(154kV )、220kV 、330kV 、500kV 、750kV 、1000kV 。
4、规程规定导线设计安全系数不应小于2.5,悬挂点设计安全系数不应小于2.25,地线安全系数应该大于导线安全系数,年均气象(耐 气象)下的安全系数不应小于4.0。
校验稀有风速和稀有覆冰气象时,导线应力不大于综合拉断力的60%,悬挂点的应力不大于综合拉断力的66%,地线的安全系数宜大于导线的设计安全系数。
5、等高悬点架空线的线长微小变化会引起弧垂和应力很大变化。
6、地线架设的一般规定:输电线路是否架设地线,应根据线路电压等级、负荷性质和系统运行方式,并结合当地已有线路的运行经验、地区雷电活动的强弱、地形地貌特点及土壤电阻率高低等来决定。
在计算耐雷水平后,通过技术经济比较,采用合理的防雷方式。
7、保护金具:1)保护架空线的防振锤、阻尼线、护线条,2)保持导线间距的间隔棒,3)电气保护的屏蔽金具(均压环、屏蔽环),4)重锤等8、相对弧垂最低点而言,架空线平均高度位于档距中央向上fm/3处。
9、 架空线平均应力公式是3cos 0mcp f γβσσ+=,公式中βσcos 0项为档距中央的应力,3mf γ可以看成距离档距中央高差引起的应力。
架空线的平均应力实际上就是架空线平均高度处的应力。
10、最大弧垂判定方法有临界温度判定法,临界比载判定法。
11、架空线的初伸长:通常将架空线的初伸长定义为架空线在年均应力(0.25σp )下,持续10年所产生的塑性和蠕变伸长。
12、补偿初伸长的方法有预拉法,增大架线应力法。
13、增大架线应力的方法:理论计算法、恒定降温法。
14、永久性塑蠕伸长:1. 绞制过程中线股间没有充分张紧,受拉后线股互相挤压,接触点局部变形而产生的挤压变形伸长;2. 架空线的最终应力应变曲线和初始应力应变曲线不同,形成的塑性伸长;3. 金属体长时间受拉,内部晶体间的位错和滑移而产生的蠕变伸长;4. 拉应力超过弹性极限,进入塑性范围而产生的塑性伸长。
输电线路设计计算公式汇总均布荷载下架空线的计算在高压架空线路的设计中,不同气象条件下架空线的弧垂、应力、和线长占有十分重要的位置,是输电线路力学研究的主要内容。
这是因为架空线的弧垂和应力直接影响着线路的正常安全运行,而架空线线长微小的变化和误差都会引起弧垂和应力相当大的改变。
设计弧垂小,架空线的拉应力就大,振动现象加剧,安全系数减少,同时杆塔荷载增大因而要求强度提高。
设计弧垂过大,满足对地距离所需杆塔高度增加,线路投资增大,而且架空线的风摆、舞动和跳跃会造成线路停电事故,若加大塔头尺寸,必然会使投资再度提高。
因此设计合适的弧垂是十分重要的。
架空线悬链方程的积分普遍形式假设一:架空线是没有刚度的柔性索链,只承受拉力而不承受弯矩。
假设二:作用在架空线上的荷载沿其线长均布;悬挂在两基杆塔间的架空线呈悬链线形状。
由力的平衡原理可得到一下结论: 1、架空线上任意一点C 处的轴向应力σx 的水平分量等于弧垂最低点处的轴向应力σ0,即架空线上轴向应力的水平分量处处相等。
σx cos θ=σ02、架空线上任意一点轴向应力的垂直分量等于该点到弧垂最低点间线长L oc 与比载γ之积。
σx sin θ=γL oc推导出: 0t gL o c γθσ= 0dy Loc dx γσ= 即 0'y L o c γσ= (4-3) 由(4-3)推导出10()dy sh x C dx γσ=+ (4-4) 结论:当比值γ/σ0一定时,架空线上任一点处的斜率于该点至弧垂最低点之间的线长成正比。
最后推到得到架空线悬链方程的普遍积分形式。
C1、C2为积分常数,其值取决于坐标系的原点位置。
0(1)20y ch x C C σγγσ=++ (4-5)等高悬点架空线的弧垂、线长和应力等高悬点架空线的悬链方程等高悬点是指架空线的两个挂点高度相同。
由于对称性,等高悬点架空线的弧垂最低点位于档距中央,将坐标原点取在该点,如图:0(1)0y ch x σγγσ=- (4-6) 由上式可以看出,架空线的悬链线具体形状完全由比值σ0 /γ决定,即无论何种架空线、何种气象条件。