最新沪教小学数学六下《5.1 有理数的意义》PPT课件

有理数的定义数的概念是随着生产和生活的需要不断发展的。

在现实生活中，我们常常遇到一些量，它们具有相反意义。

本讲的内容涉及数的扩展，我们对于数的认识从原来的正数和零扩展到负数。

所有的正负整数、正负分数和零统称为有理数。

另外，我们还要学会如何来用数轴上的点表示有理数，还要充分理解绝对值的含义。

知识梳理1.有理数及其分类、数轴1正数和负数正数就是带有正号的数(正号可以省略不写)，是大于零的数；而负数是带有负号的数，是比零小的数。

2有理数：整数和分数统称有理数。

⎧⎧⎪⎪⎨⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数整数零负整数有理数正分数分数负分数(2) 而按照正、负数来分又有如下分类：⎧⎧⎪⎨⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩正整数正有理数正分数有理数零负整数负有理数负分数 3数轴是这样的东西：规定了零点，正方向，单位长度的直线叫做数轴．4只有符号不同的两个数，叫做互为相反数。

5如果两个数的乘积为1，那么这两个数互为倒数．6相反数的数轴表现：在数轴上，位于原点两边，并且到原点的距离相等的数互为相反数。

知识梳理2. 绝对值一个数在数轴上所对应的点与原点的距离，叫做这个数的绝对值。

用符号∣а∣表示数a 的绝对值。

绝对值： 在数轴上，一个数所对应的点与原点的距离叫做这个数的绝对值．正数的绝对值是它本身；负数的绝对值是它的相反数；0的绝对值是0．两个互为相反数的数的绝对值相等00||00||00a a a a a a a a a a a >⎧≥⎧⎪===⎨⎨-<⎩⎪-<⎩或者说两个负数大小的比较因为两个负数在数轴上的位置关系是：绝对值较大的负数一定在绝对值较小的负数的左边，所以，两个负数，绝对值大的反而小。

比较两个负数大小的方法是：一、先分别求出这两个负数的绝对值；二、比较这两个绝对值的大小；三、根据“两个负数，绝对值大的反而小”做出正确的判断。

知识梳理3.综合提升有理数定义、数轴、绝对值综合运用。

【试题来源】【题目】（1）最大的负整数是 ； 最小的正整数是 ；（2）既不是整数，也不是正数的有理数是 ；（3）所有的小数都能化成分数吗？ 。

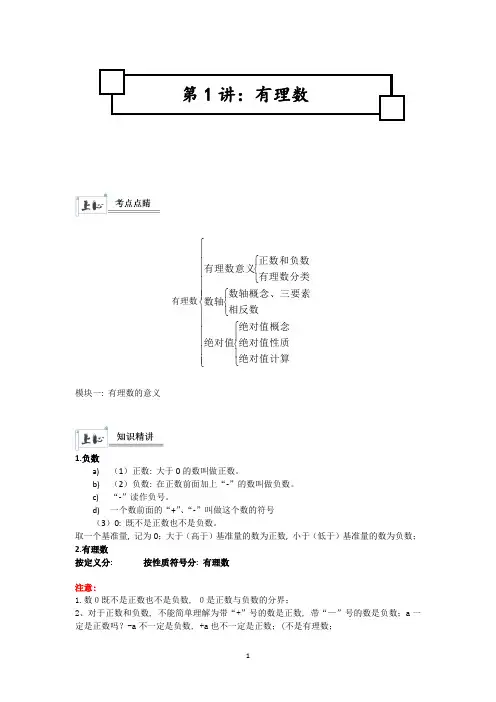
有理数⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧⎩⎨⎧绝对值计算绝对值性质绝对值概念绝对值相反数数轴概念、三要素数轴有理数分类正数和负数有理数意义模块一: 有理数的意义1.负数a)（1）正数: 大于0的数叫做正数。

b)（2）负数: 在正数前面加上“-”的数叫做负数。

c)“-”读作负号。

d)一个数前面的“+”、“-”叫做这个数的符号（3）0: 既不是正数也不是负数。

取一个基准量, 记为0；大于（高于）基准量的数为正数, 小于（低于）基准量的数为负数；2.有理数按定义分: 按性质符号分: 有理数注意:1.数０既不是正数也不是负数, ０是正数与负数的分界；2、对于正数和负数, 不能简单理解为带“+”号的数是正数, 带“—”号的数是负数；a一定是正数吗？-a不一定是负数, +a也不一定是正数；(不是有理数；第1讲：有理数3.正数和零统称为非负数；负数和零统称为非正数；正整数和零统称为非负整数；负整数和零统称为非正整数；4、0非正非负, 0是整数, 0是自然数；小数可以化为分数, 所以小数属于分数。

【例1】: 向北走2000米与向南走1000米, 若规定向北走为正, 则向北走2000米可记作, 向南走1000米, 可记作, 原地不动可记作。

【答案】: +2000m；-1000m；0m【例2】：某零件的直经尺寸在图纸上是10 0．05 （mm）, 表示这种零件的标准尺寸是______ （mm）, 合格产品的零件尺寸范围是（mm）。

【答案】: 10; 9,95-10.05【例3】: 在北京2008奥运会召开的前夕, 为了相应绿色奥运的号召, 小莉同学调查了她所在居民楼一个月内扔垃圾袋的数量, 如以每户每个月扔30个垃圾袋为基准, 超出此基数用正数表示, 不足此基数用负数表示, 其中10户居民某个月扔垃圾袋的个数如下:＋1, －4, ＋4, －7, ＋2, －2, 0, －3, ＋6, ＋3求这10户居民这个月共扔掉多少个垃圾袋？【答案】: 300【例4】: 把下列各数填在相应的集合内:π, /, -3, 2, -1, -0.58, 0, -3.14, /, 0.618, 10整数集合: ｛…｝分数集合: ｛…｝非负数集合: ｛…｝【答案】：-3,2, -1, 0,10 / , -0.58, -3.14, , 0,618 / π, 2,0,0.618,10【例5】: 下列说法正确的是（）A 有理数分为正数和负数B 有理数-a一定表示负数C 正整数、正分数、负整数、负分数统称为有理数D 有理数包括整数和分数【答案】: D相等, 实际每日生产量与计划量相比情况如下表（增加的为正数, 减少的为负数）：星期增减/辆－1+3－2+4+7－5－10（1）生产量最多的一天比生产量最少的一天多生产了辆.（2）本周总生产量是多少？是增加了还是减少了？增减数为多少？【答案】：（1）：17 (2):696,减少了, 减数为4【巩固1】:（1）如果80m表示向东走80m, 那么-6表示。

第五章《有理数》§5.1 有理数的意义一、教学目标双向细目表知识与技能 学习水平 记忆 解释 探究 理解正数、负数以及有理数的意义，会用正数、负数表示具有相反意义的量。

√过程与 方法 通过思考、归纳，完成从整数集和正分数集到有理数集的扩展。

情感态度与价值观 培养学生学习数学、应用数学的意识，激发学生学习兴趣，培养合作交流的能力。

教学重点：理解正数、负数与有理数的意义；会用正数、负数表示具有相反意义的量。

教学难点：零的意义的理解，及对于整数、正（负）数、有理数之间的相互关系。

二、教学过程 1、课前练习：（1）请说一说：5ºC —2ºC 表示什么意义？（2）说一说“48米，-10米”表示什么意思？请列举生活中用“-2。

-10”这样的数表示的实例你知道“0”的含义吗？通过本节课的学习后，我们再来回顾这个问题。

新课探索一猿人打猎,由记数,排序,产生数1,2,3,…由表示“没有”、“空位”产生0. 由分物、测量,产生分数数的概念是随着生产和生活的需要而不断发展的.新课探索二(1)思考：若到银行里去存款5000元或提款4000元,分别记作5000元或4000元,那么你能分得清哪个是存款,哪个是提款吗?新课探索二(2) 在一条东西向的马路上有一棵小树, 假如把树的位置当做0, 我们规定树的东边的位置是正,那么树的西边的位置便是负. 小明和小强从小树出发,小明向东走2千米,小强向西走1 千米,则分别记作+2千米,-1 千米.新课探索三(1)“存款”与“提款”,“向东”与“向西”,它们都是具有相反意义的量.在现实生活中,这种类似的例子很多.请列举一些这样的生活实例.用正数和负数可以表示具有相反意义的量.新课探索三(2)1.如果把收入50元记作50元(或+50元),那么下列各数分别表示什么意义?(1)20元;(2)-2.5元;(3)-80元;(4)0元.2.如果6摄氏度记作6℃,那么零下4摄氏度应记作__℃.3.若增长1.3%记作+1.3%,那么减少6.4%应记作____;-3.5%表示_______ 新课探索四(1)像+5000,+2,+50,+1.3%等数叫做________(positive number);像-4000,-1 ,-2.5,-6.4%等数叫做_______(negative number).正数前面的“+”号可省略不写,但负数前面的“-”号千万别遗漏.零既不是正数也不是负数.现在你能讲讲”0”的含义了吗?新课探索四(2)零是______与_______的分界;0℃是一个确定的温度;海拔0表示海平面的平均高度(因此“0”的意义还不仅是表示“没有”).珠穆朗玛峰的海拔高度为8844.43m,吐鲁番盆地的海拔高度为-155m,分别表示什么意思?表示珠穆朗玛峰高于海平面8844.43m,吐鲁番低于海平面155m..新课探索五例1、把数,1,-2,-2,3,,-3,2,-1,-,0,4.5,-0.3,80%分别填在表示正数和负数的圈里.新课探索六(1),1,-2,-2,3, ,-3,2,-1,-, 0,4.5,-0.3,80%可按正数,负数,零将它们分类,你还能从其它角度将它分类吗?请试一试!整数 1, -2, 3, -3, 2, -1, 0.分数,-2,,-,4.5-0.3,80%.在整数与分数范围内能否将它们再分一下.整数和分数统称为__________。

第5章第1讲：有理数的意义在以前的学习中，我们已经学习了整数、分数、正数、负数等一些知识。

这节课我们再学习一个新的知识：有理数。

那么什么是有理数呢？有理数：整数和分数，统称有理数。

这是从分类上对有理数的定义，也就是说整数和分数这两类数共同组成了有理数，即：有理数分数整数所以，凡是属于整数和分数的数，都是有理数。

我们知道整数有正负之分，可以分为正整数、负整数和零。

同样分数也有正负之分，可分为正分数和负分数。

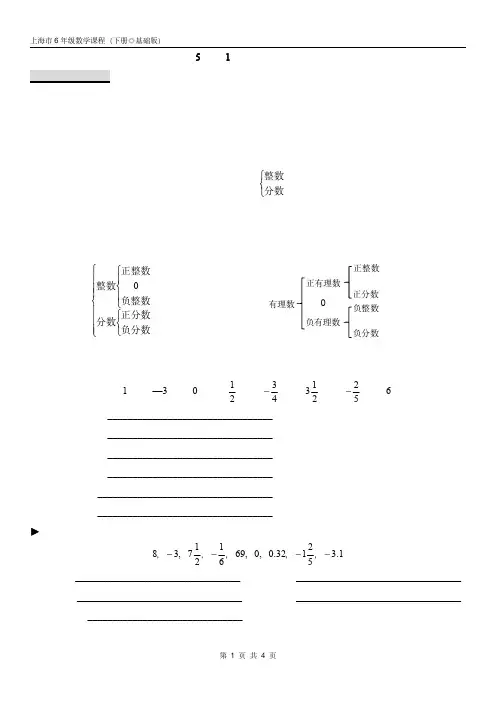
所以我们还可以对有理数按照正负进一步细分，主要有以下两种分法：有理数负分数正分数分数负整数正整数整数0这样，我们对有理数又进行了具体分类，在判断时就更加方便。

例题：将下列各数分别写在相应的横线上。

1，—3，0，21，43 ，213，52 ，6正整数：_________________________________；负整数：_________________________________；正分数：_________________________________；负分数：_________________________________；整数：___________________________________；分数：___________________________________；►习题：将下列各数分别写在相应的横线上。

1.352132.0,0,6961217,38 ，，，，，整数：_________________________________；分数：_________________________________；正数：_________________________________；负数：_________________________________；有理数：_______________________________；正整数负分数负整数正分数负有理数正有理数数有理数在有理数中，我们提到了正整数、正分数，它们都是正数；我们还提到了负整数、负分数，它们都是负数。

沪教版数学六年级下册5.1《有理数的意义》教学设计一. 教材分析《有理数的意义》是沪教版数学六年级下册第五章第一节的内容。

本节课的主要内容是有理数的定义、分类及表示方法。

学生通过学习本节课，将掌握有理数的概念，理解有理数的分类，并能运用有理数的表示方法进行简单的运算。

教材通过丰富的实例和直观的图示，引导学生认识和理解有理数的概念，培养学生的数感。

二. 学情分析六年级的学生已经掌握了实数的基本概念，具备一定的抽象思维能力。

但是，对于有理数这一概念，由于其抽象性较强，学生可能难以理解。

因此，在教学过程中，教师需要注重引导学生通过实例和实际操作来理解和掌握有理数的概念。

三. 教学目标1.知识与技能：使学生理解有理数的定义，掌握有理数的分类，学会用数轴表示有理数。

2.过程与方法：通过实例和实际操作，培养学生从具体情境中抽象出有理数的过程，发展学生的抽象思维能力。

3.情感态度与价值观：激发学生学习有理数的兴趣，培养学生的数感，感受数学与生活的密切联系。

四. 教学重难点1.重点：有理数的定义、分类和表示方法。

2.难点：有理数的分类，特别是理解正数、负数和零的概念。

五. 教学方法1.情境教学法：通过生活实例和实际操作，引导学生从具体情境中认识和理解有理数的概念。

2.启发式教学法：教师提问，引导学生思考和探索，培养学生解决问题的能力。

3.小组合作学习：学生在小组内讨论和交流，共同完成任务，培养学生的合作意识和团队精神。

六. 教学准备1.准备相关的实例和图片，用于引导学生从具体情境中认识和理解有理数的概念。

2.准备数轴，用于表示和区分有理数的不同类型。

3.准备一些练习题，用于巩固所学知识。

七. 教学过程1.导入（5分钟）教师通过展示一些生活实例，如温度、海拔等，引导学生从具体情境中认识和理解有理数的概念。

同时，教师提出问题，引导学生思考和探索，激发学生的学习兴趣。

2.呈现（10分钟）教师通过讲解和展示，向学生介绍有理数的定义、分类和表示方法。

沪教版 六年级下册数学 第一章 有理数的意义1．下列结论中，正确的是（ B ）A ．一个有理数不是正数就是负数B ．一个有理数不是整数就是分数C ．一个有理数可能是整数、分数或者0D ．以上说法都不正确2．下列结论中，正确的是（ A ）A ．自然数都是整数B ．整数都是自然数C ．0是最小的整数D ．负数不可能是整数3．在下列句子中，对0的描述正确的是（ B ）A ．0是正数B ．0是整数C ．0是负数D ．0不是自然数4．如果＋10％表示“増加10％”，那么“减少8％”可以记作（ B ）A.﹣18%B.﹣8%C.﹢2%D.﹢8%5．下面四个数中，负数是（ A ）．A.﹣3B.0C.0.2D.36．如果亏本5元记作－5元，那么盈利10元就可以记作（ ﹢10 ）元。

7．如果水位升高0.65m 记作＋0.65m ，那么水位下降0.3m 就可以记作（ ﹣0.3 ）m 。

8．气温﹣12℃表示的意义是（ 零下12℃ 或比0℃低12℃ ）9如果＋4m 表示前进4m 那么﹣2m 表示（后退2m ）10．如果扑克牌中的黑桃表示正数，梅花表示负数，那么如图所示的两张扑克牌分别表示（ ﹢6 ）和（ ﹣5 ）。

11．如图是今年3月23日某市的天气预报，请你根据图中的信息填空当天的最高温度是（ 15℃ ），当天的最大风力是（北风5级 ）12．认真观察，仔细思考，慎重填写．1、－3、－5、 ﹣7 、﹣9、 ﹣11 。

13．在﹣1、0、1、2这四个数中，既不是正数也不是负数的是（ B ）A.﹣1B. 0C. 1D. 214．如果用＋0.02克表示一只乒兵球质量超出标准质量0.02克，那么一只乒兵球质量低于标准质量0.02克记作（ B ）A ．＋0.02克B ．－0.02克C ．0克D ．＋0.04克15．北京与组约的时差为﹣13（负号表示同一时刻纽约时间比北京时间晚）如果现在是北京时间15：00，那么纽约时间是（ 2∶00 ）16．据有关资料介绍，高度每升高1km ，气温大约下降6℃，如果山脚下的气温为12℃，山顶的气温为0℃，那么山的高度大约为（ 2 ）km.17．有一组数：2、﹣3、2、﹣3、2、﹣3、2、﹣3、…，根据这个规律，得到第2016个数是多云转晴 温度：4ºC ～15ºC 风力：北风4～5级（﹣3）18．（2016・广州）中国人很早开始使用负数，中国古代数学著作《九章算术》的“方程”一章，在世界数学史上首次正式引人负数．如果收入100元记作＋100元．那么﹣80元表示（C）A．支出20元B．收入20元C．支出80元D．收入80元19．（2016湖北宜昌）如果“盈利5％”记作＋5％，那么﹣3％表示（A）A．行损3％B．亏损8％C．盈利2％D．少赚3％。

上海沪教版六年级数学下知识点总结第五章有理数5.1有理数的意义整数和分数统称为有理数有理数整数：正整数、零、负整数分数：正分数、负分数5.2正数和负数数轴：规定了原点、正方向和单位长度的直线叫数轴。

数轴的三要素：原点、单位长度、正方向。

所有的数都可以用数轴上的点来表示。

也可以用数轴来比较两个数的大小在数轴上表示的两个数，正方向的数大于负方向的数零是正数和负数的分界。

只有符号不同的两个数，我们称其中一个数为另一个数的相反数，也称为这两个数互为相反数，零的相反数是零。

一个数在数轴上所对应的点与原点的距离，叫做这个数的绝对值注意：1、一个正数的绝对值是它本身。

2、一个负数的绝对值是它的相反数。

3、零的绝对值是零。

4、两个负数，绝对值大的那个数反而小。

5.3有理数的加减有理数加法法则：1、同号两数相加，取原来的符号，并把绝对值相加。

2、异号两数相加，绝对值相等时和为零，绝对值不相等时，其和的绝对值为较大绝对值减去较小的绝对值所得的差，其和的符号取绝对值较大的加数的符号。

3、一个数同零相加，仍得这个数。

有理数加法的运算律1、交换律：a+b=b+a2、结合律：（a+b）+ c=a+(b+c)有理数的减法法则1、减去一个数，等于加上这个数的相反数2、a-b=a+(-b)5.4有理数的乘除两数相乘的符号法则正正得正，正负得负，负正得负，负负得正。

有理数的乘法法则1、两数相乘，同号得正，异号得负，并把绝对值相乘。

2、任何数与零相乘，都得零。

注意连成的符号：1、几个不等于零的数相乘，积的符号由负因数的个数决定2、当负因数有奇数个时，积为负3、当负因数有偶数个时，积为正4、几个数相乘，有因数为零，积就为零有理数除法法则1、两数相除，同号得正，异号得负，并把绝对值相除。

2、零除以任何一个不为零的数，都得零。

5.5有理数的乘方求N个相同因数的积的运算，叫做乘方。

乘法的结果叫做幂。

在a n中，a叫做底数，n叫做指数，读作a的n次方，a n看做是a的n次方结果时，读作a的n次幂。

有理数的定义数的概念是随着生产和生活的需要不断发展的。

在现实生活中，我们常常遇到一些量，它们具有相反意义。

本讲的内容涉及数的扩展，我们对于数的认识从原来的正数和零扩展到负数。

所有的正负整数、正负分数和零统称为有理数。

另外，我们还要学会如何来用数轴上的点表示有理数，还要充分理解绝对值的含义。

知识梳理1.有理数及其分类、数轴1正数和负数正数就是带有正号的数(正号可以省略不写)，是大于零的数；而负数是带有负号的数，是比零小的数。

2有理数：整数和分数统称有理数。

⎧⎧⎪⎪⎨⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数整数零负整数有理数正分数分数负分数(2) 而按照正、负数来分又有如下分类：⎧⎧⎪⎨⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩正整数正有理数正分数有理数零负整数负有理数负分数 3数轴是这样的东西：规定了零点，正方向，单位长度的直线叫做数轴． 4只有符号不同的两个数，叫做互为相反数。

5如果两个数的乘积为1，那么这两个数互为倒数．6相反数的数轴表现：在数轴上，位于原点两边，并且到原点的距离相等的数互为相反数。

知识梳理2. 绝对值一个数在数轴上所对应的点与原点的距离，叫做这个数的绝对值。

用符号∣а∣表示数a 的绝对值。

绝对值： 在数轴上，一个数所对应的点与原点的距离叫做这个数的绝对值．正数的绝对值是它本身；负数的绝对值是它的相反数；0的绝对值是0．两个互为相反数的数的绝对值相等00||00||00a a a a a a a a a a a >⎧≥⎧⎪===⎨⎨-<⎩⎪-<⎩或者说 两个负数大小的比较因为两个负数在数轴上的位置关系是：绝对值较大的负数一定在绝对值较小的负数的左边，所以，两个负数，绝对值大的反而小。

比较两个负数大小的方法是：一、先分别求出这两个负数的绝对值；二、比较这两个绝对值的大小；三、根据“两个负数，绝对值大的反而小”做出正确的判断。

知识梳理3.综合提升有理数定义、数轴、绝对值综合运用。

【试题来源】【题目】（1）最大的负整数是 ； 最小的正整数是 ；（2）既不是整数，也不是正数的有理数是 ；（3）所有的小数都能化成分数吗？ 。