当前位置：文档之家 › 高中数学人教版必修三第3章 概率全章复习 课件(共17张PPT)

高中数学人教版必修三第3章 概率全章复习 课件(共17张PPT)

  • 格式：ppt
  • 大小：531.50 KB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

人教版高中数学必修三3.随机事件的概率PPT课件(共30)

人教版高中数学必修三3.随机事件的概率PPT课件(共30)

八、知识迁移:
例、 为了估计水库中的鱼的尾数， 先从水库中捕出2 000尾鱼，给每尾鱼作 上记号（不影响其存活），然后放回水 库．经过适当的时间，让其和水库中其 余的鱼充分混合，再从水库中捕出500尾 鱼，其中有记号的鱼有40尾，试根据上 述数据，估计这个水库里鱼的尾数．
课堂感悟
概率是一门研究现实世界中广泛存在的 随机现象的科学，正确理解概率的意义是认识 、理解现实生活中有关概率的实例的关键，学 习过程中应有意识形成概率意识，并用这种意 识来理解现实世界，主动参与对事件发生的概 率的感受和探索。
课堂小结
1．随机事件发生的不确定性及频率的稳定性． (对立统一)
2．随机事件的概率的统计定义：随机事件在相 同的条件下进行大量的试验时，呈现规律性， 且频率总是接近于常数P(A)，称P(A)为事件的 概率．
3．随机事件概率的性质：0≤P(A)≤1．
作业:教材P123页T2,T3.
频率与概率的区别与联系：
√(2)明天本地下雨的机会是70%.
又例如生活中，我们经常听到这样的议论 ：“天气预报说昨天降水概率为90%，结果根 本一点雨都没下，天气预报也太不准确了。” 学了概率后，你能给出解释吗？
解：天气预报的“降水”是一个随机事 件，概率为90%指明了“降水”这个随机事 件发生的概率，我们知道：在一次试验中， 概率为90%的事件也可能不出现，因此，“ 昨天没有下雨”并不说明“昨天的降水概率 为90%”的天气预报是错误的。
值. (2)频率本身是随机的,在试验前不能确定.
做同样次数的重复试验得到事件的频率会不同,比如全班每人做 了10次掷硬币的试验,但得到正面朝上的频率可以是不同的.
(3)概率是一个确定的数,是客观存在的,与 每次试验无关. 比如,如果一个硬币是质地均匀的,则掷硬币

人教版高中数学必修三第三章第1节 3.1.1 随机事件的概率 课件(共17张PPT)

人教版高中数学必修三第三章第1节 3.1.1 随机事件的概率 课件(共17张PPT)

下表是某种油菜子在相同条件下的发芽试验结果表，请完 成表格并回答题。
每批 2 5 10 70 130 700 1500 2000 3000 粒数
发芽 2 4 9 60 116 282 639 1339 2715 的粒 数
发芽 的频 率
（1）完成上面表格： （2）该油菜子发芽的概率约是多少？
谈一谈 本节课中你们的收获？
投篮次数 进球次数 进球频率
8 10 15 20 30 40 50 6 8 12 17 25 32 39
0.75 0.80 0.80 0.85 0.83 0.80 0.78
(1) 计算表中进球的频率; (2) 这位运动员投篮一次,进球的概率约是多少?
概率约是0.8
当堂练习
1．下列说法正确的是（ ） A．任一事件的概率总在（0.1）内 B．不可能事件的概率不一定为0 C．必然事件的概率一定为1 D．以上均不对
何？
1、事件A的频数：
在相同的条件S下重复n次试验，观察某一事件 A是否出现,称n次试验中事件A出现的次数nA为 事件A出现的频数(frequency)。 2、事件A的频率： 称 率(事r件elAa出ti现ve的fr比eq例uenfnc(yA))。= nnA 为事件A出现的频
思考？ 根据定义能否得到频率的取值范围？ fn ( A) [0,1]
作业：（1）习题3.1A组第三题 （2）乒乓球比赛前裁判是如
何判断谁先发球的？为什么 （3）预习概率的意义
问题?
在生活中有许多必然事 件，不可能事件及随机事 件你能举出这样的例子吗？
实验要求：
1.六人一组每人掷10次,记录正面朝上的次数
2.规定带数字的为正面
3.记录数字汇总给组长，由组长合计总数，黑 板上填写数据

人教版高中数学必修三第三章第1节 3.1.3 概率的基本性质 课件.共16张PP

人教版高中数学必修三第三章第1节 3.1.3 概率的基本性质 课件.共16张PP
所以C1=D1。
（3）并事件（和事件）
若某事件发生当且仅当事件A发生或事件B发 生，则称此事件为事件A和事件B的并事件 （或和事件），记A作B （或AB） 。
如图：
BA B A
例.若事件K={出现1点或5点} 发生，则事件C1 = {出现1点}与事件C5 ={出现 5 点 }中至少有一个会
发生，则 KC1 C5
3.1.3 概率的基本性质
事件 的关系 和运算
概率的 几个基 本性质
（一）事件的关系和运算：
（1）包含关系
一般地，对于事件A与事件B，如果事件A发生，则 事件B一定发生，这时称事件B包含事件A（或称事
件A包含于事件B）,记作 BA （ 或 AB)
如图：
BA
例.事件C1 ={出现1点 }发生，则事件 H ={出现的
小 明 成 绩 在 60 分 以 上 的 概 率 为 P(A∪B∪C∪D)＝P(A)＋P(B)＋P(C)＋P(D) ＝0.13＋0.55＋0.16＋0.12＝0.96.
∴ 小 明 成 绩 不 及 格 的 概 率 为 P(E) ＝ 1 － P(A∪B∪C∪D)＝1－0.96＝0.04.
2.概率的基本性质： 1）必然事件概率为1，不可能事件概率
二.剖析概念，夯实基础
（二）概率的基本性质
1.概率P(A)的取值范围 （1）0≤P(A)≤1. （2）必然事件的概率是1.
（3）不可能事件的概率是0. （4）若A B, 则 P(A) ≤P(B)
二.剖析概念，夯实基础
思考：掷一枚骰子,事件C1={出现1点}，事件
C3={出现3点}则事件C1 C3 发生的频率
为0，因此0≤P(A)≤1； 2）当事件A与B互斥时，满足加法公式：

人教版高中数学必修3第三章概率《3.1.1 随机事件的概率》教学PPT

人教版高中数学必修3第三章概率《3.1.1 随机事件的概率》教学PPT

1061
0.5181
4040
2048
0.5069
12000
6019
0.5016
24000
12012
05005
30000
14984
0.4996
72088
36124
0.5011
我们看到，当试验次数很多时，出现正面的 频率值在0.5附近摆动.
上述试验表明，随机事件A在每次试验中是否 发生是不能预知的，但是在大量重复试验后，随 着试验次数的增加，事件A发生的频率呈现出一定 的规律性，这个规律性是如何体现出来的？
有些事情的发生是偶然的，有些事情的发生是必然的.
但是偶然与必然之间往往有某种内在联系.
例如，北京地区一年四季的变化有着确定的、必 然的规律，但北京地区一年里哪一天最热，哪一天最 冷，哪一天降雨量最大，那一天降雪量最大等，又是 不确定的、偶然的.
基本概念
1、随机事件: 在条件S下可能发生也可能 不发生的事件，叫做相对于 条件S的随机事件，简称随 机事件.
这些事件会发生吗？是什么事件？
不可能发生，不可能发生，不可能事件
确定事件
考察下列事件： （1）某人射击一次命中目标； （2）任意选择一个电视频道，它正在播放
新闻； （3）抛掷一个骰子出现的点数为奇数.
这些事件一定会发生吗？他们是什么事件？
可能发生也可能不发生，随机事件.
对于随机事件，知道它发生的可能性大小是 非常重要的.
2、必然事件: 在条件S下一定会发生的事 件，叫做相对于条件S的必 然事件，简称必然事件.
3、不可能事件: 在条件S下一定不会发生的事 件，叫做相对于条件S的不可 能事件，简称不可能事件.
4、确定事件: 必然事件与不可能事件统称为 相对于条件S的确定事件，简称 确定事件.

数学必修3第3章概率章末复习课件人教新课标

数学必修3第3章概率章末复习课件人教新课标

）
（2，5 （2，6
）
）
（3，5 （3，6
）
）
（4，5 （4，6
）
）
（5，5 （5，6
）
）
（6，5 （6，6
）P（A）=）1/18
2，从10件产品（其中3件次品）中，一件一件 地不放回地任意取出4件，求4件中恰有一件次 品的概率。
错解： 因为第一次有10种取法，第二次有9种取法 …，由乘法原理可知从10件取4件共有 10×9×8×7种取法，故样本空间S中基本事 件总数有10×9×8×7个。
（4）随机事件：在条件S下可能产生也可能不产 生的事件，叫相对于条件S的随机事件；
（5）频数与频率：在相同的条件S下重复n次实验
，视察某一事件A是否出现，称n次实验中事件A出
现的次数nA为事件A出现的频数；称事件A出现的
比例fn(A)=
n A为事件A出现的概率：对于给定 n
的随机事件A，如果随着实验次数的增加，事件A 产生的频率fn(A)稳定在某个常数上，把这个常数记 作P（A），称为事件A的概率。
设A＝“取出4件中恰有一件次品”，则A中含有C31 C73 种取法。
错解： 因为第一次有10种取法，第二次有9种取法…，由乘法 原理可知从10件取4件共有10×9×8×7种取法，故样本 空间S中基本事件总数有10×9×8×7个。
设A＝“取出4件中恰有一件次品”，则A中含有C31 C73 种取法。
（1） 实验总所有可能出现的基本事件只有有限个； （2） 每个基本事件出现的可能性相等
我们将具有这两个特点的概率模型称为古典概率 模型，简称古典概率。
对于古典概型，任何事件的概率为： P（A）= A包含的基本事件的个数
基本事件的总数

必修3第三章《概率》复习课

必修3第三章《概率》复习课
科目
数学
年级
高二
备课组组长
主备人
授课时间
2020年 月 日
单元
（第几单元）第三章总复习
课题
必修3第三章《概率》复习课
教材分析
随机事件的概率，随机现象的产生，频率与概率的关系与区别
课程标准
要求
通过本节课学习使学生掌握必然事件，不可能事件，确定事件，随机事件，频数与频率，概率的六种基本性质，古典概型，几何概型，互斥事件，对立事件等内容。
课前3分钟教育
课前三分钟防疫情及爱国主义教育
课型
复习课
教学目标
1、随机事件的概率；随机现象的发生；频率与概率的区别。
2、利用古典概型与几何概型可以求一些随机事件的概率；随机模拟。
教学重点
应用概率解决实际问题
教学难点
应用概率解决实际问题
教学方法
讲授法，归纳、总结、讨论、交流
学习方法
自主学习，合作学习
教学用具
教材书，课件，班班通，粉笔
课时数
2课时
设计
意图
师生
活动
师生 们共 同讨 论实 例， 提出 自己
的观 点， 老师， 学生进行 讨论。
首先
学生
们对
每一
个实
例提
出自
己的
观点，
然后
在老
师的
引导
下解
决问
题。
首先
学生
们对
每一
个实
例提
出自
己的
观点，
题。
首先第三章的有关内容与定义提问的形式来让学生想起。
（1）频率本身是随机的，在试验前___________确定，做同样次数的重复试验得到事件的频率会不同。

人教版高中数学必修三第三章第3节 3.3.1 几何概型 课件(共17张PPT)


【变式2】：圆O是边长为2的正方
形的内切圆 , 向这个正方形中随机
地投一点M,设M落在正方形中任一
点的可能性是相同的,试求点M落圆
O中的概率.
O
4
•M
知识探究（二）：几何概型的概率
【变式3】一只小虫在一个棱长为20cm盛满 水的正方体容器中游动, 假设小虫出现在容 器中的任意一个位置均为等可能的, 记“它 所在的位置距离正方体中心不超过10cm”为 事件A, 那么事件A发生的概率是多少？
B
N
N
B
B
N
BB
N
N
B
知识探究（一）：几何概型的概念
思考 3：上述每个扇形区域对应的圆弧的长度（或 扇形的面积）和它所在位置都是可以变化的，从 结论来看，甲获胜的概率与字母 B 所在扇形区域 的哪个因素有关？
B
N
N
B
B
N
BB
N
N
B
与扇形的弧长（或面积）有关.
知识探究（一）：几何概型的概念 思考 4：如果每个事件发生的概率只与构成该事 件区域的长度（面积或体积）成比例，则称这样 的概率模型为几何概型. 参照古典概型的特性， 几何概型有哪两个基本特征？
所有基本事件构成 的区域是什么？
事件A构成的区域 是什么？
在线段AB上任取一
3m
点
A
B
3m
取到线段AB上某一点 A
B
3m
线段AB（除两端外） A
B
线段CD
1m
AC DB
知识探究（二）：几何概型的概率
【变式1】：在等腰直角三角形 ABC中，在斜边AB上任取一点M，
求AM的长大于AC的长的概率.
知识探究（二）：几何概型的概率

人教版高中数学必修三第三章第1节 3.1.3 概率的基本性质 课件(共28张PPT)


事件C2={出现2点}
事件C3={出现3点}
事件C4={出现4点}
事件C5={出现5点}
事件C6={出现6点}
事件D1={出现的点数不大于1}
事件D2={出现的点数大于3}
事件D3={出现的点数小于5}
事件E ={出现的点数小于7}
事件F ={出现的点数大于6}
事件G ={出现的点数为偶数}
事件H ={出现的点数为奇数}······
（2）当事件A与事件B互斥时，满足加法公式： P(AUB)=P(A)+P(B)；
（3）若事件A与事件B为对立事件，则A∪B为必然事 件，所以P(A∪B)=P(A)+P(B)=1，于是有P(A)=1— P(B).
3、 正确理解和事件与积事件，以及互斥事件与对立事件 的区别与联系，通过教学活动，了解数学与实际生活的 密切联系，感受数学知识应用于现实世界的具体情景， 从而激发学习数学的情趣。
2020/6/7
2
教学重点
事件的关系及运算，概率的几个基本性质。
教学难点
互斥事件与对立事件的区别与联系，类比思想的渗透。
2020/6/7
3
实例导入——揭示课题
通过前面的学习，我们已经认识到:概率已不是抽 象的理论，而是我们认识世界的工具。从彩票中奖， 到证券分析；从基因工程，到法律诉讼；从市场调 查，到经济宏观调控；概率无处不在。生活需要我 们计算事件发生的概率，那概率的性质有哪些？这 节课我们一起来学习！
与集合类比，可用Venn图表示如图：
B
A
2020/6/7
7
问题探究——形成概念
不可能事件记为 Φ ，任何事件都包 含不可能事件。
2020/6/7
8

人教版高中数学必修三3.概率的基本性质PPT课件(共28)


3. 对立事件有一个发生的概率
如在掷骰子实验中，事件.G {出现的点数为偶数}；
H {出现的点数为奇数}；
P(G) = 1-P(H)=1- 1/2 = 1/2
A
B
当事件A与B对立时,则P(A∩B)＝0， P(A∪B)＝ 1， A发生的概率为
P(A)=1- P(B)
探究四：典题解析
例2 ： 如果从不包括大小王的52张扑克牌中随 1 机，到抽取红取到色一方牌张块（，（事那事件么 件C）取B的）到概的红率概心率是（是多事14少，件？问A（）：的2（）概1取）率到取是4 黑色牌（事件D）的概率是多少？
解：（1）因为C=A∪B,且A与B不会同时发生,所以 事P(C件)A=P与(A事)+件PB(B互)=斥，1 。根据概率的加法公式得
2 （此事2）件事C件与C事与件事D件是D对互立斥事，件且，CP∪(DD)为=1必-P然(C事)=件1 ，。因
2
应用提高
俗话说“三个臭皮匠顶个诸葛亮” 能顶上吗
❖ 在一次有关三国演义的知识 竞赛中，三个臭皮匠ABC能答对 题目的概率P(A)=1/3 P(B)=1/4 P(C)=1/5 （他们能答对的题目不 重复）,诸葛亮D能答对题目的概 率P(D)=2/3 ，如果将三个臭皮匠 组成一组与诸葛亮D比赛，答对 题目多者为胜方，则哪方胜？
❖（4）互斥事件的概率应怎样计算？ ❖（5) 必然事件B一定发生, 则 P(B)=1 2) 不可能事件C一定不发生, 则P(C)=0 3) 概率的取值范围为0≤P(A)≤1
2.概率的加法公式
在掷骰子实验中，事件，A {出现1点}；B {出现2点}；
匠未必能顶上一个诸葛亮．
课堂小结
❖通过这一节学习，你有哪些收获？ （比如知识、方法、能力、兴趣等 ）

高中数学必修三《第3章 概率》归纳整合课件


生是等可能的．
网络构建
专题归纳
解读第高十四考页，编辑于星期高日：考二真十三题点 四十五分。
用 M 表示“A1 被选中”这一事件，则 M＝{(A1，B1，C1)，(A1， B1，C2)，(A1，B2，C1)，(A1，B2，C2)，(A1，B3，C1)，(A1， B3，C2)}，即事件 M 由 6 个基本事件组成．故 P(M)＝168＝13. (2)用 N 表示“B1 和 C1 不全被选中”这一事件，则其对立事 件 N 表示“B1 和 C1 全被选中”这一事件． 因为 N ＝{(A1，B1，C1)，(A2，B1，C1)，(A3，B1，C1)}，即 事件 N 由 3 个基本事件组成，所以 P( N )＝138＝16. 由对立事件的概率公式得
1 2
709040＝0.897；23
608080＝0.896.
所 以 从 左到 右 依次 填 入： 1,0.8,0.9,0.857,0.892,0.897， 0.898，
0.897,0.896.
(2)由于每批种子的发芽的频率稳定在 0.897 附近，所以估计该油 菜子发芽的概率约为 0.897.
网络构建
其中直径在区间[1.48,1.52]内的零件为一等品． (1)从上述10个零件中，随机抽取1个，求这个零件为一等品的 概率． (2)从一等品零件中，随机抽取2个： ①用零件的编号列出所有可能的抽取结果； ②求这2个零件直径相等的概率．
网络构建
专题归纳
解读第高十一考页，编辑于星期高日：考二真十三题点 四十五分。
一切可能的结果组成的基本事件空间Ω＝{(A1，B1，C1)， (A1，B1，C2)，(A1，B2，C1)，(A1，B2，C2)，(A1，B3，C1) ，(A1，B3，C2)，(A2，B1，C1)，(A2，B1，C2)，(A2，B2， C1)，(A2，B2，C2)，(A2，B3，C1)，(A2，B3，C2)，(A3，B1 ，C1)，(A3，B1，C2)，(A3，B2，C1)，(A3，B2，C2)，(A3， B3，C1)，(A3，B3，C2)}，即由18个基本事件组成．由于每 一个基本事件被抽取的机会均等，因此这些基本事件的发
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例题精讲之概率的性质 8.如图，在等腰直角△ABC中， （1）过直角顶点C在∠ACB内部随机地 作一条射线CM，与线段AB交于点M， 求AM<AC的概率； （2）若是直接在线段AB上随机找一点 C M，求AM<AC的概率。
答案：
2 （1）3/4；(2) 2
A
M
B
例题精讲之概率的性质
9、在圆x2+y2-2x-2y+1=0内随机投点， 求点与圆心距离小于1/3的概率。 解:圆化为标准形式为:(x-1)2+(y-1)2=1, 这是以点C(1，1)为圆心,半径为1的圆 设“点P与圆心的距离小于1/3”为事件A, 则A成立的对应的区域是以C为圆心，半 径为1/3的圆。 所以P(A)=1/9。
例题精讲之概率的性质 2．有一人在打靶中，连续射击2次， 事件“至少有1次中靶”的对立事 件是（ ） C A.至多有1次中靶 B.2次都中靶 C.2次都不中靶 D.只有1次中靶
例题精讲之概率的性质
3、袋内分别有红、白、黑球各3、2、 1个，从中任取2个，则互斥而不对 D ）。 立的两个事件是（ A.至少有一个白球；都是白球 B.至少有一个白球；至少有一个红球 C.至少有一个白球；一个白球一个黑 球 D.至少有一个白球；红、黑球各一个
必修3第3章 概率全章复习
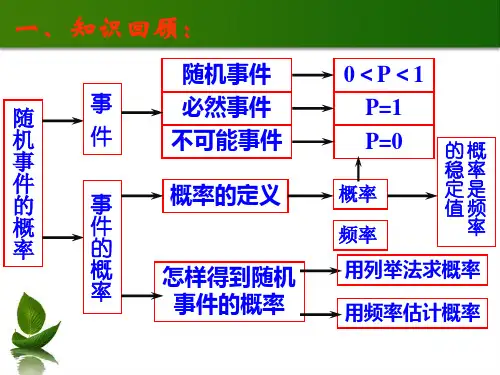
一、基础知识归纳 设Ω有n个基本事件，随机事件A包含m 个基本事件，则事件A的概率P(A)=m/n. 对任何事件A：0≤P(A)≤1.
1、古典概率定义
事件A包含的基本事件数 P(A)= 基本事件总数 当且仅当所描述的基本事件的出 现是等可能性时才成立
2、简单概率事件关系
12.若以连续掷两次骰子分别得到的点数m、n 作为P点的坐标，则点P落在圆x2+y2=16内的 概率是 ________
解析：基本事件的总数为6×6=36个，记事件A= {点P(m，n)落在圆x2+y2=16内}，则A所包含的基本事件为(1，
1)，(2，2)，(1，3)，(1，2)，(2，3)，(3，1)，(3，2)，(2，1)，
Ⅰ.互斥事件： A B 不可能同时发生的两个事件叫 做互斥事件. 对立事件：A B 且A B I 其中必有一个发生的互斥事件叫 做对立事件. 互斥是对立的 必要不充分 条件.
例题精讲之概率的性质
1.某小组有3名男生，2名女生，从中 任选2名学生参加 演讲比赛，判断 下列事件是否互斥。 1）恰有1名男生和恰有2名男生 • 是 •否 2）至少有1名男生和至少有1名女生 •否 3）至少有1名男生和全是男生 •是 4）至少有1名男生和全是女生
例题精讲之概率的性质 10.某公务员去开会，他乘火车, 轮 船,汽车,飞机去的概率分别为0.3, 0.2,0.1,0.4
（1）求他乘火车或乘飞机去的概率;
（2）求他不乘轮船去的概率；
（3）如果他去的概率为0.5，请问他 有可能是乘何交通工具去的？
11.(2009年温州测试)一个袋子有5个大小相同的球，其中有3个 黑球与2个红球，如果从中任取两个球，则恰好取到两个同色 球的概率是( ) A.1/5 B.3/10 C.2/5 D.1/2
解析：设3个黑球为A1、A2、A3，2个红球为B1、B2，则总的可 能为(A1，A2)，(A1，A3)，(A2，A3)，(A1，B1)，(A1，B2)，(A2， B1)，，(A2，B2)，(A3，B1)，(A3，B2)，(B1，B2)，共10种，其 中同色球的可能有(A1，A2)，(A1，A3)，(A2，A3)，(B1，B2)共 4种，所以概率为4/10=2/5. 答案： C
例题精讲之概率的性质
6.一个箱子内有9张票，其号数分别为 1，2，3，……，9。从中任取2张， 其号数至少有一个是奇数的概率是 多少？
P(C)=P(A)+P(B)=5/6 P(C)=1－P(C)=1－6/30=5/6
例题精讲之概率的性质
7、柜子里有3双不同的鞋，随机取2 只，试求下列事件的概率。 4/5 （1）取出的鞋不成对； （2）取出的鞋都是左脚的； 1/5 （3）取出的鞋都是同一只脚的； 2/5 （4）取出的鞋一只左脚，一只右脚， 但它们不成对。 2/5
14（2009年广州一模）某校高三年级要从3 名男生a、b、c和2名女生d、e中任选3名代 表参加学校的演讲比赛. （1）求男生a被选中的概率； （2）求男生a和女生d至少一名被选中的概 率.
解析：总的选法有 (a,b,c),(a,b,d),(a,b,e),(a,c,d),(a,c,e),(b,c,d),(b,c,e),(b,d,e),(c,d, e),(a,d,e)共10种. (1)男生a被选中的选法有6种，所以其概率为6/10=3/5. (2)考虑对立事件：男生a和女生d都没有被选中，其选法只有 (b,c,e)1种，概率为1/10，所以男生a和女生d至少一名被选中 的概率为1-1/10=9/10.
例题精讲之概率的性质
4. 抛掷一枚质地均匀的硬币，如果连 续抛掷1000次，那么第999次出现正面 朝上的概率是（ D ）
1 A. 999
1 B.之概率的性质
5.甲、乙两人下棋，两人下和棋的 概率为1/2 ，乙获胜的概率为1/5 ， 3/10 则甲获胜的概率为_______________
共8个，P=8/36 =2/9． 答案： 2/9
13.（2009年苏州模拟）设有关于x的一元二次方程 x2+2ax+b2=0． 若a是从0，1，2，3四个数中任取的一个数，b是从0，1，2三个 数中任取的一个数，求上述方程有实根的概率． 解析：设事件A为“方程a2+2ax+b2=0有实根”． 当a>0，b>0时，方程x2+2ax+b2=0有实根的充要条件为a≥b. 基本事件共12个： (0，0)，(0，1)，(0，2)，(1，0)，(1，1)，(1，2)，(2，0)，(2， 1)，(2，2)，(3，0)，(3，1)，(3，2)．其中第一个数表示a的取 值，第二个数表示b的取值． 事件A中包含9个基本事件，事件A发生的概率为 P(A)=9/12=3/4