中点四边形-文档资料
- 格式：ppt
- 大小：713.50 KB
- 文档页数：27
下载文档原格式
合集下载
中点四边形(有画板)
质疑导学
观察右图，发现问题，总结规律
A E H
B
N
D
E
M
H C
E O N B
H
D
O F G C
B
A
G D
A
O F
M G
C F
< 图 1 >
< 图 2 >
图（3）
结论：
（1）中点四边形的形状与原四边形的对角线有
密切关系。 （2）只要原四边形的两条对角线 相等 ，就能 使中点四边形是菱形； （3）只要原四边形的两条对角线 互相垂直 ， 就能使中点四边形是矩形； （4）要使中点四边形是正方形，原四边形要符 合的条件是 对角线相等且互相垂直
B
C
这个定理提供了证明线段平行以及线段成倍 分关系的根据.
自主探究
如图:点E、F、G、H分别是四边形ABCD各边中点 . 四边形EFGH是四边形ABCD的中点四边形。
1、中点四边形的定义： 顺次连接四边形各边中点所得的四边形叫做中点四边形。
2 、 任意四边形 的中点四边形是什么形?
A
E
B
已知: 如图,点E、F、G、H分别是
H
四边形 ABCD各边中点。
试判断四边形EFGH的形状，
D
F G
C
并说明理由 。
观察猜想：特殊四边形 的中点四边形是什 么 四边形呢？ E
A
A
H D G
E
B
B
H H
D F C H H D G G
F
G E B C
F
C A D
A
F
C
D
G
合作探究:
A H D E o
中点四边形
等腰梯形
A H D E G B F C
菱形
等腰梯形对角 线相等
2
E B
A
平行四边 形
E B F C
A
矩形
H
D G
菱形 矩形对角线相 等
E B F
D H
C
G
矩形
菱形
A E B F
C
菱形对角线垂Leabharlann 直1绿洲教育内部资料 真情付出，成就未来！
D
正方形
H A E B
G
正方形
C F
正方形对角线 既垂直又相等
A H D
一般梯形
E B F
G C
平行四边 形
一般梯形对角 线不相等
绿洲教育内部资料 真情付出，成就未来！
中点四边形
一、 定义： 依次连接任意一个四边形各边中点所得的四边形叫做中 点四边形。 二、 常见的中点四边形
四边形 图示 中点四边 形的形状 说明
A
一般四边 形
H
D G F C
H G D
平行四边 形 平行四边形对 角线不相等 平行四边 形 EF//FG//BD 1 EH=FG= BD 2
课题学习;中点四边形课件
04
中点四边形的推广与拓展
中点多边形的概念与性质
总结词
中点四边形的基本概念和性质
详细描述
中点四边形是指通过连接任意四边形的对角线，将四边形划分为四个三角形，其中每条 对角线上的中点连线的交点所构成的四边形。中点四边形具有一些基本的性质，如它的
四边长度相等，四个内角均为直角等。
中点多边形的构造方法
性质
总结词
中点四边形具有一些特殊的性质，如面积性质、周长性质等。
详细描述
中点四边形具有一些特殊的性质。首先，它的面积等于原平行四边形的面积的一 半。其次，它的周长等于原平行四边形的两条对角线的长度之和。此外，中点四 边形的对角线还具有一些特殊的性质，如长度性质等。
分类
总ห้องสมุดไป่ตู้词
中点四边形可以根据原平行四边形的不同类型进行分类。
中点四边形在现代数学中的应用
几何学中的中点四边形
01
在几何学中，中点四边形被广泛应用于图形变换、对称性等领
域。
代数与解析几何中的中点四边形
02
通过代数和解析几何的方法，中点四边形在解决某些数学问题
上展现出独特的优势。
计算机图形学中的中点四边形
03
在计算机图形学中，中点四边形被用于生成平滑的曲线和曲面
THANKS
感谢观看
在计算机图形学中的应用
计算机图形学是研究计算机生成和操作图形的科学，而中点四边形在其中也有着 广泛的应用。例如，在绘制几何图形时，可以利用中点四边形的性质和定理，提 高绘图的精度和效率。
在计算机动画和游戏设计中，中点四边形也有着重要的应用。通过中点四边形的 性质和定理，可以实现图形的平滑变换和动态更新，从而提高动画和游戏的真实 感和流畅度。
第19章课题学习中点四边形
第19章 课题学习 19章 中点四边形
概念回顾 一 .概念回顾 概念
矩 形
一角为直角且一组邻边相等
平行四边形
四边形
正方形
菱 形
等腰梯形
梯形
直角梯形
关于中点四边形 二.关于中点四边形 关于中点
一个四边形四边中点所连得到的四边形叫做中点四边形。 一个四边形四边中点所连得到的四边形叫做中点四边形。它的形状与原 数量关系和 有关。 四边形两条对角线的 数量关系和位置关系 有关。 平行四边形 1、连接任意一个四边形四边中点所得到的四边形一定是 四边形四边中点所得到的四边形一定是 、连接任意一个四边形 。 2、连接任意一个平行四边形四边中点所得到的四边形是 平行四边形 、连接任意一个平行四边形四边中点所得到的四边形是 。 平行四边形 3、连接任意一个菱形四边中点所得到的四边形是 、连接任意一个菱形四边中点所得到的四边形是 菱形 4、连接任意一个矩形四边中点所得到的四边形是 、连接任意一个矩形 矩形四边中点所得到的四边形是 矩形 。 菱形 。 。 。
结束
BD
∴四边形EFGH是平行四边形 四边形 是平行四边形
返回
D H A E B G C F
∵
AC⊥ AC⊥BD ∠EHG=90° °
∴
A E B
H
D G
F
C
∵ ∴
AC=BD EF=EG
A E
H D
∵
G
AC=BD EF=EG, AC ⊥ BD ∠EHG=90° ° EF=EG, ∠EHG=90° °
5、连接任意一个正方形四边中点所得到的四边形是 正方形 、连接任意一个正方形四边中点所得到的四边形是 正方形 6、连接任意一个等腰梯形四边中点所得到的四边形是 菱形 等腰梯形四边中点所得到的四边形是 、连接任意一个等腰梯形
概念回顾 一 .概念回顾 概念
矩 形
一角为直角且一组邻边相等
平行四边形
四边形
正方形
菱 形
等腰梯形
梯形
直角梯形
关于中点四边形 二.关于中点四边形 关于中点
一个四边形四边中点所连得到的四边形叫做中点四边形。 一个四边形四边中点所连得到的四边形叫做中点四边形。它的形状与原 数量关系和 有关。 四边形两条对角线的 数量关系和位置关系 有关。 平行四边形 1、连接任意一个四边形四边中点所得到的四边形一定是 四边形四边中点所得到的四边形一定是 、连接任意一个四边形 。 2、连接任意一个平行四边形四边中点所得到的四边形是 平行四边形 、连接任意一个平行四边形四边中点所得到的四边形是 。 平行四边形 3、连接任意一个菱形四边中点所得到的四边形是 、连接任意一个菱形四边中点所得到的四边形是 菱形 4、连接任意一个矩形四边中点所得到的四边形是 、连接任意一个矩形 矩形四边中点所得到的四边形是 矩形 。 菱形 。 。 。
结束
BD
∴四边形EFGH是平行四边形 四边形 是平行四边形
返回
D H A E B G C F
∵
AC⊥ AC⊥BD ∠EHG=90° °
∴
A E B
H
D G
F
C
∵ ∴
AC=BD EF=EG
A E
H D
∵
G
AC=BD EF=EG, AC ⊥ BD ∠EHG=90° ° EF=EG, ∠EHG=90° °
5、连接任意一个正方形四边中点所得到的四边形是 正方形 、连接任意一个正方形四边中点所得到的四边形是 正方形 6、连接任意一个等腰梯形四边中点所得到的四边形是 菱形 等腰梯形四边中点所得到的四边形是 、连接任意一个等腰梯形
优质课件中点四边形
答案举例 D
H
E B
G C
F
想一想,做一做
2、如图：点E、F、G、H分别是线段AB、 BC、CD、AD的中点，则四边形EFGH是 什么图形？并说明理由。
D H
A
E
G
B
F
C
复 习
A
三角形的中位线
∵ DE是△ABC的中位线
D E
1 ∴ DE∥BC， DE＝ BC 2
C
B
◈
探究一
顺次连接任意四边形各边中点，所成的四边形 是特殊的四边形吗？证明你的结论.
D
G
C
1 同理：HG ∥ AC且HG ＝ AC 2
∴EF ∥ HG且EF ＝ HG
∴四边形EFGH为平行四边形。 (一组对边平行且相等的四边形是平行四边形)
中点四边形的定义 顺次连接四边形各边中点所得的 四边形叫做中点四边形。
B
A C
D
顺次连接 任意四边形 各边中点 平行四边形 也是平行四边形 所成的四边形是平行四边形。 E 有没有更特殊？ A 矩形呢？
中点四边形
知识回顾
1
四边形之间的关系
矩形 平行四边形
正方形
菱形 四边形
等腰梯形
梯形 直角梯形
知识回顾
2
三角形 中位线 的性质 定理:三角形的中位线平行于第三边, A 且等于第三边的一半.
∵DE是△ABC的中位线,
1 ∴DE∥BC, DE BC. 2
B
D E
C
这个定理提供了证明线段平行以及线段成倍分关系 的根据.
A B H F
那么：
我思考,我进步
2
D
D
C
B
G
H
E B
G C
F
想一想,做一做
2、如图：点E、F、G、H分别是线段AB、 BC、CD、AD的中点，则四边形EFGH是 什么图形？并说明理由。
D H
A
E
G
B
F
C
复 习
A
三角形的中位线
∵ DE是△ABC的中位线
D E
1 ∴ DE∥BC， DE＝ BC 2
C
B
◈
探究一
顺次连接任意四边形各边中点，所成的四边形 是特殊的四边形吗？证明你的结论.
D
G
C
1 同理：HG ∥ AC且HG ＝ AC 2
∴EF ∥ HG且EF ＝ HG
∴四边形EFGH为平行四边形。 (一组对边平行且相等的四边形是平行四边形)
中点四边形的定义 顺次连接四边形各边中点所得的 四边形叫做中点四边形。
B
A C
D
顺次连接 任意四边形 各边中点 平行四边形 也是平行四边形 所成的四边形是平行四边形。 E 有没有更特殊？ A 矩形呢？
中点四边形
知识回顾
1
四边形之间的关系
矩形 平行四边形
正方形
菱形 四边形
等腰梯形
梯形 直角梯形
知识回顾
2
三角形 中位线 的性质 定理:三角形的中位线平行于第三边, A 且等于第三边的一半.
∵DE是△ABC的中位线,
1 ∴DE∥BC, DE BC. 2
B
D E
C
这个定理提供了证明线段平行以及线段成倍分关系 的根据.
A B H F
那么：
我思考,我进步
2
D
D
C
B
G
中点四边形PPT课件2人教版
•
30、经验是由痛苦中粹取出来的。
•
31、绳锯木断，水滴石穿。
•
32、肯承认错误则错已改了一半。
•
33、快乐不是因为拥有的多而是计较的少。
•
34、好方法事半功倍，好习惯受益终身。
•
35、生命可以不轰轰烈烈，但应掷地有声。
•
36、每临大事，心必静心，静则神明，豁然冰释。
•
37、别人认识你是你的面容和躯体，人们定义你是你的头脑和心灵。
•
17、第一个青春是上帝给的；第二个的青春是靠自己努力的。
•
18、励志照亮人生，创业改变命运。
•
19、就算生活让你再蛋疼，也要笑着学会忍。
•
20、当你能飞的时候就不要放弃飞。
•
21、所有欺骗中，自欺是最为严重的。
•
22、糊涂一点就会快乐一点。有的人有的事，想得太多会疼，想不通会头疼，想通了会心痛。
•
•
50、想像力比知识更重要。不是无知，而是对无知的无知，才是知的死亡。
•
51、对于最有能力的领航人风浪总是格外的汹涌。
•
52、思想如钻子，必须集中在一点钻下去才有力量。
•
53、年少时，梦想在心中激扬迸进，势不可挡，只是我们还没学会去战斗。经过一番努力，我们终于学会了战斗，却已没有了拼搏的勇气。因此，我们转向自身，攻击自己，成为自己最大的敌人。
51
:1
2
5 1 0.618 2
我们称点C将线段AB黄金分割，点C叫做线段AB的黄金
分割点。
A
C B
1
试试看： 你能找到五角星中黄金比吗？
E
A FGD
B
C
AG:AD=0.618:1
中点四边形知识点总结
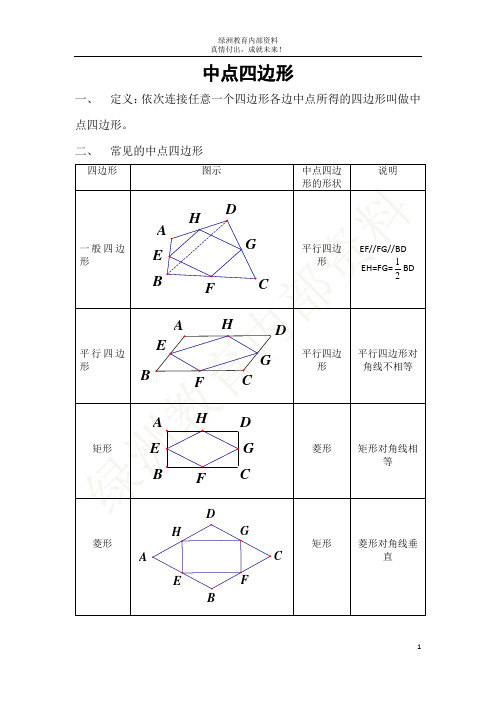
中点四边形知识点总结
嘿，朋友们！今天咱来好好唠唠中点四边形的知识点。
先说说啥是中点四边形呢？简单来讲，就是依次连接四边形各边中点所得的四边形。
就好比建房子，原来的四边形是房子的框架，中点四边形就是框架中间的那部分！比如说，有个四边形 ABCD，那连接 AB、BC、CD、DA 的中点，就得到了中点四边形。
为啥要研究中点四边形呢？那可太重要啦！它有着好多神奇的性质呢。
比如说，不管原来的四边形是什么形状，中点四边形总是平行四边形，就像不管天气怎么变，太阳总会升起一样神奇呀！你想啊，一个乱七八糟的四边形，经过这么一连接中点，嘿，就变出个平行四边形来了。
咱再深入研究一下。
如果原来的四边形是矩形，那中点四边形就是菱形啦，这像不像是丑小鸭变成了白天鹅呀！例如一个矩形的各边中点连接起来，哇塞，菱形就出现啦。
还有哦，如果原来那个四边形是正方形，那中点四边形还是正方形呢，这也太酷了吧！就好像一个超级厉害的人，不管在什么环境下都依然厉害。
“哎呀，那研究这个有啥实际用处呀？”你可能会这么问。
这用处可大啦！比如在建筑设计里，工程师们可得了解这些呀，不然怎么把房子建得稳稳当当的呢！在数学竞赛里，这也是经常考的知识点呢。
总之呀，中点四边形的知识点真的很有趣也很实用。
咱可得把它学好啦，说不定啥时候就能派上大用场呢！所以呀，大家一定要认真对待它哟，准没错！。
中点四边形
A E B
模型:连接任意四边形 各边中点所成的四边形 是平行四边形.
H
F
D G C
【思考】 • 如果把上题中的“任意四边形”改为 “平行四边形”，它的中点四边形是什么 形状呢？ • 把“任意四边形”改为“矩形”，它的 中点四边形仍是平行四边形吗？ • 再把它改为“菱形”、“正方形”呢？ • 改成“一般梯形、等腰梯形”呢？
【思考】
（1）中点四边形的形状与原四边形的什 么有密切关系？ （2）要使中点四边形是菱形，原四边形 一定要是矩形吗？ （3）要使中点四边形是矩形，原四边形 一定要是菱形吗？ （4）要使中点四边形是正方形，原四边 形一定要是正方形吗？
反思
• 重视这个模型的证明过程反映出的规律: • 对角线的关系是关键.改变四边形的形状后, 对角线具有的关系(对角线相等,对角线垂直, 对角线相等且垂直)决定了各中点所成四边 形的形状
例1 （2010山东德州）在四边形中，点 E、F、G、H分别是边AB、BC、CD、 DA的中点，如果四边形EFGH为菱形， 那么四边形ABCD是 （只要写出一 种即可）． 【关键词】特殊四边形的判定． 【答案】答案不唯一：只要是对角线相 等的四边形均符合要求．如：正方形、 矩形、等腰梯形等．
例2 点O是ΔABC所在平面内一动点，连 接OB、OC，并将AB、OB、OC、AC的 中点D、E、F、G依次连接，如果DEFG 能构成四边形： （1）如图，当O点在ΔABC内部时，证 A 明四边形DEFG是平行四边形；
中 点 四 边 形
H A G E D
B
F
C
三明十中
林华容
回顾
思考
三角形中位线的性质
定理:三角形的中位线平行于第三边,且等于第三 边的一半.
模型:连接任意四边形 各边中点所成的四边形 是平行四边形.
H
F
D G C
【思考】 • 如果把上题中的“任意四边形”改为 “平行四边形”，它的中点四边形是什么 形状呢？ • 把“任意四边形”改为“矩形”，它的 中点四边形仍是平行四边形吗？ • 再把它改为“菱形”、“正方形”呢？ • 改成“一般梯形、等腰梯形”呢？
【思考】
（1）中点四边形的形状与原四边形的什 么有密切关系？ （2）要使中点四边形是菱形，原四边形 一定要是矩形吗？ （3）要使中点四边形是矩形，原四边形 一定要是菱形吗？ （4）要使中点四边形是正方形，原四边 形一定要是正方形吗？
反思
• 重视这个模型的证明过程反映出的规律: • 对角线的关系是关键.改变四边形的形状后, 对角线具有的关系(对角线相等,对角线垂直, 对角线相等且垂直)决定了各中点所成四边 形的形状
例1 （2010山东德州）在四边形中，点 E、F、G、H分别是边AB、BC、CD、 DA的中点，如果四边形EFGH为菱形， 那么四边形ABCD是 （只要写出一 种即可）． 【关键词】特殊四边形的判定． 【答案】答案不唯一：只要是对角线相 等的四边形均符合要求．如：正方形、 矩形、等腰梯形等．
例2 点O是ΔABC所在平面内一动点，连 接OB、OC，并将AB、OB、OC、AC的 中点D、E、F、G依次连接，如果DEFG 能构成四边形： （1）如图，当O点在ΔABC内部时，证 A 明四边形DEFG是平行四边形；
中 点 四 边 形
H A G E D
B
F
C
三明十中
林华容
回顾
思考
三角形中位线的性质
定理:三角形的中位线平行于第三边,且等于第三 边的一半.
专题：中点四边形
教学内容
教师活动
预设学生行为
设计意图
【回顾交流】
（1）从定义考虑；
（2）从对角线考虑；
（3）三角形中位线定理是什么？
∵DE是△ABC的中位线
∴
【情境引入】
出示问题：一块白铁皮零料形状如图，工人师傅要从中裁出一块平行四边形白铁皮，并使四个顶点分别落在原白铁皮的四条边上，可以如何裁？
展示幻灯片，提出问题.
教师认真听取学生的小结，帮助学生完善小结的内容.
学生积极动脑，回忆本节课的学习内容，说出收获.
帮助学生梳理本节课的内容，再次温故本节课的重点知识.
【布置作业】
布置作业.
完成作业.
巩固新知识.
【课后作业】
教师布置课后巩固作业.
学生在课后能够积极、认真的完成，并且在遇到困难时寻求同伴的帮助.
给学生设置一个课后作业，对于有能力的学生起到了因材施教的作用.
多媒体展示如图，提出问题，任意四边形的中点四边形是什么形状？可以从图形上先进行猜想。
学生看幻灯片，
思考
学生独立思考.
三角形中位线是学生刚学的知识，它是本课时探究学习的理论基础，同时又加深两条线段之间的数量和位置关系，为后边原四边形的对角线关系做铺垫。
通过图形的展示，给学生以直观感，让学生经历观察-猜想-论证的过程，符合对事物的认知规律，让学生掌握科学有效的探索步骤。
目
标
解
析
为了使学生顺利完成认知构建，本节课安排在本章内容结束之后进行，一方面可以让学生对学习过的三角形的中位线和特殊平行四边形的性质与判定进行一次系统的复习，另一方面也可以让学生将中点四边形与原四边形对角线的本质关系挖掘出来，从而完成本节课的教学。
本节课的教学重点是各种四边形的中点四边形形状及其证明。难点有两个，一个是在学习中点四边形的概念后，运用已学的平行四边形和三角形中位线的相关知识多角度进行合情推理；另一个是逆向探究中点四边形的特殊性与原四边形（对角线）的本质关系。
教师活动
预设学生行为
设计意图
【回顾交流】
（1）从定义考虑；
（2）从对角线考虑；
（3）三角形中位线定理是什么？
∵DE是△ABC的中位线
∴
【情境引入】
出示问题：一块白铁皮零料形状如图，工人师傅要从中裁出一块平行四边形白铁皮，并使四个顶点分别落在原白铁皮的四条边上，可以如何裁？
展示幻灯片，提出问题.
教师认真听取学生的小结，帮助学生完善小结的内容.
学生积极动脑，回忆本节课的学习内容，说出收获.
帮助学生梳理本节课的内容，再次温故本节课的重点知识.
【布置作业】
布置作业.
完成作业.
巩固新知识.
【课后作业】
教师布置课后巩固作业.
学生在课后能够积极、认真的完成，并且在遇到困难时寻求同伴的帮助.
给学生设置一个课后作业，对于有能力的学生起到了因材施教的作用.
多媒体展示如图，提出问题，任意四边形的中点四边形是什么形状？可以从图形上先进行猜想。
学生看幻灯片，
思考
学生独立思考.
三角形中位线是学生刚学的知识，它是本课时探究学习的理论基础，同时又加深两条线段之间的数量和位置关系，为后边原四边形的对角线关系做铺垫。
通过图形的展示，给学生以直观感，让学生经历观察-猜想-论证的过程，符合对事物的认知规律，让学生掌握科学有效的探索步骤。
目
标
解
析
为了使学生顺利完成认知构建，本节课安排在本章内容结束之后进行，一方面可以让学生对学习过的三角形的中位线和特殊平行四边形的性质与判定进行一次系统的复习，另一方面也可以让学生将中点四边形与原四边形对角线的本质关系挖掘出来，从而完成本节课的教学。
本节课的教学重点是各种四边形的中点四边形形状及其证明。难点有两个，一个是在学习中点四边形的概念后，运用已学的平行四边形和三角形中位线的相关知识多角度进行合情推理；另一个是逆向探究中点四边形的特殊性与原四边形（对角线）的本质关系。
19 专题 中点四边形
专题 中点四边形【方法归纳】中点四边形的形状一般通过三角形中位线定理来证明．四边形ABCD 中，点E 、F 、G 、H 分别为AB 、BC 、CD 、AD 的中点． 1．如图，求证四边形EFGH 为平行四边形．2．（1）如图1，若四边形ABCD 是矩形，求证：四边形EFGH 是菱形． （2）如图2，若AC ＝BD ，则四边形EFGH 的形状是 ．3．（1）如图1，若四边形ABCD 是菱形，求证：四边形EFGH 是矩形． （2）如图2，若AC ⊥BD ，则四边形EFGH 的形状是 ．HGFEDCBAHGFEDC B AHGF EDCB AHG FEDCBAHGFEDC B A图1 图2图1图24．（1）如图1，若四边形ABCD 是正方形，则四边形EFGH 是 ． （2）如图2，若AC ＝BD ，AC ⊥BD ，求证：四边形EFGH 的形状是正方形．5．如图，四边形ABCD 中，AB ＝CD ，E 、F 、G 、H 分别是BD 、BC 、AC 、AD 的中点． 求证：四边形EFGH 是菱形．6．如图，CA ＝CB ，CD ＝CE ，∠ACB ＝∠DCE ＝90º，M 、N 、G 、H 分别为AE 、AB 、BD 、DE 的中点，求证：四边形MNGH 为正方形．HGF EDCB AHG FEDCBAH GF EDBAHGENMDCBA 图1 图2。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
D
E
H
A
O
C
F
G
B
17
对角线相等且垂直的四 边形的中点四边形为正 方形
18
结合刚才的证明过程，小组讨论并思考：
❖ （1）中点四边形的形状与原四边形的什么有着密
切的关系？ 对角线
❖ （2）要使中点四边形是菱形，原四边形一定要是 矩形吗？
❖ （3）要使中点四边形是矩形，原四边形一定要是
菱形吗？
B
A
G
E
E
H
AB
C
FG
D
G
C
F
19
D
“我”的命运由对角线主宰
原四边形的对角线
既不相等又不垂直 相等 垂直
相等且垂直
中点四边形
平行四边形 菱形 矩形
正方形
20
小组合作交流:
❖ 任意四边形的中点四边形都是平__行__四_边__形_； ❖ 平行四边形的中点四边形是_平__行__四_边__形__； ❖ 矩形的中点四边形是______菱_形_________； ❖ 菱形的中点四边形是________________； ❖ 正方形的中点四边形是______________； ❖ 梯形的中点四边形是________________； ❖ 直角梯形的中点四边形是____________； ❖ 等腰梯形的中点四边形是____________。
任意四边形的中点四 边形都为平行四边形
6
我思考,我进步2
顺次连接矩形各边中点所成的四边 形是什么四边形？
连结两条对角线
7
H
A
B
E
G
C
D
F
矩形的中点四边形是菱形。
8
我思考,我进步3
已顺知次:如连图接,点对E、角F线、G相、等H分的别四是边四形边形各边
中点AB所CD成各的边四中点边，形且是AC什=B么D形。 ?
25
思考题:
探究四边形中一组对边的中点 和两条对角线的中点构成的四 边形的形状？
26
谢 谢
家 提 出 宝 贵 意 见 ！
欢 迎 各 位 领 导 、 专
27
“我”的命运谁主宰
——探究中点四边形
时堰镇后港中学数学教研组
1
知识回顾 1
如下图：在三角形ABC中，点D是AB的中
点，点E是AC的中点。
DE为三角形ABC的 中位线
定理:三角形的中位线平行于第三边,
且等于第三边的一半.
A
∵DE是△ABC的中位线,
D
E
∴DE∥BC, DE 1 BC.
2
B
C
这个定理提供了证明线段平行以及线段成倍分关系
求证：四边形请E同F学GH们为画平一行画四、边看形一。看、
A
E 猜一猜证并明：证连一接证AC
H
D
G
B ∵ E、F是AB、BC边中点
1
F ∴EF∥AC且EF＝ A2 C
C
同理：HG ∥ AC且HG ＝
1
AC
2
∴EF ∥ HG且EF ＝ HG
∴四边形EFGH为平行四边形。 (一组对边平行且相等的四边形是平行四边形5 )
的依据.
2
中点四边形的定义 ❖ 顺次连接四边形各边中点所得的
四边形叫做中点四边形。
B
A C
D
3
我思,我进步1
驶向胜
想一想,做一做
利的彼 岸
给你一个四边形纸片，你能把它折成平
行四边形吗？
举例
4
我思考,我进步1
顺已次知:连如接图,任点意E、四F、边G、形H各分边别是中四点边形
所AB成CD的各四边边中形点。是什么形?
21
其它各种四边形的中点四边形边是何种四
A边矩形形A呢EBC？D 先B观察并菱猜形AD一BCD猜,再证A明.正E方形ABCBD
E
F
H
FA
CH
F
D
G
D
G
C
菱形
矩形B
D 正方G形 C
梯形ABCD
A EB
直角梯形ABCD
A EB
等腰梯形ABCD
AE B
H
FH
F
H
F
D
C
D 平行四G 边形 C 平行四G边形 D 菱形G
我思,我进步6
驶向胜
想一想,做一做
利的彼 岸
中点四边形的面积与原四边形的面积的
关系，并说出理由。
举例
A
H
E
D
B
G
F
C
24
结论:
1. 任意四边形的中点四边形都为平行 四边形。
2. 中点四边形为特殊的平行四边形的 决定因素取决于原四边形对角线是否相 等和垂直。
3.中点四边形的面积总等于原四边形 面积的一半
求证：四边形E请FG同H是学菱们形画一画、看一看、 A E 猜一猜并证一证
H
B
F
D
G
C
9
对角线相等的四边 形的中点四边形为 菱形
10
我思考,我进步4
A
E
H
B
D
F
G
C
顺次连接菱形各边中点所成的四边
形是什么四边形?
11
A
E
H
B
D
F
G
C
菱形的中点四边形是矩形。
12
我思考,我进步5
已顺知次:如连图接,点对E、角F线、G互、相H分垂别直是的四四边形边形 各边A求B中证C：D点各四所边边成中形点的EF，四G且H边是AC形矩⊥形是BD什。么四边形?
D
E
H
A
C O
F
G
B
13
对角线互相垂直的四 边形的中点四边形为 矩形
14
我思考,我进步6
顺次连接正方形各边中点所成的四 边形是什么四边形?
15
A
H
D
E
G
B
C
F
正方形的中点四边形是正方形
16
我思考,我进步5
已顺知次:如连图接,点对E、角F线、相G、等H且分别互是相四垂边直形 的 四边AB形C各D各边边中中点点，所A成C=的BD四且边AC形⊥是BD什。么 四边求形证：? 四边形EFGH是正方形
22C
填空：
❖ （1）中点四边形的形状与原四边形的对角线有 密切关系；
❖ （2）只要原四边形的两条对角线 相等 ，就能 使中点四边形是菱形；
❖ （3）只要原四边形的两条对角线 互相垂直， 就能使中点四边形是矩形；
❖ （4）要使中点四边形是正方形，原四边形要符 合的条件是 对角线相等且互相垂直 。
23
E
H
A
O
C
F
G
B
17
对角线相等且垂直的四 边形的中点四边形为正 方形
18
结合刚才的证明过程，小组讨论并思考：
❖ （1）中点四边形的形状与原四边形的什么有着密
切的关系？ 对角线
❖ （2）要使中点四边形是菱形，原四边形一定要是 矩形吗？
❖ （3）要使中点四边形是矩形，原四边形一定要是
菱形吗？
B
A
G
E
E
H
AB
C
FG
D
G
C
F
19
D
“我”的命运由对角线主宰
原四边形的对角线
既不相等又不垂直 相等 垂直
相等且垂直
中点四边形
平行四边形 菱形 矩形
正方形
20
小组合作交流:
❖ 任意四边形的中点四边形都是平__行__四_边__形_； ❖ 平行四边形的中点四边形是_平__行__四_边__形__； ❖ 矩形的中点四边形是______菱_形_________； ❖ 菱形的中点四边形是________________； ❖ 正方形的中点四边形是______________； ❖ 梯形的中点四边形是________________； ❖ 直角梯形的中点四边形是____________； ❖ 等腰梯形的中点四边形是____________。
任意四边形的中点四 边形都为平行四边形
6
我思考,我进步2
顺次连接矩形各边中点所成的四边 形是什么四边形？
连结两条对角线
7
H
A
B
E
G
C
D
F
矩形的中点四边形是菱形。
8
我思考,我进步3
已顺知次:如连图接,点对E、角F线、G相、等H分的别四是边四形边形各边
中点AB所CD成各的边四中点边，形且是AC什=B么D形。 ?
25
思考题:
探究四边形中一组对边的中点 和两条对角线的中点构成的四 边形的形状？
26
谢 谢
家 提 出 宝 贵 意 见 ！
欢 迎 各 位 领 导 、 专
27
“我”的命运谁主宰
——探究中点四边形
时堰镇后港中学数学教研组
1
知识回顾 1
如下图：在三角形ABC中，点D是AB的中
点，点E是AC的中点。
DE为三角形ABC的 中位线
定理:三角形的中位线平行于第三边,
且等于第三边的一半.
A
∵DE是△ABC的中位线,
D
E
∴DE∥BC, DE 1 BC.
2
B
C
这个定理提供了证明线段平行以及线段成倍分关系
求证：四边形请E同F学GH们为画平一行画四、边看形一。看、
A
E 猜一猜证并明：证连一接证AC
H
D
G
B ∵ E、F是AB、BC边中点
1
F ∴EF∥AC且EF＝ A2 C
C
同理：HG ∥ AC且HG ＝
1
AC
2
∴EF ∥ HG且EF ＝ HG
∴四边形EFGH为平行四边形。 (一组对边平行且相等的四边形是平行四边形5 )
的依据.
2
中点四边形的定义 ❖ 顺次连接四边形各边中点所得的
四边形叫做中点四边形。
B
A C
D
3
我思,我进步1
驶向胜
想一想,做一做
利的彼 岸
给你一个四边形纸片，你能把它折成平
行四边形吗？
举例
4
我思考,我进步1
顺已次知:连如接图,任点意E、四F、边G、形H各分边别是中四点边形
所AB成CD的各四边边中形点。是什么形?
21
其它各种四边形的中点四边形边是何种四
A边矩形形A呢EBC？D 先B观察并菱猜形AD一BCD猜,再证A明.正E方形ABCBD
E
F
H
FA
CH
F
D
G
D
G
C
菱形
矩形B
D 正方G形 C
梯形ABCD
A EB
直角梯形ABCD
A EB
等腰梯形ABCD
AE B
H
FH
F
H
F
D
C
D 平行四G 边形 C 平行四G边形 D 菱形G
我思,我进步6
驶向胜
想一想,做一做
利的彼 岸
中点四边形的面积与原四边形的面积的
关系，并说出理由。
举例
A
H
E
D
B
G
F
C
24
结论:
1. 任意四边形的中点四边形都为平行 四边形。
2. 中点四边形为特殊的平行四边形的 决定因素取决于原四边形对角线是否相 等和垂直。
3.中点四边形的面积总等于原四边形 面积的一半
求证：四边形E请FG同H是学菱们形画一画、看一看、 A E 猜一猜并证一证
H
B
F
D
G
C
9
对角线相等的四边 形的中点四边形为 菱形
10
我思考,我进步4
A
E
H
B
D
F
G
C
顺次连接菱形各边中点所成的四边
形是什么四边形?
11
A
E
H
B
D
F
G
C
菱形的中点四边形是矩形。
12
我思考,我进步5
已顺知次:如连图接,点对E、角F线、G互、相H分垂别直是的四四边形边形 各边A求B中证C：D点各四所边边成中形点的EF，四G且H边是AC形矩⊥形是BD什。么四边形?
D
E
H
A
C O
F
G
B
13
对角线互相垂直的四 边形的中点四边形为 矩形
14
我思考,我进步6
顺次连接正方形各边中点所成的四 边形是什么四边形?
15
A
H
D
E
G
B
C
F
正方形的中点四边形是正方形
16
我思考,我进步5
已顺知次:如连图接,点对E、角F线、相G、等H且分别互是相四垂边直形 的 四边AB形C各D各边边中中点点，所A成C=的BD四且边AC形⊥是BD什。么 四边求形证：? 四边形EFGH是正方形
22C
填空：
❖ （1）中点四边形的形状与原四边形的对角线有 密切关系；
❖ （2）只要原四边形的两条对角线 相等 ，就能 使中点四边形是菱形；
❖ （3）只要原四边形的两条对角线 互相垂直， 就能使中点四边形是矩形；
❖ （4）要使中点四边形是正方形，原四边形要符 合的条件是 对角线相等且互相垂直 。
23